Matrici e vettori in MQL5: Funzioni di attivazione

Introduzione

Sul tema dell'addestramento delle reti neurali sono già stati pubblicati moltissimi libri e articoli. I membri di MQL5.com hanno anche pubblicato molto materiale, tra cui diverse serie di articoli.

Qui descriveremo solo uno degli aspetti dell'apprendimento automatico — le funzioni di attivazione. Ci addentreremo nei meccanismi interni del processo.

Breve panoramica

Nelle reti neurali artificiali, una funzione di attivazione del neurone calcola il valore di un segnale di output in base ai valori di un segnale di input o di un insieme di segnali di input. La funzione di attivazione deve essere differenziabile sull'intero set di valori. Questa condizione offre la possibilità di effettuare la retropropagazione degli errori durante l'addestramento delle reti neurali. Per retropropagare l'errore, è necessario calcolare il gradiente della funzione di attivazione - il vettore delle derivate parziali della funzione di attivazione per ogni valore del vettore del segnale di input. Si ritiene che le funzioni di attivazione non lineari siano migliori per l'addestramento. Sebbene la funzione ReLU completamente lineare abbia dimostrato la sua efficacia in molti modelli.

Illustrazioni

I grafici della funzione di attivazione e delle loro derivate sono stati preparati in una sequenza monotonamente crescente da -5 a 5 come illustrazione. È stato sviluppato anche lo script che visualizza il grafico delle funzioni sul grafico dei prezzi. Viene visualizzata la finestra di dialogo di apertura del file per specificare il nome dell'immagine salvata premendo il tasto Pagina Giù.

Il tasto ESC termina lo script. Lo script stesso è allegato di seguito. Uno script simile è stato scritto dall'autore dell'articolo Retropropagazione delle reti neurali utilizzando matrici MQL5. Abbiamo utilizzato la sua idea per visualizzare il grafico dei valori delle derivate della funzione di attivazione corrispondente insieme al grafico della funzione di attivazione stessa.

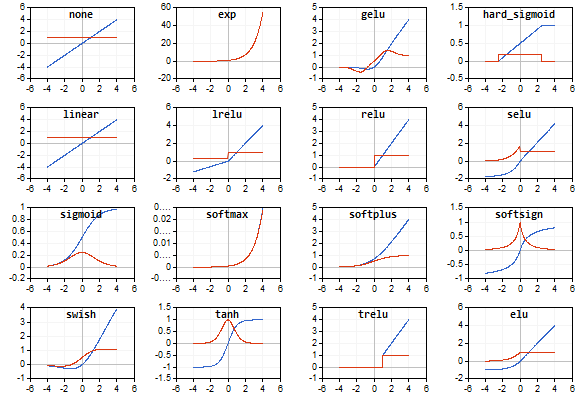
La funzione di attivazione è rappresentata in blu, mentre le derivate della funzione sono visualizzate in rosso.

Funzione di attivazione Exponential Linear Unit (ELU)

Calcolo della funzione

   if(x >= 0)
      f = x;
   else
      f = alpha*(exp(x) - 1);

Calcolo delle derivate

   if(x >= 0)
      d = 1;
   else
      d = alpha*exp(x);

Questa funzione accetta un parametro aggiuntivo "alfa". Se non specificato, il suo valore predefinito è 1.

   vector_a.Activation(vector_c,AF_ELU);      // call with the default parameter

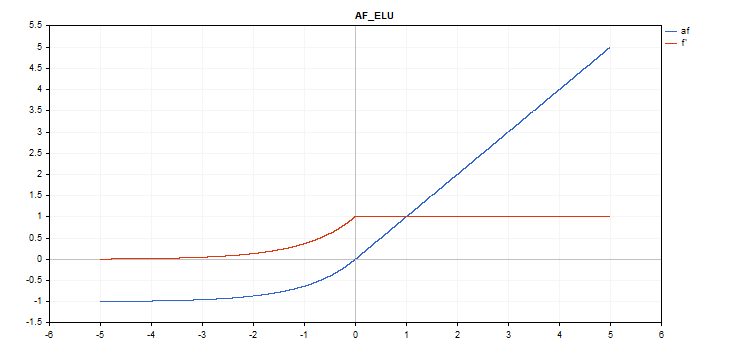
   vector_a.Activation(vector_c,AF_ELU,3.0);  // call with alpha=3.0

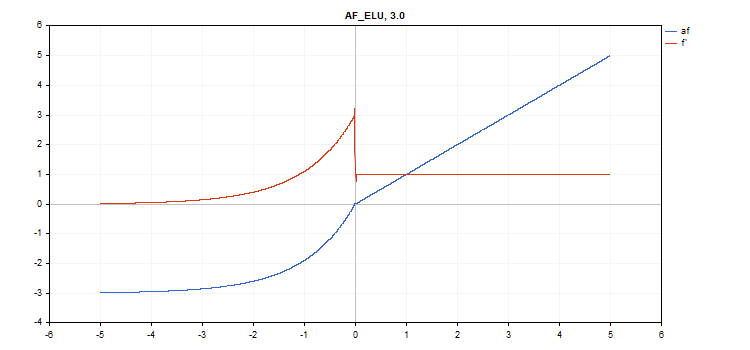
Funzione di attivazione esponenziale

Calcolo della funzione

   f = exp(x);

La stessa funzione exp serve come una derivata della funzione exp.

Come si può vedere nell'equazione di calcolo, la funzione di attivazione Esponenziale non ha parametri aggiuntivi

vector_a.Activation(vector_c,AF_EXP);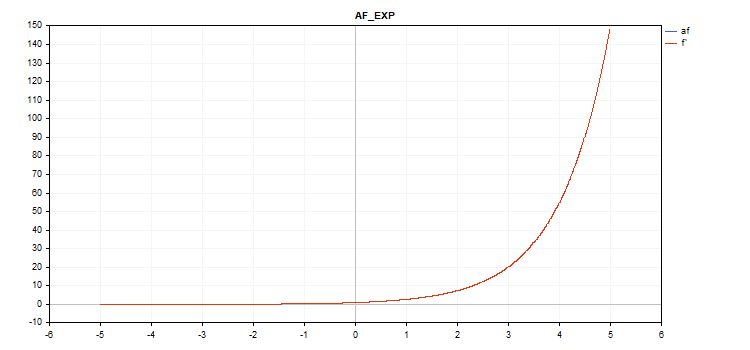

Funzione di attivazione Gaussian Error Linear Unit (GELU)

Calcolo della funzione

   f = 0.5*x*(1 + tanh(sqrt(M_2_PI)*(x+0.044715*pow(x,3)));

Calcolo delle derivate

   double x_3 = pow(x,3);
   double tmp = cosh(0.0356074*x + 0.797885*x);
   d = 0.5*tanh(0.0356774*x_3 + 0.398942*x)+(0.535161*x_3 + 0.398942*x)/(tmp*tmp) + 0.5;

Nessun parametro aggiuntivo.

vector_a.Activation(vector_c,AF_GELU);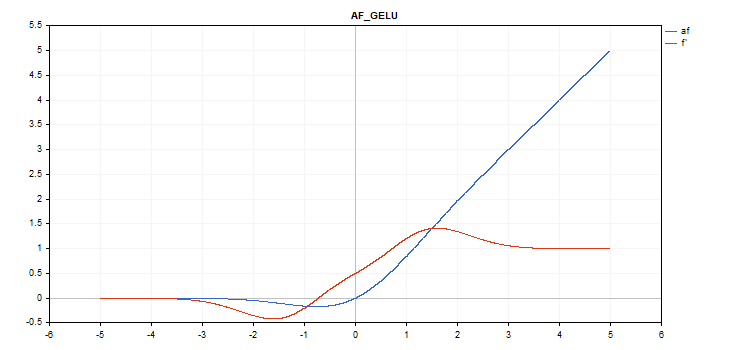

Funzione di attivazione Hard Sigmoid

Calcolo della funzione

   if(x < -2.5)
      f = 0;
   else
     {
      if(x > 2.5)
         f = 1;
      else
         f = 0.2*x + 0.5;
     }

Calcolo delle derivate

   if(x < -2.5)
      d = 0;
   else
     {
      if(x > 2.5)
         d = 0;
      else
         d = 0.2;
     }

Nessun parametro aggiuntivo.

vector_a.Activation(vector_c,AF_HARD_SIGMOID);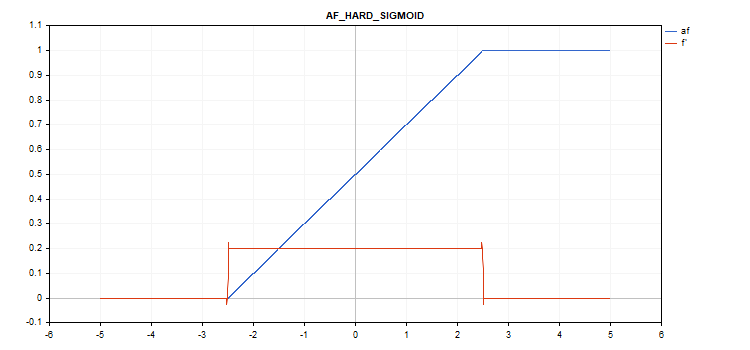

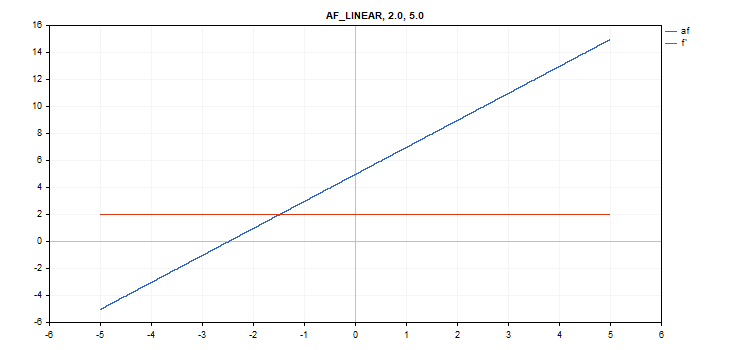
Funzione di attivazione lineare

Calcolo della funzione

   f = alpha*x + beta

Calcolo delle derivate

   d = alpha

Parametri aggiuntivi alfa = 1,0 e beta = 0,0

vector_a.Activation(vector_c,AF_LINEAR);         // call with default parameters

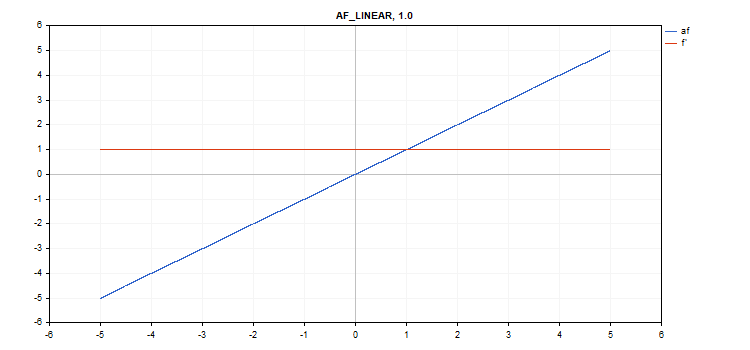
vector_a.Activation(vector_c,AF_LINEAR,2.0,5.0);  // call with alpha=2.0 and beta=5.0

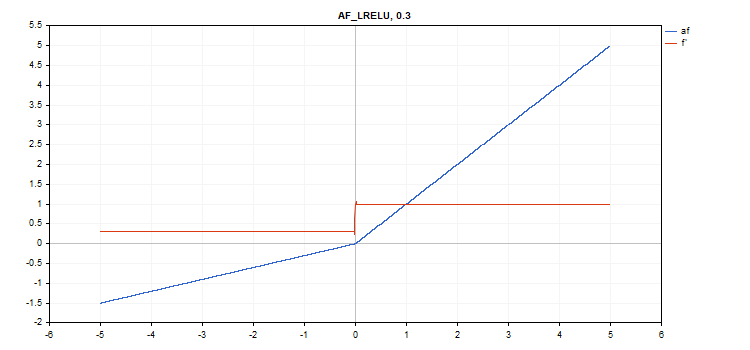
Funzione di attivazione Leaky Rectified Linear Unit (LReLU)

Calcolo della funzione

   if(x >= 0)
      f = x;
   else
      f = alpha * x;

Calcolo delle derivate

   if(x >= 0)
      d = 1;
   else
      d = alpha;

Questa funzione accetta un parametro aggiuntivo "alfa". Se non specificato, il valore predefinito è 0. 3

   vector_a.Activation(vector_c,AF_LRELU);      // call with the default parameter

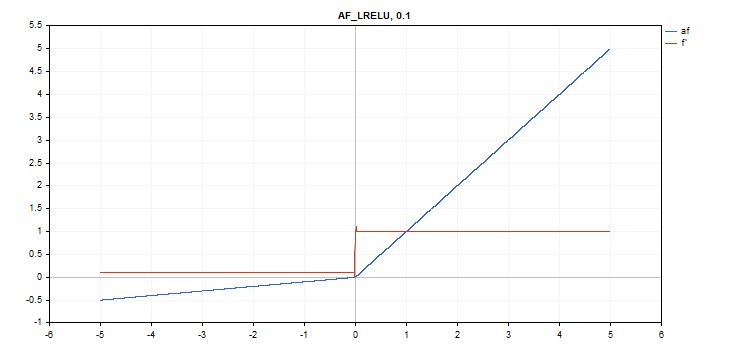
vector_a.Activation(vector_c,AF_LRELU,0.1);  // call with alpha=0.1

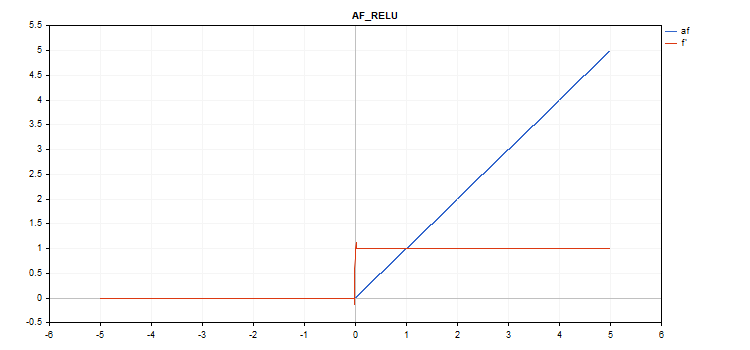
Funzione di attivazione Rectified Linear Unit (ReLU)

Calcolo della funzione

   if(alpha==0)
     {
      if(x > 0)
         f = x;
      else
         f = 0;
     }
   else
     {
      if(x >= max_value)
         f = x;
      else
         f = alpha * (x - treshold);
     }

Calcolo delle derivate

   if(alpha==0)
     {
      if(x > 0)
         d = 1;
      else
         d = 0;
     }
   else
     {
      if(x >= max_value)
         d = 1;
      else
         d = alpha;
     }

Parametri aggiuntivi alpha=0, max_value=0 e threshold=0.

vector_a.Activation(vector_c,AF_RELU);         // call with default parameters

vector_a.Activation(vector_c,AF_RELU,2.0,0.5);      // call with alpha=2.0 and max_value=0.5

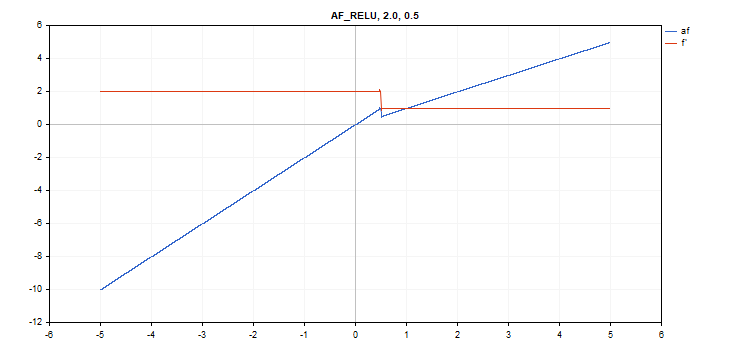
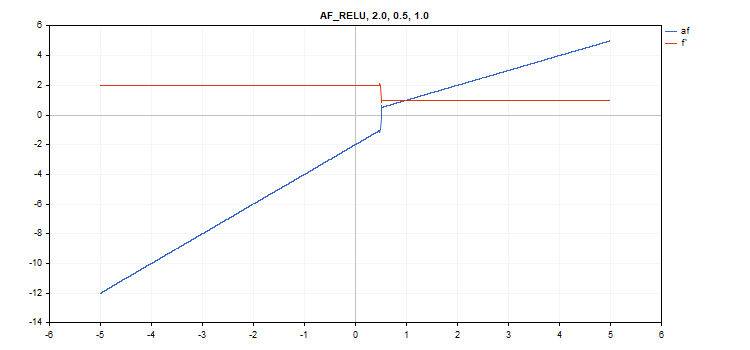
vector_a.Activation(vector_c,AF_RELU,2.0,0.5,1.0);  // call with alpha=2.0, max_value=0.5 and treshold=1.0

Funzione di attivazione Scaled Exponential Linear Unit (SELU)

Calcolo della funzione

   if(x >= 0)
      f = scale * x;
   else
      f = scale * alpha * (exp(x) - 1);

where scale = 1.05070098, alpha = 1.67326324

Calcolo delle derivate

   if(x >= 0)
      d = scale;
   else
      d = scale * alpha * exp(x);

Nessun parametro aggiuntivo.

vector_a.Activation(vector_c,AF_SELU);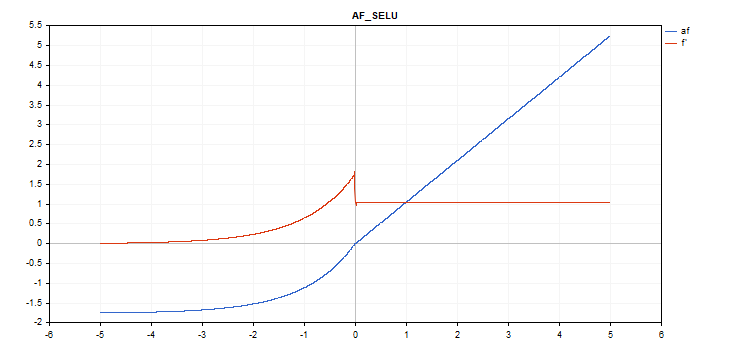

Funzione di attivazione sigmoidea

Calcolo della funzione

   f = 1 / (1 + exp(-x));

Calcolo delle derivate

   d = exp(x) / pow(exp(x) + 1, 2);

Nessun parametro aggiuntivo.

vector_a.Activation(vector_c,AF_SIGMOID);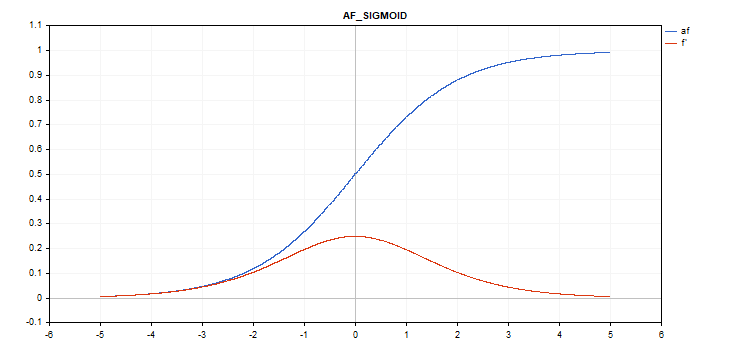

Funzione di attivazione Softplus

Calcolo della funzione

   f = log(exp(x) + 1);

Calcolo delle derivate

   d = exp(x) / (exp(x) + 1);

Nessun parametro aggiuntivo.

vector_a.Activation(vector_c,AF_SOFTPLUS);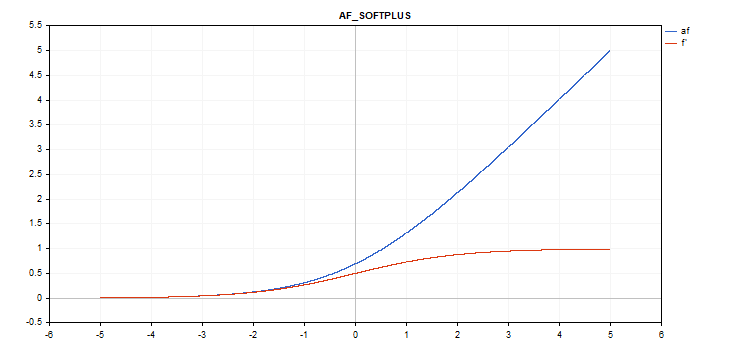

Funzione di attivazione Softsign

Calcolo della funzione

   f = x / (|x| + 1)

Calcolo delle derivate

   d = 1 / (|x| + 1)^2

Nessun parametro aggiuntivo.

vector_a.Activation(vector_c,AF_SOFTSIGN);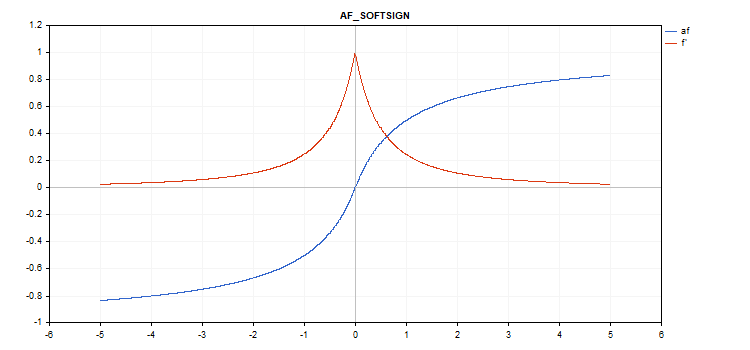

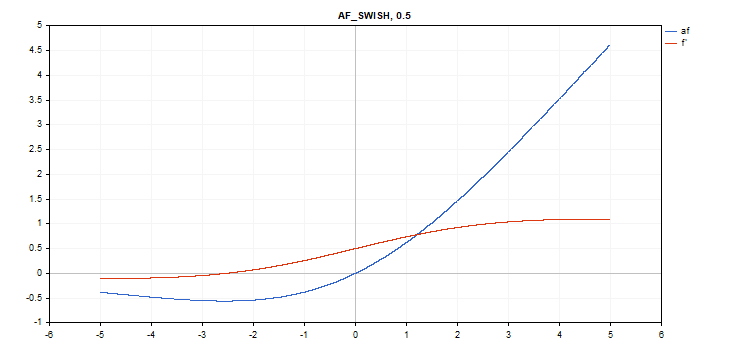
Funzione di attivazione Swish

Calcolo della funzione

   f = x / (1 + exp(-x*beta));

Calcolo delle derivate

   double tmp = exp(beta*x);
   d = tmp*(beta*x + tmp + 1) / pow(tmp+1, 2);

Parametro aggiuntivo beta = 1

vector_a.Activation(vector_c,AF_SWISH);         // call with the default parameter

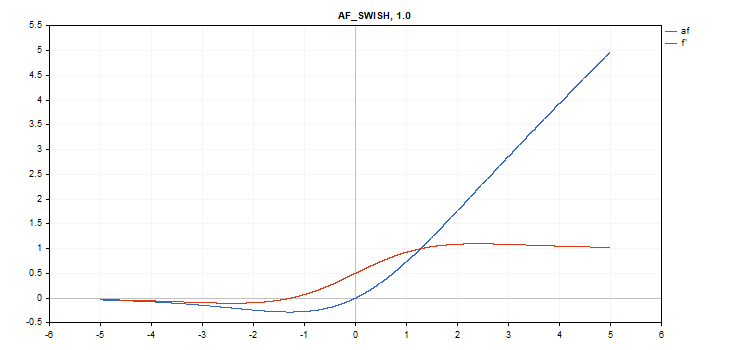
vector_a.Activation(vector_c,AF_SWISH,2.0);     // call with beta = 2.0

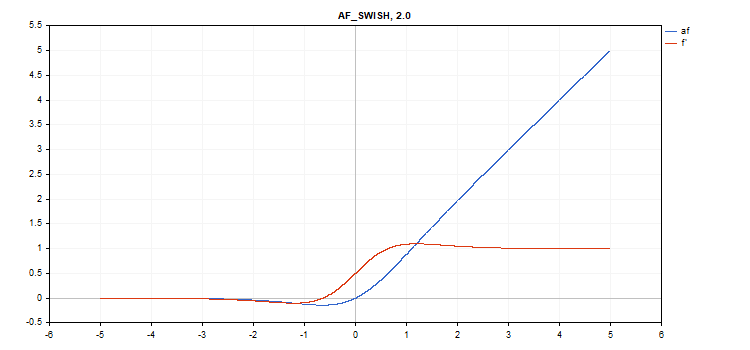
vector_a.Activation(vector_c,AF_SWISH,0.5);   // call with beta=0.5

Funzione di attivazione Hyperbolic Tangent (TanH)

Calcolo della funzione

   f = tanh(x);

Calcolo delle derivate

   d = 1 / pow(cosh(x),2);

Nessun parametro aggiuntivo.

vector_a.Activation(vector_c,AF_TANH);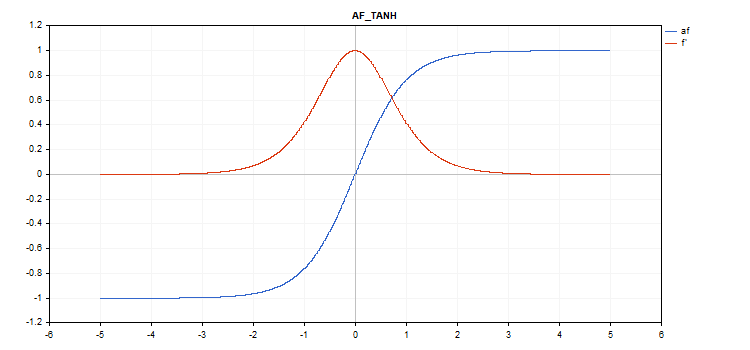

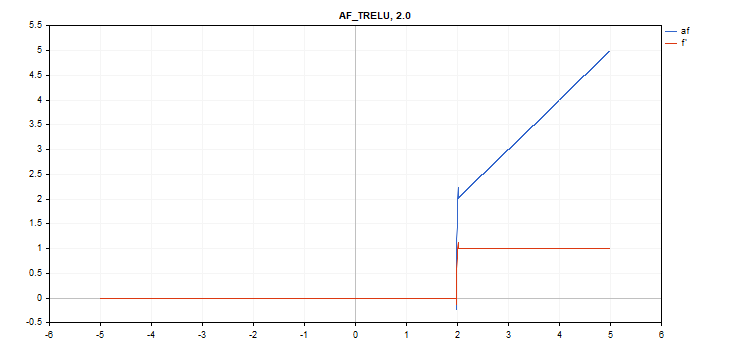
Funzione di attivazione Thresholded Rectified Linear Unit TReLU (TReLU)

Calcolo della funzione

   if(x > theta)
      f = x;
   else
      f = 0;

Calcolo delle derivate

   if(x > theta)
      d = 1;
   else
      d = 0;

Parametro aggiuntivo theta = 1

vector_a.Activation(vector_c,AF_TRELU);         // call with default parameter

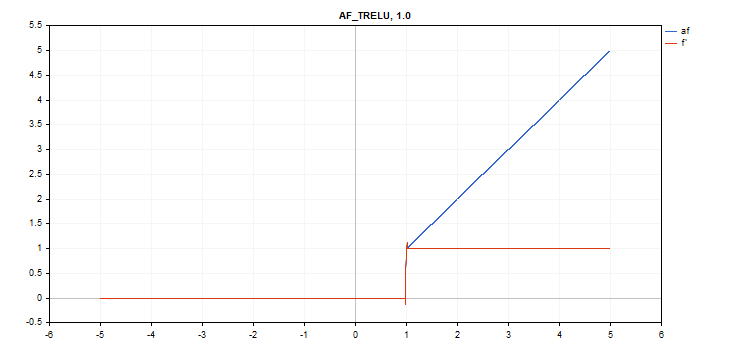
vector_a.Activation(vector_c,AF_TRELU,0.0);     // call with theta = 0.0

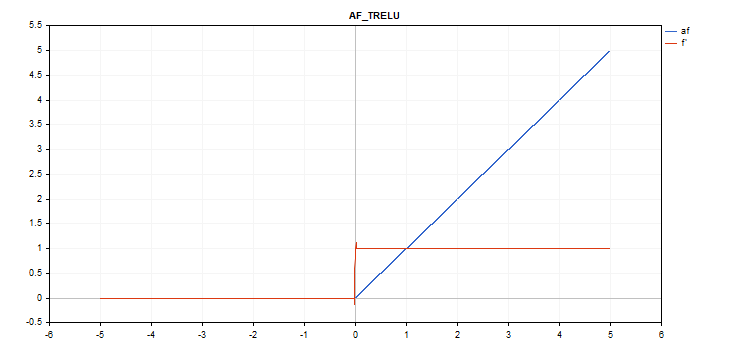
vector_a.Activation(vector_c,AF_TRELU,2.0);      // call with theta = 2.0

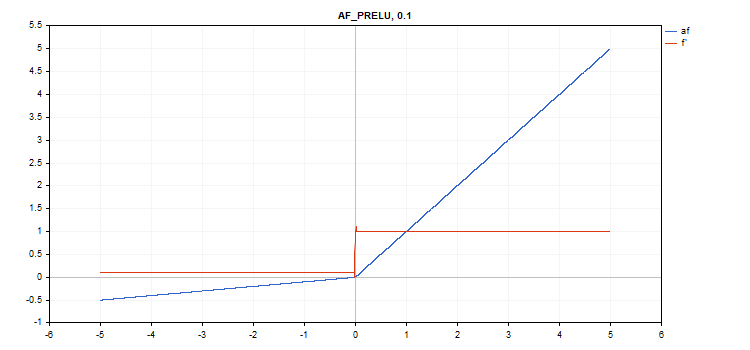
Funzione di attivazione Parametric Rectifiedl Linear Unit (PReLU)

Calcolo della funzione

   if(x[i] >= 0)
      f[i] = x[i];
   else
      f[i] = alpha[i]*x[i];

Calcolo delle derivate

   if(x[i] >= 0)
      d[i] = 1;
   else
      d[i] = alpha[i];

Parametro aggiuntivo - vettore del coefficiente 'alfa'.

vector alpha=vector::Full(vector_a.Size(),0.1);
vector_a.Activation(vector_c,AF_PRELU,alpha);

Funzione speciale Softmax

Il risultato del calcolo della funzione di attivazione Softmax non dipende solo da un valore specifico, ma anche da tutti i valori del vettore.

   sum_exp = Sum(exp(vector_a))
   f = exp(x) / sum_exp

Calcolo delle derivate

   d = f*(1 - f)

Pertanto, la somma di tutti i valori del vettore attivato è 1. Perciò, la funzione di attivazione Softmax viene molto spesso utilizzata per l'ultimo strato dei modelli di classificazione.

Grafico della funzione di attivazione vettoriale con valori da -5 a 5

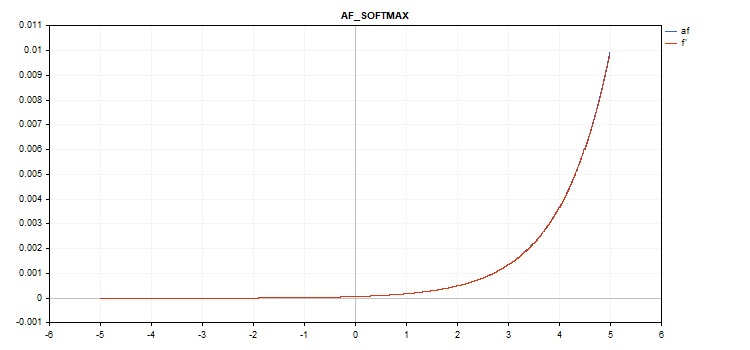
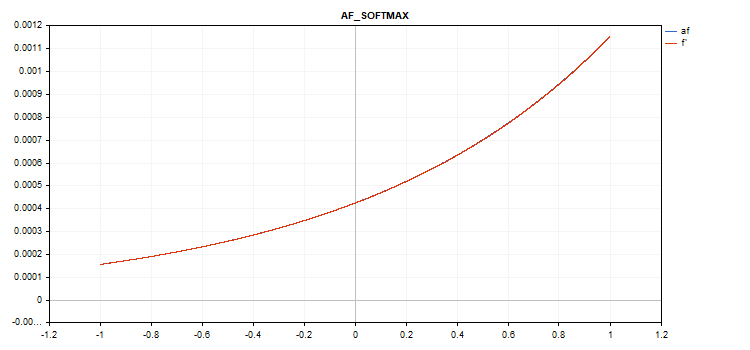
Grafico della funzione di attivazione vettoriale con valori da -1 a 1

Se non c'è una funzione di attivazione (AF_NONE)

Se non c'è una funzione di attivazione, i valori del vettore di input vengono trasferiti al vettore di output senza alcuna trasformazione. In effetti, si tratta della funzione di attivazione Lineare con alfa = 1 e beta = 0.

Conclusioni

Non esitate a familiarizzare con i codici sorgente delle funzioni di attivazione e delle derivate nel file ActivationFunction.mqh allegato di seguito.