MQL5에서 행렬 및 벡터: 활성화 함수

소개

이미 신경망 훈련에 관한 수많은 책과 기사가 출판되었습니다. MQL5.com 회원들 또한 여러 시리즈 기사를 포함하여 많은 자료를 게시했습니다.

여기서는 머신 러닝의 한 가지 측면인 활성화 함수에 대해서만 설명하겠습니다. 우리는 이 프로세스의 내부의 작동 방식에 대해 자세히 살펴볼 것입니다.

간략한 개요

인공 신경망에서 뉴런 활성화 함수는 입력 신호 또는 입력 신호 세트의 값을 기반으로 출력 신호의 값을 계산합니다. 활성화 함수는 전체 값 집합에 대해 차별화 될 수 있어야 합니다. 이 조건은 신경망을 훈련할 때 오류 역전파의 가능성을 제공합니다. 오류를 역전파 하기 위해서는 입력 신호 벡터의 각 값에 대한 활성화 함수의 부분 도함수 벡터인 활성화 함수의 기울기를 계산해야 합니다. 보통은 비선형 활성화 함수가 훈련에 더 좋다는 것이 통설입니다. 반면에 완전 선형 ReLU 함수는 많은 모델에서 그 효과를 입증했습니다.

일러스트레이션

활성화 함수와 그 도함수의 그래프는 그림과 같이 -5에서 5까지 단조롭게 증가하는 순서로 준비되었습니다. 가격 차트에 함수 그래프를 표시하는 스크립트도 개발되었습니다. Page Down 키를 누르면 저장된 이미지의 이름을 지정할 수 있는 파일 열기 대화 상자가 표시됩니다.

ESC 키는 스크립트를 종료합니다. 스크립트는 아래에 첨부되어 있습니다. 비슷한 스크립트는 MQL5 행렬을 사용한 역전파 신경망이라는 글의 작성자가 작성한 것입니다. 우리는 그 글의 작성자의 아이디어를 사용하여 활성화 함수 자체의 그래프와 함께 해당 활성화 함수 미분 값의 그래프를 표시했습니다.

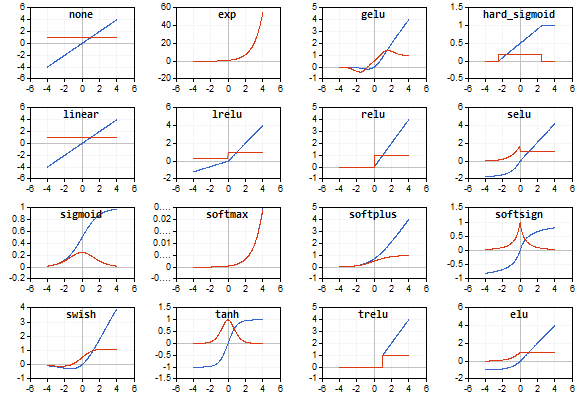
활성화 함수는 파란색으로 표시되고 함수 파생물은 빨간색으로 표시됩니다.

지수 선형 단위(ELU) 활성화 함수

함수 계산

   if(x >= 0)
      f = x;
   else
      f = alpha*(exp(x) - 1);

도함수 계산

   if(x >= 0)
      d = 1;
   else
      d = alpha*exp(x);

이 함수는 추가 '알파' 매개변수를 받습니다. 지정하지 않으면 기본값은 1입니다.

   vector_a.Activation(vector_c,AF_ELU);      // call with the default parameter

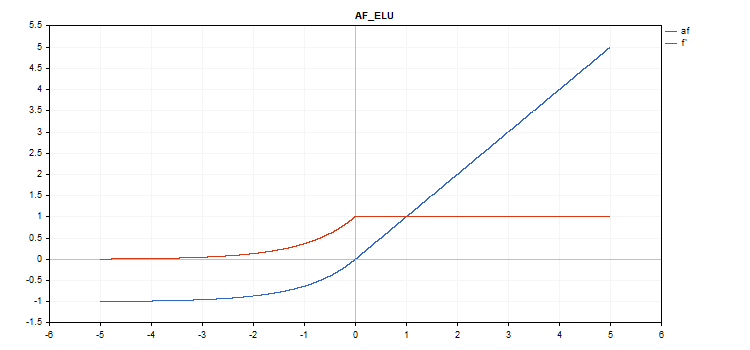
   vector_a.Activation(vector_c,AF_ELU,3.0);  // call with alpha=3.0

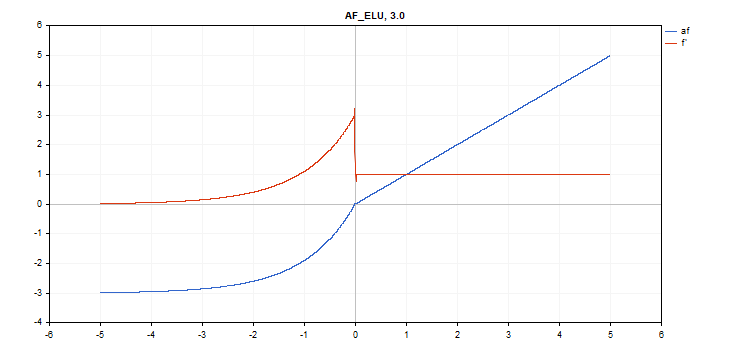
지수 활성화 기능

함수 계산

   f = exp(x);

동일한 exp 함수가 exp 함수의 파생 함수의 역할을 합니다.

계산 방정식에서 볼 수 있듯이 지수 활성화 함수에는 추가 매개 변수가 없습니다.

vector_a.Activation(vector_c,AF_EXP);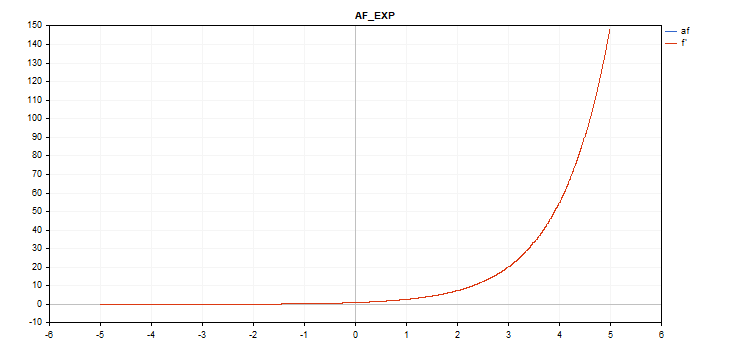

가우시안 에러 선형 단위(GELU) 활성화 함수

함수 계산

   f = 0.5*x*(1 + tanh(sqrt(M_2_PI)*(x+0.044715*pow(x,3)));

도함수 계산

   double x_3 = pow(x,3);
   double tmp = cosh(0.0356074*x + 0.797885*x);
   d = 0.5*tanh(0.0356774*x_3 + 0.398942*x)+(0.535161*x_3 + 0.398942*x)/(tmp*tmp) + 0.5;

추가 매개변수가 없습니다.

vector_a.Activation(vector_c,AF_GELU);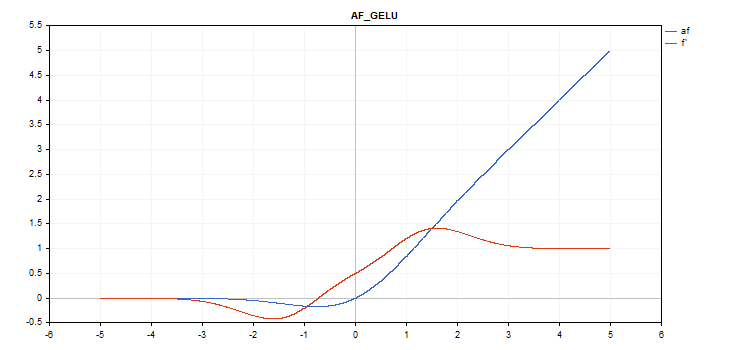

하드 시그모이드 활성화 함수

함수 계산

   if(x < -2.5)
      f = 0;
   else
     {
      if(x > 2.5)
         f = 1;
      else
         f = 0.2*x + 0.5;
     }

도함수 계산

   if(x < -2.5)
      d = 0;
   else
     {
      if(x > 2.5)
         d = 0;
      else
         d = 0.2;
     }

추가 매개변수가 없습니다.

vector_a.Activation(vector_c,AF_HARD_SIGMOID);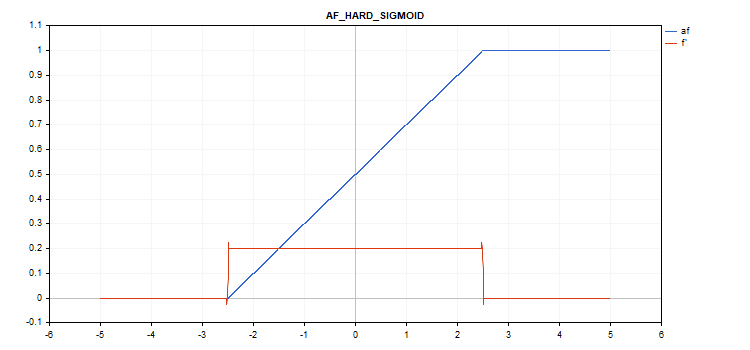

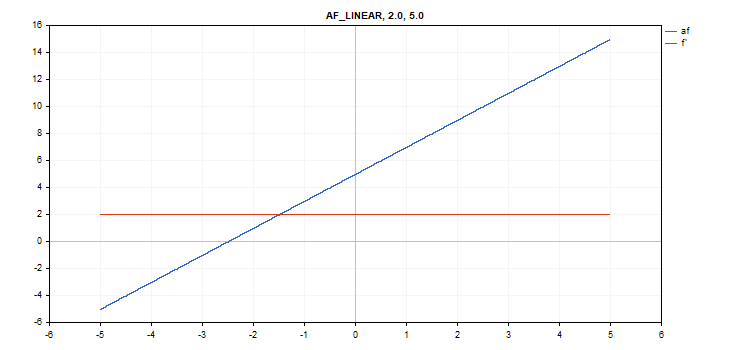
선형 활성화 함수

함수 계산

   f = alpha*x + beta

도함수 계산

   d = alpha

추가 매개변수 알파 = 1.0 및 베타 = 0.0

vector_a.Activation(vector_c,AF_LINEAR);         // call with default parameters

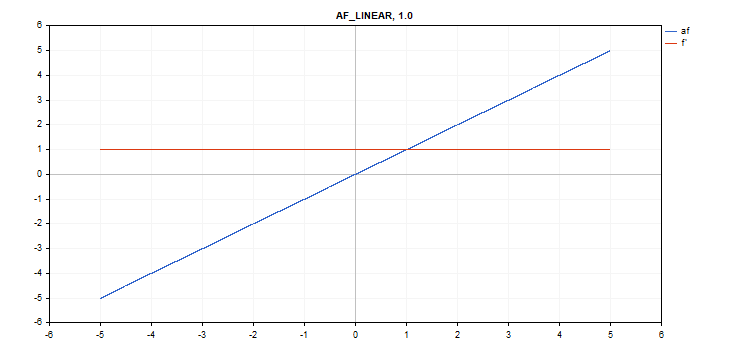
vector_a.Activation(vector_c,AF_LINEAR,2.0,5.0);  // call with alpha=2.0 and beta=5.0

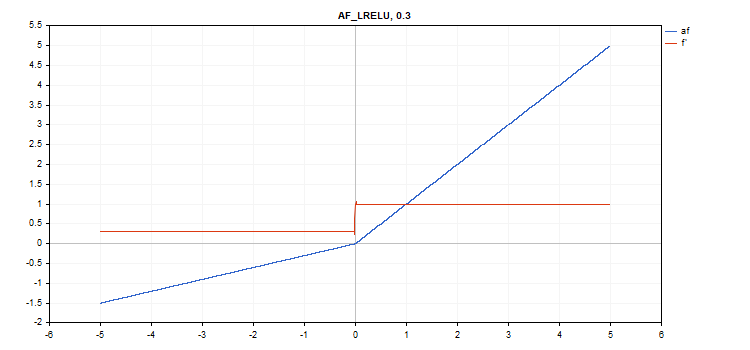
누설 정류 선형 장치(LReLU) 활성화 함수

함수 계산

   if(x >= 0)
      f = x;
   else
      f = alpha * x;

도함수 계산

   if(x >= 0)
      d = 1;
   else
      d = alpha;

이 함수는 추가 '알파' 매개변수를 받습니다. 지정하지 않으면 기본값은 0.3입니다.

   vector_a.Activation(vector_c,AF_LRELU);      // call with the default parameter

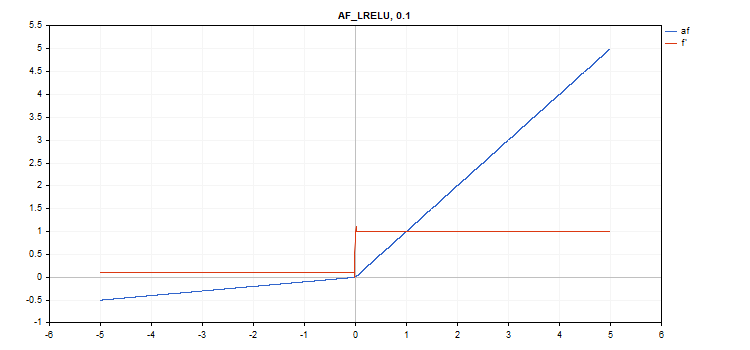
vector_a.Activation(vector_c,AF_LRELU,0.1);  // call with alpha=0.1

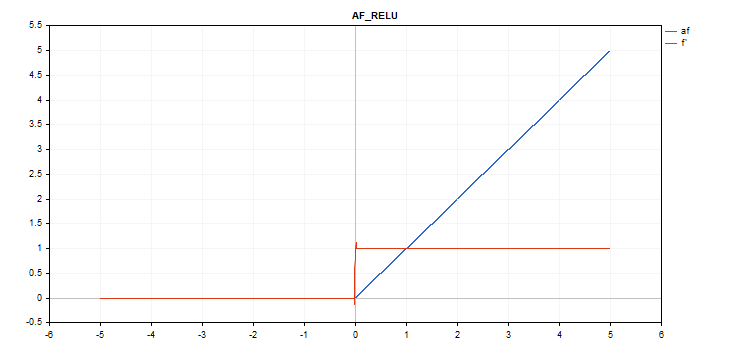
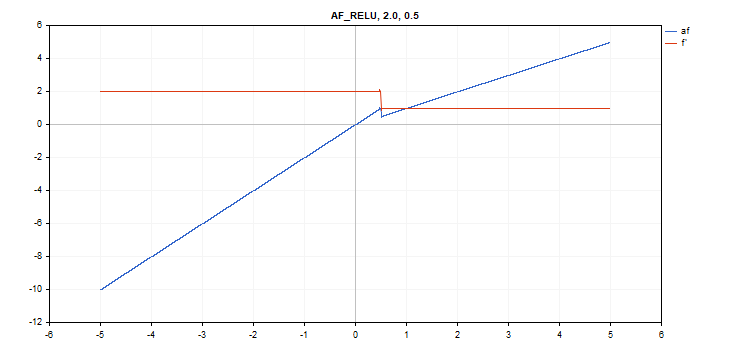
정류된 선형 장치(ReLU) 활성화 함수

함수 계산

   if(alpha==0)
     {
      if(x > 0)
         f = x;
      else
         f = 0;
     }
   else
     {
      if(x >= max_value)
         f = x;
      else
         f = alpha * (x - treshold);
     }

도함수 계산

   if(alpha==0)
     {
      if(x > 0)
         d = 1;
      else
         d = 0;
     }
   else
     {
      if(x >= max_value)
         d = 1;
      else
         d = alpha;
     }

추가 매개변수 alpha=0, max_value=0, treshold=0.

vector_a.Activation(vector_c,AF_RELU);         // call with default parameters

vector_a.Activation(vector_c,AF_RELU,2.0,0.5);      // call with alpha=2.0 and max_value=0.5

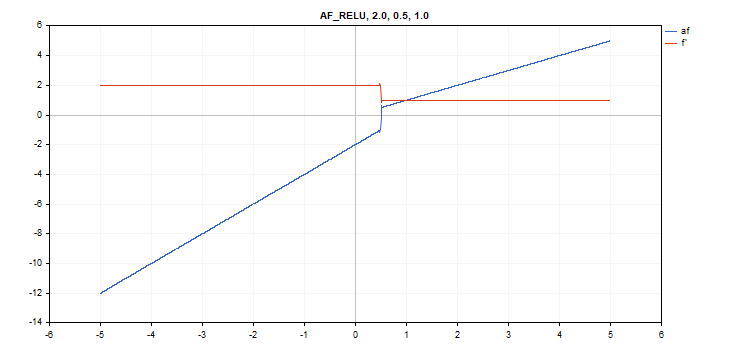
vector_a.Activation(vector_c,AF_RELU,2.0,0.5,1.0);  // call with alpha=2.0, max_value=0.5 and treshold=1.0

확장 지수 선형 단위(SELU) 활성화 함수

함수 계산

   if(x >= 0)
      f = scale * x;
   else
      f = scale * alpha * (exp(x) - 1);

where scale = 1.05070098, alpha = 1.67326324

도함수 계산

   if(x >= 0)
      d = scale;
   else
      d = scale * alpha * exp(x);

추가 매개변수가 없습니다.

vector_a.Activation(vector_c,AF_SELU);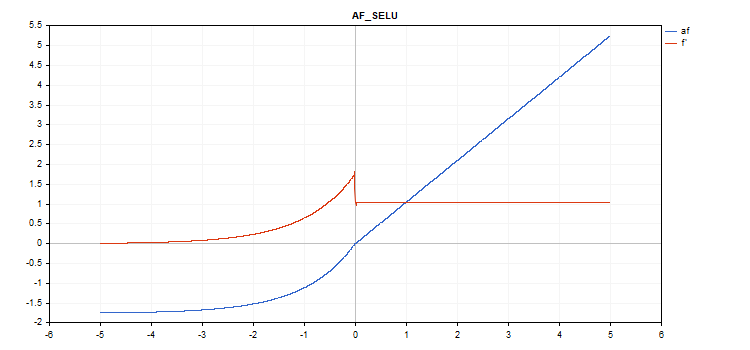

시그모이드 활성화 함수

함수 계산

   f = 1 / (1 + exp(-x));

도함수 계산

   d = exp(x) / pow(exp(x) + 1, 2);

추가 매개변수가 없습니다.

vector_a.Activation(vector_c,AF_SIGMOID);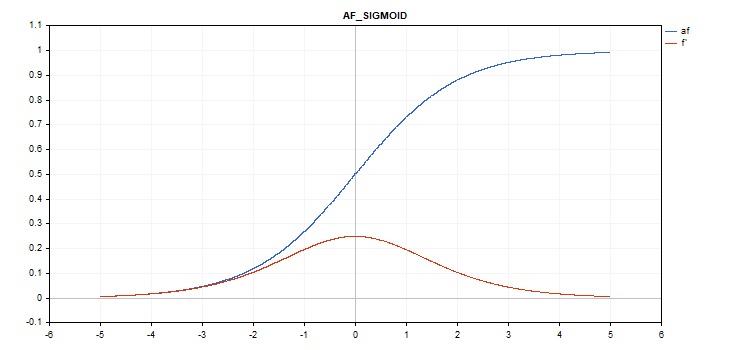

소프트플러스 활성화 함수

함수 계산

   f = log(exp(x) + 1);

도함수 계산

   d = exp(x) / (exp(x) + 1);

추가 매개변수가 없습니다.

vector_a.Activation(vector_c,AF_SOFTPLUS);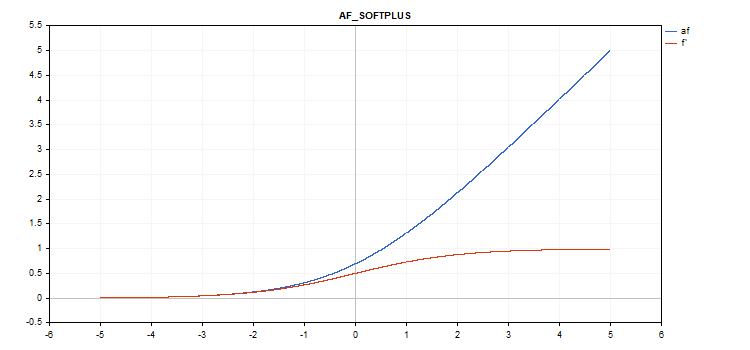

소프트사인 활성화 함수

함수 계산

   f = x / (|x| + 1)

도함수 계산

   d = 1 / (|x| + 1)^2

추가 매개변수가 없습니다.

vector_a.Activation(vector_c,AF_SOFTSIGN);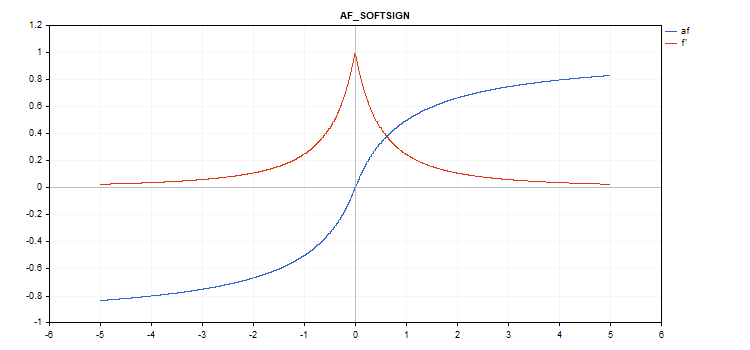

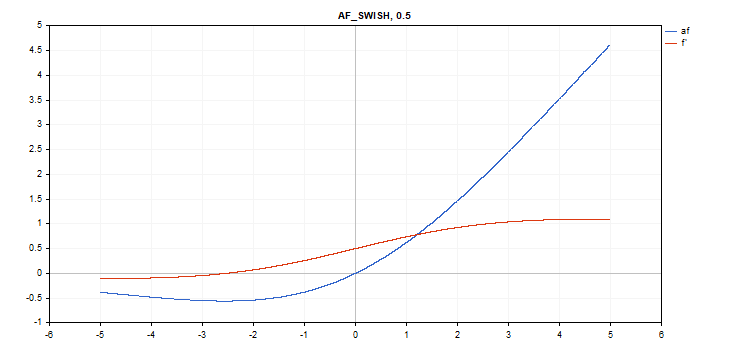
스와이시 활성화 함수

함수 계산

   f = x / (1 + exp(-x*beta));

도함수 계산

   double tmp = exp(beta*x);
   d = tmp*(beta*x + tmp + 1) / pow(tmp+1, 2);

추가 매개변수 beta = 1

vector_a.Activation(vector_c,AF_SWISH);         // call with the default parameter

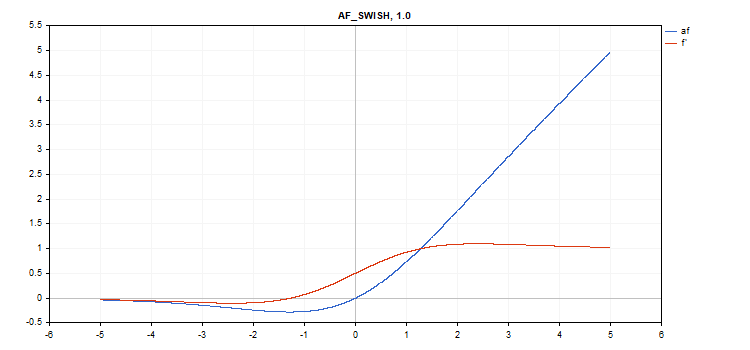
vector_a.Activation(vector_c,AF_SWISH,2.0);     // call with beta = 2.0

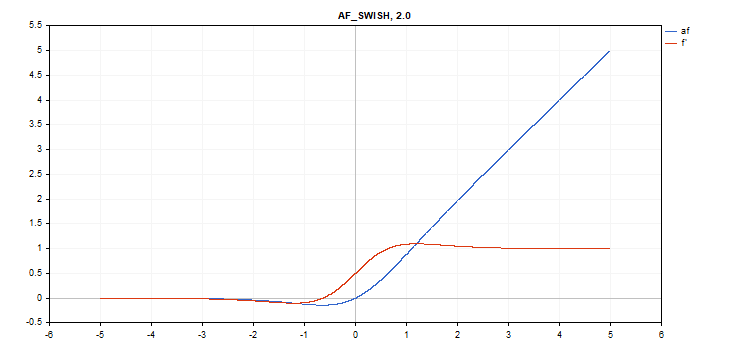
vector_a.Activation(vector_c,AF_SWISH,0.5);   // call with beta=0.5

쌍곡탄젠트(TanH) 활성화 함수

함수 계산

   f = tanh(x);

도함수 계산

   d = 1 / pow(cosh(x),2);

추가 매개변수가 없습니다.

vector_a.Activation(vector_c,AF_TANH);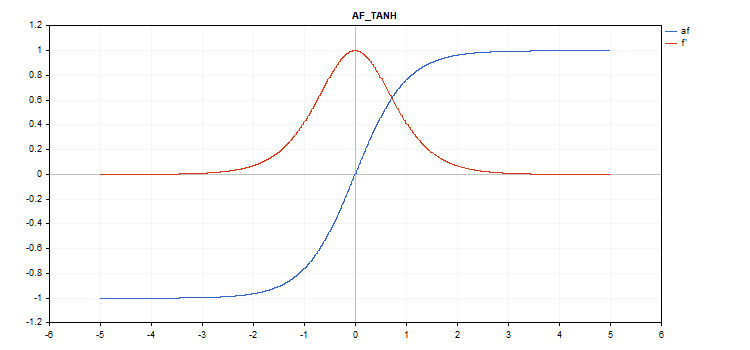

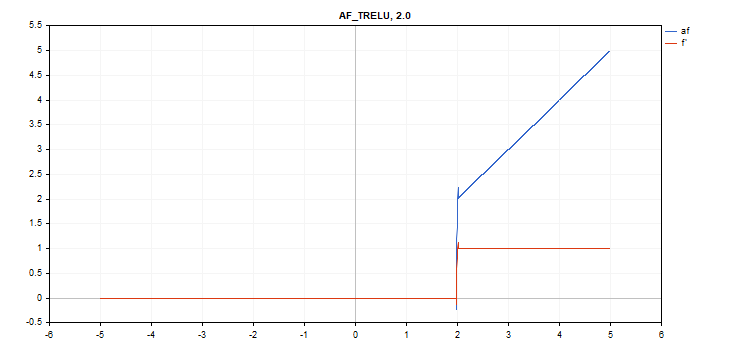
임계값 정류 선형 장치(TReLU) 활성화 함수

함수 계산

   if(x > theta)
      f = x;
   else
      f = 0;

도함수 계산

   if(x > theta)
      d = 1;
   else
      d = 0;

추가 파라미터 세타 = 1

vector_a.Activation(vector_c,AF_TRELU);         // call with default parameter

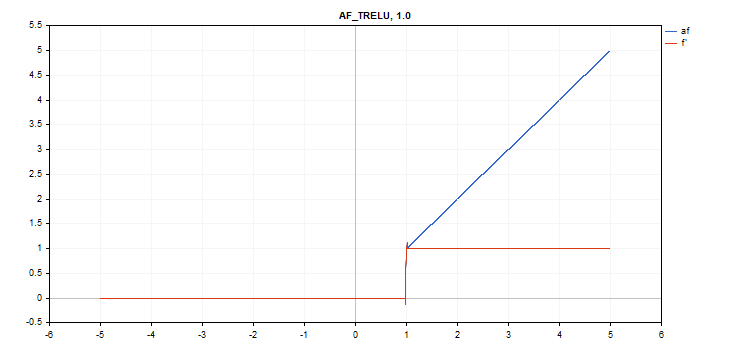
vector_a.Activation(vector_c,AF_TRELU,0.0);     // call with theta = 0.0

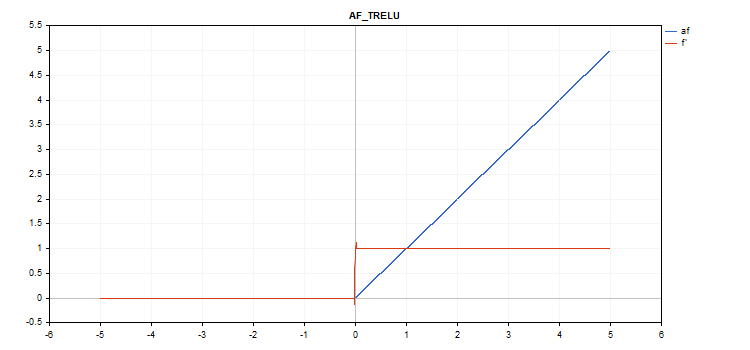
vector_a.Activation(vector_c,AF_TRELU,2.0);      // call with theta = 2.0

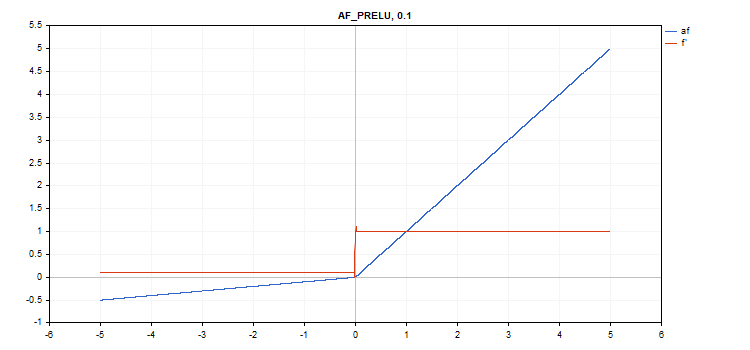
파라메트릭 정류 선형 유닛(PReLU) 활성화 함수

함수 계산

   if(x[i] >= 0)
      f[i] = x[i];
   else
      f[i] = alpha[i]*x[i];

도함수 계산

   if(x[i] >= 0)
      d[i] = 1;
   else
      d[i] = alpha[i];

추가 매개변수 - '알파' 계수 벡터.

vector alpha=vector::Full(vector_a.Size(),0.1);
vector_a.Activation(vector_c,AF_PRELU,alpha);

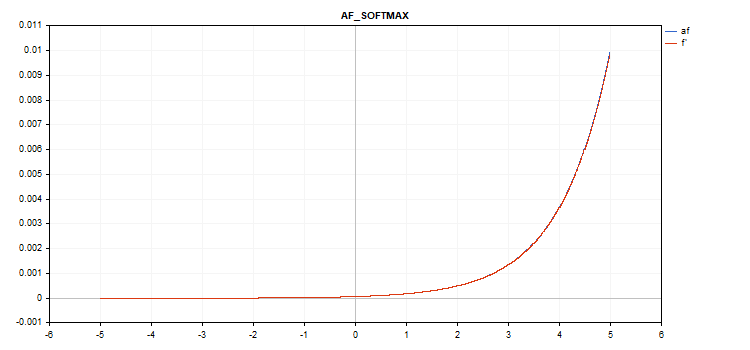
특별한 소프트맥스 함수

소프트맥스 활성화 함수를 계산한 결과는 특정 값 뿐만 아니라 모든 벡터 값에 따라 달라집니다.

   sum_exp = Sum(exp(vector_a))
   f = exp(x) / sum_exp

도함수 계산

   d = f*(1 - f)

따라서 활성화된 모든 벡터 값의 합은 1입니다. 따라서 소프트맥스 활성화 함수는 분류 모델의 마지막 계층에 자주 사용됩니다.

5에서 5까지의 값을 가진 벡터 활성화 함수 그래프

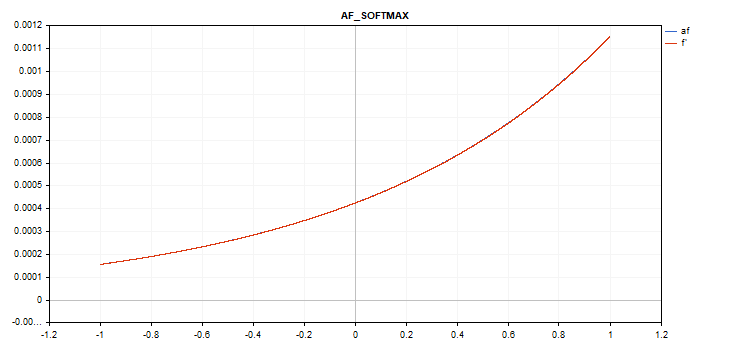
-1에서 1까지의 값을 가진 벡터 활성화 함수 그래프

활성화 함수가 없는 경우(AF_NONE)

활성화 함수가 없는 경우에 입력 벡터의 값은 아무런 변환 없이 출력 벡터로 전송됩니다. 실제로 이것은 알파 = 1, 베타 = 0인 선형 활성화 함수입니다.

결론

아래 첨부된 ActivationFunction.mqh 파일을 통해 활성화 함수 및 파생 함수의 소스 코드를 숙지하시기 바랍니다.