
Redes neurais de retropropagação em matrizes MQL5
Faz um tempinho que o aprendizado de máquina e, especificamente, as redes neurais têm feito parte das ferramentas de um trader. Dentro do universo das redes neurais, em parte de sua classificação que envolve os chamados métodos de 'aprendizado supervisionado', as redes com retropropagação de erros (backpropagation neural network, BPNN) ocupam um lugar especial. Existem várias modificações desses algoritmos. Com base neles, foram criadas, por exemplo, redes neurais profundas, recorrentes e convolucionais. Portanto, não é surpresa a quantidade de materiais sobre o assunto (e nem a quantidade de artigos neste site). Hoje, vamos explorar uma direção relativamente nova para o MQL5. O lance é que, há algum tempo, o MQL5 lançou novas funcionalidades na API para trabalhar com matrizes e vetores. Elas permitem implementar cálculos em redes neurais em modo batch, quando os dados são processados de uma vez (ou em blocos), em vez de elemento por elemento.
Com as operações matriciais, as instruções de programação que realizam as fórmulas de propagação direta e retropropagação de sinais na rede se tornam muito mais simples. Basicamente, elas se transformam em expressões de uma única linha. Isso nos permite focar em outros aspectos importantes para melhorar o algoritmo.
Neste artigo, faremos um breve resumo da teoria das redes com retropropagação de erros e criaremos classes universais baseadas nela para construir redes: as fórmulas fornecidas serão quase que 'espelhadas' no código-fonte. Assim, os novatos podem percorrer todo o 'caminho' para dominar essa tecnologia sem precisar buscar publicações externas.
Se você já está familiarizado com a teoria, pode ir direto para a segunda parte do artigo, onde examinamos exemplos de como usar as classes na prática - em script, indicador e Expert Advisor.
Introdução à teoria das redes neurais
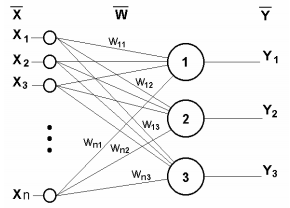
Vale lembrar que as redes neurais (RN) são compostas por elementos computacionais básicos - os neurônios, que geralmente são agrupados logicamente em camadas e conectados por conexões (sinapses), que são as 'rotas' por onde os sinais passam. O sinal é uma abstração matemática capaz de representar situações em qualquer área aplicada, inclusive no trading.
A sinapse faz a ligação entre a saída de um neurônio e a entrada de outro, sendo caracterizada por um valor chamado peso wi. O estado atual de um neurônio é definido como uma soma ponderada dos sinais que entram nas suas conexões (entradas).
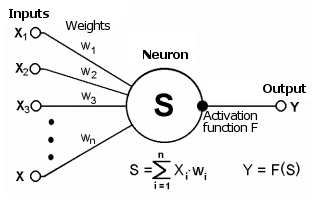
Esquema de um neurônio
Esse estado é então processado por uma função de ativação não-linear, que gera o valor de saída de um neurônio específico. A partir daí, o sinal segue pelas sinapses para os próximos neurônios conectados (se existirem) ou se torna um componente da 'resposta' da rede neural (caso o neurônio atual esteja na última camada).
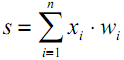 | (1) |
| | (2) |
A presença de não-linearidade potencializa as capacidades de cálculo da rede. As funções de ativação podem ser, por exemplo, a tangente hiperbólica ou a função logística (ambas fazem parte das chamadas funções em forma de S ou sigmoidais)
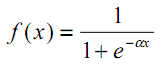 | (3) |
Veremos a seguir que o MQL5 oferece um amplo conjunto de funções de ativação incorporadas. A escolha de uma função específica deve ser baseada nas especificidades do problema a ser resolvido (seja ele de regressão, classificação). Geralmente, é possível selecionar várias funções para qualquer problema e, posteriormente, encontrar a mais adequada por meio de experimentação.
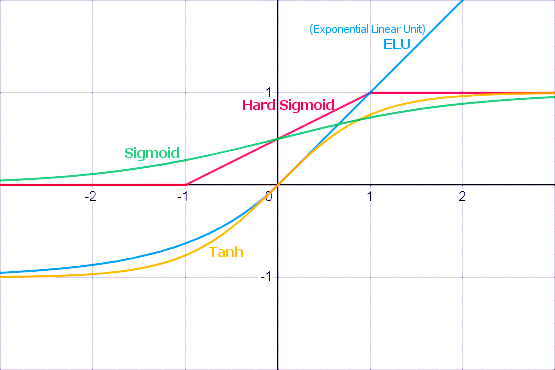
Funções de ativação populares
As funções de ativação podem possuir diferentes intervalos de valores - sendo limitadas ou ilimitadas. Por exemplo, a função sigmoide (3) mapeia os dados para o intervalo [0,+1] (sendo mais adequada para tarefas de classificação), enquanto a tangente hiperbólica direciona os dados para o intervalo [-1,+1] (sendo mais apropriada para tarefas de regressão e previsão).
Uma propriedade crucial da função de ativação é como sua derivada é definida ao longo do eixo. A existência de uma derivada finita e não-nula é fundamentalmente necessária para o algoritmo de retropropagação do erro, que será abordado adiante. Em particular, as funções em forma de S cumprem este requisito. Além disso, as funções de ativação padrão geralmente possuem uma representação analítica de sua derivada bastante simples, assegurando seu cálculo eficiente. Por exemplo, para a função sigmoide (3) temos:
| | (4) |
A rede neural de uma única camada é representada na figura a seguir.
Rede neural de camada única
O princípio de seu funcionamento é matematicamente descrito pela seguinte equação:
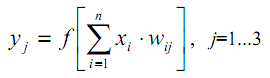 | (5) |
É claro que todos os coeficientes de peso de uma única camada podem ser resumidos em uma matriz W, onde cada elemento wij determina o valor da i-ésima conexão do j-ésimo neurônio. Dessa forma, o processo que ocorre na RN pode ser expresso em forma matricial:
| Y = F(X W) | (6) |
Onde X e Y são, respectivamente, os vetores de sinal de entrada e saída, e F(V) é a função de ativação, aplicada elemento a elemento aos componentes do vetor V.
O número de camadas e o número de neurônios em cada camada da rede dependem dos dados de entrada: suas dimensões, tamanho da amostra, lei de distribuição, entre outros fatores. Normalmente, a configuração da rede é determinada por meio de tentativas.
Para ilustração, apresentaremos um esquema de uma rede composta por duas camadas.
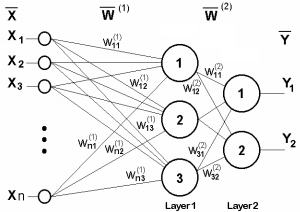
Rede neural de duas camadas
Agora, vamos abordar um detalhe anteriormente negligenciado. Observando o gráfico das funções de ativação, fica evidente que existe um valor específico T, onde as funções em forma de S apresentam a maior inclinação e transmitem eficientemente os sinais, enquanto outras funções têm um ponto de inflexão característico (ou vários desses pontos). Sendo assim, a principal atividade de cada neurônio ocorre nas proximidades de T. Geralmente, T=0 ou está próximo de 0, portanto, é conveniente ter um mecanismo para deslocar automaticamente o argumento da função de ativação para T.
Esse fenômeno não foi contemplado na fórmula (1), que deveria ter sido apresentada da seguinte maneira:
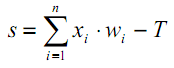 | (7) |
Esse deslocamento costuma ser implementado adicionando uma pseudo-entrada adicional à camada de neurônios, cujo valor é sempre igual a 1. Vamos atribuir a este input o número 0. Assim, temos:
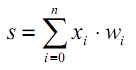 | (8) |
onde w0 = –T, x0 = 1.
O treinamento de uma rede neural com um 'supervisor' pressupõe a existência de dados de treinamento, previamente preparados e 'rotulados' por um especialista humano. Nesses dados, vetores de entrada são associados às saídas desejadas.
O processo de treinamento ocorre nas seguintes etapas:
1. Inicializar os elementos da matriz de peso (usualmente com valores aleatórios pequenos);
2. Alimentar as entradas com um dos vetores e calcular a resposta da rede; esta é a fase de propagação direta do sinal, que também será utilizada durante a operação regular da rede já treinada;
3. Calcular a diferença entre os valores de saída ideais e os obtidos, ou seja, o erro da rede, e então ajustar os pesos de acordo com uma fórmula específica (detalhada a seguir) com base nesse erro;
4. Continuar o processo em um ciclo a partir do passo 2 para todos os vetores de entrada do conjunto de dados, até que o erro seja inferior a um nível mínimo preestabelecido (conclusão bem-sucedida do treinamento) ou até que seja alcançado um número máximo pré-definido de ciclos de treinamento (em caso de falha da rede na tarefa).
No caso de uma RN de camada única, a fórmula para a modificação dos pesos é intuitiva:
| | (9) |
| | (10) |
onde δ é o erro da rede (a diferença entre a resposta produzida pela rede e o valor ideal), t e t+1 são, respectivamente, os números das iterações atual e subsequente; ν é o coeficiente de taxa de aprendizado, que se situa 0<ν<1; i é o número de entrada; j é o número do neurônio na camada.
Contudo, como proceder quando a rede tem múltiplas camadas? Aqui, introduzimos a ideia da retropropagação do erro.
Algoritmo de retropropagação do erro
Dentre as diversas estruturas de redes neurais, a estrutura multicamadas é uma das mais conhecidas. Nela, cada neurônio de uma determinada camada está conectado com todos os neurônios da camada anterior ou, no caso da primeira camada, com todas as entradas da RN. Essas RNs são conhecidas como totalmente conectadas, e é para esta estrutura que a seguinte discussão se aplica. Em muitos outros tipos de RNs, como nas convolucionais, as conexões estabelecem-se entre regiões limitadas de camadas, os chamados núcleos, o que aumenta a complexidade do endereçamento dos elementos da rede, mas não impacta a aplicabilidade do método de retropropagação.
Intuitivamente, é necessário que a informação de erro seja transmitida de alguma maneira das saídas da rede neural até as suas entradas, espalhando-se gradualmente por todas as camadas, levando em consideração a 'condutância' das conexões, isto é, os pesos.
De acordo com o método dos mínimos quadrados, a função objetivo do erro da RN a ser minimizada é:
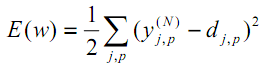 | (11) |
onde yjpᴺ é o estado de saída real do neurônio j da camada de saída N da rede neural ao processar a entrada com o padrão p; djp é o estado de saída ideal (desejado) desse neurônio.
O somatório é realizado para todos os neurônios da camada de saída e para todos os padrões processados. O coeficiente 1/2 é inserido apenas para obter uma derivada 'bonita' de E (dois são cancelados), que será usada posteriormente para treinamento (consulte a fórmula (12)) e, em qualquer caso, é 'ponderada' por um importante parâmetro de o algoritmo - velocidade (que pode ser aumentada em 2 vezes ou até mesmo mudar dinamicamente de acordo com algumas condições).
Uma das abordagens mais eficientes para minimizar uma função é fundamentada na premissa de que as melhores direções locais para extremos são indicadas pelas derivadas dessa função em um ponto específico. A derivada com sinal positivo nos conduzirá ao máximo, enquanto a derivada com sinal negativo nos guiará ao mínimo. Obviamente, os máximos e mínimos podem ser apenas locais e, para 'saltar' para o mínimo global, pode ser necessário recorrer a técnicas adicionais, mas deixaremos esse problema de fora por enquanto.
O método descrito é conhecido como método do gradiente descendente, e implica o ajuste dos coeficientes de peso com base na derivada de E, da seguinte maneira:
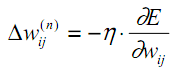 | (12) |
Aqui, wij representa o coeficiente de peso da conexão que une o neurônio i da camada n-1 ao neurônio j da camada n, e η é o coeficiente de velocidade de aprendizado.
Recordemos a configuração interna de um neurônio e, com base nela, destaquemos cada estágio de cálculos na derivada parcial conforme a fórmula (12):
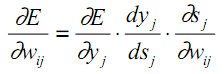 | (13) |
Como anteriormente, yj denota a saída do neurônio j, e sj é a soma ponderada de seus sinais de entrada, isto é, o argumento da função de ativação. Como o fator dyj/dsj é a derivada dessa função, isso exige que a função de ativação seja diferenciável ao longo de todo o eixo x para ser utilizada no algoritmo de retropropagação do erro em questão.
Por exemplo, no caso da tangente hiperbólica:
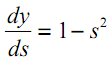 | (14) |
O terceiro fator em (13), ∂sj/∂wij, é igual à saída do neurônio yi da camada anterior (n-1). Por que isso ocorre? Vamos lembrar que numa rede multicamadas, o sinal vai da saída do neurônio da camada anterior para a entrada do neurônio da camada atual. Portanto, a fórmula (1) para sj pode ser reescrita de forma mais abrangente da seguinte maneira:
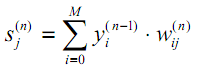 | (15) |
Aqui, M representa o número de neurônios na camada n-1, incluindo o neurônio com o estado de saída constante +1, que determina o deslocamento; yi(n-1)=xij(n) é a i-ésima entrada do neurônio j da camada n, conectada à saída do neurônio i da camada (n-1);
Quanto ao primeiro fator em (13), faz sentido decompor de acordo com as variações do erro na camada adjacente, que é mais antiga (já que os valores do erro são propagados na direção oposta):
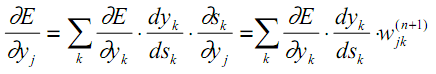 | (16) |
Aqui, a soma sobre k é realizada entre os neurônios da camada n+1.
Não é difícil observar que os dois primeiros fatores em (13) para uma camada (com índices j nos neurônios) são replicados em (16) para a próxima camada (com índices k) na forma de um coeficiente antes do peso wjk.
Vamos introduzir uma variável intermediária que incorpora esses dois fatores:
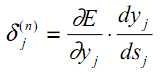 | (17) |
Como resultado, obtemos uma fórmula recursiva para calcular as grandezas δj(n) da camada n a partir das grandezas δk(n+1) da camada superior n+1.
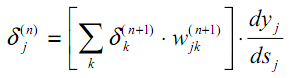 | (18) |
Para a camada de saída, a nova variável, como antes, é calculada com base na diferença entre o resultado alcançado e o desejado pela rede.
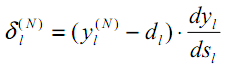 | (19) |
Comparado com (9), aqui, de forma mais rigorosa, a derivada da função de ativação é adicionada. No entanto, na camada de saída da rede neural, dependendo da tarefa, a função de ativação pode estar ausente.
Agora podemos registrar a fórmula (12) para ajustar os pesos durante o treinamento de forma mais explícita:
| | (20) |
Às vezes, para dar alguma inércia ao processo de ajuste de peso, suavizando saltos acentuados na derivada ao se mover sobre a superfície da função objetivo, a fórmula (20) é complementada pelo valor da mudança de peso na iteração anterior:
| | (21) |
onde µ é o coeficiente de inércia, e t é o número da iteração atual.
Portanto, o algoritmo completo para treinar uma rede neural usando o procedimento de retropropagação é construído da seguinte maneira:
1. Inicialize as matrizes de peso com pequenos números aleatórios.
2. Introduza um dos vetores de dados nas entradas da rede e, em um modo de operação regular, quando os sinais se propagam das entradas para as saídas, calcule o resultado geral da rede neural camada por camada usando as fórmulas de soma ponderada (15) e ativação f:
| | (22) |
Os neurônios da camada 0, a camada de entrada, são usados apenas para fornecer sinais de entrada e não possuem sinapses e funções de ativação.
| | (23) |
Iq é a q-ésima componente do vetor de entrada, aplicada à camada 0.
3. Se o erro da rede for menor que um valor pré-definido pequeno, paramos o processo com um sinal de sucesso. Se o erro for significativo, prosseguimos para as etapas seguintes.
4. Calcule para a camada de saída N: δ usando a fórmula (19), assim como as alterações nos pesos Δw usando as fórmulas (20) ou (21).
5. Para todas as outras camadas, em ordem reversa, n=N-1,...1, calcule δ e Δw usando as fórmulas (18) e (20) (ou (18) e (21)) respectivamente.
6. Ajuste todos os pesos na rede neural para a iteração t com base na iteração anterior t-1.
| | (24) |
7. Repita o processo em um ciclo a partir do passo 2.
O diagrama de sinais na rede durante o treinamento pelo algoritmo de retropropagação é ilustrado na figura seguinte.
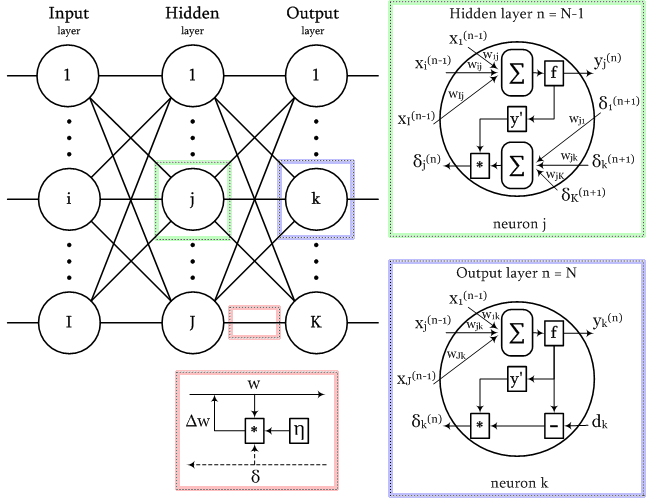
Esquema de sinais no algoritmo de retropropagação de erro
A rede é alternadamente exposta a todos os padrões de treinamento, garantindo que, metaforicamente falando, não esqueça alguns padrões enquanto aprende outros. Isso é geralmente feito de maneira aleatória, mas já que nossos dados serão colocados em matrizes e processados como um conjunto unificado, nossa implementação introduzirá outro elemento de aleatoriedade, o qual discutiremos mais adiante.
O uso de matrizes implica que os pesos de todas as camadas, além dos dados de entrada e meta de treinamento, serão representados como matrizes, e as fórmulas anteriormente mencionadas, e, consequentemente, os algoritmos, assumirão uma forma matricial. Em outras palavras, não poderemos manipular vetores individuais de entrada e dados de treinamento, e todo o ciclo do passo 2 ao passo 7 será calculado simultaneamente para todo o conjunto de dados. Esse tipo de ciclo é chamado de época de treinamento.
Visão geral das funções de ativação
O artigo vem acompanhado do script AF.mq5, que traça representações gráficas miniaturizadas de todas as funções de ativação suportadas pelo MQL5 (em azul) e suas respectivas derivadas (em vermelho). O script ajusta automaticamente as miniaturas para se adequar à janela, então, para obter imagens mais detalhadas, é recomendado ampliar ou maximizar a janela previamente. Abaixo, é apresentado um exemplo de imagem gerada por esse script.
A escolha correta da função de ativação depende do tipo de rede neural e do problema que está sendo resolvido. Além disso, é possível que uma única rede utilize diversas funções de ativação diferentes. Por exemplo, SoftMax se diferencia das demais funções ao tratar os valores de saída de uma camada não de forma individual, mas em conjunto, normalizando-os de tal maneira que podem ser interpretados como probabilidades (a soma delas é igual a 1), o que é utilizado para classificação múltipla.
Este tópico é tão extenso que exigiu um artigo separado ou uma série de artigos. Aqui nos limitaremos apenas a alertar que todas as funções têm lados positivos e negativos, o que pode levar à inoperabilidade da rede. Em particular, as funções em forma de S são caracterizadas pelo chamado problema de “gradiente de fuga”, quando os sinais começam a cair nas seções de “saturação” da curva S e, portanto, o ajuste dos pesos tende a zero) e para os monotonicamente crescentes, o problema do crescimento explosivo do gradiente ('gradiente explosivo', ou seja, pesos constantemente crescentes, até estouro numérico e obtenção de NaN (não é um número)). Ambos os problemas se tornam mais prováveis quanto maior o número de camadas na rede. Para resolvê-los, você pode usar várias técnicas, como normalização de dados (incluindo não apenas na entrada, mas também em camadas intermediárias), algoritmos de afinamento de rede (descartando neurônios (“dropout”), ignorando conexões), treinamento com lotes de dados, ruído e outras opções de regularização - algumas das quais serão analisadas e implementadas a seguir.
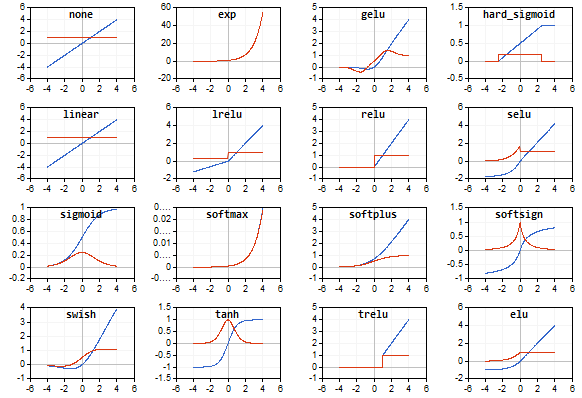
Script de demonstração com todas as funções de ativação
Implementação da rede neural na classe MatrixNet
Vamos prosseguir com a escrita da classe da rede neural, baseada nas matrizes MQL5. Dado que a rede é composta por camadas, vamos definir arrays para os coeficientes de peso e os valores de saída dos neurônios de cada camada. O número de camadas será armazenado na variável n, enquanto os pesos dos neurônios nas camadas e os sinais na saída de cada camada serão representados pelas matrizes weights e outputs, respectivamente. É importante frisar que o termo outputs refere-se aos sinais nas saídas dos neurônios de qualquer camada, e não apenas na saída da rede. Portanto, outputs[i] também descreve as camadas intermediárias, e até mesmo a camada 0, onde os dados de entrada são fornecidos.
A indexação dos arrays weights e outputs é ilustrada no seguinte esquema (as conexões de cada neurônio com a origem do deslocamento +1 não são mostradas para simplificar):
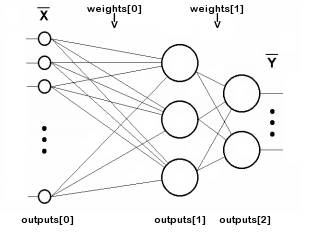
Esquema de indexação de matrizes em uma rede de duas camadas
O valor n não inclui a camada de entrada, uma vez que esta não necessita de pesos.
class MatrixNet { protected: const int n; matrix weights[/* n */]; matrix outputs[/* n + 1 */]; ENUM_ACTIVATION_FUNCTION af; ENUM_ACTIVATION_FUNCTION of; double speed; bool ready; ...
A nossa rede irá suportar dois tipos de funções de ativação (à escolha do usuário): uma para todas as camadas, exceto a de saída (armazenada em af), e uma específica para a camada de saída (na variável of). A variável speed armazena a taxa de aprendizado (coeficiente η da fórmula (20)).
A variável ready indica se a inicialização do objeto de rede foi bem-sucedida.
O construtor da rede aceita um array de inteiros, layers, que define a quantidade e o tamanho de todas as camadas. O elemento 0 estabelece o tamanho da camada de entrada pseudo, isto é, o número de recursos em cada vetor de dados de entrada. O último elemento define o tamanho da camada de saída, todos os demais definem o tamanho das camadas ocultas intermediárias. O número de camadas não pode ser inferior a dois. Para alocar memória para os arrays de matrizes, foi desenvolvido um método auxiliar chamado allocate (o qual será expandido à medida que a classe for sendo desenvolvida).
public: MatrixNet(const int &layers[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): ready(false), af(f1), of(f2), n(ArraySize(layers) - 1) { if(n < 2) return; allocate(); for(int i = 1; i <= n; ++i) { // NB: the weights matrix is transposed, i.e. indexes [row][column] specify [synapse][neuron] weights[i - 1].Init(layers[i - 1] + 1, layers[i]); } ... } protected: void allocate() { ArrayResize(weights, n); ArrayResize(outputs, n + 1); ... }
Para inicializar cada matriz de pesos, o tamanho da camada anterior layers[i - 1] é usado como o número de linhas, e adiciona-se um sinapse para a origem constante ajustável do deslocamento +1. O número de colunas é o tamanho da camada atual layers[i]. Em cada matriz de pesos, o primeiro índice se refere à camada à esquerda da matriz e o segundo, à camada à direita.
Esta numeração assegura uma escrita simplificada para a multiplicação dos vetores de sinais nas matrizes de camadas durante a propagação direta (funcionamento normal da rede). Durante a retropropagação do erro (no modo de treinamento), será necessário multiplicar o vetor de erros de cada camada superior por sua matriz de pesos transposta, a fim de recalcular os erros para a camada inferior.
Em outras palavras, como as informações dentro da rede se movem em duas direções opostas - sinais operacionais das entradas para as saídas, e erros das saídas para as entradas - as matrizes de peso em uma dessas duas direções precisam ser utilizadas em sua forma padrão, enquanto na outra devem ser transpostas. Nós adotamos como configuração padrão um layout de matriz que facilita o cálculo do sinal direto.
Preencheremos as matrizes outputs diretamente durante o processo de transmissão do sinal através da rede. Entretanto, os pesos devem ser inicializados aleatoriamente, para isso, o método randomize é chamado ao final do construtor.
public: MatrixNet(const int &layers[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): ready(false), af(f1), of(f2), n(ArraySize(layers) - 1) { ... ready = true; randomize(); } // NB: set values with appropriate distribution for specific activation functions void randomize(const double from = -0.5, const double to = +0.5) { if(!ready) return; for(int i = 0; i < n; ++i) { weights[i].Random(from, to); } }
Possuir as matrizes de peso é suficiente para implementar o fluxo direto de sinais da entrada da rede para a saída. O fato dos pesos ainda não terem sido treinados não é fundamental, cuidaremos da instrução posteriormente.
bool feedForward(const matrix &data) { if(!ready) return false; if(data.Cols() != weights[0].Rows() - 1) { PrintFormat("Column number in data %d <> Inputs layer size %d", data.Cols(), weights[0].Rows() - 1); return false; } outputs[0] = data; // input the data to the network for(int i = 0; i < n; ++i) { // expand each layer (except the last one) with one neuron for the bias signal // (there is no weight matrix to the right of the last layer, since the signal does not go further) if(!outputs[i].Resize(outputs[i].Rows(), weights[i].Rows()) || !outputs[i].Col(vector::Ones(outputs[i].Rows()), weights[i].Rows() - 1)) return false; // forward the signal from i-th layer to the (i+1)-th layer: weighted sum matrix temp = outputs[i].MatMul(weights[i]); // apply the activation function, the result is received into outputs[i + 1] if(!temp.Activation(outputs[i + 1], i < n - 1 ? af : of)) return false; } return true; }
O número de colunas na matriz de dados de entrada deve corresponder ao número de linhas na matriz de peso 0, diminuído de 1 (peso para o sinal de desvio).
O método getResults possibilita a leitura do resultado do funcionamento normal da rede. Por padrão, ele retorna a matriz de estados da camada de saída.
matrix getResults(const int layer = -1) const { static const matrix empty = {}; if(!ready) return empty; if(layer == -1) return outputs[n]; if(layer < -1 || layer > n) return empty; return outputs[layer]; }
É possível avaliar a qualidade atual do modelo através do método test: ele recebe não apenas a matriz de dados de entrada, mas também a matriz com a resposta desejada da rede.
double test(const matrix &data, const matrix &target, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { if(!ready || !feedForward(data)) return NaN(); return outputs[n].Loss(target, lf); }
Após a execução da propagação do sinal usando feedForward, calculamos aqui a medida de 'perda' do tipo determinado. Por padrão, é o erro quadrático médio (LOSS_MSE), que é aplicável para tarefas de regressão e previsão. Contudo, caso a rede seja utilizada para classificação de imagens, outro tipo de avaliação deverá ser selecionado, como por exemplo, a entropia cruzada LOSS_CCE.
No caso de erro de cálculo, o método retorna 'não um número' (NaN).
Agora, vamos abordar a retropropagação do erro. O método backProp também se inicia com a verificação da correspondência entre os tamanhos dos dados alvo e da camada de saída. Posteriormente, para a camada de saída, a derivada da função de ativação (se houver) e as 'perdas' da rede na saída, relativas aos dados alvo, são calculadas.
bool backProp(const matrix &target) { if(!ready) return false; if(target.Rows() != outputs[n].Rows() || target.Cols() != outputs[n].Cols()) return false; // output layer matrix temp; if(!outputs[n].Derivative(temp, of)) return false; matrix loss = (outputs[n] - target) * temp; // all data line by line
A matriz loss contém os valores δ da fórmula (19).
A seguir, para todas as camadas, com exceção da camada de saída, é executado um ciclo:
for(int i = n - 1; i >= 0; --i) // all layers except the output in reverse order { // remove pseudo-losses in the last element which we added as an offset source // since it is not a neuron and further error propagation is not applicable to it // (we do it in all layers except the last one where the shift element was not added) if(i < n - 1) loss.Resize(loss.Rows(), loss.Cols() - 1); matrix delta = speed * outputs[i].Transpose().MatMul(loss);
Aqui, a fórmula (20) é aplicada 'de forma espelhada': obtemos incrementos de peso com base na taxa de aprendizado η, no δ da camada atual e nas respectivas saídas da camada anterior (inferior).
Em seguida, para cada camada, computamos a fórmula (18), obtendo recursivamente os demais δ: a derivada da função de ativação (FA) é novamente utilizada, assim como a multiplicação do δ mais antigo pela matriz de peso transposta. Importante frisar que o índice i no vetor outputs[] corresponde à camada com pesos na matriz weights[i-1], já que a pseudo-camada de entrada (outputs[0]) não possui pesos. Ou seja, durante a transmissão direta do sinal, a matriz weights[0], quando aplicada a outputs[0], gera outputs[1]; weights[1] gera outputs[2], e assim por diante. Durante a retropropagação do erro, os índices se alinham: por exemplo, outputs[2] (após a diferenciação) é multiplicado pela transposta de weights[2].
if(!outputs[i].Derivative(temp, af)) return false; loss = loss.MatMul(weights[i].Transpose()) * temp;
Só após calcularmos a perda δ para a camada inferior é que podemos ajustar os pesos da matriz weights[i], isto é, corrigi-los com base no delta calculado anteriormente.
weights[i] -= delta;
}
return true;
}
Quase tudo está pronto para implementar o algoritmo de treinamento completo, com iterações por épocas e chamadas aos métodos feedForward e backProp. Contudo, é necessário retornar à teoria, pois alguns aspectos cruciais foram temporariamente deixados de lado.
Treinamento e regularização
O treinamento da RN é realizado com os dados de treino disponíveis no momento. Com base nesses dados, define-se a configuração da rede (número de camadas, quantidade de neurônios por camada, etc.), a taxa de aprendizado e outras características. Em teoria, é sempre possível construir uma rede potente o suficiente para gerar erros extremamente baixos nos dados de treinamento. Contudo, a principal força da RN, e o propósito de sua utilização, reside em sua performance eficaz em dados futuros desconhecidos (que apresentem as mesmas dependências ocultas do conjunto de treino).
O fenômeno que ocorre quando a RN treinada se ajusta excessivamente aos dados de treino, mas falha no 'teste para frente', é chamado de overfitting, e deve ser combatido a todo custo. Para isso, recorre-se à chamada regularização – a adição ao modelo ou ao método de treinamento de algumas condições extras que avaliem a capacidade de generalização da rede. Existem várias formas de regularização, incluindo:
- Análise do desempenho da rede em treinamento em um conjunto de validação adicional de dados (diferente do conjunto de treinamento);
- Exclusão aleatória de parte dos neurônios ou conexões durante o treinamento;
- Poda (pruning) da rede após o treinamento;
- Introdução de ruído nos dados de entrada;
- Reprodução artificial dos dados;
- Diminuição constante e fraca da amplitude dos pesos durante o treinamento;
- Seleção experimental do volume e configuração da rede na linha tênue, quando a rede ainda é capaz de aprender, mas já não é mais retreinada com base nos dados disponíveis;
Implementaremos algumas destas abordagens na nossa classe.
Inicialmente, vamos configurar o método de treinamento para receber não apenas os dados de entrada e saída para treinamento (parâmetros 'data' e 'target', respectivamente), mas também um conjunto de validação (que consiste igualmente em entradas e seus correspondentes vetores de saída: 'validation' e 'check').
Durante o treinamento, o erro da rede em relação aos dados de treinamento tende a diminuir de maneira bastante consistente (o termo 'geralmente' é utilizado, pois se a taxa de aprendizado ou a capacidade da rede não forem ajustadas adequadamente, o processo pode se tornar instável). Contudo, se calcularmos paralelamente o erro da rede em relação ao conjunto de validação, este, inicialmente, também diminuirá (enquanto a rede detecta as tendências mais significativas nos dados), mas em seguida começará a aumentar conforme a rede se ajusta às peculiaridades específicas da amostra de treinamento, não do conjunto de validação. Desse modo, o processo de treinamento deve ser interrompido quando o erro de validação começar a crescer. Esta abordagem é conhecida como 'parada precoce'.
Além dos dois conjuntos de dados, o método 'train' permite determinar o número máximo de épocas de treinamento ('epochs'), a precisão desejada ('accuracy', isto é, o erro médio mínimo que consideramos suficiente, quando o treinamento também é concluído com sucesso) e a maneira de calcular o erro ('lf').
A taxa de aprendizado ('speed') é configurada para ser igual à precisão ('accuracy'), porém, para permitir maior flexibilidade nas configurações, elas podem ser ajustadas separadamente, se necessário. Isso ocorre porque pretendemos implementar um ajuste automático da taxa de aprendizado, tornando o valor inicial aproximado menos relevante.
double train(const matrix &data, const matrix &target, const matrix &validation, const matrix &check, const int epochs = 1000, const double accuracy = 0.001, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { if(!ready) return NaN(); speed = accuracy; ...
Os valores de erro da rede na época atual serão armazenados nas variáveis 'mse' e 'msev' — para os conjuntos de treinamento e validação, respectivamente. Entretanto, para não reagirmos a flutuações aleatórias inevitáveis, precisaremos calcular a média dos erros em um determinado período 'p', calculado a partir do número total de épocas especificado. Os valores de erros suavizados serão armazenados nas variáveis 'msema' e 'msevma', e seus valores anteriores nas variáveis 'msemap' e 'msevmap'.
double mse = DBL_MAX; double msev = DBL_MAX; double msema = 0; // MSE averaging of the training set double msemap = 0; // MSE averaging of the training set in the previous epoch double msevma = 0; // MSE averaging of the validation dataset double msevmap = 0; // MSE averaging of the validation dataset in the previous epoch double ema = 0; // exponential smoothing factor int p = 0; // EMA period p = (int)sqrt(epochs); // empirically choose the period of the EMA averaging of errors ema = 2.0 / (p + 1); PrintFormat("EMA for early stopping: %d (%f)", p, ema);
Posteriormente, iniciamos o loop através das épocas de treinamento. Permitimos que os dados de validação não sejam fornecidos, uma vez que iremos implementar outra forma de regularização, o 'dropout'. Se o conjunto de validação não estiver vazio, calculamos o 'msev' chamando o método 'test' nele. De qualquer forma, calculamos o 'mse' chamando 'test' na amostra de treinamento. Lembrando que 'test' realiza a chamada do método 'feedForward' e calcula o erro entre o resultado da rede e os valores alvo.
int ep = 0; for(; ep < epochs; ep++) { if(validation.Rows() && check.Rows()) { // if there is validation, run it before normal pass/training msev = test(validation, check, lf); // smooth errors msevma = (msevma ? msevma : msev) * (1 - ema) + ema * msev; } mse = test(data, target, lf); // enable feedForward(data) run msema = (msema ? msema : mse) * (1 - ema) + ema * mse; ...
Em primeiro lugar, certificamo-nos de que o valor do erro é um número válido. Se não for, houve um estouro na rede ou dados inválidos foram introduzidos.
if(!MathIsValidNumber(mse)) { PrintFormat("NaN at epoch %d", ep); break; // will return NaN as error indication }
Se o novo erro for maior do que o anterior, com uma 'margem de segurança' determinada pela relação entre os tamanhos dos conjuntos de treinamento e de validação, o ciclo é interrompido.
const int scale = (int)(data.Rows() / (validation.Rows() + 1)) + 1; if(msevmap != 0 && ep > p && msevma > msevmap + scale * (msemap - msema)) { // skip the first p epochs to accumulate values for averaging PrintFormat("Stop by validation at %d, v: %f > %f, t: %f vs %f", ep, msevma, msevmap, msema, msemap); break; } msevmap = msevma; msemap = msema; ...
Se, contudo, o erro continuar a diminuir, ou pelo menos, não aumentar, registramos os novos valores de erro para comparação na próxima época.
Se o erro atingir a precisão desejada, consideramos o treinamento bem-sucedido e também interrompemos o ciclo.
if(mse <= accuracy) { PrintFormat("Done by accuracy limit %f at epoch %d", accuracy, ep); break; }
Além disso, o ciclo invoca o método virtual progress, que pode ser redefinido nas subclasses da rede, permitindo a interrupção do treinamento em resposta a determinadas ações do usuário. A implementação padrão de progress será demonstrada mais adiante.
if(!progress(ep, epochs, mse, msev, msema, msevma)) { PrintFormat("Interrupted by user at epoch %d", ep); break; }
Finalmente, se o ciclo não foi interrompido por nenhum dos critérios acima, executamos o retropropagação do erro na rede utilizando o método backProp.
if(!backProp(target)) { mse = NaN(); // error flag break; } } if(ep == epochs) { PrintFormat("Done by epoch limit %d with accuracy %f", ep, mse); } return mse; }
O método progress, por padrão, exibe métricas de treinamento no log uma vez por segundo.
virtual bool progress(const int epoch, const int total, const double error, const double valid = DBL_MAX, const double ma = DBL_MAX, const double mav = DBL_MAX) { static uint trap; if(GetTickCount() > trap) { PrintFormat("Epoch %d of %d, loss %.5f%s%s%s", epoch, total, error, ma == DBL_MAX ? "" : StringFormat(" ma(%.5f)", ma), valid == DBL_MAX ? "" : StringFormat(", validation %.5f", valid), valid == DBL_MAX ? "" : StringFormat(" v.ma(%.5f)", mav)); trap = GetTickCount() + 1000; } return !IsStopped(); }
O valor retornado true indica a continuação do treinamento, enquanto false conduz à interrupção do ciclo.
Além da 'parada precoce', a classe MatrixNet tem a capacidade de desativar aleatoriamente uma parte das suas conexões, num estilo semelhante ao 'dropout'.
O método canônico de 'dropout' implica a exclusão temporária de neurônios selecionados aleatoriamente da rede. No entanto, não podemos realizar isso sem incorrer em custos computacionais elevados, já que nosso algoritmo faz uso de operações matriciais. Para excluir neurônios de uma camada, precisaríamos reformatar as matrizes de peso e copiar partes delas a cada iteração. É muito mais simples e eficiente configurar pesos aleatórios para zero, ou seja, cortar as conexões. Naturalmente, no início de cada época, o programa deve restaurar os pesos que foram temporariamente desconectados ao seu estado anterior e, em seguida, escolher novos pesos para desconectar na próxima época.
O número de conexões temporariamente zeradas é definido pelo método enableDropOut, como uma porcentagem do total de pesos da rede. Por padrão, a variável dropOutRate é igual a 0, e o modo está desativado.
void enableDropOut(const uint percent = 10) { dropOutRate = (int)percent; }
O funcionamento do 'dropout' consiste em preservar o estado atual das matrizes de peso em um armazenamento adicional (implementado pela classe DropOutState) e anular ligações da rede escolhidas aleatoriamente. Após um ciclo de treinamento da rede nesta forma modificada, os elementos zerados nas matrizes são restaurados a partir do armazenamento e o processo é repetido: outros pesos aleatórios são selecionados e zerados, a rede é treinada com eles e assim por diante. A operação e aplicação da classe DropOutState são deixadas para o leitor compreender.
Taxa de aprendizado adaptável
Até o momento, consideramos o uso de uma taxa de aprendizado constante (a variável speed), o que não é muito prático (o aprendizado pode ser muito lento com uma taxa baixa ou instável com uma alta).
Uma das variações de adaptação da taxa de aprendizado pode ser encontrada em uma modificação especial do algoritmo de retropropagação, chamada 'rprop' (do inglês, resilient propagation ou propagação resiliente). A ideia é verificar se o sinal dos incrementos delta para cada peso é consistente entre a iteração anterior e a atual. A consistência do sinal indica que a direção do gradiente permaneceu a mesma, e nesse caso, a velocidade pode ser aumentada, mas de forma seletiva para o peso específico. Para os pesos onde o sinal do gradiente mudou, faz sentido, ao contrário, reduzir a velocidade.
Como em nossas matrizes todos os dados são calculados simultaneamente a cada época, o valor e o sinal do gradiente para cada peso são acumulados (e 'média') sobre todo o conjunto de dados. Portanto, a tecnologia é mais precisamente chamada de 'batch rprop'.
Todas as linhas de código na classe MatrixNet que implementam esta melhoria são envolvidas pelas macros BATCH_PROP. Antes de incluir o arquivo de cabeçalho MatrixNet.mqh em seu código-fonte, é recomendado habilitar a velocidade adaptativa com a diretiva:
#define BATCH_PROP
Inicialmente, note que ao invés da variável speed neste modo, é utilizado um array de matrizes speed, e também será necessário armazenar os incrementos de peso da última época no array de matrizes deltas.
class MatrixNet { protected: ... #ifdef BATCH_PROP matrix speed[]; matrix deltas[]; #else double speed; #endif
Além disso, os coeficientes de aceleração e desaceleração, bem como as velocidades máxima e mínima, são estabelecidos por quatro variáveis distintas para este propósito.
double plus; double minus; double max; double min;
A alocação de memória para novos arrays e a definição de valores padrão para as novas variáveis ocorrem no método allocate, com o qual já estamos familiarizados.
void allocate() { ArrayResize(weights, n); ArrayResize(outputs, n + 1); ArrayResize(bestWeights, n); dropOutRate = 0; #ifdef BATCH_PROP ArrayResize(speed, n); ArrayResize(deltas, n); plus = 1.1; minus = 0.1; max = 50; min = 0.0; #endif }
Para estabelecer outros valores para essas variáveis antes do início do treinamento, utilize o método setupSpeedAdjustment.
No construtor da MatrixNet, os arrays de matrizes speed e deltas são inicializados através da cópia do array da matriz weights. Isso é mais prático para obter matrizes de tamanhos semelhantes conforme as camadas da rede. O preenchimento de speed e deltas com dados significativos é realizado nas etapas subsequentes. Por exemplo, no começo do método train, em vez de simplesmente atribuir a precisão (accuracy) à variável escalar speed, esse valor é preenchido em todas as matrizes do array speed.
double train(const matrix &data, const matrix &target, const matrix &validation, const matrix &check, const int epochs = 1000, const double accuracy = 0.001, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { ... #ifdef BATCH_PROP for(int i = 0; i < n; ++i) { speed[i].Fill(accuracy); // adjust speeds on the fly deltas[i].Fill(0); } #else speed = accuracy; #endif ... }
Dentro do método backProp, a expressão que calcula os incrementos agora se refere à matriz da camada correspondente, e não a um escalar. Logo após a obtenção dos incrementos delta, o método adjustSpeed é invocado (detalhado adiante), para o qual é passado o produto delta * deltas[i], com o objetivo de comparar a direção anterior e a nova. Por fim, os novos incrementos de peso são armazenados em deltas[i] para serem analisados na próxima época.
bool backProp(const matrix &target) { ... for(int i = n - 1; i >= 0; --i) // all layers except the output in reverse order { ... #ifdef BATCH_PROP matrix delta = speed[i] * outputs[i].Transpose().MatMul(loss); adjustSpeed(speed[i], delta * deltas[i]); deltas[i] = delta; #else matrix delta = speed * outputs[i].Transpose().MatMul(loss); #endif ... } ... }
O método adjustSpeed é bastante simples. Um sinal positivo no elemento do produto matricial indica a manutenção do gradiente, e a velocidade aumenta plus vezes, mas não excedendo o valor max. Um sinal negativo indica uma mudança de gradiente, e a velocidade diminui minus vezes, mas não inferior ao valor min.
void adjustSpeed(matrix &subject, const matrix &product) { for(int i = 0; i < (int)product.Rows(); ++i) { for(int j = 0; j < (int)product.Cols(); ++j) { if(product[i][j] > 0) { subject[i][j] *= plus; if(subject[i][j] > max) subject[i][j] = max; } else if(product[i][j] < 0) { subject[i][j] *= minus; if(subject[i][j] < min) subject[i][j] = min; } } } }
Salvando e restaurando o melhor estado da rede treinada
Dessa forma, o treinamento da rede é realizado em um ciclo de iterações, chamadas épocas: em cada época, todos os vetores do conjunto de treinamento são processados pela rede, organizados em uma matriz onde as linhas são os registros e as colunas seus atributos. Por exemplo, cada registro pode armazenar uma barra de cotações, e as colunas representam os preços OHLC e volumes.
O processo de ajuste dos pesos, apesar de ser realizado com base no gradiente, possui uma natureza aleatória, no sentido de que, devido à irregularidade da função objetivo do problema e à velocidade variável, podemos ocasionalmente chegar a configurações 'piores' antes de 'descobrir' um novo mínimo de erro da rede. Em princípio, não temos garantia de que com o aumento do número de épocas, a qualidade do modelo treinado irá necessariamente melhorar e o erro da rede diminuirá.
Em vista disso, faz sentido monitorar constantemente o erro total da rede e, caso o erro após a época atual seja menor que o mínimo registrado, os pesos encontrados devem ser armazenados. Para isso, foi criado um novo array de matrizes de pesos, bem como uma estrutura chamada Stats para armazenar indicadores de aprendizado.
class MatrixNet { ... public: struct Stats { double bestLoss; // smallest error for all epochs int bestEpoch; // index of the epoch with the minimum error int epochsDone; // total number of completed epochs }; Stats getStats() const { return stats; } protected: matrix bestWeights[]; Stats stats; ...
Dentro do método train, antes de iniciar o ciclo de épocas, inicializamos a estrutura Stats para estatísticas.
double train(const matrix &data, const matrix &target, const matrix &validation, const matrix &check, const int epochs = 1000, const double accuracy = 0.001, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { ... stats.bestLoss = DBL_MAX; stats.bestEpoch = -1; DropOutState state(dropOutRate);
Dentro do próprio ciclo, ao identificar um valor de erro menor que o mínimo conhecido, salvamos todas as matrizes de pesos em bestWeights.
int ep = 0; for(; ep < epochs; ep++) { ... const double candidate = (msev != DBL_MAX) ? msev : mse; if(candidate < stats.bestLoss) { stats.bestLoss = candidate; stats.bestEpoch = ep; // save best weights from 'weights' for(int i = 0; i < n; ++i) { bestWeights[i].Assign(weights[i]); } } } ...
Após o treinamento, é fácil acessar tanto os pesos finais da rede quanto os melhores pesos.
bool getWeights(matrix &array[]) const { if(!ready) return false; ArrayResize(array, n); for(int i = 0; i < n; ++i) { array[i] = weights[i]; } return true; } bool getBestWeights(matrix &array[]) const { if(!ready) return false; if(!n || !bestWeights[0].Rows()) return false; ArrayResize(array, n); for(int i = 0; i < n; ++i) { array[i] = bestWeights[i]; } return true; }
Esses arrays de matrizes podem ser salvos em um arquivo para recuperar uma rede já treinada e pronta para uso posteriormente. Para isso, há um construtor específico.
MatrixNet(const matrix &w[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): ready(false), af(f1), of(f2), n(ArraySize(w)) { if(n < 2) return; allocate(); for(int i = 0; i < n; ++i) { weights[i] = w[i]; #ifdef BATCH_PROP speed[i] = weights[i]; // instead .Init(.Rows(), .Cols()) deltas[i] = weights[i]; // instead .Init(.Rows(), .Cols()) #endif } ready = true; }
Posteriormente, mostraremos como salvar e carregar redes prontas em um dos exemplos práticos.
Visualização do progresso do treinamento da rede
A presença do método progress, que exibe periodicamente mensagens no log, não é muito visual. Por isso, no arquivo MatrixNet.mqh, também foi implementada a classe derivada de MatrixNet chamada MatrixNetVisual, que exibe um gráfico em uma janela com as variações dos erros de treinamento ao longo das épocas.
A exibição gráfica é realizada pela classe padrão CGraphic (fornecida com o MetaTrader 5) e, mais precisamente, por uma pequena classe derivada chamada CMyGraphic.
O objeto dessa classe faz parte da MatrixNetVisual. Além disso, dentro da 'rede visualizada', há um array de 5 curvas e arrays do tipo double, que são usados para representar as linhas exibidas.
class MatrixNetVisual: public MatrixNet { CMyGraphic graphic; CCurve *c[5]; double p[], x[], y[], z[], q[], b[]; ...
Aqui estão as informações correspondentes:
No método graph, chamado a partir dos construtores da MatrixNetVisual, é criado um objeto gráfico com o tamanho da janela inteira e são adicionadas as 5 curvas mencionadas acima (CCurve).
void graph() { ulong width = ChartGetInteger(0, CHART_WIDTH_IN_PIXELS); ulong height = ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS); bool res = false; const string objname = "BPNNERROR"; if(ObjectFind(0, objname) >= 0) res = graphic.Attach(0, objname); else res = graphic.Create(0, objname, 0, 0, 0, (int)(width - 0), (int)(height - 0)); if(!res) return; c[0] = graphic.CurveAdd(p, x, CURVE_LINES, "Training"); c[1] = graphic.CurveAdd(p, y, CURVE_LINES, "Validation"); c[2] = graphic.CurveAdd(p, z, CURVE_LINES, "Val.EMA"); c[3] = graphic.CurveAdd(p, q, CURVE_LINES, "Train.EMA"); c[4] = graphic.CurveAdd(p, b, CURVE_POINTS, "Best/Minimum"); ... } public: MatrixNetVisual(const int &layers[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): MatrixNet(layers, f1, f2) { graph(); }
No método redefinido 'progress', os argumentos são adicionados aos respectivos vetores double e, posteriormente, o método 'plot' é invocado para atualizar a imagem.
virtual bool progress(const int epoch, const int total, const double error, const double valid = DBL_MAX, const double ma = DBL_MAX, const double mav = DBL_MAX) override { // fill all the arrays PUSH(p, epoch); PUSH(x, error); if(valid != DBL_MAX) PUSH(y, valid); else PUSH(y, nan); if(ma != DBL_MAX) PUSH(q, ma); else PUSH(q, nan); if(mav != DBL_MAX) PUSH(z, mav); else PUSH(z, nan); plot(); return MatrixNet::progress(epoch, total, error, valid, ma, mav); }
O método 'plot' se encarrega do preenchimento e da apresentação das curvas.
void plot() { c[0].Update(p, x); c[1].Update(p, y); c[2].Update(p, z); c[3].Update(p, q); double point[1] = {stats.bestEpoch}; b[0] = stats.bestLoss; c[4].Update(point, b); ... graphic.CurvePlotAll(); graphic.Update(); }
Sugere-se que os aspectos técnicos da visualização sejam explorados individualmente. Em breve, veremos como isso se apresenta na tela.
Script de teste
As classes pertencentes à família MatrixNet estão prontas para a primeira verificação. Isso será feito pelo script MatrixNet.mq5, no qual os dados iniciais são artificialmente gerados com base em um registro analítico conhecido. A fórmula provém da seção de ajuda sobre aprendizado de máquina, onde um exemplo próprio de treinamento pelo algoritmo de backpropagation é fornecido - não tão versátil quanto nossas classes, e, portanto, exige uma quantidade significativa de codificação (compare a quantidade de linhas usando a classe e sem ela).
f = ((x + y + z)^2 / (x^2 + y^2 + z^2)) / 3
A única diferença menor em nossa fórmula é a divisão do valor por 3, o que proporciona um intervalo de função entre 0 e 1.
A forma da função pode ser avaliada pela figura a seguir, onde as superfícies (x<->y) são exibidas para três diferentes valores de z: 0.05, 0.5 e 5.0. 0,05, 0,5 e 5,0.
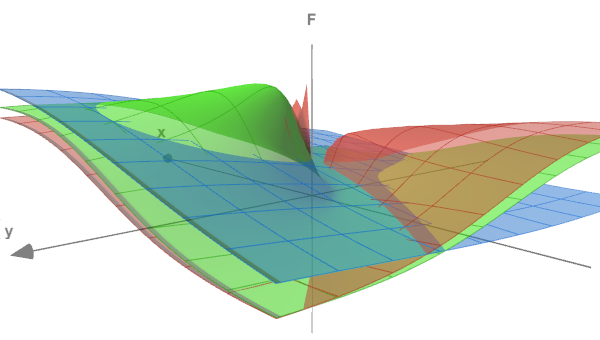
Função de teste em 3 seções
Definiremos nas variáveis de entrada do script o número de épocas de treinamento, a precisão (erro terminal) e a intensidade do ruído que, se desejado, podemos adicionar aos dados gerados (isto trará o experimento mais próximo de tarefas reais e demonstrará como a presença de ruído dificulta a detecção de dependências). Por padrão, o parâmetro RandomNoise é igual a 0, e o ruído está ausente.
input int Epochs = 1000; input double Accuracy = 0.001; input double RandomNoise = 0.0;
A função 'CreateData' se encarrega da geração de dados experimentais. Seus parâmetros matriciais 'data' e 'target' serão preenchidos com pontos da função descrita acima, em uma quantidade equivalente a 'count'. Um vetor de entrada (linha da matriz de dados) possui 3 colunas (para x, y, z). O vetor de saída (linha da matriz 'target') é o único valor f. Os pontos (x, y, z) são gerados aleatoriamente em um intervalo de -10 a +10.
bool CreateData(matrix &data, matrix &target, const int count) { if(!data.Init(count, 3) || !target.Init(count, 1)) return false; data.Random(-10, 10); vector X1 = MathPow(data.Col(0) + data.Col(1) + data.Col(2), 2); vector X2 = MathPow(data.Col(0), 2) + MathPow(data.Col(1), 2) + MathPow(data.Col(2), 2); if(!target.Col(X1 / X2 / 3.0, 0)) return false; if(RandomNoise > 0) { matrix noise; noise.Init(count, 3); noise.Random(0, RandomNoise); data += noise - RandomNoise / 2; noise.Resize(count, 1); noise.Random(-RandomNoise / 2, RandomNoise / 2); target += noise; } return true; }
A intensidade do ruído em RandomNoise é definida como a amplitude do desvio adicional das coordenadas corretas e do valor da função obtido para elas. Levando em conta que a função tem um valor máximo de 1.0, tal nível de ruído tornará a função praticamente indistinguível.
Para usar a rede neural, precisamos incluir o arquivo de cabeçalho MatrixNet.mqh. Antes dessa diretiva de pré-processador, definimos a macro BATCH_PROP para acionar o treinamento acelerado com taxa de aprendizado variável.
#define BATCH_PROP #include <MatrixNet.mqh>
Na função principal do script, estabelecemos a configuração da rede (quantidade de camadas e seus tamanhos) utilizando o array 'layers', que é passado para o construtor MatrixNetVisual. Os conjuntos de dados para treinamento e validação são gerados pela chamada dupla da função CreateData.
void OnStart() { const int layers[] = {3, 11, 7, 1}; MatrixNetVisual net(layers); matrix data, target; CreateData(data, target, 100); matrix valid, test; CreateData(valid, test, 25); ...
Na prática, os dados de entrada devem ser normalizados, depurados de outliers e verificados quanto à independência dos fatores antes de serem enviados à rede. No entanto, neste caso, somos nós que geramos os dados.
O treinamento é realizado através do método 'train', aplicado às matrizes 'data' e 'target'. Uma parada antecipada ocorrerá à medida que o desempenho no conjunto de validação/teste se deteriorar. Entretanto, em dados sem ruído, provavelmente alcançaremos a precisão necessária ou o número máximo de ciclos, dependendo do que ocorrer primeiro.
Print("Training result: ", net.train(data, target, valid, test, Epochs, Accuracy)); matrix w[]; if(net.getBestWeights(w)) { MatrixNet net2(w); if(net2.isReady()) { Print("Best copy on training data: ", net2.test(data, target)); Print("Best copy on validation data: ", net2.test(valid, test)); } }
Depois do treinamento, solicitamos as matrizes dos melhores pesos encontrados e, para verificar, construímos outra instância da rede com base nesses pesos - o objeto net2. Depois disso, executamos a rede em ambos os conjuntos de dados e registramos os erros no log.
Como o script utiliza uma rede com visualização do progresso do treinamento, iniciamos um loop de espera para o comando do usuário finalizar o script, permitindo que o usuário examine o gráfico.
while(!IsStopped()) { Sleep(1000); } }
Ao executar o script com os parâmetros padrão, podemos obter uma representação aproximada do seguinte (cada execução será diferente devido à geração aleatória dos dados e à inicialização da rede).
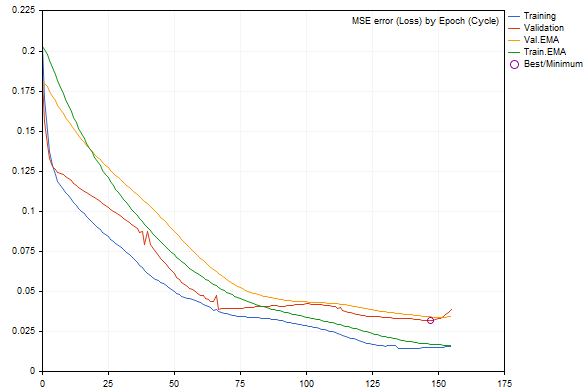
Dinâmica de mudança de erro de rede durante o treinamento
Os erros nos conjuntos de treinamento e validação são representados por linhas azuis e vermelhas, respectivamente. Suas versões suavizadas são representadas pelas linhas verde e amarela. Fica evidente que, à medida que o treinamento avança, todos os tipos de erros diminuem. No entanto, após um certo ponto, o erro de validação supera o erro do conjunto de treinamento e, mais próximo à margem direita do gráfico, seu aumento se torna perceptível, resultando em uma 'parada precoce'. A melhor configuração da rede é marcada por um círculo.
No log, veremos entradas semelhantes:
EMA for early stopping: 31 (0.062500)
Epoch 0 of 1000, loss 0.20296 ma(0.20296), validation 0.18167 v.ma(0.18167)
Epoch 120 of 1000, loss 0.02319 ma(0.02458), validation 0.04566 v.ma(0.04478)
Stop by validation at 155, v: 0.034642 > 0.034371, t: 0.016614 vs 0.016674
Training result: 0.015707719706513287
Best copy on training data: 0.015461956812387292
Best copy on validation data: 0.03211748853774414
Se começarmos a inserir ruído nos dados com o parâmetro RandomNoise, as taxas de aprendizado serão significativamente reduzidas, e se o ruído for excessivo, o erro da rede treinada aumentará ou ela deixará de aprender.
Veja, por exemplo, como fica o gráfico quando adicionamos um ruído de 3.0.
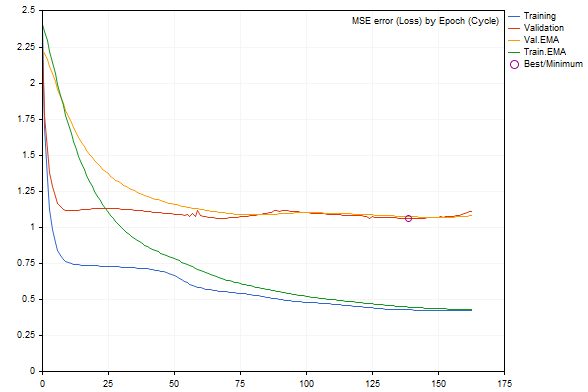
Dinâmica de erro de rede durante o treinamento com ruído adicionado
A taxa de erro, de acordo com o log, é bastante pior.
Epoch 0 of 1000, loss 2.40352 ma(2.40352), validation 2.23536 v.ma(2.23536) Stop by validation at 163, v: 1.082419 > 1.080340, t: 0.432023 vs 0.432526 Training result: 0.4244786772678285 Best copy on training data: 0.4300476339855798 Best copy on validation data: 1.062895214094978
Depois de garantir que as ferramentas da rede neural estão funcionando, vamos para exemplos mais práticos: o indicador e o EA.
Indicador preditivo
Vamos tomar como exemplo de um indicador preditivo baseado em RN o BPNNMatrixPredictorDemo.mq5. Este é uma modificação de um indicador pronto disponível no CodeBase, onde a RN é implementada em MQL5 sem o uso de matrizes, realizando a conversão de uma versão anterior do mesmo indicador a partir da linguagem C++ (com descrição detalhada, incluindo as partes relevantes da teoria da RN).
O funcionamento do indicador consiste em formar vetores de entrada de um determinado tamanho a partir de incrementos passados do preço médio EMA nos intervalos entre as barras, separadas umas das outras pela sequência de Fibonacci (1,2,3,5,8,13,21,34,55,89,144...). Com base nessas informações, é necessário prever o aumento de preço na próxima barra (à direita das barras históricas incluídas no vetor correspondente). O tamanho do vetor é determinado pelo usuário, através do tamanho da camada de entrada da RN (_numInputs). O número de camadas (até 6) e seus tamanhos são inseridos em outras variáveis de entrada.
input int _lastBar = 0; // Last bar in the past data input int _futBars = 10; // # of future bars to predict input int _smoothPer = 6; // Smoothing period input int _numLayers = 3; // # of layers including input, hidden & output (2..6) input int _numInputs = 12; // # of inputs (that is neurons in input 0-th layer) input int _numNeurons1 = 5; // # of neurons in the 1-st hidden or output layer input int _numNeurons2 = 1; // # of neurons in the 2-nd hidden or output layer input int _numNeurons3 = 0; // # of neurons in the 3-rd hidden or output layer input int _numNeurons4 = 0; // # of neurons in the 4-th hidden or output layer input int _numNeurons5 = 0; // # of neurons in the 5-th hidden or output layer input int _ntr = 500; // # of training sets / bars input int _nep = 1000; // Max # of epochs input int _maxMSEpwr = -7; // Error (as power of 10) for training to stop; mse < 10^this
Aqui também é especificado o tamanho da amostra de treinamento (_ntr), o número máximo de épocas (_nep) e o erro mínimo MSE (_maxMSEpwr).
O período de suavização do preço médio EMA é definido em _smoothPer.
Por padrão, o indicador usa os dados de treinamento a partir da última barra (_lastBar é igual a 0) e faz uma previsão para _futBars adiante. Claro que, se temos na saída da rede uma previsão para 1 barra, podemos introduzi-la gradualmente no vetor de entrada para prever várias barras subsequentes. Se inserirmos um número positivo em _lastBar, teremos uma previsão baseada no número correspondente de barras anteriores, o que nos permitirá avaliá-la visualmente (comparando com as cotações já existentes).
O indicador apresenta 3 buffers:
- linha verde clara com os valores alvo da amostra de treinamento;
- linha azul com a saída da rede na amostra de treinamento;
- linha vermelha com a previsão;
A parte aplicada do indicador na formação de conjuntos de dados e na visualização dos resultados (tanto os dados brutos quanto a previsão) não sofreu alterações.
As transformações principais ocorreram em duas funções, Train e Test - agora elas delegam integralmente o trabalho da RN para objetos da classe MatrixNet. Train instrui a rede com base nos dados coletados e retorna uma matriz com os pesos da rede (no testador, o treinamento é realizado apenas uma vez, mas quando executado online, a abertura de uma nova barra dispara um novo treinamento - isso pode ser facilmente alterado no código-fonte). Test recria a rede a partir dos pesos e executa um cálculo único padrão de previsão. Em princípio, seria mais eficiente salvar o objeto da rede treinada e usá-lo sem a necessidade de recriação. Faremos isso no próximo exemplo com um especialista, mas no caso do indicador, a estrutura original do código da versão antiga foi mantida propositalmente para facilitar a comparação das abordagens de codificação com e sem matrizes. Em particular, podemos notar que na versão matricial, somos dispensados da necessidade de 'passar' vetores através da rede em um loop, um por um, e de realizar manualmente o 'reshape' de matrizes de dados, de acordo com suas dimensões.
Com as configurações padrão, o indicador aparece no gráfico EURUSD, H1 da seguinte forma.
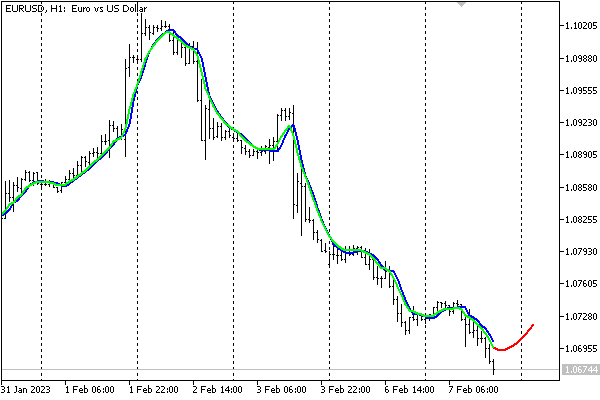
Previsão de indicador neural
Vale ressaltar que o indicador serve apenas como uma demonstração do funcionamento da RN e não é recomendado, em sua forma atual simplificada, para tomada de decisões de negociação.
Armazenamento de redes em arquivos
Os dados brutos do mercado podem mudar rapidamente, e alguns operadores consideram apropriado treinar a rede de maneira operacional (todos os dias, cada sessão, etc.) com os exemplos mais recentes. No entanto, isso pode ser dispendioso e não tão relevante para sistemas de negociação de médio e longo prazo que operam com dias. Nestes casos, é recomendável salvar a rede treinada para carregamento e utilização rápidos no futuro.
Para esse propósito, foi desenvolvida a classe MatrixNetStore, definida no arquivo de cabeçalho MatrixNetStore.mqh, no contexto do artigo. Essa classe possui os métodos 'save' e 'load', que aceitam como parâmetro M qualquer classe pertencente à família MatrixNet (atualmente, só temos duas, incluindo a MatrixNetVisual, mas isso pode ser expandido conforme a necessidade). Ambos os métodos contêm um argumento com o nome do arquivo e manipulam dados padrão da RN, como número de camadas, tamanho das mesmas, matrizes de pesos e funções de ativação.
Aqui está como a rede é salva.
class MatrixNetStore { static string signature; public: template<typename M> // M is a MatrixNet static bool save(const string filename, const M &net, Storage *storage = NULL, const int flags = 0) { // get the matrix of weights (the best weights, if any) matrix w[]; if(!net.getBestWeights(w)) { if(!net.getWeights(w)) { return false; } } // open file int h = FileOpen(filename, FILE_WRITE | FILE_BIN | FILE_SHARE_READ | FILE_SHARE_WRITE | FILE_ANSI | flags); if(h == INVALID_HANDLE) return false; // write network metadata FileWriteString(h, signature); FileWriteInteger(h, net.getActivationFunction()); FileWriteInteger(h, net.getActivationFunction(true)); FileWriteInteger(h, ArraySize(w)); // write weight matrices for(int i = 0; i < ArraySize(w); ++i) { matrix m = w[i]; FileWriteInteger(h, (int)m.Rows()); FileWriteInteger(h, (int)m.Cols()); double a[]; m.Swap(a); FileWriteArray(h, a); } // if user data is provided, write it if(storage) { if(!storage.store(h)) Print("External info wasn't saved"); } FileClose(h); return true; } ... }; static string MatrixNetStore::signature = "BPNNMS/1.0";
Vamos destacar algumas particularidades. No início do arquivo, é escrita uma assinatura para permitir a verificação da correta formatação do arquivo (essa assinatura pode ser modificada, para isso, métodos específicos foram providenciados na classe). Ademais, o método 'save' permite, quando necessário, adicionar às informações padrão sobre a rede quaisquer dados adicionais do usuário, para isso basta passar um ponteiro para o objeto da interface especial 'Storage'.
class Storage { public: virtual bool store(const int h) = 0; virtual bool restore(const int h) = 0; };
De maneira 'espelhada', é possível restaurar a rede a partir do arquivo.
class MatrixNetStore { ... template<typename M> // M is a MatrixNet static M *load(const string filename, Storage *storage = NULL, const int flags = 0) { int h = FileOpen(filename, FILE_READ | FILE_BIN | FILE_SHARE_READ | FILE_SHARE_WRITE | FILE_ANSI | flags); if(h == INVALID_HANDLE) return NULL; // check the format by signature const string header = FileReadString(h, StringLen(signature)); if(header != signature) { FileClose(h); Print("Incorrect file header"); return NULL; } // read standard network metadata set const ENUM_ACTIVATION_FUNCTION f1 = (ENUM_ACTIVATION_FUNCTION)FileReadInteger(h); const ENUM_ACTIVATION_FUNCTION f2 = (ENUM_ACTIVATION_FUNCTION)FileReadInteger(h); const int size = FileReadInteger(h); matrix w[]; ArrayResize(w, size); // read weight matrices for(int i = 0; i < size; ++i) { const int rows = FileReadInteger(h); const int cols = FileReadInteger(h); double a[]; FileReadArray(h, a, 0, rows * cols); w[i].Swap(a); w[i].Reshape(rows, cols); } // read user data if(storage) { if(!storage.restore(h)) Print("External info wasn't read"); } // create a network object M *m = new M(w, f1, f2); FileClose(h); return m; }
Com isso, estamos prontos para abordar o exemplo final do artigo - o robô de negociação.
Expert Advisor preditivo
Como estratégia para o Expert Advisor preditivo TradeNN.mq5, adotaremos um princípio bastante simples: realizar negociações na direção prevista para a próxima barra. O importante aqui é demonstrar as tecnologias de redes neurais em ação, ao invés de explorar todos os fatores observáveis para sua aplicabilidade no contexto da lucratividade.
Os dados iniciais serão os incrementos de preço em um número definido de barras, sendo possível opcionalmente analisar não apenas o símbolo atual, mas também símbolos adicionais. Isso, teoricamente, permitirá identificar interdependências (por exemplo, se um ticker segue indiretamente o outro ou suas combinações). A única saída da rede não será interpretada como preço alvo, mas, objetivando a simplificação do sistema, o sinal será analisado: se positivo - compra, se negativo - venda.
Em outras palavras, a estrutura de funcionamento da rede é, de certa maneira, híbrida: por um lado, a rede solucionará um problema de regressão, mas por outro, a ação comercial é escolhida dentre duas, como numa classificação. No futuro, pode-se aumentar o número de neurônios na camada de saída de acordo com o número de situações de negociação e aplicar a função de ativação SoftMax. No entanto, para treinar uma rede dessas, seria necessário marcar as cotações, de forma automática ou manual, de acordo com as situações.
A estratégia foi escolhida de maneira extremamente simples, a fim de focar nos parâmetros da rede e não na própria estratégia.
A lista de instrumentos analisados é introduzida no parâmetro de entrada 'Symbols', separados por vírgulas. O primeiro deve ser o símbolo do gráfico atual, pois é com este que a negociação será conduzida.
input string Symbols = "XAGUSD,XAUUSD,EURUSD"; input int Depth = 5; // Vector size (bars) input int Reserve = 250; // Training set size (vectors)
A escolha dos símbolos padrão se deve ao fato de que a prata e o ouro são considerados ativos correlacionados, e existem relativamente poucas notícias perturbadoras sobre eles (em comparação com as moedas). Portanto, em princípio, é possível tentar analisar a prata em relação ao ouro (como é feito atualmente), e também o ouro em relação à prata. Quanto ao EURUSD, este par foi adicionado por ser a base de todo o mercado, e a presença de notícias sobre ele não é relevante nesse caso, já que atua como um preditor, não uma variável a ser prevista.
Entre os outros parâmetros mais importantes está a quantidade de barras (Depth) para cada instrumento, que forma um vetor. Por exemplo, se na linha 'Symbols' 3 tickers foram definidos e o 'Depth' é 5 (por padrão), isso significa que o tamanho total do vetor de entrada da RN é 15.
O parâmetro 'Reserve' permite determinar o tamanho da amostra (número de vetores formados a partir do histórico de cotações mais recente). O valor 250 foi escolhido por padrão porque, em nosso teste, será utilizado um período gráfico diário, e 250 equivale aproximadamente a 1 ano. Logo, um 'Depth' igual a 5 equivale a uma semana.
Naturalmente, todas as configurações podem ser alteradas, assim como o período gráfico, mas em períodos mais longos, como D1, pressupõe-se que as correlações fundamentais sejam mais expressivas do que as reações espontâneas do mercado às circunstâncias imediatas.
É importante destacar também que, ao começar a rodar no testador, aproximadamente 1 ano de cotações é pré-carregado. Assim, se você quiser aumentar a quantidade de dados de treinamento em D1+, vai precisar descartar algumas barras iniciais enquanto aguarda a acumulação de uma quantidade suficiente.
Semelhante aos exemplos que vimos anteriormente, nos parâmetros, você precisa definir o número de épocas de treinamento e a precisão (que também é a velocidade inicial, e depois a velocidade será escolhida dinamicamente para cada sinapse pelo 'rprop').
input int Epochs = 1000; input double Accuracy = 0.0001; // Accuracy (and training speed)
Neste Expert Advisor, a RN vai ter 5 camadas: uma de entrada, 3 escondidas e uma de saída. O tamanho da camada de entrada é definido pelo vetor de entrada, e a segunda e terceira camadas são alocadas com o coeficiente HiddenLayerFactor. Para a penúltima camada, será usada uma fórmula empírica (veja o código-fonte abaixo) para que o tamanho dela fique entre o da camada anterior e o de saída (único).
input double HiddenLayerFactor = 2.0; // Hidden Layers Factor (to vector size) input int DropOutPercentage = 0; // DropOut Percentage
Com este exemplo de Rede Neural, vamos testar o método de regularização 'dropout'. A porcentagem de pesos escolhidos aleatoriamente para zerar é definida no parâmetro DropOutPercentage. Aqui não é fornecida uma amostra de validação, mas, se quiser, você pode combinar os dois métodos: a classe permite isso.
O parâmetro NetBinFileName serve para carregar a rede a partir de um arquivo. Os arquivos são sempre procurados com relação à pasta comum dos terminais, pois, caso contrário, para testar o Expert Advisor no testador, seria preciso especificar previamente os nomes de todas as redes necessárias no código-fonte, na diretiva #property tester_file - só assim elas seriam enviadas para o agente.
Quando o parâmetro NetBinFileName está vazio, o Expert Advisor treina uma nova rede e a salva em um arquivo com um nome temporário único. Isso é feito até mesmo durante a otimização, permitindo gerar um grande número de configurações de rede (para diferentes tamanhos de vetores, camadas, 'dropout', e profundidade do histórico).
input string NetBinFileName = ""; input int Randomizer = 0;
Adicionalmente, o parâmetro 'Randomizer' oferece a possibilidade de inicializar o gerador aleatório de maneiras distintas, habilitando assim o treinamento de múltiplas instâncias de redes para as mesmas configurações restantes. Vale ressaltar que cada rede é única por conta da randomização. Em potencial, a utilização de comitês de redes neurais, de onde se extrai uma decisão consolidada ou com base no princípio da maioria, apresenta-se como mais uma forma de regularização.
Ao mesmo tempo, estabelecer um valor específico para o 'Randomizer' possibilitará a reprodução do mesmo processo de treinamento com fins de depuração.
O armazenamento de informações de preços por símbolos é organizado utilizando a estrutura 'Closes' e um conjunto dessas estruturas 'CC': resultando em algo similar a um array de arrays.
struct Closes { double C[]; }; Closes CC[];
Os instrumentos de trabalho e suas quantidades estão reservados para o array global 'S' e para a variável 'Q': estes são preenchidos no 'OnInit'.
string S[]; int Q; int OnInit() { Q = StringSplit(StringLen(Symbols) ? Symbols : _Symbol, ',', S); ArrayResize(CC, Q); MathSrand(Randomizer); ... return INIT_SUCCEEDED; }
A função 'Calc' permite solicitar cotações para uma determinada profundidade 'Depth' a partir de um offset específico da barra: é exatamente nela que o array 'CC' é preenchido. Como essa função é chamada, veremos em breve.
bool Calc(const int offset) { const datetime dt = iTime(_Symbol, _Period, offset); for(int i = 0; i < Q; ++i) { const int bar = iBarShift(S[i], PERIOD_CURRENT, dt); // +1 for differences, +1 for model const int n = CopyClose(S[i], PERIOD_CURRENT, bar, Depth + 2, CC[i].C); for(int j = 0; j < n - 1; ++j) { CC[i].C[j] = (CC[i].C[j + 1] - CC[i].C[j]) / SymbolInfoDouble(S[i], SYMBOL_TRADE_TICK_SIZE) * SymbolInfoDouble(S[i], SYMBOL_TRADE_TICK_VALUE); } ArrayResize(CC[i].C, n - 1); } return true; }
Posteriormente, para um array específico 'CC[i].C', a função especial 'Diff' será capaz de calcular os incrementos de preço, que serão alimentados nos vetores de entrada para a rede. Uma particularidade dessa função é que ela registra todos os incrementos, exceto o último, no array 'd' passado por referência, enquanto o último incremento, que servirá como o valor alvo da previsão, é retornado diretamente.
double Diff(const double &a[], double &d[]) { const int n = ArraySize(a); ArrayResize(d, n - 1); // -1 minus the "future" model double overall = 0; for(int j = 0; j < n - 1; ++j) // left (from old) to right (toward new) { int k = n - 2 - j; overall += a[k]; d[j] = overall / sqrt(j + 1); } ... // additional normalization return a[n - 1]; }
Importa salientar que, conforme a teoria do 'passeio aleatório' de séries temporais, normalizamos as diferenças pela raiz quadrada da distância em barras (proporcional ao intervalo de confiança, caso consideremos o passado como uma previsão já cumprida). Essa não é uma abordagem canônica, mas lidar com RNs assemelha-se frequentemente à atividade de pesquisa.
O procedimento completo de seleção de fatores (por exemplo, não apenas preços, mas também indicadores, volumes) e preparação de dados para a rede (normalização, codificação) é um tópico amplo em si. É crucial facilitar ao máximo o trabalho computacional para a RN; caso contrário, ela pode não conseguir lidar com a tarefa.
Na função principal do EA OnTick, todas as operações são realizadas somente na abertura do candle/barra. Dado que o EA analisa cotações de diferentes instrumentos, é necessário sincronizá-los antes de continuar com o trabalho rotineiro. A função Sync, que não é mostrada aqui, é responsável pela sincronização. Contudo, vale ressaltar que a sincronização baseada na função Sleep é adequada mesmo para testes no modo de preços de abertura, e faremos uso desse modo mais adiante por questões de eficiência.
void OnTick() { ... static datetime last = 0; if(last == iTime(_Symbol, _Period, 0)) return; ...
A instância da rede é armazenada na variável run do tipo ponteiro automático (arquivo de cabeçalho AutoPtr.mqh), o que nos liberta da necessidade de gerenciar a liberação de memória. A variável std é destinada a armazenar a variação, que é calculada com base no conjunto de dados adquiridos das funções Calc e Diff mencionadas anteriormente. A variação será necessária para a normalização dos dados.
static AutoPtr<MatrixNet> run; static double std;
Caso o usuário forneça um nome de arquivo para carregamento no NetBinFileName, o programa tentará carregar a rede utilizando a função LoadNet (discutida posteriormente). Esta função, se bem-sucedida, retorna um ponteiro para o objeto da rede.
if(NetBinFileName != "") { if(!run[]) { run = LoadNet(NetBinFileName, std); if(!run[]) { ExpertRemove(); return; } } }
Se a rede já existir, executamos a previsão e realizamos as operações de negociação: tudo isso é gerido pela função TradeTest (discutida posteriormente).
if(run[]) { TradeTest(run[], std); } else { run = TrainNet(std); } last = iTime(_Symbol, _Period, 0); }
Se a rede ainda não existir, formamos a amostra de treinamento e treinamos a rede usando a função TrainNet: essa função também retorna um ponteiro para o novo objeto da rede e, além disso, preenche a variável std passada por referência com a variação calculada dos dados.
Note que a rede só poderá aprender depois que houver pelo menos o número solicitado de barras no histórico de todos os símbolos de trabalho. Para um gráfico online, isso provavelmente ocorrerá logo após a implementação do EA (a menos que o usuário tenha inserido um número excessivamente alto), e no testador, o histórico pré-carregado geralmente é limitado a um ano. Portanto, pode ser necessário deslocar o início da execução para o passado, a fim de acumular a quantidade necessária de barras para o treinamento até o momento de interesse.
A verificação para o número suficiente de barras é inserida no início do OnTick, mas não é discutida neste artigo (veja o código-fonte completo).
Depois de treinada, a rede começa a operar. Para o testador, isso significa que teremos uma espécie de teste prospectivo da rede já treinada. Os resultados financeiros obtidos podem ser usados para otimizações, com o objetivo de escolher a configuração de rede mais adequada ou a seleção de um comitê de redes (com configurações iguais).
A seguir, apresentamos a função TrainNet (notem as chamadas para Calc e Diff).
MatrixNet *TrainNet(double &std) { double coefs[]; matrix sys(Reserve, Q * Depth); vector model(Reserve); vector t; datetime start = 0; for(int j = Reserve - 1; j >= 0; --j) // loop through historical bars { // since close prices are used, we make +1 to the bar index if(!Calc(j + 1)) // collect data for all symbols starting with bar j to Depth bars { return NULL; // probably other symbols don't have enough history (wait) } // remember training sample start date/time if(start == 0) start = iTime(_Symbol, _Period, j); ArrayResize(coefs, 0); // calculate price difference for all symbols for Depth bars for(int i = 0; i < Q; ++i) { double temp[]; double m = Diff(CC[i].C, temp); if(i == 0) { model[j] = m; } int dest = ArraySize(coefs); ArrayCopy(coefs, temp, dest, 0); } t.Assign(coefs); sys.Row(t, j); } // normalize std = sys.Std() * 3; Print("Normalization by 3 std: ", std); sys /= std; matrix target = {}; target.Col(model, 0); target /= std; // the size of layers 0, 1, 2, 3 is derived from the data, always one output int layers[] = {0, 0, 0, 0, 1}; layers[0] = (int)sys.Cols(); layers[1] = (int)(sys.Cols() * HiddenLayerFactor); layers[2] = (int)(sys.Cols() * HiddenLayerFactor); layers[3] = (int)fmax(sqrt(sys.Rows()), fmax(sqrt(layers[1] * layers[3]), sys.Cols() * sqrt(HiddenLayerFactor))); // create and configure the network of the specified configuration ArrayPrint(layers); MatrixNetVisual *net = new MatrixNetVisual(layers); net.setupSpeedAdjustment(SpeedUp, SpeedDown, SpeedHigh, SpeedLow); net.enableDropOut(DropOutPercentage); // train the network and display the result (error) Print("Training result: ", net.train(sys, target, Epochs, Accuracy)); ...
Utilizamos a classe de rede com recurso de visualização, portanto, o progresso do treinamento será visível no gráfico. Após o treinamento, você pode remover manualmente o objeto-imagem, quando este não for mais necessário. Quando o EA é descarregado, a imagem é removida automaticamente.
A seguir, é necessário extrair da rede as melhores matrizes de peso. Além disso, checamos a possibilidade de recriar com sucesso a rede a partir destes pesos e testamos o seu desempenho nos mesmos dados.
matrix w[]; if(net.getBestWeights(w)) { MatrixNet net2(w); if(net2.isReady()) { Print("Best result: ", net2.test(sys, target)); ... } } return net; }
Finalmente, a rede é salva em um arquivo juntamente com uma string especialmente preparada, descrevendo as condições de treinamento: intervalo histórico, lista de símbolos e período gráfico, tamanho dos dados, configurações da rede.
// the most important or all EA settings can be added to the network file const string context = StringFormat("\r\n%s %s %s-%s", _Symbol, EnumToString(_Period), TimeToString(start), TimeToString(iTime(_Symbol, _Period, 0))) + "\r\n" + Symbols + "\r\n" + (string)Depth + "/" + (string)Reserve + "\r\n" + (string)Epochs + "/" + (string)Accuracy + "\r\n" + (string)HiddenLayerFactor + "/" + (string)DropOutPercentage + "\r\n"; // prepare a temporary file name const string tempfile = "bpnnmtmp" + (string)GetTickCount64() + ".bpn"; // save the network and user data to a file MatrixNetStore store; // main class unloading/loading the networks BinFileNetStorage writer(context, net.getStats(), std); // optional class wit hour information store.save(tempfile, *net, &writer); ...
A classe BinFileNetStorage mencionada aqui é específica para o nosso EA e, por meio dos métodos store/restore (interface Storage parental), lida com a nossa descrição adicional, a magnitude da normalização (que será necessária para a operação regular com novos dados), bem como as estatísticas de treinamento na forma da estrutura MatrixNet::Stats (apresentada anteriormente).
A seguir, o comportamento do EA depende se está operando no modo de otimização ou não. Durante a otimização, enviaremos o arquivo da rede do agente para o terminal usando o mecanismo de quadros (veja o código-fonte). Esses arquivos são armazenados na pasta local MQL5/Files/, numa subpasta com o nome do EA.
if(!MQLInfoInteger(MQL_OPTIMIZATION)) { // set a new name in a more understandable time format, in the common folder string filename = "bpnnm" + TimeStamp((datetime)FileGetInteger(tempfile, FILE_MODIFY_DATE)) + StringFormat("(%7g)", net.getStats().bestLoss) + ".bpn"; if(!FileMove(tempfile, 0, filename, FILE_COMMON)) { PrintFormat("Can't rename temp-file: %s [%d]", tempfile, _LastError); } } else { ... // the file will be sent from the agent to the terminal as a frame }
Em todos os outros casos (teste simples ou operação online), o arquivo é movido para a pasta comum dos terminais. Isso é feito para facilitar o carregamento subsequente através do parâmetro NetBinFileName. O fato é que, para trabalhar no testador, teríamos que especificar no código-fonte a diretiva #property tester_file com o nome específico do arquivo que planejamos introduzir no parâmetro NetBinFileName, e recompilar o EA. Sem estas manipulações, o arquivo da rede não será copiado para o agente. Portanto, é mais prático usar a pasta comum, acessível a partir de todos os agentes locais.
A função LoadNet é executada da seguinte forma:
MatrixNet *LoadNet(const string filename, double &std, const int flags = FILE_COMMON) { BinFileNetStorage reader; // optional user data MatrixNetStore store; // general metadata MatrixNet *net; std = 1.0; Print("Loading ", filename); ResetLastError(); net = store.load<MatrixNet>(filename, &reader, flags); if(net == NULL) { Print("Failed: ", _LastError); return NULL; } MatrixNet::Stats s[1]; s[0] = reader.getStats(); ArrayPrint(s); std = reader.getScale(); Print(std); Print(reader.getDescription()); return net; }
A função TradeTest invoca Calc(0) para, em seguida, obter um vetor dos incrementos de preços atuais.
bool TradeTest(MatrixNet *net, const double std) { if(!Calc(0)) return false; double coefs[]; for(int i = 0; i < Q; ++i) { double temp[]; // difference on the 0th bar is ignored, it will be predicted /* double m = */Diff(CC[i].C, temp, true); ArrayCopy(coefs, temp, ArraySize(coefs), 0); } vector t; t.Assign(coefs); matrix data = {}; data.Row(t, 0); data /= std; ...
Com base nesse vetor, a rede deve fazer uma previsão, mas antes disso, uma posição aberta existente é forçosamente fechada — nenhuma análise de correspondência entre as direções antiga e nova é feita aqui. O método ClosePosition, usado para fechar, será apresentado mais adiante. Depois, baseando-nos nos resultados do processamento direto da rede, abrimos uma nova posição na direção presumida.
ClosePosition();
if(net.feedForward(data))
{
matrix y = net.getResults();
Print("Prediction: ", y[0][0] * std);
OpenPosition((y[0][0] > 0) ? ORDER_TYPE_BUY : ORDER_TYPE_SELL);
return true;
}
return false;
}
As funções OpenPosition e ClosePosition são implementadas de maneira semelhante. Vamos apenas mostrar o ClosePosition.
bool ClosePosition() { // define an empty structure MqlTradeRequest request = {}; if(!PositionSelect(_Symbol)) return false; const string pl = StringFormat("%+.2f", PositionGetDouble(POSITION_PROFIT)); // fill in the required fields request.action = TRADE_ACTION_DEAL; request.position = PositionGetInteger(POSITION_TICKET); const ENUM_ORDER_TYPE type = (ENUM_ORDER_TYPE)(PositionGetInteger(POSITION_TYPE) ^ 1); request.type = type; request.price = SymbolInfoDouble(_Symbol, type == ORDER_TYPE_BUY ? SYMBOL_ASK : SYMBOL_BID); request.volume = PositionGetDouble(POSITION_VOLUME); request.deviation = 5; request.comment = pl; // send request ResetLastError(); MqlTradeResult result[1]; const bool ok = OrderSend(request, result[0]); Print("Status: ", _LastError, ", P/L: ", pl); ArrayPrint(result); if(ok && (result[0].retcode == TRADE_RETCODE_DONE || result[0].retcode == TRADE_RETCODE_PLACED)) { return true; } return false; }
Agora é hora para pesquisas práticas. Rodaremos o Expert Advisor no testador com as configurações padrão, no gráfico XAGUSD,D1, no modo de preços de abertura. A data inicial do teste será 01/01/2022. Isso implica que, logo após o início do Expert Advisor, a rede começará a treinar com base nos preços do ano anterior, 2021, e então negociará de acordo com seus sinais. Para visualizar o gráfico da mudança de erro ao longo das épocas, o testador deve ser executado em modo visual.
Entradas do seguinte tipo aparecerão no log, relacionadas ao treinamento da RN.
Sufficient bars at: 2022.01.04 00:00:00 Normalization by 3 std: 1.3415995381755823 15 30 30 21 1 EMA for early stopping: 31 (0.062500) Epoch 0 of 1000, loss 2.04525 ma(2.04525) Epoch 121 of 1000, loss 0.31818 ma(0.36230) Epoch 243 of 1000, loss 0.16857 ma(0.18029) Epoch 367 of 1000, loss 0.09157 ma(0.09709) Epoch 479 of 1000, loss 0.06454 ma(0.06888) Epoch 590 of 1000, loss 0.04875 ma(0.05092) Epoch 706 of 1000, loss 0.03659 ma(0.03806) Epoch 821 of 1000, loss 0.03043 ma(0.03138) Epoch 935 of 1000, loss 0.02721 ma(0.02697) Done by epoch limit 1000 with accuracy 0.024416 Training result: 0.024416206367547762 Best result: 0.024416206367547762 Check-up of saved and restored copy: bpnnm202302121707(0.0244162).bpn Loading bpnnm202302121707(0.0244162).bpn [bestLoss] [bestEpoch] [trainingSet] [validationSet] [epochsDone] [0] 0.024 999 250 0 1000 1.3415995381755823 XAGUSD PERIOD_D1 2021.01.18 00:00-2022.01.04 00:00 XAGUSD,XAUUSD,EURUSD 5/250 1000/0.0001 2.0/0 Best result restored: 0.024416206367547762
Por enquanto, preste atenção ao valor do erro final. Mais tarde, repetiremos o teste com o modo 'dropout' ativado com diferentes intensidades e compararemos os resultados.
O relatório de negociação é assim.
Exemplo de relatório de negociação de previsão
É evidente que a maior parte do comércio em 2022 não foi bem-sucedido. No entanto, no lado esquerdo, imediatamente após o ano de 2021, que forneceu a amostra de treinamento, vemos um curto período de lucratividade. Provavelmente, as regularidades encontradas pela rede continuaram a funcionar por algum tempo. Se isso é verdade, e se deveríamos ou não alterar as configurações da rede ou do conjunto de treinamento para melhorar as métricas, só pode ser descoberto para cada sistema de negociação específico através de pesquisas abrangentes. Este é um grande e meticuloso trabalho que não está relacionado à implementação interna dos algoritmos de redes neurais. Aqui, vamos nos ater a uma análise mínima.
No log, somos informados sobre o nome do arquivo contendo a rede treinada. Inseriremos este nome no testador no parâmetro NetBinFileName e expandiremos o tempo de teste, começando a partir do ano de 2021. Nesse modo, todos os parâmetros de entrada, à exceção dos dois primeiros (Symbol e Depth), não têm importância.
A negociação de teste em um intervalo de tempo ampliado apresenta a seguinte dinâmica de saldo (a amostra de treinamento é destacada em amarelo).
Curva de equilíbrio ao negociar em um intervalo prolongado, incluindo a amostra de treinamento
Como era de se esperar, a rede 'aprendeu' a especificidade do intervalo em questão, porém logo após o fim deste, ela deixa de produzir lucro.
Vamos treinar a rede duas vezes: com uma taxa de 'dropout' de 25% e 50% (o parâmetro DropOutPercentage deve ser ajustado sucessivamente para 25 e depois para 50). Para iniciar o treinamento de novas redes, limparemos o parâmetro NetBinFileName e retornaremos a data do teste para 01/01/2022.
Com um 'dropout' de 25%, obtemos um erro significativamente maior do que no primeiro caso. Mas isso é esperado, já que estamos tentando ampliar a aplicabilidade do modelo para dados fora da amostra (out-of-sample), através do endurecimento do modelo.
Epoch 0 of 1000, loss 2.04525 ma(2.04525) Epoch 125 of 1000, loss 0.46777 ma(0.48644) Epoch 251 of 1000, loss 0.36113 ma(0.36982) Epoch 381 of 1000, loss 0.30045 ma(0.30557) Epoch 503 of 1000, loss 0.27245 ma(0.27566) Epoch 624 of 1000, loss 0.24399 ma(0.24698) Epoch 744 of 1000, loss 0.22291 ma(0.22590) Epoch 840 of 1000, loss 0.19507 ma(0.20062) Epoch 930 of 1000, loss 0.18931 ma(0.19018) Done by epoch limit 1000 with accuracy 0.182581 Training result: 0.18258059873803228
Com 'dropout' de 50%, o erro aumenta ainda mais.
Epoch 0 of 1000, loss 2.04525 ma(2.04525) Epoch 118 of 1000, loss 0.54929 ma(0.55782) Epoch 242 of 1000, loss 0.43541 ma(0.45008) Epoch 367 of 1000, loss 0.38081 ma(0.38477) Epoch 491 of 1000, loss 0.34920 ma(0.35316) Epoch 611 of 1000, loss 0.30940 ma(0.31467) Epoch 729 of 1000, loss 0.29559 ma(0.29751) Epoch 842 of 1000, loss 0.27465 ma(0.27760) Epoch 956 of 1000, loss 0.25901 ma(0.26199) Done by epoch limit 1000 with accuracy 0.251914 Training result: 0.25191436104184456
A próxima imagem apresenta gráficos de treinamento nos três cenários.
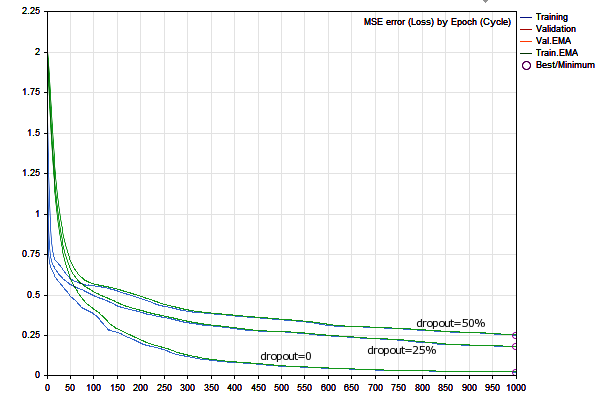
Dinâmica de aprendizado em diferentes valores de dropout
E aqui estão as curvas de saldo (a amostra de treinamento é destacada em amarelo).
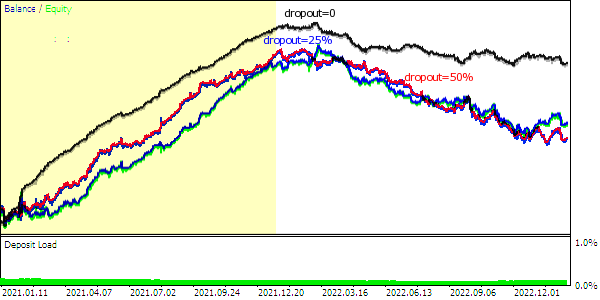
Curvas de saldo em previsões de redes com diferentes dropout
Devido ao desligamento aleatório de pesos durante o 'dropout', a linha de saldo durante o período de treinamento não é tão estável quanto na rede completa e, claro, o lucro total diminui.
Neste experimento, todas as versões perdem rapidamente a conexão com o mercado (em um ou dois meses), mas o objetivo do experimento era testar as ferramentas da rede neural criadas, e não o desenvolvimento de um sistema completo.
Em geral, a média de 'dropout' de 25% parece mais apropriada, pois um grau menor de regularização nos leva de volta ao overfitting, e um grau maior destrói as capacidades computacionais da rede. Contudo, a principal conclusão que podemos tirar preliminarmente é que a abordagem da rede neural não é uma panaceia capaz de 'salvar' qualquer sistema de negociação. As falhas podem ser devidas a suposições incorretas sobre a existência de dependências específicas, bem como aos parâmetros dos diferentes módulos do algoritmo e à preparação de dados.
Antes de descartar esta (ou qualquer outro Sistema de Negociação), é aconselhável tentar diferentes métodos para encontrar as melhores configurações para a rede, como normalmente fazemos para ajustar EAs sem a IA. Para tirar conclusões solidamente fundamentadas, será necessário coletar muito mais estatísticas.
Especificamente, podemos buscar outros grupos de símbolos ou períodos gráficos, iniciar a otimização das variáveis públicas disponíveis atualmente ou expandir a lista delas (por exemplo, funções de ativação, métodos de formação de vetores, filtragem por dias da semana, etc.).
Nesse sentido, o uso de RNs não isenta de modo algum o operador da tarefa de propor hipóteses, testar ideias e fatores significativos. A única diferença é que a otimização das configurações do sistema de negociação é complementada pelos metaparâmetros da RN.
Como experimento, vamos iniciar a otimização levando em consideração o tamanho do vetor, número de vetores, fator do tamanho das camadas ocultas e 'dropout'. Além disso, vamos incluir na otimização o parâmetro Randomizer - isso permitirá que para cada combinação de outras configurações, sejam geradas várias instâncias de redes.
- Vector size (Depth) — de 1 a 5
- Training set (Reserve) — de 50 a 400 com passo 50
- Hidden Layer Factor — de 1 a 5
- DropOut — 0, 25%, 50%
- Randomizer — de 0 a 9
Um arquivo set com as configurações está anexado. Intervalo de datas de 01/01/2022 a 15/02/2023.
Vamos escolher, por exemplo, o Profit Factor como critério de otimização, embora, considerando o pequeno número de combinações (6000) e sua enumeração completa (ao contrário da genética), isso não seja crucial.
A análise dos resultados da otimização pode ser feita exportando para um arquivo XML ou diretamente a partir do arquivo opt, por exemplo, como sugerido no programa OLAP do artigo Implementado OLAP na negociação (Parte 4): análise quantitativa e visual dos relatórios do testador ou através de outros scripts (o formato opt é aberto).
Análise estatística do relatório de otimização
Para esta captura de tela, a agregação de indicadores nas divisões solicitadas (Reserve em X - eixo horizontal, HiddenLayerFactor em Y - representado pela cor, e DropOutPercentage de 25% em Z) foi realizada por meio de um cálculo específico do fator de lucro (por células nos eixos X/Y/Z) a partir do fator de recuperação (de cada teste executado no contexto da otimização). Esta medida artificial de qualidade não é perfeita, mas é imediatamente acessível 'pronta para uso'.
Estatísticas similares ou mais familiares podem ser calculadas no Excel.
Estatisticamente, o fator da camada oculta mais vantajoso é 1 (não 2, como estava como padrão) e o tamanho do vetor é 4 (não 5). O valor de 'dropout' recomendado é de 25% ou 50%, mas definitivamente não 0%.
Como esperado, um histórico mais profundo é preferível (350 ou 400 pontos de dados, e provavelmente, um aumento adicional seria justificável).
Vamos resumir as configurações operacionais encontradas:
- Vector size = 4
- Training set = 400
- Hidden Layer Factor = 1
Como o parâmetro Randomizer foi utilizado na otimização, temos 30 instâncias de redes treinadas com esta configuração - 10 redes para cada nível de 'dropout' (0%, 25%, 50%). Nós precisamos das de 25% e 50%. Exportando o relatório de otimização para XML, podemos filtrar as entradas necessárias e obteremos uma tabela (ordenada pela lucratividade, com um filtro maior que 1):
Pass Result Profit Expected Profit Recovery Sharpe Custom Equity Trades Depth Reserve Hidden DropOut Randomizer Payoff Factor Factor Ratio DD % LayerF Perc 3838 1.35 336.02 2.41741 1.34991 1.98582 1.20187 1 1.61 139 4 400 1 25 6 838 1.23 234.40 1.68633 1.23117 0.81474 0.86474 1 2.77 139 4 400 1 25 1 3438 1.20 209.34 1.50604 1.20481 0.81329 0.78140 1 2.47 139 4 400 1 50 5 5838 1.17 173.88 1.25094 1.16758 0.61594 0.62326 1 2.76 139 4 400 1 50 9 5038 1.16 167.98 1.20849 1.16070 0.51542 0.60483 1 3.18 139 4 400 1 25 8 3238 1.13 141.35 1.01691 1.13314 0.46758 0.48160 1 2.95 139 4 400 1 25 5 2038 1.11 118.49 0.85245 1.11088 0.38826 0.41380 1 2.96 139 4 400 1 25 3 4038 1.10 107.46 0.77309 1.09951 0.49377 0.38716 1 2.12 139 4 400 1 50 6 1438 1.10 104.52 0.75194 1.09700 0.51681 0.37404 1 1.99 139 4 400 1 25 2 238 1.07 73.33 0.52755 1.06721 0.19040 0.26499 1 3.69 139 4 400 1 25 0 2838 1.03 34.62 0.24907 1.03111 0.10290 0.13053 1 3.29 139 4 400 1 50 4 2238 1.02 21.62 0.15554 1.01927 0.05130 0.07578 1 4.12 139 4 400 1 50 3
Vamos pegar a melhor, a primeira linha.
Lembre-se de que, durante a otimização, todas as redes treinadas são salvas na pasta MQL5/Arquivos/<nome do EA>/<data da otimização>. Em princípio, isso pode não ser necessário, já que o valor do Randomizer poderia ser usado para treinar uma rede semelhante novamente, mas apenas se os dados de entrada forem exatamente os mesmos. No entanto, se o histórico de cotações mudar (por exemplo, devido a uma mudança de corretor), não seria possível reproduzir a rede com as mesmas características exatas.
Os arquivos na pasta especificada têm nomes que consistem nos nomes e valores dos parâmetros otimizados. Portanto, basta fazer uma busca no sistema de arquivos:
Depth=4-Reserve=400-HiddenLayerFactor=1-DropOutPercentage=25-Randomizer=6
Suponhamos que o arquivo tenha o nome:
Depth=4-Reserve=400-HiddenLayerFactor=1-DropOutPercentage=25-Randomizer=6-3838(0.428079).bpn
onde o número entre parênteses é o erro da rede e o número antes dos parênteses é o número da corrida.
Vamos espiar o conteúdo do arquivo: apesar de ser binário, nossos metadados de treinamento foram salvos em formato de texto em sua extremidade, especificamente, indicando que o intervalo de treinamento foi de 12/01/2021 00:00 até 28/07/2022 00:00 (400 barras D1).
Copiaremos o arquivo sob um nome mais conciso, por exemplo, test3838.bpn, para a pasta geral dos terminais.
Inseriremos test3838.bpn no parâmetro NetBinFileName e 4 no parâmetro Vector size (Depth) - todos os outros parâmetros são irrelevantes se a operação for estritamente no modo de previsão.
Vamos testar a operação do EA em um período ainda mais estendido: uma vez que 2022-2023 serviu como um teste de validação para frente, vamos incorporar 2020 como um período desconhecido.
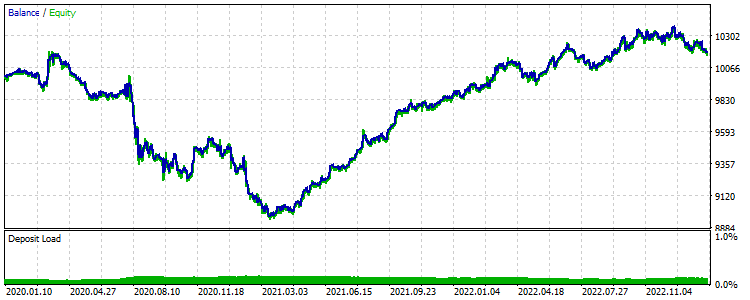
Exemplo de teste de negociação de previsão com falha fora da amostra de treinamento
Não ocorreu nenhum milagre - o sistema se mostrou deficitário em 'novos' dados. Não é difícil perceber que este quadro é característico para outras configurações.
Assim, temos duas notícias: uma boa e uma má.
A má notícia é que a ideia proposta não se mostra eficaz - pode ser que não funcione de todo, ou talvez seja um artefato da limitação do espaço de fatores explorados em nosso exemplo demonstrativo (afinal, não realizamos uma mega-otimização com bilhões de combinações e centenas de símbolos).
A boa notícia, entretanto, é que a ferramenta de rede neural sugerida permite a avaliação de ideias e fornece resultados conforme esperado (de uma perspectiva técnica).
Considerações finais
Este artigo introduz classes de redes neurais com retropropagação de erros em matrizes MQL5. A implementação não exige dependência de softwares externos, como Python, nem de recursos específicos de software e hardware (aceleradores gráficos com suporte para OpenCL). Além dos modos padrão de treinamento e uso subsequente das redes, as classes possibilitam a visualização do processo, além do salvamento e recuperação das redes em arquivos.
Graças a tais classes, o uso de redes neurais pode ser facilmente integrado a qualquer programa. Contudo, devemos lembrar que a rede é meramente uma ferramenta aplicada a um determinado material (no nosso caso: dados financeiros). Se o material não contém informação suficiente, fortemente ruidoso ou é irrelevante, nenhuma rede neural conseguirá encontrar o Graal nele.
O algoritmo de retropropagação de erro é um dos métodos básicos de treinamento mais disseminados, sobre o qual é possível construir tecnologias de rede neural mais complexas: redes recorrentes, redes convolucionais, aprendizado por reforço.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/12187
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
@Stanislav Korotky
Seus esforços para colocar o conceito de rede neural na MQL são muito apreciados. Esse é realmente um excelente trabalho para iniciantes como eu. Parabéns :)
Obrigado por atualizar o arquivo com o bug corrigido. No entanto, eu sugeriria substituir o arquivo na área de download.
Felizmente, eu li a discussão sobre o tópico e descobri que há um erro no arquivo. E agora que estava tentando procurar a correção, encontrei este link de arquivo aqui.
Espero que haja apenas esses lugares para a correção do bug, nas linhas 490-493, 500, 515-527, com a marcação //*. Se estiver em outro lugar, mencione os números das linhas ou marque //*BugFix ...
Atenciosamente
Para trabalhar com contas de compensação, é necessário adicionar uma indicação explícita de símbolo à função ClosePosition:
Fórum sobre negociação, sistemas de negociação automatizados e teste de estratégias de negociação
Discussão do artigo "Redes neurais de retropropagação em matrizes MQL5"
Stanislav Korotky, 2024.04.16 17:34
Para trabalhar com contas de compensação, você precisa especificar explicitamente o símbolo na função ClosePosition:
Um artigo que vale a pena ler.
Muito obrigado!
Obrigado, artigo muito bom!
Por algum motivo, eu o havia esquecido.