
Science des Données et Apprentissage Automatique (partie 03) : Matrices de Régression
Après de nombreux essais et beaucoup d'erreurs, le puzzle de la régression dynamique multiple est enfin résolu... continuez à lire.
Si vous avez lu avec attention les deux articles précédents, vous remarquerez que le principal problème auquel j'étais confronté était de programmer des modèles capables de gérer un plus grand nombre de variables indépendantes, c'est-à-dire de gérer dynamiquement un plus grand nombre d'entrées. Car lorsqu'il s'agit de créer des stratégies, nous sommes amenés à traiter des centaines de données, et nous voulons donc être sûrs que nos modèles peuvent répondre à cette demande.
Matrice
Pour ceux qui ont séché les cours de mathématiques, une matrice est un tableau rectangulaire de nombres, ou d'autres objets mathématiques, disposés en lignes et en colonnes, utilisée pour représenter un objet mathématique ou une propriété de cet objet.
Par exemple :
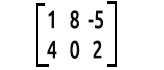
Un éléphant dans la pièce.
La façon de lire les matrices est : lignes x colonnes. La matrice de l’exemple ci-dessus est une matrice 2x3, c'est-à-dire 2 lignes et 3 colonnes.
Il ne fait aucun doute que les matrices jouent un rôle énorme dans la façon dont les ordinateurs modernes traitent l'information et calculent de grands nombres. La principale raison pour laquelle elles sont capables de le réaliser est que les données dans la matrice sont stockées sous forme de tableau que les ordinateurs lisent et manipulent facilement. Voyons donc leur application dans le machine learning.
Régression Linéaire
Les matrices permettent d'effectuer des calculs en algèbre linéaire. L'étude des matrices constitue donc une grande partie de l'algèbre linéaire. Et nous pouvons donc utiliser les matrices pour réaliser nos modèles de régression linéaire.
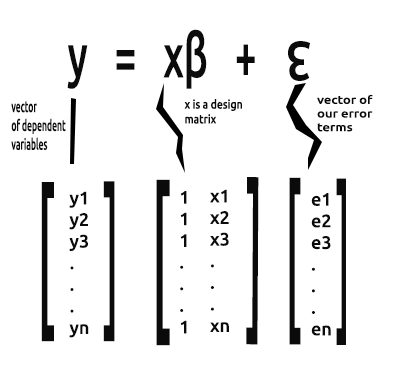
Comme nous le savons tous, l'équation d'une ligne droite est :
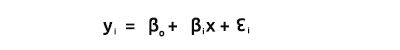
avec ∈ le terme d'erreur, Bo et Bi les coefficients d'ordonnée à l'origine et de pente respectivement.
A partir de maintenant, nous allons nous intéresser à la forme vectorielle d'une équation dans cette série d’articles. La voici :
Il s'agit de la formule d'une régression linéaire simple sous forme de matrice.
Pour un modèle linéaire simple (et d'autres modèles de régression) nous sommes généralement intéressés par la recherche des coefficients de pente et des estimateurs des moindres carrés ordinaires.
Le vecteur Beta est un vecteur contenant les bêtas
Bo etB1, comme l'explique l'équation
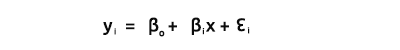
Nous nous intéressons à la recherche des coefficients car ils sont essentiels à la construction d'un modèle.
La formule pour les estimateurs des modèles sous forme vectorielle est la suivante :
C'est une formule très importante à retenir. Nous verrons bientôt comment trouver chacun des éléments de la formule.
Le produit de xTx donnera une matrice symétrique, puisque le nombre de colonnes dans xT est le même que le nombre de lignes dans x . Nous le verrons plus tard en action.
Comme nous l'avons dit précédemment, x est également appelé matrice de conception. Voici à quoi elle ressemble :
Matrice de Conception
Comme vous pouvez le voir, des 1 sont placés dans la 1ère colonne de chaque ligne de la matrice. Il s'agit de la première étape de la préparation de nos données pour la régression matricielle. Vous verrez les avantages de cette démarche à mesure que nous avancerons dans les calculs.
Ce processus est géré dans la fonction Init() de notre bibliothèque.
void CSimpleMatLinearRegression::Init(double &x[],double &y[], bool debugmode=true) { ArrayResize(Betas,2); //since it is simple linear Regression we only have two variables x and y if (ArraySize(x) != ArraySize(y)) Alert("There is variance in the number of independent variables and dependent variables \n Calculations may fall short"); m_rowsize = ArraySize(x); ArrayResize(m_xvalues,m_rowsize+m_rowsize); //add one row size space for the filled values ArrayFill(m_xvalues,0,m_rowsize,1); //fill the first row with one(s) here is where the operation is performed ArrayCopy(m_xvalues,x,m_rowsize,0,WHOLE_ARRAY); //add x values to the array starting where the filled values ended ArrayCopy(m_yvalues,y); m_debug=debugmode; }
A ce stade, lorsque nous affichons les valeurs de la matrice de conception, nous pouvons voir que les valeurs remplies d’une ligne se terminent lorsque les valeurs de x commencent.
[0] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[21] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
........
........
[693] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[714] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[735] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 4173.8 4179.2 4182.7 4185.8 4180.8 4174.6 4174.9 4170.8 4182.2 4208.4 4247.1 4217.4
[756] 4225.9 4211.2 4244.1 4249.0 4228.3 4230.6 4235.9 4227.0 4225.0 4219.7 4216.2 4225.9 4229.9 4232.8 4226.4 4206.9 4204.6 4234.7 4240.7 4243.4 4247.7
........
........
[1449] 4436.4 4442.2 4439.5 4442.5 4436.2 4423.6 4416.8 4419.6 4427.0 4431.7 4372.7 4374.6 4357.9 4381.6 4345.8 4296.8 4321.0 4284.6 4310.9 4318.1 4328.0
[1470] 4334.0 4352.3 4350.6 4354.0 4340.1 4347.5 4361.3 4345.9 4346.5 4342.8 4351.7 4326.0 4323.2 4332.7 4352.5 4401.9 4405.2 4415.8
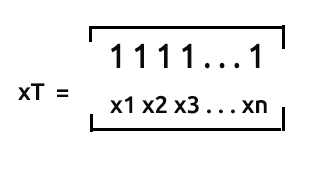
xT ou ’x transpose’ est le processus dans Matrix par lequel nous intervertissons les lignes avec les colonnes.
Cela signifie que si nous multiplions ces deux matrices :
Nous sauterons le processus de transposition d'une matrice, car la façon dont nous avons collecté nos données est sous une forme déjà transposée, bien que nous devions détransposer les valeurs x d'autre part afin de pouvoir les multiplier avec la matrice x déjà transposée.
Juste une remarque : la matrice nx2 qui n'est pas un tableau transposé ressemblera à [1 x1 1 x2 1... 1 xn]. Voyons cela.
Dé-transposition de la matrice X
Notre matrice sous forme transposée, obtenue à partir d'un fichier csv, ressemble à ceci une fois imprimée :
Matrice transposée
[
[0] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
...
...
[0] 4174 4179 4183 4186 4181 4175 4175 4171 4182 4208 4247 4217 4226 4211 4244 4249 4228 4231 4236 4227 4225 4220 4216 4226
...
...
[720] 4297 4321 4285 4311 4318 4328 4334 4352 4351 4354 4340 4348 4361 4346 4346 4343 4352 4326 4323 4333 4352 4402 4405 4416
]
Pour dé-transposer la matrice, il suffit d'échanger les lignes avec les colonnes. Le même processus inverse que la transposition de la matrice.
int tr_rows = m_rowsize, tr_cols = 1+1; //since we have one independent variable we add one for the space created by those values of one MatrixUnTranspose(m_xvalues,tr_cols,tr_rows); Print("UnTransposed Matrix"); MatrixPrint(m_xvalues,tr_cols,tr_rows);
Les choses se compliquent ici.
Nous plaçons les colonnes d'une matrice transposée à l'endroit où les lignes sont censées se trouver et inversement. Le résultat de l'exécution de cet extrait de code sera le suivant :
UnTransposed Matrix [ 1 4248 1 4201 1 4352 1 4402 ... ... 1 4405 1 4416 ]
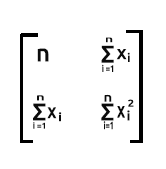
xT est une matrice 2xn, x est une nx2. Donc la matrice résultante sera une matrice 2x2
Essayons de voir à quoi ressemblera le produit de leur multiplication.
Attention: pour que la multiplication matricielle soit possible, le nombre de colonnes de la 1ère matrice doit être égal au nombre de lignes de la 2ème matrice.
Vous pouvez voir les règles de multiplication des matrices en suivant ce lien https://fr.wikipedia.org/wiki/Produit_matriciel.
La multiplication dans cette matrice est effectuée de la façon suivante :
- Ligne 1 x colonne 1
- Ligne 1 x colonne 2
- Ligne 2 x colonne 1
- Ligne 2 x colonne 2
À partir de cela, ligne 1 x colonne 1donnera la somme du produit de la ligne 1 (qui contient les valeurs de 1) et du produit de la colonne 1 (qui contient également les valeurs de 1). Ce n'est pas différent que d'incrémenter la valeur de 1 à chaque itération.
Note :
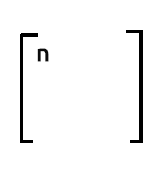
Si vous souhaitez connaître le nombre d'observations dans votre ensemble de données, vous pouvez vous fier au nombre figurant sur la 1ère ligne et la 1ère colonne de la sortie de xTx.
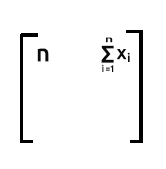
Ligne 1 x colonne 2. Puisque la ligne 1 contient les valeurs 1, lorsque nous additionnons le produit de la ligne 1 (qui contient les valeurs des 1) et de la colonne 2(qui contient les valeurs des x), le résultat sera la somme des x éléments puisque les 1 n'auront aucun effet sur la multiplication.
Ligne 2 x colonne 1. La sortie sera la somme de x puisque les valeurs de 1 de la ligne 2 n'ont aucun effet lorsqu'elles multiplient les valeurs de x qui sont sur la colonne 1.
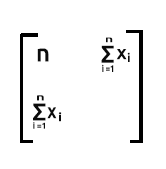
La dernière partie sera la somme des valeurs de x au carré,
puisqu'il s'agit de la somme du produit de la ligne 2, qui contient des valeurs x, et de la colonne 2, qui contient également des valeurs x.
Comme vous pouvez le voir, la sortie de la matrice est donc une matrice 2x2 dans ce cas.
Voyons comment cela fonctionne dans le monde réel, en utilisant l'ensemble de données de notre tout premier article sur la régression linéaire https://www.mql5.com/fr/articles/10459. Extrayons toutes les données et mettons-les dans un tableau x pour la variable indépendante et y pour les variables dépendantes.
//inside MatrixRegTest.mq5 script #include "MatrixRegression.mqh"; #include "LinearRegressionLib.mqh"; CSimpleMatLinearRegression matlr; CSimpleLinearRegression lr; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //double x[] = {651,762,856,1063,1190,1298,1421,1440,1518}; //stands for sales //double y[] = {23,26,30,34,43,48,52,57,58}; //money spent on ads //--- double x[], y[]; string file_name = "NASDAQ_DATA.csv", delimiter = ","; lr.GetDataToArray(x,file_name,delimiter,1); lr.GetDataToArray(y,file_name,delimiter,2); }
J'ai importé la bibliothèque CsimpleLinearRegression que nous avons créé dans le premier article
CSimpleLinearRegression lr;
Nous pourrions réutiliser certaines, comme récupérer des données dans des tableaux.
Cherchons xTx
MatrixMultiply(xT,m_xvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols); Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5); //remember?? the output of the matrix will be the row1 and col2 marked in red
Si vous prêtez attention au tableau xT[], vous pouvez voir que nous avons juste copié les valeurs x et les avons stockées dans le tableau xT[]. Pour clarifier, et comme je l'ai dit plus tôt, la façon dont nous avons collecté les données de notre fichier csv vers un tableau en utilisant la fonction GetDataToArray() nous donne des données qui sont déjà transposées.
Nous avons ensuite multiplié le tableau xT[] avec m_xvalues[] qui sont maintenant non transposés. m_xvalues est le tableau global défini pour nos valeurs x dans cette bibliothèque. C'est fait à l'intérieur de notre fonction MatrixMultiply().
void CSimpleMatLinearRegression::MatrixMultiply(double &A[],double &B[],double &output_arr[],int row1,int col1,int row2,int col2) { //--- double MultPl_Mat[]; //where the multiplications will be stored if (col1 != row2) Alert("Matrix Multiplication Error, \n The number of columns in the first matrix is not equal to the number of rows in second matrix"); else { ArrayResize(MultPl_Mat,row1*col2); int mat1_index, mat2_index; if (col1==1) //Multiplication for 1D Array { for (int i=0; i<row1; i++) for(int k=0; k<row1; k++) { int index = k + (i*row1); MultPl_Mat[index] = A[i] * B[k]; } //Print("Matrix Multiplication output"); //ArrayPrint(MultPl_Mat); } else { //if the matrix has more than 2 dimensionals for (int i=0; i<row1; i++) for (int j=0; j<col2; j++) { int index = j + (i*col2); MultPl_Mat[index] = 0; for (int k=0; k<col1; k++) { mat1_index = k + (i*row2); //k + (i*row2) mat2_index = j + (k*col2); //j + (k*col2) //Print("index out ",index," index a ",mat1_index," index b ",mat2_index); MultPl_Mat[index] += A[mat1_index] * B[mat2_index]; DBL_MAX_MIN(MultPl_Mat[index]); } //Print(index," ",MultPl_Mat[index]); } ArrayCopy(output_arr,MultPl_Mat); ArrayFree(MultPl_Mat); } } }
Pour être honnête, cette multiplication semble confuse et moche, surtout lorsque des valeurs comme
k + (i*row2); j + (k*col2);
sont utilisés. Relax ! J'ai manipulé ces index de manière à ce qu'ils puissent nous donner l'index d'une ligne et d'une colonne spécifiques. Cela aurait pu être facilement compréhensible si j'avais pu utiliser des tableaux bidimensionnels, par exemple Matrix[rows][columns] qui serait Matrix[i][k] dans ce cas Mais j'ai choisi de ne pas le faire car les tableaux multidimensionnels ont des limites et j'ai donc dû trouver une autre solution. J'ai ajouté à la fin de l'article un lien vers un code C++ simple qui, je pense, vous aidera à comprendre comment j'ai procédé. Vous pouvez également lire ce blog pour en savoir plus https://www.programiz.com/cpp-programming/examples/matrix-multiplication.
La sortie de la fonction xTx utilisant la fonction MatrixPrint() sera :
Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5);
xTx [ 744.00000 3257845.70000 3257845.70000 14275586746.32998 ]
Comme vous pouvez le voir, le premier élément de notre tableau xTx contient le nombre d'observations pour chaque donnée de notre ensemble de données. C'est pourquoi il est très important de remplir la matrice de conception avec des valeurs de 1 initialement sur la toute première colonne.
Trouvons maintenant l'inverse de la matrice xTx.
Inverse de la matrice xTx
Pour trouver l'inverse d'une matrice 2x2, on échange d'abord le premier et le dernier élément de la diagonale. Puis on ajoute des signes négatifs aux deux autres valeurs.
Voici la formule :
Pour trouver le déterminant d'une matrice : det(xTx) = Produit de la 1ère diagonale - Produit de la 2ème diagonale.
Voici comment on calculer l'inverse en code mql5 :
void CSimpleMatLinearRegression::MatrixInverse(double &Matrix[],double &output_mat[]) { // According to Matrix Rules the Inverse of a matrix can only be found when the // Matrix is Identical Starting from a 2x2 matrix so this is our starting point int matrix_size = ArraySize(Matrix); if (matrix_size > 4) Print("Matrix allowed using this method is a 2x2 matrix Only"); if (matrix_size==4) { MatrixtypeSquare(matrix_size); //first step is we swap the first and the last value of the matrix //so far we know that the last value is equal to arraysize minus one int last_mat = matrix_size-1; ArrayCopy(output_mat,Matrix); // first diagonal output_mat[0] = Matrix[last_mat]; //swap first array with last one output_mat[last_mat] = Matrix[0]; //swap the last array with the first one double first_diagonal = output_mat[0]*output_mat[last_mat]; // second diagonal //adiing negative signs >>> output_mat[1] = - Matrix[1]; output_mat[2] = - Matrix[2]; double second_diagonal = output_mat[1]*output_mat[2]; if (m_debug) { Print("Diagonal already Swapped Matrix"); MatrixPrint(output_mat,2,2); } //formula for inverse is 1/det(xTx) * (xtx)-1 //determinant equals the product of the first diagonal minus the product of the second diagonal double det = first_diagonal-second_diagonal; if (m_debug) Print("determinant =",det); for (int i=0; i<matrix_size; i++) { output_mat[i] = output_mat[i]*(1/det); DBL_MAX_MIN(output_mat[i]); } } }
Le résultat de l'exécution de ce bloc de code sera le suivant :
Diagonal already Swapped Matrix
[
14275586746 -3257846
-3257846 744
]
determinant =7477934261.0234375 Affichons l'inverse de la matrice pour voir à quoi cela ressemble :
Print("inverse xtx"); MatrixPrint(inverse_xTx,2,2,_digits); //inverse of simple lr will always be a 2x2 matrix
Le résultat sera :
[
1.9090281 -0.0004357
-0.0004357 0.0000001
]
Maintenant que nous avons l'inverse de xTx, passons à la suite.
Trouver xTy
Nous multiplions ici xT[] avec les valeurs y[] :
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //1 at the end is because the y values matrix will always have one column which is it Print("xTy"); MatrixPrint(xTy,tr_rows,1,_digits); //remember again??? how we find the output of our matrix row1 x column2
Le résultat sera :
xTy
[
10550016.7000000 46241904488.2699585
]
Référons nous à la formule :
Maintenant que nous avons l'inverse de xTx et xTy , nous pouvons terminer.
MatrixMultiply(inverse_xTx,xTy,Betas,2,2,2,1); //inverse is a square 2x2 matrix while xty is a 2x1 Print("coefficients"); MatrixPrint(Betas,2,1,5); // for simple lr our betas matrix will be a 2x1
Plus de détails sur la façon dont nous avons appelé la fonction.
Le résultat de cet extrait de code sera le suivant :
coefficients
[
-5524.40278 4.49996
]
B A M ! !! C'est le même résultat sur les coefficients que nous avons pu obtenir avec notre modèle sous forme scalaire dans la partie 01 de cette série d'articles.
Le premier nombre du tableau Bêta sera toujours la constante/intercept Y. La raison pour laquelle nous sommes capables de l'obtenir initialement est que nous avons rempli la matrice de conception avec les valeurs de 1 dans la première colonne, ce qui montre à nouveau l'importance de ce processus. Cela laisse l'espace pour que le y - intercept reste dans cette colonne.
Nous en avons terminé avec la régression linéaire simple. Voyons maintenant ce que donnera la régression multiple. Il faut être très attentif car les choses peuvent devenir délicates et compliquées à certains moments.
Résolution du casse-tête de la régression dynamique multiple
L'avantage de construire nos modèles sur une matrice est qu'il est plus facile de les mettre à l'échelle sans avoir à modifier le code. Le changement significatif que vous remarquerez dans la régression multiple est la façon dont l'inverse d'une matrice est trouvé. C'est la partie la plus difficile que j'ai passé beaucoup de temps à essayer de comprendre. Je vous donnerai plus de détails plus tard lorsque nous atteindrons cette section, mais pour l'instant, codons les choses dont nous pourrions avoir besoin dans notre bibliothèque MultipleMatrixRegression.
Nous pourrions avoir une seule bibliothèque qui pourrait gérer la régression simple et multiple en nous laissant simplement entrer les arguments de la fonction. Mais j'ai décidé de créer un autre fichier afin de clarifier les chose. Le processus sera presque le même si vous avez bien compris les calculs que nous avons effectués dans la section sur la régression linéaire simple.
Codons en premier lieu les éléments de base dont nous pouvons avoir besoin dans notre bibliothèque.
class CMultipleMatLinearReg { private: int m_handle; string m_filename; string DataColumnNames[]; //store the column names from csv file int rows_total; int x_columns_chosen; //Number of x columns chosen bool m_debug; double m_yvalues[]; //y values or dependent values matrix double m_allxvalues[]; //All x values design matrix string m_XColsArray[]; //store the x columns chosen on the Init string m_delimiter; double Betas[]; //Array for storing the coefficients protected: bool fileopen(); void GetAllDataToArray(double& array[]); void GetColumnDatatoArray(int from_column_number, double &toArr[]); public: CMultipleMatLinearReg(void); ~CMultipleMatLinearReg(void); void Init(int y_column, string x_columns="", string filename = NULL, string delimiter = ",", bool debugmode=true); };
Voici la fonction Init() :
void CMultipleMatLinearReg::Init(int y_column,string x_columns="",string filename=NULL,string delimiter=",",bool debugmode=true) { //--- pass some inputs to the global inputs since they are reusable m_filename = filename; m_debug = debugmode; m_delimiter = delimiter; //--- ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen); //--- if (m_debug) { Print("Init, number of X columns chosen =",x_columns_chosen); ArrayPrint(m_XColsArray); } //--- GetAllDataToArray(m_allxvalues); GetColumnDatatoArray(y_column,m_yvalues); // check for variance in the data set by dividing the rows total size by the number of x columns selected, there shouldn't be a reminder if (rows_total % x_columns_chosen != 0) Alert("There are variance(s) in your dataset columns sizes, This may Lead to Incorrect calculations"); else { //--- Refill the first row of a design matrix with the values of 1 int single_rowsize = rows_total/x_columns_chosen; double Temp_x[]; //Temporary x array ArrayResize(Temp_x,single_rowsize); ArrayFill(Temp_x,0,single_rowsize,1); ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //after filling the values of one fill the remaining space with values of x //Print("Temp x arr size =",ArraySize(Temp_x)); ArrayCopy(m_allxvalues,Temp_x); ArrayFree(Temp_x); //we no longer need this array int tr_cols = x_columns_chosen+1, tr_rows = single_rowsize; ArrayCopy(xT,m_allxvalues); //store the transposed values to their global array before we untranspose them MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //we add one to leave the space for the values of one if (m_debug) { Print("Design matrix"); MatrixPrint(m_allxvalues,tr_cols,tr_rows); } } }
Plus de détails sur ce qui a été écrit
ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen);
Ici, nous obtenons les colonnes x que l'on a sélectionnées (les variables indépendantes) lors de l'appel de la fonction Init dans TestScript. Nous stockons ensuite ces colonnes dans un tableau global m_XColsArray. Le fait d'avoir les colonnes dans un tableau présente des avantages puisque nous allons ensuite les lire afin de pouvoir les stocker dans le bon ordre dans le tableau de toutes les valeurs x (matrice des variables indépendantes)/matrice de conception.
Nous devons également nous assurer que toutes les lignes de nos ensembles de données sont identiques. S'il y a une différence dans une seule ligne ou dans une colonne, tous les calculs échoueront.
if (rows_total % x_columns_chosen != 0) Alert("There are variances in your dataset columns sizes, This may Lead to Incorrect calculations");
Nous transformons ensuite toutes les données des colonnes x en une matrice / matrice de conception / tableau de toutes les variables indépendantes (vous pouvez choisir de l'appeler comme vous voulez).
GetAllDataToArray(m_allxvalues);
Nous voulons également stocker toutes les variables dépendantes dans la matrice.
GetColumnDatatoArray(y_column,m_yvalues);
C'est l'étape la plus importante pour que la matrice de conception soit prête pour les calculs. L’ajout des valeurs de 1 dans la première colonne de notre matrice de valeurs x, comme dit précédemment ici.
{
//--- Refill the first row of a design matrix with the values of 1
int single_rowsize = rows_total/x_columns_chosen;
double Temp_x[]; //Temporary x array
ArrayResize(Temp_x,single_rowsize);
ArrayFill(Temp_x,0,single_rowsize,1);
ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //after filling the values of one fill the remaining space with values of x
//Print("Temp x arr size =",ArraySize(Temp_x));
ArrayCopy(m_allxvalues,Temp_x);
ArrayFree(Temp_x); //we no longer need this array
int tr_cols = x_columns_chosen+1,
tr_rows = single_rowsize;
MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //we add one to leave the space for the values of one
if (m_debug)
{
Print("Design matrix");
MatrixPrint(m_allxvalues,tr_cols,tr_rows);
}
} Cette fois-ci, nous affichons la matrice non transposée lors de l'initialisation de la bibliothèque.
C'est tout ce dont nous avons besoin sur la fonction Init pour l'instant. Appelons-la dans notre fichier multipleMatRegTestScript.mq5 (lien à la fin de l'article)
#include "multipleMatLinearReg.mqh"; CMultipleMatLinearReg matreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- string filename= "NASDAQ_DATA.csv"; matreg.Init(2,"1,3,4",filename); }
Le résultat de l'exécution du script sera (ceci n'est qu'un aperçu) :
Init, number of X columns chosen =3 "1" "3" "4" All data Array Size 2232 consuming 52 bytes of memory Design matrix Array [ 1 4174 13387 35 1 4179 13397 37 1 4183 13407 38 1 4186 13417 37 ...... ...... 1 4352 14225 47 1 4402 14226 56 1 4405 14224 56 1 4416 14223 60 ]
Trouver xTx
Ce sera ici le même processus que pour trouver la régression simple. Nous prenons les valeurs de xT qui sont les données brutes d'un fichier csv, puis nous les multiplions avec la matrice non transposée.
MatrixMultiply(xT,m_allxvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols);
Le résultat de l'affichage de la matrice xTx sera le suivant :
xTx [ 744.00 3257845.70 10572577.80 36252.20 3257845.70 14275586746.33 46332484402.07 159174265.78 10572577.80 46332484402.07 150405691938.78 515152629.66 36252.20 159174265.78 515152629.66 1910130.22 ]
Cool, ça fonctionne comme prévu.
xTx Inverse
C'est la partie la plus importante de la régression multiple .Vous devez être très attentif car les choses sont sur le point de se compliquer. Nous allons entrer dans les détails mathématiques.
Lorsque nous avons trouvé l'inverse de xTx dans la partie précédente, nous trouvions l'inverse d'une matrice 2x2. Mais nous n'en sommes plus là. Cette fois, nous trouvons l'inverse d'une matrice 4x4, car nous avons sélectionné 3 colonnes comme variables indépendantes. Lorsque nous additionnons les valeurs d'une colonne, nous obtenons 4 colonnes, ce qui nous conduit à une matrice 4x4 lorsque nous essayons de trouver l'inverse.
Nous ne pouvons plus utiliser la méthode utilisée précédemment pour trouver l'inverse cette fois. Voyons pourquoi.
La recherche de l'inverse d'une matrice à l'aide de la fonction méthode du déterminant que nous avons utilisée précédemment ne fonctionne pas lorsque les matrices sont énormes. Vous ne pouvez même pas l'utiliser pour trouver l'inverse d'une matrice 3x3.
Plusieurs méthodes ont été inventées par différents mathématiciens pour trouver l'inverse d'une matrice. L'une d'entre elles étant la classique co-matrice. Mais d'après mes recherches, la plupart de ces méthodes sont difficiles à coder et peuvent parfois prêter à confusion. Si vous souhaitez obtenir plus de détails sur les méthodes et la manière dont elles peuvent être codées, jetez un coup d'œil à ce billet de bloghttps://www.geertarien.com/blog/2017/05/15/different-methods-for-matrix-inversion/.
De toutes les méthodes existantes, j'ai choisi d'opter pour l'élimination de Gauss-Jordan parce que j'ai découvert qu'elle est fiable, facile à coder, et qu'elle est facilement évolutive. Il existe une excellente vidéo https://www.youtube.com/watch?v=YcP_KOB6KpQ qui explique bien Gauss-Jordan. J'espère qu'elle pourra vous aider à saisir le concept.
Codons maintenant le Gauss-Jordan. Si vous avez trouvé le code difficile à comprendre j'ai un code C++, pour le même code dont vous trouverez le lien ci-dessous et sur mon dépôt GitHub. Ce code pourra vous aider à comprendre comment les choses ont été faites.
void CMultipleMatLinearReg::Gauss_JordanInverse(double &Matrix[],double &output_Mat[],int mat_order) { int rowsCols = mat_order; //--- Print("row cols ",rowsCols); if (mat_order <= 2) Alert("To find the Inverse of a matrix Using this method, it order has to be greater that 2 ie more than 2x2 matrix"); else { int size = (int)MathPow(mat_order,2); //since the array has to be a square // Create a multiplicative identity matrix int start = 0; double Identity_Mat[]; ArrayResize(Identity_Mat,size); for (int i=0; i<size; i++) { if (i==start) { Identity_Mat[i] = 1; start += rowsCols+1; } else Identity_Mat[i] = 0; } //Print("Multiplicative Indentity Matrix"); //ArrayPrint(Identity_Mat); //--- double MatnIdent[]; //original matrix sided with identity matrix start = 0; for (int i=0; i<rowsCols; i++) //operation to append Identical matrix to an original one { ArrayCopy(MatnIdent,Matrix,ArraySize(MatnIdent),start,rowsCols); //add the identity matrix to the end ArrayCopy(MatnIdent,Identity_Mat,ArraySize(MatnIdent),start,rowsCols); start += rowsCols; } //--- int diagonal_index = 0, index =0; start = 0; double ratio = 0; for (int i=0; i<rowsCols; i++) { if (MatnIdent[diagonal_index] == 0) Print("Mathematical Error, Diagonal has zero value"); for (int j=0; j<rowsCols; j++) if (i != j) //if we are not on the diagonal { /* i stands for rows while j for columns, In finding the ratio we keep the rows constant while incrementing the columns that are not on the diagonal on the above if statement this helps us to Access array value based on both rows and columns */ int i__i = i + (i*rowsCols*2); diagonal_index = i__i; int mat_ind = (i)+(j*rowsCols*2); //row number + (column number) AKA i__j ratio = MatnIdent[mat_ind] / MatnIdent[diagonal_index]; DBL_MAX_MIN(MatnIdent[mat_ind]); DBL_MAX_MIN(MatnIdent[diagonal_index]); //printf("Numerator = %.4f denominator =%.4f ratio =%.4f ",MatnIdent[mat_ind],MatnIdent[diagonal_index],ratio); for (int k=0; k<rowsCols*2; k++) { int j_k, i_k; //first element for column second for row j_k = k + (j*(rowsCols*2)); i_k = k + (i*(rowsCols*2)); //Print("val =",MatnIdent[j_k]," val = ",MatnIdent[i_k]); //printf("\n jk val =%.4f, ratio = %.4f , ik val =%.4f ",MatnIdent[j_k], ratio, MatnIdent[i_k]); MatnIdent[j_k] = MatnIdent[j_k] - ratio*MatnIdent[i_k]; DBL_MAX_MIN(MatnIdent[j_k]); DBL_MAX_MIN(ratio*MatnIdent[i_k]); } } } // Row Operation to make Principal diagonal to 1 /*back to our MatrixandIdentical Matrix Array then we'll perform operations to make its principal diagonal to 1 */ ArrayResize(output_Mat,size); int counter=0; for (int i=0; i<rowsCols; i++) for (int j=rowsCols; j<2*rowsCols; j++) { int i_j, i_i; i_j = j + (i*(rowsCols*2)); i_i = i + (i*(rowsCols*2)); //Print("i_j ",i_j," val = ",MatnIdent[i_j]," i_i =",i_i," val =",MatnIdent[i_i]); MatnIdent[i_j] = MatnIdent[i_j] / MatnIdent[i_i]; //printf("%d Mathematical operation =%.4f",i_j, MatnIdent[i_j]); output_Mat[counter]= MatnIdent[i_j]; //store the Inverse of Matrix in the output Array counter++; } } //--- }
Alors appelons la fonction et affichons l'inverse d'une matrice.
double inverse_xTx[]; Gauss_JordanInverse(xTx,inverse_xTx,tr_cols); if (m_debug) { Print("xtx Inverse"); MatrixPrint(inverse_xTx,tr_cols,tr_cols,7); }
Le résultat sera :
xtx Inverse [ 3.8264763 -0.0024984 0.0004760 0.0072008 -0.0024984 0.0000024 -0.0000005 -0.0000073 0.0004760 -0.0000005 0.0000001 0.0000016 0.0072008 -0.0000073 0.0000016 0.0000290 ]
Rappelez-vous que pour trouver l'inverse d'une matrice, celle-ci doit être obligatoirement une matrice carrée. C'est pourquoi, dans les arguments de la fonction, nous avons l'argument mat_order qui est égal au nombre de lignes et de colonnes.
Trouver xTy
Trouvons maintenant le produit matriciel de la transposition de x et de Y. C’est le même processus que précédemment.
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //remember!! the value of 1 at the end is because we have only one dependent variable y
Lorsque la sortie est affichée, elle ressemble à ceci
xTy [ 10550016.70000 46241904488.26996 150084914994.69019 516408161.98000 ]
Parfait, c’est une matrice 1x4 comme prévu.
Rappelez-vous à la formule,
Nous avons maintenant tout ce dont nous avons besoin pour trouver les coefficients.
MatrixMultiply(inverse_xTx,xTy,Betas,tr_cols,tr_cols,tr_cols,1); Le résultat sera le suivant (rappelez-vous que le 1er élément de notre matrice de coefficients/bêta est la constante ou, en d'autres termes, l'ordonnée à l'origine) :
Coefficients Matrix [ -3670.97167 2.75527 0.37952 8.06681 ]
Parfait ! Laissez-moi maintenant voir avec python pour prouver que j'ai tort.
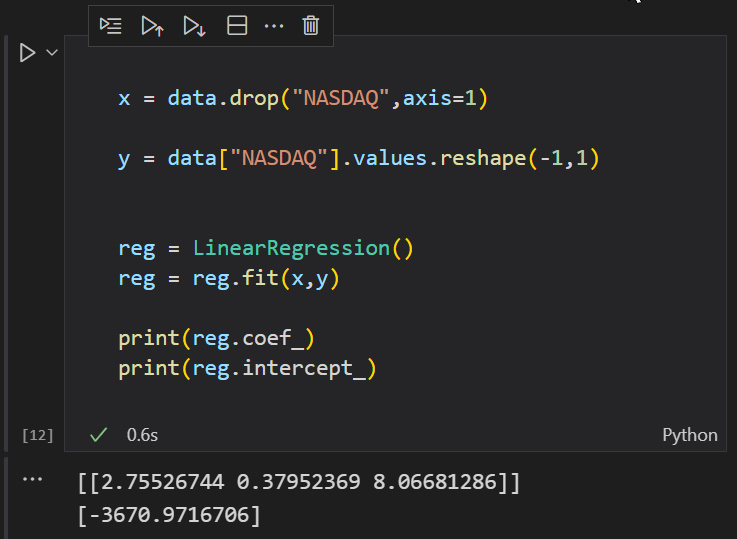
Double B A M ! ! !
Maintenant que vous l'avez, les modèles de régression dynamique multiple sont enfin possibles en mql5 ! Voyons maintenant où tout a commencé.
Tout a commencé ici :
matreg.Init(2,"1,3,4",filename);
L'idée était d'avoir une entrée de chaîne de caractères qui pourrait nous aider à mettre un nombre illimité de variables indépendantes. Il apparaît qu’en mql5, *args et *kwargs n’existe pas comme en python, qui pourraient nous laisser entrer trop d'arguments. La seule façon de procéder est donc d'utiliser la chaîne de caractères, puis de trouver un moyen de manipuler le tableau pour que le tableau unique contienne toutes nos données. Il faut ensuite trouver un moyen de les manipuler. Voir ma première tentative infructueuse pour plus d'informations https://www.mql5.com/fr/code/38894. La raison pour laquelle je dis tout cela est que je crois que quelqu'un pourrait suivre le même chemin sur ce projet ou un autre. J'explique simplement ce qui a fonctionné pour moi et ce qui n'a pas fonctionné.
Réflexions Finales
Aussi cool que cela puisse paraître, vous pouvez maintenant avoir autant de variables indépendantes que vous le souhaitez. Mais n'oubliez pas qu'il y a une limite à tout : avoir trop de variables indépendantes ou de très longues colonnes de données peut conduire à des limites de calcul de l'ordinateur. Comme vous venez de le voir, les calculs matriciels peuvent aussi donner un grand nombre de chiffres pendant les calculs.
L'ajout de variables indépendantes à un modèle de régression linéaire multiple augmentera toujours la quantité de variance dans la variable dépendante, généralement exprimée sous forme de r-carré. Donc, l'ajout d'un trop grand nombre de variables indépendantes sans justification théorique peut entraîner un modèle sur-ajusté.
Par exemple, si nous avions construit un modèle comme celui que nous avons fait dans le premier article de cette série, basé sur deux variables seulement (le NASDAQ en dépendant et le S&P500 en indépendant), notre précision aurait pu être supérieure à 95 %. Mais ce n'est peut-être pas le cas ici, car nous avons maintenant 3 variables indépendantes.
C'est toujours une bonne idée de vérifier l'exactitude de votre modèle après sa construction. Avant de construire un modèle, vous devriez également vérifier s'il existe une corrélation entre chaque variable indépendante et la cible.
Construisez toujours le modèle sur des données qui montrent une relation linéaire forte avec votre variable cible.
Merci d’avoir lu cet article ! Mon dépôt GitHub est ici https://github.com/MegaJoctan/MatrixRegressionMQL5.git.
Traduit de l’anglais par MetaQuotes Ltd.
Article original : https://www.mql5.com/en/articles/10928
Avertissement: Tous les droits sur ces documents sont réservés par MetaQuotes Ltd. La copie ou la réimpression de ces documents, en tout ou en partie, est interdite.
Cet article a été rédigé par un utilisateur du site et reflète ses opinions personnelles. MetaQuotes Ltd n'est pas responsable de l'exactitude des informations présentées, ni des conséquences découlant de l'utilisation des solutions, stratégies ou recommandations décrites.
 Développer un Expert Advisor à partir de zéro (partie 7) : Ajout du Volume au Prix (I)
Développer un Expert Advisor à partir de zéro (partie 7) : Ajout du Volume au Prix (I)
 Apprendre à concevoir un système de trading basé sur l’ATR
Apprendre à concevoir un système de trading basé sur l’ATR
 Développer un Expert Advisor à partir de zéro (partie 8) : Un saut conceptuel
Développer un Expert Advisor à partir de zéro (partie 8) : Un saut conceptuel
 Apprenez à concevoir un système de trading basé sur l’ADX
Apprenez à concevoir un système de trading basé sur l’ADX
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation

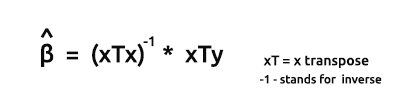
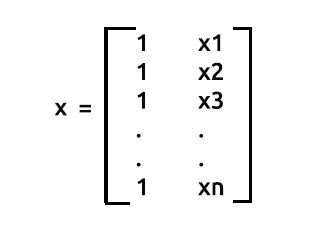
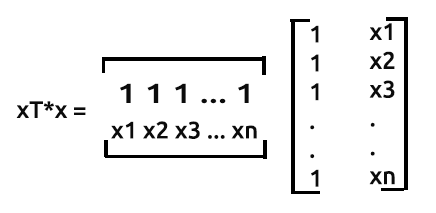

![Inverse d'une matrice [2x2] Inverse d'une matrice [2x2]](https://c.mql5.com/2/46/inverse_of_2x2_matrix.png)
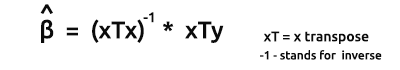
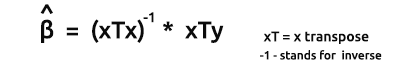
Un nouvel article Data Science and Machine Learning part 03 : Matrix Regressions a été publié :
Auteur : Omega J Msigwa