
Veri Bilimi ve Makine Öğrenimi (Bölüm 03): Matris Regresyonları
Uzun bir deneme yanılma sürecinden sonra, çoklu dinamik regresyon bilmecesi nihayet çözüldü...
Önceki iki makalede dikkat ettiyseniz, karşılaştığım en büyük sorun, daha fazla bağımsız değişkeni işleyebilen programlama modelleriydi. Burada daha fazla girdi verisinin dinamik olarak işlenmesinden bahsediyorum çünkü stratejiler oluştururken yüzlerce veri ile uğraşacağız. Bu nedenle, modellerin bu gereksinimi karşılayacağından emin olmamız gerekir.
Matris
Matematik derslerini kaçırdıysanız, bir matris, bir matematiksel nesneyi veya böyle bir nesnenin bir özelliğini temsil etmek için kullanılan, satırlar ve sütunlar halinde düzenlenmiş sayılar veya diğer matematiksel nesnelerden oluşan dikdörtgen bir dizi veya tablodur.
Örneğin:
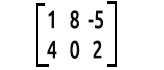
Şu detay önemlidir.
Matrisleri okuma şeklimiz satırlar çarpı sütunlardır. Yukarıda 2x3'lük bir matris var, yani 2 satır ve 3 sütundan oluşuyor.
Modern bilgisayarların bilgiyi işlemesinde ve büyük sayıları hesaplamasında kuşkusuz matrislerin büyük rolü vardır. Bunun temel nedeni, matristeki verilerin bilgisayarların okuyabileceği ve işleyebileceği dizi biçiminde depolanmasıdır. Öyleyse şimdi matrislerin makine öğrenimindeki uygulamalarını görelim.
Lineer Regresyon
Matrisler, lineer cebir hesaplamaları yapmamıza olanak tanır. Lineer cebirde önemli bir yere sahiptirler. Dolayısıyla, lineer regresyon modelleri oluşturmak için matrisleri kullanabiliriz.
Hepimizin bildiği gibi, bir doğrunun denklemi şu şekildedir:
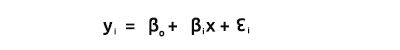
Burada ∈ hatayı temsil eder, B 0 ve B i katsayıları ise sırasıyla y-kesimi ve eğim katsayısıdır.
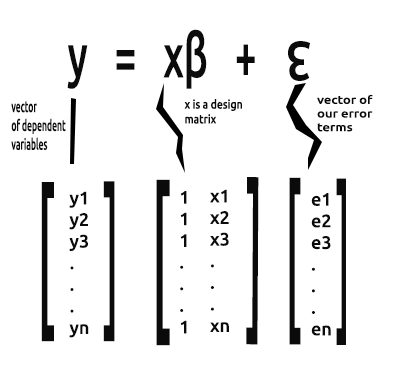
Şu andan itibaren denklemin vektör formuyla ilgileneceğiz. İşte burada:
Bu, matris biçiminde bir basit lineer regresyon formülüdür.
Bir basit lineer modelde (ve diğer regresyon modellerinde), genellikle eğim katsayılarını/sıradan en küçük kareler tahmin edicilerini ararız.
Beta vektörü, betalar içeren bir vektördür.
B 0 ve B 1 , denklemde açıklandığı şekilde:
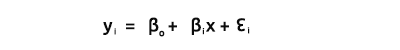
Bir model oluşturmada çok önemli oldukları için katsayıları bulmakla ilgileniyoruz.
Vektör formunda modellerin tahmin edicileri için formül şu şekildedir:
Bu çok önemli bir formüldür, ezberlenmesi gerekiyor. Formüldeki öğelerin nasıl bulunacağını aşağıdaki konularda tartışacağız.
xT'deki sütun sayısı x'teki satır sayısına eşit olduğundan, xTx çarpımı simetrik matris olacaktır. Bunu biraz sonra açıklayacağız.
Daha önce de belirtildiği gibi, x, tasarım matrisi olarak da adlandırılır, böyle bir matrisin nasıl görüneceği aşağıda anlatılmaktadır.
Tasarım Matrisi
Gördüğünüz gibi, ilk sütuna, matris dizisindeki satırlarımızın sonuna kadar sadece 1 değerlerini koyuyoruz. Bu, verilerimizi matris regresyonu için hazırlamanın ilk adımıdır. Hesaplamalarda ilerledikçe bu özel adımın avantajlarını göreceksiniz.
Bu işlemi kütüphanemizin Init() fonksiyonunda gerçekleştiriyoruz.
void CSimpleMatLinearRegression::Init(double &x[],double &y[], bool debugmode=true) { ArrayResize(Betas,2); //since it is simple linear Regression we only have two variables x and y if (ArraySize(x) != ArraySize(y)) Alert("There is variance in the number of independent variables and dependent variables \n Calculations may fall short"); m_rowsize = ArraySize(x); ArrayResize(m_xvalues,m_rowsize+m_rowsize); //add one row size space for the filled values ArrayFill(m_xvalues,0,m_rowsize,1); //fill the first row with one(s) here is where the operation is performed ArrayCopy(m_xvalues,x,m_rowsize,0,WHOLE_ARRAY); //add x values to the array starting where the filled values ended ArrayCopy(m_yvalues,y); m_debug=debugmode; }
Burada tasarım matrisinin değerlerini dolduruyoruz. Çıktı aşağıda gösterilmektedir. 1 değerlerinin doldurulmasının sonlandığı, x değerlerinin doldurulmaya başlandığı yere dikkat edin.
[ 0] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 21] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
........
........
[ 693] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 714] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 735] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 4173.8 4179.2 4182.7 4185.8 4180.8 4174.6 4174.9 4170.8 4182.2 4208.4 4247.1 4217.4
[ 756] 4225.9 4211.2 4244.1 4249.0 4228.3 4230.6 4235.9 4227.0 4225.0 4219.7 4216.2 4225.9 4229.9 4232.8 4226.4 4206.9 4204.6 4234.7 4240.7 4243.4 4247.7
........
........
[1449] 4436.4 4442.2 4439.5 4442.5 4436.2 4423.6 4416.8 4419.6 4427.0 4431.7 4372.7 4374.6 4357.9 4381.6 4345.8 4296.8 4321.0 4284.6 4310.9 4318.1 4328.0
[1470] 4334.0 4352.3 4350.6 4354.0 4340.1 4347.5 4361.3 4345.9 4346.5 4342.8 4351.7 4326.0 4323.2 4332.7 4352.5 4401.9 4405.2 4415.8
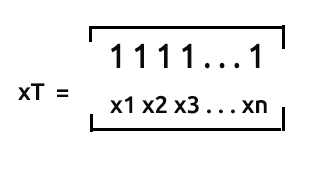
xT matrisi (x matrisinin transpozu), x matrisinin satırlarının ve sütunlarının yerleri değiştirilmiş halidir.
Ve iki matrisi çarparsak xTx matrisini elde ederiz:
Matrisi transpoze etme sürecini atlayacağız, çünkü verilerimizi toplama şeklimiz nedeniyle matris zaten transpoze formda olacaktır. Öte yandan, bu transpoze formdaki xT matrisinin x matrisi ile çarpılabilmesi adına xT matrisini ters transpoze etmemiz gerekir.
X Matrisini Ters Transpoze Etme
csv dosyasından elde edilen transpoze formdaki matrisimizin çıktısı şu şekilde görünmektedir:
Transposed Matrix
[
[ 0] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
...
...
[ 0] 4174 4179 4183 4186 4181 4175 4175 4171 4182 4208 4247 4217 4226 4211 4244 4249 4228 4231 4236 4227 4225 4220 4216 4226
...
...
[720] 4297 4321 4285 4311 4318 4328 4334 4352 4351 4354 4340 4348 4361 4346 4346 4343 4352 4326 4323 4333 4352 4402 4405 4416
]
Matrisi ters transpoze etme işleminde de, transpoze etme işlemiyle aynı şekilde satırların ve sütunların yerlerini değiştiririz.
int tr_rows = m_rowsize, tr_cols = 1+1; //since we have one independent variable we add one for the space created by those values of one MatrixUnTranspose(m_xvalues,tr_cols,tr_rows); Print("UnTransposed Matrix"); MatrixPrint(m_xvalues,tr_cols,tr_rows);
Burada işler karmaşıklaşır.
Transpoze matrisin sütunlarını satırların olması gereken yerlere ve satırlarını da sütunların olması gereken yerlere koyarız. Bu kod parçacığını çalıştırdıktan sonraki çıktı şu şekilde olacaktır:
UnTransposed Matrix [ 1 4248 1 4201 1 4352 1 4402 ... ... 1 4405 1 4416 ]
xT bir 2xn matristir, x ise bir nx2 matristir. xT*x ile ortaya çıkan matris 2x2 matris olacaktır.
Öyleyse, bu çarpımın sonucunun nasıl görüneceğini inceleyelim.
Dikkat: Matrisler çarpma için uygun olmalıdır, yani birinci matristeki sütun sayısı ikinci matristeki satır sayısına eşit olmalıdır.
Matrisleri çarpma kurallarını buradan bulabilirsiniz: https://en.wikipedia.org/wiki/Matrix_multiplication.
Matrislerimizin çarpma işlemi şu şekilde yapılır:
- 1. satır çarpı 1. sütun
- 1. satır çarpı 2. sütun
- 2. satır çarpı 1. sütun
- 2. satır çarpı 2. sütun
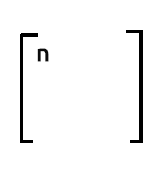
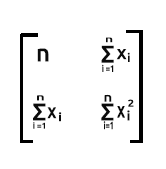
1. satır çarpı 1. sütun: matrislerimizde bu iki alanda da 1 değerleri olduğu için sonuç 1*1’lerin n kadar toplamı, yani n olacaktır.
Not:
Veri kümenizdeki gözlem sayısını bilmek istiyorsanız, xTx çıktısının ilk satır ilk sütunundaki sayıya itimat edebilirsiniz.
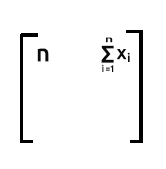
1. satır çarpı 2. sütun: 1. satırdaki her 1 değeri ile 2. sütundaki her x değerinin sırayla olan çarpımlarını topladığımızda, 1'lerin çarpma üzerinde hiçbir etkisi olmayacağından elde edilecek sonuç x değerlerinin toplamı olacaktır.
2. satır çarpı 1. sütun: 2. satırdaki her x değeri ile 1. sütundaki her 1 değerinin sırayla olan çarpımlarını topladığımızda, 1'lerin çarpma üzerinde hiçbir etkisi olmayacağından elde edilecek sonuç x değerlerinin toplamı olacaktır.
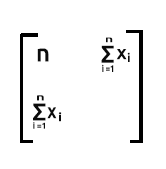
2. satır çarpı 2. sütun: 2. satırdaki her x değeri ile 2. sütundaki her x değerinin sırayla olan çarpımlarını topladığımızda, sonuç n kadar x2’lerin toplamı olacaktır.
Böylece gördüğünüz gibi, elde edilen matris 2x2'lik bir matris olur.
Şimdi bunun gerçek dünyada nasıl çalıştığını görelim. Bunu yapmak için, lineer regresyon konulu ilk makalemizdeki (https://www.mql5.com/tr/articles/10459) veri kümesini kullanalım. Verileri ayıklayalım ve bağımsız değişken için x ve bağımlı değişkenler için y dizisine koyalım.
//inside MatrixRegTest.mq5 script #include "MatrixRegression.mqh"; #include "LinearRegressionLib.mqh"; CSimpleMatLinearRegression matlr; CSimpleLinearRegression lr; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //double x[] = {651,762,856,1063,1190,1298,1421,1440,1518}; //stands for sales //double y[] = {23,26,30,34,43,48,52,57,58}; //money spent on ads //--- double x[], y[]; string file_name = "NASDAQ_DATA.csv", delimiter = ","; lr.GetDataToArray(x,file_name,delimiter,1); lr.GetDataToArray(y,file_name,delimiter,2); }
İlk makalemizde oluşturduğumuz CsimpleLinearRegression kütüphanesini buraya içe aktardım.
CSimpleLinearRegression lr;
Çünkü bu kütüphane, verileri dizilere doldurmak gibi bizim için faydalı olabilecek belirli fonksiyonları içermektedir.
xTx'i Bulma
MatrixMultiply(xT,m_xvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols); Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5); //remember?? the output of the matrix will be the row1 and col2 marked in red
xT[] dizisine dikkat ederseniz, sadece x değerlerini kopyalayıp depoladığımızı fark edeceksiniz - daha önce de belirttiğim gibi, GetDataToArray() fonksiyonunu kullanarak csv dosyamızdan diziye verileri toplama şeklimiz, bize zaten transpoze formda verileri verecektir.
Sonrasında xT[] dizisini, ters transpoze formdaki m_xvalues[] ile çarpıyoruz. m_xvalues bu kütüphanedeki x değerleri için global tanımlı bir dizidir. İşte MatrixMultiply() fonksiyonumuzun içerisindekiler:
void CSimpleMatLinearRegression::MatrixMultiply(double &A[],double &B[],double &output_arr[],int row1,int col1,int row2,int col2) { //--- double MultPl_Mat[]; //where the multiplications will be stored if (col1 != row2) Alert("Matrix Multiplication Error, \n The number of columns in the first matrix is not equal to the number of rows in second matrix"); else { ArrayResize(MultPl_Mat,row1*col2); int mat1_index, mat2_index; if (col1==1) //Multiplication for 1D Array { for (int i=0; i<row1; i++) for(int k=0; k<row1; k++) { int index = k + (i*row1); MultPl_Mat[index] = A[i] * B[k]; } //Print("Matrix Multiplication output"); //ArrayPrint(MultPl_Mat); } else { //if the matrix has more than 2 dimensionals for (int i=0; i<row1; i++) for (int j=0; j<col2; j++) { int index = j + (i*col2); MultPl_Mat[index] = 0; for (int k=0; k<col1; k++) { mat1_index = k + (i*row2); //k + (i*row2) mat2_index = j + (k*col2); //j + (k*col2) //Print("index out ",index," index a ",mat1_index," index b ",mat2_index); MultPl_Mat[index] += A[mat1_index] * B[mat2_index]; DBL_MAX_MIN(MultPl_Mat[index]); } //Print(index," ",MultPl_Mat[index]); } ArrayCopy(output_arr,MultPl_Mat); ArrayFree(MultPl_Mat); } } }
Dürüst olmak gerekirse, bu çarpma biraz kafa karıştırıcı görünüyor, özellikle şöyle şeyler kullanıldığında:
k + (i*row2); j + (k*col2);
Ama sakin olun. İndekslerle bu şekilde çalışma yöntemimiz, bize belirli bir satır ve sütundaki indeksi verebilmektedir. matris[satırlar][sütunlar] gibi iki boyutlu diziler kullansaydım bunu anlamak daha kolay olurdu, bizim durumumuzda bu matris[i][k] olurdu. Ancak çok boyutlu dizilerin sınırlamaları olduğu için yapmamaya karar verdim, bu yüzden başka bir yol bulmam gerekti. Nasıl yaptığımı anlamanıza yardımcı olacağını düşündüğüm basit bir C++ kodunu makalenin sonuna ekledim. Daha fazlasını öğrenmek istiyorsanız şu blogu okumanızı tavsiye ederim: https://www.programiz.com/cpp-programming/examples/matrix-multiplication.
xTx için MatrixPrint() fonksiyonunun başarılı çalışmasının çıktısı şu şekilde olacaktır:
Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5);
xTx [ 744.00000 3257845.70000 3257845.70000 14275586746.32998 ]
Gördüğünüz gibi, xTx dizimizdeki ilk öğe, veri kümemizdeki veriler için olan gözlem sayısıdır, bu nedenle tasarım matrisinin ilk sütununu 1 değerleriyle doldurmak çok önemlidir.
Şimdi xTx matrisinin tersini bulalım.
xTx’in Tersi
Matrisimizin tersini bulmak istiyorsak aşağıdaki formülü kullanırız. Formülün sağında gösterilen, matrisimizin ek matrisini bulmak için önce köşegenin elemanlarının yerlerini değiştiririz, ardından diğer iki değere eksi işaretleri ekleriz.
Matrisin determinantını bulmak için de: det(xTx) = Birinci köşegenin çarpımı - İkinci köşegenin çarpımı.
Mql5 kodunda matrisin tersi nasıl bulunur:
void CSimpleMatLinearRegression::MatrixInverse(double &Matrix[],double &output_mat[]) { // According to Matrix Rules the Inverse of a matrix can only be found when the // Matrix is Identical Starting from a 2x2 matrix so this is our starting point int matrix_size = ArraySize(Matrix); if (matrix_size > 4) Print("Matrix allowed using this method is a 2x2 matrix Only"); if (matrix_size==4) { MatrixtypeSquare(matrix_size); //first step is we swap the first and the last value of the matrix //so far we know that the last value is equal to arraysize minus one int last_mat = matrix_size-1; ArrayCopy(output_mat,Matrix); // first diagonal output_mat[0] = Matrix[last_mat]; //swap first array with last one output_mat[last_mat] = Matrix[0]; //swap the last array with the first one double first_diagonal = output_mat[0]*output_mat[last_mat]; // second diagonal //adiing negative signs >>> output_mat[1] = - Matrix[1]; output_mat[2] = - Matrix[2]; double second_diagonal = output_mat[1]*output_mat[2]; if (m_debug) { Print("Diagonal already Swapped Matrix"); MatrixPrint(output_mat,2,2); } //formula for inverse is 1/det(xTx) * (xtx)-1 //determinant equals the product of the first diagonal minus the product of the second diagonal double det = first_diagonal-second_diagonal; if (m_debug) Print("determinant =",det); for (int i=0; i<matrix_size; i++) { output_mat[i] = output_mat[i]*(1/det); DBL_MAX_MIN(output_mat[i]); } } }
Bu kod bloğunun çıktısı şu şekilde görünecektir:
Diagonal already Swapped Matrix
[
14275586746 -3257846
-3257846 744
]
determinant =7477934261.0234375 Nasıl göründüğünü görmek için matrisin tersini yazdıralım:
Print("inverse xtx"); MatrixPrint(inverse_xTx,2,2,_digits); //inverse of simple lr will always be a 2x2 matrix
Çıktı şu şekilde olacaktır:
[
1.9090281 -0.0004357
-0.0004357 0.0000001
]
xTx’in tersini elde ettik, hadi devam edelim.
xTy’yi Bulma
Burada xT[]'yi y[] değerleriyle çarpıyoruz.
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //1 at the end is because the y values matrix will always have one column which is it Print("xTy"); MatrixPrint(xTy,tr_rows,1,_digits); //remember again??? how we find the output of our matrix row1 x column2
Çıktı şu şekilde olacaktır:
xTy
[
10550016.7000000 46241904488.2699585
]
Formülü hatırlayalım:
xTx’in tersine ve xTy’ye sahibiz. Bir sonraki adıma geçebiliriz.
MatrixMultiply(inverse_xTx,xTy,Betas,2,2,2,1); //inverse is a square 2x2 matrix while xty is a 2x1 Print("coefficients"); MatrixPrint(Betas,2,1,5); // for simple lr our betas matrix will be a 2x1
Bu kod parçacığının çıktısı şöyle olacaktır:
coefficients
[
-5524.40278 4.49996
]
Ta-da! Bu, bu makale serimizin 1. bölümündeki skaler formdaki modelle elde ettiğimiz katsayılar için aynı sonuçtur.
Beta dizisinin ilk indeksindeki sayı her zaman sabit/y-kesimi olacaktır. Onu başlangıçta elde edebilmemizin nedeni, tasarım matrisinin ilk sütununu 1 değerleriyle doldurmuş olmamızdır. Bu da bu işlemin ne kadar önemli olduğunu bize bir kez daha gösteriyor. 1 değerleri o sütunda olması için y-kesimine yer bırakıyor.
Basit lineer regresyonla işimiz bitti. Şimdi ise çoklu regresyonun nasıl görüneceğine bakalım. Burada dikkatinizi daha fazla vermeniz gerekiyor çünkü burada işler daha zor, karmaşık ve zaman alıcı olabilir.
Çoklu Dinamik Regresyon Bulmacası Çözüldü
Modelleri matrise dayalı olarak oluşturmanın avantajı, kodu çok fazla değiştirmek zorunda kalmadan onları genişletmenin kolay olmasıdır. Çoklu regresyonda farkedeceğiniz en büyük değişiklik, matrisin tersinin nasıl bulunduğudur. Çünkü bu kısım en zor kısımdır, şahsen anlayabilmek için bu konu üzerinde çok uzun zaman harcadım. İlgili kısma geldiğimizde onun hakkında detaylı şekilde konuşacağım. Şimdi MultipleMatrixRegression kütüphanemizde ihtiyacımız olabilecek şeyleri kodlayalım.
Basit ve çoklu regresyonu işleyebilecek yalnızca bir kütüphaneye sahip olabilirdik ve sadece fonksiyon argümanlarını girebilirdik. Ancak süreç hemen hemen aynı olacağından, her şeyin nasıl çalıştığını daha net ifade edebilmek adına başka bir dosya oluşturmaya karar verdim.
Hadi sırayla ilerleyelim. Kütüphanemizde ihtiyaç duyabileceğimiz şeyleri kodlayarak başlayalım.
class CMultipleMatLinearReg { private: int m_handle; string m_filename; string DataColumnNames[]; //store the column names from csv file int rows_total; int x_columns_chosen; //Number of x columns chosen bool m_debug; double m_yvalues[]; //y values or dependent values matrix double m_allxvalues[]; //All x values design matrix string m_XColsArray[]; //store the x columns chosen on the Init string m_delimiter; double Betas[]; //Array for storing the coefficients protected: bool fileopen(); void GetAllDataToArray(double& array[]); void GetColumnDatatoArray(int from_column_number, double &toArr[]); public: CMultipleMatLinearReg(void); ~CMultipleMatLinearReg(void); void Init(int y_column, string x_columns="", string filename = NULL, string delimiter = ",", bool debugmode=true); };
Init() fonksiyonunun içerisinde olanlar:
void CMultipleMatLinearReg::Init(int y_column,string x_columns="",string filename=NULL,string delimiter=",",bool debugmode=true) { //--- pass some inputs to the global inputs since they are reusable m_filename = filename; m_debug = debugmode; m_delimiter = delimiter; //--- ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen); //--- if (m_debug) { Print("Init, number of X columns chosen =",x_columns_chosen); ArrayPrint(m_XColsArray); } //--- GetAllDataToArray(m_allxvalues); GetColumnDatatoArray(y_column,m_yvalues); // check for variance in the data set by dividing the rows total size by the number of x columns selected, there shouldn't be a reminder if (rows_total % x_columns_chosen != 0) Alert("There are variance(s) in your dataset columns sizes, This may Lead to Incorrect calculations"); else { //--- Refill the first row of a design matrix with the values of 1 int single_rowsize = rows_total/x_columns_chosen; double Temp_x[]; //Temporary x array ArrayResize(Temp_x,single_rowsize); ArrayFill(Temp_x,0,single_rowsize,1); ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //after filling the values of one fill the remaining space with values of x //Print("Temp x arr size =",ArraySize(Temp_x)); ArrayCopy(m_allxvalues,Temp_x); ArrayFree(Temp_x); //we no longer need this array int tr_cols = x_columns_chosen+1, tr_rows = single_rowsize; ArrayCopy(xT,m_allxvalues); //store the transposed values to their global array before we untranspose them MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //we add one to leave the space for the values of one if (m_debug) { Print("Design matrix"); MatrixPrint(m_allxvalues,tr_cols,tr_rows); } } }
Init() fonksiyonunda neler yapıldığı hakkında daha fazla ayrıntı
ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen);
Burada, TestScript'te Init fonksiyonu çağrılırken seçilen x sütunlarını (bağımsız değişkenler) alıyoruz ve onları m_XColsArray global dizisine depoluyoruz. Sütunları bir dizide bulundurmak, yakında onları okuyacağımız için avantajlara sahiptir. Böylece onları tüm x değerleri dizisine / tüm bağımsız değişkenler dizisine / tasarım matrisine uygun sırada depolayabiliriz.
Ayrıca veri kümelerimizdeki tüm satırların aynı olduğundan emin olmamız gerekiyor, çünkü yalnızca bir satırda veya sütunda bile farklılık olduğunda tüm hesaplamalar başarısız olacaktır.
if (rows_total % x_columns_chosen != 0) Alert("There are variances in your dataset columns sizes, This may Lead to Incorrect calculations");
Ardından tüm x sütunları verilerini tüm x değerleri dizisine / tüm bağımsız değişkenler dizisine / tasarım matrisine (adlandırmak için bunlardan birini seçebilirsiniz) depoluyoruz.
GetAllDataToArray(m_allxvalues);
Ayrıca tüm bağımlı değişkenleri de kendi matrisinde depoluyoruz.
GetColumnDatatoArray(y_column,m_yvalues);
Şimdi ise tasarım matrisini hesaplamalar için hazır hale getirmek adına çok önemli bir adıma geldik. Burada, daha önce belirttiğimiz gibi, tasarım matrisimizin ilk sütununa 1 değerlerini ekliyoruz.
{
//--- Refill the first row of a design matrix with the values of 1
int single_rowsize = rows_total/x_columns_chosen;
double Temp_x[]; //Temporary x array
ArrayResize(Temp_x,single_rowsize);
ArrayFill(Temp_x,0,single_rowsize,1);
ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //after filling the values of one fill the remaining space with values of x
//Print("Temp x arr size =",ArraySize(Temp_x));
ArrayCopy(m_allxvalues,Temp_x);
ArrayFree(Temp_x); //we no longer need this array
int tr_cols = x_columns_chosen+1,
tr_rows = single_rowsize;
MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //we add one to leave the space for the values of one
if (m_debug)
{
Print("Design matrix");
MatrixPrint(m_allxvalues,tr_cols,tr_rows);
}
} Bu sefer, kütüphaneyi başlattığımızda ters transpoze formda matrisin çıktısını alacağız.
Şimdilik Init fonksiyonunda ihtiyacımız olan şeyler bu kadar. Şimdi onu multipleMatRegTestScript.mq5 komut dosyamızda çağıralım (komut dosyası makalenin sonuna eklenmiştir).
#include "multipleMatLinearReg.mqh"; CMultipleMatLinearReg matreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- string filename= "NASDAQ_DATA.csv"; matreg.Init(2,"1,3,4",filename); }
Komut dosyası başarıyla çalıştırıldığında çıktı şu şekilde olacaktır (bu yalnızca bir genel bakıştır):
Init, number of X columns chosen =3 "1" "3" "4" All data Array Size 2232 consuming 52 bytes of memory Design matrix Array [ 1 4174 13387 35 1 4179 13397 37 1 4183 13407 38 1 4186 13417 37 ...... ...... 1 4352 14225 47 1 4402 14226 56 1 4405 14224 56 1 4416 14223 60 ]
xTx'i Bulma
Burada basit regresyonda yaptığımız aynı işlemi uyguluyoruz: csv dosyasından ham veriler olan xT’yi alıyoruz ve onu ters transpoze matrisle çarpıyoruz.
MatrixMultiply(xT,m_allxvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols);
xTx matrisi yazdırıldığında çıktı şu şekilde olacaktır:
xTx [ 744.00 3257845.70 10572577.80 36252.20 3257845.70 14275586746.33 46332484402.07 159174265.78 10572577.80 46332484402.07 150405691938.78 515152629.66 36252.20 159174265.78 515152629.66 1910130.22 ]
Çok iyi, beklendiği gibi çalışıyor.
xTx’in Tersi
Bu, çoklu regresyonun dikkat edilmesi gereken en önemli kısmıdır, çünkü bu kısımda işler çok daha karmaşık hale gelecek ve matematiğin derinliklerine ineceğiz.
Yukarıda, xTx'imizin tersini alırken 2x2'lik bir matrisin tersini alıyorduk. Bu sefer ise 4x4’lük bir matrisin tersini alacağız. 4x4’lük matrisimizde üç sütun bağımsız değişkenlerimize, bir sütunda 1 değerlerine aittir.
Daha önce matrisin tersini alırken kullandığımız yöntemi bu sefer kullanamayız. Peki neden?
Gerçek şu ki, daha önce kullandığımız determinant yöntemi büyük matrislerle çalışmaz. 3x3'lük bir matrisin tersini almak için bile kullanılamaz.
Çeşitli matematikçiler, bir matrisin tersini almak için, klasik ek matris yöntemi dahil çeşitli yöntemler keşfetmişlerdir. Ancak araştırmalarıma göre bu yöntemlerin çoğunun kodlanması gerçekten zor ve kafa karıştırıcı olabiliyor. İlgili yöntemler ve nasıl kodlanabilecekleri hakkında daha fazla bilgi edinmek istiyorsanız, şu blog yazısını okumanızı tavsiye ederim: https://www.geertarien.com/blog/2017/05/15/ Different-methods-for-matrix-inversion/.
Ben tüm yöntemlerden Gauss-Jordan eleme yöntemini seçtim. Çünkü bu yöntemin güvenilir, kodlaması daha kolay ve kolayca ölçeklenebilir olduğunu öğrendim. Gauss-Jordan eleme yöntemini iyi açıklayan harika bir video mevcut, şuradan izleyebilirsiniz: https://www.youtube.com/watch?v=YcP_KOB6KpQ. Umarım video konsepti anlamanıza yardımcı olur.
Hadi şimdi Gauss-Jordan eleme yöntemini kodlayalım. Anlamakta zorlanırsanız, aşağıdaki aynı kod parçasının C++ kodunu, linkini makalenin sonuna eklediğim GitHub'ımdan bulabilirsiniz.
void CMultipleMatLinearReg::Gauss_JordanInverse(double &Matrix[],double &output_Mat[],int mat_order) { int rowsCols = mat_order; //--- Print("row cols ",rowsCols); if (mat_order <= 2) Alert("To find the Inverse of a matrix Using this method, it order has to be greater that 2 ie more than 2x2 matrix"); else { int size = (int)MathPow(mat_order,2); //since the array has to be a square // Create a multiplicative identity matrix int start = 0; double Identity_Mat[]; ArrayResize(Identity_Mat,size); for (int i=0; i<size; i++) { if (i==start) { Identity_Mat[i] = 1; start += rowsCols+1; } else Identity_Mat[i] = 0; } //Print("Multiplicative Indentity Matrix"); //ArrayPrint(Identity_Mat); //--- double MatnIdent[]; //original matrix sided with identity matrix start = 0; for (int i=0; i<rowsCols; i++) //operation to append Identical matrix to an original one { ArrayCopy(MatnIdent,Matrix,ArraySize(MatnIdent),start,rowsCols); //add the identity matrix to the end ArrayCopy(MatnIdent,Identity_Mat,ArraySize(MatnIdent),start,rowsCols); start += rowsCols; } //--- int diagonal_index = 0, index =0; start = 0; double ratio = 0; for (int i=0; i<rowsCols; i++) { if (MatnIdent[diagonal_index] == 0) Print("Mathematical Error, Diagonal has zero value"); for (int j=0; j<rowsCols; j++) if (i != j) //if we are not on the diagonal { /* i stands for rows while j for columns, In finding the ratio we keep the rows constant while incrementing the columns that are not on the diagonal on the above if statement this helps us to Access array value based on both rows and columns */ int i__i = i + (i*rowsCols*2); diagonal_index = i__i; int mat_ind = (i)+(j*rowsCols*2); //row number + (column number) AKA i__j ratio = MatnIdent[mat_ind] / MatnIdent[diagonal_index]; DBL_MAX_MIN(MatnIdent[mat_ind]); DBL_MAX_MIN(MatnIdent[diagonal_index]); //printf("Numerator = %.4f denominator =%.4f ratio =%.4f ",MatnIdent[mat_ind],MatnIdent[diagonal_index],ratio); for (int k=0; k<rowsCols*2; k++) { int j_k, i_k; //first element for column second for row j_k = k + (j*(rowsCols*2)); i_k = k + (i*(rowsCols*2)); //Print("val =",MatnIdent[j_k]," val = ",MatnIdent[i_k]); //printf("\n jk val =%.4f, ratio = %.4f , ik val =%.4f ",MatnIdent[j_k], ratio, MatnIdent[i_k]); MatnIdent[j_k] = MatnIdent[j_k] - ratio*MatnIdent[i_k]; DBL_MAX_MIN(MatnIdent[j_k]); DBL_MAX_MIN(ratio*MatnIdent[i_k]); } } } // Row Operation to make Principal diagonal to 1 /*back to our MatrixandIdentical Matrix Array then we'll perform operations to make its principal diagonal to 1 */ ArrayResize(output_Mat,size); int counter=0; for (int i=0; i<rowsCols; i++) for (int j=rowsCols; j<2*rowsCols; j++) { int i_j, i_i; i_j = j + (i*(rowsCols*2)); i_i = i + (i*(rowsCols*2)); //Print("i_j ",i_j," val = ",MatnIdent[i_j]," i_i =",i_i," val =",MatnIdent[i_i]); MatnIdent[i_j] = MatnIdent[i_j] / MatnIdent[i_i]; //printf("%d Mathematical operation =%.4f",i_j, MatnIdent[i_j]); output_Mat[counter]= MatnIdent[i_j]; //store the Inverse of Matrix in the output Array counter++; } } //--- }
Harika, şimdi fonksiyonu çağıralım ve matrisin tersini yazdıralım:
double inverse_xTx[]; Gauss_JordanInverse(xTx,inverse_xTx,tr_cols); if (m_debug) { Print("xtx Inverse"); MatrixPrint(inverse_xTx,tr_cols,tr_cols,7); }
Çıktı şu şekilde olacaktır:
xtx Inverse [ 3.8264763 -0.0024984 0.0004760 0.0072008 -0.0024984 0.0000024 -0.0000005 -0.0000073 0.0004760 -0.0000005 0.0000001 0.0000016 0.0072008 -0.0000073 0.0000016 0.0000290 ]
Unutmayın, matrisin tersini alabilmek için matris kare matris olmalıdır. Bu nedenle fonksiyon argümanlarında satır ve sütun sayısına eşit olan mat_order argümanına sahibiz.
xTy’yi Bulma
Şimdi transpoze x ile y'nin çarpımını bulalım. Bu, daha önce yaptığımız işlemin aynısıdır.
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //remember!! the value of 1 at the end is because we have only one dependent variable y
Çıktı yazdırıldığında şu şekilde görünecektir:
xTy [ 10550016.70000 46241904488.26996 150084914994.69019 516408161.98000 ]
Çok iyi, beklendiği gibi 1x4 matris.
Formülü hatırlayalım:
Artık katsayıları bulmak için ihtiyacımız olan her şeye sahip olduğumuza göre, son kısma geçelim.
MatrixMultiply(inverse_xTx,xTy,Betas,tr_cols,tr_cols,tr_cols,1); Çıktı şu şekilde olacaktır (ve yine, katsayılarımızın/beta matrisimizin ilk öğesinin sabit veya başka bir deyişle y-kesimi olacağını unutmayın):
Coefficients Matrix [ -3670.97167 2.75527 0.37952 8.06681 ]
Harika! Şimdi Python ile görelim.
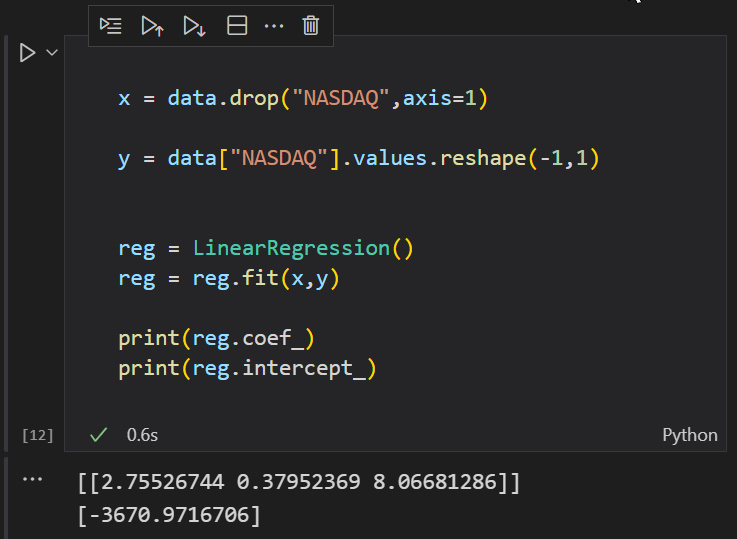
Mükemmel!!!
Artık nihayet çoklu dinamik regresyon modelleri MQL5’te kullanılabilir. Şimdi her şeyin nasıl başladığına bir göz atalım.
Her şey şu şekilde başladı:
matreg.Init(2,"1,3,4",filename);
Fikir, sınırsız sayıda bağımsız değişkenin girilmesine olanak sağlayacak bir dizge girdisi elde etmekti. Ve görünün şu ki MQL5'te, çok sayıda argüman girmemize olanak sağlayan, Python gibi dillerdeki *args ve *kwargs'a sahip olmamızın hiçbir yolu yok. Tek yol dizgeyi kullanmak ve ardından tek dizinin tüm verilerimizi içermesi için diziyi manipüle etmenin bir yolunu bulmaktı. Daha fazla bilgi için ilk başarısız denememe göz atabilirsiniz: https://www.mql5.com/tr/code/38894. Tüm bunları söylememin nedeni, birinin bu ya da başka bir projede aynı yolu izleyebileceğini düşünmemdir. Dolayısıyla, bu konuda benim için nelerin işe yarayıp nelerin yaramadığını açıklamak istedim.
Son Düşünceler
Artık istediğimiz kadar bağımsız değişkene sahip olabilmemiz kulağa ne kadar hoş gelse de, çok fazla bağımsız değişkene veya çok uzun veri kümesi sütunlarına sahip olan her şeyin bir sınırı olacağını unutmayın. Örneğin, bilgisayarın hesaplama gücünün sınırıyla karşılaşabiliriz. Yukarıda gördüğümüz gibi, matris hesaplamaları ciddi şekilde zaman alıcı olabiliyor.
Bağımsız değişkenlerin çoklu lineer regresyon modeline eklenmesi, r-kare olarak ifade edilen bağımlı değişkenin varyansının büyüklüğünü her zaman artıracaktır, bu nedenle herhangi bir teorik gerekçe olmadan çok fazla bağımsız değişken eklemek modelin aşırı uyumuna yol açabilir.
Örneğin, bu serinin ilk makalesinde yaptığımız gibi, NASDAQ bağımlı değişkeni ve S&P500 bağımsız değişkeni olmak üzere yalnızca iki değişkene dayalı bir model oluştursaydık, doğruluğumuz %95'in üzerinde olabilirdi, ancak bu sefer durum böyle olmayabilir, çünkü şimdi 3 bağımsız değişkene sahip olacağız.
Modelin doğruluğunu, onu oluşturduktan sonra kontrol etmek her zaman iyi bir fikirdir. Ayrıca modeli oluşturmadan önce her bir bağımsız değişken ile hedef arasında bir korelasyon olup olmadığını da kontrol etmemiz gerekir.
Daima hedef değişkeninizle güçlü bir lineer ilişkiye sahip verilere dayalı bir model oluşturun.
İlginiz için teşekkürler. İşte GitHub depomun linki: https://github.com/MegaJoctan/MatrixRegressionMQL5.git.
MetaQuotes Ltd tarafından İngilizceden çevrilmiştir.
Orijinal makale: https://www.mql5.com/en/articles/10928
Uyarı: Bu materyallerin tüm hakları MetaQuotes Ltd.'a aittir. Bu materyallerin tamamen veya kısmen kopyalanması veya yeniden yazdırılması yasaktır.
Bu makale sitenin bir kullanıcısı tarafından yazılmıştır ve kendi kişisel görüşlerini yansıtmaktadır. MetaQuotes Ltd, sunulan bilgilerin doğruluğundan veya açıklanan çözümlerin, stratejilerin veya tavsiyelerin kullanımından kaynaklanan herhangi bir sonuçtan sorumlu değildir.
 Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 07): Hacim profili ekleme (I)
Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 07): Hacim profili ekleme (I)
 ATR göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?
ATR göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?
 Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 08): Kavramsal sıçrama (I)
Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 08): Kavramsal sıçrama (I)
 ADX göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?
ADX göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz

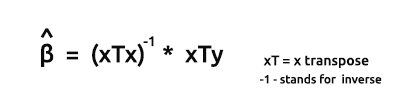
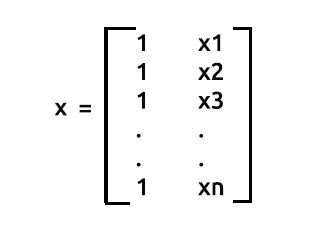
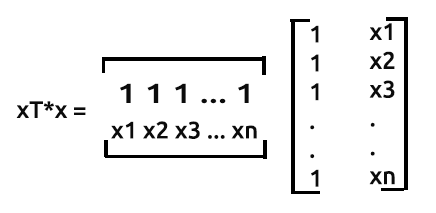

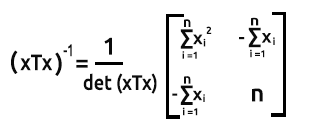
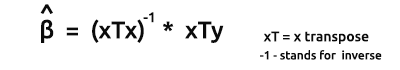
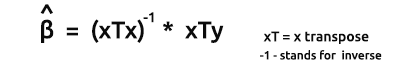
Yeni makale Veri Bilimi ve Makine Öğrenimi bölüm 03: Matris Regresyonları yayınlandı:
Yazar Omega J Msigwa