
Aprendizaje automático y data science (Parte 03): Regresión matricial
Tras un largo periodo de pruebas y errores, por fin se ha resuelto el enigma de la regresión dinámica múltiple... Continuar leyendo.
Si ha prestado atención a los dos artículos anteriores, probablemente se habrá dado cuenta de un gran problema con el que me he encontrado: la programación de modelos que puedan manejar un número mayor de variables independientes. Aquí me refiero al procesamiento dinámico de más datos de entrada, porque estamos tratando con cientos de datos a la hora de crear estrategias. Por eso debemos asegurarnos de que los modelos pueden cumplir este requisito.
Matriz
Si usted se perdió en su día la clase de matemáticas correspondiente, una matriz es un array o tabla rectangular de números u otros objetos matemáticos dispuestos en filas y columnas que se usan para representar un objeto matemático o una propiedad de dicho objeto.
Por ejemplo:
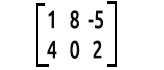
La forma en que leemos las matrices es con filas x columnas. Arriba tenemos una matriz de 2x3, lo cual significa que tenemos 2 filas y 3 columnas.
No cabe duda de que las matrices juegan un enorme papel en la forma en que las computadoras modernas procesan la información y calculan números de grandes dimensiones. La razón principal es que los datos de una matriz se almacenan como un array que las computadoras pueden leer y procesar. Así pues, vamos a ver su aplicación en el aprendizaje automático.
Regresión lineal
Las matrices permiten realizar cálculos de álgebra lineal. El estudio de las matrices constituye un gran apartado del álgebra lineal. Por lo tanto, las matrices pueden usarse para crear modelos de regresión lineal.
Como todos sabemos, la ecuación de la línea recta tiene el aspecto siguiente:
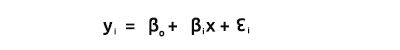
donde ∈ representa el error, y Bo y Bi son el coeficiente de intersección y, y el coeficiente de pendiente, respectivamente.
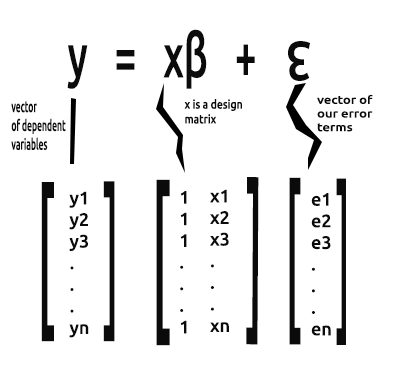
A partir de ahora, nos interesará la forma vectorial de la ecuación, aquí la tenemos:
Es una fórmula de regresión lineal simple en forma de matriz.
En un modelo lineal simple (y en otros modelos de regresión), solemos buscar los coeficientes de error de pendiente/valoraciones habituales usando el método de los mínimos cuadrados.
Entendemos por vector beta el vector que contiene valores beta.
Bo yB1, como se explica en la ecuación:
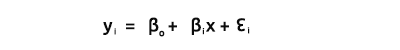
Tenemos que encontrar los coeficientes, ya que son muy importantes a la hora de construir el modelo.
Fórmula para valorar los modelos en forma vectorial:
Esta fórmula es muy importante, y debería memorizarla.
Pronto veremos cómo encontrar los elementos usando una fórmula.
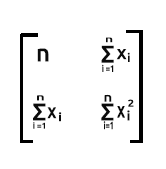
El resultado del producto xTx será una matriz simétrica, ya que el número de columnas de xT será igual al número de filas en x. Lo veremos más adelante en un ejemplo.
Como hemos dicho anteriormente,
x también se denomina matriz de diseño. Este es el aspecto que tiene dicha matriz:
Matriz de diseño
Como podemos ver, en la primera columna solo hemos colocado los valores 1 hasta el final de nuestras filas en la matriz. Este es el primer paso al preparar los datos para la regresión matricial. Verá los beneficios de este paso en particular a medida que avancemos en los cálculos.
Realizamos este proceso en la función Init() de nuestra biblioteca.
void CSimpleMatLinearRegression::Init(double &x[],double &y[], bool debugmode=true) { ArrayResize(Betas,2); //como se trata de una regresión lineal simple, solo tenemos dos variables x e y if (ArraySize(x) != ArraySize(y)) Alert("Se ha detectado una diferencia entre el número de variables independientes y dependientes \n Los cálculos podrían resultar erróneos"); m_rowsize = ArraySize(x); ArrayResize(m_xvalues,m_rowsize+m_rowsize); //añadimos un espacio con el tamaño de una fila para los valores rellenados ArrayFill(m_xvalues,0,m_rowsize,1); //rellenamos la primera línea con unidades, aquí tenemos dónde se realiza la operación ArrayCopy(m_xvalues,x,m_rowsize,0,WHOLE_ARRAY); //añadimos los valores x a la matriz, comenzando por el lugar donde se acabaron los valores rellenados ArrayCopy(m_yvalues,y); m_debug=debugmode; }
Aquí rellenaremos los valores de la matriz de diseño. El resultado se muestra abajo. Observe la línea en la que se rellenan los valores unitarios y comienzan los valores x calculados.
[ 0] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 21] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
........
........
[ 693] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 714] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 735] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 4173.8 4179.2 4182.7 4185.8 4180.8 4174.6 4174.9 4170.8 4182.2 4208.4 4247.1 4217.4
[ 756] 4225.9 4211.2 4244.1 4249.0 4228.3 4230.6 4235.9 4227.0 4225.0 4219.7 4216.2 4225.9 4229.9 4232.8 4226.4 4206.9 4204.6 4234.7 4240.7 4243.4 4247.7
........
........
[1449] 4436.4 4442.2 4439.5 4442.5 4436.2 4423.6 4416.8 4419.6 4427.0 4431.7 4372.7 4374.6 4357.9 4381.6 4345.8 4296.8 4321.0 4284.6 4310.9 4318.1 4328.0
[1470] 4334.0 4352.3 4350.6 4354.0 4340.1 4347.5 4361.3 4345.9 4346.5 4342.8 4351.7 4326.0 4323.2 4332.7 4352.5 4401.9 4405.2 4415.8
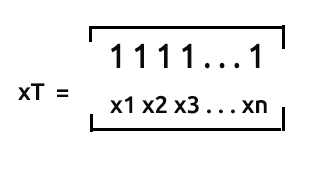
xT o transposición x es el proceso por el cual intercambiamos filas y columnas en una matriz.
Esto indica que si multiplicamos estas dos matrices...
Por ahora nos saltaremos el proceso de transposición de la matriz, porque, debido a la forma en que hemos recopilado nuestros datos, la matriz ya se encuentra en forma transpuesta. Aunque, por otra parte, será necesario realizar la transposición inversa de los valores x, para que podamos multiplicarlos por la matriz x ya transpuesta.
Es decir, para una matriz nx2 que no esté transpuesta, la matriz quedaría como [1 x1 1 x2 1 ... 1 xn]. Veamos ahora cómo funciona.
Transposición inversa de la matriz X
Nuestra matriz en forma transpuesta, derivada del archivo csv, tendrá el siguiente aspecto al imprimirse
Matriz transpuesta
[
[ 0] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
...
...
[ 0] 4174 4179 4183 4186 4181 4175 4175 4171 4182 4208 4247 4217 4226 4211 4244 4249 4228 4231 4236 4227 4225 4220 4216 4226
...
...
[720] 4297 4321 4285 4311 4318 4328 4334 4352 4351 4354 4340 4348 4361 4346 4346 4343 4352 4326 4323 4333 4352 4402 4405 4416
]
El proceso de transposición inversa consiste simplemente en intercambiar filas y columnas; es decir, lo inverso de la transposición de una matriz.
int tr_rows = m_rowsize, tr_cols = 1+1; //como tenemos una variable independiente, la añadiremos para el espacio creado con las unidades MatrixUnTranspose(m_xvalues,tr_cols,tr_rows); Print("UnTransposed Matrix"); MatrixPrint(m_xvalues,tr_cols,tr_rows);
Aquí es donde las cosas se vuelven complicadas
Ponemos las columnas de la matriz transpuesta donde deben encontrarse las filas, y las filas donde deben estar las columnas. La salida después de ejecutar este trozo de código será:
Matriz transpuesta inversa [ 1 4248 1 4201 1 4352 1 4402 ... ... 1 4405 1 4416 ]
xT es una matriz 2xn, la matriz x es nx2. La matriz final será de 2x2.
Bien, veamos cómo sería el producto de su multiplicación.
Nota: las matrices deberán ser compatibles para la multiplicación, es decir, el número de columnas de la primera matriz deberá ser igual al número de filas de la segunda.
Podrá consultar las reglas de multiplicación de las matrices aquí:
Cómo tiene lugar la multiplicación en esta matriz:
- La fila 1 multiplicada por la columna 1
- La fila 1 multiplicada por la columna 2
- La fila 2 multiplicada por la columna 1
- La fila 2 multiplicada por la columna 2
En el caso de nuestras matrices, la fila 1 multiplicada por la columna 1 será igual a la suma del producto de la fila 1, que contiene los valores de la unidad, y el producto de la columna 1, que también contiene los valores de la unidad, no se diferenciará del incremento del valor uno a uno en cada iteración.
Preste atención:
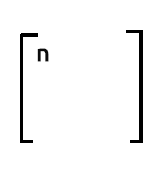
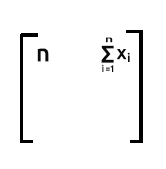
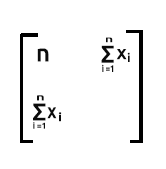
Si desea conocer el número de observaciones de su conjunto de datos, podrá basarse en el número de la primera columna de la primera fila de la salida de xTx
Fila 1 multiplicada por la columna 2. Como la fila 1 contiene unidades, cuando sumamos el producto de la fila 1 (donde tenemos unidades) y la columna 2(con valores de x), la salida será la suma de los elementos de x, porque las unidades no tienen efecto en la multiplicación.
Fila 2 multiplicada por la columna 1. El resultado será la suma de x, porque, una vez más, las unidades de la fila 2 no tendrán efecto en la multiplicación con los valores de x que están en la columna 1
La última parte es la suma de los cuadrados de los valores x.
Es la suma de los productos de la fila 2, que contiene los valores de x, y la columna 2, que también contiene los valores de x.
De esta forma, en nuestro caso terminamos con una matriz de 2x2.
Veamos ahora cómo funciona en la realidad. Para ello, usaremos el conjunto de datos de nuestro primer artículo, centrado en la regresión lineal: https://www.mql5.com/es/articles/10459
Extraemos los datos y los ponemos en un array x para la variable independiente y un array y para las variables dependientes.
//en el script MatrixRegTest.mq5 #include "MatrixRegression.mqh"; #include "LinearRegressionLib.mqh"; CSimpleMatLinearRegression matlr; CSimpleLinearRegression lr; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //double x[] = {651,762,856,1063,1190,1298,1421,1440,1518}; //ventas //double y[] = {23,26,30,34,43,48,52,57,58}; //dinero gastado en publicidad //--- double x[], y[]; string file_name = "NASDAQ_DATA.csv", delimiter = ","; lr.GetDataToArray(x,file_name,delimiter,1); lr.GetDataToArray(y,file_name,delimiter,2); }
Aquí hemos importado la biblioteca CsimpleLinearRegression que creamos en el primer artículo,
CSimpleLinearRegression lr;
porque esta biblioteca contiene ciertas funciones que necesitaremos, como la obtención de los datos en arrays.
Buscamos xTx:
MatrixMultiply(xT,m_xvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols); Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5); //¿Recuerda? En la salida de la matriz obtenemos la fila 1 y la columna 2, resaltadas en color rojo
Si presta atención al array xT[], se dará cuenta de que hemos copiado los valores de x y los hemos almacenado en este array xT[], solo para clarificar: como ya hemos dicho antes, la forma en que hemos recopilado los datos de nuestro archivo CSV en un array usando GetDataToArray() nos da los datos ya de forma transpuesta.
A continuación, multiplicamos el array xT[] por m_xvalues[], que ahora no están transpuestos. m_xvalues es un array definido globalmente para los valores de x en esta biblioteca. Y esto es lo que encontramos dentro de la función MatrixMultiply():
void CSimpleMatLinearRegression::MatrixMultiply(double &A[],double &B[],double &output_arr[],int row1,int col1,int row2,int col2) { //--- double MultPl_Mat[]; //aquí guardaremos la multiplicación if (col1 != row2) Alert("Matrix Multiplication Error, \n The number of columns in the first matrix is not equal to the number of rows in second matrix"); else { ArrayResize(MultPl_Mat,row1*col2); int mat1_index, mat2_index; if (col1==1) //Multiplicación para la matriz unidimensional { for (int i=0; i<row1; i++) for(int k=0; k<row1; k++) { int index = k + (i*row1); MultPl_Mat[index] = A[i] * B[k]; } //Print("Matrix Multiplication output"); //ArrayPrint(MultPl_Mat); } else { //si la matriz tiene más de dos dimensiones for (int i=0; i<row1; i++) for (int j=0; j<col2; j++) { int index = j + (i*col2); MultPl_Mat[index] = 0; for (int k=0; k<col1; k++) { mat1_index = k + (i*row2); //k + (i*row2) mat2_index = j + (k*col2); //j + (k*col2) //Print("index out ",index," index a ",mat1_index," index b ",mat2_index); MultPl_Mat[index] += A[mat1_index] * B[mat2_index]; DBL_MAX_MIN(MultPl_Mat[index]); } //Print(index," ",MultPl_Mat[index]); } ArrayCopy(output_arr,MultPl_Mat); ArrayFree(MultPl_Mat); } } }
Para ser sinceros, esta multiplicación parece un poco confusa, sobre todo cuando vemos cosas como
k + (i*row2); j + (k*col2);
Pero no se alarme. La forma de trabajar con los índices permite obtener un índice en una fila y una columna determinadas. Esto sería más fácil de entender si usáramos arrays bidimensionales, por ejemplo, Matrix[rows][columns], en nuestro caso, sería Matrix[i][k]. Pero hemos decidido no hacerlo porque los arrays multidimensionales tienen limitaciones, así que hemos tenido que buscar otra manera. Al final del artículo, tenemos un código C++ sencillo adjunto, que a buen seguro le ayudará a entender cómo lo hemos hecho. Si quiere saber más, le recomendamos el blog
El resultado de una salida xTx exitosa mostrada por MatrixPrint() será:
Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5); xTx [ 744.00000 3257845.70000 3257845.70000 14275586746.32998 ]
Como podrá ver, el primer elemento de nuestro array xTx contiene el número de observaciones para todos los datos de nuestro conjunto de datos, por lo que es importante rellenar la matriz de diseño con valores iguales a la unidad inicialmente en la primera columna.
Ahora vamos a encontrar la inversa de la matriz xTx.
Inversa de la matriz xTx
Para hallar la inversa de una matriz 2x2, primero se intercambian el primer y el último elemento de la diagonal y luego se añade un signo menos a los otros dos valores.
La fórmula se muestra en la siguiente imagen:
Para encontrar el determinante de una matriz det(xTx) = Producto de la primera diagonal - Producto de la segunda diagonal
Así es como podemos encontrar la inversa de la matriz en código mql5:
void CSimpleMatLinearRegression::MatrixInverse(double &Matrix[],double &output_mat[]) { // Según las reglas de las matrices, la inversa de una matriz solo se puede encontrar cuando // La matriz es idéntica, comienza con una matriz de 2x2; así que ese será nuestro punto de partida int matrix_size = ArraySize(Matrix); if (matrix_size > 4) Print("Matrix allowed using this method is a 2x2 matrix Only"); if (matrix_size==4) { MatrixtypeSquare(matrix_size); //el primer paso consistirá en intercambiar el primer y último valor de la matriz //en este punto sabemos que el último valor será igual al tamaño de la matriz menos uno int last_mat = matrix_size-1; ArrayCopy(output_mat,Matrix); // primera diagonal output_mat[0] = Matrix[last_mat]; //intercambiamos la primera matriz y la última output_mat[last_mat] = Matrix[0]; //intercambiamos la última matriz y la primera double first_diagonal = output_mat[0]*output_mat[last_mat]; // segunda diagonal //añadimos el signo menos >>> output_mat[1] = - Matrix[1]; output_mat[2] = - Matrix[2]; double second_diagonal = output_mat[1]*output_mat[2]; if (m_debug) { Print("Diagonal already Swapped Matrix"); MatrixPrint(output_mat,2,2); } //fórmula de la matriz inversa 1/det(xTx) * (xtx)-1 //el determinante es igual al producto de la primera diagonal por el producto de la segunda diagonal double det = first_diagonal-second_diagonal; if (m_debug) Print("determinant =",det); for (int i=0; i<matrix_size; i++) { output_mat[i] = output_mat[i]*(1/det); DBL_MAX_MIN(output_mat[i]); } } }
El resultado de la ejecución de este bloque de código será el siguiente:
Diagonal already Swapped Matrix
[
14275586746 -3257846
-3257846 744
]
determinant =7477934261.0234375
Imprimimos la inversa de la matriz para ver cómo queda.
Print("inverse xtx"); MatrixPrint(inverse_xTx,2,2,_digits); //la inversa de una lr simple siempre será una matriz 2x2
La conclusión sería:
[
1.9090281 -0.0004357
-0.0004357 0.0000001
]
Ahora que hemos encontrado la inversa de xTx, podemos seguir adelante.
Encontramos xTy
Aquí multiplicamos xT[] por los valores de y[].
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //al final 1, porque una matriz de valores "y" siempre tendrá una de esas columnas Print("xTy"); MatrixPrint(xTy,tr_rows,1,_digits); //una vez más, ¿recuerda? ¿Cómo encontramos el valor de salida de nuestra matriz row1 x column2?
La salida sería la siguiente:
xTy
[
10550016.7000000 46241904488.2699585
]
Mire la fórmula:
Así que ya tenemos la inversa de xTx y xTy. Procedemos al paso siguiente.
MatrixMultiply(inverse_xTx,xTy,Betas,2,2,2,1); //la inversa es una matriz cuadrada 2x2, а xty — 2x1 Print("coefficients"); MatrixPrint(Betas,2,1,5); // para una matriz lr simple con beta será 2x1
Más información sobre cómo llamamos a la función.
El resultado de este fragmento de código será el que sigue:
coefficients
[
-5524.40278 4.49996
]
¡Ta-da! Este es el mismo resultado sobre nuestros coeficientes que pudimos obtener usando el modelo en forma escalar en la primera parte de esta serie.
El número en el primer índice del array beta siempre será una constante/intercepción Y. La razón por la que podemos conseguirlo inicialmente es que hemos rellenado la matriz de diseño con valores de la unidad en la primera columna. Una vez más, esto demuestra lo importante que resulta todo el proceso, pues deja espacio en esta columna para una intersección y.
Terminamos con una simple regresión lineal. Veamos ahora cómo quedaría una regresión múltiple. Ahora hay que tener especial cuidado, porque más adelante resultará más difícil.
resolución del problema de regresión dinámica múltiple
La ventaja de construir modelos basados en una matriz es que son fáciles de escalar sin tener que modificar mucho el código a la hora de construir el modelo. El cambio significativo que notará con la regresión múltiple es cómo encontramos las matrices, porque esa parte es la más complicada: he pasado mucho tiempo tratando de entenderla. Profundizaremos en esto más adelante, cuando lleguemos a la sección correspondiente. Ahora vamos a añadir al código cosas que podrían resultar necesarias en nuestra biblioteca de Regresión Matricial Múltiple.
Podríamos tener una sola biblioteca que maneje la regresión simple y múltiple, y solo introduciríamos los argumentos de la función. Sin embargo, hemos decidido crear otro archivo para explicar cómo funcionan las cosas, ya que el proceso será muy parecido. Aquí esperamos que haya entendido los cálculos que hicimos en la sección de regresión lineal simple comentada anteriormente.
Vayamos por orden. En primer lugar, escribiremos las cosas básicas que podrían ser útiles en nuestra biblioteca.
class CMultipleMatLinearReg { private: int m_handle; string m_filename; string DataColumnNames[]; //guardamos los nombres de las columnas del archivo csv int rows_total; int x_columns_chosen; //número seleccionado de columnas x bool m_debug; double m_yvalues[]; //valores "y" o matriz de valores dependientes double m_allxvalues[]; //todos los valores x de la matriz de diseño string m_XColsArray[]; //almacenamos las x columnas elegidas en el Init string m_delimiter; double Betas[]; //array para guardar los coeficientes protected: bool fileopen(); void GetAllDataToArray(double& array[]); void GetColumnDatatoArray(int from_column_number, double &toArr[]); public: CMultipleMatLinearReg(void); ~CMultipleMatLinearReg(void); void Init(int y_column, string x_columns="", string filename = NULL, string delimiter = ",", bool debugmode=true); };
Y esto es lo que sucede dentro de la función Init()
void CMultipleMatLinearReg::Init(int y_column,string x_columns="",string filename=NULL,string delimiter=",",bool debugmode=true) { //--- algunos de los inputs se transfieren a los inputs globales, ya que se utilizan de nuevo m_filename = filename; m_debug = debugmode; m_delimiter = delimiter; //--- ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen); //--- if (m_debug) { Print("Init, number of X columns chosen =",x_columns_chosen); ArrayPrint(m_XColsArray); } //--- GetAllDataToArray(m_allxvalues); GetColumnDatatoArray(y_column,m_yvalues); // verificamos la variación en el conjunto de datos dividiendo el tamaño total de las filas por el número de columnas x seleccionadas if (rows_total % x_columns_chosen != 0) Alert("There are variance(s) in your dataset columns sizes, This may Lead to Incorrect calculations"); else { //--- rellenamos la primera fila de la matriz de diseño con valores 1 int single_rowsize = rows_total/x_columns_chosen; double Temp_x[]; //array temporal x ArrayResize(Temp_x,single_rowsize); ArrayFill(Temp_x,0,single_rowsize,1); ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //después de rellenar con unidades, rellenamos los elementos restantes con valores x //Print("Temp x arr size =",ArraySize(Temp_x)); ArrayCopy(m_allxvalues,Temp_x); ArrayFree(Temp_x); //ya no necesitamos este array int tr_cols = x_columns_chosen+1, tr_rows = single_rowsize; ArrayCopy(xT,m_allxvalues); //almacenamos los valores transpuestos en una matriz global antes de transponer de nuevo MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //añadimos para dejar espacio para los valores de unidad if (m_debug) { Print("Design matrix"); MatrixPrint(m_allxvalues,tr_cols,tr_rows); } } }
Más información sobre lo que hemos hecho.
ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen);
Aquí obtenemos las columnas x que han sido seleccionadas (variables independientes) al llamar a la función de inicialización en TestScript. A continuación, almacenamos estas columnas en el array global m_XColsArray. La ventaja de tener columnas en el array es que pronto las leeremos, y esto las mantendrá en el orden correcto en el array con todos los valores de x en la matriz de variables independientes/matriz de diseño.
También tenemos que asegurarnos de que todas las filas de nuestros conjuntos de datos sean iguales, porque si hay una diferencia en una sola fila o columna, el cálculo fallará.
if (rows_total % x_columns_chosen != 0) Alert("There are variances in your dataset columns sizes, This may Lead to Incorrect calculations");
A continuación, obtenemos todos los datos de la columna x en un array/matriz de diseño/array de todas las variables independientes (elija un nombre apropiado entre todo ello).
GetAllDataToArray(m_allxvalues);
También deberemos guardar todas las variables dependientes en la matriz.
GetColumnDatatoArray(y_column,m_yvalues);
Este es un paso muy importante: la preparación de la matriz de diseño para el cálculo. Añadimos unidades a la primera columna de nuestra matriz de valores x, como hemos mencionado antes aquí.
{
//--- rellenamos la primera fila de la matriz de diseño con valores 1
int single_rowsize = rows_total/x_columns_chosen;
double Temp_x[]; //array temporal x
ArrayResize(Temp_x,single_rowsize);
ArrayFill(Temp_x,0,single_rowsize,1);
ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //después de rellenar con unidades, rellenamos los elementos restantes con valores x
//Print("Temp x arr size =",ArraySize(Temp_x));
ArrayCopy(m_allxvalues,Temp_x);
ArrayFree(Temp_x); //ya no necesitamos este array
int tr_cols = x_columns_chosen+1,
tr_rows = single_rowsize;
MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //añadimos para dejar espacio para los valores de unidad
if (m_debug)
{
Print("Design matrix");
MatrixPrint(m_allxvalues,tr_cols,tr_rows);
}
}
Esta vez, al inicializar la biblioteca, mostraremos una matriz no transformada.
Esto es todo lo que necesitamos para la función Init. Ahora vamos a llamarla en nuestro script MultipleMatRegTestScript.mq5 (enlace al final del artículo).
#include "multipleMatLinearReg.mqh"; CMultipleMatLinearReg matreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- string filename= "NASDAQ_DATA.csv"; matreg.Init(2,"1,3,4",filename); }
Después de ejecutar con éxito el script, obtendremos en la salida (es solo un ejemplo)
Init, number of X columns chosen =3 "1" "3" "4" All data Array Size 2232 consuming 52 bytes of memory Design matrix Array [ 1 4174 13387 35 1 4179 13397 37 1 4183 13407 38 1 4186 13417 37 ...... ...... 1 4352 14225 47 1 4402 14226 56 1 4405 14224 56 1 4416 14223 60 ]
Encontramos xTx
Aquí tenemos lo mismo que hicimos con la regresión simple. Es el mismo proceso: tomamos los valores xT, que son los datos brutos del archivo csv, y luego los multiplicamos por la matriz no transformada.
MatrixMultiply(xT,m_allxvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols);
La salida al imprimir la matriz xTx será la siguiente:
xTx [ 744.00 3257845.70 10572577.80 36252.20 3257845.70 14275586746.33 46332484402.07 159174265.78 10572577.80 46332484402.07 150405691938.78 515152629.66 36252.20 159174265.78 515152629.66 1910130.22 ]
¡Magnífico! Funciona como debe.
Matriz inversa xTx
Esta es la parte más importante de la regresión múltiple a la que debemos prestar atención, porque las cosas se complican y nos adentramos en las matemáticas.
Cuando buscábamos la inversa de nuestra matriz xTx en el artículo anterior, obteníamos una matriz inversa de 2x2. Pero esta vez iremos más allá: en esta ocasión, encontraremos una matriz inversa de 4x4, porque hemos elegido 3 columnas como variables independientes, y al añadir los valores de otra columna, obtendremos 4 columnas. Estas son las que nos llevarán a la matriz 4x4 cuando tratemos de encontrar la inversa.
Esta vez no nos funcionará el método que hemos usado antes en la búsqueda de la inversa. ¡Atención, pregunta! ¿Por qué?
La cuestión es que la búsqueda de la matriz inversa utilizando el método determinante que usamos antes, no funciona con matrices grandes. Ni siquiera sirve para las matrices de 3x3.
Varios matemáticos han propuesto diferentes métodos para encontrar la inversa de la matriz, uno de los cuales es el clásico método conjugado. Sin embargo, según nuestras investigaciones, la mayoría de estos métodos son difíciles de convertir en código, y pueden resultar confusos. Si quiere saber más sobre los métodos y cómo se pueden programar, le recomendamos que lea esta entrada del blog: https://www.geertarien.com/blog/2017/05/15/different-methods-for-matrix-inversion/
De todos los métodos disponibles, hemos elegido la excepción de Gauss-Jordan. Nos parece fiable, sencillo de escribir como código y fácilmente escalable. Existe un vídeo excelente https://www.youtube.com/watch?v=YcP_KOB6KpQ que explica muy bien el método de Gauss-Jordan. Esperamos que le ayude a entender el concepto.
Bien, vamos a escribir el código del método Gauss-Jordan. Si le resulta difícil de entender, hemos implementado un código para el mismo fragmento en c++. Abajo encontrará el enlace al mismo, así como a mi GitHub. Quizá más ejemplos le ayuden a comprender cómo hemos hecho todo.
void CMultipleMatLinearReg::Gauss_JordanInverse(double &Matrix[],double &output_Mat[],int mat_order) { int rowsCols = mat_order; //--- Print("row cols ",rowsCols); if (mat_order <= 2) Alert("To find the Inverse of a matrix Using this method, it order has to be greater that 2 ie more than 2x2 matrix"); else { int size = (int)MathPow(mat_order,2); //ya que el array debe ser cuadrado // Creamos una matriz de identidad multiplicativa int start = 0; double Identity_Mat[]; ArrayResize(Identity_Mat,size); for (int i=0; i<size; i++) { if (i==start) { Identity_Mat[i] = 1; start += rowsCols+1; } else Identity_Mat[i] = 0; } //Print("Multiplicative Indentity Matrix"); //ArrayPrint(Identity_Mat); //--- double MatnIdent[]; //matriz original por el lado de la matriz de identidad start = 0; for (int i=0; i<rowsCols; i++) //operación para añadir una matriz idéntica a una original { ArrayCopy(MatnIdent,Matrix,ArraySize(MatnIdent),start,rowsCols); //añadimos la matriz de identidad al final ArrayCopy(MatnIdent,Identity_Mat,ArraySize(MatnIdent),start,rowsCols); start += rowsCols; } //--- int diagonal_index = 0, index =0; start = 0; double ratio = 0; for (int i=0; i<rowsCols; i++) { if (MatnIdent[diagonal_index] == 0) Print("Mathematical Error, Diagonal has zero value"); for (int j=0; j<rowsCols; j++) if (i != j) //if we are not on the diagonal { /* i indica las filas, mientras que j indica las columnas. Al encontrar la relación, las filas serán constantes, y al mismo tiempo incrementaremos las columnas que no estén en la diagonal en la expresión if anterior. Esto permitirá Acceder al valor de la matriz basado en las filas y columnas */ int i__i = i + (i*rowsCols*2); diagonal_index = i__i; int mat_ind = (i)+(j*rowsCols*2); //row number + (column number) AKA i__j ratio = MatnIdent[mat_ind] / MatnIdent[diagonal_index]; DBL_MAX_MIN(MatnIdent[mat_ind]); DBL_MAX_MIN(MatnIdent[diagonal_index]); //printf("Numerator = %.4f denominator =%.4f ratio =%.4f ",MatnIdent[mat_ind],MatnIdent[diagonal_index],ratio); for (int k=0; k<rowsCols*2; k++) { int j_k, i_k; //primer elemento para la columna, segundo elemento para la fila j_k = k + (j*(rowsCols*2)); i_k = k + (i*(rowsCols*2)); //Print("val =",MatnIdent[j_k]," val = ",MatnIdent[i_k]); //printf("\n jk val =%.4f, ratio = %.4f , ik val =%.4f ",MatnIdent[j_k], ratio, MatnIdent[i_k]); MatnIdent[j_k] = MatnIdent[j_k] - ratio*MatnIdent[i_k]; DBL_MAX_MIN(MatnIdent[j_k]); DBL_MAX_MIN(ratio*MatnIdent[i_k]); } } } // Operación de fila para hacer que la diagonal principal sea igual a 1 /* volvemos a nuestra matriz y el array idéntico de matrices, luego ejecutamos las operaciones necesarias para hacer su diagonal principal igual a 1 */ ArrayResize(output_Mat,size); int counter=0; for (int i=0; i<rowsCols; i++) for (int j=rowsCols; j<2*rowsCols; j++) { int i_j, i_i; i_j = j + (i*(rowsCols*2)); i_i = i + (i*(rowsCols*2)); //Print("i_j ",i_j," val = ",MatnIdent[i_j]," i_i =",i_i," val =",MatnIdent[i_i]); MatnIdent[i_j] = MatnIdent[i_j] / MatnIdent[i_i]; //printf("%d Mathematical operation =%.4f",i_j, MatnIdent[i_j]); output_Mat[counter]= MatnIdent[i_j]; //store the Inverse of Matrix in the output Array counter++; } } //--- }
Ahora llamamos a la función y mostramos la matriz inversa.
double inverse_xTx[]; Gauss_JordanInverse(xTx,inverse_xTx,tr_cols); if (m_debug) { Print("xtx Inverse"); MatrixPrint(inverse_xTx,tr_cols,tr_cols,7); }
La salida sería la siguiente:
xtx Inverse [ 3.8264763 -0.0024984 0.0004760 0.0072008 -0.0024984 0.0000024 -0.0000005 -0.0000073 0.0004760 -0.0000005 0.0000001 0.0000016 0.0072008 -0.0000073 0.0000016 0.0000290 ]
¡Recuerde! Para encontrar la inversa de una matriz, deberá tratarse de una matriz cuadrada. Por eso tenemos en los argumentos de la función el argumento mat_order, que equivale al número de filas y columnas.
Encontramos xTy
Ahora vamos a encontrar el producto matricial de la transposición de x e Y. Es el mismo proceso que hicimos antes.
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //¡Recuerde! El valor 1 al final es porque solo tenemos una variable dependiente y
Al salir, el resultado tendrá el aspecto siguiente:
xTy [ 10550016.70000 46241904488.26996 150084914994.69019 516408161.98000 ]
Genial, como esperábamos, es una matriz de 1x4.
Mire la fórmula:
Ahora que tenemos todo lo que necesitamos para encontrar los coeficientes, pasaremos a la parte final.
MatrixMultiply(inverse_xTx,xTy,Betas,tr_cols,tr_cols,tr_cols,1); La salida será (una vez más, recuerde que el primer elemento de nuestros coeficientes / matriz beta es una constante o, en otras palabras, una intersección y)
Coefficients Matrix [ -3670.97167 2.75527 0.37952 8.06681 ]
Bien, ahora vamos a hacer una prueba en Python para demostrar que estoy equivocado.
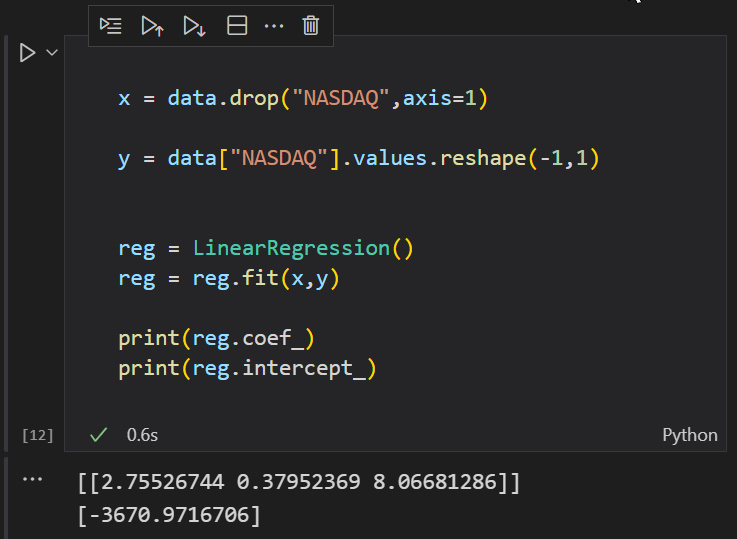
¡Hurra!
Ahora tenemos algunos modelos de regresión dinámica que por fin son posibles en mql5. Veamos de nuevo dónde comenzó todo.
Y así es como empezamos:
matreg.Init(2,"1,3,4",filename);
La idea era obtener una entrada de tipo string que permitiera introducir un número ilimitado de variables independientes. Parece que en mql5 no podemos tener *args y *kwargs de lenguajes como Python, y estos precisamente permiten introducir muchos argumentos. Así que la única forma de hacer esto es usar una cadena y luego encontrar una manera de manipular el array para que un solo array contenga todos nuestros datos. Después de eso, podremos encontrar la manera de manipularlos. Para leer más información, eche un vistazo a mi primer intento fallido: https://www.mql5.com/es/code/38894. La razón por la que digo todo esto es porque creo que alguien podría seguir el mismo camino en este u otro proyecto. Solo explico lo que nos ha funcionado y lo que no.
Reflexiones finales
Aunque suene genial, ahora podrá tener tantas variables independientes como quiera. Recuerde que hay un límite para cualquier sistema con demasiadas variables independientes o enormes columnas de conjuntos de datos. Por ejemplo, podría encontrar limitaciones en la potencia de cálculo de su computadora. Como acaba de ver, los cálculos matriciales pueden requerir mucho tiempo de computación.
La adición de variables independientes a un modelo de regresión lineal múltiple siempre aumentará la magnitud de varianza de la variable dependiente, normalmente expresada como R-cuadrado, por lo que agregar demasiadas variables independientes sin ninguna justificación teórica podría provocar el ajuste del modelo.
Por ejemplo, si construyéramos el modelo como lo hicimos en el primer artículo de esta serie, usando solo como base las dos variables dependientes NASDAQ y la independiente S&P500, nuestra precisión podría ser superior al 95%, pero podría no resultar así, porque ahora tenemos 3 variables independientes.
Siempre resulta una buena idea comprobar la precisión de un modelo después de haberlo construido. También debemos comprobar si existe una correlación entre cada variable independiente y el objetivo antes de construir el modelo.
Construya siempre sus modelos usando como base datos que tengan una fuerte relación lineal con su variable objetivo.
Gracias por su atención. Aquí tiene un enlace a mi repositorio en GitHub: https://github.com/MegaJoctan/MatrixRegressionMQL5.git
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/10928
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Aprendizaje automático y data science (Parte 04): Predicción de una caída bursátil
Aprendizaje automático y data science (Parte 04): Predicción de una caída bursátil
 Aprendiendo a diseñar un sistema de trading con MFI
Aprendiendo a diseñar un sistema de trading con MFI
 Redes neuronales: así de sencillo (Parte 17): Reducción de la dimensionalidad
Redes neuronales: así de sencillo (Parte 17): Reducción de la dimensionalidad
 El modelo de movimiento de precios y sus principales disposiciones (Parte 1): La versión del modelo más simple y sus aplicaciones
El modelo de movimiento de precios y sus principales disposiciones (Parte 1): La versión del modelo más simple y sus aplicaciones
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso

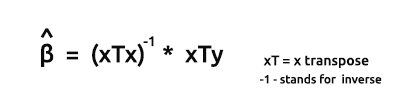
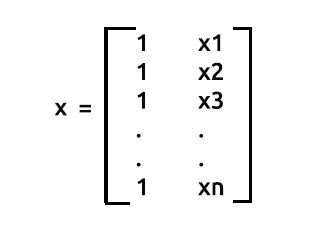
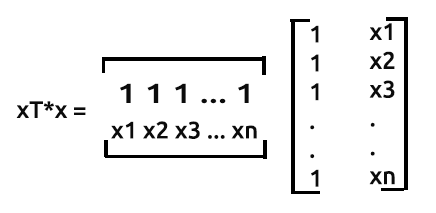

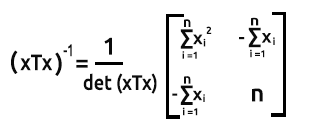
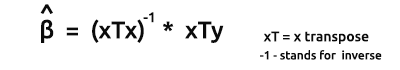
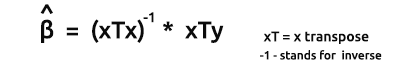
Nuevo artículo Ciencia de Datos y Aprendizaje Automático parte 03: Regresiones Matriciales ha sido publicado:
Autor: Omega J Msigwa