MetaTrader 5 / トレーディングシステム
English Русский Español Português
preview
取引におけるニューラルネットワーク：2次元接続空間モデル（最終回）

取引におけるニューラルネットワーク：2次元接続空間モデル（最終回）

MetaTrader 5 — トレーディングシステム |
22 1
Dmitriy Gizlyk
Dmitriy Gizlyk

はじめに

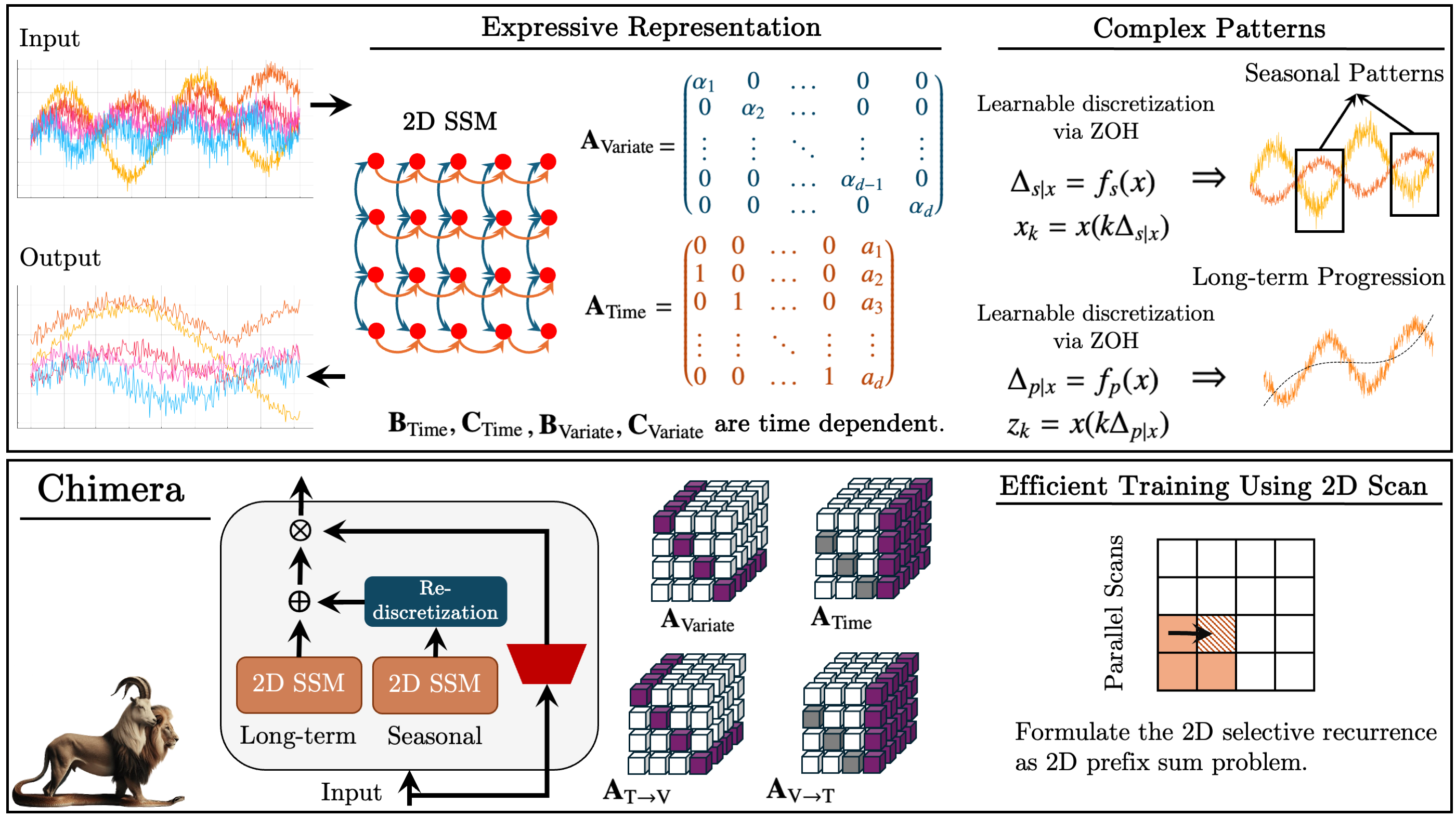
前回の記事では、Chimeraフレームワークについて紹介しました。これは時間軸と解析変数軸に沿った線形変換に基づく二次元状態空間モデル(2D-SSM)です。2つの軸に沿った状態空間モデルと、それらの相互作用を扱うメカニズムを組み合わせています。

状態空間モデル(SSM)は時系列解析で広く利用されており、複雑な依存関係をモデル化できます。しかし、従来のSSMは時間軸のみを考慮するため、多次元問題への適用は制限されていました。Chimeraは、特徴量軸（変数軸）をモデル化に組み込むことで、この制約を拡張しています。

フレームワークは2D-SSMの離散化形式で動作し、離散化ステップΔ1とΔ2を導入します。最初のパラメータは時間依存性に影響し、2つ目のパラメータは変数間の関係を制御します。Δ1の小さい値は長期トレンドの捕捉に有効であるのに対し、大きい値は季節変動を強調します。同様に、変数軸に沿った離散化は解析の詳細レベルを調整します。

正しいプロセス再構築を保証するために、フレームワークの著者は行列A1、A2（時間依存性）およびA3、A4（変数間関係）に構造的制約を導入しています。2D-SSMの因果的性質により、特徴量軸に沿った情報伝達は制限されるため、Chimeraは解析対象の前後の特徴との依存性を分析する2つのモジュールを使用します。

Chimeraフレームワークの柔軟性により、パラメータBi、Ci、Δiはデータ非依存の定数として使用することも、入力データに依存する関数として使用することも可能です。文脈依存パラメータを使用することで、複雑な多次元システムの条件に適応したモデルを構築できます。

このフレームワークは2D-SSMsを積み重ね、層間で非線形変換をおこなうことで深層モデルに近い構造を実現します。これにより、時系列をトレンド成分と季節成分に分解し、精度の高いパターン解析を可能にします。

以下は、著者らによるChimeraフレームワークの可視化です。

著者によるChimeraフレームワークの可視化

記事の実践部分では、MQL5を用いて著者の提案手法を実装するアーキテクチャを開発し、実装作業を開始しました。OpenCLプログラムに加えられた変更点を確認し、2D-SSMオブジェクトの構造を作成し、初期化メソッドを提示しました。今日は、提案手法を自分たちのモデルに統合するためのアルゴリズム構築をさらに進めます。



2D-SSMオブジェクト

前回の記事では、CNeuron2DSSMOCLオブジェクトの初期化メソッドを確認しました。このオブジェクトでは、2D-SSMの構築と学習の機能を実装することを意図しています。オブジェクト構造は以下のとおりです。

class CNeuron2DSSMOCL  :  public CNeuronBaseOCL
  {
protected:
   uint                 iWindowOut;
   uint                 iUnitsOut;
   CNeuronBaseOCL       cHiddenStates;
   CLayer               cProjectionX_Time;
   CLayer               cProjectionX_Variable;
   CNeuronConvOCL       cA;
   CNeuronConvOCL       cB_Time;
   CNeuronConvOCL       cB_Variable;
   CNeuronConvOCL       cC_Time;
   CNeuronConvOCL       cC_Variable;
   CNeuronConvOCL       cDelta_Time;
   CNeuronConvOCL       cDelta_Variable;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      feedForwardSSM2D(void);
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradientsSSM2D(void);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuron2DSSMOCL(void)  {};
                    ~CNeuron2DSSMOCL(void)  {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window_in, uint window_out, uint units_in, uint units_out, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuron2DSSMOCL; }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      Clear(void) override;
  };

本日はこの作業をさらに進めます。まず、このオブジェクトのフィードフォワードパスメソッドfeedForwardの構築アルゴリズムを考察します。

bool CNeuron2DSSMOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL *inp = NeuronOCL;
   CNeuronBaseOCL *x_time = NULL;
   CNeuronBaseOCL *x_var = NULL;

メソッドのパラメータとして、入力データオブジェクトへのポインタを受け取り、これをすぐにローカル変数に保存します。また、時間軸および特徴量軸に沿った入力データの射影オブジェクトへのポインタを保存するためのローカル変数を2つ宣言します。この段階では、まだこれらの射影を形成する必要があります。

射影を形成するために、初期化メソッドで2つの内部シーケンスを作成し、それらのオブジェクトへのポインタを動的配列cProjectionX_TimeとcProjectionX_Variableに保存しました。これらを用いて必要な射影を取得できます。

まず、時間的文脈に沿った射影を生成します。入力データオブジェクトへのポインターはすでにローカル変数に格納されています。次に、時間的文脈における射影モデルのオブジェクトを順番に処理するループを作成します。

//--- Projection Time
   int total = cProjectionX_Time.Total();
   for(int i = 0; i < total; i++)
     {
      x_time = cProjectionX_Time.At(i);
      if(!x_time ||
         !x_time.FeedForward(inp))
         return false;
      inp = x_time;
     }

ループ本体では、まずシーケンス内の次のオブジェクトへのポインタを取得します。取得したポインタの有効性を確認し、このチェックを通過した後で、そのオブジェクトのフィードフォワードメソッドを呼び出し、入力データオブジェクトへのポインタを渡します。

その後、現在のオブジェクトへのポインタを入力データを表すローカル変数に保存し、次のループ反復に進みます。

すべてのループ反復が完了すると、時間的文脈における入力データの射影を保持するローカル変数には、対応するシーケンスの最後のオブジェクトへのポインタが格納されます。このオブジェクトのバッファには、必要な射影が含まれています。

同様の手順で、特徴量的文脈における入力データの射影も取得します。

//--- Projection Variable
   inp = NeuronOCL;
   total = cProjectionX_Variable.Total();
   for(int i = 0; i < total; i++)
     {
      x_var = cProjectionX_Variable.At(i);
      if(!x_var ||
         !x_var.FeedForward(inp))
         return false;
      inp = x_var;
     }

2つの隠れ状態の4つの射影を取得するには、対応する射影オブジェクトのフィードフォワードメソッドを1回呼び出すだけで十分です。このメソッドのパラメータとして、結合された隠れ状態テンソルを保持するオブジェクトへのポインタを渡します。

   if(!cA.FeedForward(cHiddenStates.AsObject()))
      return false;

2D-SSMの残りのパラメータは文脈に依存します。したがって次に、入力データの対応する射影に基づいてモデルパラメータを生成します。この目的のため、モデルパラメータ生成オブジェクトを順番に処理し、それぞれのフィードフォワードメソッドを呼び出し、対応する入力データ射影オブジェクトへのポインタを渡します。

if(!cB_Time.FeedForward(x_time) ||
   !cB_Variable.FeedForward(x_var))
   return false;
if(!cC_Time.FeedForward(x_time) ||
   !cC_Variable.FeedForward(x_var))
   return false;
if(!cDelta_Time.FeedForward(x_time) ||
   !cDelta_Variable.FeedForward(x_var))
   return false;

この段階で、二次元状態空間モデルのパラメータの準備は完了しています。あとは隠れ状態とモデル出力の新しい値を生成するだけです。ご存じのように、前回の記事ではこれらの処理はOpenCL側で作成された別のカーネルに移動されていました。現在は、このカーネル用のラッパーメソッドを呼び出すだけで十分です。ただし、新しい隠れ状態を生成すると現在の値が上書きされ、バックプロパゲーションに必要になるため、まずデータバッファオブジェクトのポインタをスワップしてからfeedForwardSSM2Dメソッドを呼び出します。

   if(!cHiddenStates.SwapOutputs())
      return false;
//---
   return feedForwardSSM2D();
  }

次のステップは、オブジェクトのバックプロパゲーションアルゴリズムの構築です。まず、誤差勾配分配メソッドcalcInputGradientsを見てみましょう。このメソッドのパラメータとして、同じ入力データオブジェクトへのポインタを受け取りますが、今回は入力データがモデル全体の出力に与える影響に対応する誤差勾配を渡す必要があります。

bool CNeuron2DSSMOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

データの転送は、オブジェクトへの有効なポインタが存在する場合にのみ可能です。したがって、アルゴリズムの最初のステップは、受け取ったポインタのチェックをおこなうことであり、これにより解放済みまたは初期化されていないリソースへのアクセスを防ぎます。このアプローチは、計算プロセスの安定性を確保し、データ処理中の障害を防ぐために重要です。

制御ブロックを問題なく通過した後、誤差勾配の分配処理が開始されます。この処理は、モデルの出力結果のレベルから入力データに向かっておこなわれ、バックプロパゲーションの仕組みに従い、フィードフォワードパスのデータフローとは逆順で進みます。

前回の記事で述べたように、私たちは隠れ状態を生成し、2D-SSMの出力を計算するカーネルのラッパーメソッドを呼び出すことで、フィードフォワード処理を完了しました。それに対応して、誤差勾配の伝播処理は、同様のラッパーメソッドを呼び出すことで開始されますが、こちらは誤差分配をおこなうカーネル用です。このカーネル内では、2D-SSMの各要素に対して、モデル出力の形成に対する寄与に応じて、勾配が正しく分配されます。

if(!calcInputGradientsSSM2D())
   return false;

この段階でおこなわれているのは、モデルの構造コンポーネント間での勾配値の分配のみであることに注意が必要です。しかし、このカーネル内では、オブジェクトの活性化関数の導関数による値の直接的な調整はおこなわれません。そのため、モデル内部のオブジェクトに誤差勾配を伝播させる前に、これらのオブジェクトが活性化関数を持っているかを確認する必要があります。必要に応じて、非線形変換が伝播する勾配に与える影響を考慮した修正を適用するべきです。これにより、各モデルパラメータが出力信号の形成に対する実際の寄与を正しく反映して更新されることが保証されます。

//--- Deactivation
   CNeuronBaseOCL *x_time = cProjectionX_Time[-1];
   CNeuronBaseOCL *x_var = cProjectionX_Variable[-1];
   if(!x_time || !x_var)
      return false;
   if(x_time.Activation() != None)
      if(!DeActivation(x_time.getOutput(), x_time.getGradient(), x_time.getGradient(), x_time.Activation()))
         return false;
   if(x_var.Activation() != None)
      if(!DeActivation(x_var.getOutput(), x_var.getGradient(), x_var.getGradient(), x_var.Activation()))
         return false;
   if(cB_Time.Activation() != None)
      if(!DeActivation(cB_Time.getOutput(), cB_Time.getGradient(), cB_Time.getGradient(), cB_Time.Activation()))
         return false;
   if(cB_Variable.Activation() != None)
      if(!DeActivation(cB_Variable.getOutput(), cB_Variable.getGradient(), cB_Variable.getGradient(),
                                                                           cB_Variable.Activation()))
         return false;
   if(cC_Time.Activation() != None)
      if(!DeActivation(cC_Time.getOutput(), cC_Time.getGradient(), cC_Time.getGradient(), cC_Time.Activation()))
         return false;
   if(cC_Variable.Activation() != None)
      if(!DeActivation(cC_Variable.getOutput(), cC_Variable.getGradient(), cC_Variable.getGradient(), 
                                                                           cC_Variable.Activation()))
         return false;
   if(cDelta_Time.Activation() != None)
      if(!DeActivation(cDelta_Time.getOutput(), cDelta_Time.getGradient(), cDelta_Time.getGradient(), 
                                                                           cDelta_Time.Activation()))
         return false;
   if(cDelta_Variable.Activation() != None)
      if(!DeActivation(cDelta_Variable.getOutput(), cDelta_Variable.getGradient(), cDelta_Variable.getGradient(), 
                                                                                   cDelta_Variable.Activation()))
         return false;
   if(cA.Activation() != None)
      if(!DeActivation(cA.getOutput(), cA.getGradient(), cA.getGradient(), cA.Activation()))
         return false;

次に、2D-SSM内部のオブジェクトに誤差勾配を分配する処理に進みます。まず、文脈依存モデルパラメータを生成する役割を持つオブジェクトに対して、勾配値を伝播させる必要があります。ここで改めて確認すると、これらのパラメータは入力データの対応する射影に基づいて形成されます。

この段階で重要なのは、入力データ射影オブジェクトはすでにモデル出力の形成プロセスに参加しており、前の処理で誤差勾配値を受け取っているという点です。以前取得した値を保持するために、対応するデータバッファのポインタをスワップして処理をおこないます。

//--- Gradient to projections X
   CBufferFloat *grad_x_time = x_time.getGradient();
   CBufferFloat *grad_x_var = x_var.getGradient();
   if(!x_time.SetGradient(x_time.getPrevOutput(), false) ||
      !x_var.SetGradient(x_var.getPrevOutput(), false))
      return false;

次に、文脈依存パラメータを形成するオブジェクトを順番に通して誤差勾配を伝播させ、各段階で得られた勾配値を以前に保持していた値と加算し、蓄積していきます。

//--- B -> X
   if(!x_time.calcHiddenGradients(cB_Time.AsObject()) ||
      !SumAndNormilize(grad_x_time, x_time.getGradient(), grad_x_time, iWindowOut, false, 0, 0, 0, 1))
      return false;
   if(!x_var.calcHiddenGradients(cB_Variable.AsObject()) ||
      !SumAndNormilize(grad_x_var, x_var.getGradient(), grad_x_var, iWindowOut, false, 0, 0, 0, 1))
      return false;

//--- C -> X
   if(!x_time.calcHiddenGradients(cC_Time.AsObject()) ||
      !SumAndNormilize(grad_x_time, x_time.getGradient(), grad_x_time, iWindowOut, false, 0, 0, 0, 1))
      return false;
   if(!x_var.calcHiddenGradients(cC_Variable.AsObject()) ||
      !SumAndNormilize(grad_x_var, x_var.getGradient(), grad_x_var, iWindowOut, false, 0, 0, 0, 1))
      return false;

//--- Delta -> X
   if(!x_time.calcHiddenGradients(cDelta_Time.AsObject()) ||
      !SumAndNormilize(grad_x_time, x_time.getGradient(), grad_x_time, iWindowOut, false, 0, 0, 0, 1))
      return false;
   if(!x_var.calcHiddenGradients(cDelta_Variable.AsObject()) ||
      !SumAndNormilize(grad_x_var, x_var.getGradient(), grad_x_var, iWindowOut, false, 0, 0, 0, 1))
      return false;

すべての情報フローから誤差勾配の伝播が正常に完了した後、オブジェクトのポインタを元の状態に戻します。

if(!x_time.SetGradient(grad_x_time, false) ||
   !x_var.SetGradient(grad_x_var, false))
   return false;

この段階で、両文脈における入力データ射影レベルでの誤差勾配値を取得しています。次に、対応する内部射影モデルを通して勾配を伝播させる必要があります。そのために、対応するシーケンスのオブジェクトを逆順に処理するループを作成します。

//--- Projection Variable
   int total = cProjectionX_Variable.Total() - 2;
   for(int i = total; i >= 0; i--)
     {
      x_var = cProjectionX_Variable[i];
      if(!x_var ||
         !x_var.calcHiddenGradients(cProjectionX_Variable[i + 1]))
         return false;
     }

//--- Projection Time
   total = cProjectionX_Time.Total() - 2;
   for(int i = total; i >= 0; i--)
     {
      x_time = cProjectionX_Time[i];
      if(!x_time ||
         !x_time.calcHiddenGradients(cProjectionX_Time[i + 1]))
         return false;
     }

文脈射影の内部モデルを通して誤差勾配を伝播させる際には、各シーケンスの最初の層で伝播を停止することに注意してください。強調すべき点として、両方の射影シーケンスはいずれも外部プログラムからメソッドパラメータとして受け取った入力データに基づいて値を生成しています。ここで、両方の内部射影モデルから入力データオブジェクトに誤差勾配を渡す必要があります。 

このような場合に慣例ですが、まず一方の情報フローを通して誤差勾配を伝播させます。

//--- Projections -> inputs
   if(!NeuronOCL.calcHiddenGradients(x_var.AsObject()))
      return false;

次に、勾配バッファオブジェクトのポインタをスワップし、もう一方の情報フローを通して誤差を伝播させます。

   grad_x_time = NeuronOCL.getGradient();
   if(!NeuronOCL.SetGradient(x_time.getPrevOutput(), false) ||
      !NeuronOCL.calcHiddenGradients(x_time.AsObject()) ||
      !SumAndNormilize(grad_x_time, NeuronOCL.getGradient(), grad_x_time, 1, false, 0, 0, 0, 1) ||
      !NeuronOCL.SetGradient(grad_x_time, false))
      return false;
//---
   return true;
  }

最後に、両方の情報フローから得られた値を合算し、データバッファのポインタを元の状態に戻します。

ここで注意すべき点として、隠れ状態オブジェクトには誤差勾配を伝播させません。このオブジェクトはデータ保存のみを目的としており、学習可能なパラメータを含まないためです。

これで、すべての内部オブジェクトに誤差勾配値を分配する作業は完了しました。あとは、実行された処理の論理結果を呼び出し元のプログラムに返し、メソッドの実行を終了するだけです。

これをもって、CNeuron2DSSMOCLCNeuron2DSSMOCLオブジェクトのメソッド構築に用いられるアルゴリズムの確認を終了します。オブジェクトとその全メソッドの完全なコードは、付録にて参照可能です。



Chimeraモジュール

次の作業ステップは、Chimeraモジュールの構築です。フレームワークの著者は、異なる離散化レベルを持つ2つの並列2D-SSMと残差接続を使用することを提案しています。異なる離散化レベルで動作する2つの独立した状態空間モデルを組み合わせることで、依存関係のより深い解析が可能となり、マルチスケールデータに適応した高効率な予測モデルを構築できます。

異なる離散化パラメータを持つ2D-SSMを使用することで、時系列の差別化された解析が可能になります。高周波モデルは長期パターンを捉え、低周波モデルは季節サイクルの特定に焦点を当てます。この分離により、各モデルが自分のデータ領域に適応するため、情報損失や時間特徴の過剰集約による誤差が最小化され、予測精度が向上します。さらに、離散化モジュールを追加することで、2つのモデルの出力を比較可能な形式に揃えることができます。

Chimeraモジュールのもう一つの利点は、残差接続を使用する点です。残差接続により、モデルレベル間で効率的な情報伝達が保証されます。これにより、バックプロパゲーション中に勾配が保持・伝播され、勾配消失が防止されます。これは、深いモデルを学習させる際に特に重要であり、勾配降下法が数値的安定性の問題に直面しやすい状況で有効です。モデルは層間のデータ伝達中の情報損失に対してより頑健になり、長い時系列を扱う場合でも学習プロセスが安定します。

提案されたメカニズムをCNeuronChimeraオブジェクトに実装します。その構造を以下に示します。

class CNeuronChimera    :  public CNeuronBaseOCL
  {
protected:
   CNeuron2DSSMOCL    caSSM[2];
   CNeuronConvOCL     cDiscretization;
   CLayer             cResidual;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronChimera(void) {};
                    ~CNeuronChimera(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window_in, uint window_out, uint units_in, uint units_out,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronChimera; }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      Clear(void) override;
  };

提示された構造では、よく知られたオーバーライドされたメソッド群と、名前からその機能を容易に推測できるいくつかの内部オブジェクトが確認できます。

すべての内部オブジェクトは静的に宣言されており、これによりクラスのコンストラクタおよびデストラクタは空のままで構いません。すべてのオブジェクトの初期化はInitメソッドで実行されます。

bool CNeuronChimera::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window_in, uint window_out, uint units_in, uint units_out,
                          ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, units_out * window_out, optimization_type, batch))
      return false;
   SetActivationFunction(None);

メソッドのパラメータとして、作成されるオブジェクトのアーキテクチャを明確に定義する定数のセットを受け取ります。なお、このパラメータリストは、前に説明したCNeuron2DSSMOCLオブジェクトの同名メソッドから完全に継承されたものであり、内部2D-SSMsの1つのアーキテクチャを指定しています。

例によって、初期化アルゴリズムは親クラスのメソッド呼び出しから始まります。この場合は、基底の全結合層です。

次に、内部オブジェクトの初期化に進みます。前述の通り、異なる詳細レベルを持つ2つの二次元状態空間モデルを使用します。オブジェクト構造内では、内部モデルは配列caSSMとして表されています。この配列のオブジェクトを初期化するために、ループを構築します。

int index = 0;
for(int i = 0; i < 2; i++)
  {
   if(!caSSM[i].Init(0, index, OpenCL, window_in, (i + 1)*window_out, units_in, units_out, optimization, iBatch))
      return false;
   index++;
  }

最初の状態空間モデルは、外部プログラムから受け取ったパラメータを使用して初期化されます。2つ目のモデルは、出力結果に対して特徴空間の次元が倍増されており、より複雑な依存関係を捉えることが可能です。両モデルは共通の入力データセットで動作するため、主要な構成パラメータは変更されず、構造の整合性と一貫性が維持されます。

次に、追加の離散化層を初期化します。この層は、2つ目のモデルの出力を1つ目のモデルの部分空間に射影する役割を持ちます。これは標準的な畳み込み層であり、特徴空間を指定されたサイズに縮小します。

   if(!cDiscretization.Init(0, index, OpenCL, 2 * window_out, 2 * window_out, window_out, units_out, 1,
                                                                                 optimization, iBatch))
      return false;
   cDiscretization.SetActivationFunction(None);

データ損失を防ぐため、このオブジェクトでは活性化関数を無効化します。

2つの状態空間モデルの情報フローオブジェクトを初期化した後、次に残差接続の構築に進みます。この段階では、1つ以上の軸に沿ってサイズが異なる可能性のあるテンソルを合算するという問題が生じます。この問題を解決するには、まず入力データを指定された結果部分空間に射影する必要があります。この目的のため、前述の文脈射影モデルに似た内部データ射影モデルが作成されます。この手法により、データ次元を正しく揃えることができ、アーキテクチャの安定性と時間的依存性の正確な処理が保証されます。

まず、モデルオブジェクトへのポインタを格納する動的配列を準備し、これらのポインタを一時的に保持するためのローカル変数を宣言します。

//--- Residual
   cResidual.Clear();
   cResidual.SetOpenCL(OpenCL);
   CNeuronConvOCL *conv = NULL;
   CNeuronTransposeOCL *transp = NULL;

まず、データ転置オブジェクトを作成し、その後、単位系列を指定された時系列次元に射影する畳み込み層を配置します。

   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, units_in, window_in, optimization, iBatch) ||
      !cResidual.Add(transp))
     {
      delete transp;
      return false;
     }
   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, units_in, units_in, units_out, window_in, 1, optimization, iBatch) ||
      !cResidual.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

この手法により、解析対象の多変量時系列の各単位系列内の構造的依存関係を保持することができます。

続いて、入力データを特徴量軸に沿って射影する、転置オブジェクトと畳み込み層からなる別のブロックが配置されます。

   index++;
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, window_in, units_out, optimization, iBatch) ||
      !cResidual.Add(transp))
     {
      delete transp;
      return false;
     }
   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window_in, window_in, window_out, units_out, 1, optimization, iBatch) ||
      !cResidual.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

両方の畳み込み層では活性化関数を使用していない点に注意してください。これにより、入力データを情報損失を最小限に抑えて射影することが可能です。

オブジェクトの出力では、3つの情報フローを合算する予定です。このような場合に通常おこなうように、誤差勾配はすべての分岐に沿って完全に伝播させます。不要なデータコピー操作を避けるため、誤差勾配バッファのポインタを同期させます。ただし、データ射影に用いる畳み込み層は活性化関数を含む場合があります。今回のケースでは実際に使用していないため無視可能ですが、より汎用的なソリューションを構築するために、この点も考慮します。そのため、誤差勾配は活性化関数の導関数で補正した後にのみ、畳み込み層に渡されます。

   if(!SetGradient(caSSM[0].getGradient(), true))
      return false;
//---
   return true;
  }

ここまでで、処理の論理結果を呼び出し元に返し、初期化メソッドを完了します。

初期化が完了したら、feedForwardメソッドでフォワードパスアルゴリズムの実装に進みます。

bool CNeuronChimera::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   for(uint i = 0; i < caSSM.Size(); i++)
     {
      if(!caSSM[i].FeedForward(NeuronOCL))
         return false;
     }

フィードフォワードパスアルゴリズムは非常にシンプルです。メソッドのパラメータとして、入力データオブジェクトへのポインタを受け取り、それを内部の状態空間モデルに渡します。このために、内部の2D-SSMを順番に処理し、それぞれのフィードフォワードパスメソッドを呼び出すループを構築します。

すべてのループ反復が完了した後、得られた結果を比較可能な形式に射影します。

   if(!cDiscretization.FeedForward(caSSM[1].AsObject()))
      return false;

次に、入力データを結果部分空間に射影する必要があります。この目的のため、内部射影モデルのオブジェクトを順番に処理し、対応するオブジェクトのフィードフォワードパスメソッドを呼び出すループを構築します。

   CNeuronBaseOCL *inp = NeuronOCL;
   CNeuronBaseOCL *current = NULL;
   for(int i = 0; i < cResidual.Total(); i++)
     {
      current = cResidual[i];
      if(!current ||
         !current.FeedForward(inp))
         return false;
      inp = current;
     }

最後に、3つの情報フローの結果を合算し、その後データを正規化します。

   if(!SumAndNormilize(caSSM[0].getOutput(), cDiscretization.getOutput(), Output, 1, false, 0, 0, 0, 1) ||
      !SumAndNormilize(Output, current.getOutput(), Output, cDiscretization.GetFilters(), true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

その後、実行された処理の論理結果を呼び出し元プログラムに返し、メソッドの実行を完了します。

しかし、フィードフォワードパスアルゴリズムの表面的な単純さの背後では3つの情報フローが使用されており、誤差勾配の分配処理を構築するには一定の複雑さが伴います。この処理はcalcInputGradientsメソッド内で実装されます。

bool CNeuronChimera::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

メソッドのパラメータとして、入力データオブジェクトへのポインタを受け取ります。このオブジェクトに対して、モデルの最終出力に対する影響に応じた誤差勾配を渡す必要があります。そして、メソッド本体では、受け取ったポインタの関連性をすぐに確認します。このような検証の必要性については先ほど説明しました。

次に、後続オブジェクトから受け取った誤差勾配を、2つ目の2D-SSMの射影層の活性化関数で補正し、そのモデルレベルに伝播させます。

   if(!DeActivation(cDiscretization.getOutput(), cDiscretization.getGradient(), Gradient, cDiscretization.Activation()))
         return false;
   if(!caSSM[1].calcHiddenGradients(cDiscretization.AsObject()))
      return false;

同様に、内部入力データ射影モデルの最終層の活性化関数の導関数によって誤差勾配を補正し、そのシーケンス内のオブジェクトを順番に通して伝播させます。

   CNeuronBaseOCL *residual = cResidual[-1];
   if(!residual)
      return false;
   if(!DeActivation(residual.getOutput(), residual.getGradient(), Gradient, residual.Activation()))
         return false;
   for(int i = cResidual.Total() - 2; i >= 0; i--)
     {
      residual = cResidual[i];
      if(!residual ||
         !residual.calcHiddenGradients(cResidual[i + 1]))
         return false;
     }

この段階で、誤差勾配を3つの分岐すべてに沿って入力データレベルに伝えるステップに到達します。勾配の伝播中、以前に保持していた値は上書きされます。幸いにも、この問題への対処方法はすでに学んでいます。まず、1つ目の状態空間モデルから誤差勾配を伝播させます。

   if(!NeuronOCL.calcHiddenGradients(caSSM[0].AsObject()))
      return false;

次に、データバッファのポインタをスワップし、誤差勾配を2つ目の分岐に沿って伝播させ、その後、2つの情報フローからのデータを合算します。

   CBufferFloat *temp = NeuronOCL.getGradient();
   if(!NeuronOCL.SetGradient(residual.getPrevOutput(), false) ||
      !NeuronOCL.calcHiddenGradients(caSSM[1].AsObject()) ||
      !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1))
      return false;

同様の手順で、3つ目の情報フローの値も加算します。

   if(!NeuronOCL.calcHiddenGradients((CObject*)residual) ||
      !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1) ||
      !NeuronOCL.SetGradient(temp, false)
     )
      return false;
//---
   return true;
  }

すべての情報フローからのデータを合算した後にのみ、オブジェクトのポインタを元の状態に戻します。

実行された処理の論理結果を呼び出し元プログラムに返し、メソッドの実行を完了します。

これにて、MQL5を用いたChimeraフレームワークの実装アルゴリズムの解析を終了します。提示したオブジェクトおよびそのすべてのメソッドの完全なコードは、添付資料にて確認可能です。



モデルアーキテクチャ

前のセクションまでで、MQL5を用いてChimeraフレームワークの著者が提案したメソッドを実装するための広範な作業をおこないました。しかし、フレームワークの著者は、これらのオブジェクトを積み重ね、その間に非線形性を組み込んだアーキテクチャの使用を推奨しています。このようなアーキテクチャを用いることで、動作条件の変化に動的に対応できる柔軟で適応的なシステムを構築することが可能になります。したがって、ここでは学習可能モデルのアーキテクチャについて簡単に触れます。

あらかじめ述べておくと、実験の範囲内では、Chimeraアプローチをマルチタスク学習フレームワーク内で実装しています。

学習済みモデルのアーキテクチャは、CreateDescriptionsメソッド内で定義されています。

bool CreateDescriptions(CArrayObj *&actor, CArrayObj *&probability)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!probability)
     {
      probability = new CArrayObj();
      if(!probability)
         return false;
     }

メソッドのパラメータとして、モデルアーキテクチャの記述を格納するための2つの動的配列へのポインタを受け取ります。メソッド本体では、受け取ったポインタの妥当性を確認し、必要であればオブジェクトの新しいインスタンスを生成します。

まず、Actorのアーキテクチャを記述します。これには環境の状態エンコーダーブロックも含まれます。モデル入力では、環境の状態を表す未加工の生データを供給する予定です。これらのデータは、十分なサイズを持つ全結合層に渡されます。

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

次に、バッチ正規化層を配置します。この層で入力データの一次処理をおこない、比較可能な形に整えます。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

処理されたデータは、最初のChimeraモジュールに入力されます。出力として、各要素が16特徴量を持つ64要素の多次元時間系列を取得することを想定しています。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronChimera;
//--- Window
     {
      int temp[] = {BarDescr, 16}; //In, Out
      if(ArrayCopy(descr.windows, temp) < int(temp.Size()))
         return false;
     }
//--- Units
     {
      int temp[] = {HistoryBars, 64}; //In, Out
      if(ArrayCopy(descr.units, temp) < int(temp.Size()))
         return false;
     }
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

続いて、非線形性を導入するためにSoftPlus活性化関数を持つ畳み込み層を配置します。

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = 64;
   descr.window = 16;
   descr.step = 16;
   descr.window_out = 16;
   descr.activation = SoftPlus;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

同様の手順で、さらに2つのChimeraモジュールを追加し、その間に非線形性を挿入します。

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronChimera;
//--- Window
     {
      int temp[] = {16, 32}; //In, Out
      if(ArrayCopy(descr.windows, temp) < int(temp.Size()))
         return false;
     }
//--- Units
     {
      int temp[] = {64, 32}; //In, Out
      if(ArrayCopy(descr.units, temp) < int(temp.Size()))
         return false;
     }
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = 32;
   descr.window = 32;
   descr.step = 32;
   descr.window_out = 16;
   descr.activation = SoftPlus;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronChimera;
//--- Window
     {
      int temp[] = {16, 32}; //In, Out
      if(ArrayCopy(descr.windows, temp) < int(temp.Size()))
         return false;
     }
//--- Units
     {
      int temp[] = {32, 16}; //In, Out
      if(ArrayCopy(descr.units, temp) < int(temp.Size()))
         return false;
     }
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

同時に、ResNeXtフレームワークに倣って、系列の長さを短縮し、特徴空間の次元を比例的に増加させます。

次に、意思決定ヘッドが続きます。これは、3つの連続した全結合層で構成されています。

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 512;
   descr.batch = 1e4;
   descr.activation = TANH;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 256;
   descr.activation = TANH;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = NActions;
   descr.activation = SoftPlus;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

これらの層の出力は、バッチ正規化層を用いて正規化されます。

//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

前に説明したモデルと同様に、Actorの出力にはリスク管理モジュールが追加されます。

//--- layer 11
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMacroHFTvsRiskManager;
//--- Windows
     {
      int temp[] = {3, 15, NActions, AccountDescr}; //Window, Stack Size, N Actions, Account Description
      if(ArrayCopy(descr.windows, temp) < int(temp.Size()))
         return false;
     }
   descr.count = 10;
   descr.window_out = 16;
   descr.step = 4;                              // Heads
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 12
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = NActions / 3;
   descr.window = 3;
   descr.step = 3;
   descr.window_out = 3;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

次に、次の価格変動方向の確率を推定するモデルですが、これは前回の記事からほとんど変更せずに移植されています。隠れ層で使用される活性化関数にわずかな調整が加えられただけです。したがって、ここでは詳細に説明しません。モデルアーキテクチャの完全な記述は添付資料に記載されています。また、モデルの学習およびテスト用の完全なコードも添付されており、前回の作業から変更なく移植されています。



テスト

Chimeraフレームワークの著者が提案したアプローチを独自に実装した後、次は作業の最終段階に移ります。実際の履歴データを用いたモデルの学習およびテストです。

モデルの学習には、前のセクションで説明したモデルの学習時に収集された学習データセットを使用しました。このデータセットは、EUR/USD通貨ペアの2024年1年間のM1（1分足）データを用いて構築され、すべてのインジケーターのパラメータはデフォルト値のままとしています。学習データセットの作成手順の詳細は、添付リンクをご参照ください。

学習済みモデルのテストは、MetaTrader 5のストラテジーテスターで、2025年1月の履歴データを用いておこないました。その他の学習パラメータは変更していません。テスト結果を以下に示します。

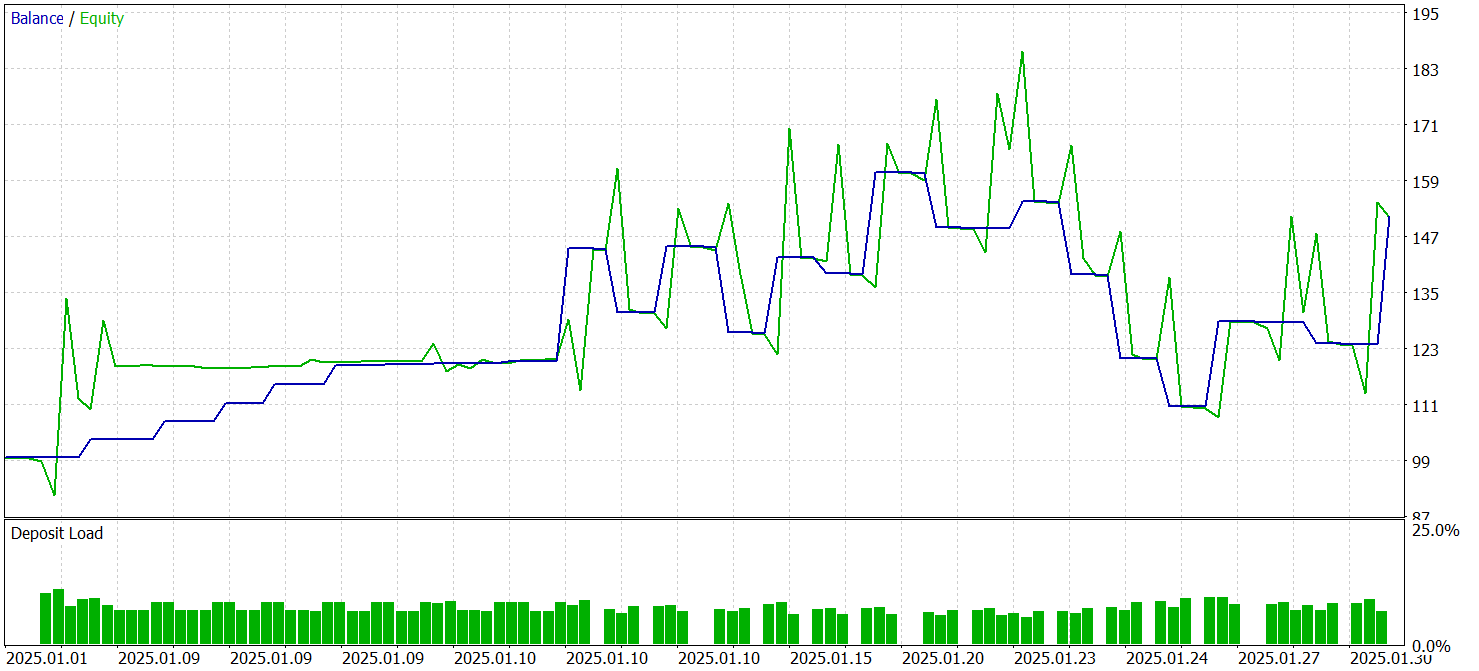
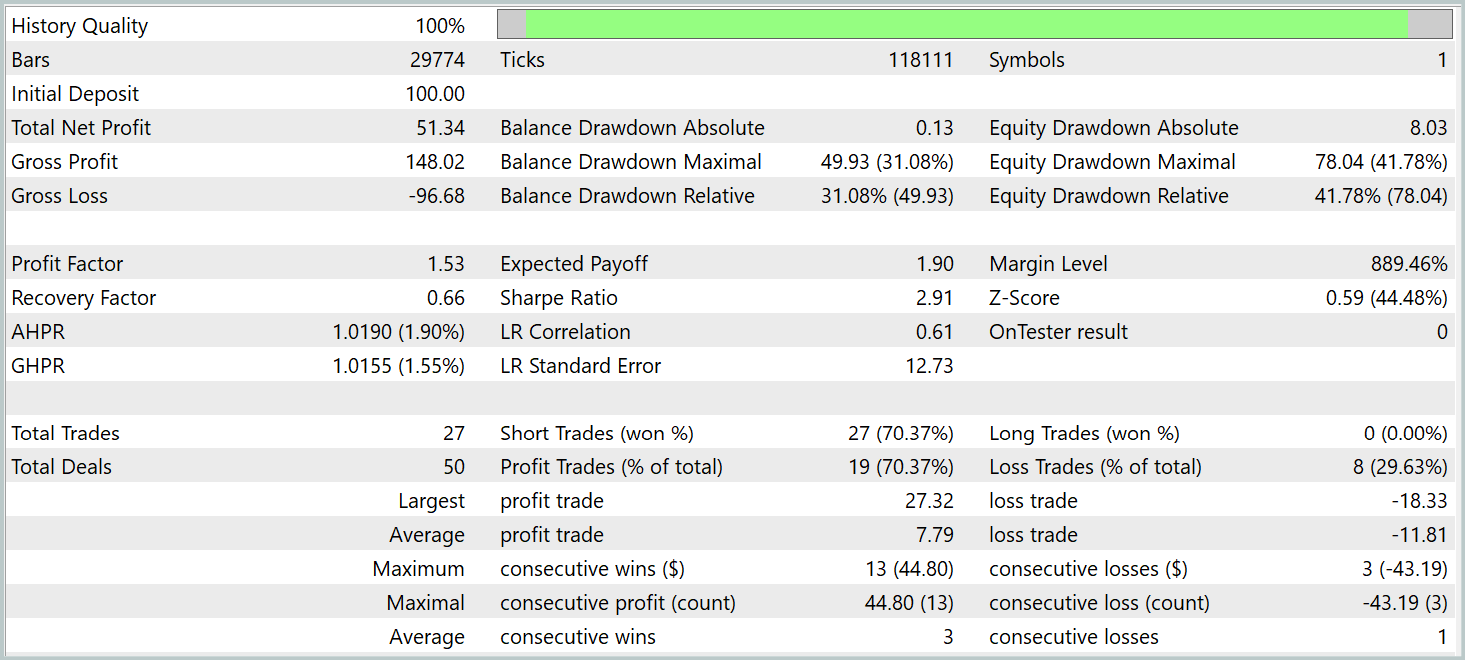
テスト結果によれば、モデルは利益を生み出すことができました。70%以上の取引が利益で終了しており、プロフィットファクターは1.53と記録されています。

しかし、いくつか注意すべき点があります。モデルはM1時間軸でテストされましたが、取引回数はわずか27回と、最小時間軸での高頻度取引としては非常に少ない数です。さらに、モデルはショートポジションのみを開いており、ここにも疑問が残ります。

ポジション保有時間も問題です。最短ポジションでも建ててからほぼ1時間後に決済されており、平均保有時間は14時間を超えます。これは、M1時間軸でテストした場合としては異常に長いです。

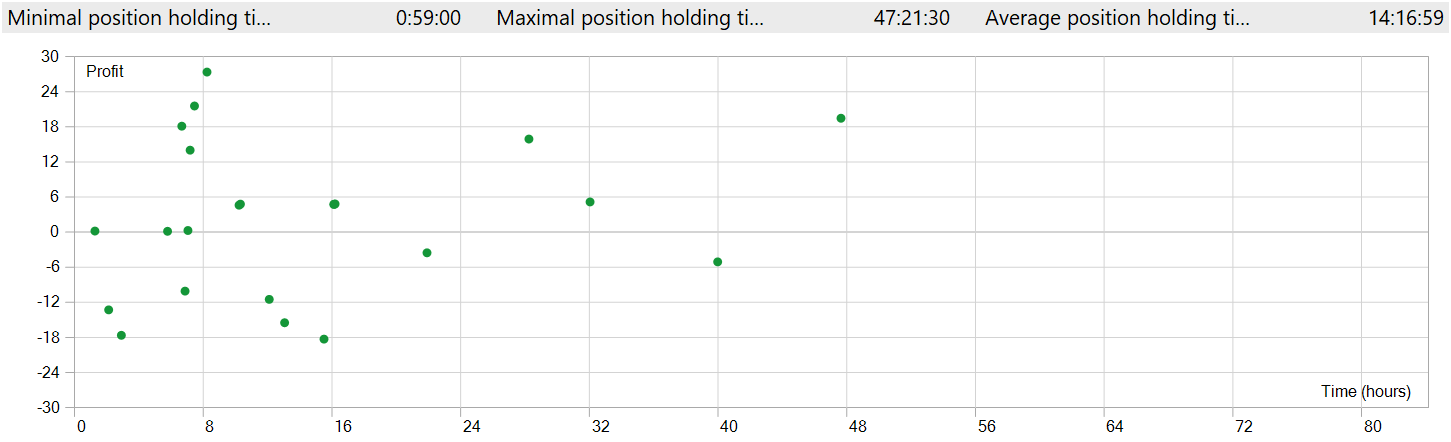
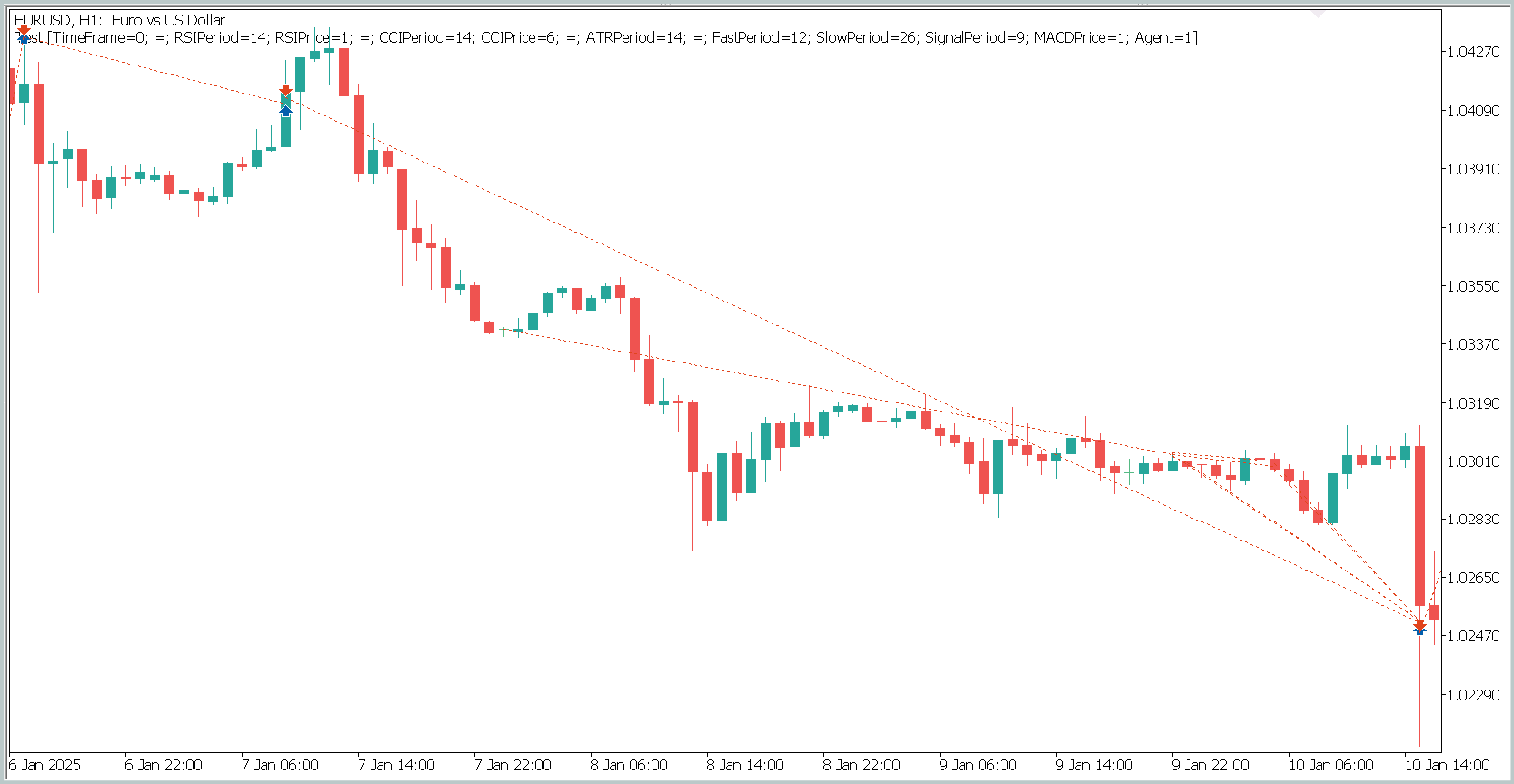
ポジションの開閉を1つのチャートウィンドウに表示するため、時間軸を上げる必要がありました。この形で見ると、グローバルトレンド方向に沿った取引が明確に観察できます。もちろん、これはM1時間軸での高頻度取引という概念とは一致しません。しかし、実装されたモデルが短期的な変動を無視しつつ、長期トレンドを捉える能力を持つことが確認できます。



結論

前回および前々回の記事では、二次元状態空間モデルに基づくChimeraフレームワークを取り上げました。このアプローチは、多変量時系列のモデリングにおいて革新的な手法を導入しており、時間軸における複雑な関係性だけでなく、特徴空間における依存関係も考慮することを可能にしています。

実践的な作業では、MQL5でフレームワークアプローチの独自の解釈を実装しました。構築したモデルは、実際の履歴データを用いて学習およびテストをおこないました。テスト結果は、やや予想外のものでした。テスト期間中、モデルは利益を生み出すことができました。しかし、期待に反して、M1タイムフレームでテストしたにもかかわらず、グローバルトレンド方向の取引が見られ、ポジションの保有時間が長いという結果になりました。


参照文献


記事で使用されているプログラム

# 名前 種類 説明
1 Research.mq5 EA サンプル収集用EA
2 ResearchRealORL.mq5
 EA
 Real-ORL法を用いたサンプル収集用EA
3 Study.mq5 EA モデル学習用EA
4 Test.mq5 EA モデルテスト用EA
5 Trajectory.mqh クラスライブラリ システム状態とモデルアーキテクチャ記述構造
6 NeuroNet.mqh クラスライブラリ ニューラルネットワークを作成するためのクラスのライブラリ
7 NeuroNet.cl コードベース OpenCLプログラムコード

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/17241

添付されたファイル |
ZIPをダウンロード
MQL5.zip (2458.9 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

最後のコメント | ディスカッションに移動 (1)
Charles Antoine Dominique Julien Fournel
Charles Antoine Dominique Julien Fournel | 18 1月 2026 において 16:22
とても興味深い！ありがとう！

グラフの結果からは、RRRの条件でクローズした方が利益が出るように思えますが、ここでのポイントはそこではありません。
1世紀前の機能で取引戦略をアップデートする 1世紀前の機能で取引戦略をアップデートする
本記事では、ラーデマッヘル関数およびウォルシュ関数を取り上げます。これらの関数を金融時系列解析にどのように適用できるかを検討し、さらに取引におけるさまざまな応用例についても考察します。
取引におけるニューラルネットワーク：2次元接続空間モデル(Chimera) 取引におけるニューラルネットワーク：2次元接続空間モデル(Chimera)
この記事では、革新的なChimeraフレームワークについて解説します。Chimeraは二次元状態空間モデルを用い、ニューラルネットワークで多変量時系列を解析する手法です。この方法は、従来手法やTransformerアーキテクチャを上回る低い計算コストで高い精度を実現します実現します。
IBMの量子コンピュータを使ってすべての価格変動パターンを解析する IBMの量子コンピュータを使ってすべての価格変動パターンを解析する
IBMの量子コンピュータを使用してすべての価格変動オプションを発見します。まるでSFの話のようですが、これが取引における量子コンピューティングの世界です。
多通貨エキスパートアドバイザーの開発（第22回）：設定のホットスワップへの移行を開始する 多通貨エキスパートアドバイザーの開発（第22回）：設定のホットスワップへの移行を開始する
定期的な最適化を自動化するのであれば、取引口座上ですでに稼働しているEAの設定を自動更新することについても検討する必要があります。これにより、ストラテジーテスター内でエキスパートアドバイザー(EA)を実行しながら、単一の実行の中でその設定を変更できるようにする必要があります。