取引におけるニューラルネットワーク：ハイブリッドグラフシーケンスモデル(GSM++)

MetaTrader 5 — トレーディングシステム | YYYY年02月DD日, 09:15

近年、自然言語処理やコンピュータビジョン分野から応用されたGraph Transformerが特に注目を集めています。長距離依存関係をモデル化できる能力や、不規則な金融構造を効率的に扱える特性により、ボラティリティ予測、市場の異常検知、最適な投資戦略の構築といったタスクにおいて有望な手法です。しかし、従来のTransformerは計算コストが高く、順序を持たないグラフ構造への適応が難しいといった根本的な課題があります。

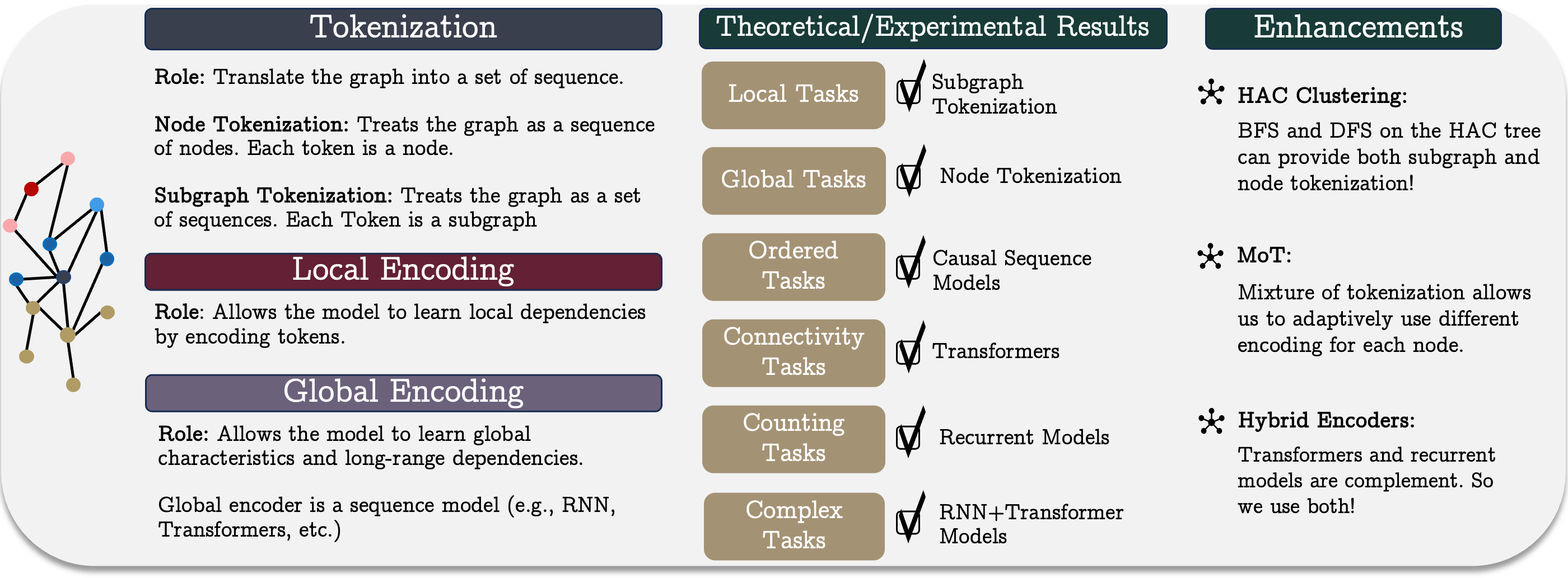
「Best of Both Worlds:Advantages of Hybrid Graph Sequence Models」の著者らは、さまざまなアーキテクチャの強みを統合した統一的なグラフシーケンスモデルであるGSM++を提案しています。このモデルは、グラフトークン化、局所ノードエンコーディング、グローバル依存関係エンコーディングという3つの主要段階を中心に構築されています。この構成は、金融システムにおける局所および大域の関係性の双方を捉えることを可能とし、幅広いタスクに適用できる高い汎用性を持っています。

提案モデルの中核をなすのが、階層的グラフトークン化手法です。この手法は、市場データをトポロジーおよび時間的特徴を保持したまま、コンパクトな系列表現へと変換します。標準的な時系列エンコーディング手法と比較して、特徴抽出の品質を向上させるとともに、大規模な市場データの処理を簡素化できます。さらに、階層的トークン化と、Transformerおよびリカレント系モデル（RNNを含む）を含むハイブリッドアーキテクチャを組み合わせることで、複数のタスクにおいて優れた性能を示します。このことから、この手法は複雑な金融データセットを扱うための強力なツールとなります。

GSM++フレームワークの著者らによる実証研究および理論解析の結果、提案モデルは従来のGraph Transformerと競合するだけでなく、複数の主要指標においてそれらを上回る性能を示すことが確認されています。

GSM++アルゴリズム

統合グラフシーケンスモデルはトークン化、局所エンコーディング、大域エンコーディングの3つの主要段階からなる概念的フレームワークとして表現されます。この手法により、複雑なグラフ構造を効率的に表現して解析でき、これは特に金融市場において重要な役割を果たします。多数の参加者や相互作用を含む複雑な市場システムでは、非線形依存関係や潜在的相関を捉える強力なモデリングツールが求められます。

トークン化は、グラフ構造を系列モデルで扱いやすい順序表現に変換する上で基本的な役割を果たします。主なトークン化戦略には、ノードまたはエッジのトークン化とサブグラフのトークン化があります。どの方法を選択するかは、グラフの構造情報がどの程度保持されるか、また解析時にどの組織的特徴を考慮するかに加え、モデルの有効性にも大きく影響します。

ノードまたはエッジのトークン化では、グラフを個々の要素の系列として扱い、要素間の接続を無視します。構造情報を保持するには、追加の位置情報や構造エンコーディングが必要です。この手法の主な欠点は、系列長がノードやエッジの数に比例するため、計算コストが高くなり、モデル学習が複雑になる点です。しかし、微視的特徴に基づく個別資産戦略の構築や、高頻度取引における短期市場変動の精密な解析、異常取引パターンの検出などの、各要素の詳細情報を活用したタスクでは非常に有効です。

サブグラフのトークン化は、グラフをサブグラフの系列として表現することで計算コストを削減し、局所構造を捉えるモデルの有効性を高めます。この手法は、相関資産のクラスタや投資家グループなど、サブグラフが局所的相互作用を表す金融応用に特に有効です。資産間の相互作用はしばしば隠れたネットワーク構造を持つため、サブグラフベースの解析は持続的な市場パターンを明らかにし、ポートフォリオ管理、流動性評価、裁定戦略において重要な役割を果たします。

それぞれのトークン化手法には利点と制約があり、タスクに応じて最適な方法を選択する必要があります。場合によっては、両手法を組み合わせたハイブリッドアプローチにより、データ表現の忠実度と計算効率、そしてモデルの有効性のバランスを最適化できます。

これらの考えに基づき、GSM++フレームワークの著者らは、ノードを類似性でクラスタリングする階層型トークン化アルゴリズム(Hierarchical Affinity Clustering, HAC)を提案しています。

アルゴリズムは、各グラフ頂点を独立したクラスタとして扱うことから始まります。各ステップで、エンコーディングの類似度に基づき「最も低コスト」とされるエッジで接続された2つのクラスタを統合します。この過程を繰り返し、最終的にグラフ全体が一つのクラスタに統合されます。その結果、根が全体のグラフを、葉が元のノードを表す階層ツリーが得られます。

この手法には2つの主な利点があります。第一に、類似した要素を近くに配置することで、モデルにおけるグラフ表現の精度が向上します。第二に、多段階のグラフエンコーディングが可能になり、柔軟な構造解析が実現します。ツリー走査には、深さ優先探索(DFS)と幅優先探索(BFS)の2つの戦略が開発されています。DFSは階層的な位置関係を反映したノード系列を生成し、BFSは類似したノードを隣接させた系列を生成します。

このトークン化手法は、グラフの局所構造を保持し、特に大域的接続の解析を必要とするタスクにおいてRNNなどのリカレント系シーケンスモデルと効率的に連携します。

さらに、階層的ポジショナルエンコーディングが導入され、ノード間の最短経路やクラスタ階層内での位置を考慮します。実験により、このエンコーディングはグラフ表現の品質を大幅に向上させることが確認されています。

ノードごとに最適なトークン化手法が異なる場合があるため、Mix of Tokenization (MoT)アプローチが提案されました。これにより、各ノードは最適なトークナイザーを選択し、その表現を組み合わせることで、最も適切なエンコーディングを利用できます。

トークン化後、データはベクトル表現に変換され、局所的なグラフ特徴の解析がおこなわれます。この段階では、グラフニューラルネットワーク(GNN)が広く使用され、ノード間の局所依存関係を効率的に捉えます。金融市場では、資産相関の解析、局所的異常の検出、微細構造データに基づく予測生成に役立ちます。GNNは複雑なパターンを抽出できるため、アルゴリズム取引や市場ボラティリティ予測にも応用されます。

大域エンコーディングは、グラフ内の長期依存関係をモデル化する上で重要です。構造要素間の複雑な関係を特定するために系列エンコーディングが適用されます。金融応用においては、マクロ経済動向のモデル化、グローバル要因が市場に与える影響の解析、深いデータ相互関係に基づく戦略立案を可能にします。金融政策や世界的経済危機の影響など、長期的な市場トレンドを扱うには、複数の時間軸にわたる複雑な依存関係を捉えられるアルゴリズムが必要です。

グラフ学習のためのシーケンスモデルを選択する際には、「どのモデルが最も効果的か」という重要な問題が生じます。標準的なアプローチでは、様々なシーケンスエンコーダを異なるトークン化手法と組み合わせることで、複数のアーキテクチャを生成できます。しかし、特定のグラフタスクに最適な構成については明確な合意はありません。

たとえば、カウントタスクでは特定タイプのノード数を判定する必要があります。因果依存性を持たない注意機構モデルでは正確な判定が困難です。この場合、順序を考慮できるRNNモデルが有効かという疑問が生じます。

解析の結果、RNNモデルの幅が異なるノードクラス数に一致する場合、正確にカウントできることが示されました。これは、順序情報が重要なタスクにおいて、RNNモデルの有効性を示しています。

アルゴリズム的推論など、一部のグラフタスクではノード順序の厳密な遵守が必要です。現代のシーケンスモデルは主に因果依存性に基づくため、グラフモデルとの統合時に考慮が必要です。過度な情報圧縮は表現の忠実度を低下させることがあります。RNNモデルでは要素間距離が大きくなると初期データへの感度が低下しますが、Transformerは感度を一定に保ちます。しかし、いずれのモデルも深さが増すと表現の崩壊が起こりやすくなります。

系列の先頭にある情報は保持されやすく、このため系列の最初と最後のトークンは中央のトークンよりも重要性を保持しやすい、いわゆるU字型の効果が観察されます。この挙動は、TransformerとRNNモデルの両方で確認されています。そのため、ノードを系列に配置する際には、重要な要素を互いに近接させることで、相互影響を最大化することが推奨されます。

接続性に関連するタスクでは、大域的なグラフ構造の解析が求められます。接続性は二値分類問題として定式化できます。研究によれば、十分な深さと埋め込みサイズを持つTransformerは、この種のタスクを効果的に解決できます。一方、RNNモデルや限定的アテンション機構を用いたTransformerでは、同等の結果を得るためにより多くのパラメータや層が必要となります。

RNNモデルは、データに自然な順序があり、トークン化がグラフ構造を尊重している場合に最も効果的です。ノードの局所性、すなわち隣接頂点間の最大距離は重要なパラメータです。局所性が限定されたグラフでは、コンパクトなRNNモデルでも接続性を効率的に判定できます。固定パラメータのTransformerでは、このようなタスクの処理は困難です。

モデル選択では、グラフ解析タスクに固有のトレードオフを理解することが重要です。異なるアーキテクチャの比較から、以下のような知見が得られます。

Transformerは、最小限のパラメータで接続性タスクに優れ、並列計算が必要な複雑なグラフに特に有効です。文脈依存の表現を形成できるため、複雑なネットワーク解析に強力です。
リカレントニューラルネットワーク(RNN)は、頂点接続が局所構造を持つグラフに適しています。必要なパラメータや計算量が少なく、省エネルギーでストリーミングデータにも適しています。
ハイブリッドモデルは、RNNとTransformerの利点を組み合わせ、計算コストと予測精度のバランスを取ります。局所的詳細と大域的文脈の両方が重要な場合に特に有効です。
状態空間モデルは、要素の順序が厳密に重要な場合に非常に効果的です。これらのモデルは長期記憶の特性を持っており、時系列解析やエージェントベースシステムにおける連続的な行動のモデリングに有用です。
スパースアテンションは、特に大規模なグラフに対するTransformerの計算コストを大幅に削減できます。しかし、その効果的な利用には、最も重要なノード接続を特定するための追加的なメカニズムが必要となる場合があり、これにより実装が複雑化することがあります。

このように、モデルの選択は入力データの構造や利用可能な計算資源に大きく依存します。大域的な依存性が強く複雑な構造を持つグラフにはTransformerが適しており、局所的な系列構造を持つグラフにはRNNが最適です。さらに、要素の順序が厳密に重要なタスクにおいては、状態空間モデルが優れた性能を発揮します。ハイブリッドアプローチは、計算効率と予測精度のバランスを可能にし、多くの応用シナリオにおいて汎用的な選択肢となります。

この分析に基づき、著者らはGSM++フレームワークを提示しています。このフレームワークは、類似性に基づく階層型ノードトークン化、局所エンコーダとしての畳み込み型グラフニューラルネットワーク、ならびにMambaモジュールとTransformerモジュールを含むハイブリッドな大域エンコーダを統合しています。

GSM++

MQL5での実装

GSM++フレームワークの著者らが提案した手法の理論的側面を検討した後、次に研究の実装に関する実践的な部分に移ります。このセクションでは、MQL5のツールを用いて、これまでに議論したアプローチに対する独自の解釈を実装することに焦点を当てます。

なお、元の手法に内在する基本的な概念は保持しているものの、実装は細部において大きく異なっている点に留意する必要があります。

まず第一に、実装では階層的類似性クラスタリング(Hierarchical Affinity Clustering,HAC)を採用しない判断をおこないました。金融商品チャート上に形成されるローソク足は、動的かつ進化的なオブジェクトであり、容易に標準化できるものではないと考えられます。その解析およびクラスタリングは、はるかに深く包括的なアプローチを必要とする、複雑で多面的なプロセスです。

そのため、これまでと同様に、解析対象となるバーの表現をトークナイズするために、学習可能なモジュールを使用します。このアプローチにより、実世界データ環境下におけるモデルの柔軟性と適応性を維持できます。これは、金融市場を扱う上で特に重要な点です。

一方で、実装では提案されているMix of Tokenization(MoT)アルゴリズムを採用していますが、タスクの特性に対応するため、やや修正および適応を加えた形となっています。GSM++フレームワークの著者らは、学習可能なクラスタリングモデルを用いて最も関連性の高い2つのトークン化アルゴリズムを選択し、それらの出力を加算して最終的な表現を生成する方法を提案しています。これに対し、この研究では、各バーに対して4種類の異なるトークンを準備し、R-MATフレームワークから借用したAttention Poolingアルゴリズムを用いてそれらの出力を統合します。

このアプローチは、より多くのデータ側面を考慮し、関連情報をより精密に抽出できるため、解析品質を大幅に向上させます。この研究では、以下のトークン化手法を使用しています。

ノードトークン化：各バーが独立した解析要素として扱われ、モデルはそこから情報を抽出します。
エッジトークン化：連続する2つのバー間の相互作用に着目し、データ内の異なる部分を結ぶ重要な関係性を強調します。
サブグラフトークン化：複数のバー間の接続を考慮することで、より複雑な構造を形成します。
単一のユニタリ系列に対するサブグラフトークン化：構造的系列を詳細に解析し、より深いレベルでのデータ処理を可能にします。

これらのトークン化手法を用いることで、個々の要素とそれらの相互関係の双方を考慮でき、各バーに対する情報表現の品質が大きく向上するとともに、モデル全体の性能も強化されます。さらに、すべてのトークンをAttention Poolingによって統合することで、モデルは最も重要な特徴に柔軟に注目でき、意思決定の精度が向上します。

このソリューションを実装するために、新たなオブジェクトであるCNeuronMoTを作成します。その構造は以下のとおりです。

class CNeuronMoT  :  public CNeuronMHAttentionPooling
  {
protected:
   CNeuronConvOCL             cNodesTokenizer;
   CNeuronConvOCL             cEdgesTokenizer;
   CNeuronConvOCL             cSubGraphsTokenizer;
   CLayer                     cUnitarSubGraphsTokenizer;
   CNeuronBaseOCL             cConcatenate;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMoT(void){};
                    ~CNeuronMoT(void){};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMoT; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

この場合の親オブジェクトはCNeuronMHAttentionPoolingであり、これは異なるトークン化のバリエーションを統合するために、モジュールの出力段階で使用されるAttention Poolingアルゴリズムをすでに実装しています。このアプローチには、いくつかの重要な利点があります。

第一に、親クラスを利用することでコードの冗長性を回避でき、Attention Poolingモジュールを他のオブジェクトやコンポーネント内で再実装する必要がなくなります。その代わりに、すでに最適化された完成度の高いアルゴリズム実装を統合できるため、高い抽象度を維持しつつ、コード保守性を大幅に向上させることができます。

第二に、トークンの統合および処理に関連するすべての操作は、親クラスの機能を通じて実行されます。これにより、システムアーキテクチャが大幅に簡素化され、リソース効率も向上します。親クラスには、アテンション処理に必要なすべてのメソッドとアルゴリズムがすでに含まれているため、機能の重複を最小限に抑えつつ、モジュール性と拡張性を高めることができます。

新しいオブジェクトの構造には、モデル実装に不可欠な、従来から用いられている仮想メソッドが含まれており、これらはオーバーライド可能です。これにより、タスク要件に応じてオブジェクトの振る舞いを柔軟にカスタマイズできます。

さらに、このクラスには、アルゴリズムで重要な役割を果たすいくつかの内部オブジェクトが含まれています。これらの具体的な役割については、クラスメソッドの実装過程において、それぞれの動作および相互関係とともに詳しく説明します。

すべての内部オブジェクトは静的として宣言されているため、コンストラクタとデストラクタを空のままにすることができます。通常どおり、宣言および継承されたすべてのオブジェクトの初期化は、Initメソッド内で処理されます。

bool CNeuronMoT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                      uint window, uint units_count,
                      ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronMHAttentionPooling::Init(numOutputs, myIndex, open_cl, window, units_count, 4, optimization_type, batch))
      return false;

メソッドのパラメータは、入力データの次元数を表す定数を受け取ります。実装では、出力も同一の次元数であることを前提としている点に注意が必要です。そのため、これらのパラメータは、同名の親クラスメソッドに即座に渡されます。親クラスメソッドには、継承されたすべてのオブジェクトおよびインターフェースに対する初期化処理がすでに実装されています。

親クラスメソッドが正常に実行されたら、新たに宣言されたオブジェクトの初期化処理に進みます。まず、ノードトークン化用オブジェクトを初期化します。このオブジェクトは畳み込み層として実装されており、畳み込みウィンドウサイズ、ストライド、およびフィルタ数は、単一の系列要素を表すベクトルと同一に設定されています。

このアプローチにより、各要素（ノード）が特定の特徴に対応するベクトルとして表現される系列データを効率的に処理できます。畳み込み処理は重要な局所特徴を抽出することを可能にし、後続のデータ処理およびトークン化の基盤を形成します。畳み込みパラメータを要素記述ベクトルに一致させることで、畳み込み層をモデル全体の構造に無理なく統合でき、すべての処理段階において効率性と一貫性を維持できます。

int index = 0;
if(!cNodesTokenizer.Init(0, index, OpenCL, iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch))
   return false;
cNodesTokenizer.SetActivationFunction(SoftPlus);

次に、エッジトークン化用の畳み込み層を初期化します。先ほどのオブジェクトとは異なり、ここでは2つの連続する要素を対象とした畳み込みウィンドウを使用します。これにより、隣接する要素間の相互作用や結合関係をモデル化することが可能となり、より深い構造解析において重要な役割を果たします。

index++;
if(!cEdgesTokenizer.Init(0, index, OpenCL, 2 * iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch))
   return false;
cEdgesTokenizer.SetActivationFunction(SoftPlus);

なお、ステップを1つとした二要素ウィンドウを用いる場合、通常は系列長が一要素分短くなる点に注意が必要です。しかし、後続のトークン統合処理では、すべての段階においてテンソルの次元互換性が求められます。そのため、実装では末尾にゼロをパディングすることで欠落する要素を補い、元の系列長を保持しています。

同様に、サブグラフトークン化用の畳み込み層を初期化します。この場合、畳み込みウィンドウを3つの系列要素へと拡張し、それ以外のパラメータはすべて維持しています。

index++;
if(!cSubGraphsTokenizer.Init(0, index, OpenCL, 3 * iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch))
   return false;
cSubGraphsTokenizer.SetActivationFunction(SoftPlus);

すべてのトークン化レベルにおいて、SoftPlus活性化関数を適用します。この選択にはいくつかの利点があります。SoftPlusは滑らかで単調増加な関数であり、急激な不連続を回避できるため、学習の安定性が向上します。ReLUとは異なり、SoftPlusにはゼロから正の値への急激な遷移が存在しないため、「デッドニューロン」の問題を防ぐことができます。

また、SoftPlusの導関数は常に正であるため、逆伝播時における良好な微分可能性が確保され、重み更新を滑らかにおこなうことができます。これは、精密かつ安定したパラメータ調整を必要とする複雑なニューラルネットワークにおいて、特に重要です。

すべてのトークン化レベルにSoftPlusを適用することで、モデルの柔軟性と安定性が向上し、複雑な系列データの処理および解析において不可欠な滑らかさと堅牢性を確保できます。

多次元時系列における単一ユニタリ系列のトークン生成には、複数の逐次的な処理が必要となります。この機能を実現するために、いくつかの連続した操作を内部モデルとして統合し、動的配列cUnitarSubGraphsTokenizerに格納されたオブジェクトへのポインタを保持します。

まず、動的配列を初期化し、オブジェクトポインタを一時的に格納するためのローカル変数を宣言します。

cUnitarSubGraphsTokenizer.Clear();
cUnitarSubGraphsTokenizer.SetOpenCL(OpenCL);
CNeuronConvOCL *conv = NULL;
CNeuronTransposeOCL *transp = NULL;

ユニタリ系列を扱いやすくするために、入力データを転置します。

index++;
transp = new CNeuronTransposeOCL();
if(!transp ||
   !transp.Init(0, index, OpenCL, iUnits, iWindow, optimization, iBatch) ||
   !cUnitarSubGraphsTokenizer.Add(transp))
  {
   delete transp;
   return false;
  }

次に、畳み込み層を用いてサブグラフトークンを生成します。ここでも3要素からなるサブグラフを解析します。各要素は単一の値で表現され、解析される変数の数はユニタリ系列の数に対応します。

index++;
conv = new CNeuronConvOCL();
if(!conv ||
   !conv.Init(0, index, OpenCL, 3, 1, 1, iUnits, iWindow, optimization, iBatch) ||
   !cUnitarSubGraphsTokenizer.Add(conv))
  {
   delete conv;
   return false;
  }
conv.SetActivationFunction(SoftPlus);

このアプローチにより、各ユニタリ系列内の遷移やパターンを詳細に解析することが可能となります。

生成された値は、その後元の状態に転置して戻されます。

index++;
transp = new CNeuronTransposeOCL();
if(!transp ||
   !transp.Init(0, index, OpenCL, iWindow, iUnits, optimization, iBatch) ||
   !cUnitarSubGraphsTokenizer.Add(transp))
  {
   delete transp;
   return false;
  }
transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

最後に、異なるトークン化手法から得られた結果を結合する役割を持つオブジェクトを初期化します。

   index++;
   if(!cConcatenate.Init(0, index, OpenCL, 4 * iWindow * iUnits, optimization, iBatch))
      return false;
   cConcatenate.SetActivationFunction(None);
//---
   return true;
  }

なお、結合用オブジェクトでは、活性化関数は意図的に無効化しています。もちろん、すべてのトークン生成オブジェクトには同じ活性化関数を使用しています。活性化関数を結合オブジェクトに移すことも可能であり、その場合は逆伝播における勾配分配アルゴリズムが若干簡略化される可能性があります。しかし一般的には、個々のトークン生成オブジェクトで異なる活性化関数を使用できるようにしています。この場合、結合オブジェクトに活性化関数を指定すると、データが歪んでしまうだけです。

メソッドの最後に、実行された操作の論理結果を呼び出し元プログラムに返します。

次に、feedForwardメソッドにおいてフィードフォワード処理のアルゴリズムを実装する必要があります。アルゴリズムは非常にシンプルです。

bool CNeuronMoT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cNodesTokenizer.FeedForward(NeuronOCL))
      return false;
   if(!cEdgesTokenizer.FeedForward(NeuronOCL))
      return false;
   if(!cSubGraphsTokenizer.FeedForward(NeuronOCL))
      return false;

このメソッドは、入力データを保持するオブジェクトへのポインタを受け取ります。このポインタは、各トークン化レベルに対応する内部オブジェクトのメソッドに渡されます。

ユニタリ系列におけるトークン生成では、内部モデル内のオブジェクトを順番に反復処理するループが実行されます。

   CNeuronBaseOCL *prev = NeuronOCL, *current = NULL;
   for(int i = 0; i < cUnitarSubGraphsTokenizer.Total(); i++)
     {
      current = cUnitarSubGraphsTokenizer[i];
      if(!current ||
         !current.FeedForward(prev))
         return false;
      prev = current;
     }

生成されたすべてのトークンは、系列要素を表す単一のテンソルに集約されます。

   if(!Concat(cNodesTokenizer.getOutputIndex(), cEdgesTokenizer.getOutputIndex(),
              cSubGraphsTokenizer.getOutputIndex(), current.getOutputIndex(),
              cConcatenate.getOutputIndex(), iWindow, iWindow, iWindow, iWindow, iUnits))
      return false;

生成されたテンソルは、同名の親クラスメソッドに渡され、最終的なグラフ表現が得られます。

   return CNeuronMHAttentionPooling::feedForward(cConcatenate.AsObject());
  }

実行された処理の論理結果を呼び出し元プログラムに返し、メソッドの実行を完了します。

概念的にはシンプルですが、feedForwardメソッドは4つの並列情報ストリームを実行するため、勾配分配が複雑になります。このアルゴリズムは、calcInputGradientsメソッド内で実装されています。

bool CNeuronMoT::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

このメソッドは、同じ入力元データオブジェクトへのポインタを受け取ります。今回はさらに、入力データがモデル出力に与える影響量に応じた誤差勾配も渡す必要があります。データは有効なオブジェクトにのみ渡すことができるため、まずポインタの有効性を確認します。

その後、後続オブジェクトから得られた誤差勾配は、親クラスを介してトークン結合オブジェクトに下流方向へ分配されます。

if(!CNeuronMHAttentionPooling::calcInputGradients(cConcatenate.AsObject()))
   return false;

次に、勾配はすべての情報ストリーム間で分割されます。

CNeuronBaseOCL *current = cUnitarSubGraphsTokenizer[-1];
if(!current ||
   !DeConcat(cNodesTokenizer.getGradient(), cEdgesTokenizer.getGradient(),
             cSubGraphsTokenizer.getGradient(), current.getGradient(),
             cConcatenate.getGradient(), iWindow, iWindow, iWindow, iWindow, iUnits))
   return false;

次に、誤差勾配をすべての情報ストリームに分配する必要があります。

結合オブジェクトからは、活性化関数の導関数による調整がまだおこなわれていない誤差勾配が取得されます。そのため、各情報ストリームの処理を開始する前に、対応する活性化関数の導関数に従って値を調整する必要があります。

まず、単変量系列に沿って誤差勾配を分配します。まず、活性化関数が存在するかを確認し、必要に応じて取得した値を調整します。

if(current.Activation() != None &&
   !DeActivation(current.getOutput(), current.getGradient(),
                 current.getGradient(), current.Activation()))
   return false;

次に、内部モデル内のオブジェクトに対して逆伝播ループを実行し、関連するメソッドを順次呼び出します。

for(int i = cUnitarSubGraphsTokenizer.Total() - 2; i >= 0; i--)
  {
   current = cUnitarSubGraphsTokenizer[i];
   if(!current ||
      !current.calcHiddenGradients(cUnitarSubGraphsTokenizer[i + 1]))
      return false;
  }

その後、誤差勾配を入力元データレベルまで伝播させます。

if(!NeuronOCL.calcHiddenGradients(current.AsObject()))
   return false;

この段階では、誤差勾配は1つのブランチを通じてのみ入力データ層に伝播されています。残りの3つのブランチについても同様の処理をおこなう必要があります。

以前取得した値を保持するために、対応するデータバッファのポインタをスワップして処理をおこないます。

CBufferFloat *temp = NeuronOCL.getGradient();
if(!NeuronOCL.SetGradient(current.getPrevOutput(), false))
   return false;

これにより、以前に取得したデータが保存されたことを確認した上で、残りのブランチに沿って勾配を伝播します。ここでも順次、活性化関数の存在を確認し、必要に応じて対応する導関数に基づき値を調整します。

if(cNodesTokenizer.Activation() != None &&
   !DeActivation(cNodesTokenizer.getOutput(), cNodesTokenizer.getGradient(),
                 cNodesTokenizer.getGradient(), cNodesTokenizer.Activation()))
   return false;
if(!NeuronOCL.calcHiddenGradients(cNodesTokenizer.AsObject()) ||
   !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1))
   return false;

続いて、誤差勾配を入力元データレベルまで伝播させ、以前に蓄積された値と合算します。同様の操作を次のブランチについても繰り返します。

if(cEdgesTokenizer.Activation() != None &&
   !DeActivation(cEdgesTokenizer.getOutput(), cEdgesTokenizer.getGradient(),
                 cEdgesTokenizer.getGradient(), cEdgesTokenizer.Activation()))
   return false;
if(!NeuronOCL.calcHiddenGradients(cEdgesTokenizer.AsObject()) ||
   !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1))
   return false;

if(cSubGraphsTokenizer.Activation() != None &&
   !DeActivation(cSubGraphsTokenizer.getOutput(), cSubGraphsTokenizer.getGradient(),
                 cSubGraphsTokenizer.getGradient(), cSubGraphsTokenizer.Activation()))
   return false;
if(!NeuronOCL.calcHiddenGradients(cSubGraphsTokenizer.AsObject()) ||
   !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1))
   return false;

すべての情報ストリームにおける誤差勾配の伝播が正常に完了した後、ポインタを元の状態に戻し、操作の論理的結果を呼び出し元に返してメソッドを完了します。

   if(!NeuronOCL.SetGradient(temp, false))
      return false;
//---
   return true;
  }

これで、適応型混合トークン化オブジェクトCNeuronMoTのメソッドにおけるアルゴリズム構築のレビューは終了です。オブジェクトおよびそのすべてのメソッドの完全な実装は、添付ファイルで提供されています。

本記事はここまでとなりますが、作業はまだ完了していません。ここで短い休憩を取り、次回に作業を続けます。

結論

本記事では、ハイブリッドグラフ系列モデル(GSM++)を活用する革新的なアプローチについて検討しました。これにより、グラフ構造の強力な表現能力と系列データ解析を組み合わせることが可能となります。GSM++は、予測や解析において高い精度を発揮し、複雑な金融データを効率的に処理します。また、計算リソースの使用を最適化できるため、大規模データを扱う際にも非常に有用です。特に、急速に変化する市場状況に適応できる点が、GSM++の大きな強みです。

実践セクションでは、提案手法に対する独自の解釈を実装し、混合トークン化モジュールを構築しました。次回の記事では、この作業を完了させ、実際の過去データを用いた実装の有効性検証も行う予定です。

参照文献

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	サンプル収集用EA
2	ResearchRealORL.mq5	EA	Real-ORL法を用いたサンプル収集用EA
3	Study.mq5	EA	モデル学習用EA
4	Test.mq5	EA	モデルテスト用EA
5	Trajectory.mqh	クラスライブラリ	システム状態とモデルアーキテクチャ記述構造
6	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
7	NeuroNet.cl	コードベース	OpenCLプログラムコード

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/17279

添付されたファイル |

ZIPをダウンロード

MQL5.zip (2482.85 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

ディスカッションに移動

コードベースにコードを公開する方法：実践ガイド

本記事では、MQL5ソースコードベースにさまざまな種類のターミナルプログラムを投稿する方法を、実際の事例を用いて解説します。

中心力最適化(CFO)アルゴリズム

本記事では、重力の法則にヒントを得た中心力最適化(Central Force Optimization, CFO)アルゴリズムを紹介します。このアルゴリズムは、物理的引力の原理を用いて最適化問題を解決する手法を探究するものです。ここでは、「より重い」解が、成功度の低い解を引き寄せる仕組みを扱います。

初心者からエキスパートへ：MQL5リスク強制EAによる取引規律の自動化

多くのトレーダーにとって、口座が破綻する最大の要因は、リスクルールを理解していることと、それを一貫して守ることの間にあるギャップです。感情による判断の上書き、リベンジトレード、あるいは単純な見落としによって、どれほど優れた戦略であっても容易に崩壊してしまいます。本記事では、リスク強制エキスパートアドバイザー(Risk Enforcement EA)を開発することで、MetaTrader 5プラットフォームを、あなたの取引ルールを一切の例外なく執行する揺るぎない監督者へと変えていきます。ディスカッションにぜひご参加ください。

多通貨エキスパートアドバイザーの開発（第24回）：新しい戦略の追加(II)

本記事では、引き続き、作成済みの自動最適化システムに新しい戦略を連携する方法を見ていきます。最適化プロジェクト作成EAと、第2ステージおよび第3ステージのEAにどのような変更を加える必要があるかを見てみましょう。