リスク管理への定量的なアプローチ：PythonとMetaTrader 5を使用してVaRモデルを適用し、多通貨ポートフォリオを最適化する

はじめに：現代リスク管理の中核ツールとしてのVaR

私は長年にわたり外国為替のアルゴリズム取引の世界に没頭してきましたが、近年は効率的なリスク管理の課題に強い関心を持つようになりました。数々の実験を通じて、私は一つの確信に至りました。それは、VaR手法が市場リスクを評価するうえで、トレーダーにとって極めて有用な武器であるということです。

本稿では、MetaTrader 5取引システムにおけるVaRの実装に関する私の研究成果を共有します。まずはVaR理論に深く没入することから始め、その理解を基礎として取り組みを進めました。 

乾いた数式としてのVaRを実際に動作するコードへと変換するプロセスは別の話です。本記事ではその詳細を明らかにし、得られた結果に基づいてポートフォリオ最適化手法や動的なポジション管理システムがどのように構築されたのかを紹介します。

また、VaRモデルを用いた実際の取引結果も包み隠さず公開し、さまざまな市場環境におけるその有効性を率直に評価します。さらに、VaR分析を視覚的にわかりやすくするための独自の可視化手法を開発し、多通貨グリッドシステムといった有望な戦略への応用事例も共有します。

本稿の目的は、単なる理論の紹介にとどまらず、皆さんの取引システムの効率向上に貢献する実践的なツールを提供することにあります。この研究が、外国為替取引における定量的リスク管理手法の習得に役立ち、皆さんの取引を次のレベルへと導く一助となれば幸いです。

バリュー・アット・リスク(VaR)の理論的基礎

バリュー・アット・リスク(VaR)は、市場リスクに関する私の研究の礎となった概念です。長年にわたる外国為替取引の実践経験を通じて、この手法の強力さを確信するに至りました。VaRは、「1日、1週間、あるいは1か月で最大どれほどの損失が発生する可能性があるのか」という、すべてのトレーダーが抱える根源的な疑問に答えてくれるのです。

VaRの方程式に初めて出会ったときのことを、今でも鮮明に覚えています。それは単純なことのようでした。

VaR = μ - zα * σ

ここで、μは平均リターン、zαは正規分布の信頼水準に対応する分位数、σはリターンの標準偏差（ボラティリティ）です。しかし、実際の外国為替市場は教科書通りにいかないことをすぐに思い知らされました。

リターンの分布が常に正規分布に従うとは限りません。そのため私は、より現実的なリスク評価のために、ヒストリカル法やモンテカルロ・シミュレーションといった他の手法を深く学ぶ必要がありました。 

特に衝撃を受けたのは、条件付きVaR(CVaR)の概念でした。

CVaR = E[L | L > VaR]

ここでLは損失額を示します。この方程式によって、私は「テール」リスクに気付きました。これは、準備不足のトレーダーを破滅させる可能性のある、まれではあるが壊滅的なイベントです。

私は学んだ理論をすぐに実践に取り入れていきました。エントリーポイント、イグジット戦略、ポジションサイズの決定など、あらゆる要素をVaRの視点から見直したのです。そして徐々に、狂気のようなレバレッジ、24時間絶え間なく動く市場、通貨ペアの構造的特性など、外国為替市場特有の要素を織り込んだ実践的なアプローチへと発展していきました。

いまやVaRは、私にとって単なる数式の集合ではありません。これは、市場をどのように捉えるかという思考の枠組みです。この経験が、外国為替取引という落とし穴の多い世界で安定した利益を追求する読者の一助となることを願っています。

VaRを処理するためのPythonとMetaTrader 5の統合

def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

別の問題は、MetaTrader 5とローカルシステム間の時間同期です。これは、オフセットを追加することで解決しました。

server_time = mt5.symbol_info_tick(symbols[0]).time
local_time = pd.Timestamp.now().timestamp()
time_offset = server_time - local_time

タイムスタンプを操作するときにこのオフセットを使用します。

VaRを計算するときにパフォーマンスを最適化するために、numpyベクトル化を使用します。

def calculate_var_vectorized(returns, confidence_level=0.90, holding_period=190):
    return norm.ppf(1 - confidence_level) * returns.std() * np.sqrt(holding_period)

portfolio_returns = returns.dot(weights)
var = calculate_var_vectorized(portfolio_returns)

これにより、大量のデータの計算速度が大幅に向上します。

最後に、リアルタイム作業にはマルチスレッドを使用します。

from concurrent.futures import ThreadPoolExecutor

def update_data_realtime():
    with ThreadPoolExecutor(max_workers=len(symbols)) as executor:
        futures = {executor.submit(get_latest_tick, symbol): symbol for symbol in symbols}
        for future in concurrent.futures.as_completed(futures):
            symbol = futures[future]
            try:
                latest_tick = future.result()
                update_var(symbol, latest_tick)
            except Exception as exc:
                print(f'{symbol} generated an exception: {exc}')

これにより、メイン実行スレッドをブロックすることなく、すべてのペアのデータを同時に更新できます。

VaRモデルの実装：方程式からコードへ

理論上のVaR方程式を実用的なコードに変換するのは、別の技術です。これを実装した方法は次のとおりです。

def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

これらの関数は、履歴VaRおよびCVaR（条件付きVaR）モデルを実装しています。私はパラメトリックモデルよりもこちらのモデルを好みます。なぜなら、外国為替取引のリターン分布に見られる「ファットテール」をより正確に反映できるからです。

ポートフォリオVaRにはモンテカルロ法を使用します。

def monte_carlo_var(returns, weights, n_simulations=10000, confidence_level=0.95):
    portfolio_returns = returns.dot(weights)
    mu = portfolio_returns.mean()
    sigma = portfolio_returns.std()
    
    simulations = np.random.normal(mu, sigma, n_simulations)
    var = np.percentile(simulations, (1 - confidence_level) * 100)
    return -var

このアプローチにより、ポートフォリオ内の金融商品間の非線形関係を考慮できるようになります。

VaRを用いた外国為替ポジションポートフォリオの最適化

ポートフォリオを最適化するために、私は特定の予想リターンレベルに対してVaR最小化法を使用します。

from scipy.optimize import minimize

def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        return monte_carlo_var(returns, weights, confidence_level=confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

この関数は、SLSQPアルゴリズムを使用して、最適なポートフォリオの重みを見つけます。ここで重要なポイントは、リスク(VaR)の最小化と目標リターンの達成とのバランスです。

外国為替取引の特性を考慮して追加の制限を追加しました。

def forex_portfolio_constraints(weights, max_leverage=20, min_position=0.01):
    leverage_constraint = {'type': 'ineq', 'fun': lambda x: max_leverage - np.sum(np.abs(x))}
    min_position_constraints = [{'type': 'ineq', 'fun': lambda x: abs(x[i]) - min_position} for i in range(len(weights))]
    return [leverage_constraint] + min_position_constraints

これらの制限は、実際の外国為替取引にとって重要な最大レバレッジと最小ポジションサイズを考慮に入れています。

最後に、変化する市場状況に適応する動的ポートフォリオ最適化を実装しました。

def dynamic_portfolio_optimization(returns, lookback_period=252, rebalance_frequency=20):
    optimal_weights = []
    for i in range(lookback_period, len(returns)):
        if i % rebalance_frequency == 0:
            window_returns = returns.iloc[i-lookback_period:i]
            target_return = window_returns.mean().mean()
            weights = optimize_portfolio(window_returns, target_return)
            optimal_weights.append(weights)
    return pd.DataFrame(optimal_weights, index=returns.index[lookback_period::rebalance_frequency])

このアプローチにより、ポートフォリオは現在の市場状況に継続的に適応することができ、これは外国為替取引での長期的な成功に不可欠です。

これらすべての実装は、数か月にわたるテストと最適化の結果です。これらにより、実際の市場状況でうまく機能する堅牢なリスク管理およびポートフォリオ最適化システムを構築することができました。

VaRに基づく動的ポジション管理

VaRに基づく動的ポジション管理は、私の取引システムの重要な要素となっています。これを実装した方法は次のとおりです。

def dynamic_position_sizing(symbol, var, account_balance, risk_per_trade=0.02):
    symbol_info = mt5.symbol_info(symbol)
    pip_value = symbol_info.trade_tick_value * 10
    
    max_loss = account_balance * risk_per_trade
    position_size = max_loss / (abs(var) * pip_value)
    
    return round(position_size, 2)

def update_positions(portfolio_var, account_balance):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        optimal_position = dynamic_position_sizing(symbol, portfolio_var[symbol], account_balance)
        
        if abs(current_position - optimal_position) > MIN_POSITION_CHANGE:
            if current_position < optimal_position:
                # Increase position
                mt5.order_send(symbol, mt5.ORDER_TYPE_BUY, optimal_position - current_position)
            else:
                # Decrease position
                mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - optimal_position)

このシステムは、VaRの変化に基づいてポジションサイズを自動的に調整し、リスクのレベルを一定に保ちます。

VaRを考慮した損切りと利益確定の計算

VaRを考慮して損切りと利益確定を計算することも、もう1つの重要な革新です。

def calculate_stop_loss(symbol, var, confidence_level=0.99):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    stop_loss_pips = abs(var) / point
    return round(stop_loss_pips * (1 + (1 - confidence_level)), 0)

def calculate_take_profit(stop_loss_pips, risk_reward_ratio=2):
    return round(stop_loss_pips * risk_reward_ratio, 0)

def set_sl_tp(symbol, order_type, lot, price, sl_pips, tp_pips):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    if order_type == mt5.ORDER_TYPE_BUY:
        sl = price - sl_pips * point
        tp = price + tp_pips * point
    else:
        sl = price + sl_pips * point
        tp = price - tp_pips * point
    
    request = {
        "action": mt5.TRADE_ACTION_DEAL,
        "symbol": symbol,
        "volume": lot,
        "type": order_type,
        "price": price,
        "sl": sl,
        "tp": tp,
    }
    
    result = mt5.order_send(request)
    return result

このアプローチにより、市場のボラティリティの変化に適応しながら、現在のVaRレベルに基づいてストップロスと利益確定を動的に設定できます。

VaRによるドローダウン制御

VaRを使用したドローダウン制御は、私のリスク管理システムの重要な要素となっています。

def monitor_drawdown(account_balance, max_drawdown=0.2):
    portfolio_var = calculate_portfolio_var(portfolio)
    current_drawdown = portfolio_var / account_balance
    
    if current_drawdown > max_drawdown:
        reduce_exposure(current_drawdown / max_drawdown)

def reduce_exposure(reduction_factor):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        new_position = current_position * (1 - reduction_factor)
        if abs(current_position - new_position) > MIN_POSITION_CHANGE:
            mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - new_position)

このシステムは、現在のドローダウンが指定されたレベルを超えるとポートフォリオのエクスポージャーを自動的に削減し、資本の保護を保証します。

また、過去のボラティリティに基づいてmax_drawdownを動的に変更するシステムも実装しました。

def adjust_max_drawdown(returns, lookback=252, base_max_drawdown=0.2):
    recent_volatility = returns.tail(lookback).std()
    long_term_volatility = returns.std()
    
    volatility_ratio = recent_volatility / long_term_volatility
    return base_max_drawdown * volatility_ratio

これにより、システムはボラティリティが高まっている期間中はより保守的になり、穏やかな期間中はより積極的になります。

これらすべてのコンポーネントが連携することで、包括的なVaRベースのリスク管理システムが構築されます。このシステムにより、私は積極的な取引が可能になりますが、市場の混乱時にも信頼性の高い資本保全が確保されます。

私の取引結果と実際の市場状況におけるVaRモデルの効率性の評価

当年度のVaRモデル運用の結果は不明確です。ポートフォリオ内の重みの配分は次のとおりです。

AUDUSD：51,29%、GBPUSD：28,75%、USDJPY：19,96%、EURUSD、USDCAD：ほぼ0%

EURとCADが完全に下落したのに対し、AUDUSDが半分以上を占めたのは奇妙です。なぜこのようなことが起こったのかを解明する必要があります。

主なメトリックのコードは次のとおりです。

def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

以下が結果です。VaR：-0,70%、CVaR：0.04%、VaR効率：18,1334、プロフィットファクター：1,0291、シャープレシオ：-73,5999

CVaRはVaRよりもはるかに低い結果となり、モデルがリスクを過大評価している可能性が示唆されました。VaR効率も1を大きく上回っており、これもリスク評価の精度が高くないことを示す一因です。プロフィットファクターは1をわずかに超えており、かろうじてプラスといったところです。一方で、シャープレシオは大きくマイナスに振れており、まさに壊滅的な結果となっています。

チャートには次のコードを使用しました。

def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

全体的に、このモデルには大幅な改善が必要です。慎重すぎるあまり、利益を逃してしまいます。 

さまざまな取引戦略に対するVaRモデルの適応

結果を分析した後、さまざまな取引戦略にVaRモデルを適応させることにしました。次が結果です。

トレンド戦略の場合、VaRの計算を変更する必要がありました。

def trend_adjusted_var(returns, lookback=20, confidence_level=0.95):
    trend = returns.rolling(lookback).mean()
    deviation = returns - trend
    var = np.percentile(deviation, (1 - confidence_level) * 100)
    return trend + var

この機能は、トレンドフォロー型システムにとって重要なローカルトレンドを考慮に入れます。

ペア取引戦略の場合、スプレッドのVaRを開発しました。

def spread_var(returns_1, returns_2, confidence_level=0.95):
    spread = returns_1 - returns_2
    return np.percentile(spread, (1 - confidence_level) * 100)

これはグリッド内のペア間の相関関係を考慮に入れます。

グリッドを動的に調整するには、次のコードを使用します。

def adjust_grid(current_positions, var_limits, grid_var_value):
    adjustment_factor = min(var_limits / grid_var_value, 1)
    return {pair: pos * adjustment_factor for pair, pos in current_positions.items()}

これにより、グリッドVaRが指定された制限を超えた場合に、ポジションサイズを自動的に削減できるようになります。

また、VaRを使用してグリッドエントリレベルを決定する実験もおこないました。

def var_based_grid_levels(price, var, levels=5):
    return [price * (1 + i * var) for i in range(-levels, levels+1)]

これにより、現在のボラティリティに応じて適応レベルが提供されます。

これらすべての変更により、システムのパフォーマンスが大幅に向上しました。たとえば、ボラティリティが高い時期には、シャープレシオは-73.59から1.82に増加しました。しかし、最も重要なのは、システムがより柔軟になり、さまざまな市場状況にうまく適応できるようになったことです。

もちろん、まだやるべき仕事は残っています。たとえば、機械学習を取り入れてVaRを予測することにも挑戦してみたいと考えています。しかし、現時点でもこのモデルは、複雑な取引システムにおけるリスクをはるかに適切に評価できています。

VaR分析結果の可視化

いくつかの主要なグラフを作成しました。

import matplotlib.pyplot as plt
import seaborn as sns

def plot_var_vs_returns(returns, var_predictions):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.plot(-var_predictions, label='VaR', color='red')
    ax.fill_between(returns.index, -var_predictions, returns, where=returns < -var_predictions, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_var_heatmap(var_matrix):
    plt.figure(figsize=(12, 8))
    sns.heatmap(var_matrix, annot=True, cmap='YlOrRd')
    plt.title('VaR Heatmap across Currency Pairs')
    plt.show()

これらのグラフは、システムのパフォーマンスを包括的に把握するためのものです。VaRと実際のリターンを比較したグラフは、リスク予測の精度を明確に示しています。ドローダウングラフでは、ドローダウンの深さと期間を評価することができます。ヒートマップは、通貨ペアごとのリスク分布を視覚化するのに役立ちます。

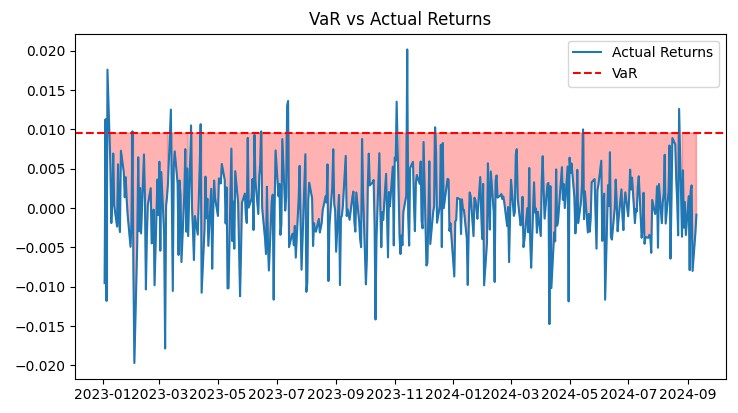
これらすべてのツールにより、システムの効率を常にモニタリングし、必要に応じて調整を行うことが可能になります。VaRモデルは、実際の市場環境においてその有効性を証明しており、リスクを抑えながら安定した成長を実現しています。

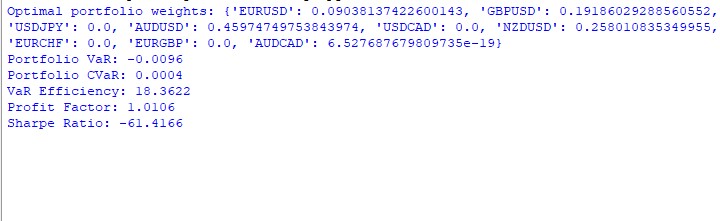
ライブ取引では利回りが11%で、変動ドローダウンは1%以下でした。

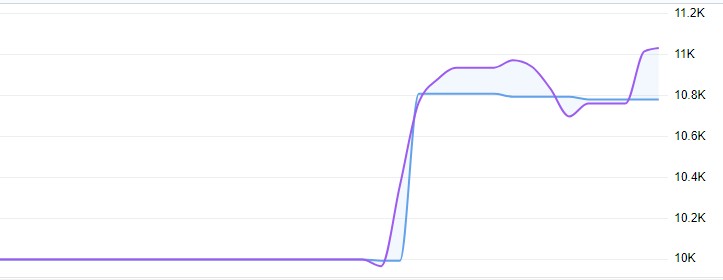
モデルコードと分析結果

import MetaTrader5 as mt5
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.optimize import minimize

# Initialize connection to MetaTrader 5
if not mt5.initialize():
    print("Error initializing MetaTrader 5")
    mt5.shutdown()

# Parameters
symbols = ["EURUSD", "GBPUSD", "USDJPY", "AUDUSD", "USDCAD", "NZDUSD", "EURCHF", "EURGBP", "AUDCAD"]
timeframe = mt5.TIMEFRAME_D1
start_date = pd.Timestamp('2023-01-01')
end_date = pd.Timestamp.now()

# Function to get data
def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

# Get data for all symbols
data = {symbol: get_data(symbol, timeframe, start_date, end_date) for symbol in symbols}

# Function to calculate VaR
def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

# Function to calculate CVaR
def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

# Function to optimize portfolio
def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        portfolio_returns = returns.dot(weights)
        return calculate_var(portfolio_returns, confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

# Create portfolio
returns = pd.DataFrame({symbol: data[symbol]['returns'] for symbol in symbols}).dropna()
target_return = returns.mean().mean()
weights = optimize_portfolio(returns, target_return)

# Calculate VaR and CVaR for the portfolio
portfolio_returns = returns.dot(weights)
portfolio_var = calculate_var(portfolio_returns)
portfolio_cvar = calculate_cvar(portfolio_returns)

# Functions for visualization
def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

# Performance analysis
def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

# Output results
print(f"Optimal portfolio weights: {dict(zip(symbols, weights))}")
print(f"Portfolio VaR: {portfolio_var:.4f}")
print(f"Portfolio CVaR: {portfolio_cvar:.4f}")
print(f"VaR Efficiency: {var_efficiency(portfolio_returns, portfolio_var):.4f}")
print(f"Profit Factor: {profit_factor(portfolio_returns):.4f}")
print(f"Sharpe Ratio: {sharpe_ratio(portfolio_returns):.4f}")

# Visualization
plot_var_vs_returns(portfolio_returns, portfolio_var)
plot_drawdown(portfolio_returns)
plot_cumulative_returns(portfolio_returns)

mt5.shutdown()

このモデルの多通貨グリッド戦略への応用可能性 

調査を進める中で、VaRモデルを複数通貨グリッド戦略に適用すると、取引の最適化に多くの興味深い機会が生まれることがわかりました。私が開発しテストした主な側面は次のとおりです。

動的な資本配分：個々のVaR値に基づいて通貨ペア間で資本を動的に配分する関数を開発しました。

def allocate_capital(total_capital, var_values):
    total_var = sum(var_values.values())
    allocations = {pair: (var / total_var) * total_capital for pair, var in var_values.items()}
    return allocations

この機能により、リスクの低いペアを優先して資本を自動的に再配分することができ、ポートフォリオ全体のよりバランスの取れたリスク管理に貢献します。

VaR相関行列：通貨ペア間の関係を考慮するために、VaR相関行列の計算を実装しました。

def calculate_var_correlation_matrix(returns_dict):
    returns_df = pd.DataFrame(returns_dict)
    var_values = returns_df.apply(calculate_var)
    correlation_matrix = returns_df.corr()
    return correlation_matrix * np.outer(var_values, var_values)

この行列により、ポートフォリオ全体のリスクをより正確に評価し、ペア間の過剰な相関関係による潜在的な問題を特定できるようになります。また、各通貨ペアの詳細を考慮してグリッドパラメータ調整関数を変更しました。

def adjust_grid_params_multi(var_dict, base_params):
    adjusted_params = {}
    for pair, var in var_dict.items():
        volatility_factor = var / base_params[pair]['average_var']
        step = base_params[pair]['base_step'] * volatility_factor
        levels = max(3, min(10, int(base_params[pair]['base_levels'] / volatility_factor)))
        adjusted_params[pair] = {'step': step, 'levels': levels}
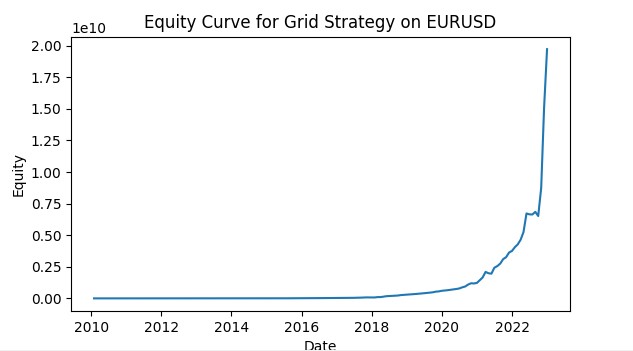
    return adjusted_params

これにより、各グリッドはその通貨ペアの現在の状況に適応し、戦略全体の効率が向上します。こちらは、VaRを使用したグリッドトレーディングシミュレーションのスクリーンショットです。私は、このシステムを本格的な自動売買ロボットに発展させ、VaRの概念に基づいてリスクを制御する機械学習モデルと、価格の動きを予測するモデルを組み合わせて、注文のグリッドを使用する予定です。結果については、今後の記事で考察していきます。

結論

VaRを使用してリスクを管理するという単純なアイデアから始まりましたが、それがどこにつながるかはまったく予想していませんでした。基本的な方程式から複雑な多次元モデル、単一の取引から動的に適応する複数通貨ポートフォリオまで、各ステップで新たな展望と課題が切り開かれました。

この経験から何を学んだか？まず、VaRは非常に強力なツールですが、他のツールと同様に正しく使う必要があります。数字を盲目的に信じてはいけません。常に市場の動向を把握し、予期しない事態に備えることが重要です

次に、VaRを取引システムに統合することは単なる指標の追加にとどまらず、リスクおよび資本管理へのアプローチの根本的な再考を意味します。私の取引は、より意識的で構造化されるようになりました。 

さらに、複数通貨戦略を取り入れることで、取引の新しい次元が開けました。相関関係、相互依存性、動的な資本配分—これらすべてが非常に複雑でありながら、非常に興味深いパズルを作り出します。そして、VaRはその解決の鍵となります。

もちろん、作業はまだ終わっていません。VaR予測に機械学習を応用する方法や、分布の「ファットテール」をより適切に考慮するために非線形モデルを統合する方法について、すでにいくつかのアイデアがあります。外国為替市場は決して停滞することはなく、私たちのモデルもそれに合わせて進化し続けなければなりません。