ニューラルネットワークが簡単に(第90回):時系列の周波数補間(FITS)
はじめに
時系列分析は、金融市場における意思決定において重要な役割を担っています。金融分野における時系列データは複雑で動的であるため、効率的な処理手法が求められます。
高度な時系列分析の研究では、洗練されたモデルや手法が開発されていますが、これらのモデルは計算量が多く、動的な金融市場においては実用的でないことがしばしばあります。特に、意思決定が迅速におこなわれるべき場面では、これらのモデルはほとんど適用できません。
さらに、最近ではモバイルデバイスを使用してリソースが限られた環境で経営上の意思決定をおこなう場面が増えており、これにより、意思決定に使用するモデルに対してさらに高い要求が求められています。
このような背景の中で、時系列データを周波数領域で表現することで、観測されたパターンをより効率的かつコンパクトに表現できる可能性があります。たとえば、スペクトルデータや高振幅周波数分析の活用は、重要な特徴量を識別するのに役立ちます。
前回の記事では、周波数領域を用いて時系列パターンを検出するFEDformer法について説明しました。しかし、この手法で用いられているTransformerは、軽量なモデルとは言えません。そこで、複雑で計算コストが大きいモデルの代わりに、論文「FITS:Modeling Time Series with 10k Parameters」では、時系列の周波数補間(FITS: Frequency Interpolation Time Series)手法が提案されています。この手法は、時系列分析と予測においてコンパクトで効率的なソリューションを提供します。FITSは、周波数領域での補間を活用して、分析対象の時間セグメントのウィンドウを拡張し、計算オーバーヘッドを最小限に抑えながら時間的特徴を効率的に抽出できるようにします。
FITS法の著者は、この手法の次のような利点を強調しています。
- パラメータ数が少なく、軽量なモデルであるためリソースが限られたデバイスでの使用に最適である。
- 複雑なニューラルネットワークを用いて、信号の振幅と位相に関する情報を効率的に収集し、時系列データ分析の効率を向上させる。
1. FITSアルゴリズム
周波数領域での時系列分析により、データを損失することなく、信号を正弦波成分の線形結合に分解することができます。これらの成分は、それぞれ固有の周波数、初期位相、および振幅を持っています。時系列の予測は複雑になることがありますが、個々の正弦波成分の予測は、時間シフトに基づいて正弦波の位相を調整するだけで済むため、比較的簡単です。このようにシフトされた正弦波を線形に結合することで、分析した時系列の予測値を得ることができます。
このアプローチにより、分析された時系列ウィンドウの周波数特性を効果的に維持することができます。また、時間ウィンドウと予測期間の間で、意味のあるシーケンスが保たれます。
ただし、時間領域で各正弦波成分を予測するのには非常に手間がかかります。この問題を解決するために、FITS法の著者は、よりコンパクトで情報豊富なデータ表現として、複素周波数領域の使用を提案しています。
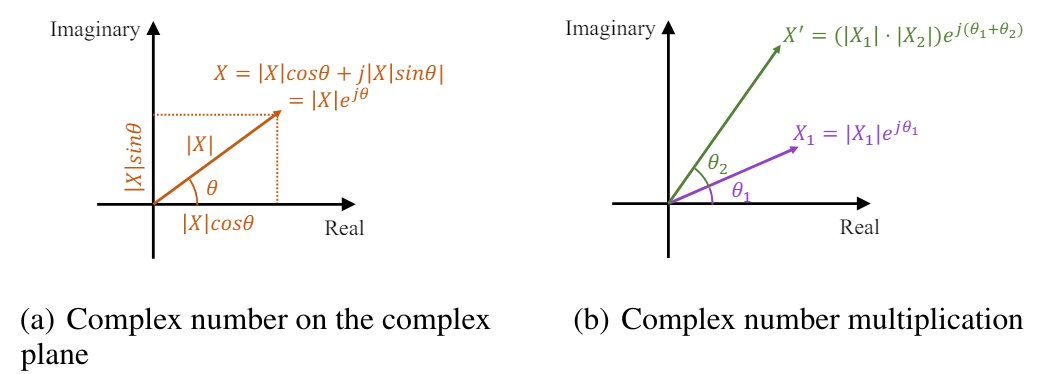
高速フーリエ変換(FFT)は、離散時系列信号を時間領域から複素周波数領域に効率的に変換する手法です。フーリエ解析において、複素周波数領域は、各周波数成分が複素数で表されるシーケンスで特徴づけられます。この複素数は、成分の振幅と位相を反映し、信号の完全な記述を提供します。周波数成分の振幅は、時間領域におけるその成分の大きさ、すなわち強度を示します。一方、位相はその成分がもたらす時間シフトや遅延を示します。数学的には、周波数成分に関連付けられた複素数は、指定された振幅と位相を持つ複素指数関数として表現されます。
![]()
ここで、X(f)は周波数fの周波数成分に関連する複素数です。
|X(f)|は成分の振幅です。
θ(f)は成分の位相です。
複素平面では、指数要素は、長さが振幅に等しく、角度が位相に等しいベクトルとして表すことができます。
![]()
したがって、周波数領域の複素数は、フーリエ変換における各周波数成分の振幅と位相を表す簡潔かつエレガントな方法を提供します。
信号の時間シフトは、周波数領域での位相シフトに対応します。複素周波数領域では、この位相シフトは複素指数の単位要素と対応する位相の乗算として表現できます。シフトされた信号の振幅は依然として|X(f)|であり、位相は時間に対する線形シフトを示します。
したがって、振幅のスケーリングと位相シフトは、複素数の乗算として同時に表現することができます。
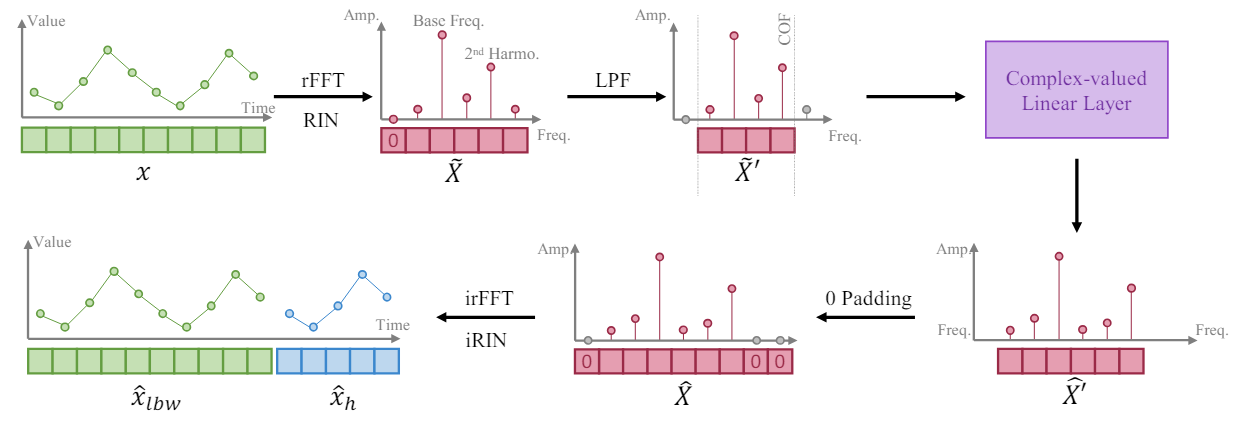
FITS法の著者は、時系列が長いほど周波数表現の周波数分解能が高くなるという事実に基づき、入力データの分析ウィンドウの周波数表現を補間することで時系列セグメントを拡張するようにモデルを訓練します。著者は、この補間を訓練するために単一の複素線形層を使用することを提案しており、その結果、モデルは補間プロセス中に振幅スケーリングと位相シフトを複素数の乗算として学習できます。FITSアルゴリズムでは、高速フーリエ変換(FFT)を使用して時系列セグメントを複素周波数領域に投影します。補間後、周波数表現は逆FFTを使用して時間領域に戻されます。
しかし、このようなセグメントの平均を取ると、複素周波数表現で非常に大きなゼロ周波数成分が発生します。この問題を解決するために、受信信号は可逆正規化(RevIN)に渡され、これにより平均がゼロのインスタンスが得られます。
さらに、FITSの著者は、FITSにローパスフィルター(LPF)を追加してモデルのサイズを縮小しています。ローパスフィルターは、指定されたカットオフ周波数を超える高周波成分を効果的に除去し、重要な時系列情報を保持しつつモデル表現を圧縮します。
FITSは周波数領域で動作しますが、逆FFT後の平均二乗誤差(MSE)などの標準的な損失関数を使用して時間領域で訓練されます。これにより、さまざまな後続の時系列問題に適応できる汎用的なアプローチが提供されます。
予測タスクにおいて、FITSは計画期間に合わせて遡及分析ウィンドウを生成します。これにより、予測と遡及分析を制御でき、モデルは遡及分析ウィンドウを正確に再構築するように学習します。引用された論文でおこなわれた分析では、事後洞察と予測監視を組み合わせることで、特定のシナリオでパフォーマンスが向上する可能性が示されています。
再構成タスクでは、FITSは指定されたサブサンプリングレートに基づいて入力時系列セグメントをサブサンプリングし、次に周波数補間を実行してダウンサンプリングされたセグメントを元の形式に戻します。このようにして、損失を使った直接制御が適用され、信号の正確な再構成が保証されます。
モデル結果テンソルの長さを制御するために、FITSの著者は𝜂(補間率)というパラメータを導入しました。これは、モデル結果テンソルの必要なサイズと元のデータテンソルの対応するサイズの比率を示します。
ローパスフィルター(LPF)を適用する場合、複素層の入力データテンソルのサイズはLPFのカットオフ周波数(COF)に対応することに注意が必要です。周波数補間を実行した後、複素周波数表現は、結果のテンソルの必要なサイズまでゼロで埋められます。逆FFTを適用する前に、ゼロ周波数成分として追加のゼロを導入します。
FITSにLPFを組み込む主な目的は、重要な情報を保持しつつモデルボリュームを圧縮することですLPFは、特定のカットオフ周波数(COF)を超える周波数成分を破棄することで、より簡潔な周波数領域表現を実現します。LPFは、モデルの学習能力を超える成分を除去しながら、時系列の関連情報を保持します。これにより、入力時系列の意味のあるコンテンツの大部分が保持されます。実験結果では、周波数領域で元の表現の4分の1のみが保持されている場合でも、フィルタ処理された信号の歪みが最小限であることが示されています。また、LPFでフィルタ処理された高周波成分には、時系列モデリングに本質的に無関係なノイズが含まれていることがわかっています。
ここで重要なのは、適切なカットオフ周波数(COF)の選択です。この問題に対処するため、FITSの著者は支配的な周波数の高調波成分に基づく手法を提案しています。優位周波数の整数倍である高調波は、時系列信号の波形を形成する上で重要な役割を果たします。カットオフ周波数をこれらの高調波と比較することで、信号の構造や周期性に関連する周波数成分が保持され、ノイズや不要な高周波成分を抑制しながら意味のある情報を抽出することができます。
原作者によるFITS法の視覚化を以下に示します。
2. MQL5での実装
FITS法の理論的側面について検討した後、次に、MQL5を使用して提案されたアプローチを実際に実装する段階に進みます。
これまで通り、提案されたアプローチを使用しますが、解決しようとしている問題の詳細により、実装は著者のアルゴリズムのビジョンと若干異なる場合があります。
2.1 FFTの実装
上記の手法の理論的な説明から、この手法は直接および逆高速フーリエ変換(FFT)に基づいていることがわかります。高速フーリエ変換を使用することで、まず解析対象の信号を周波数領域に変換し、次に予測されたシーケンスを元の時系列表現に戻すことができます。この場合、高速フーリエ変換には2つの主要な利点があります。
- 他の同様の変換と比較した操作の高速性
- 逆変換を直接変換として表現する能力
ここで重要なのは、タスクの枠組みにおいて、多変量時系列に対するFFTの実装が必要であるという点です。実際には、多変量シーケンス内の各単一時系列に対してFFTを適用します。
実装におけるほとんどの数学的な演算はOpenCLに転送されます。これにより、独立したデータを持つ多くの同様の演算を複数の並列スレッドに分散させ、計算にかかる時間を短縮できます。OpenCL側で高速フーリエ変換の演算が実行され、各並列スレッドで個別のユニタリ時系列の分解をおこないます。
次に、FFTカーネルの形式で操作を実行するアルゴリズムを示します。カーネルのパラメータとして、4つのデータ配列へのポインタを渡します。ここでは、入力データとその操作結果を格納する2つの配列を使用します。1つの配列には複素数の実部(信号振幅)が含まれ、もう1つの配列には虚部(位相)が含まれます。
しかし、注意すべき点は、信号の虚部を常にカーネルに渡すわけではないことです。例えば、入力時系列を分解する際には、この虚部が存在しません。この場合、解決策は非常に簡単で、欠落しているデータをゼロで埋めることです。この状況に対応するために、カーネルのパラメータとしてinput_complexフラグを導入し、ゼロで満たされた別のバッファを渡さないようにします。
さらに、FFTに使用されるCooley-Tukeyアルゴリズムは、シーケンスの長さが2の累乗である場合にのみ適用できます。この条件は重大な制約となりますが、これは解析される信号の準備段階で対応できます。具体的には、シーケンスの欠落している部分をゼロで埋めることで、この制限を解決できます。ここでも、データの無駄なコピーを避けるために、カーネルパラメータとしてinput_windowとoutput_windowという2つの変数を追加します。input_windowでは解析対象のシーケンスの実際の長さを示し、output_windowでは分解結果ベクトルのサイズ(2の累乗)を指定します。この場合、ユニタリシーケンスのサイズに関する情報を扱っています。
最後に、reverseというパラメータがあります。これは、変換の方向(直接変換または逆変換)を指定します。
__kernel void FFT(__global float *inputs_re, __global float *inputs_im, __global float *outputs_re, __global float *outputs_im, const int input_window, const int input_complex, const int output_window, const int reverse ) { size_t variable = get_global_id(0);
カーネル本体では、まず、分析対象のユニタリ シーケンスを指すスレッド識別子を定義します。ここでは、データバッファのシフトやその他の必要な定数も定義します。
const ulong N = output_window; const ulong N2 = N / 2; const ulong inp_shift = input_window * variable; const ulong out_shift = output_window * variable;
次のステップでは、入力データを特定の順序で再ソートし、FFTアルゴリズムを少し最適化します。
uint target = 0; for(uint position = 0; position < N; position++) { if(target > position) { outputs_re[out_shift + position] = (target < input_window ? inputs_re[inp_shift + target] : 0); outputs_im[out_shift + position] = ((target < input_window && input_complex) ? inputs_im[inp_shift + target] : 0); outputs_re[out_shift + target] = inputs_re[inp_shift + position]; outputs_im[out_shift + target] = (input_complex ? inputs_im[inp_shift + position] : 0); } else { outputs_re[out_shift + position] = inputs_re[inp_shift + position]; outputs_im[out_shift + position] = (input_complex ? inputs_im[inp_shift + position] : 0); } unsigned int mask = N; while(target & (mask >>= 1)) target &= ~mask; target |= mask; }
次に、ネストループでデータの直接変換が実行されます。外側のループでは、長さ 2、4、8、... nのセグメントのFFT反復を構築します。
float real = 0, imag = 0; for(int len = 2; len <= (int)N; len <<= 1) { float w_real = (float)cos(2 * M_PI_F / len); float w_imag = (float)sin(2 * M_PI_F / len);
ループ本体では、ループ長1ポイントあたりの引数回転の乗数を定義し、分析対象のシーケンス内のブロックを反復処理するためのネストされたループを構成します。
for(int i = 0; i < (int)N; i += len) { float cur_w_real = 1; float cur_w_imag = 0;
ここでは、現在の位相回転の変数を宣言し、ブロック内の要素に対して別のネストされたループを構成します。
for(int j = 0; j < len / 2; j++) { real = cur_w_real * outputs_re[out_shift + i + j + len / 2] - cur_w_imag * outputs_im[out_shift + i + j + len / 2]; imag = cur_w_imag * outputs_re[out_shift + i + j + len / 2] + cur_w_real * outputs_im[out_shift + i + j + len / 2]; outputs_re[out_shift + i + j + len / 2] = outputs_re[out_shift + i + j] - real; outputs_im[out_shift + i + j + len / 2] = outputs_im[out_shift + i + j] - imag; outputs_re[out_shift + i + j] += real; outputs_im[out_shift + i + j] += imag; real = cur_w_real * w_real - cur_w_imag * w_imag; cur_w_imag = cur_w_imag * w_real + cur_w_real * w_imag; cur_w_real = real; } } }
ループ本体では、まず分析対象の要素を変更し、次に次の反復の現在のフェーズ変数の値を変更します。
バッファ要素の変更は、追加のメモリを割り当てることなく「インプレース」で実行されることに注意してください。
ループシステムの反復が完了したら、reverseフラグの値を確認します。逆変換を実行する場合は、結果バッファ内のデータを再ソートします。この場合、取得した値をシーケンス内の要素数で割ります。
if(reverse) { outputs_re[0] /= N; outputs_im[0] /= N; outputs_re[N2] /= N; outputs_im[N2] /= N; for(int i = 1; i < N2; i++) { real = outputs_re[i] / N; imag = outputs_im[i] / N; outputs_re[i] = outputs_re[N - i] / N; outputs_im[i] = outputs_im[N - i] / N; outputs_re[N - i] = real; outputs_im[N - i] = imag; } } }
2.2 予測分布の実部と虚部を組み合わせる
上記のカーネルを使用すると、直接および逆高速フーリエ分解を実行できます。これにより、私たちのニーズは十分に満たされます。ただし、FITS法には注意すべき点がもう1つあります。この手法の作成者は、複雑なニューラルネットワークを使用してデータを補間します。複素ニューラルネットワークの詳細な紹介については、「A Survey of Complex-Valued Neural Networks」を読むことをお勧めします。この実装では、実数部と虚数部を個別に補間し、次の式に従ってそれらを結合する既存のニューラル層クラスを使用します。
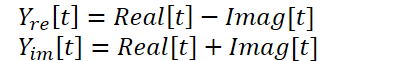
これらの操作を実行するには、ComplexLayerカーネルを作成します。カーネルアルゴリズムは非常に単純です。行列の行と列を指す2次元のスレッドを識別するだけです。データバッファのシフトを決定し、単純な数学的演算を実行します。
__kernel void ComplexLayer(__global float *inputs_re, __global float *inputs_im, __global float *outputs_re, __global float *outputs_im ) { size_t i = get_global_id(0); size_t j = get_global_id(1); size_t total_i = get_global_size(0); size_t total_j = get_global_size(1); uint shift = i * total_j + j; //--- outputs_re[shift] = inputs_re[shift] - inputs_im[shift]; outputs_im[shift] = inputs_im[shift] + inputs_re[shift]; }
ComplexLayerGradientバックプロパゲーション カーネルも同様の方法で構築されます。添付ファイルを使用してこのコードを調べることができます。
これでOpenCLプログラム側の操作は終了です。
2.3 FITSメソッドクラスの作成
OpenCLプログラムのカーネルでの作業が終了したら、メインプログラムに移り、FITS法の著者が提案したアプローチを実装するためにCNeuronFITSOCLクラスを作成します。この新しいクラスはニューラル層の基底クラスであるCNeuronBaseOCLから派生します。新しいクラスの構造は以下のようになります。
class CNeuronFITSOCL : public CNeuronBaseOCL { protected: //--- uint iWindow; uint iWindowOut; uint iCount; uint iFFTin; uint iIFFTin; //--- CNeuronBaseOCL cInputsRe; CNeuronBaseOCL cInputsIm; CNeuronBaseOCL cFFTRe; CNeuronBaseOCL cFFTIm; CNeuronDropoutOCL cDropRe; CNeuronDropoutOCL cDropIm; CNeuronConvOCL cInsideRe1; CNeuronConvOCL cInsideIm1; CNeuronConvOCL cInsideRe2; CNeuronConvOCL cInsideIm2; CNeuronBaseOCL cComplexRe; CNeuronBaseOCL cComplexIm; CNeuronBaseOCL cIFFTRe; CNeuronBaseOCL cIFFTIm; CBufferFloat cClear; //--- virtual bool FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false); virtual bool ComplexLayerOut(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im); virtual bool ComplexLayerGradient(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); public: CNeuronFITSOCL(void) {}; ~CNeuronFITSOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_out, uint count, float dropout, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual int Type(void) const { return defNeuronFITSOCL; } virtual void SetOpenCL(COpenCLMy *obj); virtual void TrainMode(bool flag); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); };
新しいクラスの構造には、内部ニューラル層オブジェクトの宣言がかなり多く含まれています。これは、モデルの予想されるシンプルさを考慮すると奇妙に思えるかもしれません。しかし、データ補間を担当する4つのネストされたニューラル層(cInsideRe*およびcInsideIm*)のパラメータのみを訓練することに注意してください。その他のオブジェクトは、中間データバッファとして機能します。メソッドを実装する際には、それらの目的を考慮する必要があります。
また、CNeuronDropoutOCL層が2つあることにも注意が必要です。この実装では、特定のカットオフ周波数を決定するLFPは使用しません。ここで、周波数特性のセットをサンプリングする効率について述べているFEDformer法の著者の実験を思い出しました。そこで、ドロップアウト層を使用して、ランダムな周波数特性の特定の数をゼロに設定することにしました。
すべての内部オブジェクトを静的として宣言するため、クラスのコンストラクタとデストラクタは空のままにできます。オブジェクトとすべてのローカル変数は、Initメソッドで初期化されます。通常どおり、メソッドパラメータでは、オブジェクトの必要な構造を一意に決定できる変数を指定します。ここでは、ユニタリ入力および出力データシーケンスのウィンドウサイズ(windowとwindow_out)、ユニタリ時系列の数(count)、およびゼロ化された周波数特性の割合(dropout)を指定します。統合層を構築しており、ソースデータと結果の両方のウィンドウサイズは、FFTアルゴリズムの要件に関係なく、任意の正の数にできることに注意してください。前述のように、指定されたアルゴリズムでは、2の累乗のいずれかに等しい入力サイズが必要です。
bool CNeuronFITSOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_out, uint count, float dropout, ENUM_OPTIMIZATION optimization_type, uint batch) { if(window <= 0) return false; if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * count, optimization_type, batch)) return false;
メソッド本体では、まず小さな制御ブロックを実行し、入力ウィンドウのサイズ (正の数である必要があります) を確認して、同じ名前の親クラス メソッドを呼び出します。ご存知のとおり、親クラスメソッドは追加の制御と継承されたオブジェクトの初期化を実装します。
制御ブロックを正常に通過した後、受信したパラメータをローカル変数に保存します。
//--- Save constants
iWindow = window;
iWindowOut = window_out;
iCount = count;
activation=None;
直接FFTと逆FFTのテンソルのサイズを、取得した対応するパラメータに最も近い2の大きな累乗の形式で決定します。
//--- Calculate FFT and iFFT size int power = int(MathLog(iWindow) / M_LN2); if(MathPow(2, power) != iWindow) power++; iFFTin = uint(MathPow(2, power)); power = int(MathLog(iWindowOut) / M_LN2); if(MathPow(2, power) != iWindowOut) power++; iIFFTin = uint(MathPow(2, power));
次に、ネストされたオブジェクトを初期化するブロックがあります。cInputs*オブジェクトは、直接FFTの入力データバッファとして使用されます。そのサイズは、指定されたブロックの入力におけるユニタリシーケンスのサイズと分析されるシーケンスの数の積に等しくなります。
if(!cInputsRe.Init(0, 0, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cInputsIm.Init(0, 1, OpenCL, iFFTin * iCount, optimization, iBatch)) return false;
直接フーリエ分解cFFT*の結果を記録するオブジェクトも同様のサイズです。
if(!cFFTRe.Init(0, 2, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cFFTIm.Init(0, 3, OpenCL, iFFTin * iCount, optimization, iBatch)) return false;
次に、ドロップアウトオブジェクトを宣言します。それらのサイズは前のものと同じです。
if(!cDropRe.Init(0, 4, OpenCL, iFFTin * iCount, dropout, optimization, iBatch)) return false; if(!cDropIm.Init(0, 5, OpenCL, iFFTin * iCount, dropout, optimization, iBatch)) return false;
シーケンス補間には、1つの隠れ層と層間のtanh活性化を持つMLPを使用します。ブロックの出力では、逆FFTブロックの要件に従ってデータを受信します。
if(!cInsideRe1.Init(0, 6, OpenCL, iFFTin, iFFTin, 4*iIFFTin, iCount, optimization, iBatch)) return false; cInsideRe1.SetActivationFunction(TANH); if(!cInsideIm1.Init(0, 7, OpenCL, iFFTin, iFFTin, 4*iIFFTin, iCount, optimization, iBatch)) return false; cInsideIm1.SetActivationFunction(TANH); if(!cInsideRe2.Init(0, 8, OpenCL, 4*iIFFTin, 4*iIFFTin, iIFFTin, iCount, optimization, iBatch)) return false; cInsideRe2.SetActivationFunction(None); if(!cInsideIm2.Init(0, 9, OpenCL, 4*iIFFTin, 4*iIFFTin, iIFFTin, iCount, optimization, iBatch)) return false; cInsideIm2.SetActivationFunction(None);
補間結果をcComplex*オブジェクトに結合します。
if(!cComplexRe.Init(0, 10, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cComplexIm.Init(0, 11, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false;
FITS法によれば、補間されたシーケンスは逆フーリエ分解され、その際に周波数特性が時系列に変換されます。この演算結果をcIFFTオブジェクトに書き込みます。
if(!cIFFTRe.Init(0, 12, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cIFFTIm.Init(0, 13, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false;
さらに、欠落した値を補うために使用するゼロ値の補助バッファを宣言します。
if(!cClear.BufferInit(MathMax(iFFTin, iIFFTin)*iCount, 0)) return false; cClear.BufferCreate(OpenCL); //--- return true; }
すべてのネストされたオブジェクトが正常に初期化されたら、メソッドを完了します。
次のステップは、クラス機能の実装です。ただし、フィードフォワードメソッドとバックプロパゲーションメソッドに直接進む前に、上記で構築されたカーネルを実行キューに配置する機能を実装するための準備作業をおこなう必要があります。このようなカーネルには同様のアルゴリズムが存在します。この記事の枠組みの中では、高速フーリエ変換カーネルCNeuronFITSOCL::FFTを呼び出すメソッドのみを検討します。
bool CNeuronFITSOCL::FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false) { uint global_work_offset[1] = {0}; uint global_work_size[1] = {iCount};
メソッドのパラメータでは、必要な4つのデータバッファ(入力データ用に2つ、結果用に2つ)へのポインタと、操作方向のフラグを渡します。
メソッド本体では、タスク空間を定義します。ここでは、分析対象のシーケンスの数に対応する1次元の問題空間を使用します。
次に、カーネルにパラメータを渡します。まず、ソースデータバッファへのポインタを渡します。
if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_inputs_re, inp_re.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_inputs_im, (!!inp_im ? inp_im.GetIndex() : inp_re.GetIndex()))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
信号の虚数部のバッファがなくてもカーネルを起動できることに注意してください。前述の通り、これを実現するためにカーネルでinput_complexフラグを使用しています。ただし、必要なパラメータをすべてカーネルに渡さない場合、ランタイムエラーが発生します。したがって、虚数部バッファがない場合は、信号の実数部バッファへのポインタを指定し、対応するフラグにfalseを指定する必要があります。
if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_input_complex, int(!!inp_im))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
次に、結果バッファへのポインタを渡します。
if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_outputs_re, out_re.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_outputs_im, out_im.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
入力ウィンドウと出力ウィンドウのサイズも渡します。後者は2の累乗です。ウィンドウサイズは定数から取得するのではなく、計算することに注意してください。これは、このメソッドを異なるバッファ、つまり異なる入力ウィンドウと出力ウィンドウで実行される直接フーリエ変換と逆フーリエ変換の両方に対応させるためです。
if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_input_window, (int)(inp_re.Total() / iCount))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_output_window, (int)(out_re.Total() / iCount))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
最後のパラメータとして、逆変換アルゴリズムを使用するかどうかを示すフラグを渡します。
if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_reverse, int(reverse))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
カーネルを実行キューに入れます。
if(!OpenCL.Execute(def_k_FFT, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
各段階で操作のプロセスを制御し、実行された操作の論理値を呼び出し元に返します。
同じ名前のカーネルが呼び出されるCNeuronFITSOCL::ComplexLayerOutと CNeuronFITSOCL::ComplexLayerGradientメソッドは、同様の原理に基づいて構築されています。これらは添付ファイルで確認できます。
準備作業を終えたら、CNeuronFITSOCL::feedForwardメソッドで説明されているフィードフォワードパスアルゴリズムの構築に進みます。
メソッドのパラメータでは、ニューラル層のオブジェクトへのポインタを受け取り、入力データを渡す前にそのオブジェクトを確認します。メソッド本体では、受け取ったポインタをすぐに確認します。
bool CNeuronFITSOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
FITSでは、データの事前正規化が必要です。データの正規化は前のニューラル層で実行されるものと想定し、このクラスではこの手順を省略します。
取得したデータを、直接高速フーリエ変換を使用して周波数応答領域に変換します。これをおこなうには、適切なメソッドを呼び出します (そのアルゴリズムは上記に示されています)。
//--- FFT if(!FFT(NeuronOCL.getOutput(), NULL, cFFTRe.getOutput(), cFFTIm.getOutput(), false)) return false;
ドロップアウト層を使用して、結果として得られる周波数特性にギャップを設けます。
//--- DropOut if(!cDropRe.FeedForward(cFFTRe.AsObject())) return false; if(!cDropIm.FeedForward(cFFTIm.AsObject())) return false;
その後、予測値の大きさによって周波数特性を補間します。
//--- Complex Layer if(!cInsideRe1.FeedForward(cDropRe.AsObject())) return false; if(!cInsideRe2.FeedForward(cInsideRe1.AsObject())) return false; if(!cInsideIm1.FeedForward(cDropIm.AsObject())) return false; if(!cInsideIm2.FeedForward(cInsideIm1.AsObject())) return false;
信号の実数部と虚数部の個別の補間を組み合わせてみましょう。
if(!ComplexLayerOut(cInsideRe2.getOutput(), cInsideIm2.getOutput(), cComplexRe.getOutput(), cComplexIm.getOutput())) return false;
逆分解によって出力信号を時間領域に戻します。
//--- iFFT if(!FFT(cComplexRe.getOutput(), cComplexIm.getOutput(), cIFFTRe.getOutput(), cIFFTIm.getOutput(), true)) return false;
結果として得られる予測系列は、後続のニューラル層に渡す必要があるシーケンスのサイズを超える可能性があることに注意してください。したがって、信号の実数部から必要なブロックを選択します。
//--- To Output if(!DeConcat(Output, cIFFTRe.getGradient(), cIFFTRe.getOutput(), iWindowOut, iIFFTin - iWindowOut, iCount)) return false; //--- return true; }
各ステップで結果を制御することを忘れないでください。すべての反復が完了したら、実行された操作の論理結果を呼び出し元に返します。
フィードフォワードパスを実装した後、バックプロパゲーションメソッドの構築に進みます。CNeuronFITSOCL::calcInputGradientsメソッドは、最終結果への影響に応じて、すべての内部オブジェクトと前層に誤差勾配を伝播します。
bool CNeuronFITSOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
パラメータでは、メソッドは前層のオブジェクトへのポインタを受け取ります。このオブジェクトに誤差勾配を渡す必要があります。そして、メソッド本体では、受け取ったポインタの関連性をすぐに確認します。
次の層から取得した誤差勾配は、すでにGradientバッファに格納されています。ただし、これには信号の実数部のみが含まれており、指定された予測深度までのデータしか含まれていません。逆変換から得られる全信号の水平方向で、実数部と虚数部の両方の誤差勾配が必要です。このようなデータを生成するために、次の2つの仮定に基づいて進めます。
- フィードフォワードパス内の逆フーリエ変換ブロックの出力では、離散的な時系列値を取得することが期待されます。この場合、信号の実数部は必要な時系列に対応し、虚数部は「0」に等しい(または「0」に近い)と見なします。したがって、虚数部の誤差は、その値の反対の符号に等しくなります。
- 指定された計画期間を超えた予測値の精度についての情報がないため、予想される偏差は無視し、その誤差を「0」とみなします。
//--- Copy Gradients if(!SumAndNormilize(cIFFTIm.getOutput(), GetPointer(cClear), cIFFTIm.getGradient(), 1, false, 0, 0, 0, -1)) return false;
if(!Concat(Gradient, GetPointer(cClear), cIFFTRe.getGradient(), iWindowOut, iIFFTin - iWindowOut, iCount)) return false;
また、誤差勾配は時系列形式で提示されることにも注意してください。ただし、予測は周波数領域でおこなわれました。したがって、誤差勾配を周波数領域に変換する必要もあります。この操作では、高速フーリエ変換を使用します。
//--- FFT if(!FFT(cIFFTRe.getGradient(), cIFFTIm.getGradient(), cComplexRe.getGradient(), cComplexIm.getGradient(), false)) return false;
周波数特性を実部と虚部の2つのMLPに分配します。
//--- Complex Layer if(!ComplexLayerGradient(cInsideRe2.getGradient(), cInsideIm2.getGradient(), cComplexRe.getGradient(), cComplexIm.getGradient())) return false;
次に、MLPを通して誤差勾配を分配します。
if(!cInsideRe1.calcHiddenGradients(cInsideRe2.AsObject())) return false; if(!cInsideIm1.calcHiddenGradients(cInsideIm2.AsObject())) return false; if(!cDropRe.calcHiddenGradients(cInsideRe1.AsObject())) return false; if(!cDropIm.calcHiddenGradients(cInsideIm1.AsObject())) return false;
ドロップアウト層を通じて、誤差勾配を直接フーリエ変換ブロックの出力に伝播します。
//--- Dropout if(!cFFTRe.calcHiddenGradients(cDropRe.AsObject())) return false; if(!cFFTIm.calcHiddenGradients(cDropIm.AsObject())) return false;
ここで、誤差勾配を周波数領域から時系列に変換する必要があります。この操作は逆変換を使用して実行されます。
//--- IFFT if(!FFT(cFFTRe.getGradient(), cFFTIm.getGradient(), cInputsRe.getGradient(), cInputsIm.getGradient(), true)) return false;
そして最後に、実際の誤差勾配の必要な部分だけを前層に渡します。
//--- To Input Layer if(!DeConcat(NeuronOCL.getGradient(), cFFTIm.getGradient(), cFFTRe.getGradient(), iWindow, iFFTin - iWindow, iCount)) return false; //--- return true; }
いつものように、メソッド本体内のすべての操作の実行プロセスを制御し、最後に操作の正しさの論理値を呼び出し元に返します。
誤差誤差勾配伝播プロセスの後には、モデルパラメータの更新がおこなわれます。このプロセスは、CNeuronFITSOCL::updateInputWeightsメソッドで実装されています。すでに述べたように、クラスで宣言された多くのオブジェクトの中で、MLP層のみが学習パラメータを含んでいます。したがって、以下のメソッドでこの層のパラメータを調整します。
bool CNeuronFITSOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cInsideRe1.UpdateInputWeights(cDropRe.AsObject())) return false; if(!cInsideIm1.UpdateInputWeights(cDropIm.AsObject())) return false; if(!cInsideRe2.UpdateInputWeights(cInsideRe1.AsObject())) return false; if(!cInsideIm2.UpdateInputWeights(cInsideIm1.AsObject())) return false; //--- return true; }
ファイル操作メソッドを使用する場合、訓練可能なパラメータを含まない内部オブジェクトが多数あるという事実も考慮する必要があります。価値のない大量の情報を保存しても意味がありません。したがって、データ保存メソッドCNeuronFITSOCL::Saveでは、最初に同じ名前の親クラスメソッドを呼び出します。
bool CNeuronFITSOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false;
その後、アーキテクチャ定数を保存します。
//--- Save constants if(FileWriteInteger(file_handle, int(iWindow)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iWindowOut)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iCount)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iFFTin)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iIFFTin)) < INT_VALUE) return false;
MLPオブジェクトを保存します。
//--- Save objects if(!cInsideRe1.Save(file_handle)) return false; if(!cInsideIm1.Save(file_handle)) return false; if(!cInsideRe2.Save(file_handle)) return false; if(!cInsideIm2.Save(file_handle)) return false;
ドロップアウトブロックオブジェクトをさらに追加してみましょう。
if(!cDropRe.Save(file_handle)) return false; if(!cDropIm.Save(file_handle)) return false; //--- return true; }
これで完了です。残りのオブジェクトにはデータバッファのみが含まれており、その情報は1回のフォワード/バックワード パス実行内でのみ関連します。したがって、それらを保存せず、ディスク領域を節約します。ただし、すべてにコストが伴います。データ読み込みメソッドCNeuronFITSOCL::Loadのアルゴリズムを複雑にする必要があります。
bool CNeuronFITSOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false;
このメソッドでは、まずデータ保存メソッドをミラーリングします。
- 同じ名前の親クラスのメソッドを呼び出す。
- 定数をロードし、データファイルの末尾に到達したことを制御する。
//--- Load constants if(FileIsEnding(file_handle)) return false; iWindow = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iWindowOut = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iCount = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iFFTin = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iIFFTin = uint(FileReadInteger(file_handle)); activation=None;
- MLPとDropoutパラメータを読み込む。
//--- Load objects if(!LoadInsideLayer(file_handle, cInsideRe1.AsObject())) return false; if(!LoadInsideLayer(file_handle, cInsideIm1.AsObject())) return false; if(!LoadInsideLayer(file_handle, cInsideRe2.AsObject())) return false; if(!LoadInsideLayer(file_handle, cInsideIm2.AsObject())) return false; if(!LoadInsideLayer(file_handle, cDropRe.AsObject())) return false; if(!LoadInsideLayer(file_handle, cDropIm.AsObject())) return false;
ここで、不足しているオブジェクトを初期化する必要があります。ここでは、クラス初期化メソッドのコードの一部を繰り返します。
//--- Init objects if(!cInputsRe.Init(0, 0, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cInputsIm.Init(0, 1, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cFFTRe.Init(0, 2, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cFFTIm.Init(0, 3, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cComplexRe.Init(0, 8, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cComplexIm.Init(0, 9, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cIFFTRe.Init(0, 10, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cIFFTIm.Init(0, 11, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cClear.BufferInit(MathMax(iFFTin, iIFFTin)*iCount, 0)) return false; cClear.BufferCreate(OpenCL); //--- return true; }
これで、新しいCNeuronFITSOCLクラスのメソッドとそのアルゴリズムの説明は終了です。このクラスとそのすべてのメソッドの完全なコードは、添付ファイルで確認できます。添付ファイルには、この記事で使用したすべてのプログラムも含まれています。それでは、モデル訓練アーキテクチャの検討に移りましょう。
2.4 モデルアーキテクチャ
FITS法は、時系列分析と予測のために提案されました。環境状態エンコーダーでは提案されたアプローチが使用されることはすでにご想像のとおりです。そのアーキテクチャはCreateEncoderDescriptionsメソッドで説明されています。
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
メソッドパラメータでは、作成されたモデルのアーキテクチャを保存するための動的配列オブジェクトへのポインタを受け取ります。そして、メソッド本体では、受け取ったポインタの関連性をすぐに確認します。必要に応じて、動的配列オブジェクトの新しいインスタンスを作成します。
いつものように、環境の現在の状態を表す「生の」データをモデルに入力します。
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
データはバッチ正規化層で前処理されます。これにより、データが比較可能な形式になり、モデル訓練プロセスの安定性が向上します。
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
入力データは多変量時系列です。各データブロックには、履歴データの1つのローソク足を表すさまざまなパラメータが含まれています。ただし、データセット内のユニタリシーケンスを分析するには、結果のテンソルを転置する必要があります。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = HistoryBars; descr.window = BarDescr; if(!encoder.Add(descr)) { delete descr; return false; }
この段階で、準備作業は完了したとみなすことができ、ユニタリ時系列の分析と予測に進むことができます。このプロセスを新しいクラスのオブジェクトに実装します。
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFITSOCL; descr.count = BarDescr; descr.window = HistoryBars; descr.activation = None; descr.window_out = NForecast; if(!encoder.Add(descr)) { delete descr; return false; }
このクラスの本体では、提案されたFITSメソッドのほぼすべてを実装しました。ニューラル層の出力には予測値があります。したがって、予測値のテンソルを期待される結果の次元に転置するだけです。
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = BarDescr; descr.window = NForecast; if(!encoder.Add(descr)) { delete descr; return false; }
また、入力データの統計分布の以前に削除したパラメータを追加する必要があります。
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
ご覧のとおり、環境のその後の状態を分析および予測するためのモデルは、FITS法の作成者が約束したとおり、非常に簡潔です。同時に、モデルアーキテクチャに加えた変更は、入力データの量や形式にまったく影響を与えませんでした。モデルの出力形式も変更していません。したがって、以前に作成したActorおよびCriticモデル アーキテクチャを変更せずに使用できます。さらに、以前に構築したEA(エキスパートアドバイザー)を使用して環境と対話し、モデルを訓練したり、以前に収集した訓練データセットを使用したりできます。変更する必要があるのは、環境状態の潜在表現層へのポインタだけです。
#define LatentLayer 3
ここで使用されているすべてのプログラムの完全なコードは添付ファイルにあります。テストしてみましょう。
3. テスト
FITS法について理解し、MQL5を使用して提案されたアプローチの実装に真剣に取り組みました。次は、実際の履歴データを使用して作業の結果をテストします。前回と同様に、H1時間枠のEURUSD履歴データを使用してモデルを訓練およびテストします。モデルを訓練するには、2023年全体の履歴データを使用します。訓練されたモデルをテストするには、2024年1月からのデータを使用します。
モデルの訓練プロセスについては、前回の記事で説明しました。まず、環境状態エンコーダーを訓練して、後続の状態を予測します。次に、Actorの動作方策を繰り返し訓練して、最大の収益性を実現します。
予想通り、エンコーダーモデルは非常に軽量であることがわかりました。学習プロセスは比較的高速でスムーズです。モデルはサイズが小さいにもかかわらず、前回の記事で説明したFEDformerモデルに匹敵するパフォーマンスを発揮します。ここで注目すべきは、モデルのサイズがほぼ84倍小さいことです。

しかし、Actorの方策訓練フェーズは期待外れな結果に終わりました。このモデルは特定の履歴セクションでのみ収益性を発揮します。以下のバランスグラフでは、テストセクションを超えた部分において、月の最初の10日間に非常に急速な成長が見られます。しかし、次の10日間では収益性の高い取引がまれで、損失が発生しています。3番目の10日間では収益性の高い取引と損失の取引がほぼ同等になっています。

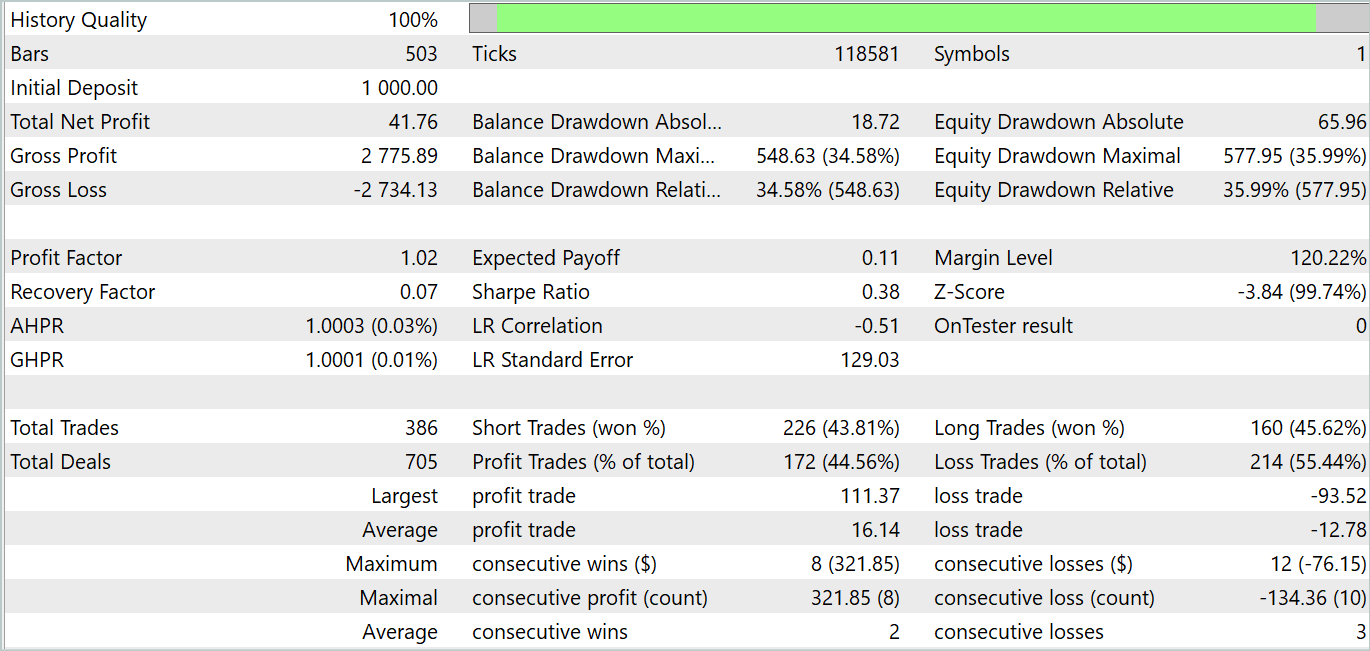
全体として、今月はわずかな収益がありました。ここで注目すべき点は、最大および平均の収益性の高い取引の規模が、対応する損失指標を上回っていることです。ただし、収益性の高い取引の数が全体の半分未満であるため、平均収益性の高い取引の優位性が打ち消されています。
また注目すべき点として、テスト結果がFEDformer法の著者による結論を部分的に裏付けていることが挙げられます。入力データに明確な周期性がないため、 DFTではトレンドの変化の瞬間を判断できません。
結論
本記事では、時系列分析と予測のための新しいFITS法について説明しました。この手法の主な特徴は、周波数領域における時系列の分析と予測にあります。この手法では、直接および逆高速フーリエ変換アルゴリズムを使用するため、モデルの入力と出力において、使い慣れた離散時系列を操作できます。この機能により、提案された軽量アーキテクチャを、時系列分析や予測が利用される多くの分野に実装することが可能です。
実践的な部分では、MQL5を使用して提案されたアプローチのビジョンを実装しました。実際の履歴データを用いてモデルの訓練とテストをおこないましたが、残念ながらテストでは期待された結果は得られませんでした。ただし、この結果は提案されたアプローチの特定の実装にのみ関連するものであることに留意したいと思います。原著者のアルゴリズムを使用した場合、結果は異なる可能性があります。
参照文献
- FITS:Modeling Time Series with 10k Parameters
- A Survey of Complex-Valued Neural Networks
- この連載の他の記事記事
記事で使用されているプログラム
| # | 名前 | 種類 | 詳細 |
|---|---|---|---|
| 1 | Research.mq5 | EA | コレクションEAの例 |
| 2 | ResearchRealORL.mq5 | EA | Real-ORL法による事例収集のためのEA |
| 3 | Study.mq5 | EA | モデル訓練EA |
| 4 | StudyEncoder.mq5 | EA | エンコード訓練EA |
| 5 | Test.mq5 | EA | モデルをテストするEA |
| 6 | Trajectory.mqh | クラスライブラリ | システム状態記述の構造体 |
| 7 | NeuroNet.mqh | クラスライブラリ | ニューラルネットワークを作成するためのクラスのライブラリ |
| 8 | NeuroNet.cl | コードベース | OpenCLプログラムコードライブラリ |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14913
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 PythonとMQL5でロボットを開発する(第2回):モデルの選択、作成、訓練、Pythonカスタムテスター
PythonとMQL5でロボットを開発する(第2回):モデルの選択、作成、訓練、Pythonカスタムテスター
 多通貨エキスパートアドバイザーの開発(第12回):プロップトレーディングレベルのリスクマネージャーの育成
多通貨エキスパートアドバイザーの開発(第12回):プロップトレーディングレベルのリスクマネージャーの育成
 チャート上で取引を視覚化する(第1回):分析期間の選択
チャート上で取引を視覚化する(第1回):分析期間の選択
 ニューラルネットワークの実践:直線関数
ニューラルネットワークの実践:直線関数
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索