Redes neuronales: así de sencillo (Parte 90): Interpolación frecuencial de series temporales (FITS)
Introducción
El análisis de series temporales desempeña un papel importante en la toma de decisiones en los mercados financieros. Los datos de las series temporales del sector financiero suelen ser complejos y dinámicos, y su procesamiento requiere métodos eficaces.
La investigación reciente en el análisis de series temporales ha conducido al desarrollo de modelos y métodos sofisticados, pero estos modelos suelen requerir importantes recursos computacionales, lo cual los hace menos adecuados para su uso en el entorno dinámico de los mercados financieros, es decir, cuando el tiempo de decisión se convierte en parte de una estrategia exitosa.
Además, hoy en día, cada vez se toman más decisiones de gestión a través de dispositivos móviles, cuyos recursos también son limitados. Este hecho impone requisitos adicionales a los modelos usados en la toma de tales decisiones.
En este contexto, la representación de las series temporales en el dominio de la frecuencia puede ofrecer una representación más eficaz y compacta de los patrones observados. Por ejemplo, el uso de datos espectrales y el análisis de frecuencias de gran amplitud pueden ayudar a identificar características importantes.
Ya nos familiarizamos en su momento con el método FEDformer, que utiliza el dominio de la frecuencia para encontrar patrones en una serie temporal. Sin embargo, el Transformer que usa no es un modelo ligero. En lugar de modelos complejos que requieren un gran gasto de recursos informáticos, en el artículo "FITS: Modeling Time Series with 10k Parameters" se presentó el método de Interpolación Frecuencial de Series Temporales (Frequency Interpolation Time Series — FITS). Es una solución compacta y eficaz para el análisis y la previsión de series temporales. El método FITS utiliza la interpolación en el dominio de la frecuencia para ampliar la ventana del segmento temporal analizado, lo cual permite extraer de forma eficaz las características temporales sin grandes recursos informáticos.
Los autores del FITS destacan las siguientes ventajas de su método:
- El FITS es un modelo ligero con pocos parámetros, lo cual lo convierte en una opción ideal para su uso en dispositivos con recursos limitados.
- El FITS utiliza una compleja red neuronal para recopilar información sobre la amplitud y la fase de la señal, lo que mejora la eficacia del análisis de datos de series temporales.
1. Algoritmo FITS
El análisis de series temporales en el dominio de la frecuencia permite descomponer una señal en una combinación lineal de componentes sinusoidales sin pérdida de datos. Cada uno de estos componentes posee una frecuencia, una fase inicial y una amplitud únicas. Mientras que la predicción de una serie temporal puede ser una tarea compleja, la predicción de componentes sinusoidales individuales resulta relativamente más sencilla, ya que solo requiere ajustar la fase de la onda sinusoidal según el desplazamiento temporal. Las ondas sinusoidales desplazadas de este modo se combinan linealmente para obtener los valores de previsión de las series temporales analizadas.
Este enfoque nos permite preservar eficazmente las características de frecuencia de la ventana de la serie temporal analizada. En este caso, además, se mantiene la coherencia semántica entre la ventana temporal y el horizonte de predicción.
No obstante, predecir cada componente sinusoidal en el dominio temporal puede llevar bastante tiempo. Para resolver este problema, los autores del método FITS proponen usar un dominio de frecuencia complejo, que proporciona una representación más compacta e informativa de los datos.
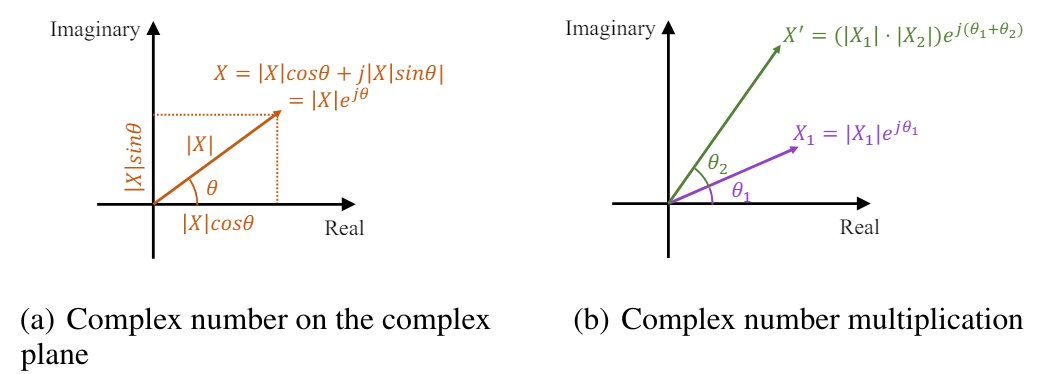
La transformada rápida de Fourier (FFT) transforma eficazmente las señales de series temporales discretas del dominio del tiempo al dominio de la frecuencia compleja. En el análisis de Fourier, el dominio de la frecuencia compleja se representa usando una secuencia en la que cada componente de frecuencia se caracteriza por un número complejo. Este número complejo refleja la amplitud y la fase del componente, ofreciendo una descripción completa. La amplitud de un componente de frecuencia representa la magnitud o fuerza de ese componente en la señal original en el dominio del tiempo. Por el contrario, la fase indica el desplazamiento temporal o retraso introducido por este componente. Matemáticamente, el número complejo asociado a la componente de frecuencia puede representarse como un elemento exponencial complejo con una amplitud y una fase concretas:
![]()
donde X(f) es un número complejo asociado al componente de frecuencia en la frecuencia f,
|X(f)| es la amplitud del componente,
θ(f) es la fase del componente.
En el plano complejo, el elemento exponencial puede representarse como un vector con una longitud igual a la amplitud y un ángulo igual a la fase:
![]()
Así, el número complejo en el dominio de la frecuencia ofrece una forma concisa y elegante de representar la amplitud y la fase de cada componente de frecuencia en la transformada de Fourier.
El desplazamiento temporal de la señal se corresponde con el desplazamiento de fase en el dominio de la frecuencia. En el dominio de la frecuencia compleja, dicho desplazamiento de fase puede expresarse como la multiplicación del elemento unitario del exponente complejo por la fase correspondiente. La señal desplazada sigue teniendo una amplitud |X(f)|, mientras que la fase muestra un desplazamiento lineal en el tiempo.
Así, el escalado de amplitud y el desplazamiento de fase pueden expresarse de forma simultánea como una multiplicación de números complejos.
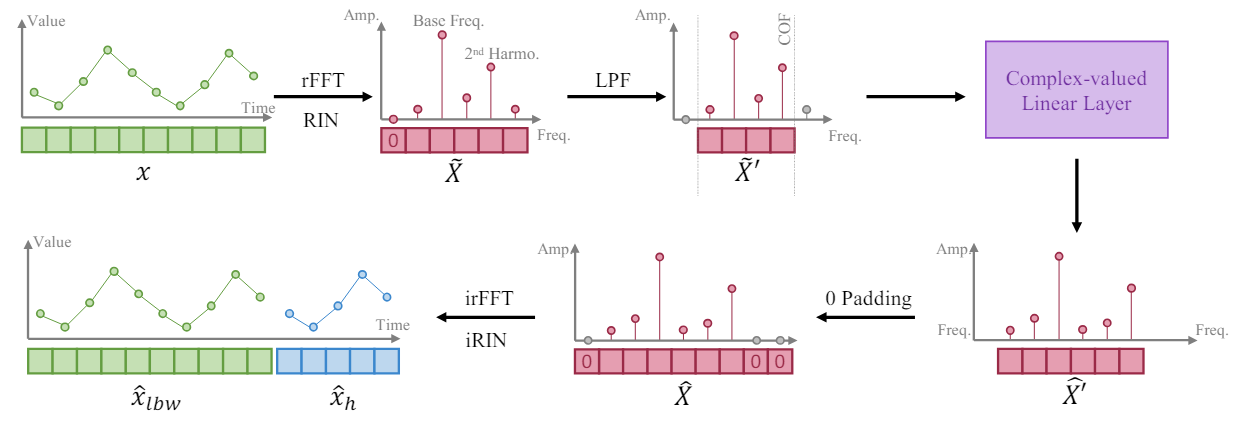
Guiados por el hecho de que una serie temporal más larga ofrece una mayor resolución en su representación frecuencial, los autores del método FITS entrenan al modelo para que amplíe un segmento de la serie temporal interpolando la representación frecuencial de la ventana analizada de datos de origen. Así, proponen utilizar una única capa lineal compleja para entrenar dicha interpolación. Como resultado, el modelo puede aprender el escalado de amplitud y el desplazamiento de fase como una multiplicación de números complejos durante el proceso de interpolación. El algoritmo FITS usa la transformada rápida de Fourier para proyectar segmentos de series temporales en el dominio de una frecuencia compleja. Y tras la interpolación, la representación en la frecuencia se proyecta de nuevo en la representación en el tiempo utilizando la FFT inversa.
Sin embargo, la media de dichos segmentos generará un componente de frecuencia cero muy grande en su representación de frecuencia compleja. Para resolver este problema, la señal obtenida se someterá a una normalización reversible (RevIN), que permite obtener una instancia con media cero.
Además, los autores del método incluyen un filtro de paso bajo (LPF) en el FITS para reducir el tamaño del modelo. El filtro de paso bajo elimina eficazmente los componentes de alta frecuencia por encima de una cierta frecuencia de corte, densificando la representación del modelo y conservando al mismo tiempo la información importante de las series temporales.
A pesar de funcionar en el dominio de la frecuencia, el FITS se entrena en el dominio del tiempo utilizando funciones de pérdida estándar como el error cuadrático medio (MSE) tras la transformada rápida de Fourier inversa. Esto ofrece un enfoque versátil adaptado a diversos problemas de series temporales posteriores.
En el caso de las tareas de previsión, el FITS genera una ventana de análisis retrospectivo junto con un horizonte de planificación. Esto permite controlar la previsión y el análisis retrospectivo, con modelos recomendados para reconstruir con precisión la ventana de análisis retrospectivo. El análisis del autor muestra que la combinación de retrospectiva y supervisión de las previsiones puede provocar una mejora de los resultados en determinados escenarios.
Para las tareas de reconstrucción, el FITS submuestrea el segmento de la serie temporal original según una determinada frecuencia de submuestreo. A continuación, se realiza una interpolación frecuencial para restaurar el segmento muestreado a su forma original. De esta manera, se aplica un control directo con pérdidas para garantizar una reconstrucción precisa de la señal.
Para controlar la longitud del tensor de resultados del modelo, los autores del método introducen una tasa de interpolación (denotada como 𝜂), que es el cociente del tamaño requerido del tensor de resultados del modelo por el tamaño correspondiente del tensor de datos original.
Cabe destacar que al aplicar un filtro de paso bajo (LPF), el tamaño del tensor de datos de origen de nuestra capa compleja se corresponde con la frecuencia de corte (COF) del LPF. Una vez realizada la interpolación frecuencial, la representación de frecuencias complejas se aumentará con ceros hasta alcanzar el tamaño deseado del tensor resultante. Antes de aplicar la FFT inversa, se introduce un cero adicional como componente de frecuencia cero de la representación.
El objetivo principal de incluir el LPF en el FITS es comprimir el volumen del modelo conservando información importante. El LPF lo consigue descartando los componentes de frecuencia por encima de una determinada frecuencia de corte (COF), lo cual da lugar a una representación más concisa en el dominio de la frecuencia. El LPF almacena la información relevante de la serie temporal mientras descarta los componentes que superan las capacidades de entrenamiento del modelo. De este modo, se conserva gran parte del contenido significativo de la serie temporal original. Los experimentos realizados por los autores del método demuestran que la señal filtrada presenta una distorsión mínima incluso cuando solo se conserva una cuarta parte de la representación original en el dominio de la frecuencia. Además, los componentes de alta frecuencia filtrados por los LPF suelen contener ruido intrínsecamente irrelevante para el modelado eficaz de las series temporales.
La selección de una frecuencia de corte (COF) adecuada sigue siendo una tarea no trivial. Para resolver este problema, los autores del FITS proponen un método basado en el contenido armónico de la frecuencia dominante. Los armónicos, que son múltiplos enteros de la frecuencia dominante, juegan un papel importante en la conformación de la onda de la serie temporal. Al comparar la frecuencia de corte con estos armónicos, conservamos los componentes de frecuencia correspondientes vinculados a la estructura y periodicidad de la señal. Este enfoque aprovecha el acoplamiento intrínseco entre frecuencias para extraer información sustancial al tiempo que suprime el ruido y los componentes de alta frecuencia innecesarios.
La visión del autor del FITS se presenta a continuación.
2. Implementación con MQL5
Tras familiarizarnos con los aspectos teóricos del método FITS,, podemos pasar a la aplicación práctica de los planteamientos propuestos usando MQL5.
Como de costumbre, usaremos los enfoques propuestos, pero nuestra implementación resultará ligeramente distinta de la visión del autor del algoritmo debido a las especificidades del problema a resolver.
2.1 Aplicación de la FFT
De la descripción teórica del método presentada anteriormente se desprende que este se basa en la descomposición rápida de Fourier directa e inversa. Con su ayuda, primero trasladaremos la señal analizada al dominio de las características de frecuencia y, a continuación, la secuencia predicha se retornará a la representación de series temporales. En este caso, cabe destacar dos ventajas de la transformada rápida de Fourier:
- la velocidad de las operaciones en comparación con otras transformaciones similares;
- la posibilidad de expresar la transformación inversa usando la transformación directa.
Aquí cabe señalar que en nuestro problema necesitaremos implementar la FFT de una serie temporal multidimensional, que en la práctica será la misma FFT aplicada a cada serie temporal unitaria de nuestra secuencia multidimensional.
Recuerde que la mayor parte de las operaciones matemáticas de nuestras implementaciones se han trasladado a OpenCL. Esto nos permitirá distribuir la ejecución de un gran número de operaciones de un solo tipo con datos independientes entre varios flujos paralelos, y así reducir el tiempo de ejecución de las operaciones. También realizaremos operaciones rápidas de descomposición de Fourier en el lado OpenCL. En cada uno de los flujos paralelos, realizaremos una descomposición de una serie temporal unitaria independiente.
Formalizaremos el algoritmo de las operaciones como un kernel FFT. En los parámetros del kernel, transmitiremos los punteros a 4 arrays de datos. Aquí utilizaremos dos arrays, cada uno para los datos de origen y los resultados de las operaciones. Un array contendrá la parte real del valor complejo (la amplitud de la señal), mientras que el segundo contendrá la parte imaginaria (su fase).
Sin embargo, cabe señalar que no siempre suministraremos la parte imaginaria de la señal a la entrada del kernel. Por ejemplo, al descomponer la serie temporal original, simplemente no dispondremos de ella. En esta situación, la solución será bastante sencilla: sustituiremos los datos que faltan por valores nulos. Y para evitar transmitir un búfer aparte relleno de valores nulos, simplemente crearemos la bandera input_complex en los parámetros del kernel.
El segundo punto a tener en cuenta será que el algoritmo Cooley-Tukey para la FFT que utilizamos solo funcionará para secuencias cuya longitud sea de grado 2. Y esta condición impondrá serias limitaciones, podemos decir incluso que supondrá una limitación en la preparación de la señal que se va a analizar. El método funcionará bien si rellenamos los elementos que faltan en la secuencia con valores cero. Nuevamente, para evitar el copiado innecesario de datos para reformatear las series temporales, añadiremos dos variables en los parámetros del kernel: input_window y output_window. En el primero especificaremos la longitud real de la secuencia a analizar, mientras que en el segundo indicaremos el tamaño del vector de resultados de la descomposición, que será de grado 2. Permítanme aclarar que en este caso estaremos hablando del tamaño de una secuencia unitaria.
Un parámetro adicional, inverse, indicará el sentido de la operación: la transformación directa o inversa.
__kernel void FFT(__global float *inputs_re, __global float *inputs_im, __global float *outputs_re, __global float *outputs_im, const int input_window, const int input_complex, const int output_window, const int reverse ) { size_t variable = get_global_id(0);
En el cuerpo del kernel, primero definiremos un identificador de flujo que nos señalará la secuencia unitaria que se va a analizar. Aquí es donde definiremos los desplazamientos en los búferes de datos y otras constantes requeridas.
const ulong N = output_window; const ulong N2 = N / 2; const ulong inp_shift = input_window * variable; const ulong out_shift = output_window * variable;
El siguiente paso consistirá en reordenar los datos de origen en un orden específico que nos permitirá optimizar ligeramente el algoritmo FFT.
uint target = 0; for(uint position = 0; position < N; position++) { if(target > position) { outputs_re[out_shift + position] = (target < input_window ? inputs_re[inp_shift + target] : 0); outputs_im[out_shift + position] = ((target < input_window && input_complex) ? inputs_im[inp_shift + target] : 0); outputs_re[out_shift + target] = inputs_re[inp_shift + position]; outputs_im[out_shift + target] = (input_complex ? inputs_im[inp_shift + position] : 0); } else { outputs_re[out_shift + position] = inputs_re[inp_shift + position]; outputs_im[out_shift + position] = (input_complex ? inputs_im[inp_shift + position] : 0); } unsigned int mask = N; while(target & (mask >>= 1)) target &= ~mask; target |= mask; }
A continuación vendrá la transformación directa de los datos, que se realizará en un sistema de ciclos anidados. En el ciclo exterior, construiremos las iteraciones del FFT para segmentos de longitudes 2, 4, 8, .... n.
float real = 0, imag = 0; for(int len = 2; len <= (int)N; len <<= 1) { float w_real = (float)cos(2 * M_PI_F / len); float w_imag = (float)sin(2 * M_PI_F / len);
En el cuerpo del ciclo, definiremos un multiplicador para rotar el argumento 1 punto de la longitud del ciclo y organizaremos un ciclo anidado de enumeración de los bloques de la secuencia analizada.
for(int i = 0; i < (int)N; i += len) { float cur_w_real = 1; float cur_w_imag = 0;
Aquí declararemos las variables de rotación de la fase actual y organizaremos otro ciclo anidado de enumeración de los elementos del bloque.
for(int j = 0; j < len / 2; j++) { real = cur_w_real * outputs_re[out_shift + i + j + len / 2] - cur_w_imag * outputs_im[out_shift + i + j + len / 2]; imag = cur_w_imag * outputs_re[out_shift + i + j + len / 2] + cur_w_real * outputs_im[out_shift + i + j + len / 2]; outputs_re[out_shift + i + j + len / 2] = outputs_re[out_shift + i + j] - real; outputs_im[out_shift + i + j + len / 2] = outputs_im[out_shift + i + j] - imag; outputs_re[out_shift + i + j] += real; outputs_im[out_shift + i + j] += imag; real = cur_w_real * w_real - cur_w_imag * w_imag; cur_w_imag = cur_w_imag * w_real + cur_w_real * w_imag; cur_w_real = real; } } }
En el cuerpo del ciclo, primero modificaremos los elementos que se van a analizar y luego cambiaremos el valor de las variables de la fase actual para la siguiente iteración.
Tenga en cuenta que la modificación de los elementos del búfer se realizará "in situ" sin asignar memoria adicional.
Una vez completadas las iteraciones del sistema de ciclos, comprobaremos el valor de la bandera inverse. Y en el caso de realizar una conversión inversa, reordenaremos los datos en el búfer de resultados. En este caso, dividiremos los valores obtenidos por el número de elementos de la secuencia.
if(reverse) { outputs_re[0] /= N; outputs_im[0] /= N; outputs_re[N2] /= N; outputs_im[N2] /= N; for(int i = 1; i < N2; i++) { real = outputs_re[i] / N; imag = outputs_im[i] / N; outputs_re[i] = outputs_re[N - i] / N; outputs_im[i] = outputs_im[N - i] / N; outputs_re[N - i] = real; outputs_im[N - i] = imag; } } }
2.2 Combinación de las partes real e imaginaria de la distribución de previsiones
El kernel presentado anteriormente nos permitirá realizar la descomposición rápida de Fourier directa e inversa, lo cual en principio cubrirá nuestras necesidades en esta materia. Pero deberemos considerar otra cosa sobre el método FITS. Los autores del método utilizan una compleja red neuronal para interpolar los datos. Para estudiar con mayor detalle las redes neuronales complejas, le sugiero leer el artículo "A Survey of Complex-Valued Neural Networks". En esta implementación, usaremos clases existentes de capas neuronales que interpolarán por separado las partes real e imaginaria y luego las combinarán utilizando una fórmula:
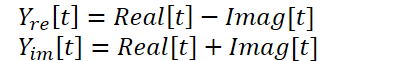
Para realizar estas operaciones, crearemos el kernel ComplexLayer. El algoritmo del kernel es bastante sencillo. Solo tendremos que identificar el flujo en dos dimensiones que nos señalará la fila y la columna de las matrices. Luego determinaremos los desplazamientos en los búferes de datos y realizaremos operaciones matemáticas sencillas.
__kernel void ComplexLayer(__global float *inputs_re, __global float *inputs_im, __global float *outputs_re, __global float *outputs_im ) { size_t i = get_global_id(0); size_t j = get_global_id(1); size_t total_i = get_global_size(0); size_t total_j = get_global_size(1); uint shift = i * total_j + j; //--- outputs_re[shift] = inputs_re[shift] - inputs_im[shift]; outputs_im[shift] = inputs_im[shift] + inputs_re[shift]; }
El kernel de propagación inversa del error ComplexLayerGradient se construirá de forma similar. Le sugiero que se familiarice con su código en el archivo adjunto.
Con esto daremos por terminado el trabajo con la parte OpenCL del programa.
2.3 Creación de una clase de método FITS
Una vez completados los kernels del programa OpenCL, pasaremos al programa principal donde crearemos la clase CNeuronFITSOCL para implementar los enfoques propuestos por los autores del método FITS. Después crearemos una nueva clase heredando la clase básica de capas neuronales CNeuronBaseOCL. A continuación, mostraremos la estructura de la nueva clase.
class CNeuronFITSOCL : public CNeuronBaseOCL { protected: //--- uint iWindow; uint iWindowOut; uint iCount; uint iFFTin; uint iIFFTin; //--- CNeuronBaseOCL cInputsRe; CNeuronBaseOCL cInputsIm; CNeuronBaseOCL cFFTRe; CNeuronBaseOCL cFFTIm; CNeuronDropoutOCL cDropRe; CNeuronDropoutOCL cDropIm; CNeuronConvOCL cInsideRe1; CNeuronConvOCL cInsideIm1; CNeuronConvOCL cInsideRe2; CNeuronConvOCL cInsideIm2; CNeuronBaseOCL cComplexRe; CNeuronBaseOCL cComplexIm; CNeuronBaseOCL cIFFTRe; CNeuronBaseOCL cIFFTIm; CBufferFloat cClear; //--- virtual bool FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false); virtual bool ComplexLayerOut(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im); virtual bool ComplexLayerGradient(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); public: CNeuronFITSOCL(void) {}; ~CNeuronFITSOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_out, uint count, float dropout, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual int Type(void) const { return defNeuronFITSOCL; } virtual void SetOpenCL(COpenCLMy *obj); virtual void TrainMode(bool flag); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); };
No resulta difícil darse cuenta de que en la estructura de la nueva clase se declarará un gran número de objetos internos de la capa neuronal. Y esto provocará cierta disonancia en el contexto de la declarada simplicidad del modelo. Sin embargo, debemos decir de entrada que entrenaremos solo los parámetros de las 4 capas neuronales anidadas responsables de la interpolación de datos (cInsideRe* y cInsideIm*). El resto actuarán como búferes de datos intermedios, cuyo propósito conoceremos durante la implementación de los métodos.
Aquí es donde también deberemos destacar la presencia de 2 capas CNeuronDropoutOCL. En esta implementación, hemos decidido no utilizar la LFP, que implica definir algún tipo de frecuencia de corte. Y aquí he recordado los experimentos de los autores del método FEDformer, que hablan de la eficacia del muestreo de un conjunto de características de frecuencia. Así que he decidido utilizar la capa Dropout para concentrarme en una respuesta de frecuencia aleatoria.
Todos los objetos internos los declararemos como estáticos, lo que nos permitirá dejar el constructor y el destructor de la clase "vacíos". La inicialización directa de los objetos y de todas las variables locales se realizará en el método Init. Como es habitual, los parámetros del método especificarán variables que permiten definir sin ambigüedad la estructura requerida del objeto. Aquí veremos los tamaños de la ventana de la secuencia unitaria de datos de origen y los resultados (window y window_out), el número de series temporales unitarias (count) y la proporción de características de frecuencia puestas a cero (dropout). Cabe señalar que estamos construyendo una capa unificada, y el tamaño de la ventana tanto de los datos de entrada como de los resultados podrá ser cualquier número positivo sin estar limitado a los requisitos del algoritmo FFT. Recordemos que el algoritmo anterior requerirá un tamaño de datos de origen igual a una potencia de 2.
bool CNeuronFITSOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_out, uint count, float dropout, ENUM_OPTIMIZATION optimization_type, uint batch) { if(window <= 0) return false; if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * count, optimization_type, batch)) return false;
En el cuerpo del método, primero organizaremos un pequeño bloque de control donde comprobaremos el tamaño de la ventana de datos de origen (debe ser un número positivo) y llamaremos al método homónimo de la clase padre. Como ya sabrá, el método de la clase padre implementa un control adicional y la inicialización de los objetos heredados.
Tras pasar con éxito el bloque de control, guardaremos los parámetros obtenidos en variables locales.
//--- Save constants
iWindow = window;
iWindowOut = window_out;
iCount = count;
activation=None;
Definiremos las dimensiones de los tensores para las FFT directa e inversa como las potencias mayores de 2 más próximas a los parámetros obtenidos correspondientes.
//--- Calculate FFT and iFFT size int power = int(MathLog(iWindow) / M_LN2); if(MathPow(2, power) != iWindow) power++; iFFTin = uint(MathPow(2, power)); power = int(MathLog(iWindowOut) / M_LN2); if(MathPow(2, power) != iWindowOut) power++; iIFFTin = uint(MathPow(2, power));
Después vendrá el bloque de inicialización de objetos anidados. Los objetos cInputs* se utilizarán como búferes de datos de entrada para la FFT directa. Su tamaño será igual al producto del tamaño de la secuencia unitaria a la entrada de este bloque y el número de secuencias que hay que analizar.
if(!cInputsRe.Init(0, 0, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cInputsIm.Init(0, 1, OpenCL, iFFTin * iCount, optimization, iBatch)) return false;
Los objetos para registrar los resultados de la descomposición de Fourier directa cFFT* tendrán un tamaño similar.
if(!cFFTRe.Init(0, 2, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cFFTIm.Init(0, 3, OpenCL, iFFTin * iCount, optimization, iBatch)) return false;
A continuación, declararemos los objetos Dropout. No resulta difícil adivinar que tendrán el mismo tamaño que los anteriores.
if(!cDropRe.Init(0, 4, OpenCL, iFFTin * iCount, dropout, optimization, iBatch)) return false; if(!cDropIm.Init(0, 5, OpenCL, iFFTin * iCount, dropout, optimization, iBatch)) return false;
Para la interpolación de secuencias, utilizaremos un MLP con una capa oculta y activación tanh entre capas. A la salida del bloque, obtendremos los datos según los requisitos del bloque de FFT inversa.
if(!cInsideRe1.Init(0, 6, OpenCL, iFFTin, iFFTin, 4*iIFFTin, iCount, optimization, iBatch)) return false; cInsideRe1.SetActivationFunction(TANH); if(!cInsideIm1.Init(0, 7, OpenCL, iFFTin, iFFTin, 4*iIFFTin, iCount, optimization, iBatch)) return false; cInsideIm1.SetActivationFunction(TANH); if(!cInsideRe2.Init(0, 8, OpenCL, 4*iIFFTin, 4*iIFFTin, iIFFTin, iCount, optimization, iBatch)) return false; cInsideRe2.SetActivationFunction(None); if(!cInsideIm2.Init(0, 9, OpenCL, 4*iIFFTin, 4*iIFFTin, iIFFTin, iCount, optimization, iBatch)) return false; cInsideIm2.SetActivationFunction(None);
Combinaremos los resultados de la interpolación en objetos cComplex*.
if(!cComplexRe.Init(0, 10, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cComplexIm.Init(0, 11, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false;
Según el método FITS, las secuencias interpoladas se someterán a una descomposición inversa de Fourier en la que las características de frecuencia se transformarán en series temporales. Escribiremos los resultados de esta operación en objetos cIFFT.
if(!cIFFTRe.Init(0, 12, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cIFFTIm.Init(0, 13, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false;
Además, declararemos un búfer auxiliar de valores cero con el que completaremos los valores que falten.
if(!cClear.BufferInit(MathMax(iFFTin, iIFFTin)*iCount, 0)) return false; cClear.BufferCreate(OpenCL); //--- return true; }
Una vez que todos los objetos anidados se hayan inicializado correctamente, finalizaremos el método.
El siguiente paso será implementar la funcionalidad de la clase. Pero antes de pasar directamente a los métodos de pasada directa e inversa, tendremos que hacer algunos trabajos preparatorios para implementar la funcionalidad necesaria para poner los kernels construidos anteriormente en la cola de ejecución. El algoritmo de estos kernels será homogéneo. Y dentro del ámbito de este artículo, consideraremos solo el método de llamada al kernel de transformada rápida de Fourier CNeuronFITSOCL::FFT.
bool CNeuronFITSOCL::FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false) { uint global_work_offset[1] = {0}; uint global_work_size[1] = {iCount};
En los parámetros del método transmitiremos los punteros a los 4 búferes de datos con los que trabajaremos (2 de datos de origen y 2 de resultados) y la bandera de dirección de las operaciones.
En el cuerpo del método, definiremos el espacio de tareas. Aquí utilizaremos un espacio de problemas unidimensional en cuanto al número de secuencias que hay que analizar.
Y luego transmitiremos los parámetros al kernel. En primer lugar, los punteros a los búferes de datos de origen.
if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_inputs_re, inp_re.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_inputs_im, (!!inp_im ? inp_im.GetIndex() : inp_re.GetIndex()))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Aquí vale la pena señalar que permitiremos la posibilidad de ejecutar el kernel sin el búfer de la parte imaginaria de la señal. Como recordará, utilizamos la bandera input_complex para esto en el kernel. Sin embargo, si no transmitimos todos los parámetros necesarios al kernel, obtendremos un error de ejecución. Por lo tanto, si no hay búfer de la parte imaginaria, apuntaremos el puntero al búfer de la parte real de la señal y especificaremos false para el indicador correspondiente.
if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_input_complex, int(!!inp_im))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
A continuación, transmitiremos los punteros a los búferes de resultados.
if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_outputs_re, out_re.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_outputs_im, out_im.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
El tamaño de las ventanas de datos de origen y resultados; este último es de grado 2. Tenga en cuenta que estamos calculando los tamaños de las ventanas en lugar de tomarlos de las constantes. Esto se debe a que utilizaremos este método para las transformadas de Fourier directa e inversa, que se efectuarán con diferentes búferes y, por tanto, con diferentes ventanas de datos de entrada y resultados.
if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_input_window, (int)(inp_re.Total() / iCount))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_output_window, (int)(out_re.Total() / iCount))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Por último, transmitiremos una bandera para indicar el uso del algoritmo de transformación inversa.
if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_reverse, int(reverse))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Y pondremos el kernel en la cola de ejecución.
if(!OpenCL.Execute(def_k_FFT, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
En cada paso, controlaremos el proceso de las operaciones y retornaremos al programa de llamada el valor lógico de las operaciones realizadas.
Los métodos CNeuronFITSOCL::ComplexLayerOut y CNeuronFITSOCL::ComplexLayerGradient, que llaman a los kernels homónimos, se basarán en un principio similar. Le sugiero a familiarizarse con ellos en los anexos.
Una vez completado el trabajo preparatorio, procederemos a construir el algoritmo de pasada directa descrito en el método CNeuronFITSOCL::feedForward.
En los parámetros, el método obtendrá un puntero al objeto de la capa neuronal precedente que nos pasa los datos de origen. Y en el cuerpo del método comprobaremos inmediatamente el puntero recibido.
bool CNeuronFITSOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Aquí debemos decir que el método FITS implica una normalización previa de los datos. Asumiremos que se ha efectuado la normalización de los datos en las capas neuronales precedentes y omitiremos este dicho dentro de esta clase.
Luego trasladaremos los datos obtenidos al dominio de las características de frecuencia usando una transformada rápida de Fourier directa. Para ello, llamaremos al método correspondiente, cuyo algoritmo se presenta más arriba.
//--- FFT if(!FFT(NeuronOCL.getOutput(), NULL, cFFTRe.getOutput(), cFFTIm.getOutput(), false)) return false;
Reduciremos las características de frecuencia resultantes utilizando capas Dropout.
//--- DropOut if(!cDropRe.FeedForward(cFFTRe.AsObject())) return false; if(!cDropIm.FeedForward(cFFTIm.AsObject())) return false;
A continuación, interpolaremos las características de frecuencia al tamaño de los valores predichos.
//--- Complex Layer if(!cInsideRe1.FeedForward(cDropRe.AsObject())) return false; if(!cInsideRe2.FeedForward(cInsideRe1.AsObject())) return false; if(!cInsideIm1.FeedForward(cDropIm.AsObject())) return false; if(!cInsideIm2.FeedForward(cInsideIm1.AsObject())) return false;
Y combinaremos las interpolaciones separadas de las partes real e imaginaria de la señal.
if(!ComplexLayerOut(cInsideRe2.getOutput(), cInsideIm2.getOutput(), cComplexRe.getOutput(), cComplexIm.getOutput())) return false;
Después retornaremos la señal obtenida al dominio temporal mediante descomposición inversa.
//--- iFFT if(!FFT(cComplexRe.getOutput(), cComplexIm.getOutput(), cIFFTRe.getOutput(), cIFFTIm.getOutput(), true)) return false;
Aquí cabe señalar que la serie predicha resultante podría superar el tamaño de la secuencia que tenemos que transmitir a la capa neuronal posterior. Por lo tanto, extraeremos solo el bloque que necesitamos de la parte real de la señal.
//--- To Output if(!DeConcat(Output, cIFFTRe.getGradient(), cIFFTRe.getOutput(), iWindowOut, iIFFTin - iWindowOut, iCount)) return false; //--- return true; }
No se olvide de supervisar el proceso de las operaciones en cada paso. Y al final de todas las iteraciones, retornaremos el resultado lógico de las operaciones realizadas al programa de llamada.
Tras implementar el pasada directa, construiremos los métodos de pasada inversa. Y aquí empezaremos con el método CNeuronFITSOCL::calcInputGradients, encargado de distribuir el gradiente de error a todos los objetos internos y la capa anterior según su influencia en el resultado final.
bool CNeuronFITSOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
En los parámetros, el método obtendré el puntero al objeto de la capa anterior al que vamos a pasar el gradiente de error. En el cuerpo del método comprobaremos directamente la relevancia del puntero recibido.
El gradiente de error obtenido de la capa posterior ya está almacenado en el búfer Gradient. Sin embargo, solo contendrá la parte real de la señal. Y solo para una profundidad de previsión determinada. Necesitaremos el gradiente de error tanto para la parte real como para la imaginaria en el horizonte de la señal completa a partir de la transformada inversa. Para generar estos datos, partiremos de dos supuestos:
- A la salida del bloque de la transformada inversa de Fourier de pasada directa, esperaremos obtener los valores de las series temporales discretas. En este caso, la parte real de la señal corresponderá a la serie temporal requerida, mientras que la parte imaginaria será igual (o cercana) a "0". Por lo tanto, el error de la parte imaginaria será igual a su valor tomado con el signo opuesto.
- Como no tenemos información sobre la corrección de los valores previstos más allá del horizonte de planificación dado, simplemente despreciaremos las posibles desviaciones y consideraremos el error para ellas como "0".
//--- Copy Gradients if(!SumAndNormilize(cIFFTIm.getOutput(), GetPointer(cClear), cIFFTIm.getGradient(), 1, false, 0, 0, 0, -1)) return false;
if(!Concat(Gradient, GetPointer(cClear), cIFFTRe.getGradient(), iWindowOut, iIFFTin - iWindowOut, iCount)) return false;
A continuación, fíjese en que tendremos el gradiente de error representado como una serie temporal. Realizaremos la previsión en el dominio de la frecuencia. Por lo tanto, también tendremos que convertir el gradiente de error al dominio de la frecuencia. Y esta operación implicará la aplicación de una transformada rápida de Fourier.
//--- FFT if(!FFT(cIFFTRe.getGradient(), cIFFTIm.getGradient(), cComplexRe.getGradient(), cComplexIm.getGradient(), false)) return false;
Luego distribuiremos las características de frecuencia entre los 2 MLP de las partes real e imaginaria.
//--- Complex Layer if(!ComplexLayerGradient(cInsideRe2.getGradient(), cInsideIm2.getGradient(), cComplexRe.getGradient(), cComplexIm.getGradient())) return false;
A continuación, distribuiremos el gradiente de error a través del MLP.
if(!cInsideRe1.calcHiddenGradients(cInsideRe2.AsObject())) return false; if(!cInsideIm1.calcHiddenGradients(cInsideIm2.AsObject())) return false; if(!cDropRe.calcHiddenGradients(cInsideRe1.AsObject())) return false; if(!cDropIm.calcHiddenGradients(cInsideIm1.AsObject())) return false;
A través de la capa Dropout llevaremos el gradiente de error a la salida del bloque de la transformada directa de Fourier.
//--- Dropout if(!cFFTRe.calcHiddenGradients(cDropRe.AsObject())) return false; if(!cFFTIm.calcHiddenGradients(cDropIm.AsObject())) return false;
Y ahora tendremos que convertir el gradiente de error del dominio de la frecuencia a una serie temporal. Realizaremos esta operación utilizando la transformación inversa.
//--- IFFT if(!FFT(cFFTRe.getGradient(), cFFTIm.getGradient(), cInputsRe.getGradient(), cInputsIm.getGradient(), true)) return false;
Por último, transferiremos a la capa anterior solo la parte necesaria del gradiente de error real.
//--- To Input Layer if(!DeConcat(NeuronOCL.getGradient(), cFFTIm.getGradient(), cFFTRe.getGradient(), iWindow, iFFTin - iWindow, iCount)) return false; //--- return true; }
Como siempre, controlaremos el proceso de ejecución de todas las operaciones en el cuerpo del método, y al final devolveremos al programa de llamada un valor lógico sobre la corrección de las operaciones ejecutadas.
A la distribución del gradiente de error le seguirá el proceso de actualización de los parámetros del modelo, que se implementará en el método CNeuronFITSOCL::updateInputWeights. Como hemos mencionado antes, entre los muchos objetos declarados en la clase, los parámetros entrenados solo contendrán capas MLP. Ajustaremos sus parámetros en el método anterior.
bool CNeuronFITSOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cInsideRe1.UpdateInputWeights(cDropRe.AsObject())) return false; if(!cInsideIm1.UpdateInputWeights(cDropIm.AsObject())) return false; if(!cInsideRe2.UpdateInputWeights(cInsideRe1.AsObject())) return false; if(!cInsideIm2.UpdateInputWeights(cInsideIm1.AsObject())) return false; //--- return true; }
La presencia de un gran número de objetos internos que no contienen parámetros entrenables, también imprimirá su huella en los métodos de trabajo con archivos. Estará de acuerdo conmigo en que no tiene especial sentido almacenar cantidades considerables de información sin valor alguno. Por consiguiente, en el método CNeuronFITSOCL::Save, primero llamaremos al método homónimo de la clase padre.
bool CNeuronFITSOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false;
Después guardaremos las constantes de la arquitectura.
//--- Save constants if(FileWriteInteger(file_handle, int(iWindow)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iWindowOut)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iCount)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iFFTin)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iIFFTin)) < INT_VALUE) return false;
Y guardaremos los objetos MLP.
//--- Save objects if(!cInsideRe1.Save(file_handle)) return false; if(!cInsideIm1.Save(file_handle)) return false; if(!cInsideRe2.Save(file_handle)) return false; if(!cInsideIm2.Save(file_handle)) return false;
Luego añadiremos más objetos del bloque Dropout.
if(!cDropRe.Save(file_handle)) return false; if(!cDropIm.Save(file_handle)) return false; //--- return true; }
Y ya está. Los demás objetos solo contendrán búferes de datos cuya información solo será relevante dentro de un ciclo de pasada directa-inversa. Por lo tanto, no los guardaremos y así ahorraremos espacio en el disco. No obstante, pagaremos este ahorro complicando el algoritmo del método de carga de datos CNeuronFITSOCL::Load.
bool CNeuronFITSOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false;
En él, primero repetiremos a la inversa el método de almacenamiento de datos:
- Después llamaremos al método homónimo de la clase padre.
- Y cargaremos las constantes. Al mismo tiempo, controlamos que se llegue al final del archivo de datos.
//--- Load constants if(FileIsEnding(file_handle)) return false; iWindow = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iWindowOut = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iCount = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iFFTin = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iIFFTin = uint(FileReadInteger(file_handle)); activation=None;
- Luego leeremos los parámetros MLP y Dropout.
//--- Load objects if(!LoadInsideLayer(file_handle, cInsideRe1.AsObject())) return false; if(!LoadInsideLayer(file_handle, cInsideIm1.AsObject())) return false; if(!LoadInsideLayer(file_handle, cInsideRe2.AsObject())) return false; if(!LoadInsideLayer(file_handle, cInsideIm2.AsObject())) return false; if(!LoadInsideLayer(file_handle, cDropRe.AsObject())) return false; if(!LoadInsideLayer(file_handle, cDropIm.AsObject())) return false;
E inicializaremos los objetos restantes. Aquí estaremos repitiendo parte del código del método de inicialización de la clase.
//--- Init objects if(!cInputsRe.Init(0, 0, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cInputsIm.Init(0, 1, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cFFTRe.Init(0, 2, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cFFTIm.Init(0, 3, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cComplexRe.Init(0, 8, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cComplexIm.Init(0, 9, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cIFFTRe.Init(0, 10, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cIFFTIm.Init(0, 11, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cClear.BufferInit(MathMax(iFFTin, iIFFTin)*iCount, 0)) return false; cClear.BufferCreate(OpenCL); //--- return true; }
Con esto concluiremos nuestro trabajo de descripción de los métodos de nuestra nueva clase CNeuronFITSOCL y sus algoritmos. Podrá encontrar el código completo de esta clase y todos sus métodos en el archivo adjunto. Todos los programas utilizados en la preparación de este artículo también se encuentran allí. Ahora podemos comenzar a describir la arquitectura de los modelos entrenados.
2.4 Arquitectura del modelo
El método FITS se ha propuesto para el análisis y la previsión de series temporales. Y creo que ya habrá adivinado que utilizaremos los planteamientos propuestos en el Codificador del estado del entorno. Su arquitectura se describirá en el método CreateEncoderDescriptions.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
En los parámetros del método obtendremos el puntero al objeto de array dinámico para guardar la arquitectura del modelo creado. En el cuerpo del método comprobaremos directamente la relevancia del puntero recibido. De ser necesario, crearemos una nueva instancia del objeto de array dinámico.
Como siempre, suministraremos a la entrada del modelo los datos "brutos" que describen el estado actual del entorno.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
El procesamiento inicial de los datos recibidos se realizará en la capa de normalización por lotes, que permitirá convertir los datos a una forma comparable y aumentar la estabilidad del proceso de entrenamiento del modelo.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Nuestros datos de origen serán series temporales multidimensionales. Cada bloque de datos secuenciales contendrá distintos parámetros que describirán una vela de datos históricos. Sin embargo, para analizar las secuencias unitarias de nuestro conjunto de datos, necesitaremos transponer el tensor resultante.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = HistoryBars; descr.window = BarDescr; if(!encoder.Add(descr)) { delete descr; return false; }
Llegados a este punto, podemos dar por concluido el trabajo preparatorio y pasar al análisis directo y la previsión de series temporales unitarias. Realizaremos este proceso en el objeto de nuestra nueva clase.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFITSOCL; descr.count = BarDescr; descr.window = HistoryBars; descr.activation = None; descr.window_out = NForecast; if(!encoder.Add(descr)) { delete descr; return false; }
Cabe mencionar aquí que hemos implementado casi todo el método FITS propuesto en el cuerpo de nuestra clase. Y a la salida de la capa neuronal ya tenemos los valores predichos. Todo lo que tendremos que hacer es transponer el tensor de valores predichos a la dimensionalidad de los resultados esperados.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = BarDescr; descr.window = NForecast; if(!encoder.Add(descr)) { delete descr; return false; }
Y añadir los parámetros previamente retirados de la distribución estadística de los datos de origen.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Como podemos ver, el modelo de análisis y predicción de los estados del entorno posteriores ha resultado bastante corto, tal y como habían prometido los autores del método FITS. Al mismo tiempo, los cambios que hemos introducido en la arquitectura del modelo no han afectado en absoluto al volumen ni al formato de los datos de entrada. Tampoco hemos cambiado el formato de los resultados del modelo. Esto nos permitirá utilizar sin cambios las arquitecturas de los modelos del Actor y el Crítico creadas anteriormente. Además, podremos utilizar asesores para la interacción con el entorno y el entrenamiento de modelos previamente construidos, así como muestras de entrenamiento ya recopiladas. Lo único que deberemos cambiar es el puntero a la capa de representación latente del estado del entorno.
#define LatentLayer 3
El código completo de todos los programas utilizados en la elaboración del artículo figura en el anexo. Vamos a pasar ahora a comprobar los resultados del trabajo realizado.
3. Simulación
Ya nos hemos familiarizado con el método FITS y realizado un trabajo bastante serio sobre la aplicación de los enfoques propuestos utilizando herramientas MQL5. Ahora ha llegado el momento de probar la eficacia de esta solución con datos históricos reales. Al igual que antes, entrenaremos y probaremos los modelos con los datos históricos de EURUSD y el marco temporal H1. El entrenamiento se realizará con los datos históricos de todo el año 2023. Y probaremos el modelo entrenado con los datos de enero de 2024.
Entrenaremos los modelos de forma similar al proceso descrito en el artículo anterior. Primero entrenaremos el codificador de estados del entorno para predecir los estados posteriores. Y luego entrenaremos iterativamente la política de comportamiento del Actor para obtener la máxima rentabilidad.
Como era de esperar, el modelo del Codificador ha resultado bastante ligero. El proceso de entrenamiento ha sido relativamente rápido y fluido. A pesar de su pequeño tamaño, el modelo demuestra un rendimiento comparable al modelo FEDformer analizado en el último artículo. Aquí cabe señalar que el modelo es casi 84 veces más pequeño.

No obstante, en la fase de entrenamiento de la política del Actor, nos hemos llevado una decepción. El modelo solo es capaz de mostrar rendimiento en segmentos históricos aislados. En el gráfico de balance sin pruebas que figura a continuación, se observa una subida bastante rápida en la primera década del mes. Pero la segunda década se caracteriza por la tendencia a perder fondos del depósito con raras operaciones rentables. La tercera década se acerca a la paridad de transacciones rentables y no rentables.

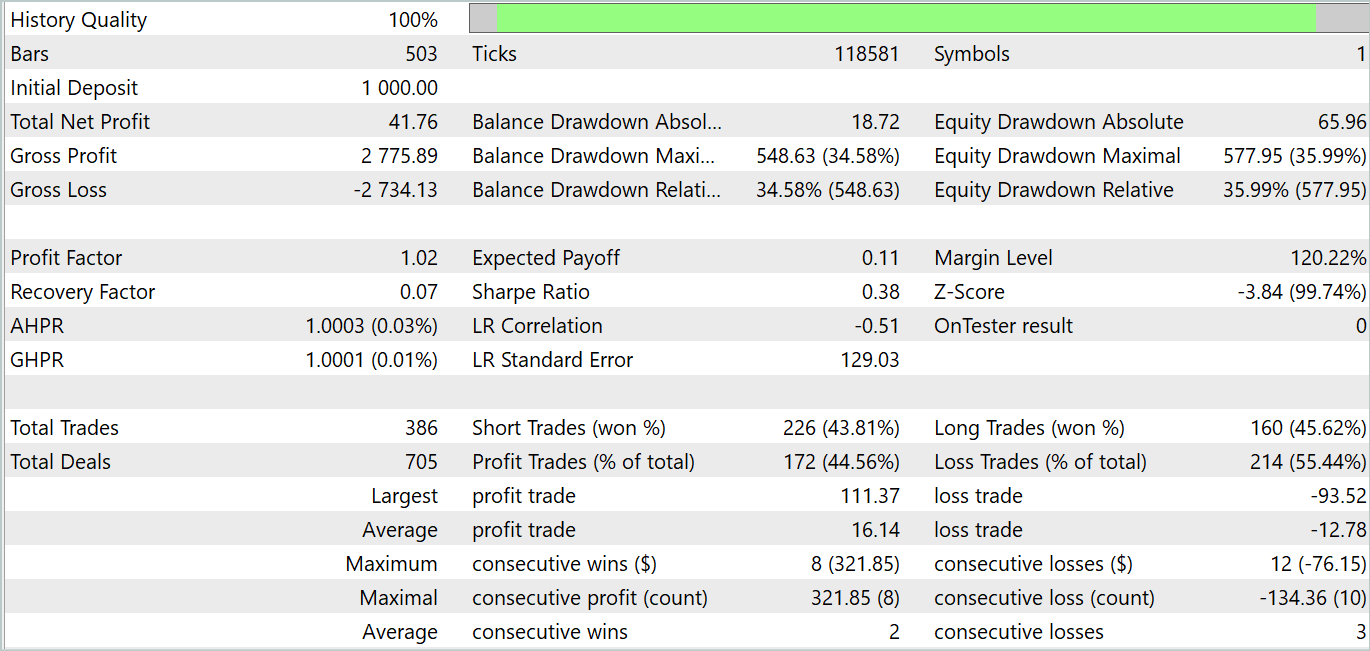
En conjunto, el mes ha sido ligeramente positivo. Cabe señalar aquí que la magnitud de las transacciones rentable máxima y media supera las cifras de las pérdidas correspondientes. Sin embargo, el número de transacciones rentables es inferior a la mitad, lo que nivela la superioridad de la transacción rentable media.
Debemos señalar que los resultados de las pruebas confirman parcialmente las conclusiones extraídas por los autores del método FEDformer: debido a la ausencia de periodicidad pronunciada en los datos iniciales, la DFT no es capaz de determinar el momento del cambio de tendencia.
Conclusión
En este artículo se presenta un nuevo método de análisis y previsión de series temporales, el FITS. La característica clave de este método es el análisis y la predicción de series temporales en el dominio de la frecuencia. Al mismo tiempo, gracias al uso del algoritmo de transformada rápida de Fourier directa e inversa, podemos trabajar con las series temporales discretas habituales a la entrada y salida del modelo. Esta característica permite aplicar la arquitectura ligera propuesta en muchos ámbitos en los que se utilizan el análisis y la previsión de series temporales.
En la parte práctica de este artículo, hemos implementado nuestra visión de los enfoques propuestos usando MQL5. Asimismo, hemos entrenado y probado los modelos con datos históricos reales. Por desgracia, los resultados de las pruebas no han dado el resultado deseado. Sin embargo, querría señalar que los resultados presentados solo son relevantes para la aplicación presentada de los enfoques propuestos. El uso del algoritmo del autor puede arrojar resultados distintos.
Enlaces
- FITS: Modeling Time Series with 10k Parameters
- A Survey of Complex-Valued Neural Networks
- Otros artículos de la serie
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de cobros de ejemplo Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | StudyEncoder.mq5 | Asesor | Asesor de entrenamiento del Codificador |
| 5 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 6 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 7 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/14913
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Características del Wizard MQL5 que debe conocer (Parte 27): Medias móviles y el ángulo de ataque
Características del Wizard MQL5 que debe conocer (Parte 27): Medias móviles y el ángulo de ataque
 Análisis de sentimientos y aprendizaje profundo para operar con EA y backtesting con Python
Análisis de sentimientos y aprendizaje profundo para operar con EA y backtesting con Python
 Desarrollamos un asesor experto multidivisa (Parte 11): Comenzamos a automatizar el proceso de optimización
Desarrollamos un asesor experto multidivisa (Parte 11): Comenzamos a automatizar el proceso de optimización
 Cómo crear cualquier tipo de Trailing Stop y conectarlo a un asesor experto
Cómo crear cualquier tipo de Trailing Stop y conectarlo a un asesor experto
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso