ニューラルネットワークの実践：直線関数

はじめに

皆様を歓迎し、ニューラルネットワークに関する新しい記事をお読みいただけることを大変嬉しく思います。

前回の「ニューラルネットワークの実践：最小二乗法」稿では、では、非常にシンプルなケースを取り上げ、使用しているデータセットを最もよく表す方程式の見つけ方について説明しました。このシステムで生成された方程式は非常に単純で、1つの変数のみを使用しています。計算方法についてはすでに説明していますので、ここではその要点をまとめます。データベース内の利用可能な値に基づいて方程式を構築するためには、解析数学と代数計算に関する相当な知識が必要です。また、使用しているデータベースにどのようなデータが含まれているかを理解しておくことも重要です。

この記事は教育的な目的が広くあるため、読者にとって難解な内容にはしたくありません。計算を深く理解したいと考えている方には、このトピックに関連する資料の学習をお勧めします。特に、解析数学と代数微積分を中心に勉強する必要があります。このプロセスを理論的で退屈なものにしないために、まずはゲーム理論を学ぶことをお勧めします。ゲーム理論では、無限の計算を単調に復習することなく、楽しみながら計算や分析に慣れることができるからです。

このトピックについては、よく説明されていて理解しやすい資料がWeb上にたくさん存在します。しかし、この記事では数学の詳細には触れず、コードに焦点を当てているため、数学的な問題に興味がない方でも安心してお読みいただけます。数学的な問題は非常に奥深く、完全に理解するには時間を要するため、ほとんどの読者にとっては興味のない領域かもしれません。

したがって、この記事では、データベース内のデータを表す関数を得るいくつかの方法について簡単に説明します。統計や確率の研究を用いて結果を解釈する方法については詳細に触れません。この問題の数学的側面について深く知りたい方にお任せします。これらの問いを検討することは、ニューラルネットワークの研究において非常に重要です。ここでは、このテーマを冷静に掘り下げていきます。

一般的な形式で方程式を作成する

まずは計算を始めましょう。（またかと思うかもしれませんが）落ち着いてください、親愛なる読者の皆さん。これから何をするか心配する必要はありません。今回はもっと優しく進めることをお約束します。今日の目標は、より一般的な直線方程式を生成できるシステムを構築することです。そして、数式の背後にある数学的な開発については深く掘り下げず、皆さんを驚かせないようにします。前回の記事では、基本的なアイデアと原則に基づいて数学的な方程式を開発する過程を示しましたが、今回はこれらの方程式が実際に何を意味するのかを理解することに焦点を当てます。できるだけわかりやすく進めるよう努力しますので、最初は混乱するかもしれませんが、安心してお読みください。全体がどのように展開するかを見ていきましょう。ここでは、数学のさまざまな研究を統合して、データベースに含まれる情報に基づいてニューラルネットワークに知識を学習させる方法を示します。

始める前に、1つだけ明確にしておきたいことがあります。ここで扱うのは、データベースに新しい情報を受け取らないニューラルネットワークです。つまり、データベースはすでに完全に作成されており、そこに存在する情報を最もよく表す方程式を生成するだけです。後に、他のメカニズムを使用して、新しい情報が既存のデータと関連しているかどうかをフィルタリングすることが可能です。このようなメカニズムは通常、人工知能の分野に属しますが、これは別の議論の対象です。

では、コードの例に戻りましょう。この例では、2次元平面にプロット可能な2つのデータセットが既にあります。つまり、X座標とY座標のみを使用します。データを冷静に分析すると、それが直線に近い形で表現できることがわかり、目的の方程式は比較的簡単に作成できます。ただし、方程式が曲線や三角関数である場合もありますので、一概には言えません。しかし、1歩ずつ進み、まずは単純なケースから始めましょう。取得したい方程式の形式を理解することが重要です。

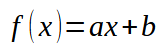
ここで、定数<a>の値は傾きを表し、定数<b>は交点を示します。<b>が0の場合、関数の根も0になります。前回の記事では、<b>が0の際にこの係数を計算する方法を説明しました。また、同じ記事の最後で、両方の値を調整し、上記の線形関数を構築する方法についても触れました。定数<b>の値を変更すると、関数の根も変化することを再度思い出してください。この理解は、多項式を使用してシステムを解く上で非常に重要です。今回は前回の記事から適応した方法を使用します。

こうした値を試行錯誤で見つける試みは、プログラミングでは「ブルートフォース」と呼ばれ、すべての可能な値を試す方法です（これは最善の方法からは程遠いものですが）。この方法は実行可能ですが、通常は処理時間が非常に長くなります。特に私たちのケースでは、多くの時間と労力がかかりますが、完全に実行可能です。しかし、変数の数が大幅に増えると、手動でおこなうかブルートフォースでおこなうかにかかわらず、このプロセスは非現実的になります。

とはいえ、力任せに計算をおこなう方法を選んだ場合でも、前回の記事では定数<b>が0の際の傾きを計算する方法を示しました。この方法により、データベース内のデータ量に関係なく、角度係数を比較的簡単かつ迅速に見つけることが可能でした。唯一の制約は、結果の方程式が直線である必要があるという点です。しかし、定数<b>が0でない場合、この計算は機能しません。これによって得られるのは、どの方向に移動するかの大まかなアイデアに過ぎません。この点については後ほど詳しく説明します。今は、冒頭で説明したような既知の関数に基づいて作業を進めていきます。

一般的な解法について考えてみましょう。使用する多項式の種類を知っておくことが必要です。この知識がなければ、最も単純なケースでも、データを最もよく表す方程式を見つけるのに非常に時間がかかります。したがって、次に説明するすべての内容は、この事前の知識に基づいていることを思い出してください。

最小二乗法をあらゆるケースに一般化してみましょう。そのためには、使用する多項式の種類を理解する必要があります。直線を生成する単純な多項式から始め、この多項式は以下の式を用いて一般化できます。

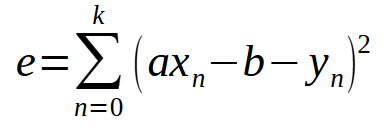
ちょっと待ってください、これは前回の記事で見たのと同じ式ではないでしょうか。そうです。基本的には同じことですが、変数<b>が0であると仮定しなくなったため、式に含まれています。この合計を展開すると、前回の記事でおこなったことに似たものになります。ただし、理解を深めるためには、この計算を一般化する際に、変数<a>と<b>の両方に関する導関数を考慮する必要があります。これにより、以下に示す定義が得られます。

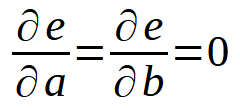
つまり、すべては前回の記事でおこなったことと同じです。ただし、この原則は直線の方程式に限定されません。どちらの場合でも同じアプローチを使用できます。たとえば、データセットを放物線として表現することが最適である場合、データベース内のデータを用いて二次方程式を見つける方法を考える必要があります。最後の2つの定義は次のように変換されます。

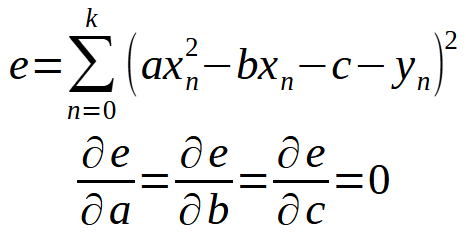
したがって、方程式を生成する方法を見つけるために新しい項を開発する必要があります。この場合は、2次方程式になります。つまり、2次方程式がデータベース内のすべての情報を表示できるように、定数を見つける必要があります。ただし、直線方程式を使用するケースに戻り、<b>が0でないと仮定して計算を続けると、まず次の方程式が得られます。

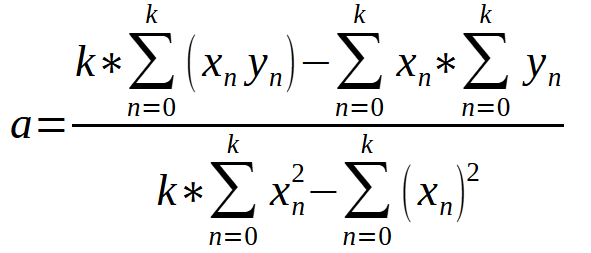
この式によって、データベースに含まれるデータに基づいて<a>の値を計算できます。

定数<a>の値が得られたら、次の式を用いて定数<b>を見つけることができます。

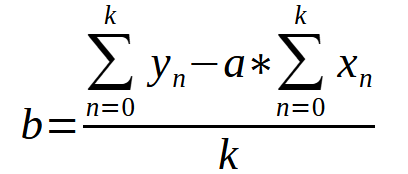
どちらの場合も、値<k>はグラフ上の点の数です。方程式だけを見ると、混乱して複雑なものに思えるかもしれません。また、これらの式をプログラミング言語でどのようにコードに変換するか分からない場合もあるでしょう。これによって、手動で実行せずに定数の値を取得することができるようになります。これは、前回の記事でおこなったことです。この数学的形式をプログラミング言語形式（この場合はMQL5）に変換しますが、他の言語を使用しても同様の結果が得られます。以下は、これらの方程式がMQL5コードでどのように表示されるかを示しています。

28. //+------------------------------------------------------------------+
29. void Func_01(void)
30. {
31.     int A[]={
32.                   -100, -150,
33.                    -80,  -50,
34.                     30,   80,
35.                    100,  120
36.             };
37. 
38.     int vx, vy;
39.     uint k;
40.     double ly, err, dx, dy, dxy, dx2, a, b;
41.     string s0 = "";
42. 
43.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
44.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
45. 
46.     err = dx = dy = dxy = dx2 = 0;
47.     k = 0;    
48.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++, k++)
49.     {
50.         vx = A[c1++];
51.         vy = A[c1++];
52.         dx += vx;
53.         dy += vy;
54.         dxy += (vx * vy);
55.         dx2 += MathPow(vx, 2);
56.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
57.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle))) - global.Const_B;
58.         s0 += StringFormat("%.4f || ", MathAbs(ly));
59.         canvas.LineVertical(global.x + vx, global.y - vy, global.y + (int)(ly - vy), ColorToARGB(clrPurple));
60.         err += MathPow(ly, 2);
61.     }
62.     a = ((k * dxy) - (dx * dy)) / ((k * dx2) - MathPow(dx, 2));
63.     b = (dy - (a * dx)) / k;
64.     PlotText(3, StringFormat("Error: %.8f", err));
65.     PlotText(4, s0);
66.     PlotText(5, StringFormat("f(x) = %.4fx %c %.4f", a, (b < 0 ? '-' : '+'), MathAbs(b)));
67. }
68. //+------------------------------------------------------------------+

このフラグメントで何が起こっているのかを考えてみましょう。46行目と47行目では、すべての変数を0に初期化しています。これは、変数が0から始まることを明示的に示すためですが、コンパイラは通常、変数を暗黙的に0に初期化するため、この初期化を省略することも可能です。52行目では、すべてのX値の合計を計算し、53行目ではY値の合計を計算します。54行目では、X値とY値の積の合計を求め、最後に55行目でX値の二乗の合計を計算します。

これらの計算は、これまで見てきた数式で使用されており、実際には非常にシンプルです。言い換えれば、計算は見た目ほど複雑ではなく、スムーズに進行します。上記の計算はすべて、これまでに検討した式で使用されます。今回はかなりシンプルになりました。

次に、直線の方程式で使用される定数の値を計算する必要があります。具体的には、傾きを計算する62行目と、切片の値を求める63行目が関わります。数式をプログラムによる計算に変換することの簡単さにお気づきでしょうか。数学の理解を主張しながら、それをプログラミング用語に翻訳できない人がいますが、私の意見では、こうした人々は自分自身を欺いています。なぜなら、数式をコードとして表現することは、文章を読むのと同じくらい容易だからです。もちろん、数式を理解していなければ、計算を実行するための指示をコンピューターに伝えることは不可能です。

次に、結果の方程式をプロットします。これは66行目でおこなわれ、計算された値が特定のデータセットに最適かどうかを視覚的に確認できます。以下のGIFでは、31行目の行列Aで指定された値を用いてプログラムを実行した結果を示しています。

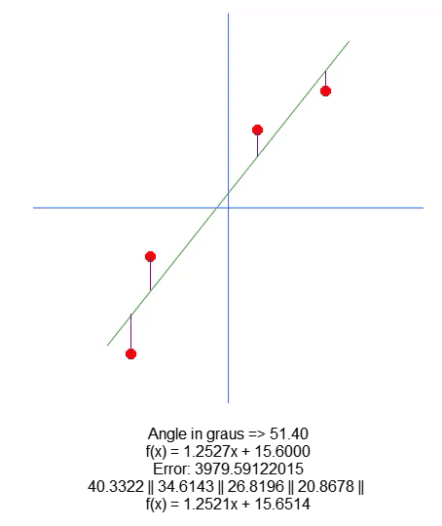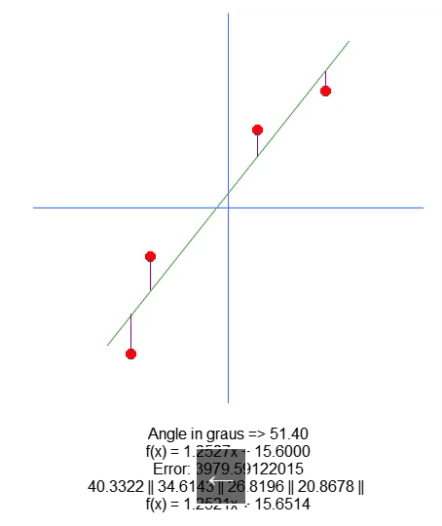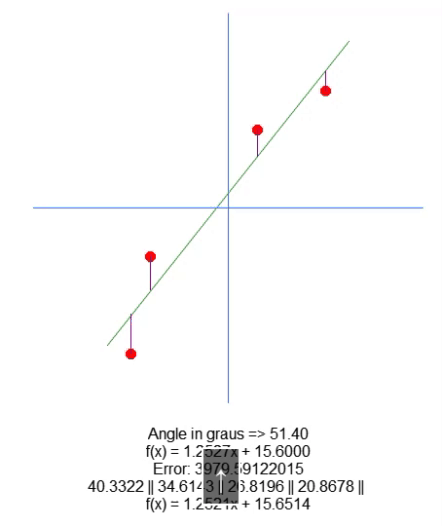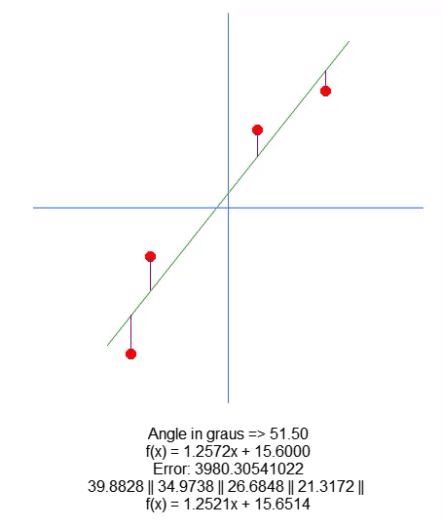
理想的な点を見つける試みを通じて、誤差値がどのように変化するかを確認します。理想的な直線の方程式と、矢印を用いてプロットしようとしている直線の方程式を比較することで、非常に正確な設定が得られます。完璧な一致は達成できませんが、理想に非常に近い値を得ることができます。この理解は重要です。なぜなら、まもなくこの特性を別の方法で学習することになるからです。

では、計算された値に近づく方法があるのかと疑問に思うかもしれません。答えははい、あります。これを実現するには、以下のコードに示すように、プログラム内の値を変更するだけです。

void NewAngle(const char direct, const char updow, const double step = 0.1)

変更する値はステップ引数です。ここでは、コード内で0.1のステップを使用していますが、より小さい値や大きい値を設定することもできます。小さい値を使用すると、プログラムが計算値に到達するまでに時間がかかりますが、変動が少なくなり、誤差の精度が高くなります。ただし、どちらか一方が他方を上回ることを忘れないでください。100% 完璧な解決策は存在しませんが、理想的なバランスポイントを見つけることが重要です。

直線方程式を計算できるコードが完成したら、行列Aの値を自由に変更し、任意の条件や知識ベースを作成できます。使用する変数の型を変更するだけでよい場合もあります。ここではintegerを使用していますが、doubleやfloatなどの浮動小数点データ型に変更することで、計算結果に影響を与えずに直線方程式を取得できます。ただし、データベース内のデータが2次方程式で最もよく表される場合は、前述の通り、データベースを最適に表現する定数システムを見つけるために計算を調整する必要があります。すべてはコンテキストに依存します。考えられるすべてのケースに対して100%効果的なソリューションは存在しません。

この直線方程式を計算する方法が唯一の方法だと考えている場合は、あなたの知識にはまだ限界があります。このトピックで得たのと同じ値を導く別の方法を示すために、新しいセクションを学び、その概念を分割していきます。このセクションは、次の記事で扱う内容の序章となります。

擬似逆行列

これまでの説明では、全体的に複雑で、コードへの実装が難しいように思えました。これは、必要な変更をそれぞれ適切に生成されたコードに組み込む必要があるからです。しかし、変数が常に変動する状況においては、コードを記述するよりも優れたアプローチがあります。少なくとも、私はそう考えています。変数の数が頻繁に変わる場合、私はスカラー計算から行列計算に移行することを好みます。行列演算を使用することで、複数の時間変数を作成することなく、さまざまな要因を考慮することができます。行列因数分解のコードを作成することが非常に難しいと感じ、多くの人がその仕組みを理解せずに実行するためのライブラリに依存していることを知っています。計算方法がわからないため、これらのライブラリに頼ることが多いのです。

以前、行列分解に関する2つの記事を執筆しました。これらの記事では、行列分解演算を実行するために必要な基本的な要素について説明しました。行列を計算に使用することで、多くの問題がより簡単かつ迅速に解決できることがわかります。

これらは「行列分解：基本」および「行列分解：より実用的なモデリング」稿です。このトピックについてさらに深く学びたい方は、これらの記事を読んで実際にテストしてみることをお勧めします。もちろん、これらの記事では基本的な内容しか取り上げていませんが、その内容を理解すれば、このセクションでの進行がスムーズになるでしょう。

ここでは、前のトピックで得た値を行列を使用して見つけます。これからの作業を理解するには、行列の加算方法を知っておく必要があります。これはプログラミングの問題ではなく、これらの計算をプログラミングすること自体は比較的簡単だからです。少なくとも、行列を使った計算の基本的な知識が必要です。この分野についての知識を前提としていますので、計算の実行方法については詳しく説明しません。専門家である必要はありませんが、基本を知っていることが重要です。

さて、データベースがあり、その内容を数式として保存したいという前提に戻り、直線の方程式を見つける方法を考えます。一見すると、これは天才だけが達成できるような非常に難しいことに思えるかもしれません。しかし、実際にはそうではありません。前のトピックと同様のプロセスをおこないますが、少し異なるアプローチを取ります。

まずは基本から始めましょう。誤差方程式を以下の図に示します。

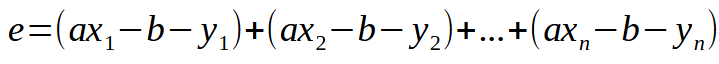
これは方程式のスカラー形式ですが、同じ方程式を行列形式で表すことも可能です。

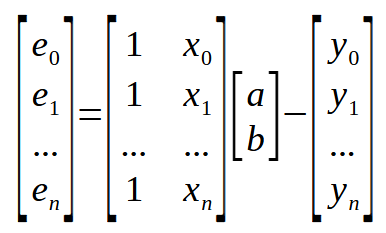
この行列表現は、何も追加されていない、前の図とまったく同じものです。ただし、この行列表現はさらに簡略化可能です。次のように表現できます。

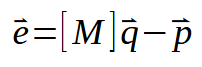
この表現は一見複雑に見えるかもしれませんが、実際にはスカラー計算が行うことを正確に表現しています。このコンパクトな形式の行列分解では、数式に記述する要素が少なくなるため、計算の実行方法をより良く理解できるでしょう。ここで、ベクトル<e>は、x値を含む行列<M>に、探している定数を含むベクトル<q>を乗じたものに等しいことを示しています。これらの定数には、傾きと切片が含まれます。次に、y値を含む行列の値を表すベクトル<p>を減算します。

ここで、重要な点を思い出してください。定数<a>と<b>の誤差に対する導関数を求めており、これは簡単に計算できます。これで、計算に使用する点の位置が明確になりました。したがって、これを行列形式で表すと次のようになります。

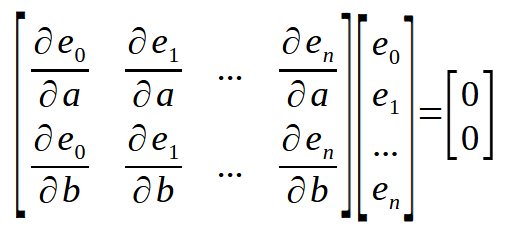
ここに小さな詳細があります。

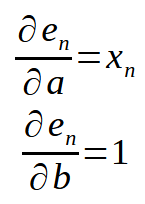
<n>がコード内の配列インデックスを表すことを覚えておけば、上記の式は以下のように書き直せます。

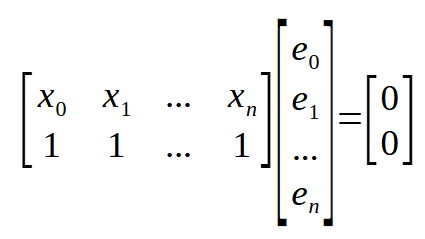
ここで、非常に興味深いことがわかりました。上の行列を見ると、同じ結果が示されていることが確認できます。他の場所にも同様の結果が示されていますが、この行列は転置されているだけで、これにより式がさらに簡潔になっています。下の画像をご覧ください。

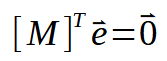
次のステップは、すでに持っているデータにいくつかの置換を加えることです。こうして次の定式が得られます。

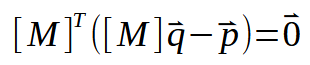
ここで、上記の計算または式（お好きな名前で呼んでください）を展開してみましょう。次のようになります。

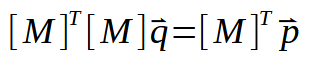
ここで転置行列を反転すると、次のようになります。

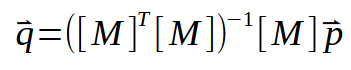
この結果は非常に素晴らしく興味深い因数分解であり、それを作成した人物は実際に2020年のノーベル数学賞に値するほどの業績を残しています。この定式化は、作成者にちなんで ムーア・ペンローズ逆行列と呼ばれています。これは、傾きと切片というまさに私たちが探している要素を提供してくれます。そして、これらの値はベクトル <q> に含まれています。このタイプの計算は、さまざまなプログラムで実装でき、その多くは計算処理専用に設計されています。たとえば、SCILabを使用すると、以下に示すプログラムを使って傾きと交点の値を計算できます。

clc;
clear;
clf;

x=[-100; -80; 30; 100];
y=[-150; -50; 80; 120];

A = [ones(x), x];

plot(x, y, 'ro');
zoom_rect([-150, -180, 180, 180]);
xgrid;

x = pinv(A) * y;
b = x(1);
a = x(2);

x =[-120:1:120];
y = a * x + b;

plot(x, y, 'b-');

実行結果は下記に示されています。

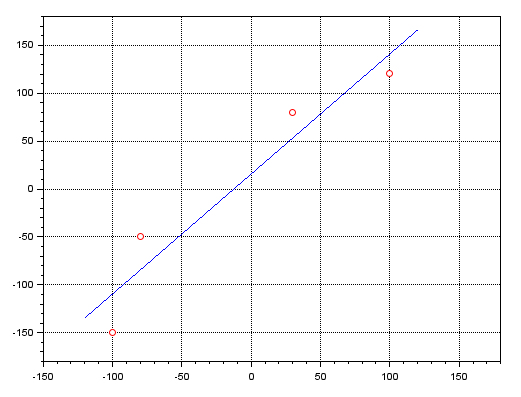
赤い点は、MQL5プログラムで得られた同じ点の位置を示しています。青い線は、擬似逆行列を用いて得られた直線方程式の結果を表しています。同様の処理は、MATLABやExcelなどの他のプログラムでも実行可能です。このことは、擬似逆行列がさまざまな分野で非常に有用である理由を示しています。

この擬似逆行列の興味深さを実感するためには、方程式の行列や使用されるベクトルをわずかに変更するだけで、あらゆる種類の多項式を非常に効率的に解決できることがわかります。

最終的な考察

擬似逆行列は、行列を用いて実行すべき因数分解です。このため、定数<a>と<b>を見つけるための具体的なプログラムはこの記事では示しません。何が起こっているのかを深く理解するためには、特定の説明を考慮する必要があります。単にコードを示すだけでは不十分です。行列演算は、その特異性から、より多くの注意を要します。手動で計算する場合、演算は比較的簡単ですが、これをプログラムで実行するとなると、話はまったく異なります。行列を用いた因数分解に関する他の記事でも、その内容は一般的ではなく、非常に特定的です。しかし、私たちの目的には、より一般的なコードが必要です。そうでないと、擬似逆行列を正しく計算することができません。