ニューラルネットワークが簡単に（第88回）：Time-series Dense Encoder (TiDE)

はじめに

時系列予測問題の解法として、回帰モデル、畳み込みモデル、グラフモデルなど、あらゆるニューラルネットワークアーキテクチャが研究されています。中でも、特に注目すべき成果はTransformerアーキテクチャをベースにしたモデルで実証されています。これまでの連載でも、そういったアルゴリズムをいくつか紹介してきました。しかし、最近の研究では、Transformerベースのモデルが期待されていたほどの性能を発揮しない可能性があることが指摘されています。実際、いくつかの時系列予測ベンチマークでは、単純な線形モデルが同等かそれ以上のパフォーマンスを示す場合もあります。とはいえ、線形モデルにも欠点があります。それは、時系列データと時間に依存しない共変量との間の非線形関係をモデル化するには適していない点です。

時系列分析と予測の分野における研究は、次第に2つの方向に分かれています。1つは、Transformerの可能性がまだ十分に発揮されていないと考え、アーキテクチャの効率を改善しようとするもの。もう1つは、線形モデルの弱点を最小限に抑えることに焦点を当てたものです。後者のアプローチを代表するのが、「Long-term Forecasting with TiDE:Time-series Dense Encoder」と題された論文です。この論文では、一般的なベンチマークにおいて、既存のディープラーニングモデルよりも優れた性能を発揮する、シンプルで効率的な時系列予測のためのディープラーニングアーキテクチャが提案されています。このモデルは、多層パーセプトロン (MLP) を基盤にしており、驚くほどシンプルです。自己注意(Self-Attention)メカニズムや回帰層、畳み込み層を使用していないため、Transformerベースの解決策とは異なり、予測期間やコンテキストの長さに対して線形的な計算スケーラビリティを持ちます。

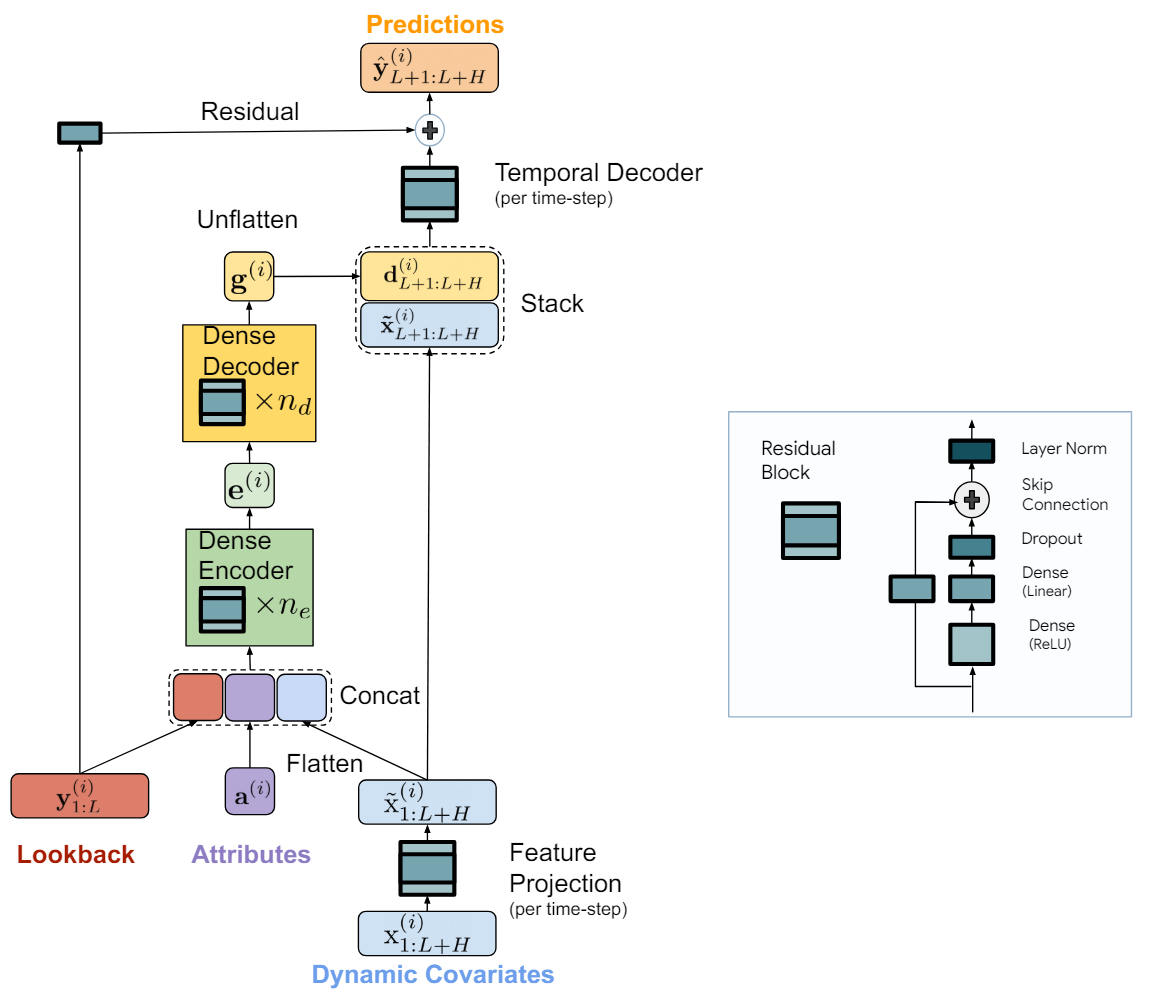
Time-series Dense Encoder (TiDE)モデルは、MLPを使って共変量と過去の時系列データをエンコードし、将来の共変量とともに予測時系列をデコードします。

この手法の著者は、この簡略化された線形モデルであるTiDEを解析し、LDS（線形動的システム）において、設計行列の最大特異値が1でない場合でも、TiDEがほぼ最適な誤差を達成できることを示しました。さらに、この結果はシミュレーションデータでの経験的テストによっても確認されており、線形モデルがLSTMやTarnsformerよりも優れていることが明らかになりました。

一般的な実世界の時系列予測ベンチマークにおいて、TiDEは従来のベースラインとなるニューラルネットワークモデルと比べて、より優れた、あるいは同等の結果を達成しました。さらに、TiDEは最高性能のTransformerベースモデルと比較して、本番環境で5倍速く、訓練では10倍以上の速度を誇ります。

1. TiDEアルゴリズム

TiDE (Time-series Dense Encoder)モデルは、長期時系列予測のためのシンプルで効率的なMLPベースのアーキテクチャです。このアルゴリズムでは、過去のデータや共変量を処理できるように、MLPを用いて非線形性が追加されています。モデルは各データチャンネルに独立して適用され、入力は一度に1つの時系列の過去データと共変量です。モデルの重みは、データセット全体を使ってグローバルに訓練されます。

モデルの重要な構成要素はMLPの閉ループブロックです。MLPは1つの隠れ層とReLU活性化関数を持ち、完全に線形なスキップ接続も含まれています。また、隠れ層から出力へのマッピングをおこなう線形層ではドロップアウトが使用され、出力には正規化層も組み込まれています。

TiDEモデルは論理的にエンコードセクションとデコードセクションに分かれています。エンコードセクションには、特徴射影ステップとそれに続く密なMLPエンコーダが含まれます。デコードセクションでは、密デコーダに続いて時間デコーダが配置されています。密エンコーダと密デコーダは、1つのブロックにまとめることも可能ですが、この手法の著者は異なるサイズの隠れ層を使用しているため、これらを別々のブロックとして扱っています。さらに、デコーダブロックの最後の層はユニークで、その出力サイズは予測期間と一致させる必要があります。

エンコードステップの目的は、時系列の履歴と共変量を密な特徴表現にマッピングすることです。TiDEモデルにおけるエンコードプロセスには、2つの重要なステップがあります。

まず、閉ループブロックを使用して、各時間ステップにおける共変量（過去のコンテキストと予測地平線の両方）を低次元の投影にマッピングします。

次に、すべての過去と未来の共変量をプールして平滑化し、静的な属性と過去の時系列データと組み合わせます。その後、複数の閉ループブロックを含む密エンコーダを使ってこれらを埋め込みにマッピングします。TiDEモデルのデコードプロセスでは、エンコードされた潜在表現を将来の時系列予測にマッピングします。これには、密デコーダと時間デコーダの2つの操作が含まれます。

密デコーダは、エンコーダブロックと同様の複数の閉ループブロックのスタックで構成されており、エンコーダの出力を入力として予測状態のベクトルにマッピングします。

最終的な予測は、時間デコーダを用いて生成されます。時間デコーダは、デコードされたベクトルと予測期間の共変量を組み合わせ、予測地平線の各時間ステップ（t番目）にマッピングする閉ループブロックです。これにより、将来の共変量と時系列予測との間に接続が追加され、特定の時間ステップにおける共変量が実際の値に強く影響する場合に有効です。例えば、暦日ごとのニュースイベントなどが該当します。

時間デコーダの値には、分析された時系列の過去を計画期間ベクトルに線形にマッピングするグローバル残差接続の値を加えます。これにより、純粋な線形モデルは常にTiDEモデルのサブクラスであることが保証されます。

以下は、著者によるこの手法の視覚化です。

モデルはミニバッチ勾配降下法を用いて訓練されます。この手法の著者は、損失関数としてMSEを使用しています。各エポックでは、訓練データから作成できるすべての過去と予測のペアが含まれるため、ミニバッチ間で一部の時間点が重複する場合もあります。

2. MQL5での実装

TiDEアルゴリズムの理論的側面について考察したので、次にMQL5使った実践的な実装に進みましょう。

前述の通り、TiDETiDE手法の主要な構成要素は閉ループブロックです。このブロックでは著者は全結合層を用いていますが、それぞれのブロックは独立したチャンネルに適用されます。ここでのブロックの訓練可能なパラメータは、グローバルに訓練され、すべての多次元時系列チャンネルで共通です。

実装においては、分析対象となる多次元時系列データの各独立チャンネルに対して、並列計算をおこなうことが重要です。以前、同様の状況では、複数の畳み込みフィルターを使用する畳み込み層を用いました。この畳み込み層では、ウィンドウサイズがストライドに等しく、1チャンネルのデータ量に相当します。ここで、畳み込み層のウィンドウサイズは、分析する時系列の履歴の深さに等しいことがポイントです。

畳み込み層を使うところまで来たので、閉ループ畳み込みブロックについて思い出してみましょう。これは、CCMRメソッドを実装するときに作成したものです。注意深く見ると、いくつかの違いがあることに気付くでしょう。例えば、CCMRの実装では正規化層が含まれていましたが、今回の文脈では、この違いを考慮しないことにします。そのため、以前に作成したCResidualConvブロックを使用して、新しいモデルを構築することにします。

これで、提案するTiDEアルゴリズムの基本的な構成要素が完成しました。後は、これらのブロックを組み合わせて、アルゴリズム全体を構築するだけです。

2.1 TiDEアルゴリズムクラス

提案されたアプローチを、新しいクラスCNeuronTiDEOCLに実装してみましょう。このクラスは、ニューラル層の基本クラスであるCNeuronBaseOCLを継承しています。新しいクラスのアーキテクチャでは、以下の4つの主要なパラメータが必要となり、それぞれに対応するローカル変数を宣言します。

• iHistory：分析する時系列履歴の深さ
• iForecast：時系列の予測期間
• iVariables：分析対象となる変数（チャンネル）の数
• iFeatures：時系列に含まれる共変量の数

class CNeuronTiDEOCL :  public CNeuronBaseOCL
  {
protected:
   uint              iHistory;
   uint              iForecast;
   uint              iVariables;
   uint              iFeatures;
   //---
   CResidualConv     acEncoderDecoder[];
   CNeuronConvOCL    cGlobalResidual;
   CResidualConv     acFeatureProjection[2];
   CResidualConv     cTemporalDecoder;
   //---
   CNeuronBaseOCL    cHistoryInput;
   CNeuronBaseOCL    cFeatureInput;
   CNeuronBaseOCL    cEncoderInput;
   CNeuronBaseOCL    cTemporalDecoderInput;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                        CBufferFloat *SecondGradient, 
                                        ENUM_ACTIVATION SecondActivation = None);

public:
                     CNeuronTiDEOCL(void) {};
                    ~CNeuronTiDEOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint history, uint forecast, uint variables, uint features, 
                          uint &encoder_decoder[], ENUM_OPTIMIZATION optimization_type, 
                          uint batch);
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual int       Type(void)        const                      {  return defNeuronTiDEOCL; }
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
  };

ご覧の通り、変数にはエンコーダとデコーダのブロック数は含まれていません。実装では、エンコーダとデコーダをacEncoderDecoder[]ブロックの配列にまとめています。この配列のサイズは、過去のデータをエンコードし、予測された時系列値をデコードするために使用される閉ループブロックの総数を示します。

さらに、時系列共変量の射影は2つのブロックに分割されています（acFeatureProjection[2]）。その一方では、過去のデータをエンコードするための共変量の投影が生成され、もう一方では予測値をデコードします。

加えて、時間デコーダブロックcTemporalDecoderも追加されます。グローバル残差接続には、cGlobalResidual畳み込み層を使用します。

また、中間値を書き込むために4つのローカル全結合層を宣言します。各層の具体的な目的は、実装プロセスで説明されます。

クラス内のすべてのオブジェクトをstaticとして宣言しているため、コンストラクタとデストラクタは空のままにできます。

オーバーライド可能なメソッドのセットは非常に標準的です。いつものように、クラスオブジェクトの初期化メソッドCNeuronTiDEOCL::Initから考え始めましょう。

bool CNeuronTiDEOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint history, 
                          uint forecast, uint variables, uint features, uint &encoder_decoder[],
                          ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, forecast * variables, 
                            optimization_type, batch))
      return false;

パラメータには、必要なアーキテクチャを実装するために必要なすべての情報を受け取ります。メソッド本体では、まず親クラスの同じメソッドを呼び出す。このメソッドは、受け取ったパラメータの最低限必要な制御と、継承したオブジェクトの初期化を実装しています。

親クラスの初期化メソッド操作が正常に実行された後、キー定数の値を保存します。

   iHistory = MathMax(history, 1);
   iForecast = forecast;
   iVariables = variables;
   iFeatures = MathMax(features, 1);

次に内部オブジェクトの初期化に移ります。まず共変量射影ブロックを初期化します。

   if(!acFeatureProjection[0].Init(0, 0, OpenCL, iFeatures, iHistory * iVariables, 1, 
                                                                 optimization, iBatch))
      return false;
   if(!acFeatureProjection[1].Init(0, 1, OpenCL, iFeatures, iForecast * iVariables, 1, 
                                                                 optimization, iBatch))
      return false;

実験では、分析対象の時系列における共変量に関する先験的な知識は使用していません。その代わりに、タイムスタンプの時間高調波をシーケンスに投影しています。これにより、分析された多次元時間チャンネルの各チャンネル（変数）に対して独自の投影を生成します。

密エンコーダとデコーダの隠れ層の次元はencoder_decoder[]配列の形で得られます。この配列のサイズは、エンコーダとデコーダに含まれる閉ループブロックの総数を示しており、配列の各要素の値は対応するブロックの次元を示します。エンコーダへの入力は、過去の時系列データと共変量の投影を連結したベクトルです。デコーダの出力では、予測水平線に対応するベクトルを取得する必要があります。そのためには、デコーダ出力の必要なサイズに合わせたブロックをもう1つ追加する必要があります。

   int total = ArraySize(encoder_decoder);
   if(ArrayResize(acEncoderDecoder, total + 1) < total + 1)
      return false;
   if(total == 0)
     {
      if(!acEncoderDecoder[0].Init(0, 2, OpenCL, 2 * iHistory, iForecast, iVariables,
                                                                 optimization, iBatch))
         return false;
     }
   else
     {
      if(!acEncoderDecoder[0].Init(0, 2, OpenCL, 2 * iHistory, encoder_decoder[0], iVariables, 
                                                                          optimization, iBatch))
         return false;
      for(int i = 1; i < total; i++)
         if(!acEncoderDecoder[i].Init(0, i + 2, OpenCL, encoder_decoder[i - 1], 
                                          encoder_decoder[i], iVariables, optimization, iBatch))
            return false;
      if(!acEncoderDecoder[total].Init(0, total + 2, OpenCL, encoder_decoder[total - 1],
                                                   iForecast, iVariables, optimization, iBatch))
         return false;
     }

次に、時間デコーダブロックとグローバルフィードバック層を初期化します。

   if(!cGlobalResidual.Init(0, total + 3, OpenCL, iHistory, iHistory, iForecast, iVariables, 
                                                                        optimization, iBatch))
      return false;
   cGlobalResidual.SetActivationFunction(TANH);
   if(!cTemporalDecoder.Init(0, total + 4, OpenCL, 2 * iForecast, iForecast, iVariables, 
                                                                        optimization, iBatch))
      return false;

次の2点に注意してください。

1. 時間デコーダは、予測時系列値と予測共変量の投影を連結した行列を入力として受け取ります。このブロックの出力として、調整された予測時系列値を取得します。
2. 各CResidualConvブロックの出力では、データが正規化されます。具体的には、各チャンネルの平均値は0、分散は1になります。グローバル閉ループブロックのデータを比較可能な形にするため、cGlobalResidual層の活性化関数として双曲正接（tanh）を使用します。

次のステップでは、中間データを格納するための補助オブジェクトを初期化します。具体的には、解析した多変量時系列の履歴データをcHistoryInputに、外部プログラムから取得した共変量をcFeatureInputに保存します。

   if(!cHistoryInput.Init(0, total + 5, OpenCL, iHistory * iVariables, optimization, iBatch))
      return false;
   if(!cFeatureInput.Init(0, total + 6, OpenCL, iFeatures, optimization, iBatch))
      return false;

cEncoderInputには、過去のデータと共変量の投影を連結した行列を記述します。

   if(!cEncoderInput.Init(0, total + 7, OpenCL, 2 * iHistory * iVariables, optimization,iBatch))
      return false;

密デコーダの出力は、予測値の共変量と連結され、cTemporalDecoderInputに書き込まれます。

   if(!cTemporalDecoderInput.Init(0, total + 8, OpenCL, 2 * iForecast * iVariables, 
                                                                         optimization, iBatch))
      return false;

クラスオブジェクトの初期化メソッドの最後に、データバッファの入れ替えをおこない、クラスの各要素のデータバッファ間で誤差勾配の余分なコピーを排除します。

   if(cGlobalResidual.getGradient() != Gradient)
      if(!cGlobalResidual.SetGradient(Gradient))
         return false;
   if(cTemporalDecoder.getGradient() != getGradient())
      if(!cTemporalDecoder.SetGradient(Gradient))
         return false;
//---
   return true;
  }

クラスインスタンスの初期化が完了したら、CNeuronTiDEOCL::feedForwardメソッドで説明されているフィードフォワードアルゴリズムの構築に移ります。メソッドのパラメータには、入力データを含む2つのオブジェクトへのポインタを受け取ります。これは過去の多変量時系列データで、前のニューラル層からの結果バッファと、別のデータバッファとして表現された共変量の形をしています。

bool CNeuronTiDEOCL::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   if(!NeuronOCL || !SecondInput)
      return false;

メソッド本体では、受け取ったポインタが適切かどうかを即座に確認します。

次に、受け取った入力データを内部オブジェクトにコピーする必要があります。しかし、全情報量を転送するのではなく、データバッファへのポインタをチェックし、必要であればコピーするだけです。

   if(cHistoryInput.getOutputIndex() != NeuronOCL.getOutputIndex())
     {
      CBufferFloat *temp = cHistoryInput.getOutput();
      if(!temp.BufferSet(NeuronOCL.getOutputIndex()))
         return false;
     }
   if(cFeatureInput.getOutputIndex() != SecondInput.GetIndex())
     {
      CBufferFloat *temp = cFeatureInput.getOutput();
      if(!temp.BufferSet(SecondInput.GetIndex()))
         return false;
     }

準備作業をおこなった後、過去のデータを予測値の次元に投影します。これは一種の自己回帰モデルです。

   if(!cGlobalResidual.FeedForward(NeuronOCL))
      return false;

共変量の過去値と予測値への予測を作成します。

   if(!acFeatureProjection[0].FeedForward(NeuronOCL))
      return false;
   if(!acFeatureProjection[1].FeedForward(cFeatureInput.AsObject()))
      return false;

次に、履歴データと対応する共変量射影行列を連結します。

   if(!Concat(NeuronOCL.getOutput(), acFeatureProjection[0].getOutput(), 
              cEncoderInput.getOutput(), iHistory, iHistory, iVariables))
      return false;

密エンコーダとデコーダブロックの動作のループを作成します。

   uint total = acEncoderDecoder.Size();
   CNeuronBaseOCL *prev = cEncoderInput.AsObject();
   for(uint i = 0; i < total; i++)
     {
      if(!acEncoderDecoder[i].FeedForward(prev))
         return false;
      prev = acEncoderDecoder[i].AsObject();
     }

デコーダの出力と予測値の共変量の射影を連結します。

   if(!Concat(prev.getOutput(), acFeatureProjection[1].getOutput(), 
              cTemporalDecoderInput.getOutput(), iForecast, iForecast, iVariables))
      return false;

連結された行列は時間デコーダブロックに供給されます。

   if(!cTemporalDecoder.FeedForward(cTemporalDecoderInput.AsObject()))
      return false;

フィードフォワード演算の最後に、2つのデータストリームの結果を合計し、その結果を独立したチャンネル間で正規化します。

   if(!SumAndNormilize(cGlobalResidual.getOutput(), cTemporalDecoder.getOutput(), Output, 
                                                                         iForecast, true))
      return false;
//---
   return true;
  }

フィードフォワードパスに続いて、2層からなるバックプロパゲーションパスがおこなわれます。まず、CNeuronTiDEOCL::calcInputGradientsメソッドで、最終結果に対する影響度に従って、すべての内部オブジェクトと外部入力の間に誤差勾配を分配します。パラメータには、入力データの誤差勾配を書き込むためのオブジェクトへのポインタを受け取ります。

bool CNeuronTiDEOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                          CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!cTemporalDecoderInput.calcHiddenGradients(cTemporalDecoder.AsObject()))
      return false;

データバッファのスワッピングを使うので、クラスの誤差勾配からネストしたオブジェクトの関連するバッファにデータをコピーする必要はありません。そこで、ネストしたブロックの誤差勾配分布メソッドを逆の順序で呼び出します。

まず、時間デコーダブロックを通して誤差勾配を伝播させます。演算結果は、密デコーダと予測された時系列共変量の投影に分配されます。

   int total = (int)acEncoderDecoder.Size();
   if(!DeConcat(acEncoderDecoder[total - 1].getGradient(), acFeatureProjection[1].getGradient(),
                cTemporalDecoderInput.getGradient(), iForecast, iForecast, iVariables))
      return false;

その後、密エンコーダとデコーダブロックに誤差勾配を分配します。

   for(int i = total - 2; i >= 0; i--)
      if(!acEncoderDecoder[i].calcHiddenGradients(acEncoderDecoder[i + 1].AsObject()))
         return false;
   if(!cEncoderInput.calcHiddenGradients(acEncoderDecoder[0].AsObject()))
      return false;

密エンコーダの入力データのレベルでの誤差勾配は、多変量時系列の履歴データと対応する共変量にまたがって分布します。

   if(!DeConcat(cHistoryInput.getGradient(), acFeatureProjection[0].getGradient(),
                cEncoderInput.getGradient(), iHistory, iHistory, iVariables))
      return false;

次に、活性化関数の微分によってグローバルフィードバック層の誤差勾配を調整します。

   if(cGlobalResidual.Activation() != None)
     {
      if(!DeActivation(cGlobalResidual.getOutput(), cGlobalResidual.getGradient(),
                       cGlobalResidual.getGradient(), cGlobalResidual.Activation()))
         return false;
     }

誤差勾配を入力データレベルまで下げます。

   if(!NeuronOCL.calcHiddenGradients(cGlobalResidual.AsObject()))
      return false;

ここでは、2番目のデータストリームの誤差勾配も、前の層の活性化関数の導関数で調整します。

   if(NeuronOCL.Activation()!=None)
      if(!DeActivation(cHistoryInput.getOutput(),cHistoryInput.getGradient(),
                       cHistoryInput.getGradient(),SecondActivation))
        return false;

その後、両方のデータストリームから誤差勾配を合計します。

   if(!SumAndNormilize(NeuronOCL.getGradient(), cHistoryInput.getGradient(),
                       NeuronOCL.getGradient(), iHistory, false, 0, 0, 0, 1))
      return false;

この段階で、誤差勾配を多変量時系列の履歴データレベルに伝播させました。次に、誤差勾配を共変量に伝播させる必要があります。

ここで言及しておくべきことは、今回の実験の枠組みでは、このプロセスが必須ではないという点です。共変量には、式で定義されたタイムスタンプの高調波を使用します。この公式は学習過程で調整されることはありません。しかし、「将来への備え」を考慮して、共変量レベルまで勾配を伝播させるプロセスを構築しています。これにより、今後の実験で時系列の共変量を学習するさまざまなモデルを試すことが可能になります。

そこで、過去のデータの共変量から誤差勾配を伝播させます。得られた値は、共変量勾配のバッファに転送されます。

   if(!cFeatureInput.calcHiddenGradients(acFeatureProjection[0].AsObject()))
      return false;
   if(!SumAndNormilize(cFeatureInput.getGradient(), cFeatureInput.getGradient(), SecondGradient,
                                                               iFeatures, false, 0, 0, 0, 0.5f))
      return false;

その後、予測値の共変量の勾配を求め、2つのデータストリームの結果を合計します。

   if(!cFeatureInput.calcHiddenGradients(acFeatureProjection[1].AsObject()))
      return false;
   if(!SumAndNormilize(SecondGradient, cFeatureInput.getGradient(), SecondGradient, iFeatures, 
                                                                          false, 0, 0, 0, 1.0f))
      return false;

必要に応じて、活性化関数の微分の誤差勾配を調整します。

   if(SecondActivation!=None)
      if(!DeActivation(SecondInput,SecondGradient,SecondGradient,SecondActivation))
        return false;
//---
   return true;
  }

バックプロパゲーションパスの第2ステップは、モデルの訓練パラメータを調整することです。この機能は、CNeuronTiDEOCL::updateInputWeightsメソッドに実装されています。このメソッドのアルゴリズムは非常にシンプルです。訓練可能なパラメータを持つすべての内部オブジェクトの対応するメソッドを1つずつ呼び出すだけです。

bool CNeuronTiDEOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
//---
   if(!cGlobalResidual.UpdateInputWeights(cHistoryInput.AsObject()))
      return false;
   if(!acFeatureProjection[0].UpdateInputWeights(cHistoryInput.AsObject()))
      return false;
   if(!acFeatureProjection[1].UpdateInputWeights(cFeatureInput.AsObject()))
      return false;
//---
   uint total = acEncoderDecoder.Size();
   CNeuronBaseOCL *prev = cEncoderInput.AsObject();
   for(uint i = 0; i < total; i++)
     {
      if(!acEncoderDecoder[i].UpdateInputWeights(prev))
         return false;
      prev = acEncoderDecoder[i].AsObject();
     }
//---
   if(!cTemporalDecoder.UpdateInputWeights(cTemporalDecoderInput.AsObject()))
      return false;
//---
   return true;
  }

ファイルの操作方法について一言加えたいと思います。ディスク容量を節約するため、キー定数と訓練可能なパラメータを持つオブジェクトのみを保存します。

bool CNeuronTiDEOCL::Save(const int file_handle)
  {
   if(!CNeuronBaseOCL::Save(file_handle))
      return false;
//---
   if(FileWriteInteger(file_handle, (int)iHistory, INT_VALUE) < INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle, (int)iForecast, INT_VALUE) < INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle, (int)iVariables, INT_VALUE) < INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle, (int)iFeatures, INT_VALUE) < INT_VALUE)
      return false;
//---
   uint total = acEncoderDecoder.Size();
   if(FileWriteInteger(file_handle, (int)total, INT_VALUE) < INT_VALUE)
      return false;
   for(uint i = 0; i < total; i++)
      if(!acEncoderDecoder[i].Save(file_handle))
         return false;
   if(!cGlobalResidual.Save(file_handle))
      return false;
   for(int i = 0; i < 2; i++)
      if(!acFeatureProjection[i].Save(file_handle))
         return false;
   if(!cTemporalDecoder.Save(file_handle))
      return false;
//---
   return true;
  }

しかし、これはデータロードメソッドCNeuronTiDEOCL::Load のアルゴリズムに若干の複雑さをもたらします。以前と同様に、このメソッドはデータをロードするためのファイルハンドルをパラメータとして受け取ります。まず、親オブジェクトのデータをロードします。

bool CNeuronTiDEOCL::Load(const int file_handle)
  {
   if(!CNeuronBaseOCL::Load(file_handle))
      return false;

 次に、キー定数の値を読み込みます。

   if(FileIsEnding(file_handle))
      return false;
   iHistory = (uint)FileReadInteger(file_handle);
   if(FileIsEnding(file_handle))
      return false;
   iForecast = (uint)FileReadInteger(file_handle);
   if(FileIsEnding(file_handle))
      return false;
   iVariables = (uint)FileReadInteger(file_handle);
   if(FileIsEnding(file_handle))
      return false;
   iFeatures = (uint)FileReadInteger(file_handle);
   if(FileIsEnding(file_handle))
      return false;

次に、密エンコーダとデコーダブロックからデータをロードする必要があります。ここで最初のニュアンスに遭遇します。データファイルからブロックスタックのサイズを読み取ります。acEncoderDecoder配列の現在のサイズより大きくても小さくてもかまいません。必要であれば、配列のサイズを調整します。

   int total = FileReadInteger(file_handle);
   int prev_size = (int)acEncoderDecoder.Size();
   if(prev_size != total)
      if(ArrayResize(acEncoderDecoder, total) < total)
         return false;

次に、ループを実行してファイルからブロックデータを読み込みます。しかし、追加された配列要素のデータをロードするメソッドを呼び出す前に、それらを初期化する必要があります。以前に作成されたオブジェクトは、前のステップで初期化されているため、これは適用されません。

   for(int i = 0; i < total; i++)
     {
      if(i >= prev_size)
         if(!acEncoderDecoder[i].Init(0, i + 2, OpenCL, 1, 1, 1, ADAM, 1))
            return false;
      if(!LoadInsideLayer(file_handle, acEncoderDecoder[i].AsObject()))
         return false;
     }

次に、グローバル残差、共変量投影、時間デコーダのオブジェクトをロードします。ここではすべてが単純明快です。

   if(!LoadInsideLayer(file_handle, cGlobalResidual.AsObject()))
      return false;
   for(int i = 0; i < 2; i++)
      if(!LoadInsideLayer(file_handle, acFeatureProjection[i].AsObject()))
         return false;
   if(!LoadInsideLayer(file_handle, cTemporalDecoder.AsObject()))
      return false;

この時点で、すべての保存データをロードした。しかし、まだ補助オブジェクトがあり、クラスの初期化アルゴリズムと同様に初期化します。

   if(!cHistoryInput.Init(0, total + 5, OpenCL, iHistory * iVariables, optimization, iBatch))
      return false;
   if(!cFeatureInput.Init(0, total + 6, OpenCL, iFeatures, optimization, iBatch))
      return false;
   if(!cEncoderInput.Init(0, total + 7, OpenCL, 2 * iHistory * iVariables, optimization,iBatch))
      return false;
   if(!cTemporalDecoderInput.Init(0, total + 8, OpenCL, 2 * iForecast * iVariables,optimization,
                                                                                        iBatch))
      return false;

必要であれば、データバッファを交換します。

   if(cGlobalResidual.getGradient() != Gradient)
      if(!cGlobalResidual.SetGradient(Gradient))
         return false;
   if(cTemporalDecoder.getGradient() != getGradient())
      if(!cTemporalDecoder.SetGradient(Gradient))
         return false;
//---
   return true;
  }

この新しいクラスのすべてのメソッドの完全なコードは、以下の添付ファイルにあります。そこには、この記事で説明しなかったクラスの補助メソッドもあります。アルゴリズムは非常にシンプルなので、自分で勉強することができます。モデルの訓練アーキテクチャの検討に移りましょう。

2.2 訓練用モデルアーキテクチャ

お察しの通り、新しいTiDEメソッドクラスが環境状態エンコーダアーキテクチャに追加されました。同様に、時系列の将来の状態を予測するために、これまでに検討されたすべてのアルゴリズムについても同じことをおこないました。覚えているように、CreateEncoderDescriptionsメソッドでエンコーダのアーキテクチャを記述します。このメソッドのパラメータには、作成するモデルのアーキテクチャを記述するための動的配列オブジェクトへのポインタが渡されます。

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

メソッド本体では、受け取ったポインタを確認し、必要であれば動的配列オブジェクトの新しいインスタンスを生成します。

端末から受信した生の履歴データをモデルに供給します。

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

データはバッチ正規化層で前処理され、比較可能な形式に変換されます。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

環境の状態を表す過去のデータを収集しながら、ローソク足の文脈でデータを形成します。TiDE法のアルゴリズムは、各特徴の独立したチャンネルの文脈でデータを分析することを意味します。以前に収集した経験再生バッファを新しいモデルの訓練に活用できるように、データ収集ブロックの再設計はおこなわれませんでした。その代わりに、入力データを必要な形に変換するためのデータ転置層を追加します。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

次に、TiDEメソッドが実装された新しい層が登場します。

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTiDEOCL;

分析における独立チャネルの数は、環境状態のローソク足1本を記述するベクトルのサイズに等しくなります。

   descr.count = BarDescr;

分析履歴の深さと予測期間は、対応する定数によって決定されます。

   descr.window = HistoryBars;
   descr.window_out = NForecast;

タイムスタンプは、年、月、週、日の4つの高調波のベクトルとして表現されます。

   descr.step = 4;

密エンコーダデコーダブロックのアーキテクチャは、クラスを構築するときに説明したように、値の配列として指定されます。

   {
      int windows[]={HistoryBars,2*EmbeddingSize,EmbeddingSize,2*EmbeddingSize,NForecast};
      if(ArrayCopy(descr.windows,windows)<=0)
        return false;
   }

すべての活性化関数はクラスの内部オブジェクトで指定されているので、ここでは指定しません。

   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

データはCNeuronTiDEOCL正規化されることに注意が必要です。予測値のバイアスを補正するために、独立したチャンネル内で単純な線形バイアス関数を実行する活性化関数のない畳み込み層を使用します。

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   descr.step = NForecast;
   descr.window_out = NForecast;
   descr.activation=None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

次に、予測値を入力データ表現の次元に転置します。

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

入力データの分布の統計変数を返します。

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = BarDescr*NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

環境状態エンコーダのアーキテクチャが変更されたため、注意すべき点が2つあります。1つ目は、環境の予測値の隠れ状態抽出層へのポインタです。

#define        LatentLayer             4

2つ目は、この隠された状態の大きさです。前回の記事では、状態エンコーダの出力は、過去のデータと予測値の記述でした。今回は予測値のみです。したがって、ActorとCriticのモデルアーキテクチャを適切に調整する必要があります。

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic)
  {
//---
........
........
//--- Actor
........
........
//--- layer 2-12
   for(int i = 0; i < 10; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronCrossAttenOCL;
        {
         int temp[] = {1, BarDescr};
         ArrayCopy(descr.units, temp);
        }
        {
         int temp[] = {EmbeddingSize, NForecast};
         ArrayCopy(descr.windows, temp);
        }
      descr.window_out = 32;
      descr.step = 4;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!actor.Add(descr))
        {
         delete descr;
         return false;
        }
     }
........
........
//--- Critic
........
........
//--- layer 2-12
   for(int i = 0; i < 10; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronCrossAttenOCL;
        {
         int temp[] = {1, BarDescr};
         ArrayCopy(descr.units, temp);
        }
        {
         int temp[] = {EmbeddingSize, NForecast};
         ArrayCopy(descr.windows, temp);
        }
      descr.window_out = 32;
      descr.step = 4;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!critic.Add(descr))
        {
         delete descr;
         return false;
        }
     }
........
........
//---
   return true;
  }

この実装では、ActorとCriticのモデルにおいてTransformerのアルゴリズムを使用していることに注意してください。また、予測値の独立したチャネルに対してクロスアテンションを実施します。しかし、ローソク足の文脈で予測値へのクロスアテンションを使用する実験も可能です。これを実施することに決めた場合は、エンコーダの隠れ状態層へのポインタ、分析されたオブジェクトの数、および1つのオブジェクトの説明ウィンドウのサイズを変更することを忘れないでください。

2.3 状態エンコーダ学習アドバイザー

次の段階はモデルの訓練です。ここで、モデル訓練EAのアルゴリズムに改良が必要です。まず第一に、これは環境状態エンコーダモデルでの作業に関するものであり、新しいクラスがこのモデルに追加されたからです。今回は、モデル訓練用EA「...\Experts\TiDE\StudyEncoder.mq5」のメソッドの詳細な説明は省略します。ここでは、モデルの訓練メソッドである「Train」のみに注目してみましょう。

//+------------------------------------------------------------------+
//| Train function                                                   |
//+------------------------------------------------------------------+
void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);
//---
   vector<float> result, target;
   bool Stop = false;
//---
   uint ticks = GetTickCount();

メソッドの始まりは、以前の記事で説明したアルゴリズムに従います。準備作業も含まれています。

この後、モデルの訓練ループが続きます。ループの本体では、経験再生バッファから軌跡とその状態をサンプリングします。

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * 
                               (Buffer[tr].Total - 2 - NForecast));
      if(i <= 0)
        {
         iter--;
         continue;
        }

前回同様、環境の状態を表す過去のデータを読み込みます。

      bState.AssignArray(Buffer[tr].States[i].state);

しかし今は、予測値を生成するために、より多くの共変量データが必要です。モデルを構築する際、環境状態のタイムスタンプ高調波を使用することにしました。モデルが過去と予測値への投影を学習することを期待しましょう。

タイムスタンプハーモニックバッファを用意しましょう。

      bTime.Clear();
      double time = (double)Buffer[tr].States[i].account[7];
      double x = time / (double)(D'2024.01.01' - D'2023.01.01');
      bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_MN1);
      bTime.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_W1);
      bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_D1);
      bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      if(bTime.GetIndex() >= 0)
         bTime.BufferWrite();

Environment State Encoderのフィードフォワードパスメソッドを呼び出せるようになりました。

      //--- State Encoder
      if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, 
                                          (CBufferFloat*)GetPointer(bTime)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

次に、前回同様、目標値を用意します。

      //--- Collect target data
      if(!Result.AssignArray(Buffer[tr].States[i + NForecast].state))
         continue;
      if(!Result.Resize(BarDescr * NForecast))
         continue;

エンコーダのバックプロパゲーションメソッドを呼ビ出します。

      if(!Encoder.backProp(Result, GetPointer(bTime), GetPointer(bTimeGradient)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

ここで注意すべきは、バックプロパゲーションパスメソッドのパラメータには、ターゲット値に加えて、タイムスタンプ高調波とその誤差勾配のバッファへのポインタを指定する必要があるということです。一見すると、誤差勾配を使用せず、勾配の代わりに高調波そのもののバッファで代用することも可能に思えますが、調和誤差の勾配は今後使用しないため、高調波自体も次の反復で書き直されます。では、なぜメモリ上に余分なバッファを作る必要があるのでしょうか。

しかし、この軽率な行動には注意が必要です。誤差勾配を伝播させた後にモデルのパラメータを調整する際、各層はその層の出力と入力データの誤差勾配を使用します。したがって、タイムスタンプ高調波を誤差勾配で上書きすると、過去のデータと予測状態の共変量に対する投影パラメータを更新する際に、歪んだ重み勾配が得られることになります。その結果、モデルパラメータの調整が歪んでしまい、モデルの訓練が予測できない方向に進む可能性があります。

エンコーダのフィードフォワードとバックワードパス操作が正常に完了したら、訓練の進捗状況をユーザーに通知し、訓練ループの次の反復に移ります。

      if(GetTickCount() - ticks > 500)
        {
         double percent = double(iter) * 100.0 / (Iterations);
         string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", percent, 
                                                         Encoder.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

モデル訓練プロセスは、指定された回数のループ反復が完了するまで繰り返されます。この数値はループの外部パラメータで指定されます。訓練終了後、銘柄チャートのコメント欄を消去します。

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder",
                                                        Encoder.getRecentAverageError());
   ExpertRemove();
//---
  }

訓練結果の情報を端末のログに出力し、EAを終了させます。

また、Actor and Criticモデル訓練EA「...\Experts\TiDE\Study.mq5」も修正されますが、その詳細については今は触れません。上記の説明に基づけば、EAコードの中から似たようなブロックを簡単に見つけることができます。完全なEAコードは添付ファイルにあります。添付ファイルには、環境との相互作用や訓練データの収集に関するEAも含まれており、同様の編集が施されています。

3. テスト

新しい時系列予測手法であるTime-series Dense Encoder (TiDE)を学びました。MQL5を使用して、この提案されたアプローチのビジョンを実装しました。

前述の通り、以前のモデルの入力データの構造を保持しているため、過去に収集したデータを用いて新しいモデルを訓練できます。

すべてのモデルは、EURUSD銘柄のH1時間枠の履歴データを使用して訓練されています。時間の経過とともに、EAの使用期間も変化します。現時点では、モデルの訓練には2023年からの実際の履歴データを使用しています。訓練済みモデルは、MetaTrader 5のストラテジーテスターで2024年1月のデータを使ってテストされます。テスト期間は訓練期間に続き、訓練データセットに含まれていない新しいデータに対するモデルの性能を評価します。同時に、モデル学習時には物理的に未知であった新たに入力されたデータに対してリアルタイムで実行されるモデル運用期間にも、非常に類似した条件を提供することを目指しています。

これまでの多くの記事と同様に、環境状態エンコーダモデルは口座の状態やポジションから独立しています。したがって、環境との相互作用が1回だけの訓練サンプルであっても、将来の状態を予測する精度を得るまでモデルを訓練することが可能です。当然ながら、「望ましい予測精度」はモデルの能力を超えることはできません。無理をしても意味はありません。

環境状態を予測するモデルの訓練を終えた後、次の段階であるActorの行動方策の訓練に移ります。このステップでは、ActorモデルとCriticモデルを繰り返し訓練し、一定の期間ごとに経験再生バッファを更新します。

経験再生バッファの更新とは、Actorの現在の行動方策に基づいて、環境との相互作用経験を追加収集することを意味します。私たちが研究している金融市場の環境は非常に多面的であるため、経験再生バッファにはそのすべてを完全に集めることはできません。Actorの現在の政策行動が捉える環境はほんの一部に過ぎません。このデータを分析することで、Actorの行動方策を最適化するための小さな一歩を踏み出します。このセグメントの境界線に近づくと、更新されたActor方策からわずかに可視エリアを広げて追加データを収集する必要があります。

こうした繰り返しの結果、訓練データセットとテストデータセットの両方で利益を生み出せるActor方策を訓練しました。

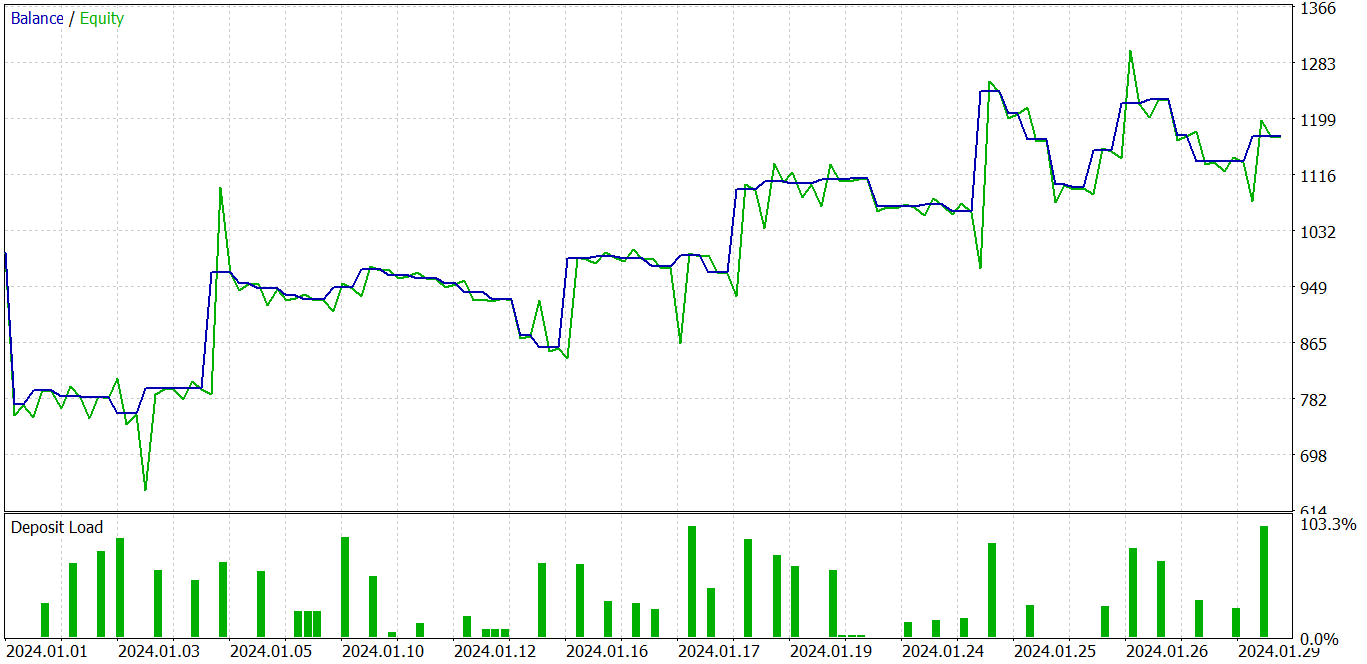
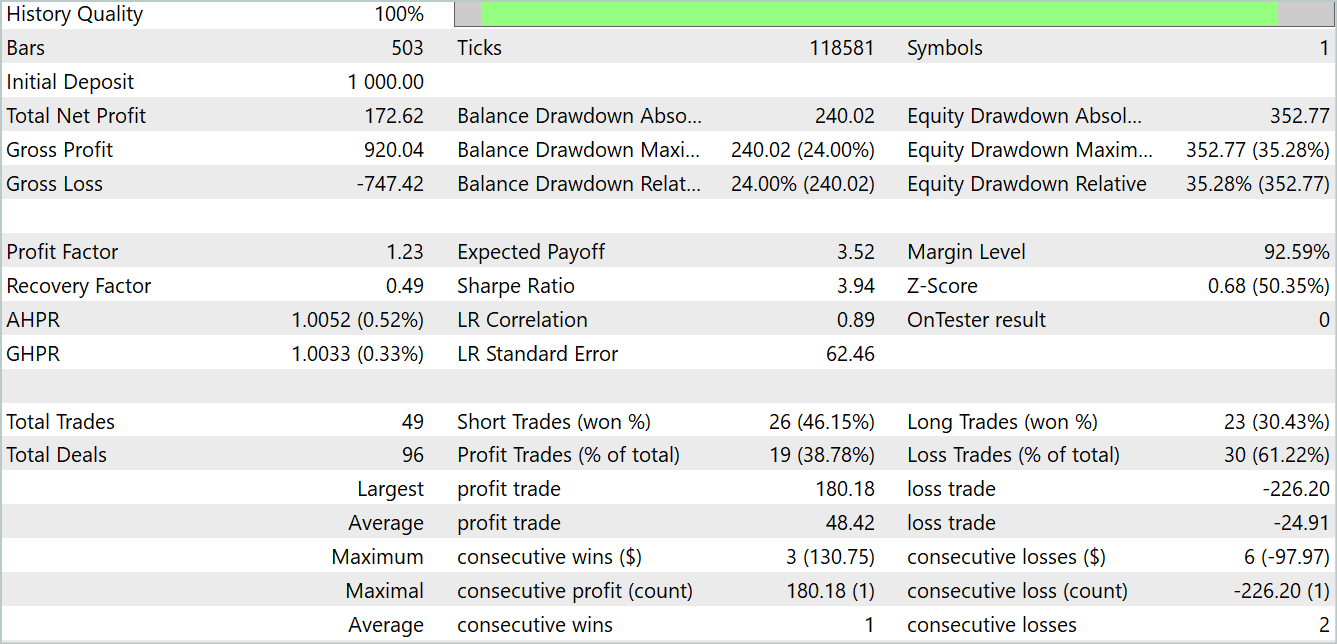
上のチャートでは、最初に負け取引があり、その後明確な利益トレンドに変化しています。収益性の高い取引の割合は40％未満ですが、利益が出ている取引1件につき、ほぼ2件の負け取引があります。しかし、不採算取引は採算取引よりもかなり小さいことが観察されます。平均的な利益取引は、平均的な損失取引のほぼ2倍の額です。このような要因により、テスト期間中に利益を上げることが可能となりました。テスト結果によると、プロフィットファクターは1.23でした。

結論

この記事では、時系列の長期予測用に設計されたオリジナルのTiDE (Time-series Dense Encoder)モデルに触れました。このモデルは古典的な線形モデルやTransformerとは異なり、多層パーセプトロン（MLP）を過去のデータと共変量の符号化、さらには将来の予測の復号化の両方に使用しています。

本手法の著者による実験は、MLPモデルの使用が時系列分析と予測の問題を解決する上で大きな可能性を秘めていることを実証しました。さらに、TiDEはTransformerとは異なり、線形計算複雑度を持つため、大量のデータを扱う際に効率的です。

この記事の実用的な部分では、提案されたアプローチのビジョンをオリジナルとは少し異なる形で実装しました。それにもかかわらず、得られた結果は、提案されたアプローチが非常に効率的であることを証明しています。また、モデルの訓練プロセスは、先に説明したTransformerよりもはるかに速いことが分かりました。

参照文献

• Long-term Forecasting with TiDE:Time-series Dense Encoder
• この連載の他の記事記事

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	コレクションEAの例
2	ResearchRealORL.mq5	EA	Real-ORL法による事例収集のためのEA
3	Study.mq5	EA	モデル訓練EA
4	StudyEncoder.mq5	EA	エンコード訓練EA
5	Test.mq5	EA	モデルをテストするEA
6	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
7	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
8	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ