神经网络变得简单（第 88 部分）：时间序列密集编码器（TiDE）

MetaTrader 5 — 交易系统 | 27 一月 2025, 10:03

188

Dmitriy Gizlyk

概述

可能所有已知的神经网络架构都已根据其解决时间序列预测问题的能力进行了研究，包括递归、卷积、和图形模型。由基于变换器架构的模型展现出的结果最值得关注。本系列文章中还呈现了若干种这样的算法。不过，最近的研究表明，基于变换器的架构也许没有预期的那么强大。在某些时间序列预测基准上，简单的线性模型能展示出相当、甚至更好的性能。然而，不幸的是，这种线性模型存在缺点，若时间序列的协变量与时间无关，则其不适合为非线性关系建模。

时间序列分析和预测领域的进一步研究分为两个方向。一些人看中尚未完全发挥潜力的变换器，并正致力于提高该类架构的效率。其他人则尝试把线性模型的缺点最小化。标题为《搭配 TiDE 进行长期预测：时间序列密集编码器》的论文所指正是第二个方向。本文针对时间序列预测提出了一种简单高效的深度学习架构，在流行的基准中，该架构达成的性能优于现有的深度学习模型。所提出的基于多层感知器（MLP）的模型超简单，且不包括自关注机制、递归层或卷积层。因此，与许多基于变换器的解决方案不同，它在上下文长度和预测横向范围层面，具有线性计算可扩展性。

时间序列密集编码器（TiDE）模型利用 MLP 针对以往时间序列和协变量一同编码，并配合未来协变量一起，解码预测时间序列。

该方法的作者分析了简化的线性模型 TiDE，并展现出当 LDS 设计矩阵的最大奇异值不同于 1 时，该线性模型能在线性动态系统（LDS）中达成近乎最优的误差。依据模拟数据的测试，它们得到实证：线性模型的性能优于 LSTM 和变换器。

依据流行的真实世界时间序列预测基准，相比以前的基线神经网络模型，TiDE 达成了更好或相似的结果。同时，TiDE 的生产速度比基于变换器的最佳模型快 5 倍，训练速度快 10 倍以上。

1. TiDE 算法

TiDE（Time-series Dense Encoder — 时间序列密集编码器）模型是一种简单高效的基于 MLP 的架构，进行长期时间序列预测。该算法的作者以 MLP 的形式添加了非线性，如此它们就能处理过去的数据和协变量。该模型应用于独立的数据通道，即模型输入是一条时间序列的某个过去时刻、及协变量。在这种情况下，模型权重依据整个数据集进行全局训练，即它们对于所有独立通道都是相同的。

该模型的关键组件是 MLP 闭环模块。MLP 有一个隐藏层和 ReLU 激活。它还有一个完全线性的跳接。该方法的作者在线性层上使用 Dropout,，将隐藏层映射到输出端，并在输出端使用归一化层。

TiDE 模型在逻辑上分为编码和解码部分。编码器部分包含一个特征投影步骤，后跟一个密集 MLP 编码器。解码部分由一个密集解码器，后随一个时态解码器组成。密集编码器和密集解码器可以组合到一个模块。不过，该方法的作者将它们分开，因为它们在两个模块中使用了不同大小的隐藏层。此外，解码器模块的最后一层是唯一的：其输出大小必须与规划横向范围匹配。

编码步骤的目标是将时间序列的历史记录和协变量映射到密集特征表示。TiDE 模型中的编码有两个关键步骤。

最初，使用闭环模块将每个时间步长（在历史背景和预测横向范围内）的协变量映射到低维投影。

然后，我们将所有过去和未来投影协变量进行汇集和平滑处理，并将它们与静态属性和过去的时间序列相结合。之后，我们用包含多个闭环模块的密集编码器，将它们映射到一个嵌入。TiDE 模型中的解码将编码的潜在表示映射到时间序列的未来预测值。它还包括两个操作：密集解码器和时态解码器。

密集解码器是若干闭环模块的一个堆叠，类似于编码器模块。它取编码器的输出作为输入，并将其映射到预测状态的向量。

模型输出使用时态解码器生成最终预测。时态解码器是相同的闭环模块，将已解码向量映射到预测横向范围的第 t 个时间步长，并结合预测区间的投影协变量。该操作在未来协变量与时间序列预测之间添加了连接。如果某些协变量在特定时间步上对实际值具有很强的直接影响，这可能很实用。例如，单一日历日的新闻背景。

对于时态解码器的数值，我们加上全局残差连接的数值，其会把过去已分析时间序列线性映射到规划横向范围向量。这确保了纯线性模型始终是 TiDE 模型的子类。

作者对该方法的可视化如下表示。

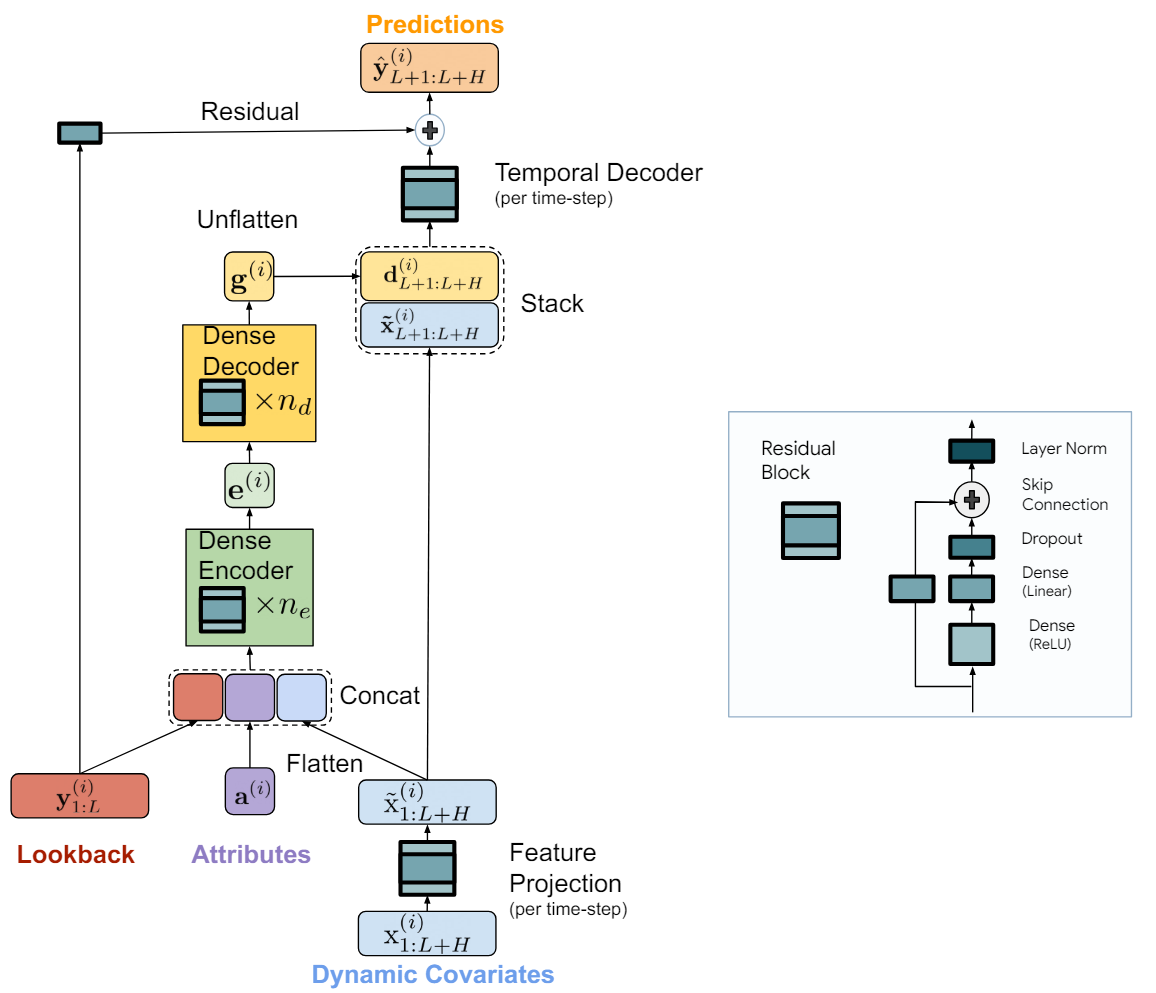
该模型采用小批量梯度下降进行训练。该方法的作者利用 MSE 作为损失函数。每局次包括依据训练区间构造的以往所有对和预测横向范围。因此，两个小批量就能重叠时间点。

2. 利用 MQL5 实现

我们已研究了 TiDE 算法的理论层面。现在我们可以转到利用 MQL5 实施这些方式的实现。

如上所述，我们正在研究的 TiDE 方法的主要 “构建模块” 是一个闭环模块。在该模块中，该方法的作者使用了全连接层。不过，注意模型中这样的每个模块都被应用到分开的独立通道。在这种情况下，模块的可训练参数是经全局性训练，并且对于所分析多维时间序列的所有通道都相同。

当然，在我们的实现中，我们希望针对正在分析的多维时间序列的所有独立通道实现并行计算。在类似情况下，我们之前采用的是带有多个卷积滤波器的卷积层。这种卷积层的窗口大小等于它的步幅，与一个通道的数据量相对应。我认为这很明显，它等于所分析时间序列历史的深度。

既然我们已经到了使用卷积层的地步，那我们回顾一下我们在实现 CCMR 方法时创建的闭环卷积模块。如果您认真阅读过，您也许注意到差异：CCMR 实现用到了归一化层。不过，在本文的上下文中，我决定忽略模块架构中的这种差异。因此，我们将使用之前创建的 CResidualConv 模块来构建一个新模型。

如此，我们得到所提议 TiDE 算法的基本“构建模块”。现在我们需要由这些模块组装整个算法。

2.1TiDE 算法类

我们在新的 CNeuronTiDEOCL 类中实现所提议方式，它继承自神经层基类 CNeuronBaseOCL。我们新类的架构需要 4 个关键参数，我们将为其声明局部变量：

iHistory – 所分析时间序列的历史深度
iForecast – 时间序列预测横向范围
iVariables – 所分析变量（通道）的数量
iFeatures – 时间序列中的协变量数量

class CNeuronTiDEOCL :  public CNeuronBaseOCL
  {
protected:
   uint              iHistory;
   uint              iForecast;
   uint              iVariables;
   uint              iFeatures;
   //---
   CResidualConv     acEncoderDecoder[];
   CNeuronConvOCL    cGlobalResidual;
   CResidualConv     acFeatureProjection[2];
   CResidualConv     cTemporalDecoder;
   //---
   CNeuronBaseOCL    cHistoryInput;
   CNeuronBaseOCL    cFeatureInput;
   CNeuronBaseOCL    cEncoderInput;
   CNeuronBaseOCL    cTemporalDecoderInput;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                        CBufferFloat *SecondGradient, 
                                        ENUM_ACTIVATION SecondActivation = None);

public:
                     CNeuronTiDEOCL(void) {};
                    ~CNeuronTiDEOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint history, uint forecast, uint variables, uint features, 
                          uint &encoder_decoder[], ENUM_OPTIMIZATION optimization_type, 
                          uint batch);
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual int       Type(void)        const                      {  return defNeuronTiDEOCL; }
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
  };

如您所见，这些变量不包括模型的编码器或解码器的模块数量。在我们的实现中，我们将编码器和解码器组合成一个 acEncoderDecoder[] 模块数组。该数组的大小将指定为编码历史数据和解码预测时间序列值的闭环模块的总数。

此外，我们将时间序列协变量的投影切分为 2 个模块（acFeatureProjection[2]）。在其中之一，我们将生成协变量的投影来编码历史数据；而在第二个里 - 解码预测值。

我们还将添加一个时态解码器模块 cTemporalDecoder。对于全局残差连接，我们将使用 cGlobalResidual 卷积层。

此外，我们声明了 4 个局部全连接层来写入中间值。在实现过程中会说明每一层的具体目的。

我们已经将类中的所有对象声明为静态，这允许我们将类构造函数和析构函数留“空”。

可重写方法集都非常标准。如常，我们首先研究类对象初始化方法 CNeuronTiDEOCL::Init。

bool CNeuronTiDEOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint history, 
                          uint forecast, uint variables, uint features, uint &encoder_decoder[],
                          ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, forecast * variables, 
                            optimization_type, batch))
      return false;

在参数中，该方法接收实现所需架构的所有必要信息。在方法主体中，我们首先调用父类的相同方法，其针对收到的参数和继承对象的初始化，实现最小必要控制。

父类初始化方法执行操作成功后，我们保存关键常量的数值。

   iHistory = MathMax(history, 1);
   iForecast = forecast;
   iVariables = variables;
   iFeatures = MathMax(features, 1);

然后我们转至初始化内部对象。首先，我们初始化协变量投影模块。

   if(!acFeatureProjection[0].Init(0, 0, OpenCL, iFeatures, iHistory * iVariables, 1, 
                                                                 optimization, iBatch))
      return false;
   if(!acFeatureProjection[1].Init(0, 1, OpenCL, iFeatures, iForecast * iVariables, 1, 
                                                                 optimization, iBatch))
      return false;

请注意，在我们的实验中，我们没有用到任何有关所分析时间序列的协变量的先验知识。取而代之，我们将时间戳的时间谐量投影到序列上。在如此行事中，我们为所分析多维时间通道的每个通道（变量）生成自己的投影。

我们以 encoder_decoder[] 数组的形式获得密集编码器和解码器的隐藏层的维度。数组大小表示编码器和解码器中闭环模块的总数。数组元素的数值表示相应模块的维度。记住，编码器的输入是历史时间序列数据与协变量投影的级联向量。在解码器的输出端，我们需要获得与预测横向范围相对应的向量。为了满足后者，我们在解码器的输出处添加另一个所需大小的模块。

   int total = ArraySize(encoder_decoder);
   if(ArrayResize(acEncoderDecoder, total + 1) < total + 1)
      return false;
   if(total == 0)
     {
      if(!acEncoderDecoder[0].Init(0, 2, OpenCL, 2 * iHistory, iForecast, iVariables,
                                                                 optimization, iBatch))
         return false;
     }
   else
     {
      if(!acEncoderDecoder[0].Init(0, 2, OpenCL, 2 * iHistory, encoder_decoder[0], iVariables, 
                                                                          optimization, iBatch))
         return false;
      for(int i = 1; i < total; i++)
         if(!acEncoderDecoder[i].Init(0, i + 2, OpenCL, encoder_decoder[i - 1], 
                                          encoder_decoder[i], iVariables, optimization, iBatch))
            return false;
      if(!acEncoderDecoder[total].Init(0, total + 2, OpenCL, encoder_decoder[total - 1],
                                                   iForecast, iVariables, optimization, iBatch))
         return false;
     }

接下来，我们初始化时态解码器模块和全局反馈层。

   if(!cGlobalResidual.Init(0, total + 3, OpenCL, iHistory, iHistory, iForecast, iVariables, 
                                                                        optimization, iBatch))
      return false;
   cGlobalResidual.SetActivationFunction(TANH);
   if(!cTemporalDecoder.Init(0, total + 4, OpenCL, 2 * iForecast, iForecast, iVariables, 
                                                                        optimization, iBatch))
      return false;

注意以下两点：

时态解码器接收所预测时间序列数值和预测协变量投影的级联矩阵作为输入。在模块的输出端，我们会收到调整后的所预测时间序列数值。
在每个 CResidualConv 模块的输出端，数据被归一化：每个通道的平均值等于 “0”，方差等于 “1”。为了将全局闭环模块的数据转换为可比较的形式，我们将使用双曲正切（tanh）作为 cGlobalResidual 层的激活函数。

在下一步中，我们初始化存储中间数据的辅助对象。我们将所分析多员时间序列的历史数据，以及从外部程序获得的协变量分别保存在 cHistoryInput 和 cFeatureInput 当中。

   if(!cHistoryInput.Init(0, total + 5, OpenCL, iHistory * iVariables, optimization, iBatch))
      return false;
   if(!cFeatureInput.Init(0, total + 6, OpenCL, iFeatures, optimization, iBatch))
      return false;

我们在 cEncoderInput 中编写历史数据和协变量投影的级联矩阵。

   if(!cEncoderInput.Init(0, total + 7, OpenCL, 2 * iHistory * iVariables, optimization,iBatch))
      return false;

密集解码器的输出将与预测值协变量级联，并写入 cTemporalDecoderInput。

   if(!cTemporalDecoderInput.Init(0, total + 8, OpenCL, 2 * iForecast * iVariables, 
                                                                         optimization, iBatch))
      return false;

在类对象初始化方法的末尾，我们将交换数据缓冲区，以便剔除在类中各个元素的数据缓冲区之间额外复制误差梯度。

   if(cGlobalResidual.getGradient() != Gradient)
      if(!cGlobalResidual.SetGradient(Gradient))
         return false;
   if(cTemporalDecoder.getGradient() != getGradient())
      if(!cTemporalDecoder.SetGradient(Gradient))
         return false;
//---
   return true;
  }

类实例初始化完成后，我们转到构造前馈算法，如 CNeuronTiDEOCL::feedForward 方法中所述。在方法参数中，我们接收指向 2 个包含输入数据的对象指针。这是历史多元时间序列数据，其形式为来自前一个神经层的结果缓冲区，及表示为单独数据缓冲区的协变量。

bool CNeuronTiDEOCL::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   if(!NeuronOCL || !SecondInput)
      return false;

在方法主体中，我们立即检查收到的指针是否相关。

接下来，我们需要将接收到的输入数据复制到内部对象之中。不过，取代传送全部信息，我们仅检查指向数据缓冲区的指针，并在必要时复制它们。

   if(cHistoryInput.getOutputIndex() != NeuronOCL.getOutputIndex())
     {
      CBufferFloat *temp = cHistoryInput.getOutput();
      if(!temp.BufferSet(NeuronOCL.getOutputIndex()))
         return false;
     }
   if(cFeatureInput.getOutputIndex() != SecondInput.GetIndex())
     {
      CBufferFloat *temp = cFeatureInput.getOutput();
      if(!temp.BufferSet(SecondInput.GetIndex()))
         return false;
     }

准备工作完毕，我们将历史数据投影到预测值的维度之中。这是一种自回归模型。

   if(!cGlobalResidual.FeedForward(NeuronOCL))
      return false;

我们生成历史和预测值的协变量投影。

   if(!acFeatureProjection[0].FeedForward(NeuronOCL))
      return false;
   if(!acFeatureProjection[1].FeedForward(cFeatureInput.AsObject()))
      return false;

然后，我们将历史数据与相应的协变量投影矩阵连接起来。

   if(!Concat(NeuronOCL.getOutput(), acFeatureProjection[0].getOutput(), 
              cEncoderInput.getOutput(), iHistory, iHistory, iVariables))
      return false;

创建密集编码器和解码器模块的操作循环。

   uint total = acEncoderDecoder.Size();
   CNeuronBaseOCL *prev = cEncoderInput.AsObject();
   for(uint i = 0; i < total; i++)
     {
      if(!acEncoderDecoder[i].FeedForward(prev))
         return false;
      prev = acEncoderDecoder[i].AsObject();
     }

我们将解码器的输出与预测值协变量的投影连接起来。

   if(!Concat(prev.getOutput(), acFeatureProjection[1].getOutput(), 
              cTemporalDecoderInput.getOutput(), iForecast, iForecast, iVariables))
      return false;

级联矩阵被投喂到时间解码器模块。

   if(!cTemporalDecoder.FeedForward(cTemporalDecoderInput.AsObject()))
      return false;

在前馈操作结束时，我们将 2 个数据流的结果相加，并跨越独立通道对出品的结果归一化。

   if(!SumAndNormilize(cGlobalResidual.getOutput(), cTemporalDecoder.getOutput(), Output, 
                                                                         iForecast, true))
      return false;
//---
   return true;
  }

前馈通验之后是反向传播通验，它由 2 层组成。首先，我们根据 CNeuronTiDEOCL::calcInputGradients 方法中，根据最终结果对其影响，在所有内部对象和外部输入之间分派误差梯度。在参数中，该方法接收指向对象的指针，用于写入输入数据的误差梯度。

bool CNeuronTiDEOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                          CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!cTemporalDecoderInput.calcHiddenGradients(cTemporalDecoder.AsObject()))
      return false;

由于我们用到了数据缓冲区的交换，因此无需将数据从类的误差梯度复制到嵌套对象的相应缓冲区之中。故此，我们以逆向顺序调用嵌套模块的误差梯度分布方法。

首先，我们通过时态解码器模块传播误差梯度。我们将跨越密集解码器和所预测时间序列协变量的投影分派运算结果。

   int total = (int)acEncoderDecoder.Size();
   if(!DeConcat(acEncoderDecoder[total - 1].getGradient(), acFeatureProjection[1].getGradient(),
                cTemporalDecoderInput.getGradient(), iForecast, iForecast, iVariables))
      return false;

之后，我们将误差梯度分派到密集编码器和解码器模块之中。

   for(int i = total - 2; i >= 0; i--)
      if(!acEncoderDecoder[i].calcHiddenGradients(acEncoderDecoder[i + 1].AsObject()))
         return false;
   if(!cEncoderInput.calcHiddenGradients(acEncoderDecoder[0].AsObject()))
      return false;

密集编码器输入数据层级的误差梯度被分派到跨越多元时间序列和相应协变量的历史数据之中。

   if(!DeConcat(cHistoryInput.getGradient(), acFeatureProjection[0].getGradient(),
                cEncoderInput.getGradient(), iHistory, iHistory, iVariables))
      return false;

接下来，我们通过激活函数的导数来调整全局反馈层的误差梯度。

   if(cGlobalResidual.Activation() != None)
     {
      if(!DeActivation(cGlobalResidual.getOutput(), cGlobalResidual.getGradient(),
                       cGlobalResidual.getGradient(), cGlobalResidual.Activation()))
         return false;
     }

输入数据层级的误差梯度更低。

   if(!NeuronOCL.calcHiddenGradients(cGlobalResidual.AsObject()))
      return false;

此处我们还将通过上一层激活函数的导数来调整第二个数据流的误差梯度。

   if(NeuronOCL.Activation()!=None)
      if(!DeActivation(cHistoryInput.getOutput(),cHistoryInput.getGradient(),
                       cHistoryInput.getGradient(),SecondActivation))
        return false;

之后，我们将两个数据流的误差梯度相加。

   if(!SumAndNormilize(NeuronOCL.getGradient(), cHistoryInput.getGradient(),
                       NeuronOCL.getGradient(), iHistory, false, 0, 0, 0, 1))
      return false;

在该阶段，我们已将误差梯度传播到多元时间序列的历史数据层级。现在我们需要将误差梯度传播到协变量。

此处应当说，于我们正在进行的实验框架内，这个过程是不必要的。对于协变量，我们采用由公式给出的时间戳谐量。在学习期间，该公式不会进行调整。不过，我们创建了一个将梯度传播到协变量层级的过程，且会留意“面向未来”。在后续的实验中，我们能够尝试学习时间序列协变量的不同模型。

故此，我们传播来自历史数据协变量的误差梯度。获得的数值将传送到协变量梯度缓冲区。

   if(!cFeatureInput.calcHiddenGradients(acFeatureProjection[0].AsObject()))
      return false;
   if(!SumAndNormilize(cFeatureInput.getGradient(), cFeatureInput.getGradient(), SecondGradient,
                                                               iFeatures, false, 0, 0, 0, 0.5f))
      return false;

之后，我们获得已预测值的协变量的梯度，并将 2 个数据流的结果相加。

   if(!cFeatureInput.calcHiddenGradients(acFeatureProjection[1].AsObject()))
      return false;
   if(!SumAndNormilize(SecondGradient, cFeatureInput.getGradient(), SecondGradient, iFeatures, 
                                                                          false, 0, 0, 0, 1.0f))
      return false;

如有必要，我们会针对激活函数导数的误差调整梯度。

   if(SecondActivation!=None)
      if(!DeActivation(SecondInput,SecondGradient,SecondGradient,SecondActivation))
        return false;
//---
   return true;
  }

反向传播传递的第二步是调整模型的训练参数。该功能在 CNeuronTiDEOCL::updateInputWeights 方法中实现。该方法算法十分简单。我们简单地逐一调用具有可训练参数的所有内部对象的相应方法。

bool CNeuronTiDEOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
//---
   if(!cGlobalResidual.UpdateInputWeights(cHistoryInput.AsObject()))
      return false;
   if(!acFeatureProjection[0].UpdateInputWeights(cHistoryInput.AsObject()))
      return false;
   if(!acFeatureProjection[1].UpdateInputWeights(cFeatureInput.AsObject()))
      return false;
//---
   uint total = acEncoderDecoder.Size();
   CNeuronBaseOCL *prev = cEncoderInput.AsObject();
   for(uint i = 0; i < total; i++)
     {
      if(!acEncoderDecoder[i].UpdateInputWeights(prev))
         return false;
      prev = acEncoderDecoder[i].AsObject();
     }
//---
   if(!cTemporalDecoder.UpdateInputWeights(cTemporalDecoderInput.AsObject()))
      return false;
//---
   return true;
  }

我想说几句文件操作方法。为了节省磁盘空间，我们仅保存可训练参数的关键常量和对象。

bool CNeuronTiDEOCL::Save(const int file_handle)
  {
   if(!CNeuronBaseOCL::Save(file_handle))
      return false;
//---
   if(FileWriteInteger(file_handle, (int)iHistory, INT_VALUE) < INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle, (int)iForecast, INT_VALUE) < INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle, (int)iVariables, INT_VALUE) < INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle, (int)iFeatures, INT_VALUE) < INT_VALUE)
      return false;
//---
   uint total = acEncoderDecoder.Size();
   if(FileWriteInteger(file_handle, (int)total, INT_VALUE) < INT_VALUE)
      return false;
   for(uint i = 0; i < total; i++)
      if(!acEncoderDecoder[i].Save(file_handle))
         return false;
   if(!cGlobalResidual.Save(file_handle))
      return false;
   for(int i = 0; i < 2; i++)
      if(!acFeatureProjection[i].Save(file_handle))
         return false;
   if(!cTemporalDecoder.Save(file_handle))
      return false;
//---
   return true;
  }

不过，这会导致数据加载方法 CNeuronTiDEOCL::Load 的算法变得复杂。如前，该方法在参数中接收一个加载数据文件的句柄。首先，我们加载父对象数据。

bool CNeuronTiDEOCL::Load(const int file_handle)
  {
   if(!CNeuronBaseOCL::Load(file_handle))
      return false;

然后我们读取关键常量的数值。

   if(FileIsEnding(file_handle))
      return false;
   iHistory = (uint)FileReadInteger(file_handle);
   if(FileIsEnding(file_handle))
      return false;
   iForecast = (uint)FileReadInteger(file_handle);
   if(FileIsEnding(file_handle))
      return false;
   iVariables = (uint)FileReadInteger(file_handle);
   if(FileIsEnding(file_handle))
      return false;
   iFeatures = (uint)FileReadInteger(file_handle);
   if(FileIsEnding(file_handle))
      return false;

接下来，我们需要从密集编码器和解码器模块加载数据。此处，我们遇到了第一个细微差别。我们从数据文件中读取模块堆叠大小。它可能大于或小于 acEncoderDecoder 数组的当前尺寸。如有必要，我们调整数组大小。

   int total = FileReadInteger(file_handle);
   int prev_size = (int)acEncoderDecoder.Size();
   if(prev_size != total)
      if(ArrayResize(acEncoderDecoder, total) < total)
         return false;

接下来，我们运行一个循环，并从文件中读取模块数据。不过，在调用方法加载添加数组元素数据之前，我们需要初始化它们。这不适用于以前创建的对象，因为它们已在早前的步骤中初始化。

   for(int i = 0; i < total; i++)
     {
      if(i >= prev_size)
         if(!acEncoderDecoder[i].Init(0, i + 2, OpenCL, 1, 1, 1, ADAM, 1))
            return false;
      if(!LoadInsideLayer(file_handle, acEncoderDecoder[i].AsObject()))
         return false;
     }

接下来，我们加载全局残差、协变量投影、和时态解码器对象。此处的一切都直截了当。

   if(!LoadInsideLayer(file_handle, cGlobalResidual.AsObject()))
      return false;
   for(int i = 0; i < 2; i++)
      if(!LoadInsideLayer(file_handle, acFeatureProjection[i].AsObject()))
         return false;
   if(!LoadInsideLayer(file_handle, cTemporalDecoder.AsObject()))
      return false;

此刻，我们已经加载了所有保存的数据。但我们仍有辅助对象，我们像类初始化算法一样初始化它们。

   if(!cHistoryInput.Init(0, total + 5, OpenCL, iHistory * iVariables, optimization, iBatch))
      return false;
   if(!cFeatureInput.Init(0, total + 6, OpenCL, iFeatures, optimization, iBatch))
      return false;
   if(!cEncoderInput.Init(0, total + 7, OpenCL, 2 * iHistory * iVariables, optimization,iBatch))
      return false;
   if(!cTemporalDecoderInput.Init(0, total + 8, OpenCL, 2 * iForecast * iVariables,optimization,
                                                                                        iBatch))
      return false;

如有必要，交换数据缓冲区。

   if(cGlobalResidual.getGradient() != Gradient)
      if(!cGlobalResidual.SetGradient(Gradient))
         return false;
   if(cTemporalDecoder.getGradient() != getGradient())
      if(!cTemporalDecoder.SetGradient(Gradient))
         return false;
//---
   return true;
  }

这个新类的所有方法的完整代码在下面的附件中提供。在那里，您还能找到本文中未讨论的类辅助方法。它们的算法非常简单，因此您可自行研究它们。我们转到研究模型训练架构。

2.2进行训练的模型架构

您也许已经猜到了，新的 TiDE 方法类已被添加到环境状态编码器架构之中。我们对之前研究过的所有预测时间序列未来状态的算法所做相同。如您所知，我们在 CreateEncoderDescriptions 方法中描述了编码器架构。在方法参数中，我们收到一个指向动态数组对象的指针，用于写入我们正在创建的模型的架构。

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

在方法主体中，我们检查收到的指针，并在必要时创建动态数组对象的新实例。

我们把自终端接收的原始历史数据投喂给模型。

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

数据在批量归一化层中进行预处理，并在其中转换为可比较的形式。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

在收集描述环境状态的历史数据时，我们形成蜡条上下文数据。TiDE 方法算法意味着在单个特征的独立通道的上下文中分析数据。为了预留先前收集的经验回放缓冲区来训练新模型的可能性，我们没有重新设计数据收集模块。取而代之，我们添加了一个数据转置层，将输入数据转换为所需的形式。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

接下来是我们的新层，其中实现了 TiDE 方法。

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTiDEOCL;

分析中独立通道的数量等于描述环境状态的一根烛条的向量大小。

   descr.count = BarDescr;

所分析历史的深度和预测横向范围由相应的常量判定。

   descr.window = HistoryBars;
   descr.window_out = NForecast;

我们的时间戳由 4 个谐量的向量表示：年、月、周、和日。

   descr.step = 4;

密集编码器-解码器模块的架构被指定为数值数组，如构造类时所解释的那样。

   {
      int windows[]={HistoryBars,2*EmbeddingSize,EmbeddingSize,2*EmbeddingSize,NForecast};
      if(ArrayCopy(descr.windows,windows)<=0)
        return false;
   }

所有激活函数都在类的内部对象中指定，故我们在此不用指定它们。

   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

注意，数据在 CNeuronTiDEOCL 层内被多次归一化。为了校正预测值的乖离，我们将用到一个没有激活函数的卷积层，它在独立通道内执行简单的线性乖离函数。

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   descr.step = NForecast;
   descr.window_out = NForecast;
   descr.activation=None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

然后，我们将预测值转置到输入数据表示的维度中。

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

返回输入数据分布的统计变量。

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = BarDescr*NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

由于环境状态编码器架构发生了变化，因此有 2 点需要注意。第一个是指向环境预测值的隐藏状态提取层的指针。

#define        LatentLayer             4

第二个是这个隐藏状态的大小。在上一篇文章中，状态编码器的输出是历史数据和预测值的描述。这次我们仅有预测值。因此，我们需要对扮演者和评论者模型架构进行相应的调整。

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic)
  {
//---
........
........
//--- Actor
........
........
//--- layer 2-12
   for(int i = 0; i < 10; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronCrossAttenOCL;
        {
         int temp[] = {1, BarDescr};
         ArrayCopy(descr.units, temp);
        }
        {
         int temp[] = {EmbeddingSize, NForecast};
         ArrayCopy(descr.windows, temp);
        }
      descr.window_out = 32;
      descr.step = 4;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!actor.Add(descr))
        {
         delete descr;
         return false;
        }
     }
........
........
//--- Critic
........
........
//--- layer 2-12
   for(int i = 0; i < 10; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronCrossAttenOCL;
        {
         int temp[] = {1, BarDescr};
         ArrayCopy(descr.units, temp);
        }
        {
         int temp[] = {EmbeddingSize, NForecast};
         ArrayCopy(descr.windows, temp);
        }
      descr.window_out = 32;
      descr.step = 4;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!critic.Add(descr))
        {
         delete descr;
         return false;
        }
     }
........
........
//---
   return true;
  }

请注意，在该实现中，我们仍然在扮演者和评论者模型中使用变换器算法。我们还针对预测值的独立通道实现了交叉关注。不过，您也可以试验在蜡烛上下文中使用针对已预测值的交叉关注。如果您决定这样做，不要忘记更改指向编码器隐藏状态层的指针，以及所分析对象的数量，及一个对象的描述窗口大小。

2.3状态编码器学习智能系统

下一阶段是训练模型。于此，我们需要对模型训练 EA 的算法加以改进。首先，这与搭配环境状态编码器模型操作有关。因为新类已添加到该模型之中。在本文中，我不会提供模型训练 EA “...\Experts\TiDE\StudyEncoder.mq5” 的详解。我们仅专注于模型训练方法 'Train'。

//+------------------------------------------------------------------+
//| Train function                                                   |
//+------------------------------------------------------------------+
void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);
//---
   vector<float> result, target;
   bool Stop = false;
//---
   uint ticks = GetTickCount();

该方法的开头遵循前面文章中讨论的算法。它包含准备工作。

后随模型训练循环。在循环主体中，我们从经验回放缓冲区取样轨迹及据其的状态。

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * 
                               (Buffer[tr].Total - 2 - NForecast));
      if(i <= 0)
        {
         iter--;
         continue;
        }

如前，我们加载描述环境状态的历史数据。

      bState.AssignArray(Buffer[tr].States[i].state);

但现在我们需要更多的协变量数据来生成预测值。在构造模型时，我们决定使用环境状态的时间戳谐量。我们希望该模型能够依据历史值和预测值学习其投影。

我们准备一个时间戳谐量缓冲区。

      bTime.Clear();
      double time = (double)Buffer[tr].States[i].account[7];
      double x = time / (double)(D'2024.01.01' - D'2023.01.01');
      bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_MN1);
      bTime.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_W1);
      bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_D1);
      bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      if(bTime.GetIndex() >= 0)
         bTime.BufferWrite();

现在我们可以调用环境状态编码器的前馈通验方法。

      //--- State Encoder
      if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, 
                                          (CBufferFloat*)GetPointer(bTime)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

接下来，如前，我们准备目标值。

      //--- Collect target data
      if(!Result.AssignArray(Buffer[tr].States[i + NForecast].state))
         continue;
      if(!Result.Resize(BarDescr * NForecast))
         continue;

我们调用编码器的反向传播方法。

      if(!Encoder.backProp(Result, GetPointer(bTime), GetPointer(bTimeGradient)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

于此应当注意的是，在反向传播方法的参数中，除了目标值之外，我们还指定了指向时间戳谐量缓冲区、及其误差梯度的指针。初看，我们未用到误差梯度，并且可用谐量缓冲区的替身取代梯度。因为我们在进一步的工作中不使用谐量误差的梯度。还有，谐量替身将在下一次迭代中重写。那么为什么要在内存中创建一个额外的缓冲区呢？

但我想警告您不要轻率地采取这种做法。传播误差梯度后，我们调整模型参数。为了调整权重，每个层都在层的输出和输入数据里用到误差梯度。因此，如果我们用误差梯度覆盖时间戳谐量，那么当依据历史数据和预测状态的协变量更新投影参数时，我们将得到失真的权重梯度。接踵而至，我们将得到模型参数的失真调整。在这种情况下，模型训练将朝着不可预测的方向进行。

在编码器的前馈和后馈通验操作成功完成后，我们会通知用户训练进度，并转到训练循环的下一次迭代。

      if(GetTickCount() - ticks > 500)
        {
         double percent = double(iter) * 100.0 / (Iterations);
         string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", percent, 
                                                         Encoder.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

重复模型训练过程，直到完成指定数量的循环迭代。该数字在循环的外部参数中指定。完成训练后，我们清除品种图表上的注释区域。

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder",
                                                        Encoder.getRecentAverageError());
   ExpertRemove();
//---
  }

我们将有关训练结果的信息输出到终端日志，并启动 EA 终止。

相关修改也在扮演者和评论者模型训练 EA “...\Experts\TiDE\Study.mq5” 中进行。不过，我们现在不再赘述它们。基于上面提供的描述，您可以在 EA 代码中轻松找到类似的模块。完整的 EA 代码可在附件中找到。该附件还包含与环境交互的 EA，和训练数据集合，其中包含类似的编辑。

3. 测试

我们已经领略了一种预测时间序列的新方法：时间序列密集编码器（TiDE）。我们已利用 MQL5 实现了提议方法的愿景。

如前所述，我们预留了以前模型中输入数据的结构，故我们能用以前收集的数据来训练新模型。

我要提醒您，所有模型都采用 EURUSD 品种， H1 时间帧的历史数据进行训练。随着时间的推移，我们的 EA 的区间也会发生变化。此刻，我采用 2023 年的真实历史数据来训练我的模型。然后采用 2024 年 1 月的数据在 MetaTrader 5 策略测试器中测试已训练模型。测试区间跟在训练区间之后，从而评估模型在新数据上的性能，新数据不包括在训练数据集当中。同时，我们希望为模型运行期间提供非常相似的条件，它实时运行所依据的新接收数据，其在模型训练时物理未知。

与之前的许多文章一样，环境状态编码器模型与账户状态和持仓无关。因此，我们甚至可以依据训练样本来训练模型，只需与环境进行一次交互，直到获得预测未来状态所需的准确性。自然而然，“所需的预测准确性”不能超过模型的能力。您不能从自己的头顶跳过。

预测环境状态的模型训练完毕之后，我们转到第二阶段 — 训练扮演者行为政策。在该步骤中，我们将迭代训练扮演者和评论者模型，并在特定时段更新经验回放缓冲区。

更新经验回放缓冲区是指环境交互经验的额外集合，同时考虑到扮演者的当前行为政策。因为我们研究的金融市场环境是相当多方面的。故此，我们无法在经验回放缓冲区中完整收集它的所有表现形式。我们只是捕获扮演者当前政策动作的一个小环境。通过分析这些数据，我们朝着优化扮演者的行为政策迈出了一小步。当接近此区段的边界时，我们需要通过将可见区域略微扩展到已更新扮演者政策之外来收集额外数据。

作为这些迭代的结果，我训练了一个能够在训练和测试数据集上均产生盈利的扮演者政策。

模型测试结果

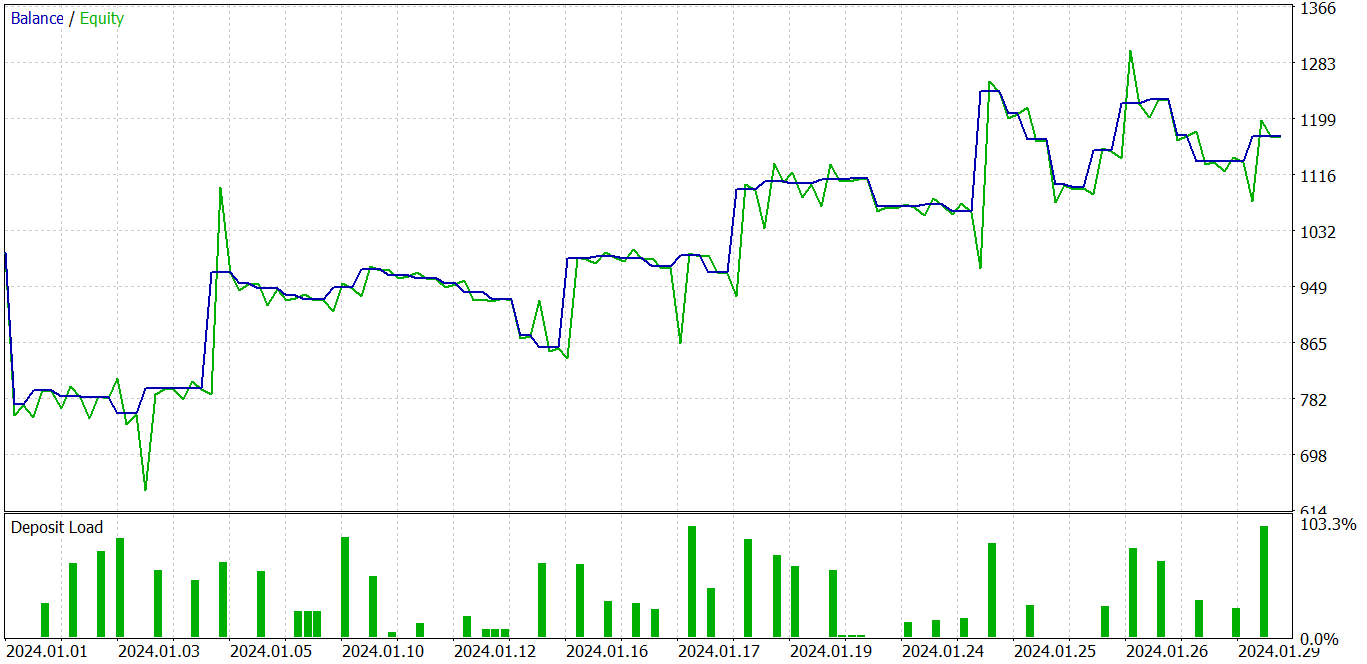
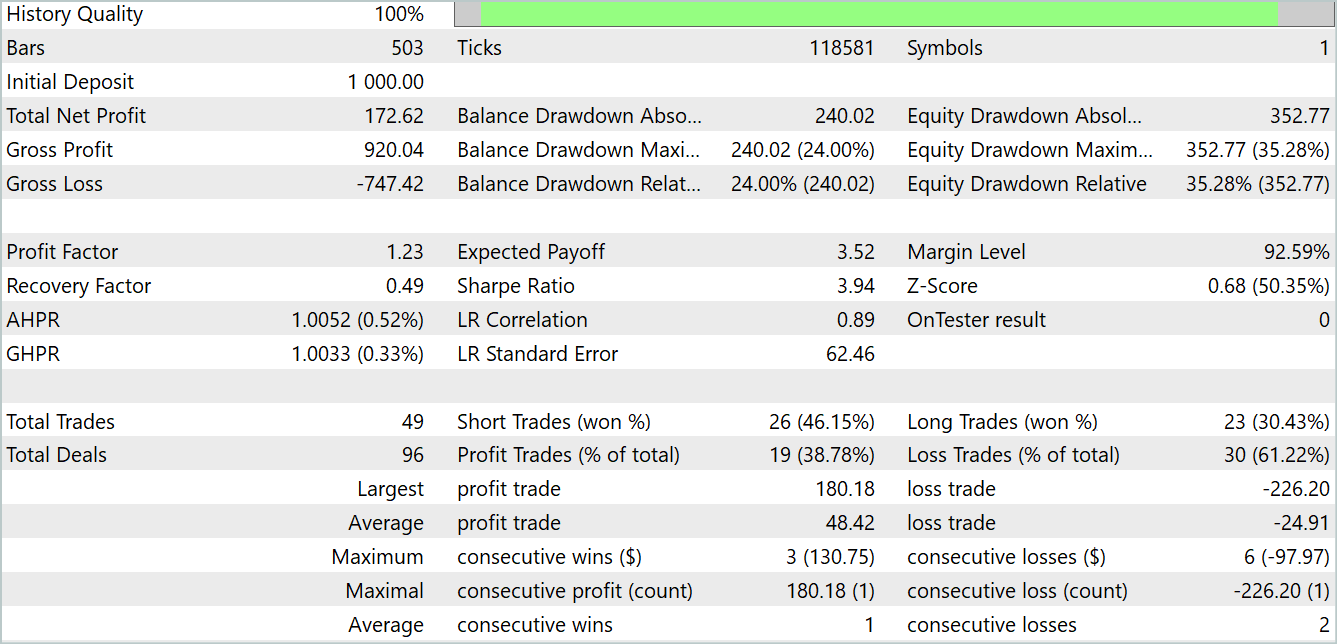
在上面图表中，我们看到一开始是亏损交易，然后转变为明显的盈利趋势。盈利交易的份额低于 40%。每 2 笔盈利交易几乎有 1 笔亏损交易。然而，我们观察到无盈利交易明显小于有盈利交易。平均盈利交易几乎是平均亏损交易的 2 倍。所有这些都令模型能够在测试期间获利。根据测试结果，盈利因子为 1.23。

结束语

在本文中，我们领略了原始的 TiDE（时间密集编码器）模型，该模型专为时间序列的长期预测而设计。该模型不同于经典的线性模型和转换器，因为它使用多层感知器（MLP）为过去的数据和协变量进行编码，并用于解码未来的预测。

该方法作者进行的实验表明，使用 MLP 模型在解决时间序列分析和预测问题方面具有巨大潜力。此外，与变换器不同，TiDE 具有线性计算复杂性，这令它在处理大数据时效率更高。

在本文的实践部分，我们已实现了对所提议方法的愿景，其与原方案略有不同。无论如何，所获结果证明，所提议的方式相当有效。此外，模型训练过程比前面讨论过的变换器快得多。

参考

文中所用程序

#	名称	类型	说明
1	Research.mq5	EA	样本收集 EA
2	ResearchRealORL.mq5	EA	运用 Real-ORL 方法收集示例的 EA
3	Study.mq5	EA	模型训练 EA
4	StudyEncoder.mq5	EA	编码训练 EA
5	Test.mq5	EA	模型测试 EA
6	Trajectory.mqh	类库	系统状态定义结构
7	NeuroNet.mqh	类库	创建神经网络的类库
8	NeuroNet.cl	代码库	OpenCL 程序代码库