知っておくべきMQL5ウィザードのテクニック（第31回）：損失関数の選択

はじめに

MQL5ウィザードは、この連載で紹介したように、さまざまなアイデアを試す実験台として機能します。時には、複数の実装方法を持つカスタムシグナルが登場することがあります。このシナリオは、学習率に関する2つの記事やバッチ正規化について触れた最後の記事でも見られました。それぞれのテーマが、複数のカスタムシグナルの可能性を示したように、損失関数も複数の形式が存在し、同様の状況にあります。

テスト結果を目標と比較する方法は1つではありません。MQL5で利用できる14種類の損失関数(ENUM_LOSS_FUNCTION)の列挙を考えると、それぞれが機械学習の訓練において独自の方法を提供しているというわけではないかもしれません。しかし重要なのは、それぞれに微妙な違いがあり、これらの違いが、訓練するネットワークやアルゴリズムの特性に応じて慎重に選択されるべきであるという点です。

損失関数に加えて、ENUM_REGRESSION_METRICを利用することも可能ですが、これは統計的な指標であり、学習後にアルゴリズムのパフォーマンスを評価するために適しているため、この記事では取り上げません。特に、最終的な出力が複数の次元を持つ場合、このメトリクスは非常に有用です。しかし、今回は目的関数に焦点を当てて議論を進めます。

適切な損失尺度の選択は極めて重要です。なぜなら、ニューラルネットワーク（本記事で扱う機械学習アルゴリズム）は、回帰器や分類器のようなカテゴリに分類される場合があり、また教師あり学習や教師なし学習のように異なるタイプにも分類されるからです。さらに、強化学習のような手法は、損失関数の利用と適用において多面的なアプローチが必要になることもあります。

つまり、損失関数が多様な形式を持つ理由は、単に種類が多いからというだけではなく、解くべき「問題」自体（ニューラルネットワークの種類）が多様だからです。損失関数は、訓練において、テストされたパラメータが目標からどれだけずれているかを定量化することで、その問題解決に貢献します。

教師あり学習の損失関数は直感的に理解できますが、教師なし学習の理想的な損失関数というのは少し異なるアプローチが必要になります。例えば、コホネンマップやクラスタリングのような教師なし学習においても、データ間の距離やギャップを測定する際には標準化された基準が必要であり、損失関数はこの役割を担っています。

損失関数の概要

MQL5では、損失関数を定量化するために最大14種類の手法が提供されています。応用例を検討する前に、これらのすべてについて簡単に説明しておきます。ここで重要なポイントは、損失がスカラー値ではなくベクトルとして扱われ、損失勾配を表す点です。また、これらの数式を実装するMQL5のコードは、すべて内蔵のベクトル関数から実行されるため、共有されることはありません。様々な損失関数をテストするための簡単なスクリプトを以下に示します。

#property  script_show_inputs
input ENUM_LOSS_FUNCTION __loss = LOSS_HUBER;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
      vector _a = {1.0, 2.0, 4.0};
      vector _b = {4.0, 12.0, 36.0 };
      
      vector _loss = _a.LossGradient(_b,__loss); 
      
      printf(__FUNCSIG__+" for: "+EnumToString(__loss));
      Print(" loss gradient is: ",_loss);
      PrintFormat(" while loss is: %.5f. ",_a.Loss(_b,__loss));
  }
//+------------------------------------------------------------------+

まずは 損失平均二乗誤差です。この損失関数は非常に広く使用されており、その目的は予測値と目標値（実測値）の差を二乗して測定することです。これにより、誤差の大きさを数値化します。これは、誤差が常に正になることを保証し（大きさに焦点を当て）、二乗することで大きな誤差に対して大きなペナルティを課します。さらに、MSEは対象となる変数の二乗単位で表されるため、解釈が比較的容易です。その計算式を以下に示します。

ここで

• nは目的変数と比較変数の次元サイズ（通常、これらの変数はベクトル形式）
• iはベクトル空間内のインデックス
• y^ は出力または予測ベクトル
• yはターゲットベクトル

その長所は、大きな誤差に敏感であることと、勾配が滑らかなので勾配降下最適化手法に適していることです。短所は外れ値に敏感なことでしょう。

次は 損失平均-絶対誤差(Mean absolute error)（英語）関数です。これもMSEと同様に広く使われている損失関数で、誤差の大きさに注目し、方向は考慮しません。上記のMSEとの違いは、二乗をおこなわないため、大きな値に特別な重みを与えないことです。二乗をおこなわないため、誤差の単位がターゲットベクトルの単位と一致し、MSEよりも解釈が容易になります。この式は上記のものと似ていますが、次のようになります。

ここで

• n、i、y、y^は、上記のMSEと同じ値を表します

主な利点は、二乗をおこなわないため外れ値や大きな誤差の影響を受けにくい点と、目標の単位を維持しやすく解釈が簡単である点です。しかし、勾配の挙動はMSEほど滑らかではありません。微分すると、出力が+1.0、-1.0、またはゼロのいずれかになるため、これらが交互に繰り返され、MSEのように学習プロセスがスムーズに収束しにくくなります。特に回帰の場面では、この点が問題になる可能性があります。また、すべての誤差を等しく扱うことは、収束プロセスにおいてある程度不利に働くこともあります。

次は、カテゴリカルクロスエントロピー(categorical cross entropy)（英語）です。これは、厳密な多次元空間において、予測された確率分布と実際の確率分布との間の差を測定する損失関数です。MQL5の損失関数アルゴリズムでは、MAEやMSEをベクトル出力として利用し、それらの個々の誤差が合計されないため、多次元的な扱いとなりますが、その式が示唆するように、これらの誤差は簡単にスカラーとして扱うこともできます。一方、カテゴリカルクロスエントロピー(CCE)は、常に多次元的な出力を持ちます。この計算式は次のようになります。

ここで

• Nはクラス数またはデータポイントのベクトルサイズ
• yは実測値または目標値
• pは予測値またはネットワーク出力値
• logは自然対数

CCEは本来回帰器ではなく分類器向けの損失関数であり、特に学習時にデータセットの分類に複数のクラスが存在する場合に適しています。主にグラフィックや画像処理の分野で使われますが、取引への応用も考えられないわけではありません。CCEの特筆すべき点は、との相性が非常に良いことです。ソフトマックスは、入力値を正規化して、それらの総和が1となる確率分布を出力します。これにより、特定のデータポイントがどのクラスに属するかの確率を計算するという目的に適しています。CCEの重要な要素の一つは、対数成分が自信のある不正確な予測を、自信のない予測よりも重く罰することです。これは、ワンホットエンコーディングという実践から生じるもので、目標値は正規化され、正しいクラスには完全な重み（通常1.0）が与えられ、それ以外のクラスには0が割り当てられます。CCEは最適化の際に滑らかな勾配を提供し、誤った予測には上記のようなペナルティ効果があるため、モデルがより自信を持って正確な予測をおこなうよう促します。クラス間の母集団の大きさが不均衡な中で訓練をおこなう場合、競技場を均等にするために重み付け調整を実施することができます。しかし、あまりに多くのクラスが提示された場合、過剰適合の危険性があるため、モデルが鑑定すべきクラスの数を決定する際には予防措置を講じる必要があります。

次は 二値エントロピー関数(BCE)です。BCEもまた、複数のクラスを扱うのが得意なCCEとは異なり、2クラスの設定において予測値と目標値とのギャップを定量化します。この損失関数の出力は0.0から1.0の範囲に制限されており、以下の式によって導かれます：

ここで

• 上記の他の損失関数と同様、Nはサンプルサイズ
• yは予測値
• pは予測値
• logは自然対数

BCEにおいては、2つのクラスは通常ポジティブクラスとネガティブクラスと呼ばれます。したがって、本質的にBCEの出力は、データ点がポジティブクラスに属する確率として理解されます。この値は0.0から1.0の範囲にあり、ハードシグモイド関数が適切なペアリング活性化関数として利用されます。MQL5の組み込み活性化関数から得られるベクトル出力は、ポジティブクラスとネガティブクラスの確率を含むベクトルとして生成されます。

カルバック・ライブラー情報量は、上で見てきたベクトルギャップ法に似た、もう1つの興味深い損失関数アルゴリズムです。その公式は次式で与えられます。

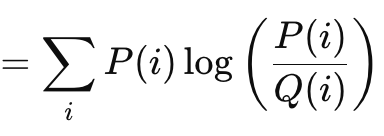
ここで

• Pは予想される確率
• Qは実際の確率

出力の範囲は、発散がないことを示す0から無限大までとなっています。これらの正の値は、予測が「真実」からどれだけ離れているかを示す明確な指標です。前述の式で示したように、合計が関与するのはスカラー出力をターゲットとする場合のみです。MQL5に内蔵されているベクトル実装は、逆伝播を実行する際のデルタや最終的な勾配の計算において、より適切で必要なベクトル出力を提供します。カルバック・ライブラー情報量は情報理論に基づいており、その柔軟性から強化学習や変分オートエンコーダへの応用が進められています。しかし、その欠点には、非対称性、ゼロ値に対する敏感さ、出力の束縛がないことによる解釈の難しさが挙げられます。片方のクラスにゼロの確率が与えられると、もう一方のクラスは自動的に無限の値を持つため、ゼロの感度は重要です。非対称性は、与えられた確率の適切な解釈を妨げるだけでなく、転移学習をより困難にします（Kが与えられた場合のPの確率は、Pが与えられた場合のKの確率とは逆ではないため）。さらに、順方向確率と逆方向確率の和は、あらかじめ決められた値ではなく、無限大の場合もあれば、そうでない場合もあります。

これに基づいて導かれるのがコサイン類似度です。コサイン類似度は、これまで見てきたベクトルギャップ測定とは異なり、方向性を考慮します。計算式は以下の通りです。

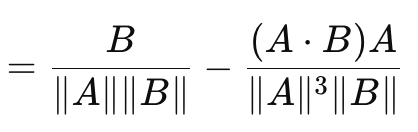
ここで

• A.Bは2つのベクトルの内積
• ||A||とB||はその大きさまたは規範

上の式は、ベクトルAに対する損失勾配を表していますが、ベクトルBに対するそれは別の逆式となります。AとBの余弦を合計しても、固定または任意の定数にはならないため、余弦類似度は不等式の三角形を満たさず、真のメトリックではありません（AとBの余弦類似度とBとCの余弦類似度は、必ずしもAとCの余弦類似度以上とは限りません）。その一方で、余弦類似度の利点はスケール不変性です。提供される値が問題のベクトルの大きさに依存しないため、大きさではなく方向が重要な場合に特に有用です。また、他の手法よりも計算量が少なく、非常に深いネットワークやTransformer、あるいはその両方を扱う場合には、特に重要な考慮点となります。コサイン類似度は、各ベクトル値の個々の大きさよりも、推測される方向（意味）がより適切な指標となるような、高次元データ（例えば、大規模言語モデルのテキスト埋め込みなど）に高い適用性があります。ただし、コサイン類似度にはすべてのタスクに適しているわけではないという欠点があります。特に、学習時のベクトルの大きさが重要な状況では適していません。さらに、いずれかのベクトルのノルムが0（すべての値が0）の場合、余弦類似度は定義されません。また、前述したように、不等辺三角形のルールを満たさないことから、真のメトリックとは見なされません。この点が重要となる例としては、幾何学的ディープラーニング、グラフベースのニューラルネットワーク、シャムネットワークからの対比損失などが挙げられます。これらの使用例では、いずれも方向性よりも大きさが重要です。しかし、MQL5でコサイン類似度を適用する際に重要なのは、機械学習により適しているコサイン近接度が使用される点です。コサイン近接度は、角度の余弦の距離に相当し、余弦類似度を1から引くことで得られます。

ポアソン損失勾配関数(Poisson regression)（英語）は，可算データや離散データのモデリングに適しています。前述の損失関数と同様に、ベクトルデータ型の内蔵関数によって実装されています。その公式は以下のように表されます。

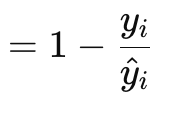
ここで

• y は（インデックスiの）ターゲットベクトル値
• y^は予測値

勾配値はベクトル形式で返されます。この方がバックプロパゲーション処理に役立つからです。また、これらは元のポアソン関数のスカラーリターン式の1次微分です。

ここで

• 勾配の公式

この例では、トレーダーがニューラルネットワークに与えることができる離散データのタイプには、価格バーのローソク足の種類や、以前のバーが強気、弱気、またはフラットであるかどうかが含まれます。このユースケースは、データをカウントするシナリオをカバーしており、たとえば、最近の歴史からさまざまなローソク足の価格バーのパターンを考慮したニューラルネットワークは、将来の10本の価格バーの標準的なサンプルの中で、予想される特定のローソク足の種類の数を返すように訓練されることができます。その係数は対数率比であるため解釈が容易で、ポアソン回帰とよく整合しているため、訓練後の分析もポアソン回帰を用いて簡単におこなえます。また、カウント予測は常にプラス（非負）であることが保証されます。一方で、良い特徴には分散仮定があり、平均と分散が常に同じか、ほとんど同じ値であると仮定されます。もしこれが成り立たない場合、損失関数はうまく機能しません。特特に入力データ内のカウント数が多い外れ値に対して敏感であり、自然対数の使用はNaNや無効な結果を引き起こす可能性があります。加えて、ポアソン回帰の適用は正の整数データに限定されるため、価格変動を予測する場合など、連続的な負の予測が必要なシナリオには使用できません。

フーバー損失で、MQL5がベクトルデータ型で提供するもののサンプリングは終わりです。他にも、双曲余弦の対数、カテゴリヒンジ、二乗ヒンジ、ヒンジ、平均二乗対数誤差、平均絶対パーセンテージ誤差など、まだ取り上げていないクラスの損失関数があります。これらの損失関数は、ニューラルネットワークが回帰器であるか分類器であるかにとって重要ではありません。フーバー損失は次式で与えられます。

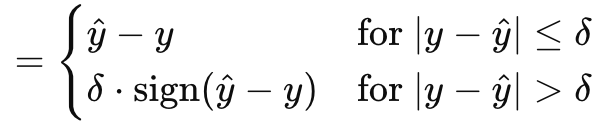
ここで

• y^は予測値
• yはターゲット
• デルタは、関係が線形から二次関数に変化する損失入力値

勾配は、元のフーバー損失のように、真の値または目標値と予測値との比較に応じて、2つの方法のいずれかで計算できます。これは一次関数と二次関数の一部であり、入力パラメータが調整されたときの目標値と予測値の差のマッピングを表しています。フーバー損失はロバスト回帰(robust regression)（英語）で優位性を持ち、MAE（平均絶対誤差）とMSE（平均二乗誤差）の長所を組み合わせています。外れ値の影響を受けにくく、小さな誤差に対してはMAEよりも安定しているためです。この損失関数は完全に微分可能であるため、勾配降下法に理想的であり、デルタのおかげで適応性があります。デルタが小さいとMAEのような働きをし、デルタが大きいとMSEのような働きをします。これにより、ロバスト性と感度のトレードオフをコントロールすることが可能です。欠点としては、フーバー損失は比較的複雑で、その式は区分的であるだけでなく、理想的なデルタの計算と決定が煩雑な作業になることが多いです。このため、私が参照できなかった標準の行列およびベクトルライブラリに基づいていると思われるMQL5実装では、フーバー損失およびフーバー損失勾配の組み込み関数のデルタ値がどのように計算されるかは公開されていません。様々な活性化関数と組み合わせることができますが、線形活性化がより適していると推奨されることが多いです。

回帰モデルの損失関数

では、これらの損失アルゴリズムのうち、どれが回帰ネットワークに最適なのでしょうか。答えは、MSE、MAE、フーバー損失です。その理由は次の通りです。回帰ネットワークは、カテゴリカルラベルや離散データではなく、連続的な数値を予測することを目的としているからです。これは、これらのネットワークの出力層が、通常、広範囲にわたる実数値を生成することを意味します。回帰タスクの性質上、最適化において予測値と真値の間の偏差を最小化する必要があります。分類ネットワークとは異なり、出力を列挙する必要が少なく、数があらかじめわかっていることが多いです。

したがって、MSEに行き着きます。すでにみたように、MSEは、大きな誤差に対して大きな二次的ペナルティを課すため、回帰ネットワークを効率的に実行するために、狭い偏差に向けて勾配降下法と最適化を導きます。また、滑らかで微分しやすいため、回帰ネットワークが扱う連続データにも自然に適合します。

回帰ネットワークは外れ値の影響も受けやすく、そのため外れ値に強い損失関数が必要です。そこでMAEが登場します。MAEは、誤差に線形的なペナルティを課すため、MSEよりも外れ値の影響を受けにくくなっています。さらに、MAEはロバストな誤差測定を提供し、ノイズの多いデータでも有用です。

最後に、回帰ネットワークは小さな誤差に対する感度とロバスト性の間のバランスを取る必要があります。これらの特性はハイパー損失関数が提供するもので、最適化プロセス全体を通して滑らかさを保ちます。

これら3つの「理想的な」損失関数をすべてゼロにした状態で、回帰ネットワークで使用する際に考慮すべき理想的な活性化関数は何でしょうか。公式には、線形活性化と同一性活性化が推奨されており、後者は、データの変動を可能な限り捉えるためにネットワーク出力の大きさを保持します。これら2つの活性化関数は、その出力が束縛されない性質により、ネットワークのフィードフォワード処理と訓練を通じてデータの損失がないことを意味します。個人的には、有界出力が好ましいと考えていますので、負と正の両方の実数を捕らえるソフトサインやTANHを選びたいと思います。これらの活性化関数は出力を-1.0から+1.0に制約します。この出力の制約は、勾配の爆発と消失といった問題を避けるために重要です。

分類モデルの損失関数

分類ニューラルネットワークについてはどうでしょうか。損失関数と活性化関数の選択はどうなるのでしょう。ここでの選択プロセスはそれほど変わりません。基本的にはネットワークの主要な特性を見て、それに基づいて選択をおこないます。

分類ネットワークは、あらかじめ定義されたカテゴリのプールから離散的なクラスラベルを予測することを目的としています。これらのネットワークは、各クラスの尤度を示す確率を出力し、損失を最小化することで予測精度を最大化することを主な目標としています。そのため、損失関数の選択は、ネットワークを訓練してクラスを正確に識別する上で重要な役割を果たします。これらの主要な特徴から、 MQL5によって提供されている損失関数の中で、分類ネットワークに最も適した2つの主要な損失関数として、カテゴリクロスエントロピーと二値クロスエントロピーが挙げられます。

二値クロスエントロピー（BCE）は、2つの可能性のあるカテゴリから分類をおこないますが、実際には予測数は2つ以上になることが多く、このバッチの大きさが勾配ベクトルのノルムを決定します。つまり、勾配ベクトルの各インデックスにおける値は、共有式で強調したようにBCE損失関数の偏導関数となり、これらの値がバックプロパゲーションで使用されます。しかし、ネットワークの出力値は、前述のように正のクラスに対する確率となり、出力ベクトルの各投影値に対する確率となります。

BCEは分類ネットワークに適しています。なぜなら、確率が正のクラスを指すため、容易に解釈できるからです。バッチから正しいクラスの対数尤度を最大化することに重点を置いているため、各出力値の様々な確率に敏感です。これは定数ではなく変数として微分できるため、逆伝播における勾配計算をスムーズかつ効率的におこなうことができます。

CCEは、2つ以上のカテゴリを分類できるようにすることでBCEを拡張し、出力ベクトルのノルムまたはサイズは常に、それぞれに確率が与えられるクラスの数となります。これは、例えば5つの値まで予測することができ、それぞれの値がすべて真か偽かのどちらかであるBCEとは異なります。CCEでは、出力サイズはクラスの数と一致するように接頭辞が付けられます。前述のワンホットエンコーディングは、予測とのギャップを測定する前にターゲットベクトルを正規化するのに有効です。

これと組み合わせる活性化の理想的な形は、0.0から+1.0の範囲でアウトバウンドする関数です。これにはソフトマックス、シグモイド、ハードシグモイドが含まれます。

テスト

そのため、回帰MLPと分類器の2つのテストをおこないます。このテストの目的は、本稿で取り上げた損失関数と活性化のアイデアをMQL5とEAの形で実装することを実証することです。これらのテスト結果は、添付のコードをライブ口座に導入し、使用することを保証するものではなく、むしろ、読者が取引システムを適切と判断した場合、ブローカーのリアルティックのデータを長期間にわたってテストし、自分自身の注意を払うように促すものです。いつものように、実稼働環境への配備は、満足のいく結果が得られる相互検証またはフォワードウォークテストが実施された後にのみおこなうのが理想的です。

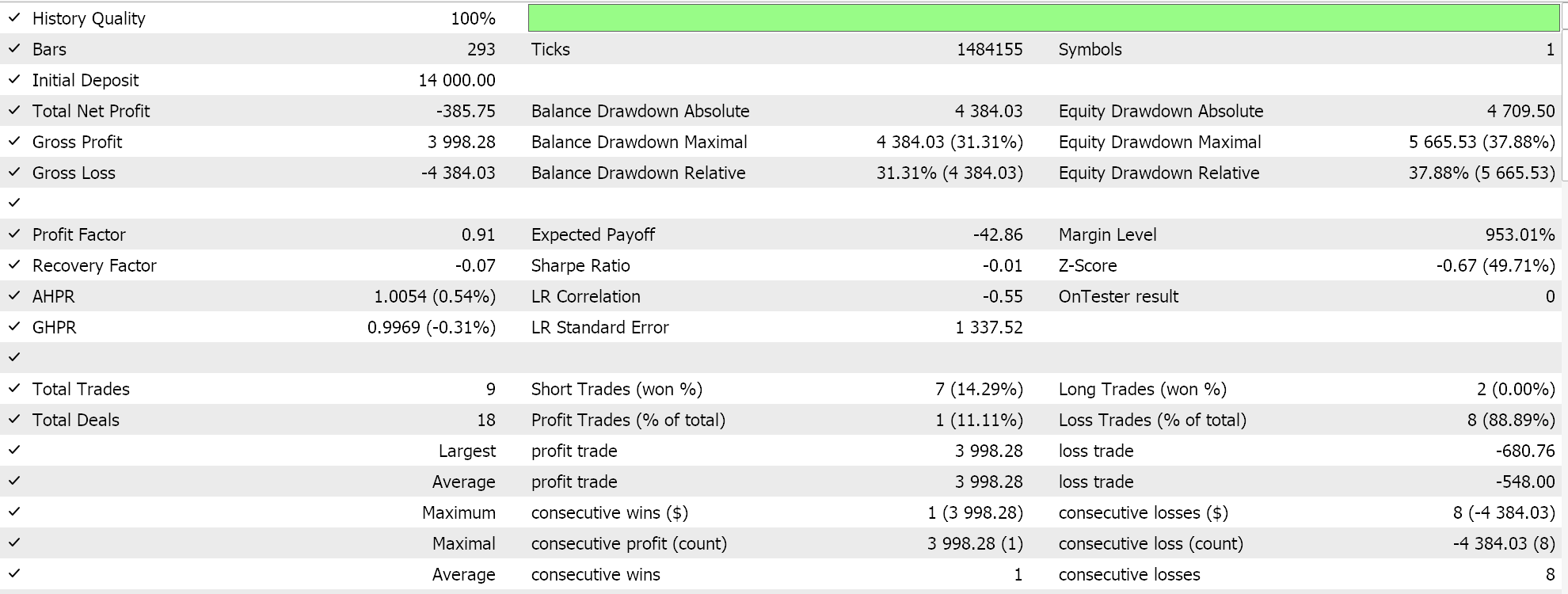
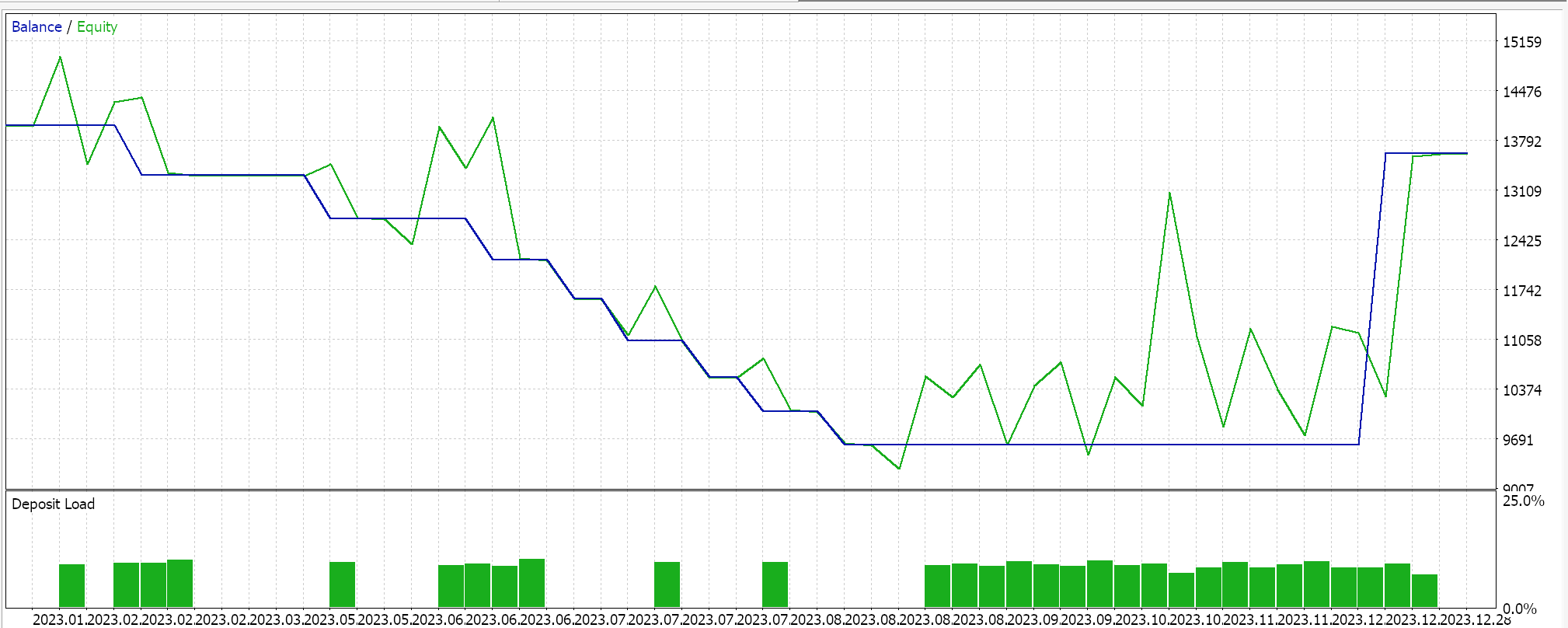
昨年2023年のGBPCHFを日足でテストします。回帰ネットワークを取得するには、前回の記事で紹介したCmlpクラスを参照します。入力データは価格変動率（ポイントではない）なので、TANH活性化フーバー損失関数を使用してテストし、システムがどの程度取引可能かを確認できます。カスタムシグナルのロングとショートの条件は、MQL5では以下のように実装されています。

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalRegr::LongCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[0] > 0.0)
   {  result = int(round(100.0*(fabs(_out[0])/(fabs(_out[0])+fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1))))));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[0],  result);return(0);
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalRegr::ShortCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[0] < 0.0)
   {  result = int(round(100.0*(fabs(_out[0])/(fabs(_out[0])+fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1))))));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[0],  result);return(0);
   return(result);
}

また、新しい価格バーごとに、ネットワークの学習と同時に、履歴データに対するEAのテストもおこないます。これも重要な決定事項で、短期的な行動にネットワークが過剰にフィットするのを避けるため、訓練は6カ月に1回、あるいはあらかじめ決めた別の長い期間に実施されます。この回帰ネットワークは4-7-1の3層サイズ（数字は層のサイズを表す）になっており、最近の 4 つの価格変更が入力として機能し、単一の出力が次の価格変更であることを意味します。

2023年のGBPCHFを日足でテストすると、次のようなレポートが得られます。

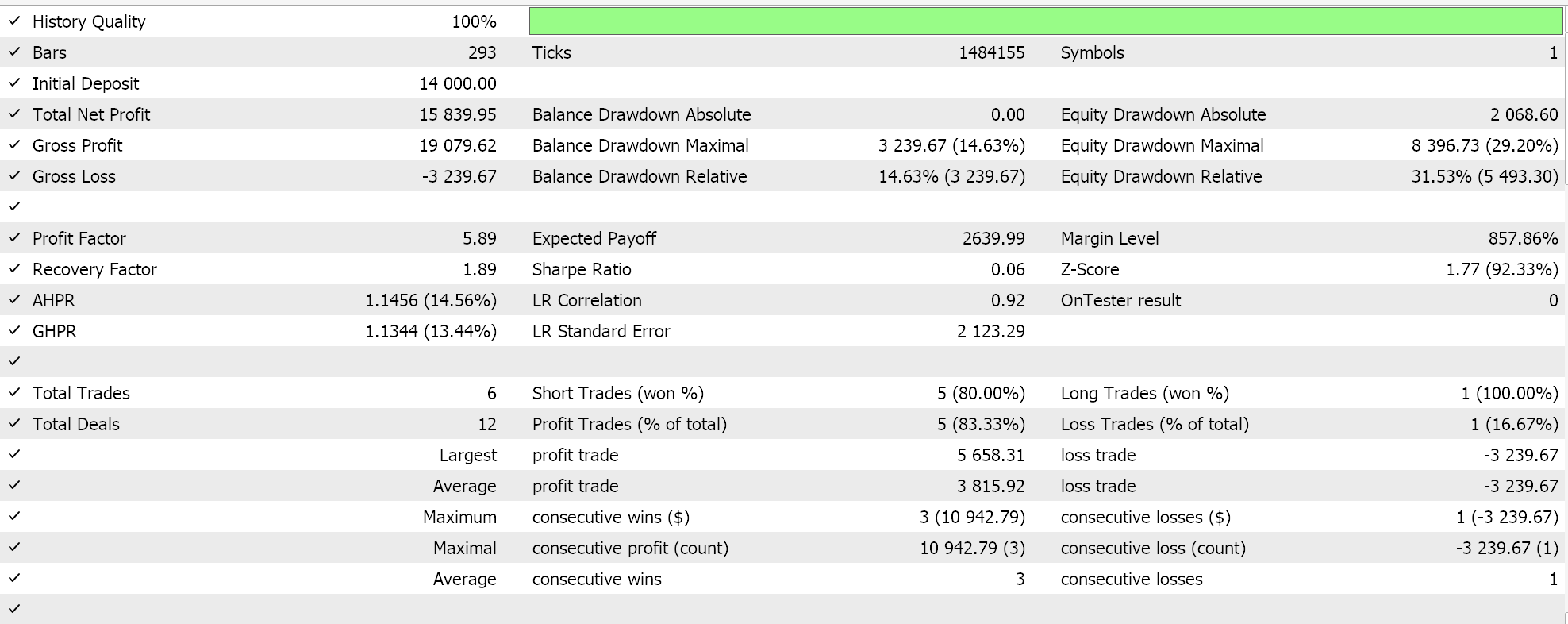
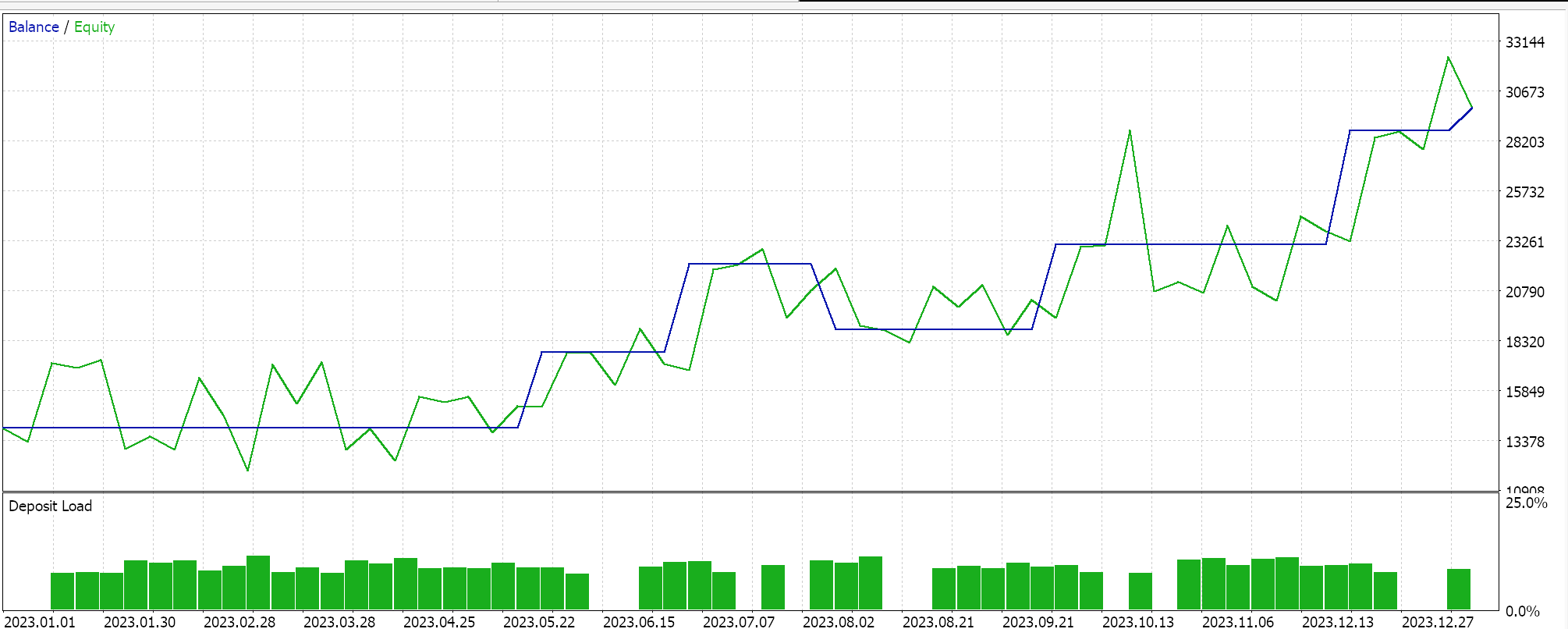
分類器ネットワークでは、引き続き「Cmlp」クラスをベースとして使用し、入力データは過去3回の価格帯の分類とします。これは、3-6-3のシンプルなMLPネットワーク (これも3層のみ) に入力されます。ここでは3つの分類が可能であり、損失関数はCCEであるため、最終的な出力層もサイズが3で、確率分布として機能するようにする必要があります。売買条件の生成は、MQL5では以下のように実装されています。

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalClas::LongCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[2] > _out[1] && _out[2] > _out[0])
   {  result = int(round(100.0 * _out[2]));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[2],  result);return(0);
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalClas::ShortCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[0] > _out[1] && _out[0] > _out[2])
   {  result = int(round(100.0 * _out[0]));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[0],  result);return(0);
   return(result);
}

分類器EAでも同様のテストをおこなったところ、以下のような結果が得られました。

添付のコードは、ウィザードアセンブリを使用してEAを生成します。ガイドはこちらとこちら.です。

結論

まとめると、ニューラルネットワークのような機械学習アルゴリズムを開発する際に、MQL5で利用可能な損失関数の遍歴を見てきました。皮肉なことに、網羅的ではないほど長いリストが存在しますが、爆発や消失勾配と効率を回避することに重点を置き、以前の記事で説明した特定の活性化関数と組み合わせてうまく機能するいくつかの重要な損失関数を強調しました。利用可能な損失関数の多くは、出力が制限されていないという理由だけでなく、これらのネットワークの主要な特性要件に適合していないため、一般的な回帰ネットワークや分類ネットワークに必ずしも適しているわけではありません。そのため、検討された損失関数は、利用可能な損失関数の中では少数にとどまりました。