Redes neuronales: así de sencillo (Parte 88): Codificador de series temporales totalmente conectadas (TiDE)

Introducción

Probablemente todas las arquitecturas de redes neuronales conocidas, incluidos los modelos recurrentes, convolucionales y de grafos, se han investigado para resolver problemas de previsión de series temporales. Pero los resultados más notables los demuestran los modelos basados en la arquitectura del Transformer. En esta serie de artículos también hemos presentado varios algoritmos de este tipo. No obstante, investigaciones recientes han demostrado que las arquitecturas basadas en el Transformer pueden resultar menos potentes de lo esperado. En algunas series temporales de referencia, los modelos lineales simples pueden ofrecer resultados comparables o incluso mejores. Pero, por desgracia, estos modelos lineales poseen desventajas, ya que no son adecuados para modelar relaciones no lineales entre una secuencia de series temporales y covariables independientes del tiempo.

Podemos decir que la investigación futura en el campo del análisis y la previsión de series temporales se dividirá en 2 ramas. Algunos ven el potencial incompleto del Transformer y trabajan para mejorar la eficiencia de esta clase de arquitecturas. Otros trabajan para minimizar las desventajas de los modelos lineales. El artículo "Long-term Forecasting with TiDE: Time-series Dense Encoder" pertenece a la segunda rama. Este artículo propone una arquitectura de aprendizaje profundo simple y eficiente para la predicción de series temporales, que proporciona un mejor rendimiento que los modelos de aprendizaje profundo existentes en puntos de referencia populares. El modelo basado en el perceptrón multicapa (MLP) presentado es notablemente simple y no tiene mecanismos de Self-Attention, recurrentes o de capas convolucionales. Por lo tanto, posee una escalabilidad computacional lineal con respecto a la longitud del contexto y el horizonte de predicción, a diferencia de muchas soluciones basadas en el Transformer.

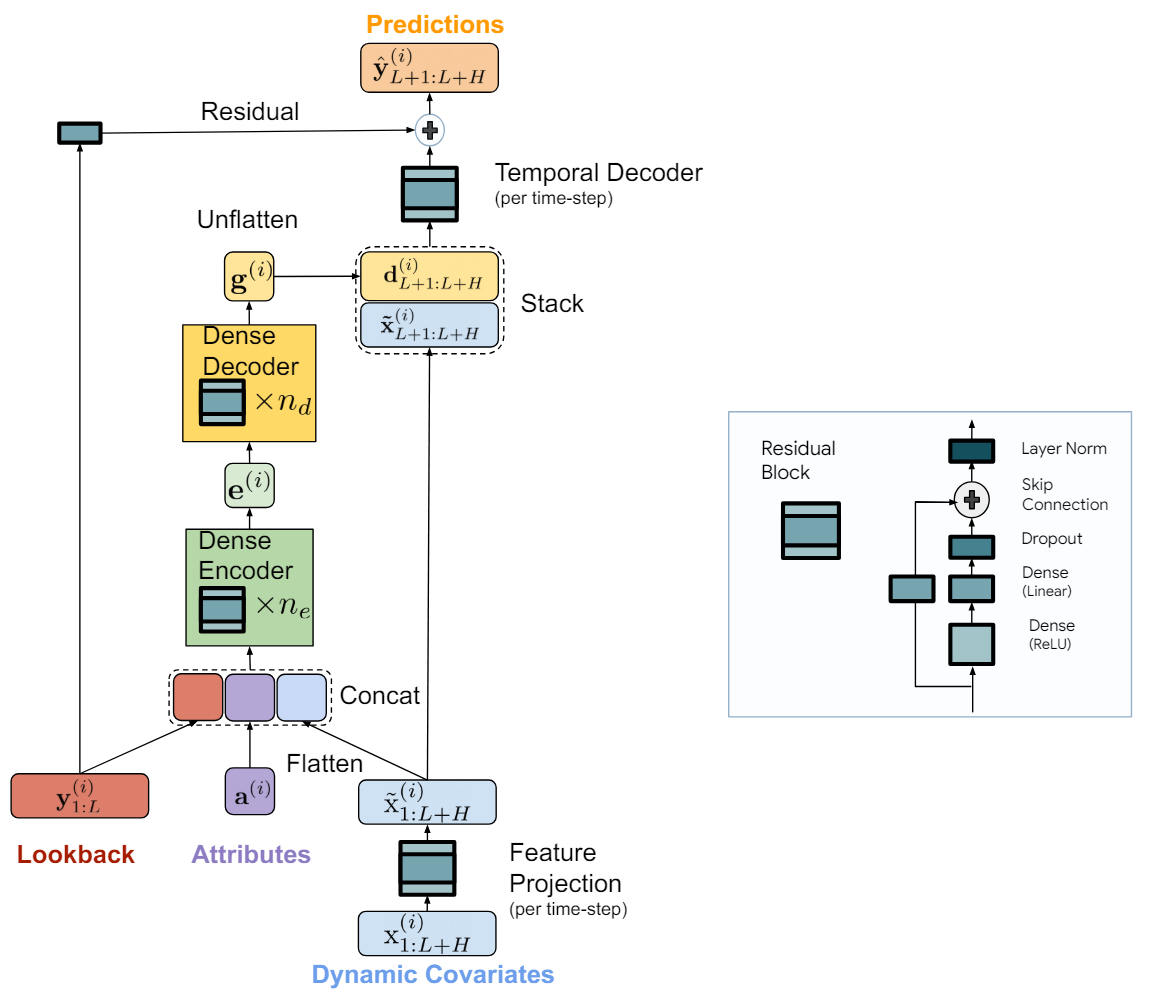
El modelo Time-series Dense Encoder (TiDE) usa MLP para codificar series temporales pasadas junto con covariables y descodificar las series temporales predichas junto con las covariables futuras.

Los autores del método analizan un modelo TiDE lineal simplificado y demuestran que este modelo lineal puede conseguir un error casi óptimo en sistemas dinámicos lineales (LDS) cuando la matriz de construcción LDS tiene un valor singular máximo distinto de 1. Luego lo prueban empíricamente con datos simulados en los que el modelo lineal supera a las LSTM y a los Transformers.

En las pruebas de referencia de predicción de series temporales del mundo real, TiDE obtiene resultados mejores o similares a los modelos de redes neuronales básicas anteriores. El funcionamiento de TiDE, por su parte, es 5 veces más rápido, mientras que el entrenamiento es más de 10 veces más rápido, en comparación con el mejor modelo basado en el Transformer.

1. Algoritmo TiDE

El modelo se denomina TiDE (Time-series Dense Encoder) y supone una arquitectura simple y eficiente basada en MLP para la previsión de series temporales a largo plazo. Los autores del algoritmo añaden no linealidades en forma de MLP para poder procesar datos y covariables pasados.

El modelo se aplica a canales de datos independientes, es decir, las entradas del modelo son el pasado y las covariables de una serie temporal cada vez. En este caso, los pesos del modelo se entrenan globalmente usando el conjunto de datos completo, es decir, son uniformes para todos los canales independientes.

El componente clave del modelo es la unidad MLP de retroalimentación, que supone un MLP de una sola capa oculta con activación ReLU. También dispone de una conexión de atajo completamente lineal. Los autores del método utilizan Dropout en una capa lineal que asigna una capa oculta a la salida, y usan la normalización de capas en la salida.

El modelo TiDE se divide lógicamente en secciones de codificación y descodificación. La sección de codificación contiene un paso de proyección de características seguido de un codificador MLP denso. La sección de descodificación consta de un descodificador denso seguido de un descodificador temporal.

El codificador denso y el decodificador denso pueden combinarse en una sola unidad. No obstante, los autores del método separan los dos porque utilizan diferentes tamaños de capas ocultas en los dos bloques. Además, la última capa del bloque decodificador es única en el sentido de que su tamaño de salida debe coincidir con el horizonte de planificación.

La tarea de la etapa de codificación consiste en representar el pasado y las covariables de las series temporales en una representación densa de características. La codificación en el modelo TiDE consta de dos pasos clave.

En primer lugar, se usa un bloque de retroalimentación para representar las covariables en cada paso temporal (tanto en el contexto de la historia como en el horizonte de previsión) en una proyección de dimensionalidad inferior.

Luego fusionamos y suavizamos todas las covariables proyectadas pasadas y futuras y las combinamos con atributos estáticos y series temporales pasadas. A continuación, las representamos en la incorporación utilizando un codificador denso que contiene múltiples bloques de retroalimentación.

La descodificación en el modelo TiDE presenta las representaciones latentes codificadas en los futuros valores predichos de series temporales. También incluye dos operaciones: un descodificador denso y un descodificador temporal.

El decodificador denso es una pila de múltiples bloques de realimentación similares a los bloques del codificador. Toma los resultados del codificador como entrada y los representa en un vector de representaciones predictivas de estado.

La salida del modelo usa un descodificador temporal para generar las predicciones finales. El decodificador temporal es el mismo bloque de realimentación que asigna el vector decodificado al paso temporal t-ésimo del horizonte de previsión, combinado con las covariables proyectadas del periodo de previsión.

Esta operación añade la relación de las covariables del periodo de previsión a los valores de previsión de la serie temporal, lo cual puede resultar útil si algunas covariables tienen un fuerte efecto directo sobre el valor real en un paso de tiempo concreto. Por ejemplo, las noticias de fondo en determinados días naturales.

A los valores del decodificador temporal se añaden los valores de la conexión residual global, que representa linealmente el pasado de las series temporales analizadas con el vector del horizonte de planificación. Esto garantiza que el modelo puramente lineal sea siempre una subclase del modelo TiDE.

Más abajo le presentamos la visualización del método por parte del autor.

El modelo se entrena usando el descenso de gradiente por minipaquetes. Los autores del método utilizan el error cuadrático medio (MSE) como función de pérdida. Cada época incluye todos los pares de horizonte pasado y horizonte previsto que pueden construirse partiendo del periodo de entrenamiento. Es decir, dos minipaquetes pueden tener puntos temporales superpuestos.

2. Implementación con MQL5

Tras analizar los aspectos teóricos del algoritmo TiDE, vamos a implementar los enfoques propuestos usando MQL5.

Como ya hemos mencionado, el principal "ladrillo" del método TiDE que estamos considerando es el bloque de retroalimentación. En él, los autores del método usan capas totalmente conectadas. Pero debemos señalar que cada unidad de este tipo en el modelo se aplica a un canal independiente. En este caso, los parámetros entrenados del bloque se entrenarán a nivel global y serán uniformes para todos los canales de las series temporales multidimensionales analizadas.

Obviamente, en nuestra aplicación nos gustaría implementar el cálculo paralelo para todos los canales independientes de las series temporales multidimensionales que estamos analizando. En casos semejantes, ya hemos usado muchas veces capas convolucionales con varios filtros de convolución. El tamaño de la ventana de dicha capa convolucional será igual a su paso y se corresponderá con el volumen de datos de un canal. Creo que resulta obvio que será igual a la profundidad de la historia de la serie temporal que estamos analizando.

Y ya que hemos llegado al uso de capas convolucionales, me acuerdo del bloque de retroalimentación que creamos al implementar el método CCMR. El lector atento encontrará una diferencia en la presencia de las capas de normalización que hemos usado en la aplicación anterior. Sin embargo, para los objetivos de este artículo, hemos decidido ignorar esta diferencia en la arquitectura de bloques y utilizar el bloque ya preparado CResidualConv para construir un nuevo modelo.

Bien, ya tenemos el "ladrillo" básico del algoritmo TiDE propuesto. Ahora deberemos ensamblar todo el algoritmo a partir de estos bloques.

2.1 Clase del algoritmo TiDE

Envolveremos la implementación de los enfoques propuestos en una nueva clase CNeuronTiDEOCL, que crearemos como heredera de la clase básica de capas neuronales de nuestro modelo CNeuronBaseOCL. Para la arquitectura de nuestra nueva clase, los parámetros clave serán 4 parámetros para los que declararemos variables locales:

• iHistory — profundidad de la historia analizada de la serie temporal;
• iForecast — horizonte de previsión de series temporales;
• iVariables — número de variables (canales) analizados;
• iFeatures — número de covariables de series temporales.

class CNeuronTiDEOCL :  public CNeuronBaseOCL
  {
protected:
   uint              iHistory;
   uint              iForecast;
   uint              iVariables;
   uint              iFeatures;
   //---
   CResidualConv     acEncoderDecoder[];
   CNeuronConvOCL    cGlobalResidual;
   CResidualConv     acFeatureProjection[2];
   CResidualConv     cTemporalDecoder;
   //---
   CNeuronBaseOCL    cHistoryInput;
   CNeuronBaseOCL    cFeatureInput;
   CNeuronBaseOCL    cEncoderInput;
   CNeuronBaseOCL    cTemporalDecoderInput;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                        CBufferFloat *SecondGradient, 
                                        ENUM_ACTIVATION SecondActivation = None);

public:
                     CNeuronTiDEOCL(void) {};
                    ~CNeuronTiDEOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint history, uint forecast, uint variables, uint features, 
                          uint &encoder_decoder[], ENUM_OPTIMIZATION optimization_type, 
                          uint batch);
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual int       Type(void)        const                      {  return defNeuronTiDEOCL; }
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
  };

Como podemos observar, entre las variables mencionadas no figura el número de bloques ni en el modelo de Codificador ni en el de Decodificador. En nuestra implementación, hemos combinado el Codificador y el Decodificador en el array de bloques acEncoderDecoder[]. El tamaño de este array nos indicará el número total de bloques de retroalimentación utilizados para codificar los datos históricos y descodificar los valores predichos de la serie temporal.

Además, dividiremos la proyección de las covariables de las series temporales en 2 bloques (acFeatureProjection[2]). En uno, generaremos una proyección de covariables para codificar los datos históricos, mientras que en el otro generaremos una proyección de covariables para descodificar los valores predichos.

Asimismo, añadiremos un bloque de decodificador temporal cTemporalDecoder. Y para la conexión residual global, usaremos la capa convolucional cGlobalResidual.

Además, declararemos 4 capas locales totalmente conectadas para registrar los valores intermedios. Conoceremos la finalidad específica de cada capa durante la implementación.

Hemos declarado todos los objetos de nuestra clase como estáticos, lo cual nos permitirá dejar el constructor y el destructor de la clase "vacíos".

Tengo que decir que el conjunto de métodos redefinidos es bastante estándar. Como siempre, empezaremos con el método de inicialización del objeto de la clase CNeuronTiDEOCL::Init.

bool CNeuronTiDEOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint history, 
                          uint forecast, uint variables, uint features, uint &encoder_decoder[],
                          ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, forecast * variables, 
                            optimization_type, batch))
      return false;

En los parámetros, el método obtendrá toda la información necesaria para implementar la arquitectura requerida. Y en el cuerpo del método llamaremos primero al método homónimo de la clase padre, en el que se implementará el control mínimo necesario de los parámetros obtenidos y la inicialización de los objetos heredados.

Tras ejecutar con éxito las operaciones del método de inicialización de la clase padre, almacenaremos los valores de las constantes clave.

   iHistory = MathMax(history, 1);
   iForecast = forecast;
   iVariables = variables;
   iFeatures = MathMax(features, 1);

Y luego procederemos a inicializar los objetos internos. Primero inicializaremos los bloques de proyección de covariables.

   if(!acFeatureProjection[0].Init(0, 0, OpenCL, iFeatures, iHistory * iVariables, 1, 
                                                                 optimization, iBatch))
      return false;
   if(!acFeatureProjection[1].Init(0, 1, OpenCL, iFeatures, iForecast * iVariables, 1, 
                                                                 optimization, iBatch))
      return false;

Aquí deberemos decir que en nuestro experimento no utilizaremos ningún conocimiento a priori sobre las covariables de las series temporales analizadas. En su lugar, proyectaremos el armónico temporal de la marca temporal sobre la secuencia. Al hacerlo, generaremos proyecciones propias para cada canal (variable) del canal temporal multidimensional analizado.

Luego obtendremos las dimensiones de las capas ocultas del codificador y decodificador denso como un array encoder_decoder[]. El tamaño del array indicará el número total de bloques de realimentación en el codificador y el decodificador. Mientras que el valor de los elementos del array indicará la dimensionalidad del bloque correspondiente. Recordemos que la entrada del codificador supone un vector concatenado de datos de series temporales históricas con una proyección de covariables. Y que la salida del descodificador debe ser un vector que se corresponda con el horizonte de predicción. Para cumplir este último requisito, añadiremos otro bloque a la salida del descodificador del tamaño requerido.

   int total = ArraySize(encoder_decoder);
   if(ArrayResize(acEncoderDecoder, total + 1) < total + 1)
      return false;
   if(total == 0)
     {
      if(!acEncoderDecoder[0].Init(0, 2, OpenCL, 2 * iHistory, iForecast, iVariables,
                                                                 optimization, iBatch))
         return false;
     }
   else
     {
      if(!acEncoderDecoder[0].Init(0, 2, OpenCL, 2 * iHistory, encoder_decoder[0], iVariables, 
                                                                          optimization, iBatch))
         return false;
      for(int i = 1; i < total; i++)
         if(!acEncoderDecoder[i].Init(0, i + 2, OpenCL, encoder_decoder[i - 1], 
                                          encoder_decoder[i], iVariables, optimization, iBatch))
            return false;
      if(!acEncoderDecoder[total].Init(0, total + 2, OpenCL, encoder_decoder[total - 1],
                                                   iForecast, iVariables, optimization, iBatch))
         return false;
     }

A continuación, inicializaremos el bloque de decodificador temporal y la capa de realimentación global.

   if(!cGlobalResidual.Init(0, total + 3, OpenCL, iHistory, iHistory, iForecast, iVariables, 
                                                                        optimization, iBatch))
      return false;
   cGlobalResidual.SetActivationFunction(TANH);
   if(!cTemporalDecoder.Init(0, total + 4, OpenCL, 2 * iForecast, iForecast, iVariables, 
                                                                        optimization, iBatch))
      return false;

Aquí hay dos puntos que merece la pena destacar:

1. El decodificador temporal obtendrá como entrada una matriz concatenada de valores de series temporales predichas y proyecciones de covariables predichas. Mientras que a la salida del bloque obtendremos los valores predichos corregidos de las series temporales.
2. La salida de cada bloque CResidualConv normalizará los datos: la media de cada canal será "0" y la varianza será "1". Para convertir los datos del bloque de retroalimentación global a una forma comparable, utilizaremos la tangente hiperbólica (tanh) como función de activación de la capa cGlobalResidual.

El siguiente paso consistirá en inicializar los objetos auxiliares para guardar los datos intermedios. Luego almacenaremos los datos históricos de las series temporales multidimensionales analizadas y las covariables obtenidas del programa externo en cHistoryInput y cFeatureInput, respectivamente.

   if(!cHistoryInput.Init(0, total + 5, OpenCL, iHistory * iVariables, optimization, iBatch))
      return false;
   if(!cFeatureInput.Init(0, total + 6, OpenCL, iFeatures, optimization, iBatch))
      return false;

Después escribiremos la matriz concatenada de datos históricos y proyecciones de covariables en cEncoderInput.

   if(!cEncoderInput.Init(0, total + 7, OpenCL, 2 * iHistory * iVariables, optimization,iBatch))
      return false;

Los resultados del decodificador denso se concatenarán con las covariables de los valores predichos y se escribirán en cTemporalDecoderInput.

   if(!cTemporalDecoderInput.Init(0, total + 8, OpenCL, 2 * iForecast * iVariables, 
                                                                         optimization, iBatch))
      return false;

Al final del método de inicialización del objeto de clase, realizaremos un intercambio de búferes de datos para evitar el copiado innecesario de gradientes de error entre los búferes de datos de los elementos individuales de nuestra clase.

   if(cGlobalResidual.getGradient() != Gradient)
      if(!cGlobalResidual.SetGradient(Gradient))
         return false;
   if(cTemporalDecoder.getGradient() != getGradient())
      if(!cTemporalDecoder.SetGradient(Gradient))
         return false;
//---
   return true;
  }

Una vez inicializada la instancia de la clase, procederemos a construir el algoritmo de pasada directa, descrito en el método CNeuronTiDEOCL::feedForward. En los parámetros del método obtendremos los punteros a 2 objetos que contienen los datos de origen. Se trata de los datos históricos de las series temporales multidimensionales en forma de búfer de resultados de la capa neuronal anterior y las covariables representadas en búferes de datos independientes.

bool CNeuronTiDEOCL::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   if(!NeuronOCL || !SecondInput)
      return false;

En el cuerpo del método, comprobaremos inmediatamente la relevancia de los punteros recibidos.

A continuación, tendremos que copiar los datos de origen obtenidos en los objetos internos, pero en lugar de transferir toda la información, solo comprobaremos los punteros a los búferes de datos y los copiaremos si es necesario.

   if(cHistoryInput.getOutputIndex() != NeuronOCL.getOutputIndex())
     {
      CBufferFloat *temp = cHistoryInput.getOutput();
      if(!temp.BufferSet(NeuronOCL.getOutputIndex()))
         return false;
     }
   if(cFeatureInput.getOutputIndex() != SecondInput.GetIndex())
     {
      CBufferFloat *temp = cFeatureInput.getOutput();
      if(!temp.BufferSet(SecondInput.GetIndex()))
         return false;
     }

Tras el trabajo preparatorio, proyectaremos los datos históricos en la dimensionalidad de los valores previstos. Una especie de modelo autorregresivo.

   if(!cGlobalResidual.FeedForward(NeuronOCL))
      return false;

Y generaremos las proyecciones de las covariables a los valores históricos y previstos.

   if(!acFeatureProjection[0].FeedForward(NeuronOCL))
      return false;
   if(!acFeatureProjection[1].FeedForward(cFeatureInput.AsObject()))
      return false;

A continuación, concatenaremos los datos históricos con la matriz de proyección de covariables correspondiente.

   if(!Concat(NeuronOCL.getOutput(), acFeatureProjection[0].getOutput(), 
              cEncoderInput.getOutput(), iHistory, iHistory, iVariables))
      return false;

Y organizaremos un ciclo de operaciones de bloques del codificador y el decodificador densos.

   uint total = acEncoderDecoder.Size();
   CNeuronBaseOCL *prev = cEncoderInput.AsObject();
   for(uint i = 0; i < total; i++)
     {
      if(!acEncoderDecoder[i].FeedForward(prev))
         return false;
      prev = acEncoderDecoder[i].AsObject();
     }

Luego concatenaremos los resultados del descodificador con la proyección de las covariables de los valores predichos.

   if(!Concat(prev.getOutput(), acFeatureProjection[1].getOutput(), 
              cTemporalDecoderInput.getOutput(), iForecast, iForecast, iVariables))
      return false;

La matriz concatenada se suministrará y servirá como datos de entrada para el bloque de decodificador temporal.

   if(!cTemporalDecoder.FeedForward(cTemporalDecoderInput.AsObject()))
      return false;

Al final de las operaciones de pasada directa, sumaremos los resultados de los 2 flujos de datos y normalizaremos el resultado obtenido dentro de canales independientes.

   if(!SumAndNormilize(cGlobalResidual.getOutput(), cTemporalDecoder.getOutput(), Output, 
                                                                         iForecast, true))
      return false;
//---
   return true;
  }

A la pasada directa le seguirá, como siempre, el pasada inversa, que constará de 2 pasos. Primero distribuiremos el gradiente de error entre todos los objetos internos y entradas externas según su impacto en el resultado final en el método CNeuronTiDEOCL::calcInputGradients. En los parámetros, el método obtendrá los punteros a los objetos para registrar los gradientes de error de los datos originales.

bool CNeuronTiDEOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                          CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!cTemporalDecoderInput.calcHiddenGradients(cTemporalDecoder.AsObject()))
      return false;

Recordemos que al intercambiar los búferes de datos, no tendremos necesidad de copiar los datos de los gradientes de error de nuestra clase a los búferes correspondientes de los objetos anidados. Por lo tanto, pasaremos directamente a llamar a los métodos de distribución del gradiente de error de nuestros bloques anidados en orden inverso al paso anterior.

Primero pasaremos el gradiente de error por el bloque de decodificador temporal. Luego distribuiremos el resultado de las operaciones entre el decodificador denso y la proyección de las covariables de la serie predicha.

   int total = (int)acEncoderDecoder.Size();
   if(!DeConcat(acEncoderDecoder[total - 1].getGradient(), acFeatureProjection[1].getGradient(),
                cTemporalDecoderInput.getGradient(), iForecast, iForecast, iVariables))
      return false;

A continuación, distribuiremos el gradiente de error por el bloque del codificador y el decodificador densos.

   for(int i = total - 2; i >= 0; i--)
      if(!acEncoderDecoder[i].calcHiddenGradients(acEncoderDecoder[i + 1].AsObject()))
         return false;
   if(!cEncoderInput.calcHiddenGradients(acEncoderDecoder[0].AsObject()))
      return false;

Después distribuiremos el gradiente de error al nivel de los datos de origen del codificador denso entre los datos históricos de las series temporales multidimensionales y las covariables correspondientes.

   if(!DeConcat(cHistoryInput.getGradient(), acFeatureProjection[0].getGradient(),
                cEncoderInput.getGradient(), iHistory, iHistory, iVariables))
      return false;

Luego ajustaremos el gradiente de error de la capa de realimentación global usando la derivada de la función de activación.

   if(cGlobalResidual.Activation() != None)
     {
      if(!DeActivation(cGlobalResidual.getOutput(), cGlobalResidual.getGradient(),
                       cGlobalResidual.getGradient(), cGlobalResidual.Activation()))
         return false;
     }

Y bajaremos el gradiente de error al nivel de los datos de origen.

   if(!NeuronOCL.calcHiddenGradients(cGlobalResidual.AsObject()))
      return false;

Aquí corregiremos la derivada de la función de activación de la capa anterior según el gradiente de error del segundo flujo de datos.

   if(NeuronOCL.Activation()!=None)
      if(!DeActivation(cHistoryInput.getOutput(),cHistoryInput.getGradient(),
                       cHistoryInput.getGradient(),SecondActivation))
        return false;

A continuación, sumaremos los gradientes de error de ambos flujos de datos.

   if(!SumAndNormilize(NeuronOCL.getGradient(), cHistoryInput.getGradient(),
                       NeuronOCL.getGradient(), iHistory, false, 0, 0, 0, 1))
      return false;

En este paso, transferiremos el gradiente de error al nivel de datos históricos de las series temporales multidimensionales. Y solo nos quedará transmitir el gradiente de error a las covariables.

Aquí debemos decir que este proceso resulta redundante en el ámbito del experimento que estamos realizando. Al fin y al cabo, utilizamos como covariables los armónicos de la marca temporal, que vienen dados por la fórmula. Y no se corrige en el proceso de entrenamiento. Pero, aun así, estamos creando un proceso de transmisión de gradiente a nivel de covariable con un proceso de "preparación para el futuro". Como en experimentos posteriores pueden utilizarse diferentes modelos de entrenamiento de series temporales covariantes.

Primero bajaremos el gradiente de error a partir de las covariables de los datos históricos. Y transferiremos los valores obtenidos al búfer de gradiente de covariables.

   if(!cFeatureInput.calcHiddenGradients(acFeatureProjection[0].AsObject()))
      return false;
   if(!SumAndNormilize(cFeatureInput.getGradient(), cFeatureInput.getGradient(), SecondGradient,
                                                               iFeatures, false, 0, 0, 0, 0.5f))
      return false;

Después, obtendremos los gradientes de las covariables predichas y sumaremos el resultado de los 2 flujos de datos.

   if(!cFeatureInput.calcHiddenGradients(acFeatureProjection[1].AsObject()))
      return false;
   if(!SumAndNormilize(SecondGradient, cFeatureInput.getGradient(), SecondGradient, iFeatures, 
                                                                          false, 0, 0, 0, 1.0f))
      return false;

Si es necesario, corregiremos el gradiente de error usando la derivada de la función de activación.

   if(SecondActivation!=None)
      if(!DeActivation(SecondInput,SecondGradient,SecondGradient,SecondActivation))
        return false;
//---
   return true;
  }

El segundo paso de la pasada inversa consistirá en ajustar los parámetros entrenados del modelo. Esta funcionalidad se organiza en el método CNeuronTiDEOCL::updateInputWeights. El algoritmo de este método es bastante simple. Lo único que haremos es llamar uno a uno al método correspondiente de todos los objetos internos que tengan parámetros entrenados.

bool CNeuronTiDEOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
//---
   if(!cGlobalResidual.UpdateInputWeights(cHistoryInput.AsObject()))
      return false;
   if(!acFeatureProjection[0].UpdateInputWeights(cHistoryInput.AsObject()))
      return false;
   if(!acFeatureProjection[1].UpdateInputWeights(cFeatureInput.AsObject()))
      return false;
//---
   uint total = acEncoderDecoder.Size();
   CNeuronBaseOCL *prev = cEncoderInput.AsObject();
   for(uint i = 0; i < total; i++)
     {
      if(!acEncoderDecoder[i].UpdateInputWeights(prev))
         return false;
      prev = acEncoderDecoder[i].AsObject();
     }
//---
   if(!cTemporalDecoder.UpdateInputWeights(cTemporalDecoderInput.AsObject()))
      return false;
//---
   return true;
  }

Me gustaría decir unas palabras sobre los métodos de trabajo con archivos. Para ahorrar espacio en disco, solo guardaremos las constantes clave y los objetos con parámetros entrenados.

bool CNeuronTiDEOCL::Save(const int file_handle)
  {
   if(!CNeuronBaseOCL::Save(file_handle))
      return false;
//---
   if(FileWriteInteger(file_handle, (int)iHistory, INT_VALUE) < INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle, (int)iForecast, INT_VALUE) < INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle, (int)iVariables, INT_VALUE) < INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle, (int)iFeatures, INT_VALUE) < INT_VALUE)
      return false;
//---
   uint total = acEncoderDecoder.Size();
   if(FileWriteInteger(file_handle, (int)total, INT_VALUE) < INT_VALUE)
      return false;
   for(uint i = 0; i < total; i++)
      if(!acEncoderDecoder[i].Save(file_handle))
         return false;
   if(!cGlobalResidual.Save(file_handle))
      return false;
   for(int i = 0; i < 2; i++)
      if(!acFeatureProjection[i].Save(file_handle))
         return false;
   if(!cTemporalDecoder.Save(file_handle))
      return false;
//---
   return true;
  }

Sin embargo, esto acarreará cierta complejidad en el algoritmo del método de carga de datos CNeuronTiDEOCL::Load. Al igual que antes, el método obtendrá el handle del archivo para cargar los datos en los parámetros. En primer lugar, cargaremos los datos del objeto padre.

bool CNeuronTiDEOCL::Load(const int file_handle)
  {
   if(!CNeuronBaseOCL::Load(file_handle))
      return false;

 A continuación, leeremos los valores de las constantes básicas.

   if(FileIsEnding(file_handle))
      return false;
   iHistory = (uint)FileReadInteger(file_handle);
   if(FileIsEnding(file_handle))
      return false;
   iForecast = (uint)FileReadInteger(file_handle);
   if(FileIsEnding(file_handle))
      return false;
   iVariables = (uint)FileReadInteger(file_handle);
   if(FileIsEnding(file_handle))
      return false;
   iFeatures = (uint)FileReadInteger(file_handle);
   if(FileIsEnding(file_handle))
      return false;

Y luego tendremos que cargar los datos del bloque del codificador y el decodificador densos. Pero aquí nos espera ya el primer matiz. Nosotros leeremos el tamaño de la pila de bloques del archivo de datos. Y este puede ser mayor o menor que el tamaño actual de nuestro array acEncoderDecoder. Así que, de ser necesario, ajustaremos el tamaño del array.

   int total = FileReadInteger(file_handle);
   int prev_size = (int)acEncoderDecoder.Size();
   if(prev_size != total)
      if(ArrayResize(acEncoderDecoder, total) < total)
         return false;

A continuación, organizaremos un ciclo y leeremos los datos del bloque desde el archivo. Sin embargo, antes de que podamos llamar al método para cargar los datos de los elementos del array añadidos, necesitaremos inicializarlos. Esto no se aplica a los objetos creados previamente, ya que se han inicializado en pasos anteriores.

   for(int i = 0; i < total; i++)
     {
      if(i >= prev_size)
         if(!acEncoderDecoder[i].Init(0, i + 2, OpenCL, 1, 1, 1, ADAM, 1))
            return false;
      if(!LoadInsideLayer(file_handle, acEncoderDecoder[i].AsObject()))
         return false;
     }

A continuación, cargaremos objetos de retroalimentación global, las proyecciones de covariables y el decodificador temporal. Aquí no se observan obstáculos ocultos.

   if(!LoadInsideLayer(file_handle, cGlobalResidual.AsObject()))
      return false;
   for(int i = 0; i < 2; i++)
      if(!LoadInsideLayer(file_handle, acFeatureProjection[i].AsObject()))
         return false;
   if(!LoadInsideLayer(file_handle, cTemporalDecoder.AsObject()))
      return false;

En este punto, hemos cargado todos los datos guardados, pero nos quedan objetos auxiliares, que inicializaremos de forma similar al algoritmo de inicialización de clases.

   if(!cHistoryInput.Init(0, total + 5, OpenCL, iHistory * iVariables, optimization, iBatch))
      return false;
   if(!cFeatureInput.Init(0, total + 6, OpenCL, iFeatures, optimization, iBatch))
      return false;
   if(!cEncoderInput.Init(0, total + 7, OpenCL, 2 * iHistory * iVariables, optimization,iBatch))
      return false;
   if(!cTemporalDecoderInput.Init(0, total + 8, OpenCL, 2 * iForecast * iVariables,optimization,
                                                                                        iBatch))
      return false;

Y, si es necesario, realizaremos el intercambio de búferes de datos.

   if(cGlobalResidual.getGradient() != Gradient)
      if(!cGlobalResidual.SetGradient(Gradient))
         return false;
   if(cTemporalDecoder.getGradient() != getGradient())
      if(!cTemporalDecoder.SetGradient(Gradient))
         return false;
//---
   return true;
  }

Podrá ver el código completo de todos los métodos de nuestra nueva clase en el archivo adjunto. Allí también encontrará los métodos auxiliares de la clase que no han sido analizados en este artículo. Su algoritmo es bastante sencillo de aprender de forma autónoma. Vamos a pasar ahora a examinar la arquitectura de los modelos entrenados.

2.2 Arquitectura de los modelos entrenados

Creo que no resulta difícil adivinar que hemos introducido una nueva clase de método TiDE en la arquitectura del Codificador del estado del entorno. Esto es exactamente lo que hemos hecho con todos los algoritmos de predicción de estados futuros de una serie temporal comentados anteriormente. Como recordará, describimos la arquitectura del Codificador en el método CreateEncoderDescriptions. En los parámetros del método especificado obtendremos el puntero a un objeto de array dinámico para registrar la arquitectura del modelo creado.

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

En el cuerpo del método comprobaremos el puntero obtenido y, si es necesario, crearemos una nueva instancia del objeto de array dinámico.

Como antes, introduciremos los datos históricos de origen recibidos del terminal en la entrada del modelo.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Los datos resultantes se procesarán inicialmente en la capa de normalización por lotes, donde se les dará una forma comparable.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Aquí me gustaría recordarle que durante la recopilación de los datos históricos de la descripción del entorno, generaremos los datos usando como base las velas. En cambio, el algoritmo del método TiDE analizará los datos considerando los canales independientes de características individuales. Para conservar la capacidad de usar los búferes de reproducción de experiencias recopilados previamente para entrenar el nuevo modelo, no rediseñaremos el bloque de recopilación de datos. En su lugar, añadiremos una capa de transposición de datos que dará a los datos de origen el aspecto requerido.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y luego estará nuestra nueva capa de aplicación de los enfoques del método TiDE.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTiDEOCL;

El número de canales independientes que debemos analizar será igual al tamaño del vector de descripción de una vela del estado del entorno.

   descr.count = BarDescr;

En este caso, la profundidad de la historia analizada y el horizonte de los valores previstos vendrán determinados por las constantes correspondientes.

   descr.window = HistoryBars;
   descr.window_out = NForecast;

Representaremos la marca temporal como un vector de 4 armónicos: año, mes, semana y día.

   descr.step = 4;

La arquitectura del bloque de codificador-decodificador denso se especificará como un array de valores, tal y como se explica en la construcción de la clase.

   {
      int windows[]={HistoryBars,2*EmbeddingSize,EmbeddingSize,2*EmbeddingSize,NForecast};
      if(ArrayCopy(descr.windows,windows)<=0)
        return false;
   }

Todas las funciones de activación se especificarán en los objetos internos de la clase, por lo que no especificaremos esto aquí.

   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Recordemos que dentro de la capa CNeuronTiDEOCL , la normalización de los datos se realizará varias veces. Y utilizaremos una capa convolucional sin función de activación para corregir el desplazamiento de los valores predichos, que realiza una función de desplazamiento lineal simple dentro de canales independientes.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   descr.step = NForecast;
   descr.window_out = NForecast;
   descr.activation=None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación, transpondremos los valores predichos a la dimensionalidad de la representación original de los datos.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y retornaremos los indicadores estadísticos de la distribución de los datos originales.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = BarDescr*NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Debido al cambio en la arquitectura del Codificador del entorno, habrá 2 cosas a tener en cuenta. La primera será el puntero a la capa de extracción de estados ocultos de los valores del entorno predichos.

#define        LatentLayer             4

La segunda será el tamaño de este estado oculto. A diferencia del artículo anterior, donde la salida del codificador de estados era una descripción de los datos históricos y los valores predichos, ahora solo tendremos los valores predichos. Por consiguiente, deberemos realizar los ajustes oportunos en las arquitecturas de los modelos del Actor y el Crítico.

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic)
  {
//---
........
........
//--- Actor
........
........
//--- layer 2-12
   for(int i = 0; i < 10; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronCrossAttenOCL;
        {
         int temp[] = {1, BarDescr};
         ArrayCopy(descr.units, temp);
        }
        {
         int temp[] = {EmbeddingSize, NForecast};
         ArrayCopy(descr.windows, temp);
        }
      descr.window_out = 32;
      descr.step = 4;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!actor.Add(descr))
        {
         delete descr;
         return false;
        }
     }
........
........
//--- Critic
........
........
//--- layer 2-12
   for(int i = 0; i < 10; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronCrossAttenOCL;
        {
         int temp[] = {1, BarDescr};
         ArrayCopy(descr.units, temp);
        }
        {
         int temp[] = {EmbeddingSize, NForecast};
         ArrayCopy(descr.windows, temp);
        }
      descr.window_out = 32;
      descr.step = 4;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!critic.Add(descr))
        {
         delete descr;
         return false;
        }
     }
........
........
//---
   return true;
  }

Nótese que en esta implementación mantendremos el uso de los algoritmos del Transformer en los modelos del Actor y el Crítico. Al hacerlo, ejecutaremos la atención cruzada respecto a canales independientes de valores de previsión. Sin embargo, también podremos experimentar con el uso de la atención cruzada respecto a los valores de previsión en una sección de velas. No se olvide de cambiar el puntero de la capa de estado oculto del codificador, así como el número de objetos analizados y el tamaño de la ventana de descripción del objeto.

2.3 Asesor de entrenamiento del codificador de estado

La siguiente etapa de nuestro trabajo será el entrenamiento de los modelos. Y aquí necesitábamos algunas mejoras en el algoritmo de los asesores de entrenamiento de modelos. En primer lugar, mejoraremos el trabajo con el modelo de codificador del estado del entorno. Después de todo, este es el modelo en el que añadiremos una nueva clase. En este artículo, no consideraremos con detalle todos los métodos del asesor de entrenamiento del modelo "...\Experts\TiDE\StudyEncoder.mq5", nos centraremos solo en el método de entrenamiento directo del modelo Train.

//+------------------------------------------------------------------+
//| Train function                                                   |
//+------------------------------------------------------------------+
void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);
//---
   vector<float> result, target;
   bool Stop = false;
//---
   uint ticks = GetTickCount();

El principio del método conservará el algoritmo comentado en los artículos anteriores. Aquí podemos ver el consabido trabajo preparatorio.

Le sigue un ciclo de entrenamiento del modelo, en cuyo cuerpo simularemos la trayectoria desde el búfer de reproducción de experiencias y el estado en él.

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * 
                               (Buffer[tr].Total - 2 - NForecast));
      if(i <= 0)
        {
         iter--;
         continue;
        }

AL igual que antes, cargaremos los datos históricos de la descripción del entorno.

      bState.AssignArray(Buffer[tr].States[i].state);

Pero ahora necesitaremos más datos de covariables para generar valores predictivos. Al construir el modelo, acordamos utilizar el armónico de fechas del estado del entorno. Y es de esperar que el modelo aprenda su proyección hacia valores históricos y previstos.

Luego prepararemos el búfer de armónico de la marca temporal.

      bTime.Clear();
      double time = (double)Buffer[tr].States[i].account[7];
      double x = time / (double)(D'2024.01.01' - D'2023.01.01');
      bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_MN1);
      bTime.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_W1);
      bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_D1);
      bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      if(bTime.GetIndex() >= 0)
         bTime.BufferWrite();

Y ahora podremos llamar al método de pasada directa del codificador del estado del entorno.

      //--- State Encoder
      if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, 
                                          (CBufferFloat*)GetPointer(bTime)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

A continuación, prepararemos los valores objetivo como antes.

      //--- Collect target data
      if(!Result.AssignArray(Buffer[tr].States[i + NForecast].state))
         continue;
      if(!Result.Resize(BarDescr * NForecast))
         continue;

Y realizaremos una llamada al método de pasada inversa del Codificador.

      if(!Encoder.backProp(Result, GetPointer(bTime), GetPointer(bTimeGradient)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Nótese aquí que en los parámetros del método de pasada inversa, además de los valores objetivo, especificaremos los punteros a los búferes de los armónicos de marca temporal y sus gradientes de error. A primera vista, no utilizamos gradientes de error y podríamos haber sustituido los gradientes por un búfer de los armónicos propios. Al fin y al cabo, en futuros trabajos no utilizaremos los gradientes de error de armónicos. Y los propios armónicos se sobrescribirán en la siguiente iteración. ¿Para qué crear un búfer adicional en la memoria?

Quiero advertirle contra este movimiento precipitado. La cuestión es que tras la distribución del gradiente de error, realizaremos un ajuste de los parámetros del modelo. Para ajustar los pesos, cada capa utilizará el gradiente de error en la salida de la capa y los datos originales. En consecuencia, si sobrescribimos los armónicos de la marca temporal con los gradientes de error, obtendremos gradientes distorsionados de los coeficientes de peso cuando actualicemos los parámetros de su proyección sobre las covariables de los datos históricos y los estados predichos. Y como consecuencia, obtendremos un ajuste distorsionado de los parámetros del modelo. No creo que haga falta decir que, en tal caso, el entrenamiento de los modelos irá en una dirección impredecible.

Una vez ejecutadas con éxito las operaciones de pasada directa e inversa del Codificador, informaremos al usuario del progreso del proceso de entrenamiento y pasaremos a la siguiente iteración del ciclo de entrenamiento.

      if(GetTickCount() - ticks > 500)
        {
         double percent = double(iter) * 100.0 / (Iterations);
         string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", percent, 
                                                         Encoder.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

El proceso de entrenamiento del modelo se repetirá hasta que se completa el número especificado de iteraciones del ciclo, especificado en los parámetros del ciclo externo. Y una vez finalizado el entrenamiento, borraremos el campo de comentarios de la ficha del instrumento.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder",
                                                        Encoder.getRecentAverageError());
   ExpertRemove();
//---
  }

Después enviaremos los resultados del entrenamiento del modelo al registro del terminal e inicializaremos la finalización del asesor experto.

En el asesor de entrenamiento del modelo del Actor y del Crítico "...\Experts\TiDE\Study.mq5" también realizaremos ajustes similares en el modelo de Codificador del entorno. Pero no nos detendremos ahora en su descripción. Después de todo, con la descripción anterior podremos encontrar fácilmente bloques similares en el código del EA por nosotros mismos. Asimismo, usted podrá encontrar el código completo del EA en el archivo adjunto. Los asesores de interacción con el entorno y de recogida de datos de entrenamiento también se presentarán allí y contendrán ediciones similares.

3. Simulación

Más arriba, nos hemos familiarizado con el nuevo método Time-series Dense Encoder(TiDE) de previsión de series temporales e implementado nuestra visión de los enfoques propuestos usando MQL5.

Como ya hemos mencionado, hemos conservado la estructura de los datos de origen de los modelos anteriores, lo cual nos permite utilizar datos recopilados previamente para entrenar los nuevos modelos.

Permítanme recordarles que todos los modelos son entrenados con los datos históricos de EURUSD y el marco temporal H1. Resulta natural que, a medida que se escriban los artículos, también cambie el tiempo fuera de nuestra ventana. Por el momento, utilizaremos los datos históricos reales de 2023 para entrenar los modelos. La prueba de los modelos entrenados se realizará en el simulador de estrategias de MetaTrader 5 para los datos de enero de 2024. El periodo de pruebas seguirá al de entrenamiento para evaluar las capacidades del modelo con nuevos datos fuera de la muestra de entrenamiento. De este modo, maximizaremos las condiciones cuando el modelo se ejecute en tiempo real con datos recién llegados que resulten físicamente desconocidos en el momento en que se entrena el modelo.

Como en varios artículos anteriores, el modelo de codificador del estado del entorno será independiente del estado de la cuenta y de las posiciones abiertas. Por tanto, podremos entrenar el modelo incluso en una muestra de entrenamiento con una sola pasada de interacción con el entorno hasta obtener la precisión deseada en la predicción de estados futuros. Naturalmente, la "precisión de predicción deseada" no podrá superar las capacidades del propio modelo. Debemos recordar que "no se le pueden pedir peras al olmo".

Tras entrenar el modelo de predicción de los estados del entorno, pasaremos a la segunda etapa: el entrenamiento de la política de comportamiento del Actor. En esta fase, entrenaremos de forma iterativa los modelos del Actor y el Crítico con actualizaciones periódicas del búfer de reproducción de experiencias.

Recordemos que al actualizar el búfer de reproducción de experiencias, nos estaremos refiriendo a la recopilación adicional de la experiencia de interacción con el entorno respecto a la política de comportamiento actual del Actor. Al fin y al cabo, el entorno de los mercados financieros que estamos analizando es bastante polifacético, y no podemos recopilar plenamente todas sus manifestaciones en el búfer de reproducción de experiencias. Solo tomaremos un diminuto corte del pequeño entorno de acciones de la actual política del Actor. Analizando el corte obtenido, daremos un pequeño paso hacia la optimización de la política de comportamiento de nuestro Actor. Y a medida que nos acercamos a los límites de esta corte, tendremos que recoger datos adicionales implicando la zona visible en las proximidades de la política del Actor actualizada.

Como resultado de las iteraciones anteriores, podremos entrenar una política del Actor capaz de generar beneficios tanto en las muestras de entrenamiento como en las de prueba.

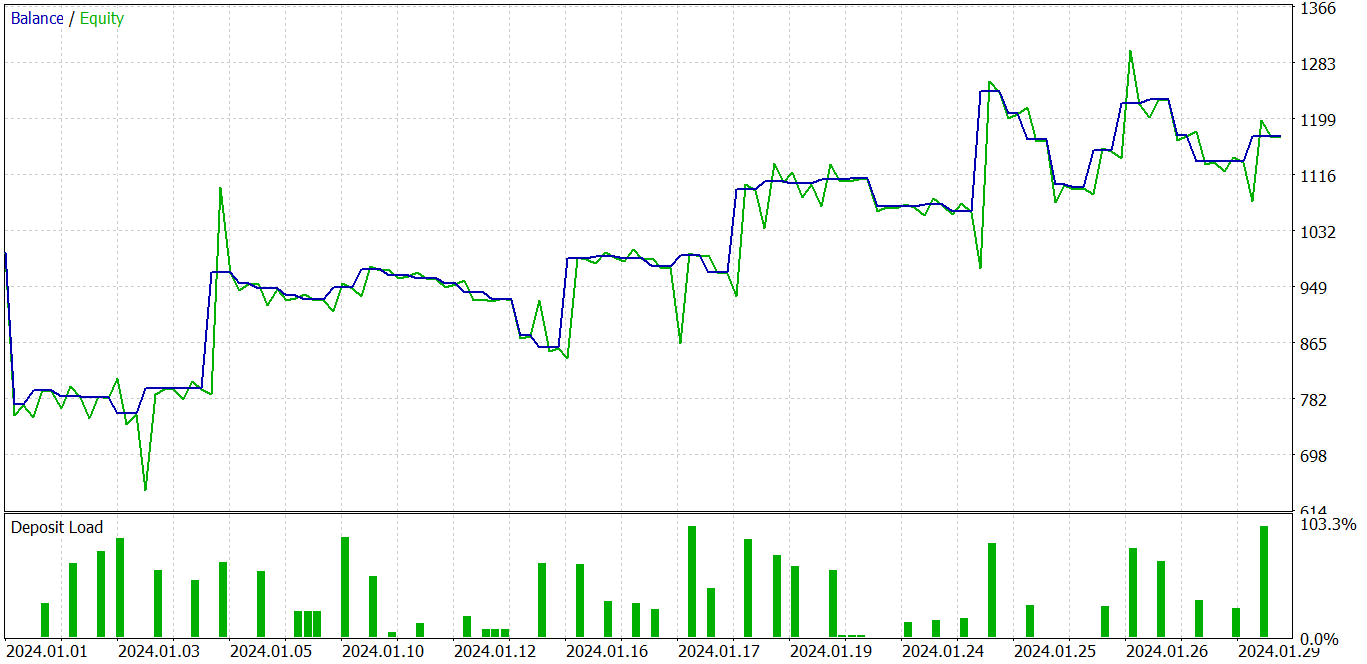
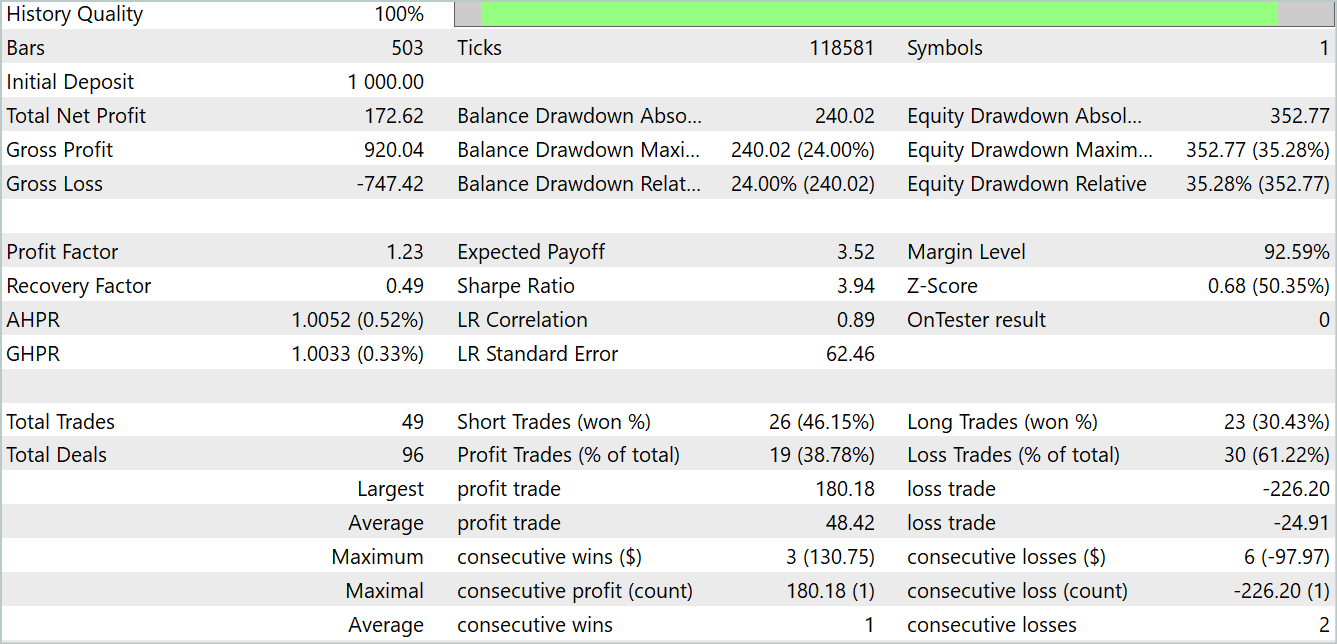
En el gráfico anterior, podemos ver una operación perdedora al principio, a la que sigue una clara tendencia rentable. Sí, la proporción de transacciones rentables es inferior al 40%. Prácticamente por cada transacción rentable tenemos 2 perdedoras. No obstante, observamos que las transacciones perdedoras son mucho menores que las rentables. La media de transacciones rentables es casi 2 veces superior a la media de transacciones perdedoras. Todo ello permite al modelo obtener beneficios en el periodo de prueba. Al final de la prueba, el factor de beneficio ha sido de 1,23.

Conclusión

En este artículo hemos presentado el modelo original TiDE (Time-series Dense Encoder) para la previsión de series temporales a largo plazo. Este modelo difiere de los modelos lineales clásicos y de los transformadores en que utiliza perceptrones multicapa (MLP) tanto para codificar los datos y covariables pasados como para descodificar predicciones futuras.

Los experimentos implementados por los autores del método demuestran que la aplicación de modelos MLP tiene un gran potencial en el campo de la resolución de problemas de análisis y previsión de series temporales. Además, el TiDE tiene una complejidad computacional lineal, a diferencia del Transformer, lo cual lo hace más eficiente a la hora de tratar grandes cantidades de datos.

En la parte práctica del presente artículo, hemos plasmado nuestra visión de los enfoques propuestos, que difiere ligeramente de la del autor. No obstante, los resultados obtenidos nos permiten destacar la eficacia del enfoque propuesto. Y sí, el entrenamiento de modelos resulta mucho más rápido que el de los Transformers comentado anteriormente.

Enlaces

• Long-term Forecasting with TiDE: Time-series Dense Encoder
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de cobros de ejemplo Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	StudyEncoder.mq5	Asesor	Asesor de entrenamiento del Codificador
5	Test.mq5	Asesor	Asesor para la prueba de modelos
6	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
7	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
8	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL