MetaTrader 5 / 例
English Русский Deutsch Português
preview
母集団アルゴリズムのハイブリダイゼーション：逐次構造と並列構造

母集団アルゴリズムのハイブリダイゼーション：逐次構造と並列構造

MetaTrader 5 — 例 | 19 8月 2024, 14:53
23 0
Andrey Dik
Andrey Dik

内容

1. はじめに
2. GWOとCOAの実験
3. ESGとSDSmの実験
4. 終わりに


1. はじめに

最適化アルゴリズムハイブリダイゼーションの3つの主な選択肢を考えてみましょう。

1. アルゴリズム検索戦略を1つに混ぜる：各アルゴリズムは、それぞれ独自のスキルと能力を備えています。両者の論理構造を混ぜることで、成功という共通の追求においてさまざまな特性が生まれます。これはさまざまなスタイルのダンスで、それぞれのステップが全体の動きを補い、引き立てます。このようなアプローチの例として、以前の記事で取り上げた遺伝的アルゴリズムと組み合わせたバクテリア採餌最適化があります。

2. バトンタッチのように、反復を一方の部分的な作業と他方の最終的な作業に分けることで、各アルゴリズムを一貫して動作させます。アルゴリズムはスポーツチームのようなもので、それぞれがレースの各ステージに特化しています。両者の間でバトンを渡すということは、知識と結果の伝達を意味し、よく調整されたチームの調和のように、ある段階から次の段階へのスムーズで効率的な移行を生み出し、反復の総数は変わりません。

3. 各アルゴリズムの並列動作と、それに続く独自の最良の結果の組み合わせは、各アルゴリズムが共通の世界というキャンバスに独自のエネルギーを注ぎ込む芸術家である集団的創造性に似ています。各反復で、最良の結果が結合されます。一筆一筆が、研究中の問題の理解を補完し、拡大し、最適解の共通ビジョンを生み出します。

このようなアルゴリズムハイブリダイゼーションは、異なるアプローチや戦略をクリエイティブに組み合わせる大きな機会を提供し、新たな発見や最適化の改善につながります。芸術の世界においてさまざまなスタイルやテクニックがユニークな作品の創造を促すように、さまざまなアルゴリズムを調和的に組み合わせることで、最適な結果を導き出し、複雑な問題を効率的に探索することができます。

選択肢の空間における一歩一歩が重要な、最適解検索の世界では、検索するだけでなく、望む結果を得るために自信を持って検索することも重要です。以前の記事でおこなった母集団最適化アルゴリズムの分野における実験的研究では、最大点に到達するために最小点にアルゴリズムを強制的に配置させるというもので、成功の初期条件依存性という重要な側面が明らかになりました。最小点から離れるのが難しく、効率が落ちるものもありましたが、開始位置にほとんど依存せず、普遍的な安定性を示す輝かしいアルゴリズムもありました。プロセスの初期段階でその空間の探索に成功したものもあれば、後の段階で結果を改善しようと試みたアルゴリズムもありました。各アルゴリズムが持つこれらのユニークな特徴をうまく利用することで、それぞれの長所を伸ばし、短所を減らすことができます。さまざまな戦略を組み合わせることで、空間をうまく探索し、作業のさまざまな段階で結果を改善できる、より効率的な手法につながるでしょう。標準化のおかげで、アルゴリズムのハイブリダイゼーションがより身近になったことも付け加えておきたいと思います。現在では、すべての母集団アルゴリズムが1つのクラスにまとめられており、創造的な組み合わせやまったく新しい可能性への扉が開かれています。


2. GWOとCOAの実験

この実験では、性能も特徴も異なる2つのアルゴリズムを取り上げます。GWOとCOAmです。GWOがランキング表の最下位に位置しているのに対し、COAmは中位に位置しています。逐次操作と並列操作でこれらの組み合わせを使用して、どのような結果が得られるか試してみましょう。この記事では、検索戦略の論理的要素を混ぜることは考えません。なぜなら、これは各アルゴリズムの組み合わせに非常に特有なことであり、1つの記事の枠内で考えることはできないからです。

灰色オオカミオプティマイザ(GWO)は、灰色オオカミの群れの狩りをシミュレートしたメタヒューリスティック確率的アルゴリズムです。
GWOアルゴリズムの主な特徴は以下の通りです。

  • 群れの行動をシミュレート：このアルゴリズムは、オオカミの群れの階層構造を利用しており、それぞれのオオカミが異なる役割（アルファ、ベータ、デルタ、オメガ）を果たします。
  • 最大値を探す：アルファ、ベータ、デルタのオオカミは最も適応力が高いとされ、獲物に最も近く、他のオオカミはこれらのオオカミに近づく傾向があります。GWOは急速に全域的極値に向かいます。
  • 適応力：アルゴリズムが機能するにつれて、オオカミは常に配置を変え、変化する状況に適応できるようになります。

カッコー最適化アルゴリズム(COAm)は、自然から着想を得た最新のヒューリスティックアルゴリズムのひとつです。一部のカッコー種の寄生が元になっています。
COAmアルゴリズムの主な特徴は以下の通りです。

  • カッコーの行動をシミュレート：このアルゴリズムは、カッコーが他の鳥の巣に卵を産み付けるという繁殖戦略を用いています。
  • 最大値を探す：巣の中の卵は最適化問題の可能な解と解釈され、カッコーの卵は新しい解を表します。
  • 適応力：カッコーの卵が巣主の卵より高品質であれば、巣主の卵は置き換えられことになります。そうでなければ、巣主の卵が巣に残ります。
したがって、これらのアルゴリズムのハイブリダイゼーションは、それらの利点を組み合わせて、より効率的に最適化問題を解くことができるようになると考えられます。図1は、GWOとCOAmの動作のシーケンス図です。第1段階が終了し、GWOにいくつかの反復が割り当てられると、1つのアルゴリズムのエージェントの状態があと1つのアルゴリズムに移されます。各エージェントは新しい種に生まれ変わり（この場合、オオカミはカッコーに変わる）、個体群の中での地位は維持されます。

    GWOCOA

    図1：ハイブリッドアルゴリズム、GWO+COA

    では、予想される成り行きを見てみましょう。

    1. 開始
       - 限られたリソースである1万回の反復から始めるので、最適解を得るためには各反復が重要です。
    2. ステップ1（反復0～5000）
       - 総反復回数を半分に分け、GWOアルゴリズムから始めます。
       - 探索空間全体にオオカミが急速に拡散します。期間の半ばまでに、オオカミはすぐに潜在的な全域的極値に収束します。
    3. ステップ2（反復5000～10000）
       - 最初の5000回の反復の後、これらのオオカミの位置をカッコーの位置とします。
       - レヴィの飛行によるカッコー検索は、極限をさらに洗練させるためのバトンを受け取ります。
    4. 結果
    - このGWOアルゴリズムとレヴィの飛行を用いたカッコー探索の組み合わせの結果、限られた反復回数で、より正確で安定した大域的極値を達成できるようになると期待されています。

    従って、この戦略を用いることで、収束の速さと結果の正確さのバランスを確保しながら、限られた反復回数で大域的極値探索を最適化することができます。

    C_AO_GWO_COAmクラスを宣言します。このクラスはC_AOクラスを継承します。クラスのコンストラクタで、popSize母集団サイズやGWOとCOAmアルゴリズム間のratioのような最適化パラメータのデフォルト値を設定します。このクラスでは、2つのアルゴリズムの逐次操作を使用することができます。処理は通常と同じで、テストスタンドを変更することなく使用することができます。

    このクラスでは、パラメータの設定(SetParams)、最適化の初期化(Init)、大域解の移動(Moving)と更新(Revision)、エージェントへの座標値の挿入(Injection)のメソッドも定義しています。

    このクラスの重要な変数には、ratio（GWOとCOAmの比率）、およびそれぞれ灰色オオカミオプティマイザとカッコー最適化アルゴリズムを実装するためのC_AO_GWOとC_AO_COAmクラスオブジェクトがあります。

    また、各アルゴリズム（GWOとCOAm）のエポック数と現在のエポックを追跡するための変数を持っています。

    //——————————————————————————————————————————————————————————————————————————————
class C_AO_GWO_COAm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_GWO_COAm () { }
  C_AO_GWO_COAm ()
  {
    ao_name = "GWO_COAm";
    ao_desc = "Grey Wolf Optimizer and Cuckoo Optimization Algorithm M";

    popSize = 50;    //population size
    ratio   = 0.5;   //the ratio of GWO and COAm

    ArrayResize (params, 2);

    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "ratio";   params [1].val = ratio;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    ratio   = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving    ();
  void Revision  ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  double ratio;  //the ratio of GWO and COAm

  private: //-------------------------------------------------------------------
  C_AO_GWO  AO1;
  C_AO_COAm AO2;

  int epochCount;
  int epochNow;

  int epochGWO;
  int epochCOAm;
};
//——————————————————————————————————————————————————————————————————————————————

    C_AO_GWO_COAmクラスのInitメソッドは、最適化プロセスの初期化に使用されます。ここで初期値が設定され、エージェントが作成され、GWOとCOAmアルゴリズムの初期化パラメータが設定されます。

    1. 標準的な初期化の成功は、StandardInitメソッドを使用して検証されます。StandardInitメソッドは、渡されたパラメータを使用して最小検索範囲と最大検索範囲を設定します。
    2. GWOとCOAmの各アルゴリズムのエポック数は、ratioとエポック数(epochCount)の合計に基づいて計算されます。
    3. GWOおよびCOAmアルゴリズムのパラメータは、SetParamsおよびInitメソッドを使用して設定および初期化されます。
    4. このメソッドは、初期化に成功すればtrueを返します。

    このメソッドは、与えられたパラメータと制約条件下で問題を最適化するためのGWOとCOAmアルゴリズムの初期設定と初期化を提供します。

    //——————————————————————————————————————————————————————————————————————————————
bool C_AO_GWO_COAm::Init (const double &rangeMinP  [], //minimum search range
                          const double &rangeMaxP  [], //maximum search range
                          const double &rangeStepP [], //step search
                          const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochCount   = epochsP;
  epochNow     = 0;

  epochGWO  = int(epochCount *ratio);
  epochCOAm = epochCount - epochGWO;

  AO1.params [0].val = popSize;
  AO2.params [0].val = popSize;

  AO1.SetParams ();
  AO2.SetParams ();

  AO1.Init (rangeMinP, rangeMaxP, rangeStepP, epochGWO);
  AO2.Init (rangeMinP, rangeMaxP, rangeStepP, epochCOAm);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_GWO_COAmクラスのMovingメソッドのコードでは、変数epochNowの値が1つ増えます。epochNowカウンタは、GWOとCOAmがそれぞれ動作する段階を決定するために使用されます。

    epochNowがepochGWOよりも小さい場合、AO1 (GWO)オブジェクトに対してMovingメソッドが呼ばれ、その後「AO1.a」エージェント配列の要素が「a」エージェント配列にコピーされます。

    epochNowがepochGWOに等しい場合、AO2 (COAm)オブジェクト上でMovingメソッドが呼び出され、「AO1.a」配列の値が 「AO2.a」配列の対応する要素に挿入されます。これはまさにオオカミがカッコウに変化する現象です。最後に、「AO2.a」配列の全要素が「a」配列にコピーされ、実行プログラムの「a」エージェントにアクセスします。

    このメソッドは、選択されたGWOとCOAmアルゴリズムに従って、各最適化エポックでエージェントが順次移動することを保証します。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Moving ()
{
  epochNow++;

  if (epochNow < epochGWO)
  {
    AO1.Moving ();
    for (int i = 0; i < popSize; i++)
    {
      a [i] = AO1.a [i];
    }
    return;
  }

  AO2.Moving ();

  if (epochNow == epochGWO)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        AO2.Injection (i, c, AO1.a [i].c [c]);
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    a [i] = AO2.a [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

    Revisionメソッドは、算出されたエージェントの適応値を、対応するアルゴリズムのエージェントに送信します。

    epochNowおよびepochGWO変数の値に応じて、GWOまたはCOAmアルゴリズムに対して以下のアクションが実行されます。

    1. 適応値をエージェントにコピーする
    2. Revisionメソッドを実行する
    3. 大域解を更新する

    したがって、このメソッドは、対応するアルゴリズムの現在の実行段階に応じて、GWOとCOAmアルゴリズムからの解で大域解を更新するロジックを実装しています。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Revision ()
{
  if (epochNow < epochGWO)
  {
    for (int i = 0; i < popSize; i++) AO1.a [i].f = a [i].f;

    AO1.Revision ();

    if (AO1.fB > fB)
    {
      fB = AO1.fB;
      ArrayCopy (cB, AO1.cB, 0, 0, WHOLE_ARRAY);
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++) AO2.a [i].f = a [i].f;

    AO2.Revision ();

    if (AO2.fB > fB)
    {
      fB = AO2.fB;
      ArrayCopy (cB, AO2.cB, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    このハイブリッドアルゴリズムの動作を可視化すると、次のような現象が浮き彫りになります。GWOはしばしば局所的な極値で立ち往生し、その急速な動きを早々に止めてしまいます。対照的に、COAアルゴリズムは様々な結果の軌跡を残し、時に印象的な終点の範囲を作り出します。

    Hilly

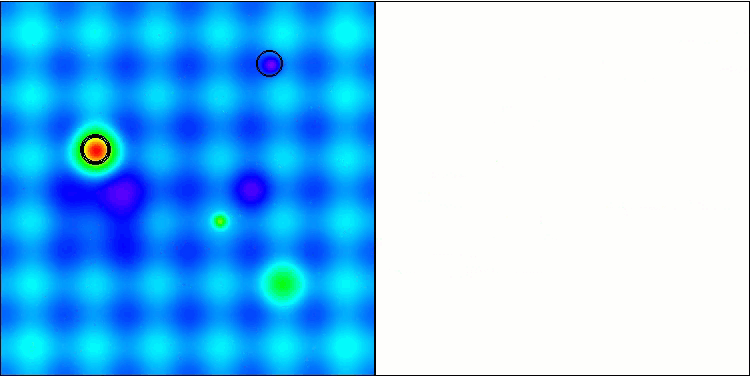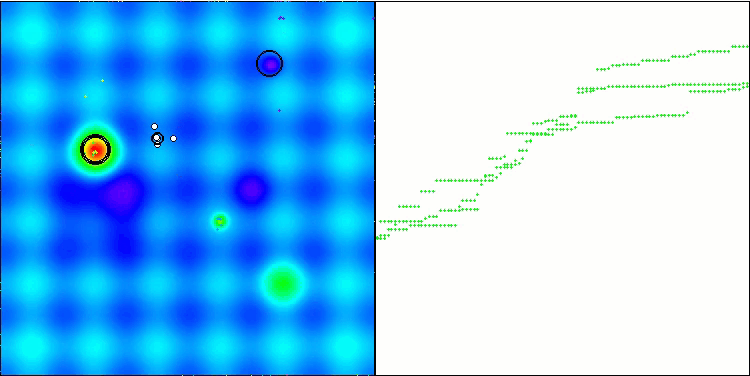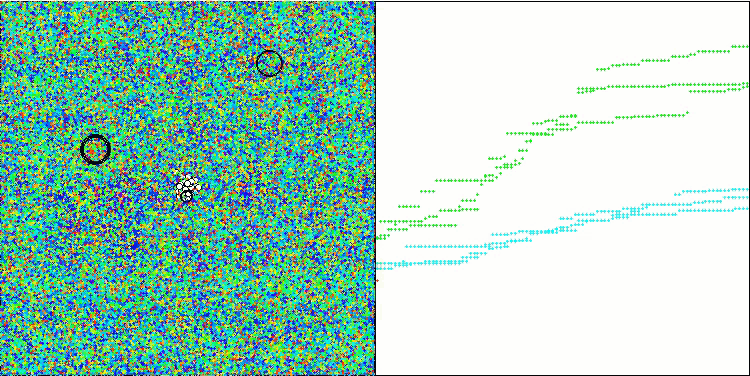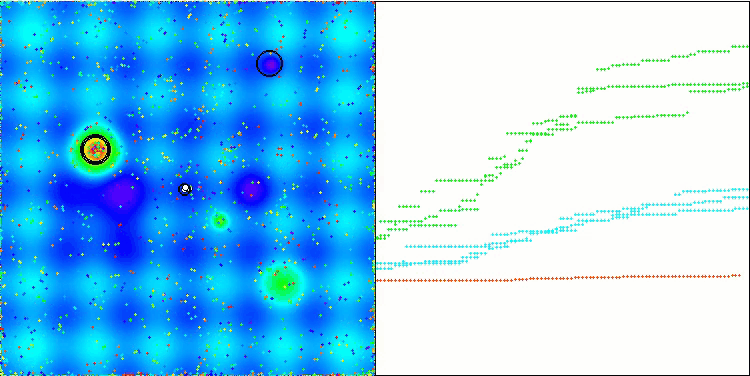
    Hillyテスト関数のGWO-COAm

    Forest

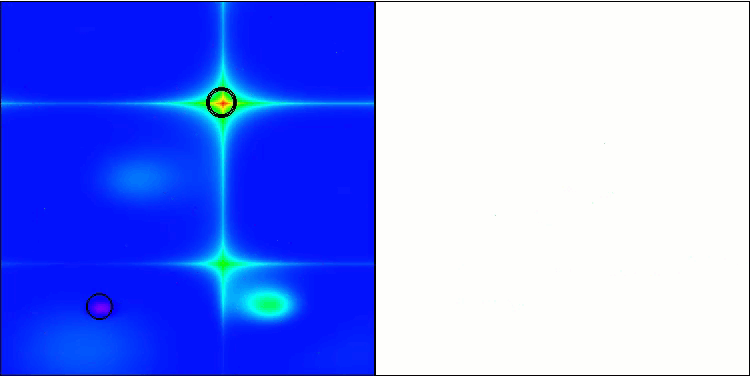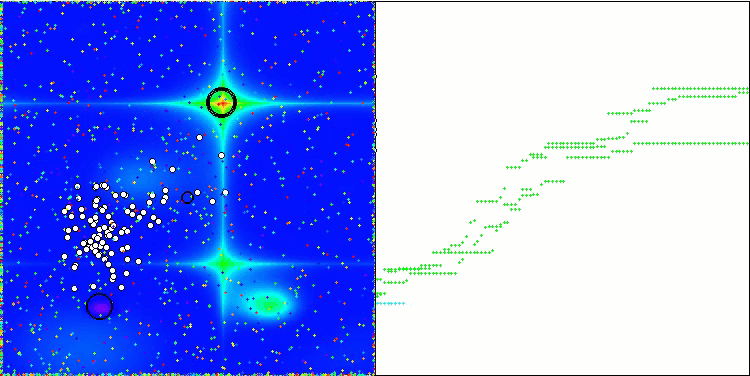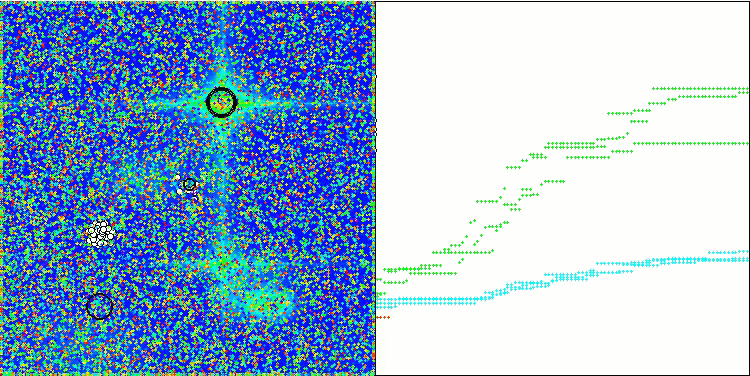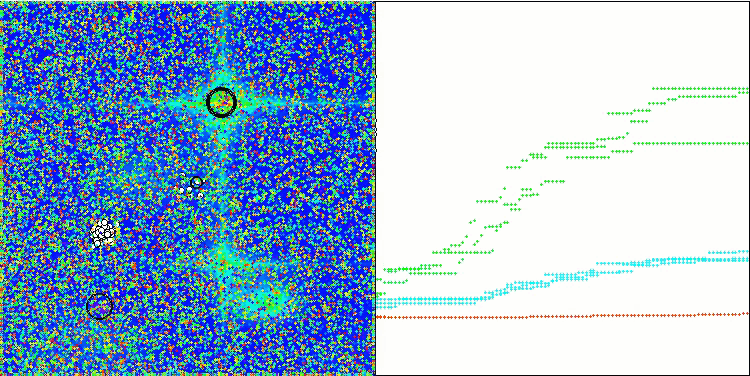
    Forestテスト関数のGWO-COAm

    Megacity

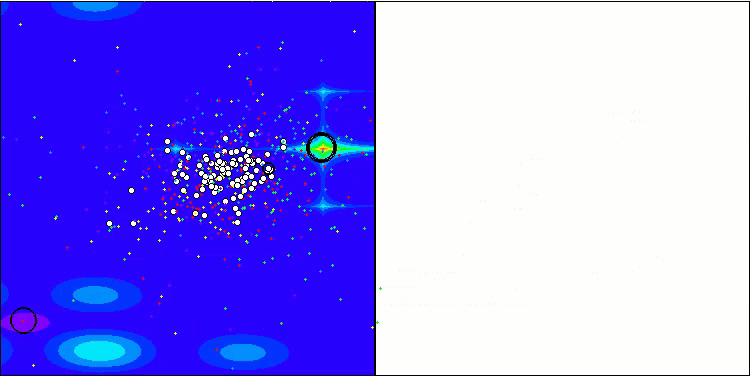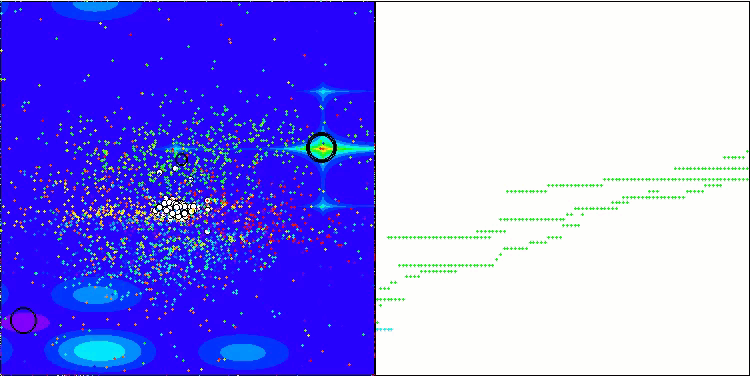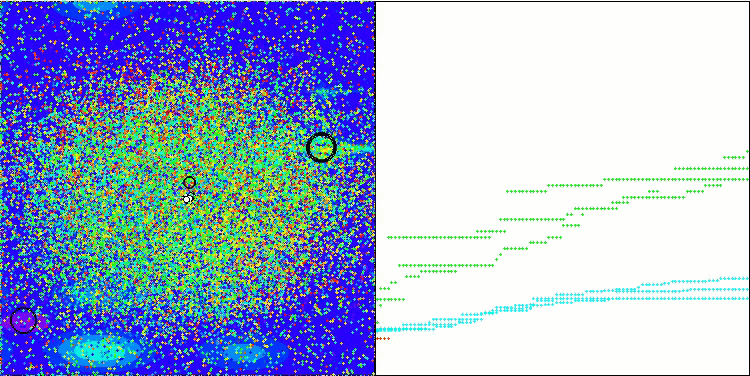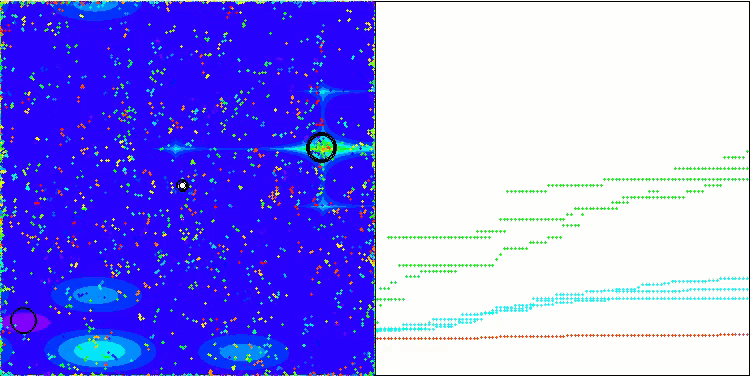
    Megacityテスト関数のGWO-COAm

    そこで、GWOアルゴリズムとCOAmアルゴリズムを順次組み合わせてハイブリッドアルゴリズムを作成する実験をおこないました。しかし、これは望ましい結果（ベストのパフォーマンスを向上させる）にはつながりませんでした。GWOはしばしば極大値で止まって動きが止まる一方、COAmアルゴリズムはバトンを受け取ることができず、実験実行回数によって最終結果に大きなばらつきがあるのが特徴です。

    GWO-COAmテストスタンドの結果（逐次構造）は次の通りです。

    GWO_COAm|Grey Wolf Optimizer and Cuckoo Optimization Algorithm M|50.0|0.3|
    =============================
    5 Hilly's; Func runs:10000; result:0.729041499138184
    25 Hilly's; Func runs:10000; result:0.4465971838522985
    500 Hilly's; Func runs:10000; result:0.2685674823439256
    =============================
    5 Forest's; Func runs:10000; result:0.6963174902735325
    25 Forest's; Func runs:10000; result:0.347940898514357
    500 Forest's; Func runs:10000; result:0.16776831572853218
    =============================
    5 Megacity's; Func runs:10000; result:0.5492307692307692
    25 Megacity's; Func runs:10000; result:0.2464615384615385
    500 Megacity's; Func runs:10000; result:0.10724615384615484
    =============================
    All score:3.55917 (39.55%)

    結果は、COAm単独作戦と遜色ありません。改善は見られますが、残念ながら些細なものです。ただし、個々の独立した実行では、COAmが同等の結果を出すこともあります。

    独立して動作するだけでなく、共通の目標のために互いに最適解を交換する2つのアルゴリズムのエージェントの最適な位置を各反復で交換する並列作業を組み合わせたハイブリッドを作成してみましょう。

    次に、GWOとCOAmアルゴリズムの並列演算を使用してみましょう。そのためには、ジョイントアルゴリズムのクラスを変える必要はありません。大幅な変更が必要なメソッドのコードのみを提供します。

    逐次構成とは異なり、ここでは両アルゴリズムのMovingメソッドを一度に起動します。この後、これらのアルゴリズムのエージェントを結合クラスのエージェントにコピーし、その後適応度関数を計算します。したがって、このメソッドは2つのオブジェクトAO1とAO2のデータを現在オブジェクトの配列「a」に結合します。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Moving ()
{
  AO1.Moving ();
  AO2.Moving ();

  int cnt = 0;
  for (int i = 0; i < popSize / 2; i++)
  {
    a [cnt] = AO1.a [i];
    cnt++;
  }

  for (int i = 0; i < popSize / 2; i++)
  {
    a [cnt] = AO2.a [i];
    cnt++;
  }
}
//——————————————————————————————————————————————————————————————————————————————

    並列操作構造のMovingメソッドの違いは次のとおりです。適合値をAO1およびAO2オブジェクトエージェントに転送し、それらのRevisionメソッドを実行して大域的な解を更新した後、エージェントは1つのアルゴリズムから別のアルゴリズムにペアでコピーされます。つまり、2つの最良のエージェントがアルゴリズム間で交換されることで、両アルゴリズムが互いの最良の特性を充実させ、問題解決のパフォーマンスを向上させることができます。このアプローチにより、各アルゴリズムが達成した最良解を共有することができます。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Revision ()
{
  int cnt = 0;

  for (int i = 0; i < popSize / 2; i++)
  {
    AO1.a [i].f = a [cnt].f;
    cnt++;

    if (AO1.a [i].f > fB)
    {
      fB = AO1.a [i].f;
      ArrayCopy (cB, AO1.a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  for (int i = 0; i < popSize / 2; i++)
  {
    AO2.a [i].f = a [cnt].f;
    cnt++;

    if (AO2.a [i].f > fB)
    {
      fB = AO2.a [i].f;
      ArrayCopy (cB, AO2.a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  AO1.Revision ();
  AO2.Revision ();
  
  S_AO_Agent temp [];
  ArrayResize (temp, popSize / 2);
  
  for (int i = 0; i < 2; i++) temp [i] = AO1.a [i]; 

  for (int i = 0; i < 2; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      AO1.Injection (i, coords - 1, AO2.a [i].c [c]);
      AO2.Injection (i, coords - 1, temp  [i].c [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    GWO-COAmテストスタンドの結果（平行構造）は次の通りです。

    GWO_COAm|Grey Wolf Optimizer and Cuckoo Optimization Algorithm M|50.0|
    =============================
    5 Hilly's; Func runs:10000; result:0.6930620289919492
    25 Hilly's; Func runs:10000; result:0.4389512737634269
    500 Hilly's; Func runs:10000; result:0.26733735583025275
    =============================
    5 Forest's; Func runs:10000; result:0.6512995888741085
    25 Forest's; Func runs:10000; result:0.33119611021722106
    500 Forest's; Func runs:10000; result:0.16858175021299981
    =============================
    5 Megacity's; Func runs:10000; result:0.4615384615384615
    25 Megacity's; Func runs:10000; result:0.23015384615384615
    500 Megacity's; Func runs:10000; result:0.1059538461538471
    =============================
    All score:3.34807 (37.20%)

    残念ながら、パフォーマンスの向上は見られません。


    3. ESGとSDSmの実験

    上述したGWOとCOAmのハイブリダイゼーションオプションでは、「重みカテゴリ」が異なるアルゴリズムが使用されました。互いに補完し合えるように、似たような能力を持つアルゴリズムを使用するのが合理的です。そこで、逐次構造と並列構造を用いて、さらに2つの実験をおこないます。これを実現するために、ESGとSDSmアルゴリズムを使用します。

    この2つのアルゴリズムをハイブリッドに組み合わせることで、ランダム性とソーシャルダイナミクスのユニークな組み合わせを生み出すことができます。

    確率拡散探索(SDSm)は母集団最適化アルゴリズムです。

    アルゴリズムの主な特徴は以下の通りです。

    • 解の部分的評価：エージェントは仮説（探索問題に対する解の候補）の部分的な評価をおこない、アルゴリズムの計算量を減らします。
    • 有望な解の配布：エージェントは直接個体的なコミュニケーションを通じて、仮説に関する情報を交換します。質の高い解は、同じ仮説を持つエージェントのクラスタから特定することができます。
    • 数学的正当性：SDSmには深い数学的根拠があり、信頼性と予測性を高めています。

    SDSmは、ランダム探索と拡散を組み合わせた進化的最適化手法で、高次元空間の最適化問題を解きます。

    社会集団の進化(ESG)は、多母集団最適化アルゴリズムです。

    アルゴリズムの主な特徴は以下の通りです。

    • 社会的グループ：このアルゴリズムは、個々の粒子ではなく、協力と経験の交換によって結ばれた社会的集団によって作動します。各集団には意思決定の中心があり、最適化エージェントとして粒子の集合を持ちます。
    • 集団的な動き：社会的集団内の粒子は相互作用し、パラメータ空間で一緒に動きます。これにより、各集団はパラメータ空間の異なる領域を探索し、見つかった最適解に関する情報を共有することができます。
    • 局地的および大域的の経験：各社会的集団は、その中で最適解に関する情報（局所的経験）を保存しています。また、全集団の中で総合的なベストスコアもあります（大域的経験）。

    ESGは、収束性が高く、必要な計算量が少ないシンプルなアーキテクチャです。

    逐次操作と並列操作の実験をおこなうためのコードは、GWOとCOAmの代わりにこれらのクラスの対応するオブジェクトの宣言を置き換える必要があることを除けば、上記とまったく同じです。

    ESG-SDSmテストスタンドの結果（逐次構造）は次の通りです。

    ESG_SDSm|Evolution_of_Social_Groups and Stochastic Diffusion Search M|200.0|0.5|
    =============================
    5 Hilly's; Func runs:10000; result:0.9642488921252973
    25 Hilly's; Func runs:10000; result:0.7526240638447592
    500 Hilly's; Func runs:10000; result:0.2961693434072249
    =============================
    5 Forest's; Func runs:10000; result:0.9897783503200446
    25 Forest's; Func runs:10000; result:0.7608845505131734
    500 Forest's; Func runs:10000; result:0.2130287247171918
    =============================
    5 Megacity's; Func runs:10000; result:0.82
    25 Megacity's; Func runs:10000; result:0.5421538461538462
    500 Megacity's; Func runs:10000; result:0.11932307692307798
    =============================
    All score:5.45821 (60.65%)

    ESG-SDSmテストスタンドの結果（平行構造）は次の通りです。

    ESG_SDSm|Evolution_of_Social_Groups and Stochastic Diffusion Search M|200.0|
    =============================
    5 Hilly's; Func runs:10000; result:0.9561232188424761
    25 Hilly's; Func runs:10000; result:0.7493199026465321
    500 Hilly's; Func runs:10000; result:0.3176797705433513
    =============================
    5 Forest's; Func runs:10000; result:0.9726744619317564
    25 Forest's; Func runs:10000; result:0.7494321306074204
    500 Forest's; Func runs:10000; result:0.22498291462144127
    =============================
    5 Megacity's; Func runs:10000; result:0.836923076923077
    25 Megacity's; Func runs:10000; result:0.5261538461538462
    500 Megacity's; Func runs:10000; result:0.13435384615384738
    =============================
    All score:5.46764 (60.75%)

    逐次と並列のハイブリダイゼーション構造の結果は、確率的アルゴリズムの通常の誤差に非常に近いことが判明しました。これらのアルゴリズムの個別演算結果よりもわずかに低くなります。


    4. まとめ

    本稿でハイブリダイゼーションの構成要素として検討したアルゴリズムは、現在のランキング表のさまざまな位置をカバーし、各アルゴリズムの性能の違いが全体的な結果に与える影響を理解するために選択しました。バランスの取れた分析と最終結果への影響を公平に比較するために、検索能力においてアルゴリズムがほぼ同等であることが重要なのでしょうか。

    本稿では、様々な最適化アルゴリズムをハイブリダイゼーションの構成要素として考えました。ここでの目標は、現在のランキング表で異なるポジションを占めるアルゴリズムを幅広くカバーし、各アルゴリズムのパフォーマンスの違いが全体的な結果にどのように影響するかを調べることでした。

    検索能力においてアルゴリズムがほぼ同等であることが重要かどうかは、まだ未解決の問題です。最良の解決策を見つけることが主な目的であれば、これは問題ではないかもしれません。

    実験には、GWOやCOAなど、その能力が大きく異なるアルゴリズムを選択しました。これらのアルゴリズムは、最適化に対する2つの異なるアプローチを表しており、これらを組み合わせることで貴重な教訓を得ることができます。対照的に、ESGやSDSmのような性能のよく似たアルゴリズムも選択しました。

    以下は現在のアルゴリズムのランキング表です。これまで説明したすべてのアルゴリズムが含まれており、新しいデータが入手可能になれば更新されます。

    表

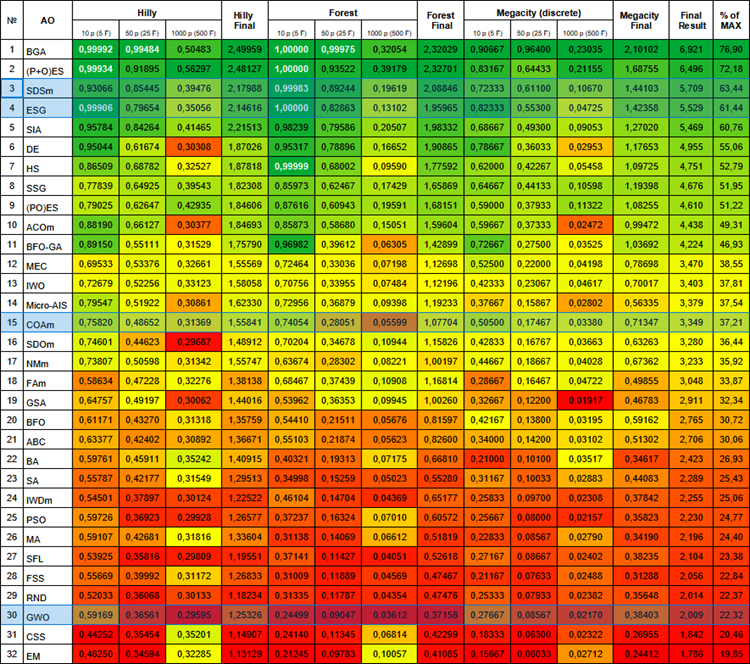
    母集団アルゴリズムの評価表

    ESGとSDSmアルゴリズムエージェントの並列作業とベストポジションの交換、そして逐次構造を組み合わせたハイブリッド方式を作ろうとしたとき、曖昧な現象に遭遇しました。研究の過程で、この2つのアプローチを組み合わせても、相乗効果や強化にはつながらず、平均的な結果にしかならないことがわかりました。これらの異なる戦略間の相互作用が十分に効率的でなかったために、それぞれの核となる原則が完全に統合されなかったのでしょう。

    実験の結果、このような条件下では、逐次的なハイブリダイゼーション構造も並列的なハイブリダイゼーション構造も望ましい結果をもたらさないことが明らかになり、うまく組み合わせるためのアルゴリズムを慎重に選択することの重要性が浮き彫りになりました。アルゴリズムが初期段階で一定の性質を備えていることが必要です。つまり、検索がうまくても精緻化が不十分であったり、あるいはその逆であったりします。この場合のみ、ハイブリダイゼーション手法が両方のアルゴリズムの性能を向上させることができます。アルゴリズミックロジックの融合によるハイブリダイゼーションの成功体験（最初の構造による）は、このアプローチの可能性を浮き彫りにしていますが、最適な結果を得るためには、自明ではない努力、慎重な介入、共同融合ロジックの開発が必要です。

    この観察は、アルゴリズムの個々の特性だけでなく、ハイブリダイゼーションの文脈における相互作用の重要性を浮き彫りにしています。自然界で、異なる種の組み合わせが独自の適応をもたらすように、最適化の世界でもアルゴリズムの組み合わせには微調整と調和が必要です。おそらく、予想外の組み合わせや失敗の中にこそ、最適化の分野における新たな発見や改善の鍵があるのでしょう。

    この経験は、ハイブリッド最適化手法を作成する際に、アルゴリズムを注意深く分析し、選択することの重要性を浮き彫りにしています。最適解を見出すことに成功するためには、各アルゴリズムの個々の特性だけでなく、特定のタスクの枠内での相互作用も考慮に入れる必要があります。

    試し、創造し、組み合わせるのです。いつものように、すべてのツールとソースコードを以下に添付します。

    MetaQuotes Ltdによってロシア語から翻訳されました。
    元の記事: https://www.mql5.com/ru/articles/14389

    添付されたファイル |
    ZIPをダウンロード
    The_world_of_AO_Hybrid.zip (41 KB)
    警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

    この著者による他の記事

    ディスカッションに移動
    最適化アルゴリズムの効率における乱数生成器の品質の役割 最適化アルゴリズムの効率における乱数生成器の品質の役割
    この記事では、メルセンヌ・ツイスタ乱数生成器を取り上げ、MQL5の標準的な乱数生成器と比較します。また、乱数生成器の品質が最適化アルゴリズムの結果に与える影響についても調べます。
    手動取引のリスクマネージャー 手動取引のリスクマネージャー
    この記事では、手動取引用のリスクマネージャークラスをゼロから書く方法について詳しく説明します。このクラスは、自動化プログラムを使用するアルゴリズムトレーダーが継承するための基本クラスとしても使用できます。
    ニューラルネットワークが簡単に（第80回）：Graph Transformer Generative Adversarial Model (GTGAN) ニューラルネットワークが簡単に（第80回）：Graph Transformer Generative Adversarial Model (GTGAN)
    この記事では、2024年1月に導入された、グラフ制約のある建築レイアウト生成の複雑な問題を解くためのGTGAN (Graph Transformer Generative Adversarial Model)アルゴリズムについて知ろうと思います。
    多通貨エキスパートアドバイザーの開発（第5回）：可変ポジションサイズ 多通貨エキスパートアドバイザーの開発（第5回）：可変ポジションサイズ
    前回開発中のエキスパートアドバイザー(EA)は、固定されたポジションサイズのみを使用して取引をおこなうことができました。これはテスト用には許容できますが、実際の口座で取引する場合にはお勧めできません。可変のポジションサイズで取引できるようにしましょう。