Hybridization of population algorithms. Sequential and parallel structures

Contents

1. Introduction
2. Experimenting with GWO and COA
3. Experimenting with ESG and SDSm
4. Conclusions

1. Introduction

Let's consider three main options for hybridizing optimization algorithms:

1. Mixing algorithm search strategies into one. Each algorithm features its own set of skills and abilities. Mixing their logical structures provides a variety of properties in the common pursuit of success. This is a dance of various styles, where each step complements and enhances the overall movement. An example of such an approach is the Bacterial Foraging Optimization combined with the genetic algorithm discussed in one of the previous articles.

2. Consistent operation of each of the algorithms by dividing iterations into partial work of one and the final work of the other, like passing a baton. Algorithms are like sports teams, each of which specializes in its own stage of the race. Passing the baton between them implies the transfer of knowledge and results, creating a smooth and efficient transition from one stage to the next, like the harmony of a well-coordinated team, leaving the total number of iterations unchanged.

3. The parallel operation of each algorithm with the subsequent combination of unique best results resembles collective creativity, where each algorithm is an artist, putting its unique energy into the common world canvas. At each iteration, the best results are merged. Each stroke complements and expands the understanding of the problem under study, creating a common vision of the optimal solution.

These algorithmic hybridization options provide significant opportunities for creative combinations of different approaches and strategies, leading to new discoveries and improvements in optimization. Just like in the world of art a variety of styles and techniques inspire the creation of unique works, the harmonious combination of different algorithms can lead to optimal results and efficient exploration of complex problems.

In the world of finding optimal solutions, where every step in the space of options matters, it is important not only to search, but also to find with confidence to achieve the desired result. The experimental study we conducted in a previous article in the field of population optimization algorithms, where we forced algorithms to be placed at the global minimum point in order to reach the global maximum point, revealed an important aspect: the dependence of success on initial conditions. Some algorithms had difficulty leaving the minimum point, losing efficiency, but others were shining examples of universal stability with little dependence on the starting position. Some of them successfully explored the space early in the process, while others attempted to improve the results in later stages. These unique features of each algorithm can be successfully used, enhancing their positive aspects and reducing their disadvantages. We hope that combining different strategies can lead to more efficient methods that can successfully explore space and improve results at different stages of the work. It is important to add that thanks to standardization, hybridization of algorithms has become more accessible. Now all population algorithms are brought into a single class, which opens the door to creative combinations and completely new possibilities.

2. Experimenting with GWO and COA

For this experiment, we will take two algorithms that have different performance and features: GWO and COAm. While GWO is located at the very bottom of the ranking table, COAm is located in the middle. Let's try to find out what results can be achieved using their combinations in sequential and parallel operation. We will not consider mixing logical elements of search strategies in this article, since this is very specific to each combination of algorithms and cannot be considered within the framework of one article.

Grey Wolf Optimizer (GWO) is a metaheuristic stochastic algorithm based on the simulated hunting of a pack of gray wolves.
GWO algorithm main features:

• Simulating pack behavior. The algorithm uses a hierarchical structure of a wolf pack, where each wolf plays a different role (alpha, beta, delta, omega).
  
• Search for a global maximum. Alpha, beta and delta wolves are considered the most adaptable and are closest to the prey, while other wolves tend to get closer to them. GWO is rapidly heading towards a potential global extreme.
  
• Adaptability. As the algorithm works, the wolves are constantly rearranging themselves, which allows them to adapt to changing conditions.
  

Cuckoo Optimization Algorithm (COAm) is one of the latest heuristic algorithms inspired by nature. It is based on the parasitism of some cuckoo species.
COAm algorithm main features:

• Simulating cuckoo behavior. The algorithm uses a cuckoo breeding strategy, where the cuckoo lays its eggs in the nests of other birds.
• Search for a global maximum. The eggs in the nest are interpreted as possible solutions to the optimization problem, and the cuckoo egg represents the new solution.
  
• Adaptability. If the cuckoo egg is of higher quality than the parent egg, then it will be replaced. Otherwise, the parent egg will remain in the nest.

Thus, hybridizing these algorithms will presumably allow their combined advantages to be used to solve optimization problems more efficiently. Figure 1 shows a sequential diagram of the GWO and COAm operation. Upon completion of the first stage, when some iterations are allocated to GWO, the states of agents of one algorithm are transferred to another. Each of the agents is reborn into a new species (in this case the wolf turns into a cuckoo) where the position of the individuals is maintained in the population.

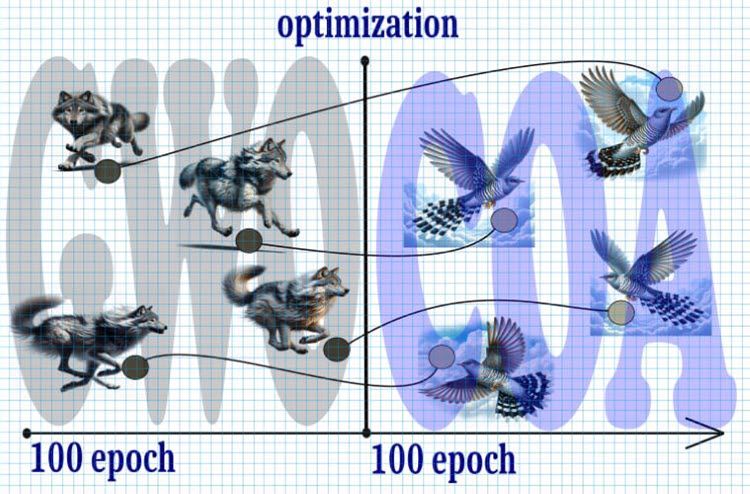
Figure 1. Hybrid algorithm, GWO+COA

Let's take a look at the probable course of events:

1. Start:
   - We start with 10,000 iterations, which is a limited resource, so each iteration is critical to achieve the optimal solution.
2. Step 1 (0—5000 iterations):
   - Divide the total number of iterations in half and start with the GWO algorithm.
   - Due to the rapid spread of wolves across the search space, they quickly converge to a potential global extremum by the middle of the period.
3. Step 2 (5000 — 10000 iterations):
   - After the first 5000 iterations, we adopt the position of the wolves to the position of the cuckoos at these points.
   - Cuckoo search with the Levy flight receives the baton to further refine the extremum.
4. Result:
- It is expected that as a result of this combination of GWO algorithms and cuckoo search with Levy flight, we will be able to achieve a more accurate and stable global extremum in a limited number of iterations.

Thus, the use of this strategy will allow optimizing the search for a global extremum in a limited number of iterations ensuring a balance between the speed of convergence and the accuracy of the result.

Declare the "C_AO_GWO_COAm" class, which is an inheritor of the "C_AO" class. The class constructor sets default values for optimization parameters such as the "popSize" population size and the "ratio" between the GWO and COAm algorithms. The class will allow using the sequential operation of two algorithms, while handling it will remain the same as usual and will allow us to use our test stand without changes.

The class also defines the methods for setting parameters (SetParams), initializing optimization (Init), moving (Moving) and updating (Revision) the global solution, and inserting (Injection) coordinate values into agents.

Important variables in the class include "ratio" (the ratio between GWO and COAm), as well as C_AO_GWO and C_AO_COAm class objects for implementing the Grey Wolf Optimizer and Cuckoo Optimization Algorithm, respectively.

The class also has variables to track the number of epochs and the current epoch for each of the algorithms (GWO and COAm).

//——————————————————————————————————————————————————————————————————————————————
class C_AO_GWO_COAm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_GWO_COAm () { }
  C_AO_GWO_COAm ()
  {
    ao_name = "GWO_COAm";
    ao_desc = "Grey Wolf Optimizer and Cuckoo Optimization Algorithm M";

    popSize = 50;    //population size
    ratio   = 0.5;   //the ratio of GWO and COAm

    ArrayResize (params, 2);

    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "ratio";   params [1].val = ratio;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    ratio   = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving    ();
  void Revision  ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  double ratio;  //the ratio of GWO and COAm

  private: //-------------------------------------------------------------------
  C_AO_GWO  AO1;
  C_AO_COAm AO2;

  int epochCount;
  int epochNow;

  int epochGWO;
  int epochCOAm;
};
//——————————————————————————————————————————————————————————————————————————————

The Init method in the C_AO_GWO_COAm class is used to initialize the optimization process. This is where initial values are set, agents are created, and initialization parameters are set for the GWO and COAm algorithms.

1. The success of standard initialization is verified using the StandardInit method, which uses the passed parameters to set the minimum and maximum search range.
2. The number of epochs for each of the GWO and COAm algorithms is calculated based on the "ratio" and the total number of epochs (epochCount).
3. Parameters for the GWO and COAm algorithms are set and initialized using the SetParams and Init methods.
4. The method returns "true" if initialization is successful.

The method provides the initial setup and initialization of the GWO and COAm algorithms to optimize the problem with given parameters and constraints.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_GWO_COAm::Init (const double &rangeMinP  [], //minimum search range
                          const double &rangeMaxP  [], //maximum search range
                          const double &rangeStepP [], //step search
                          const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochCount   = epochsP;
  epochNow     = 0;

  epochGWO  = int(epochCount *ratio);
  epochCOAm = epochCount - epochGWO;

  AO1.params [0].val = popSize;
  AO2.params [0].val = popSize;

  AO1.SetParams ();
  AO2.SetParams ();

  AO1.Init (rangeMinP, rangeMaxP, rangeStepP, epochGWO);
  AO2.Init (rangeMinP, rangeMaxP, rangeStepP, epochCOAm);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

The value of the "epochNow" variable increases by one in the code of the Moving method of the C_AO_GWO_COAm class. The "epochNow" counter is used to determine the stages, at which GWO and then COAm respectively operate.

If "epochNow" is less than "epochGWO", then the Moving method is called for the AO1 (GWO) object, after which the elements of the "AO1.a" agent array are copied to the "a" agent array.

If "epochNow" is equal to "epochGWO", the Moving method is called on the "AO2" (COAm) object, and the values from the "AO1.a" array are then inserted into the corresponding elements of the "AO2.a" array, i.e. this is the very transformation of wolves into cuckoos. Finally, all elements of the "AO2.a" array are copied into the "a" array to access the "a" agents in the executing program.

This method ensures that the agents move sequentially at each optimization epoch in accordance with the selected GWO and COAm algorithms.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Moving ()
{
  epochNow++;

  if (epochNow < epochGWO)
  {
    AO1.Moving ();
    for (int i = 0; i < popSize; i++)
    {
      a [i] = AO1.a [i];
    }
    return;
  }

  AO2.Moving ();

  if (epochNow == epochGWO)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        AO2.Injection (i, c, AO1.a [i].c [c]);
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    a [i] = AO2.a [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

The Revision method transmits the calculated fitness value of the agents to the corresponding agents of the algorithms.

Depending on the value of the "epochNow" and "epochGWO" variables, the following actions are performed for the GWO or COAm algorithms:

1. Copying the fitness value to agents.
2. Executing the Revision method.
3. Performing a global solution update.
   

Thus, the method implements the logic of updating the global solution with the solution from the GWO and COAm algorithms, depending on the current stage of execution of the corresponding algorithms.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Revision ()
{
  if (epochNow < epochGWO)
  {
    for (int i = 0; i < popSize; i++) AO1.a [i].f = a [i].f;

    AO1.Revision ();

    if (AO1.fB > fB)
    {
      fB = AO1.fB;
      ArrayCopy (cB, AO1.cB, 0, 0, WHOLE_ARRAY);
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++) AO2.a [i].f = a [i].f;

    AO2.Revision ();

    if (AO2.fB > fB)
    {
      fB = AO2.fB;
      ArrayCopy (cB, AO2.cB, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

The visualization of the hybrid algorithm operation highlights the following phenomenon: GWO often gets stuck in local extrema, prematurely stopping its rapid movement. In contrast, the COA algorithm leaves behind a trail of varied results creating a sometimes impressive range of end points.

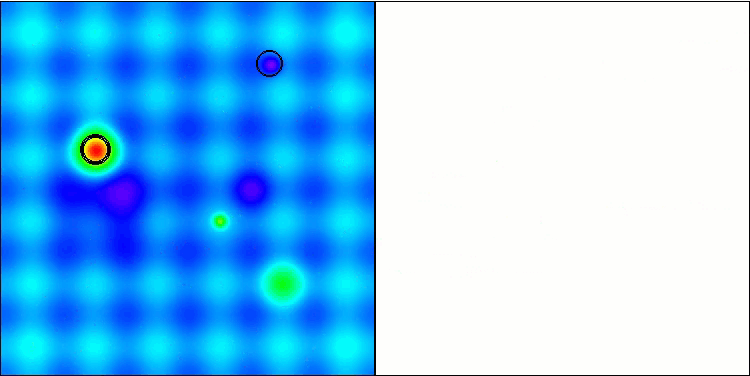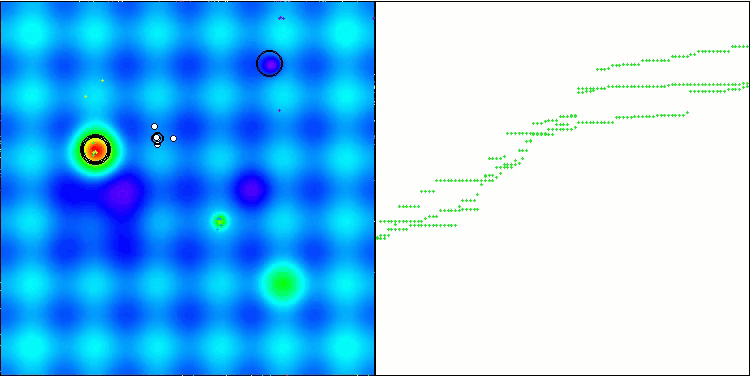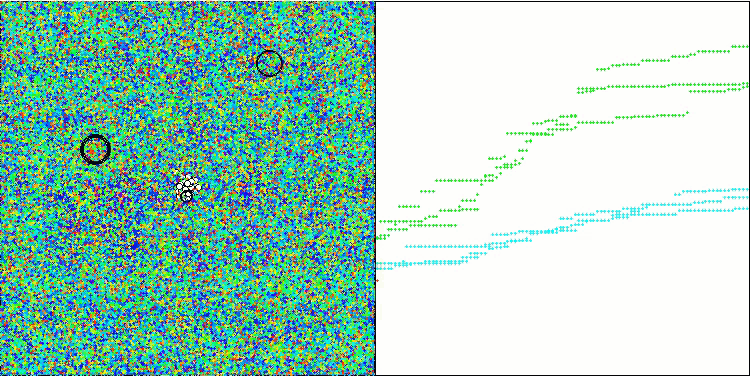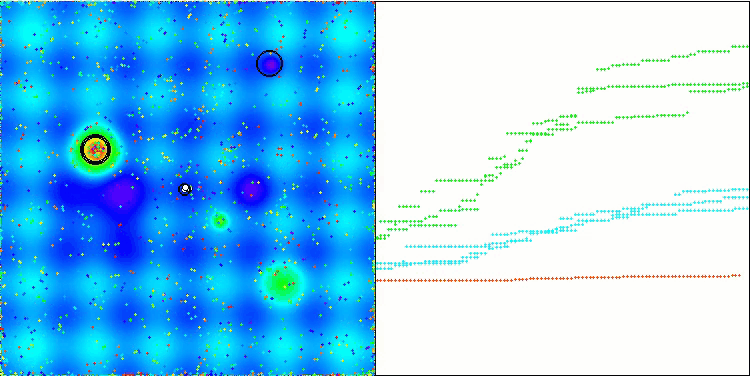
GWO-COAm on the Hilly test function

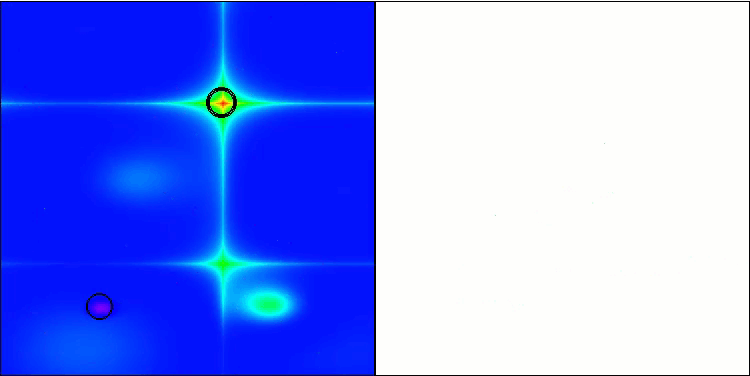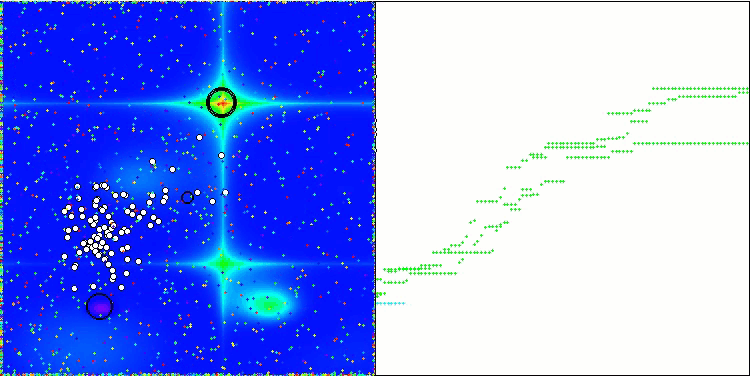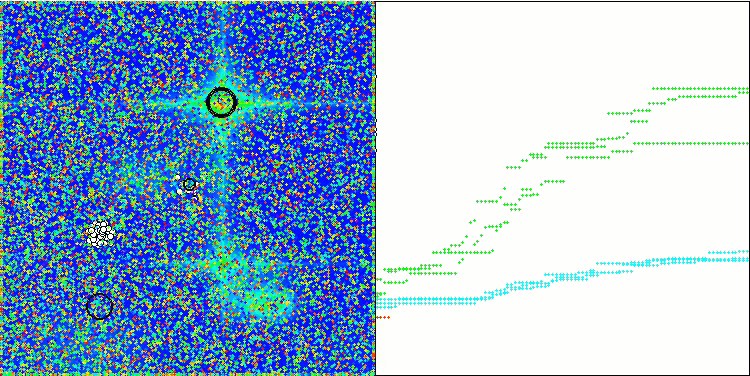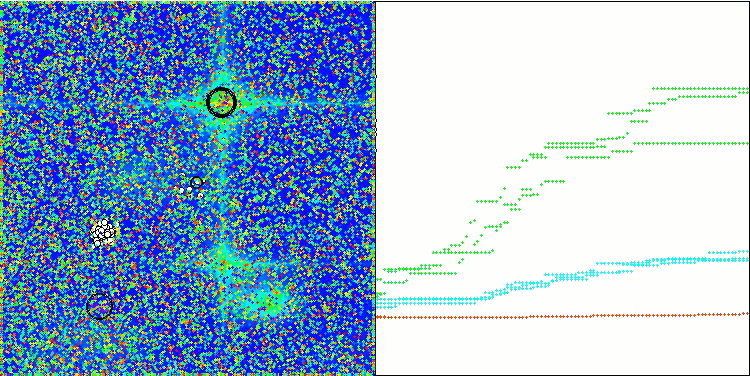
GWO-COAm on the Forest test function

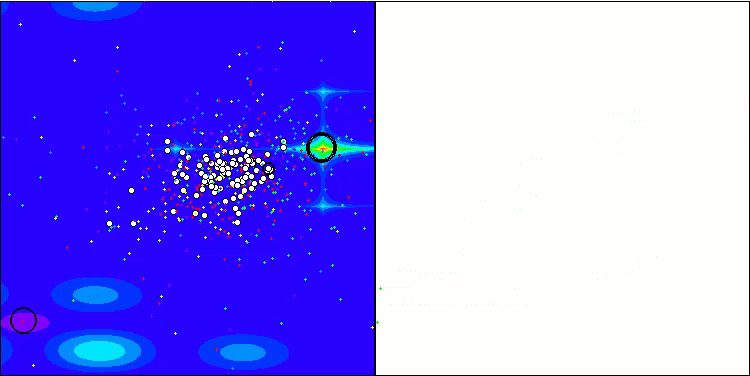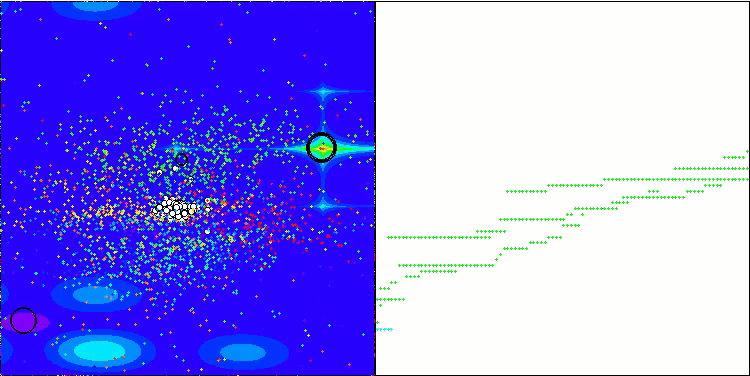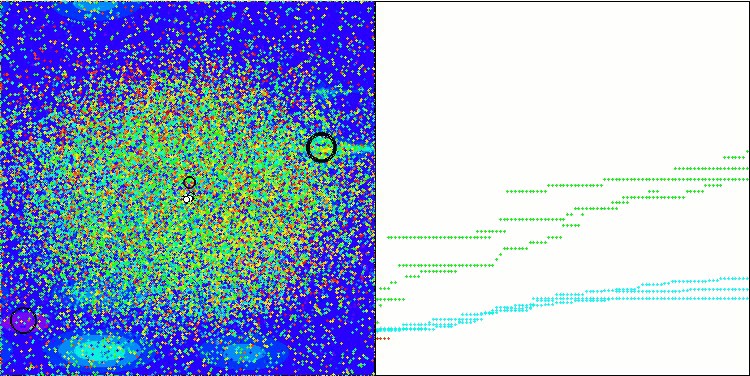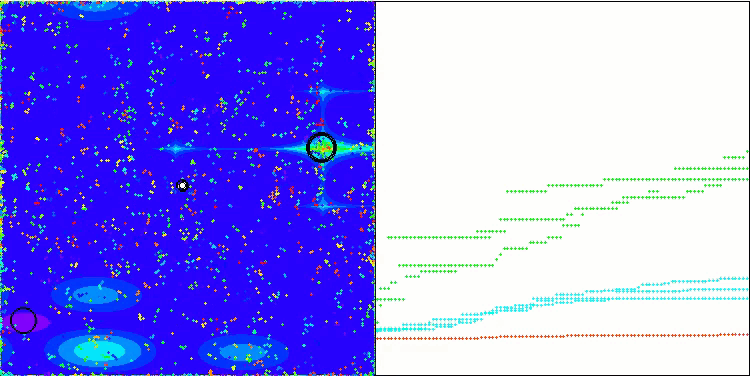
GWO-COAm on the Megacity test function

So, we conducted an experiment trying to create a hybrid algorithm by combining the GWO and COAm algorithms sequentially. However, this did not lead to the desired results (improving the performance of the best one). GWO often gets stuck in local maxima and stops moving, while the COAm algorithm was unable to pick up the baton and is characterized by a large scatter in the final results, depending on the number of experimental runs.

GWO-COAm test stand results (sequential structure):

GWO_COAm|Grey Wolf Optimizer and Cuckoo Optimization Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.729041499138184
25 Hilly's; Func runs: 10000; result: 0.4465971838522985
500 Hilly's; Func runs: 10000; result: 0.2685674823439256
=============================
5 Forest's; Func runs: 10000; result: 0.6963174902735325
25 Forest's; Func runs: 10000; result: 0.347940898514357
500 Forest's; Func runs: 10000; result: 0.16776831572853218
=============================
5 Megacity's; Func runs: 10000; result: 0.5492307692307692
25 Megacity's; Func runs: 10000; result: 0.2464615384615385
500 Megacity's; Func runs: 10000; result: 0.10724615384615484
=============================
All score: 3.55917 (39.55%)

The result is comparable to that of COAm separate operation. There is an improvement, but, unfortunately, it is insignificant. However, in individual independent runs, COAm sometimes produces comparable results.

Let's try to create a hybrid that combines parallel work with the exchange at each iteration of the best positions of the agents of two algorithms that will not only work independently, but also exchange the best solutions with each other for a common goal.

Now let's try to use the parallel operation of the GWO and COAm algorithms. To do this, we practically do not have to change the class of the joint algorithm. I will only provide the code of the methods that require significant changes.

Unlike the sequential structure, here we launch the Moving methods of both algorithms at once. After this, copy the agents of these algorithms into the agents of the combined class for subsequent fitness function calculation. Thus, the method combines the data from two objects "AO1" and "AO2" into the "a" current object array.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Moving ()
{
  AO1.Moving ();
  AO2.Moving ();

  int cnt = 0;
  for (int i = 0; i < popSize / 2; i++)
  {
    a [cnt] = AO1.a [i];
    cnt++;
  }

  for (int i = 0; i < popSize / 2; i++)
  {
    a [cnt] = AO2.a [i];
    cnt++;
  }
}
//——————————————————————————————————————————————————————————————————————————————

The differences of the Moving method for the parallel operation structure are as follows: after transferring fitness values to the "AO1" and "AO2" object agents, executing their Revision methods and updating the global solution, the agents are copied from one algorithm to another in pairs. This means that the two best agents are exchanged between the algorithms, which helps both algorithms enrich each other's best characteristics and improve their performance in solving problems. This approach allows the best solutions achieved by each algorithm to be shared.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Revision ()
{
  int cnt = 0;

  for (int i = 0; i < popSize / 2; i++)
  {
    AO1.a [i].f = a [cnt].f;
    cnt++;

    if (AO1.a [i].f > fB)
    {
      fB = AO1.a [i].f;
      ArrayCopy (cB, AO1.a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  for (int i = 0; i < popSize / 2; i++)
  {
    AO2.a [i].f = a [cnt].f;
    cnt++;

    if (AO2.a [i].f > fB)
    {
      fB = AO2.a [i].f;
      ArrayCopy (cB, AO2.a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  AO1.Revision ();
  AO2.Revision ();
  
  S_AO_Agent temp [];
  ArrayResize (temp, popSize / 2);
  
  for (int i = 0; i < 2; i++) temp [i] = AO1.a [i]; 

  for (int i = 0; i < 2; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      AO1.Injection (i, coords - 1, AO2.a [i].c [c]);
      AO2.Injection (i, coords - 1, temp  [i].c [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

GWO-COAm test stand results (parallel structure):

GWO_COAm|Grey Wolf Optimizer and Cuckoo Optimization Algorithm M|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6930620289919492
25 Hilly's; Func runs: 10000; result: 0.4389512737634269
500 Hilly's; Func runs: 10000; result: 0.26733735583025275
=============================
5 Forest's; Func runs: 10000; result: 0.6512995888741085
25 Forest's; Func runs: 10000; result: 0.33119611021722106
500 Forest's; Func runs: 10000; result: 0.16858175021299981
=============================
5 Megacity's; Func runs: 10000; result: 0.4615384615384615
25 Megacity's; Func runs: 10000; result: 0.23015384615384615
500 Megacity's; Func runs: 10000; result: 0.1059538461538471
=============================
All score: 3.34807 (37.20%)

Unfortunately, there are no performance improvements.

3. Experimenting with ESG and SDSm

In the GWO and COAm hybridization options discussed above, algorithms from different "weight categories" were used. It is reasonable to use algorithms that are similar in capabilities so that they truly complement each other. Therefore, we will conduct two more experiments using sequential and parallel structures. To achieve this, we will use the ESG and SDSm algorithms.

Combining these two algorithms into a hybrid can create a unique combination of randomness and social dynamics.

Stochastic Diffusion Search (SDSm) is a population optimization algorithm.

The main features of the algorithm:

• Partial evaluation of solutions. Agents conduct partial evaluation of hypotheses (candidate solutions to the search problem), which reduces the computational complexity of the algorithm.
• Distributing promising solutions. The agents exchange information about the hypotheses through direct personal communication. High-quality solutions can be identified from clusters of agents with the same hypothesis.
• Mathematical justification. SDSm has a deep mathematical basis, making it more reliable and predictable.

SDSm is an evolutionary optimization method that combines random search and diffusion to solve optimization problems in high-dimensional spaces.

Evolution of Social Groups (ESG) is a multi-population optimization algorithm.

The main features of the algorithm:

• Social groups. The algorithm does not operate with individual particles, but with social groups united by cooperation and exchange of experience. Each group has its own decision center and a set of particles as optimization agents.
• Collective movement. Particles within social groups interact and move together in parameter space. This allows groups to explore different regions of the parameter space and share information about the best solutions found.
• Local and global experience. Each social group stores information about the best solution within it (local experience). There is also an overall best score among all groups (global experience).

ESG is a simple architecture with high convergence and low computational requirements.

The code for conducting experiments on sequential and parallel operation is exactly the same as above, except that we need to replace the declaration of the corresponding objects of these classes instead of GWO and COAm.

ESG-SDSm test stand results (sequential structure):

ESG_SDSm|Evolution_of_Social_Groups and Stochastic Diffusion Search M|200.0|0.5|
=============================
5 Hilly's; Func runs: 10000; result: 0.9642488921252973
25 Hilly's; Func runs: 10000; result: 0.7526240638447592
500 Hilly's; Func runs: 10000; result: 0.2961693434072249
=============================
5 Forest's; Func runs: 10000; result: 0.9897783503200446
25 Forest's; Func runs: 10000; result: 0.7608845505131734
500 Forest's; Func runs: 10000; result: 0.2130287247171918
=============================
5 Megacity's; Func runs: 10000; result: 0.82
25 Megacity's; Func runs: 10000; result: 0.5421538461538462
500 Megacity's; Func runs: 10000; result: 0.11932307692307798
=============================
All score: 5.45821 (60.65%)

ESG-SDSm test stand results (parallel structure):

ESG_SDSm|Evolution_of_Social_Groups and Stochastic Diffusion Search M|200.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9561232188424761
25 Hilly's; Func runs: 10000; result: 0.7493199026465321
500 Hilly's; Func runs: 10000; result: 0.3176797705433513
=============================
5 Forest's; Func runs: 10000; result: 0.9726744619317564
25 Forest's; Func runs: 10000; result: 0.7494321306074204
500 Forest's; Func runs: 10000; result: 0.22498291462144127
=============================
5 Megacity's; Func runs: 10000; result: 0.836923076923077
25 Megacity's; Func runs: 10000; result: 0.5261538461538462
500 Megacity's; Func runs: 10000; result: 0.13435384615384738
=============================
All score: 5.46764 (60.75%)

The results for the sequential and parallel hybridization structures turned out to be very close fitting into the usual error of stochastic algorithms. They are slightly lower than the separate operation results of these algorithms.

4. Summary

The algorithms considered in this article as components for hybridization were selected to cover various positions in the current ranking table and to understand the impact of the different performance of each algorithm on the overall result. Is it important for the algorithms to be roughly equal in search ability to ensure a balanced analysis and a fair comparison of their impact on the final result?

In this article, we consider various optimization algorithms as components for hybridization. Our goal is to cover a wide range of algorithms that occupy different positions in the current ranking table to find out how the different performance of each algorithm affects the overall result.

Whether it is important for algorithms to be roughly equal in search ability remains an open question. This may not matter if the main goal is to find the best solution.

For experiments, we chose algorithms that differ greatly in their capabilities, such as GWO and COA. These algorithms represent two different approaches to optimization, and combining them can teach us valuable lessons. In contrast, we also selected algorithms that are very similar in performance, such as ESG and SDSm.

Below is the current rating table of algorithms. It includes all the algorithms we have discussed and will be updated as new data becomes available.

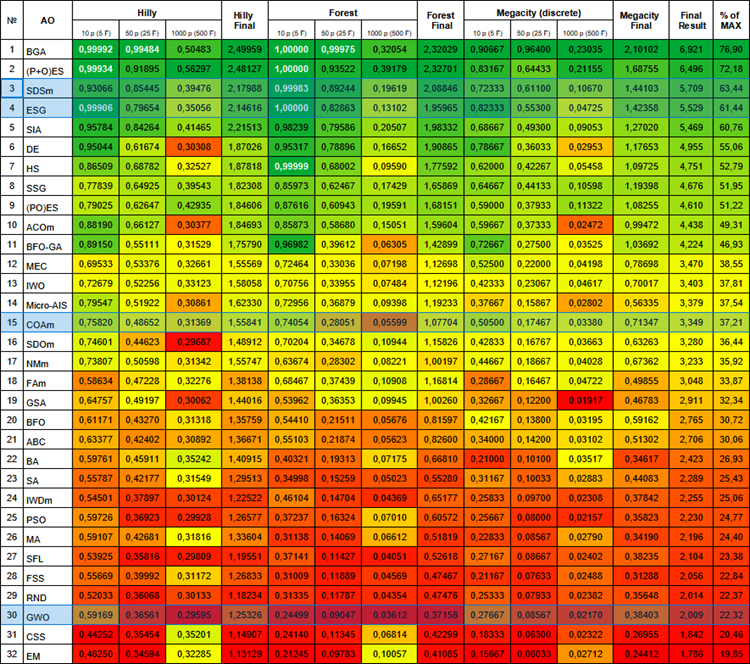
Rating table of population algorithms

When trying to create a hybrid method combining parallel work and exchange of the best positions of the ESG and SDSm algorithm agents, as well as in the sequential structure, we encountered an ambiguous phenomenon. In the course of our research, we found out that combining these two approaches did not lead to synergy and enhancement, but to an average result. It is likely that the interaction between these different strategies has not been efficient enough, preventing the full integration of their core principles.

As a result of the experiments, it became clear that both sequential and parallel hybridization structures did not lead to the desired results under these conditions, highlighting the importance of careful selection of algorithms for successful combination. It is necessary that the algorithms initially have certain qualities: either they search well and are poorly refined, or vice versa. Only in this case can hybridization methods improve the performance of both algorithms. The successful experience of hybridization through the fusion of algorithmic logic (according to the first structure) highlights the potential of this approach, however, it requires non-trivial effort, careful intervention and the development of joint fusion logic to achieve optimal results.

This observation highlights the importance of not only the individual characteristics of algorithms, but also their interactions in the context of hybridization. Just as in nature, where the combination of different species can lead to unique adaptations, in the world of optimization, the combination of algorithms requires fine tuning and harmony. Perhaps, it is in unexpected combinations and failed attempts that we find the keys to new discoveries and improvements in the field of optimization.

This experience highlights the importance of careful analysis and selection of algorithms when creating hybrid optimization methods. It is necessary to take into account not only the individual characteristics of each algorithm, but also their interaction within the framework of a specific task in order to achieve successful results in finding optimal solutions.

Try, experiment, create and combine. As always, all tools and source codes are attached below.