最適化アルゴリズムの効率における乱数生成器の品質の役割

MetaTrader 5 — テスター | 19 8月 2024, 14:55

はじめに

最適化アルゴリズムの使用に関して、多くの読者が、高品質の乱数生成器を使用することがいかに重要であるかを疑問に思っています。この質問に対する答えは、一見したほど単純ではありません。ただし、母集団アルゴリズムは圧倒的に確率的探索に基づいているため、乱数の質がアルゴリズムの探索能力に大きな影響を与えることは直感的に理解できます。

一緒にこの問題を調べましょう。その前に、乱数生成器の種類と、それが結果に与える影響、そして信頼できるオプションはどこにあるのかを考えておく必要があります。

乱数生成器(random number generator: RNG)は、数字や値のシーケンスを作成するアルゴリズムまたはデバイスであり、数字はランダムに見えます。コンピュータ科学や数学では、このようなシーケンスは、真のランダム過程ではなく、決定論的アルゴリズムによって生成されるため、通常「擬似乱数」と呼ばれることに注意することが重要です。

乱数生成器には大きく分けて2種類あります。

1. 疑似乱数生成器(PRG)：これらの生成器は、数学的な方程式やアルゴリズムを使用して、ランダムに見える数字のシーケンスを作成します。生成器は「シード」と呼ばれる初期値で初期化され、呼ばれるたびに、シーケンスの次の数字を生成します。アルゴリズムとシードの適切な選択により、PSGは擬似乱数シーケンスが必要とされる多くの用途に有用です。
2. ハードウェア乱数生成器(TRNG)：これらの生成器は、放射性崩壊ノイズや量子ノイズなどの真にランダムなプロセスを使用して乱数を生成します。このような生成器は、暗号や宝くじなど、高度な乱数性が要求される分野でよく使用されています。

疑似乱数生成器は、標準的なプログラミング言語ライブラリに組み込まれているものなど、プログラミングでよく使用されます。

プログラミング言語に組み込まれた乱数生成器の精度は、乱数生成に使用される特定の実装とアルゴリズムに依存します。MQL5、Python、C++、C#、Javaなど、最近のプログラミング言語のほとんどは、ほとんどの一般的なアプリケーションでかなり質の高い乱数を提供する擬似乱数生成器を内蔵しています。

一般的に、プログラミング言語に内蔵されている乱数生成器は、ほとんどの一般的なタスクに適していますが、高いレベルの乱数性やセキュリティが要求されるタスクについては、特殊なソリューションを検討する価値があります。

高度な乱数性とセキュリティを必要とするタスクには、乱数生成のための特別なソリューションを使用することができます。これらのソリューションには、以下のようなものがあります。

1. 暗号乱数生成器：これらの生成器は、高度なセキュリティが要求される暗号化アプリケーションでの使用を目的としています。乱数性、予測への耐性、暗号解読への耐性を提供します。
2. ハードウェア乱数生成器：これらの生成器は、熱雑音や量子現象などの物理的プロセスを利用して乱数を生成します。真にランダムな数値を提供し、高度な乱数性が要求される分野で広く利用されています。
3. 乱数生成ライブラリ：プログラミング言語の標準的な組み込み生成器よりも複雑なアルゴリズムを提供する、特別なライブラリがあります。例えば、OpenSSLライブラリは、乱数生成を含む暗号機能を提供します。

プログラミング言語の組み込み乱数生成器で使用できる最も一般的なアルゴリズムには、以下のようなものがあります。

1. 線形合同法(Linear Congruential Generator: LCG)：擬似乱数を生成するための最も単純で最も広く使用されているアルゴリズムの1つです。周期が短く、乱数性が低いという欠点があります。
2. メルセンヌ・ツイスタ：このアルゴリズムは周期が長く、乱数性が高いため、多くのプログラミング言語でよく使用されています。
3. Xorshift：擬似乱数生成アルゴリズムの一群で、乱数性が高く、高速です。
4. PCG (Permuted Congruential Generator)：この比較的新しいクラスの生成器は、乱数性の質と性能のバランスがとれています。

乱数生成器の選択は、タスクの特定の要件に依存します。以下は、決断に役立つ場合のあるいくつかの考慮事項です。

1. 乱数性の質：用途に高いレベルの乱数性が必要な場合、特に暗号化目的の場合は、暗号論的擬似乱数生成器(Cryptographically Secure Pseudo-Random Number Generator: CSPRNG)のような特殊な暗号化乱数生成器を使用するのが最善です。
2. 性能：乱数生成の速度を重視するのであれば、XorshiftやPCGのような高性能なアルゴリズムの方が望ましいかもしれません。
3. 周期と品質：メルセンヌ・ツイスタのように、周期が長く乱数性の質が高いアルゴリズムもあります。
4. 使いやすさ：開発者によっては、乱数生成器に簡単にアクセスでき、使いやすいことが重要な場合もあります。このような場合には、標準的なプログラミング言語ライブラリで提供されているような、組み込みの生成器が便利です。

暗号化レベルのセキュリティが必要な場合は、PythonのCryptoRandomやJavaのSecureRandomなど、専用の暗号化乱数生成器を使用することをお勧めします。性能と乱数性の質のバランスを求めるのであれば、メルセンヌ・ツイスタやPCGのようなアルゴリズムがよいでしょう。

また、安全性と乱数性はシステムの信頼性と安全性において重要な役割を果たすため、生成器の選択は思慮深く、特定の用途の要件に適したものでなければならないことを忘れてはなりません。ただし、この記事で興味があるのは、RNGの品質が最適化アルゴリズムの結果に与える影響についてです。この文脈でのみ研究を進めるつもりです。

メルセンヌ・ツイスタ

数多くの乱数生成器がある中で、許容できる速度を維持しながら高品質の生成をおこなうものを見つけるのは容易ではありません。結局のところ、生成速度は最適化プロセス全体の実行時間に大きな影響を与えます。

したがって、信頼性の高い生成器を選択することは、乱数の品質と生成速度のバランスを必要とする重要な問題です。このプロセスに無駄な時間を費やすことなく、十分な生成品質を確保できる最適なソルーションを見つける必要があります。

ハードウェア生成器は、ほとんどのユーザーにとってアクセスが難しいので、ここでは即座に検討対象から外します。ソフトウェア生成器の中では、高品質のメルセンヌ生成器が広く知られています。

メルセンヌ・ツイスタは、1997年に松本眞と西村拓士によって開発された擬似乱数生成アルゴリズムです。この乱数生成アルゴリズムは、長周期で乱数の質が良く、比較的高性能であるため、最も広く使用されている乱数生成アルゴリズムの1つです。

メルセンヌ・ツイスタの主な特徴は次の通りです。

長周期：メルセンヌ・ツイスタは周期が非常に長いので、数列が繰り返され始める前に膨大な数のユニークな擬似乱数を生成することができます。
良質の乱数性：このアルゴリズムでは乱数の質が保証されます。つまり、生成される数値は乱数の統計的性質に一致します。
性能：メルセンヌ・ツイスタは高性能で、多くの用途に使用できる魅力的な選択肢です。

メルセンヌ・ツイスタの動作原理は、擬似乱数を生成する線形回帰法に基づいています。このアルゴリズムでは、生成器の状態として大きな数（通常は32ビットまたは64ビット）を使用します。これが、次の擬似乱数を生成するために複雑な演算を使用して変換されます。ここでは64ビット生成器を使用します。

64ビット数用のメルセンヌ・ツイスタアルゴリズムに基づく擬似乱数生成器を実装したMersenneTwister64クラスについて考えてみましょう。以下は、そのメソッドと機能の簡単な説明です。

Init ：乱数生成器の初期化メソッド。シード（初期値）を引数に取り、クラスの内部変数を設定します。MT配列（メルセンヌ配列）は、シードに基づいた値で満たされます。
RND_ulong：ランダムな64ビット符号なし整数を返すメソッド。現在のインデックスが312より大きい場合、MT配列の値を更新するためにtwist()メソッドが呼ばれます。その後、ビット単位のシフトとビット単位のXOR演算を数回おこない、乱数を生成します。インデックス値は、結果を返す前に1でインクリメントされます。
RND_ulong_In_Range：指定した範囲（境界を含む）内のランダムな 64 ビット符号なし整数を返すメソッド。minとmaxが等しい場合はminが返されます。minがmaxより大きい場合、minとmaxの値が入れ替わります。次にRND_ulong()メソッドが呼ばれ、指定された範囲に収まるようにシフトとスケーリングがおこなわれた乱数が生成されます。
twist：MT配列の「ミキシング」操作をおこなう内部メソッド。各配列要素について、ビット単位のシフト演算とビット単位のXOR演算を用いて、隣接する要素の組み合わせがおこなわれます。インデックス値は、シャッフル操作の実行後に0に設定されます。

//——————————————————————————————————————————————————————————————————————————————
class MersenneTwister64
{
public: //--------------------------------------------------------------------

  void Init (ulong seed)
  {
    index = 312;

    MT [0] = seed;
    for (int i = 1; i < 312; i++)
    {
      MT [i] = (6364136223846793005 * (MT [i - 1] ^ (MT [i - 1] >> 62)) + i) & 0xFFFFFFFFFFFFFFFF;
    }
  }

  //from 0 to 18 446 744 073 709 551 615
  ulong RND_ulong ()
  {
    if (index >= 312)
    {
      twist ();
    }

    ulong y = MT [index];
    y = y ^ (y >> 29) & 0x5555555555555555;
    y = y ^ (y << 17) & 0x71D67FFFEDA60000;
    y = y ^ (y << 37) & 0xFFF7EEE000000000;
    y = y ^ (y >> 43);

    index++;
    return y;
  }

  ulong RND_ulong_In_Range (ulong min, ulong max)
  {
    if (min == max) return min;
    if (min > max)
    {
      ulong temp = min;
      min = max;
      max = temp;
    }
    return min + RND_ulong () % (max - min + 1);
  }

private: //-------------------------------------------------------------------
  ulong MT [312];
  int index;

  void twist ()
  {
    for (int i = 0; i < 312; i++)
    {
      ulong y = (MT [i] & 0x8000000000000000) + (MT [(i + 1) % 312] & 0x7FFFFFFFFFFFFFFF);
      MT [i] = MT [(i + 156) % 312] ^ (y >> 1);
      if (y % 2 != 0)
      {
        MT [i] = MT [i] ^ 0xB5026F5AA96619E9;
      }
    }
    index = 0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

乱数生成器とテスト結果の比較

MQL5に組み込まれている乱数生成器（以下、「標準」と呼ぶ）とメルセンヌ・ツイスタという2つの乱数生成器の働きを視覚的に比較してみましょう。そのために、2つの画像を生成し、その見た目を分析しました。一見したところ、どちらの画像にもパターンや周期性はなく、デザインも均質です。生成器間に明らかな視覚的な違いは見られません。

StandRND

標準生成器で生成された画像

MersRND

メルセンヌ・ツイスタ生成器で生成された画像

しかし、より客観的な乱数生成器の比較のためには、乱数性の程度と生成された数値の統計的特性を評価できる統計的検定を使用することが推奨されます。目視による評価には限界があり、真の乱数性から隠れた系統的な逸脱を検出できるとは限らないことに注意することが重要です。

したがって、生成器をより正確に比較するために、より信頼性の高い結果を得るために、統計的検定による追加分析を実施します。一様性に興味があるので、ランダムに生成された数字がどの程度一様であるかを評価する統計的検定であるカイ二乗検定を使用します。この場合、10,000の観測があり、それぞれが10,000の生成値を含みます。

カイ2乗検定（χ²検定）が、データ分布の均等性を検定するために使用されます。これにより、観測された度数が、一様分布で予想される度数とどの程度一致するかを判断することができます。

10,000の観測から1を引いた自由度9,999におけるカイ二乗検定（χ²検定）における有意水準0.05の臨界値は10232.73727です。この値は、カイ二乗検定で予想される度数と観察される度数を比較するのに使用される定数です。これは分布のカイ二乗表から取られ、観測値と期待値の差がどの程度有意かを判断するのに役立ちます。

カイ二乗検定をおこなうときは、計算された統計量を臨界値と比較します。計算された統計量が臨界値より大きければ、分布が期待される分布と一致するという帰無仮説を棄却することができます。そうでなければ帰無仮説が受け入れられます。

テストスクリプトのコードの一部を見てみましょう（一般的に、スクリプトは画像を構築し、生成器の実行時間を測定し、カイ二乗検定を計算する）。

observedとexpectedの2つの配列が作成され、初期化されます。observed配列は、各BoxesNumber区間で観測された乱数数を格納するために使用されます。expected配列には、生成器が完全な一様分布で動作していた場合に、各ビン内の乱数の期待値が格納されます。

このコードでは、次にStandardRND変数の値を確認し、どの乱数生成器を使用するかを指定します。StandardRNDがtrueの場合、MQL5の標準乱数生成器が使用されます。そうでない場合は、メルセンヌ・ツイスタ生成器が使用されます。このループは乱数を発生させ、その区間だけ配列observedの対応する要素をインクリメントします。

乱数が生成された後、カイ二乗統計量が計算されます。各区間について「(observed - expected)^2 / expected」値が計算され、chiSquareStatistic変数に合計されます。chiSquareCriticalValueの臨界値は、有意水準0.05*に設定されます。

比較結果はコードの最後に表示されます。chiSquareStatisticの値がchiSquareCriticalValueより大きければ、帰無仮説を棄却するというメッセージが表示されます。分布は予想と異なります。そうでない場合は、帰無仮説を棄却しないというメッセージが表示されます。

*：有意水準0.05（または5%）は、最も一般的な有意水準の1つであり、科学研究の多くの分野で広く使用されています。つまり、有意水準0.05の統計的検定をおこなう場合、5%の確率で第１種の過誤が発生することを許容します。統計学における有意水準とは、結果の統計的有意性を判断するために用いられる閾値のことです。これは通常α（アルファ）と表記され、第１種の過誤の確率、すなわち真の帰無仮説を棄却する確率を表します。

int observed [];
ArrayResize     (observed, BoxesNumber);
ArrayInitialize (observed, 0);

int expected [];
ArrayResize     (expected, BoxesNumber);
ArrayInitialize (expected, ThrowsNumber / BoxesNumber);

if (StandardRND)
{
  Print ("Standard, ", ThrowsNumber, " throws, ", BoxesNumber, " boxes");
  for (int i = 0; i < ThrowsNumber; i++)
  {
    observed [rndS.RNDintInRange (0, BoxesNumber - 1)]++;
  }
}
else
{
  Print ("Mersenne, ", ThrowsNumber, " throws, ", BoxesNumber, " boxes");
  for (int i = 0; i < ThrowsNumber; i++)
  {
    observed [(int)rndM.RND_ulong_In_Range (0, BoxesNumber  - 1)]++;
  }
}

// Calculate the chi-square statistic
double chiSquareStatistic = 0;
for (int i = 0; i < ArraySize(observed); i++)
{
  chiSquareStatistic += MathPow(observed[i] - expected[i], 2) / expected[i];
}

// Critical value for the significance level of 0.05
double chiSquareCriticalValue = 10232.73727; //10000

// Output results
if (chiSquareStatistic > chiSquareCriticalValue)
{
  Print("We reject the null hypothesis: The distribution differs from the expected one.");
}
else
{
  Print("We do not reject the null hypothesis: The distribution is consistent with the expected one.");
}

統計と標準生成器の実行時間を計算するために、スクリプトを5回実行してみましょう。メルセンヌ・ツイスタ生成器の実行時間も同時に測定されます。ツイスタと標準生成器の実行時間の商として、実行時間の差を計算します。

2024.03.18 20:54:33.456    stand:120353 mcs
2024.03.18 20:54:33.456    mers :397920 mcs
2024.03.18 20:54:33.456    diff :3.3062740438543283
2024.03.18 20:54:33.459    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:33.854    We reject the null hypothesis:The distribution differs from the expected one.
2024.03.18 20:54:38.802    stand:121670 mcs
2024.03.18 20:54:38.802    mers :403180 mcs
2024.03.18 20:54:38.802    diff :3.3137174323991125
2024.03.18 20:54:38.805    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:39.194    We reject the null hypothesis:The distribution differs from the expected one.
2024.03.18 20:54:43.767    stand:121222 mcs
2024.03.18 20:54:43.767    mers :400986 mcs
2024.03.18 20:54:43.767    diff :3.3078649090099157
2024.03.18 20:54:43.770    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:44.156    We reject the null hypothesis:The distribution differs from the expected one.
2024.03.18 20:54:48.476    stand:119246 mcs
2024.03.18 20:54:48.476    mers :400319 mcs
2024.03.18 20:54:48.476    diff :3.3570853529678146
2024.03.18 20:54:48.479    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:48.873    We reject the null hypothesis:The distribution differs from the expected one.
2024.03.18 20:54:53.144    stand:119309 mcs
2024.03.18 20:54:53.144    mers :404502 mcs
2024.03.18 20:54:53.144    diff :3.390372897266761
2024.03.18 20:54:53.148    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:53.553    We reject the null hypothesis:The distribution differs from the expected one.

期待される一様乱数分布からの系統的な逸脱があることを示すカイ二乗検定を使ってテストしたところ、残念なことに、標準乱数発生器は5つのテストのすべてで不合格となりました。

次に、メルセンヌ・ツイスターをテストし、両生成器の実行時間を測定し続けます。

2024.03.18 20:55:48.133    stand:115447 mcs
2024.03.18 20:55:48.133    mers :413258 mcs
2024.03.18 20:55:48.133    diff :3.57963394458063
2024.03.18 20:55:48.138    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:55:49.504    We do not reject the null hypothesis:The distribution is consistent with the expected one.
2024.03.18 20:55:56.340    stand:117433 mcs
2024.03.18 20:55:56.340    mers :402337 mcs
2024.03.18 20:55:56.340    diff :3.4260982858310696
2024.03.18 20:55:56.346    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:55:57.717    We do not reject the null hypothesis:The distribution is consistent with the expected one.
2024.03.18 20:56:05.837    stand:120129 mcs
2024.03.18 20:56:05.837    mers :400705 mcs
2024.03.18 20:56:05.837    diff :3.3356225391037966
2024.03.18 20:56:05.843    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:56:07.219    We do not reject the null hypothesis:The distribution is consistent with the expected one.
2024.03.18 20:56:12.206    stand:119980 mcs
2024.03.18 20:56:12.206    mers :397436 mcs
2024.03.18 20:56:12.206    diff :3.312518753125521
2024.03.18 20:56:12.211    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:56:13.582    We do not reject the null hypothesis:The distribution is consistent with the expected one.
2024.03.18 20:56:18.837    stand:118140 mcs
2024.03.18 20:56:18.837    mers :397565 mcs
2024.03.18 20:56:18.837    diff :3.3652023023531403
2024.03.18 20:56:18.842    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:56:20.220    We do not reject the null hypothesis:The distribution is consistent with the expected one.

メルセンヌ渦は5つのテスト（カイ二乗検定の実行）すべてで課題に対処しました。同時に、この生成器には重大な欠点があることもわかります。ツイスタは標準的な生成器の約3.4倍遅く、最適化アルゴリズムの速度に大きく影響します。

さて、ここからが最も興味深い部分、つまりこの研究のハイライトです。乱数生成器の品質が最適化結果にどの程度影響するかを調べるテストを実施します。覚えていらっしゃるかもしれませんが、標準生成器が[0;32,767]の範囲の数字を生成する一方、64ビットのメルセンヌ・ツイスタは[0;18,446,744,073,709,551,615]の範囲の数字を生成します。

実験をおこなうために、50のHilly関数を選択し、各関数について10,000回の反復をおこないました。なぜHillyの50の特徴量を選んだのでしょうか。なぜHillyなのでしょうか。第一に、この数は、アルゴリズムが適応度関数の限られた回数の実行で100%の収束を達成できないように選択されました。これにより、乱数生成器の種類による使い方の違いを観察することが可能になりました。第二に、Hilly関数を選択したのは、その滑らかさによるもので、離散的な検定関数を使用した場合の乱数生成にはない自然な結果の散らばりを避けることができます。より信頼性が高く、統計的に有意なデータを得るために、実験を20回繰り返し、結果を平均化しました。最適化アルゴリズムとしてはBGAを選択しました。BGAは、私たちの評価表で第1位であり、同時に滑らかな関数で結果のばらつきが非常に小さいことを示しています。

結果の出力から、BGAアルゴリズムでは、標準乱数生成器とメルセンヌ発生器の両方を使用した場合、最適化結果はほぼ同じであることがわかります。差は小数点第3位までしか見ることができませんが、ここでの目的にとっては重要ではなく、かなり小さいと考えられます。

//Standard
C_AO_BGA:50:50:1.0:3:0.001:0.7:16
=============================
50 Hilly's; Func runs:10000; result:0.9257245560389498
=============================
All score:0.92572

//Mersenne
C_AO_BGA:50:50:1.0:3:0.001:0.7:16
=============================
50 Hilly's; Func runs:10000; result:0.9221148477644971
=============================
All score:0.92211

アルゴリズムの動作を可視化したところ、アルゴリズムロジック内で2つの異なるタイプの乱数生成器を使用しても、大きなずれは見つかりませんでした。結果のばらつきの差は、アルゴリズム操作自体のばらつきの範囲内です。

BGA標準RND

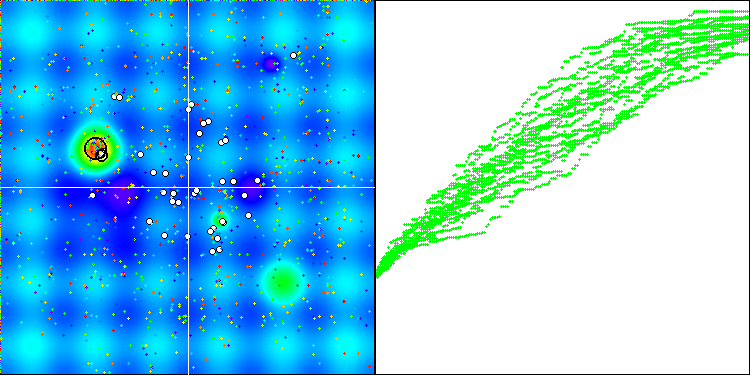
標準生成器によるBGA

BGAメルセンヌRND

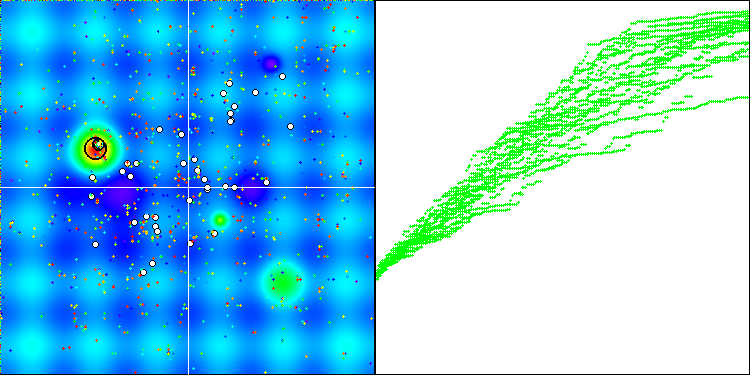
メルセンヌ・ツイスタによるBGA

乱数生成器の品質は最適化アルゴリズムの性能に影響しない、というのが予備的な結論です。

BGA最適化アルゴリズムで上記の生成器を使用した場合の結果に若干の違いがあるのは、BGAでは染色体の各ビットが他のビットから独立して生成されるためではないかと仮定してみましょう。実際、乱数生成器の役割は、ブール演算の「イエス/ノー」操作に集約され、「イエス」と「ノー」の発生数の差は、わずか1000分の1パーセントにすぎません。

つまり、バイナリ遺伝的アルゴリズムでは、乱数生成器を使用することに違いはありません。この結論は一見してまったくわかりませんでしたが、他の最適化アルゴリズム、特に座標によって[min, max]で囲まれた空間全体で連続的な確率を使用するアルゴリズムではそうなのでしょうか。

得られた主張を確認するため、あるいは反論するために、もう少し実験をしてみましょう。今回は、評価表のトップクラスであり、ロジック内で乱数を使用した多数の演算を使用し、検索空間全体に連続確率を適用する (P_O)ES アルゴリズムを取り上げます。

(P_O)ESを標準乱数生成器で5回テストしました。

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs:10000; result:0.9611258962207798
=============================
All score:0.96113

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs:10000; result:0.9515388684155862
=============================
All score:0.95154

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs:10000; result:0.9374143219597522
=============================
All score:0.93741

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs:10000; result:0.9408961932771648
=============================
All score:0.94090

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs:10000; result:0.9533447716768805
=============================
All score:0.95334

(P_O)ESをメルセンヌ・ツイスタ生成器で5回テストしました。

C_AO_(P_O)ES:100:150:0.02:8.0:10

=============================
50 Hilly's; Func runs:10000; result:0.9726583883537465
=============================
All score:0.97266

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs:10000; result:0.9699307111435692
=============================
All score:0.96993

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs:10000; result:0.9864631937799934
=============================
All score:0.98646

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs:10000; result:0.9608040257741147
=============================
All score:0.96080

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs:10000; result:0.9540192199550924
=============================
All score:0.95402

実験結果からわかるように、最初の一連の実験は、アルゴリズムにおける標準乱数生成器の使用に関するものでした。結果の平均値は約0.95であり、メルセンヌ・ツイスタを使用した場合の平均値は0.96であることがわかります。これは大きな差ではありませんが、メルセンヌ・ツイスタが存在する場合の方が、実験結果がまだ高いことを示しています。しかし、このアルゴリズムを使用する時間は、標準的なアルゴリズムの実行時間を3.5倍上回ることに留意してください。

まとめ

多くのトレーダーを悩ませる疑問に終止符を打つべく、興味深い実験をおこないました。最適化アルゴリズムと併用する場合、乱数生成器の品質は重要かということです。このような研究は公開されているのを見たことがありません。

BGAのようなブール演算を使用するアルゴリズムや、DE（母集団の親を選ぶのに乱数を使用する差分進化(Differential Evolution)）のような小さな離散範囲の乱数を使用するアルゴリズムでは、RNGの質はほとんど役割を果たしません。

(P_O)ESのような、最適化されたパラメータの全範囲にわたって新しい解を生成するために乱数を使用する他のアルゴリズム（ほとんどの母集団アルゴリズムは類似している）では、RNGは測定誤差に適合する小さな役割を果たします。より高品質のメルセンヌ・ツイスタ生成器は、標準的なものより3.5倍遅いことが重要です。

最適化問題では、品質と計算時間のバランスが確かに重要な役割を果たします。結局、この場合はスピードを選択します。高品質生成器の使用によるアルゴリズム結果の増加は測定誤差の範囲内ですが、スピードは大幅に低下します。

実施されたテストのコードが記載されたアーカイブを以下に添付します。この記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14413

添付されたファイル |

ZIPをダウンロード

The_world_of_AO_RND_quality.zip (24.24 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。