Redes neuronales: así de sencillo (Parte 49): Soft Actor-Critic

Introducción

Continuamos nuestra introducción a los algoritmos para resolver problemas mediante aprendizaje por refuerzo en un espacio continuo de acciones. En artículos anteriores, ya nos hemos familiarizado con los algoritmos Deep Deterministic Policy Gradient (DDPG) y Twin Delayed Deep Deterministic policy gradient (TD3). En este artículo, le presento otro algoritmo: el Soft Actor-Critic (SAC). Este algoritmo se presentó por primera vez en el artículo "Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor" (enero de 2018). El método se introdujo casi al mismo tiempo que el TD3 y tiene algunas similitudes, pero también existen diferencias en los algoritmos. El objetivo principal del SAC es maximizar la recompensa esperada dada la máxima entropía de la política, lo cual permite encontrar una variedad de soluciones óptimas en entornos estocásticos.

1. El algoritmo Soft Actor-Critic (SAC)

Al empezar a analizar el algoritmo SAC, probablemente debamos señalar inmediatamente que no es un sucesor directo del método TD3 (ni viceversa), aunque tienen algunas similitudes. Ambos métodos:

• son algoritmos off-policy
• explotan los enfoques DDPG
• usan 2 Críticos.

Sin embargo, a diferencia de los dos métodos anteriores, el SAC utiliza la política estocástica del Actor, lo cual permite al algoritmo explorar diferentes estrategias y encontrar soluciones óptimas dada la máxima variedad de acciones de los actores.

Hablando de la estocasticidad del entorno, entendemos que en el estado S, al realizarse la acción A, obtenemos la recompensa R en el rango [Rmin, Rmax] con una cierta probabilidad Psa.

El SAC utiliza un Actor con una política estocástica. Esto significa que un Actor en el estado S puede elegir una cierta acción A' de todo el espacio de acciones con una cierta probabilidad Pa'. En otras palabras, la política del Actor en cada estado concreto permite elegir no una acción óptima concreta, sino cualquiera de las acciones posibles (pero con una cierta probabilidad). Y en el proceso de entrenamiento, el Actor aprende esta distribución de probabilidad de maximizar la recompensa.

Esta propiedad de la política estocástica del Actor nos permite investigar diferentes estrategias y descubrir soluciones óptimas que puedan quedar ocultas al utilizar políticas deterministas. Además, la política estocástica del Actor tiene en cuenta la incertidumbre del entorno. En presencia de ruido o factores aleatorios, estas políticas pueden ser más resistentes y adaptativas al generar una variedad de acciones para interactuar eficazmente con el entorno.

No obstante, el aprendizaje estocástico de la política del Actor también realiza ajustes durante el aprendizaje. El aprendizaje por refuerzo clásico pretende maximizar el rendimiento esperado. Durante el aprendizaje, podemos decir que para cada acción S, elegiremos la acción A* que tenga la mayor probabilidad de darnos el mayor rendimiento. Este enfoque determinista construye una clara dependencia St →At →St+1 ⇒ R y no deja lugar a la estocasticidad de las acciones. Para entrenar una política estocástica, los autores del algoritmo Soft Actor-Critic introducen la regularización de entropía en según la recompensa.

En este contexto, la entropía (H) es una medida de la incertidumbre o diversidad de la política, mientras que el parámetro ɑ>0 es el coeficiente de temperatura y permite equilibrar la exploración del entorno y el funcionamiento del modelo.

Permítanme recordarles que la entropía supone una medida de la incertidumbre de una variable aleatoria y se define mediante la fórmula

Nótese que estamos hablando del logaritmo de la probabilidad de seleccionar una acción en el rango de valores [0, 1]. Y en este intervalo de valores admisibles el gráfico de la función de entropía es decreciente y se sitúa en la zona de valores positivos. Así, cuanto menor sea la probabilidad de seleccionar una acción, mayor será la recompensa y el modelo se verá incentivado a explorar el entorno.

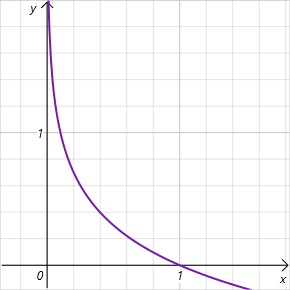
Como podemos ver, esto plantea exigencias bastante elevadas en la selección del hiperparámetro ɑ. Actualmente, existen varias implementaciones del algoritmo SAC. Entre ellas, se encuentra el enfoque clásico de parámetros fijos. Resulta bastante común encontrar implementaciones con una disminución gradual del parámetro. Es fácil ver que cuando ɑ=0 llegamos al aprendizaje por refuerzo determinista. Además, existen varios enfoques para optimizar el parámetro ɑ según el propio modelo durante el proceso de aprendizaje.

Ya nos hemos aclarado con la función de recompensa. Vamos a pasar ahora al entrenamiento del Crítico. De forma similar a TD3, el SAC entrena 2 modelos del Crítico en paralelo utilizando MSE como función de pérdida. El valor más bajo de los dos modelos objetivo del Crítico se utilizará para el valor previsto del estado futuro, pero hay dos diferencias fundamentales.

En primer lugar, tenemos la función de recompensa comentada anteriormente. Utilizaremos la regularización de la entropía tanto para los estados actuales como para los futuros. Obviamente, con un factor de descuento aplicado al valor del siguiente estado del sistema.

La segunda diferencia radica en el Actor. El SAC no utiliza el modelo objetivo del Actor. Se utiliza un único modelo del Actor entrenado para seleccionar una acción en el estado actual y en los siguientes. Así, haremos hincapié en que la consecución de recompensas futuras se logra utilizando las políticas actuales. Además, el uso de un único modelo del Actor reducirá los gastos de memoria y computación.

 

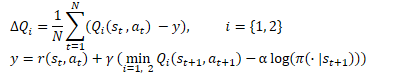
Para entrenar las políticas del Actor, utilizaremos enfoques de DDPG. Así, obtendremos el gradiente de error de la acción usando la retropropagación del gradiente de error del coste previsto de la acción a través del modelo del Crítico. Pero a diferencia de TD3 (donde solo utilizamos el modelo del Crítico 1), los autores de SAC sugieren utilizar un modelo con un coste de acción estimado más bajo.

Hay otro punto que señalar aquí. Durante el aprendizaje, cambiaremos la política, lo cual provocará un cambio en las acciones del Actor en un estado particular del sistema. Además, el uso de la política estocástica del Actor también contribuirá a la diversidad de las acciones del Actor. Al mismo tiempo, entrenaremos los modelos con los datos de un búfer de reproducción de experiencia con recompensas por otras acciones del agente. Aquí, nos guiaremos por el supuesto teórico de que nos movemos hacia la maximización de la recompensa predictiva en el proceso de aprendizaje del Actor. Así, en cualquier estado S, el coste de una acción con la nueva política πnew será inferior al coste de una acción en la antigua política πold.

Es una suposición bastante subjetiva, pero totalmente coherente con nuestro paradigma de aprendizaje de modelos. Y para no acumular posibles errores, puedo recomendarle que durante el aprendizaje actualice el búfer de reproducción de experiencia más a menudo para reflejar las actualizaciones de la política del Actor.

La actualización de los modelos objetivo se suavizará utilizando el coeficiente τ, de forma similar a TD3.

Y una diferencia más con el método TD3: el algoritmo SAC no utiliza el retraso en el entrenamiento del Actor y la actualización de los modelos objetivo. Aquí, todos los modelos se actualizan en cada paso de entrenamiento.

Vamos a resumir el algoritmo SAC:

• La regularización de la entropía se introducirá en la función de recompensa.
• Al principio del proceso de aprendizaje, los modelos del Actor y los 2 Críticos se inicializarán con parámetros aleatorios.
• Como resultado de la interacción con el entorno, se rellenará el búfer de reproducción de experiencia. Luego almacenaremos el estado del entorno, la acción, el estado posterior y la recompensa.
• Una vez rellenado el búfer de experiencia, entrenaremos los modelos
• Recuperamos aleatoriamente el conjunto de datos del búfer de reproducción de experiencia
• Definimos una acción para un estado futuro dada la política actual del Actor
• Determinamos el valor pronosticado del estado futuro utilizando la política actual de al menos 2 modelos objetivo de los Críticos.
• Actualizamos los modelos de los Críticos
• Actualizamos la política del Actor
• Actualizamos los modelos objetivo.

El proceso de entrenamiento del modelo es iterativo y se repite hasta obtener el resultado deseado o alcanzarse un extremo mínimo en el gráfico de la función de pérdida de los Críticos.

2. Implementación usando MQL5

Tras la familiarizarnos con la teoría del algoritmo SAC, procederemos a implementarlo usando las herramientas MQL5. Y lo primero a lo que nos enfrentaremos es a la determinación de la probabilidad de una acción. En realidad es una cuestión bastante sencilla para la aplicación tabular de la política del Actor, pero causa dificultades si utilizamos redes neuronales. Al fin y al cabo, no llevamos estadísticas de los estados del entorno ni de las acciones realizadas, estas se encuentran "cosidas" a los parámetros personalizables de nuestro modelo. A este respecto, me acordé del aprendizaje Q distribuido. Recuerde que hablamos de estudiar la distribución de probabilidad de la recompensa esperada. El aprendizaje Q distribuido nos permite obtener una distribución de probabilidad para un número determinado de valores de recompensa de intervalo fijo, mientras que el modelo de la función Q totalmente parametrizada (FQF) nos permite estudiar tanto los valores del intervalo como sus probabilidades.

2.1 Creación de una nueva clase de capa neuronal

Heredando de la clase CNeuronFQF, crearemos una nueva clase de capa neuronal para implementar el algoritmo propuesto CNeuronSoftActorCritic. El conjunto de métodos de la nueva clase es bastante estándar, pero existen algunas peculiaridades.

En concreto, hemos decidido utilizar parámetros de regularización de entropía ajustables en nuestra aplicación. Para ello, hemos añadido la capa neural cAlphas. Esta implementación usa una capa de tipo CNeuronConcatenate, ya que utilizaremos la inserción del estado actual y la distribución cuantílica en la salida para decidir el tamaño de los coeficientes.

Además, hemos añadido un búfer independiente para registrar los valores de entropía que luego utilizaremos en la función de recompensa.

Los dos objetos añadidos se declararán como estáticos, lo cual nos permitirá dejar vacíos el constructor y el destructor de la clase.

class CNeuronSoftActorCritic  :  public CNeuronFQF
  {
protected:
   CNeuronConcatenate   cAlphas;
   CBufferFloat         cLogProbs;
 
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronSoftActorCritic(void) {};
                    ~CNeuronSoftActorCritic(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint actions, uint quantiles, 
                          uint numInputs, ENUM_OPTIMIZATION optimization_type, uint batch);
   virtual bool      calcAlphaGradients(CNeuronBaseOCL *NeuronOCL);
   virtual bool      GetAlphaLogProbs(vector<float> &log_probs)       { return (cLogProbs.GetData(log_probs) > 0); }
   virtual bool      CalcLogProbs(CBufferFloat *buffer);
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual int       Type(void) override        const                 {  return defNeuronSoftActorCritic;          }
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Primero analizaremos el método de inicialización de la clase Init. Los parámetros del método repiten completamente los parámetros del método análogo de la clase padre. En el cuerpo del método, llamaremos directamente al método de la clase padre. Utilizaremos esta técnica muy a menudo. Después de todo, la clase padre implementa todos los controles necesarios, así como la inicialización de todos los objetos heredados. Una única comprobación de los resultados de la ejecución del método de la clase padre sustituirá al control total de las operaciones mencionadas. Todo lo que deberemos hacer es inicializar los objetos añadidos.

Primero inicializaremos la capa de cálculo de coeficientes ɑ. Como hemos mencionado antes, suministraremos a la entrada de este modelo una inserción del estado actual cuyo tamaño será igual al tamaño de la capa neuronal anterior. Ahora vamos a añadir una distribución cuantílica en la salida de la capa actual, que estará contenida en la capa interna cQuantile2 (declarada e inicializada en la clase padre). A la salida de la capa cAlphas, planeamos obtener los coeficientes de temperatura para cada acción individual. Como consecuencia, el tamaño de la capa será igual al número de acciones.

Los coeficientes deberán ser no negativos. Para cumplir este requisito, definiremos Sigmoid como la función de activación de esta capa.

Al final del método, inicializaremos el búfer de entropía con valores cero. Su tamaño también será igual al número de acciones. Y crearemos directamente un búfer en el contexto OpenCL actual.

bool CNeuronSoftActorCritic::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                  uint actions, uint quantiles, uint numInputs, 
                                  ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronFQF::Init(numOutputs, myIndex, open_cl, actions, quantiles, numInputs, optimization_type, batch))
      return false;
//---
   if(!cAlphas.Init(0, 0, OpenCL, actions, numInputs, cQuantile2.Neurons(), optimization_type, batch))
      return false;
   cAlphas.SetActivationFunction(SIGMOID);
//---
   if(!cLogProbs.BufferInit(actions, 0) || !cLogProbs.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

A continuación, pasaremos a la aplicación del proceso de pasada directa. Aquí debemos decir que tomaremos prestado directamente el proceso de aprendizaje de cuantiles y la distribución de probabilidad de la clase padre, al completo y sin ningún cambio. No obstante, añadiremos la organización del proceso de determinación de los coeficientes de temperatura y el cálculo de los valores de entropía. Además, si para el cálculo de los coeficientes de temperatura solo necesitamos llamar a la pasada directa de la capa cAlphas, la determinación de los valores de entropía deberá realizarse partiendo de "0".

Tenemos que calcular la entropía para cada acción del Actor. En esta fase, esperaremos que no haya un gran número de acciones aquí. Pero como todos los datos iniciales están en la memoria contextual de OpenCL, resultará lógico transferir nuestras operaciones a este entorno. Y primero crearemos el kernel SAC_AlphaLogProbs OpenCL del programa para implementar esta funcionalidad.

En los parámetros del kernel, transmitiremos 5 búferes de datos y 2 constantes:

• outputs — búfer de resultados, contiene sumas ponderadas de la probabilidad de los valores cuantílicos para cada acción
• quantiles — valores medios de los cuantiles (búfer de resultados de la capa interna cQuantile2)
• probs — tensor de probabilidad (búfer de resultados de la capa interna cSoftMax)
• alphas — vector de coeficientes de temperatura
• log_probs — vector de valores de entropía (en este caso, el búfer para registrar los resultados)
• count_quants — número de cuantiles para cada acción
• activation — tipo de función de activación.

Debemos señalar de inmediato que la clase CNeuronFQF no utilizará la función de activación de salida. Incluso diría que va en contra de su esencia. De hecho, la distribución de los valores medios de los cuantiles de la recompensa esperada está delineada por la propia recompensa real durante el entrenamiento del modelo. En nuestro caso, sin embargo, a la salida de la capa esperaremos algún valor de acción del Actor de una distribución continua. Debido a diversas circunstancias técnicas o de otro tipo, el alcance de las acciones permisibles de un agente puede verse limitado a cierto marco. Y eso es algo que nos permite precisamente la función de activación. No obstante, para obtener una verdadera estimación de la probabilidad, para nosotros es muy importante que la función de activación se aplique ya después de haber determinado la probabilidad de la acción real. Por ello, hemos añadido su realización a este kernel.

__kernel void SAC_AlphaLogProbs(__global float *outputs,
                                __global float *quantiles,
                                __global float *probs,
                                __global float *alphas,
                                __global float *log_probs,
                                const int count_quants,
                                const int activation
                               )
  {
   const int i = get_global_id(0);
   int shift = i * count_quants;
   float quant1 = -1e37f;
   float quant2 = 1e37f;
   float prob1 = 0;
   float prob2 = 0;
   float value = outputs[i];

En el cuerpo del kernel, identificaremos el flujo actual de operaciones. Este nos dará el número de secuencia de la acción analizada. Y luego determinaremos el desplazamiento en los topes de cuantiles y probabilidades.

Después declararemos las variables locales. Para determinar la probabilidad de una acción en concreto, necesitaremos encontrar los 2 cuantiles más cercanos. En la variable quant1 escribiremos la media del cuantil más próximo a la parte inferior, mientras que en la variable quant2 escribiremos el valor medio del cuantil más cercano por arriba. En la fase inicial, inicializaremos las variables especificadas con valores extremos conocidos. Luego almacenaremos las probabilidades correspondientes en las variables prob1 y prob2, que inicializaremos con valores cero. Al fin y al cabo, a nuestro juicio, la probabilidad de obtener tales valores extremos será "0".

A continuación, almacenaremos el valor buscado del búfer en la variable local value.

Permíteme recordarle que, debido a las peculiaridades de la organización de la memoria contextual de OpenCL, el acceso a las variables locales resulta mucho más rápido que la obtención de los datos del búfer de memoria global. Y trabajando con variables locales aumentaremos el rendimiento de todo el programa OpenCL.

Ahora que hemos almacenado el valor buscado en una variable local, podremos aplicar sin problemas la función de activación al búfer de resultados de la capa neuronal.

   switch(activation)
     {
      case 0:
         outputs[i] = tanh(value);
         break;
      case 1:
         outputs[i] = 1 / (1 + exp(-value));
         break;
      case 2:
         if(value < 0)
            outputs[i] = value * 0.01f;
         break;
      default:
         break;
     }

A continuación, organizaremos un ciclo de enumeración de todos los valores medios de los cuantiles y buscaremos los más próximos. 

Aquí debemos señalar que no hemos clasificado los valores medios de los cuantiles. Las determinaciones de la media ponderada no se ven afectadas por ello y ya hemos renunciado anteriormente a realizar operaciones innecesarias. Por lo tanto, con una alta probabilidad los cuantiles más próximos al valor buscado no se encontrarán en los elementos vecinos del búfer de cuantiles. Por lo tanto, iteraremos por todos los valores.

Una cosa más, para no escribir en ambas variables los valores de un cuantil para el límite inferior utilizaremos el operador lógico ">=", y para el límite superior estrictamente "<". Cuando se encuentre un cuantil más cercano que el cuantil previamente almacenado, sobrescribiremos el valor en las variables correspondientes previamente declaradas con la media del cuantil y su probabilidad.

   for(int q = 0; q < count_quants; q++)
     {
      float quant = quantiles[shift + q];
      if(value >= quant && quant1 < quant)
        {
         quant1 = quant;
         prob1 = probs[shift + q];
        }
      if(value < quant && quant2 > quant)
        {
         quant2 = quant;
         prob2 = probs[shift + q];
        }
     }

Cuando se completen todas las iteraciones del ciclo, nuestras variables locales contendrán los datos de los cuantiles más cercanos. Y el valor que buscamos estará en algún punto intermedio. Sin embargo, nuestro conocimiento de la distribución de probabilidad de las acciones se limita a la distribución aprendida. En este caso, usaremos la hipótesis de dependencia lineal de la probabilidad entre los 2 cuantiles más próximos. Dado un número suficientemente grande de cuantiles, y considerando el rango limitado de la distribución de valores del dominio de acciones reales, nuestra suposición no estará lejos de la verdad.

   float prob = fabs(value - quant1) / fabs(quant2 - quant1);
   prob = clamp((1-prob) * prob1 + prob * prob2, 1.0e-3f, 1.0f);
   log_probs[i] = -alphas[i] * log(prob);
  }

Tras determinar la probabilidad de acción, determinaremos la entropía de acción y multiplicaremos el valor resultante por el coeficiente de temperatura. Para evitar valores de entropía demasiado grandes, hemos limitado el límite inferior de la probabilidad a 0,001.

Con esto concluiremos nuestro trabajo sobre los kernels de pasada directa y pasaremos al programa principal. Aquí crearemos un método de pasada directa de nuestra clase CNeuronSoftActorCritic::feedForward.

Como recordará, aquí estamos explotando ampliamente las capacidades de los métodos virtuales en los objetos heredados. Por lo tanto, los parámetros de este método repetirán completamente los métodos similares de todas las clases consideradas anteriormente.

En el cuerpo del método, primero realizaremos una llamada al método de pasada directa de la clase padre y al método similar de la capa de cálculo del coeficiente de temperatura. Aquí solo necesitaremos controlar los resultados de la ejecución de los métodos anteriores.

bool CNeuronSoftActorCritic::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!CNeuronFQF::feedForward(NeuronOCL))
      return false;
   if(!cAlphas.FeedForward(GetPointer(cQuantile0), cQuantile2.getOutput()))
      return false;

A continuación deberemos calcular el componente de entropía de la función de recompensa. Para ello, organizaremos el proceso de puesta en marcha del kernel comentado anteriormente. Lo ejecutaremos en el espacio unidimensional de tareas según el número de acciones analizadas.

   uint global_work_offset[1] = {0};
   uint global_work_size[1] = {Neurons()};

Como siempre, antes de poner el kernel en la cola de ejecución, organizaremos el proceso de transmisión de los datos de origen a sus parámetros.

   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_alphas, cAlphas.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_log_probs, cLogProbs.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_outputs, getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_probs, cSoftMax.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_quantiles, cQuantile2.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_SAC_AlphaLogProbs, def_k_sac_alp_count_quants, (int)(cSoftMax.Neurons() / global_work_size[0])))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_SAC_AlphaLogProbs, def_k_sac_alp_activation, (int)activation))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

Tenga en cuenta que no comprobaremos ningún búfer. La cuestión es que todos los búferes utilizados ya han superado el control en la etapa de pasada directa del método de la clase padre y la capa de cálculo del coeficiente de temperatura. Lo único que no se ha comprobado es el búfer interno para registrar los resultados del kernel, pero se trata de un objeto interno cuya creación hemos controlado en la fase de inicialización del objeto de clase. No existe acceso desde un programa externo al objeto, y la probabilidad de obtener un error en este punto es bastante baja. Así que asumiremos este riesgo en favor de la rapidez de nuestro programa.

Al final del método, pondremos el kernel en la cola de ejecución y comprobaremos el resultado de las operaciones.

   if(!OpenCL.Execute(def_k_SAC_AlphaLogProbs, 1, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

Me gustaría señalar de nuevo que en este caso estaremos comprobando el resultado de colocar el kernel en la cola de ejecución, pero no los resultados de las operaciones dentro del kernel. Para obtener los resultados, deberemos cargar los datos del búfer cLogProbs en la memoria principal. Esta funcionalidad se implementará en el método GetAlphaLogProbs. El código del método cabe en una línea y se mostrará en el bloque de descripción de la estructura de la clase.

Con esto hemos finalizado nuestro trabajo sobre la organización del proceso de pasada directa por clase, y podemos proceder a crear la funcionalidad de la pasada inversa. Debemos decir que la mayor parte de la funcionalidad ya está implementada en el método de la clase padre, y, por extraño que parezca, ni siquiera redefiniremos el método de distribución del gradiente de error a través de la capa neuronal. La cuestión es que la distribución del gradiente de error en la regularización de la entropía no encaja del todo en nuestro marco general. El gradiente de error en la acción lo obtendremos del modelo del Crítico desde su última capa, e incluiremos la propia regularización de la entropía en la función de recompensa. Como consecuencia, su error también estará en el nivel de predicción de la recompensa, es decir, en la capa de resultados del Crítico, y aquí es donde nos surgen dos cuestiones:

1. La introducción de un búfer de gradiente adicional rompería el modelo que hemos construido para virtualizar los métodos de pasada inversa.
2. En la fase de pasada inversa del Actor, simplemente no tendremos los datos de error del Crítico. Será necesario crear un nuevo proceso para todo el modelo.

Hemos decidido arreglárnoslas, por así decirlo, "con lo mínimo" y hemos creado un nuevo proceso paralelo solo para el gradiente de error de regularización entrópica sin una revisión completa del proceso de retropropagación del error en el modelo.

En primer lugar, crearemos el kernel en el programa OpenCL. Su código es bastante sencillo, solo tendremos que multiplicar el gradiente de error resultante por la entropía. Y luego corregiremos el valor obtenido usando la derivada de la función de activación de la capa de cálculo del coeficiente de temperatura.

__kernel void SAC_AlphaGradients(__global float *outputs,
                                 __global float *gradient,
                                 __global float *log_probs,
                                 __global float *alphas_grad,
                                 const int activation
                                )
  {
   const int i = get_global_id(0);
   float out = outputs[i];
//---
   float grad = -gradient[i] * log_probs[i];
   switch(activation)
     {
      case 0:
         out = clamp(out, -1.0f, 1.0f);
         grad = clamp(grad + out, -1.0f, 1.0f) - out;
         grad = grad * max(1 - pow(out, 2), 1.0e-4f);
         break;
      case 1:
         out = clamp(out, 0.0f, 1.0f);
         grad = clamp(grad + out, 0.0f, 1.0f) - out;
         grad = grad * max(out * (1 - out), 1.0e-4f);
         break;
      case 2:
         if(out < 0)
            grad = grad * 0.01f;
         break;
      default:
         break;
     }
//---
   alphas_grad[i] = grad;
  }

Aquí debemos señalar que para simplificar el cálculo, simplemente multiplicaremos el gradiente por el valor del búfer log_probs. Como recordará, en la pasada directa escribimos aquí el valor de entropía teniendo en cuenta el coeficiente de temperatura. Y matemáticamente deberemos dividir el valor del búfer por este valor. Pero para la temperatura, utilizaremos la sigmoide como función de activación. Por lo tanto, su valor estará siempre en el intervalo [0,1]. La división por un número positivo inferior a 1 solo aumentará el gradiente de error. Y en este caso, no haremos esto a propósito.

Una vez completado el kernel SAC_AlphaGradients, procederemos a trabajar en el programa principal y crearemos el método CNeuronSoftActorCritic::calcAlphaGradients. En este punto, primero pondremos el kernel en la cola de ejecución y solo después llamaremos a los métodos de los objetos internos. Por ello, organizaremos un bloque de controles antes de iniciar el proceso.

bool CNeuronSoftActorCritic::calcAlphaGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL || !NeuronOCL.getGradient() ||
      !NeuronOCL.getGradientIndex()<0)
      return false;

A continuación, definiremos el espacio de tareas del kernel y transmitiremos los datos iniciales a sus parámetros.

   uint global_work_offset[1] = {0};
   uint global_work_size[1] = {Neurons()};
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaGradients, def_k_sac_alg_outputs, cAlphas.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaGradients, def_k_sac_alg_alphas_grad, cAlphas.getGradientIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaGradients, def_k_sac_alg_gradient, NeuronOCL.getGradientIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaGradients, def_k_sac_alg_log_probs, cLogProbs.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_SAC_AlphaGradients, def_k_sac_alg_activation, (int)cAlphas.Activation()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

Después pondremos el kernel en la cola de ejecución y no nos olvidaremos de supervisar las operaciones.

   if(!OpenCL.Execute(def_k_SAC_AlphaGradients, 1, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }

Al final del método, llamaremos al método de pasada inversa de nuestra capa interna de cálculo del coeficiente de temperatura.

   return cAlphas.calcHiddenGradients(GetPointer(cQuantile0), cQuantile2.getOutput(), cQuantile2.getGradient());
  }

Además, redefiniremos el método para actualizar los parámetros de la capa neuronal CNeuronSoftActorCritic::updateInputWeights. El algoritmo de este método es bastante sencillo, solo llama a métodos similares de la clase padre y los objetos internos. El código completo de este método se encuentra en los archivos anexos. Allí también encontrará el código completo de todos los métodos y clases usados en este artículo. Esto incluye los métodos de trabajo con los archivos de nuestra nueva clase, en los que no nos detendremos ahora.

2.2 Modificación de la clase CNet

Una vez completada la nueva clase, declararemos las constantes para mantener los kernels creados, sin olvidarnos de añadir nuevos kernels al proceso de inicialización del objeto de contexto y del programa OpenCL. Hemos repetido esta funcionalidad más de 50 veces al crear cada nuevo kernel, así que no nos detendremos en ella.

En cuanto a nosotros, ha llegado el momento de recordar que la funcionalidad de nuestra biblioteca carece de la capacidad de acceder directamente a una capa neuronal específica. El proceso completo de interacción se construye a través de la funcionalidad de la operación del modelo en su conjunto a nivel de la clase CNet. Así, para obtener los valores del componente de entropía para el usuario, crearemos el método CNet::GetLogProbs.

En los parámetros, el método obtendrá el puntero al vector para escribir los valores.

En el cuerpo del método, organizaremos un bloque de controles con una reducción paso a paso del nivel de los objetos. Primero comprobaremos la existencia de un objeto matriz dinámico de capas neuronales. Luego descenderemos un nivel más y comprobaremos el puntero del objeto de la última capa neuronal. A continuación, bajaremos aún más y comprobaremos el tipo de la última capa neuronal. Esta debería ser nuestra nueva capa CNeuronSoftActorCritic.

bool CNet::GetLogProbs(vectorf &log_probs)
  {
//---
   if(!layers)
      return false;
   int total = layers.Total();
   if(total <= 0 || !layers.At(total - 1))
      return false;
   CLayer *layer = layers.At(total - 1);
   if(!layer.At(0) || layer.At(0).Type() != defNeuronSoftActorCritic)
      return false;
//---
   CNeuronSoftActorCritic *neuron = layer.At(0);

Solo después de superar con éxito todos los niveles de control pasaremos al método similar de nuestra capa neural.

   return neuron.GetAlphaLogProbs(log_probs);
  }

Tenga en cuenta que en esta fase nos limitaremos a la última capa del modelo. Esto implica que la capa solo podrá utilizarse como última capa del Actor.

Una cosa más: este método solo lee datos del búfer y no iniciará su proceso de cálculo. Por lo tanto, su invocación solo tendrá sentido tras la pasada directa del Actor. De hecho, no se trata de una limitación de ningún tipo: en nuestra representación, la regularización de la entropía solo se usará para generar la recompensa durante la recopilación de datos primarios y el entrenamiento del modelo. En estos procesos, la pasada directa del Actor con la generación de la acción respecto a la ejecución resulta primordial.

Para las necesidades de la pasada inversa, crearemos el método CNet::AlphasGradient. Como ya hemos comentado, la distribución del gradiente de entropía va más allá del proceso que hemos construido anteriormente. Esto también se reflejará en el algoritmo de este método. Construiremos el método de tal forma que sea llamado a través del Crítico, mientras que transmitiremos el puntero al objeto del Actor en los parámetros del método.

El algoritmo del bloque de control de este método también estará estructurado en consecuencia. Primero comprobaremos que el puntero al objeto del Actor esté actualizado y que tenga la última capa CNeuronSoftActorCritic.

bool CNet::AlphasGradient(CNet *PolicyNet)
  {
   if(!PolicyNet || !PolicyNet.layers)
      return false;
   int total = PolicyNet.layers.Total();
   if(total <= 0)
      return false;
   CLayer *layer = PolicyNet.layers.At(total - 1);
   if(!layer || !layer.At(0))
      return false;
   if(layer.At(0).Type() != defNeuronSoftActorCritic)
      return true;
//---
   CNeuronSoftActorCritic *neuron = layer.At(0);

La segunda parte del bloque de control realizará comprobaciones similares para la última capa del Crítico. Aquí, por supuesto, no habrá ninguna restricción sobre el tipo de capa neuronal.

   if(!layers)
      return false;
   total = layers.Total();
   if(total <= 0 || !layers.At(total - 1))
      return false;
   layer = layers.At(total - 1);

Solo después de superar todos los controles pasaremos al método de distribución del gradiente de nuestra nueva capa neuronal.

   return neuron.calcAlphaGradients((CNeuronBaseOCL*) layer.At(0));
  }

Debemos decir honestamente que el uso de un modelo totalmente parametrizado nos permite determinar las probabilidades de las acciones individuales, pero no permite crear una política del Actor verdaderamente estocástica. La estocasticidad del actor implica el muestreo de acciones a partir de una distribución aprendida, algo que no podemos organizar en el lado del contexto de OpenCL. En el autocodificador variacional, para resolver dicho problema, utilizamos el truco de la reparametrización y un vector de valores aleatorios generados al margen del programa principal. Pero en este caso, necesitaremos cargar una distribución de probabilidad para el muestreo. En su lugar, en la fase de recopilación de bases de ejemplos, muestrearemos los valores en algún entorno del valor estimado (de forma similar a TD3) y, a continuación, solicitaremos al modelo la entropía de dichas acciones. Para ello, crearemos el método CNet::CalcLogProbs. Su algoritmo recuerda la construcción del método GetLogProbs, pero a diferencia del anterior, en los parámetros recibiremos un puntero al búfer de datos con los valores muestreados. Y como resultado del funcionamiento del método en el propio búfer obtendremos sus probabilidades.

El código completo de todas las clases y sus métodos se encuentra en el archivo adjunto.

2.3 Creación de un modelo de entrenamiento de asesores

Una vez que hemos terminado de crear nuevos objetos para nuestro modelo, pasaremos a organizar el proceso de creación y entrenamiento del mismo. Como antes, usaremos 3 asesores en este proceso:

• Research — recopilación de una base de datos de ejemplos
• Study — entrenamiento de modelos
• Test — comprueba los resultados obtenidos.

Con el fin de reducir la longitud del artículo y ahorrarle tiempo al lector, nos centraremos solo en los cambios realizados en las versiones de los asesores expertos similares del artículo anterior para organizar el algoritmo en consideración.

Lo primero y más importante será la arquitectura del modelo. Aquí solo hemos cambiado la última capa Actor, sustituyéndola por la nueva clase CNeuronSoftActorCritic. Hemos indicado el tamaño de la capa según el número de acciones, y 32 cuantiles para cada acción (como recomiendan los autores del método FQF).

Asimismo, hemos utilizado una sigmoide como función de activación, de forma similar a los experimentos del artículo anterior.

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic)
  {
//--- Actor
.........
.........
//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftActorCritic;
   descr.count = NActions;
   descr.window_out = 32;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- Critic
.........
.........
//---
   return true;
  }

El algoritmo del asesor experto "...\SoftActorCritic\Research.mq5" lo hemos tomado casi sin cambios del artículo anterior. Ni el bloque de recopilación de datos históricos ni el bloque de ejecución de operaciones comerciales han sufrido cambios. Los únicos cambios los hemos realizado en la función OnTick en cuanto a la recompensa del entorno. Como ya hemos mencionado, el algoritmo SAC añade la regularización de la entropía a la función de recompensa.

Al igual que antes, utilizaremos como recompensa la variación relativa del valor del balance de la cuenta. También añadiremos una penalización por no tener posiciones abiertas. Pero ahora deberemos añadir la regularización de la entropía. Para este propósito, hemos creado el método CalcLogProbs más arriba. No obstante, hay un pequeño detalle: La distribución cuantílica de nuestra clase almacenará los valores hasta la función de activación. Ya en el proceso de toma de decisiones, utilizaremos los resultados activados del modelo del Actor. Como función de activación en la salida del Actor, utilizaremos una sigmoide.

Mediante transformaciones matemáticas llegaremos a

Utilizaremos esta propiedad y ajustaremos las acciones muestreadas a la forma deseada. A continuación, trasladaremos los datos del vector al búfer de datos y, si es posible, trasladaremos la información a la memoria contextual OpenCL. 

Tras realizar este trabajo preparatorio, solicitaremos al Actor la entropía de las acciones realizadas.

Nótese que hemos obtenido la entropía de las 6 acciones considerando el coeficiente de temperatura, pero nuestra recompensa supondrá un número para evaluar la totalidad del estado actual y la acción. En esta implementación, utilizaremos el valor de entropía total, que encaja bien en el contexto de las probabilidades y logaritmos. Al fin y al cabo, la probabilidad de un suceso complejo es igual al producto de las probabilidades de los sucesos que lo componen, mientras que el logaritmo del producto es igual a la suma del logaritmo de los multiplicadores individuales. No obstante, admito otros enfoques. Su idoneidad para cada caso concreto puede comprobarse durante el proceso de entrenamiento. No tema experimentar.

void OnTick()
  {
//---
.........
.........
//---
   float reward = Account[0];
   if((buy_value + sell_value) == 0)
      reward -= (float)(atr / PrevBalance);
   for(ulong i = 0; i < temp.Size(); i++)
      sState.action[i] = temp[i];
   temp.Clip(0.001f, 0.999f);
   temp = MathLog((temp - 1.0f) * (-1.0f) / temp) * (-1);
   Result.AssignArray(temp);
   if(Result.GetIndex() >= 0)
      Result.BufferWrite();
   if(Actor.CalcLogProbs(Result))
     {
      Result.GetData(temp);
      reward += temp.Sum();
     }
   if(!Base.Add(sState, reward))
      ExpertRemove();
  }

Los cambios más significativos se han realizado en el proceso de entrenamiento del modelo en el asesor "...\SoftActorCritic\Study.mq5". Echemos un vistazo más de cerca a la función Train del asesor experto especificado. Aquí se organizará todo el proceso de entrenamiento del modelo.

Al principio de la función, muestrearemos el conjunto de datos del búfer de reproducción de experiencia, como hemos hecho anteriormente.

void Train(void)
  {
   int total_tr = ArraySize(Buffer);
   uint ticks = GetTickCount();
//---
   for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++)
     {
      int tr = (int)((MathRand() / 32767.0) * (total_tr - 1));
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2));

A continuación, determinaremos el valor previsto del estado futuro. El algoritmo seguirá un proceso similar en la aplicación del método TD3. Una diferencia será la ausencia del modelo objetivo del Actor. Aquí, utilizaremos el modelo del Actor entrenado para determinar la acción en el estado futuro.

      //--- Target
      State.AssignArray(Buffer[tr].States[i + 1].state);
      float PrevBalance = Buffer[tr].States[i].account[0];
      float PrevEquity = Buffer[tr].States[i].account[1];
      Account.Clear();
      Account.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance);
      Account.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance);
      Account.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity);
      Account.Add(Buffer[tr].States[i + 1].account[2]);
      Account.Add(Buffer[tr].States[i + 1].account[3]);
      Account.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance);
      Account.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance);
      Account.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance);
      //---
      if(Account.GetIndex() >= 0)
         Account.BufferWrite();

Luego rellenaremos los búferes de datos de origen y llamaremos a los métodos de pasada directa del Actor y a los 2 modelos de destino del Crítico.

      if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         ExpertRemove();
         break;
        }
      //---
      if(!TargetCritic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
         !TargetCritic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

Como en el método TD3, para entrenar al Crítico, utilizaremos el menor valor predicho del valor de estado, pero en este caso, estaremos añadiendo un componente entrópico.

      vector<float> log_prob;
      if(!Actor.GetLogProbs(log_prob))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }
      TargetCritic1.getResults(Result);
      float reward = Result[0];
      TargetCritic2.getResults(Result);
      reward = Buffer[tr].Revards[i] + DiscFactor * (MathMin(reward, Result[0]) + log_prob.Sum() - Buffer[tr].Revards[i + 1]);

Nótese aquí que, en el proceso de almacenamiento de la trayectoria, hemos mantenido la cantidad acumulada de recompensas hasta el final de la pasada, considerando el factor de descuento. La recompensa por cada transición de estado individual implicará una regularización entrópica. Para entrenar los modelos del Crítico, ajustaremos la recompensa acumulada guardada para corregir el uso de la política actualizada. Para ello, tomaremos la diferencia entre el valor mínimo previsto del estado posterior, teniendo en cuenta el componente de entropía, y la recompensa acumulada de ese estado almacenada en el búfer de reproducción de experiencia. El valor resultante se ajustará usando un factor de descuento y se añadirá al valor almacenado del estado actual. En este caso, utilizaremos la hipótesis del coste de acción no decreciente durante el proceso de optimización del modelo.

A continuación, nos enfrentaremos a la fase de entrenamiento de los modelos de los Críticos. Para ello, rellenaremos los búferes de datos con el estado actual del sistema.

      //--- Q-function study
      State.AssignArray(Buffer[tr].States[i].state);
      PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
      PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
      Account.Update(0, (Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
      Account.Update(1, Buffer[tr].States[i].account[1] / PrevBalance);
      Account.Update(2, (Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
      Account.Update(3, Buffer[tr].States[i].account[2]);
      Account.Update(4, Buffer[tr].States[i].account[3]);
      Account.Update(5, Buffer[tr].States[i].account[4] / PrevBalance);
      Account.Update(6, Buffer[tr].States[i].account[5] / PrevBalance);
      Account.Update(7, Buffer[tr].States[i].account[6] / PrevBalance);
      //---
      Account.BufferWrite();

Tenga en cuenta que en este caso ya no estaremos buscando un búfer de descripción del estado de la cuenta en el contexto de OpenCL. Simplemente llamaremos al método para mover los datos al contexto inmediatamente después de guardar los datos. Esto es posible gracias a que todos los modelos se ejecutan en el mismo contexto OpenCL. Ya hemos hablado de las ventajas de este enfoque. Al llamar a los métodos de pasada directa de los modelos de destino, el búfer ya se habrá creado en el contexto. De lo contrario, obtendríamos un error al ejecutarlos. Por lo tanto, en esta fase ya no perderemos tiempo ni recursos en comprobaciones innecesarias.

Tras cargar los datos, llamaremos al método de pasada directa del Actor y cargaremos el componente de entropía de la recompensa.

      if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }
      //---
      Actor.GetLogProbs(log_prob);

En esta fase tendremos todos los datos que necesitamos para los pasada directa e inversa de los Críticos. Pero en esta fase, nos hemos desviado ligeramente del algoritmo del autor. La cuestión es que los autores del método, tras actualizar los parámetros del Crítico, proponen utilizar el Crítico con la valoración mínima para actualizar la política del Actor. Según nuestras observaciones, a pesar de las desviaciones en las estimaciones, el gradiente de error entre acciones prácticamente no varía, así que hemos decidido alternar los modelos del Crítico. En las iteraciones pares, actualizaremos el modelo del Crítico 2 basándonos en las acciones del búfer de reproducción de experiencia, mientras que la política del Actor se entrenará usando como base las primeras valoraciones del Crítico.

      Actions.AssignArray(Buffer[tr].States[i].action);
      if(Actions.GetIndex() >= 0)
         Actions.BufferWrite();
//---
      if((iter % 2) == 0)
        {
         if(!Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
            !Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         Result.Clear();
         Result.Add(reward-log_prob.Sum());
         if(!Critic1.backProp(Result, GetPointer(Actor)) ||
            !Critic1.AlphasGradient(GetPointer(Actor)) ||
            !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer) ||
            !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         Result.Update(0,Buffer[tr].Revards[i]);
         if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
        }

En las iteraciones impares, cambiaremos el uso de los modelos del Crítico.

      else
        {
         if(!Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
            !Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         Result.Clear();
         Result.Add(reward);
         if(!Critic2.backProp(Result, GetPointer(Actor)) ||
            !Critic2.AlphasGradient(GetPointer(Actor)) ||
            !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer) ||
            !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         Result.Update(0,Buffer[tr].Revards[i]);
         if(!Critic1.backProp(Result, GetPointer(Actions), GetPointer(Gradient)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
        }

Observe la secuencia en la que se llaman los métodos de pasada inversa. En primer lugar, realizaremos una pasada inversa del Crítico. Luego pasaremos el gradiente por el componente entrópico. A continuación, realizaremos una pasada inversa a través del bloque de procesamiento primario de datos del Actor. Esto nos permitirá adaptar las capas de convolución a los requisitos del Crítico, y solo entonces realizaremos una pasada inversa completa del Actor para optimizar su política de acción.

Al final de las operaciones de la función, actualizaremos los modelos objetivo y mostraremos un mensaje informativo al usuario para que supervise visualmente el proceso de aprendizaje.

      //--- Update Target Nets
      TargetCritic1.WeightsUpdate(GetPointer(Critic1), Tau);
      TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau);
      //---
      if(GetTickCount() - ticks > 500)
        {
         string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", 
                                    iter * 100.0 / (double)(Iterations), Critic1.getRecentAverageError());
         str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", 
                                    iter * 100.0 / (double)(Iterations), Critic2.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }
   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", Critic1.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", Critic2.getRecentAverageError());
   ExpertRemove();
//---
  }

Podrá encontrar el código completo del asesor en el archivo adjunto. Allí también encontrará el código del asesor de pruebas. Los cambios introducidos son similares a los cambios del asesor de recopilación de datos primarios, así que no nos detendremos en ellos.

3.Pruebas

El entrenamiento y las pruebas del modelo se han realizado con los datos históricos del marco temporal H1 en EURUSD para el periodo de enero a mayo de 2023. Tanto los parámetros de los indicadores como los hiperparámetros al completo los hemos utilizado como establecidos por defecto.

Muy a mi pesar, debo admitir que durante la elaboración del artículo no he sido capaz de entrenar un modelo capaz de generar beneficios en la muestra de entrenamiento. Según los resultados de la prueba, mi modelo he perdido un 3,8% durante los 5 meses del periodo de entrenamiento. 

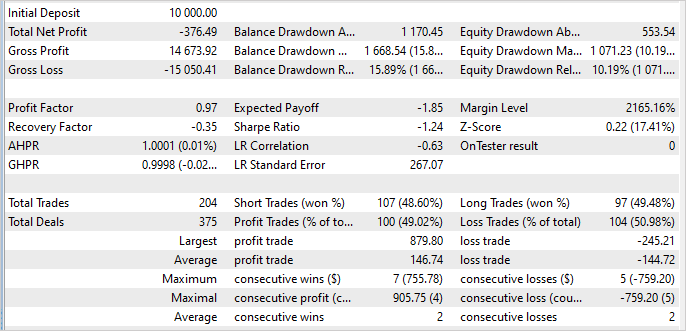
En el lado positivo, la operación rentable máxima es 3,6 veces superior a la pérdida máxima por 1 operación. La media de operaciones rentables es solo ligeramente superior a la media de operaciones perdedoras. Pero aquí la proporción de operaciones rentables es del 49%. En esencia, ese 1% no ha bastado para llegar a 0.

En cuanto a los datos fuera de la muestra de entrenamiento, la situación se ha mantenido prácticamente sin cambios. Incluso el porcentaje de transacciones rentables ha aumentado hasta el 51%. Sin embargo, el valor de la operación rentable media ha disminuido, y hemos vuelto a tener pérdidas.

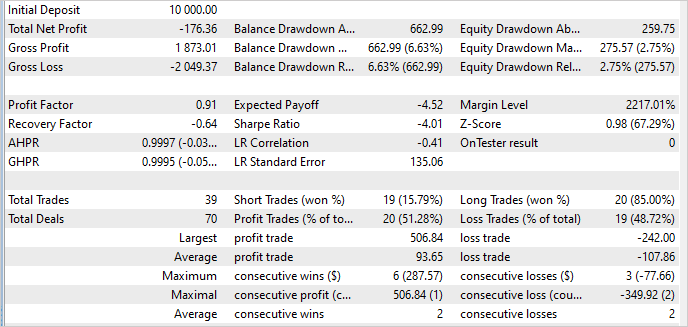
La estabilidad del rendimiento del modelo fuera de la muestra de entrenamiento supone un factor positivo. Pero la cuestión sigue siendo cómo evitar las pérdidas. Tal vez la causa resida en los cambios que hemos introducido en nuestro algoritmo, o tal vez en un coeficiente de temperatura inflado, lo cual estimula una mayor exploración del mercado.

Otra posibilidad es que exista demasiada variación en los valores de acción muestreados. Al muestrear una acción con probabilidad cercana a "0" la elevada entropía sobreestima sus recompensas y esto distorsiona la política del Actor. Para encontrar la causa, necesitaremos pruebas adicionales, cuyos resultados me aseguraré de compartir con usted.

Conclusión

En este trabajo, hemos introducido el algoritmo Soft Actor-Critic (SAC) para resolver problemas en un espacio continuo de acciones. El SAC se basa en la idea de maximizar la entropía de la política, permitiendo al agente explorar diferentes estrategias y encontrar soluciones óptimas en entornos estocásticos dada la máxima variedad de acciones.

Los autores del método propusieron el uso de la regularización de entropía, que se añade a la función de entrenamiento objetivo. Esto permite que el algoritmo estimule la exploración de nuevas acciones y evite que se fije demasiado rígidamente en determinadas estrategias.

Hemos implementado este método utilizando herramientas MQL5, pero desafortunadamente no hemos podido entrenar una estrategia rentable. No obstante, el modelo entrenado muestra un rendimiento estable dentro y fuera de la muestra de entrenamiento. Lo cual demuestra la capacidad del método para generalizar la experiencia adquirida y transmitirla a estados del entorno desconocidos.

Nuestro objetivo es encontrar oportunidades para aprender políticas de Actor rentables; más adelante, presentaremos al lector los resultados de este trabajo.

Enlaces

• Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor
• Soft Actor-Critic Algorithms and Applications
• Redes neuronales: así de sencillo (Parte 48): Métodos para reducir la sobreestimación de los valores de la función Q

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	Study.mq5	Asesor	Asesor de entrenamiento del agente
3	Test.mq5	Asesor	Asesor para la prueba de modelos
4	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
5	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
6	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL