離散ハートレー変換
はじめに
1942年、ラルフ・ハートレーは、記事「A More Symmetrical Fourier Analysis Applied to Transmission Problems」の中でフーリエ変換の類似物を提案しました。
フーリエ変換(FT)と同様に、ハートレー変換(HT)は元の信号を三角関数の和に変換します。しかし、それらの間には1つの大きな違いがあります。FTは実数値を複素数に変換しますが、HTは実数値のみを提供します。この違いのため、ハートレー変換は普及しませんでした。科学者や技術者はそれに何の利点も見出さず、通常のフーリエ変換を使い続けたのです。1983年、Ronald Bracewell(英語)は、ハートレー変換の離散バージョンを発表しました。
理論を少々
離散ハートレー変換(DHT)(英語)は、離散時系列の分析と処理に使用できます。信号のフィルタリング、スペクトルの分析などが可能になります。DHTの能力は離散フーリエ変換の能力に劣りません。ただし、DFTとは異なり、DHTは実数のみを使用するため、実際の実装がより便利であり、その適用結果はより視覚的です。
N個の実数h[0]…h[N-1]があるとします。離散ハートレー変換を使用して、それらからN個の実数H[0]…H[N-1]を取得します。
この変換により、信号を時間領域から周波数領域に転送できるようになります。これを利用すると、元の信号内の特定の高調波の影響がどの程度大きいかを推定できます。H[0]には信号に関する基本情報が含まれます。H[1]…H[N-1]は追加データを提供します。これらの数値は、元の信号における特定の高調波がどの程度強いかを示します。これらの数値のインデックスは、この高調波が元の信号に何サイクル収まるかを示します。言い換えれば、指数が高いほど高調波周波数が高くなります。
逆ハートレー変換は、周波数領域から時間領域に移動するために使用されます。その方程式は次のようになります。
どちらの方程式でも、cas(cosおよびsin)関数は三角関数の和を表します。
ただし、差で置き換えることは可能です。変革の本質は変わりません。では、DHTを実践する方法を見てみましょう。
離散ハートレー変換の導入
DHTは信号を時間領域から周波数領域に変換しますが、これによって実際的な利益を得ることができるでしょうか。
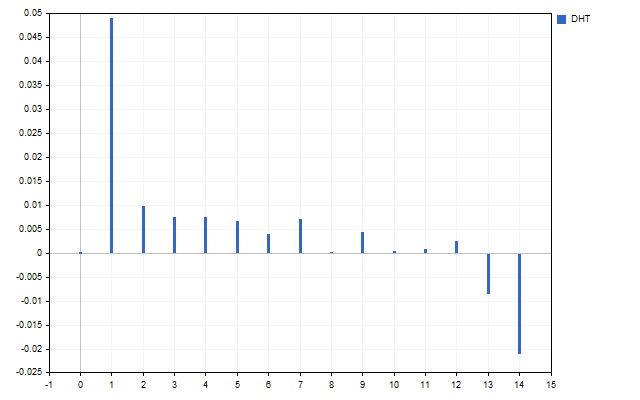
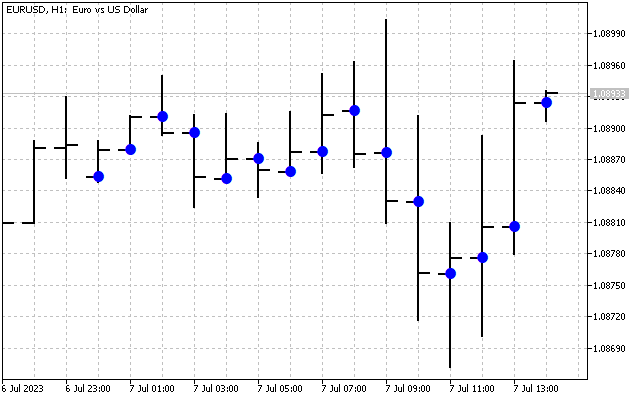
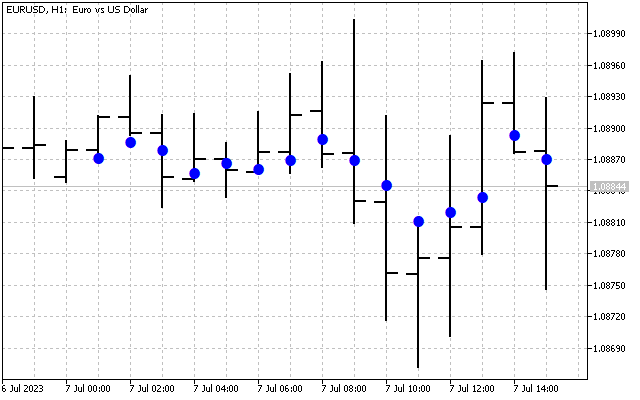
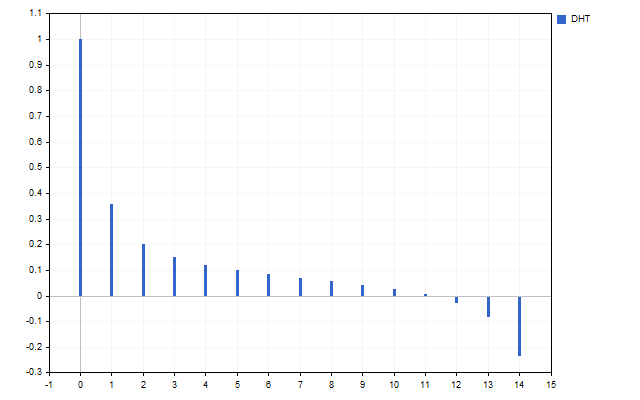
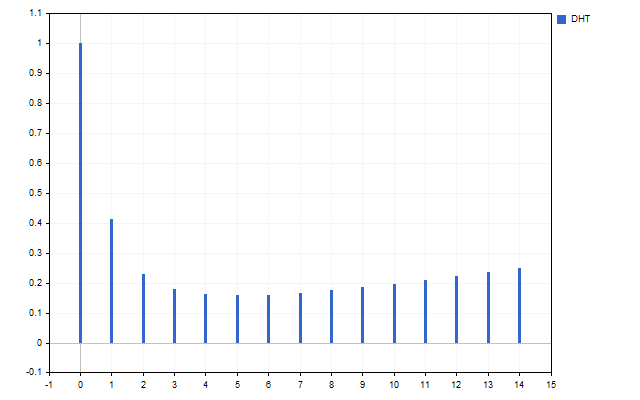
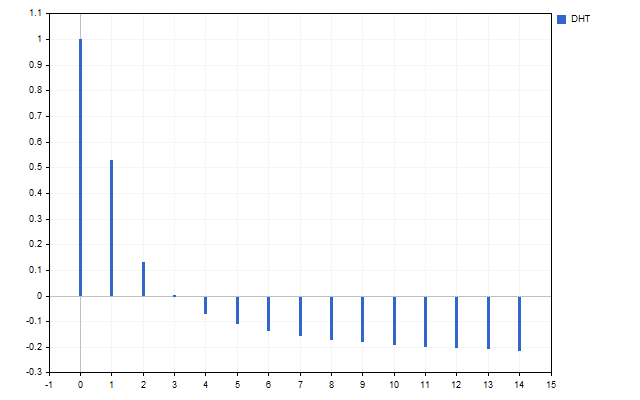
15の始値をシグナルとして考えてみましょう。この時系列のスペクトルは次のようになります(スケールの違いによりH[0]は表示されていません)。
この図は、高調波が異なれば強度も異なることを明確に示しています。しかし、このスペクトルで何ができるのでしょうか。
単純移動平均を例に挙げてみましょう。その方程式は非常に簡単です。
価格の1つをゼロに設定すると、指標はどうなるでしょうか。何も良いものは得られそうにありません。しかし、周波数領域ではこれが可能です。任意の数の高調波をゼロにすることができます。
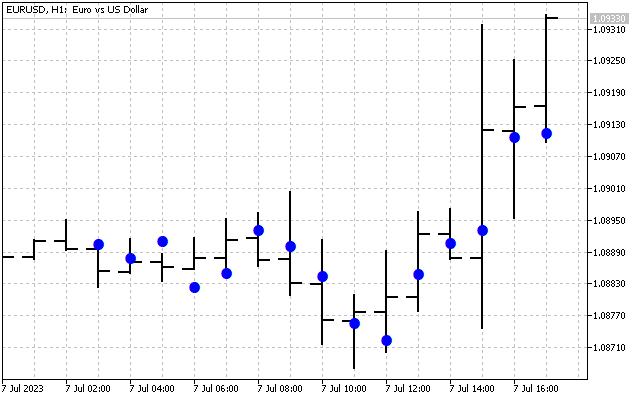
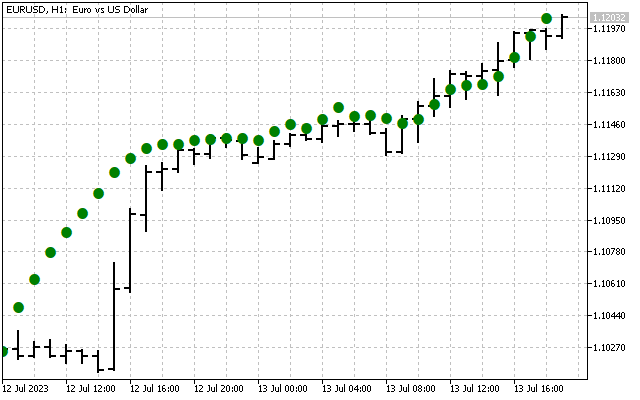
元の信号は次のようになります。
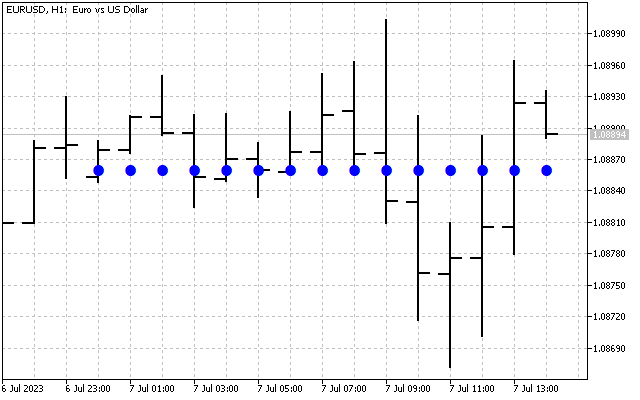
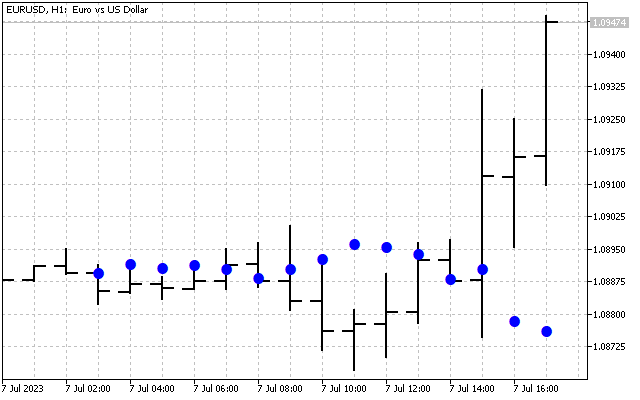
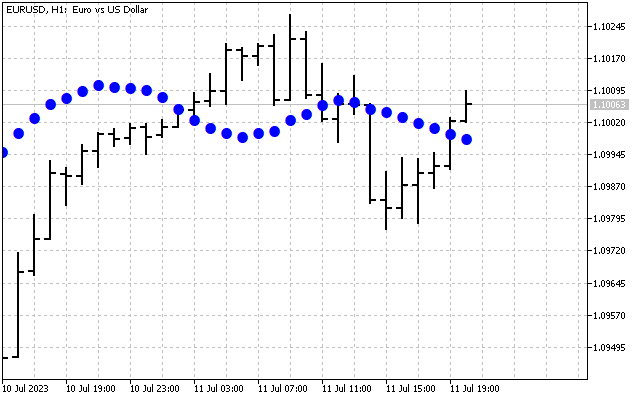
次に、H[1]~H[14]のすべての高調波をゼロに設定しましょう。これで、元の信号に関する基本的な情報だけが得られました。このスペクトルに逆ハートレー変換を適用してみましょう。
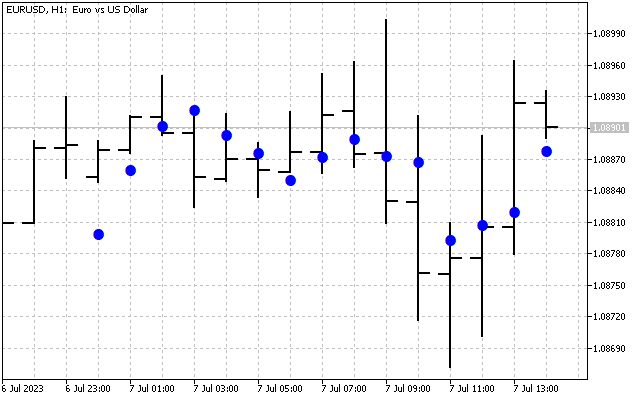
次に、最高周波数H[10]–H[14]の高調波を削除します。ハートレー変換では次の結果が得られます。
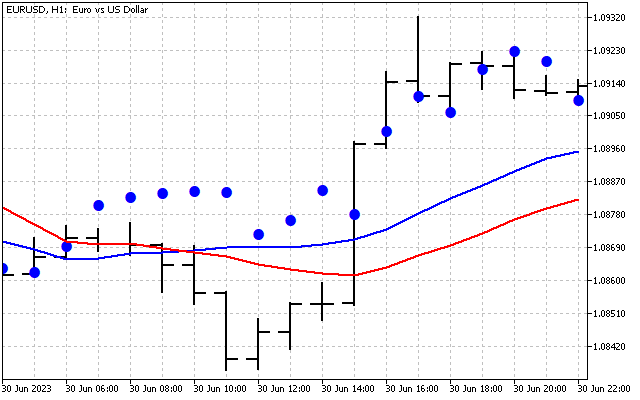
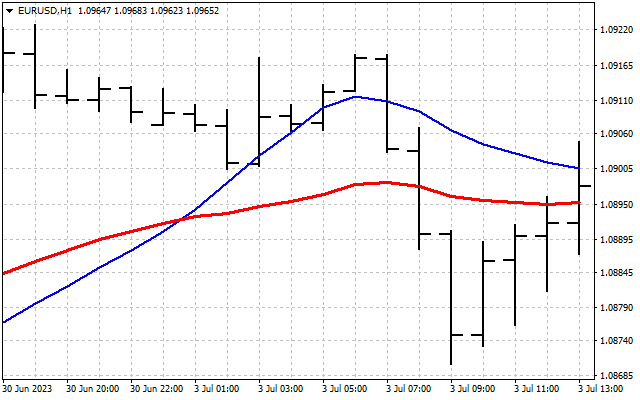
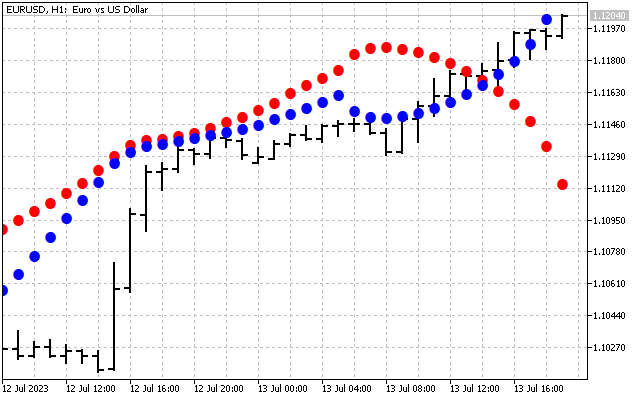
元の信号を平滑化しました。ここでは、ハートレー変換を実際に適用する最初の方法を示します。まず、周波数領域で時系列を平滑化できます。その後、取得された値は通常の指標の入力に転送されます。例として2つの移動平均を見てみましょう。そのうちの1つは通常どおり価格に適用されます(赤線)。2番目はDHT値(青線)に適用されます。
信号スペクトルを処理する方法は、一部の高調波を無効にすることだけではありません。たとえば、指定された数値で割ることにより、すべての高調波を一度に減衰できます。
あるいは、周波数に応じて各高調波を減衰させることもできます。周波数が高いほど、減衰も大きくなります。
いずれの場合も、平滑化された時系列が得られます。高調波を2倍に減衰させた信号は次のようになります。
スペクトルを処理する別の方法は、最も強い高調波のみを残すことです。これをおこなうには、すべての高調波の平均を見つける必要があります。
絶対値がこの平均を超えるものだけを残します。
そうすれば、メイン信号と最も強い高調波のみが得られます。
もう1つの信号処理オプションは、高調波値を反転できることです。この場合、再構成された信号は逆位相になります。
この場合、信号の鏡面反射を受け取ることになります。つまり、上昇傾向が下降傾向に置き換えられ、その逆も同様です。このアプローチは、支持と抵抗のレベルを計算するときに役立ちます。
ソース信号のスペクトルを処理するためのすべてのオプションは、個別に使用することも、相互に組み合わせて使用することもできます。たとえば、最初に最も強い高調波のみを残し、次にその符号を反対に変更することができます。この場合、結果は逆トレンドのインパルスの可能性を示します。
最適なスペクトルを持つ指標
線形指標はすべて係数のセットです。これらの係数にハートレー変換を適用すると、指標のスペクトル特性が得られます。
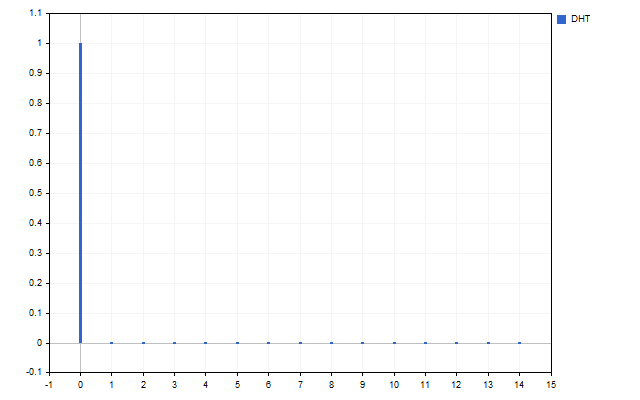
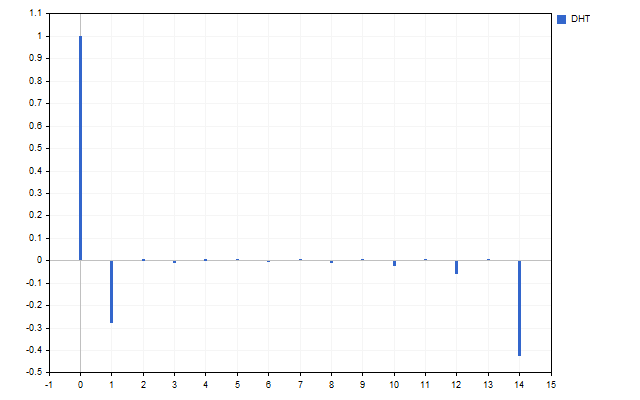
SMAがローパスフィルターであることはわかっています。この発言を確認してみましょう。この指標のすべての係数は1/Nに等しくなります。ハートレー変換は、この指標スペクトルを提供します。
見てわかるように、SMAはメイン信号H[0]のみを通過させますが、他のすべての高調波は完全に抑制されます。
スペクトル(指標の周波数特性)は互いに大きく異なる場合があります。たとえば、LWMAは入力信号のすべての高調波を通過させます。
一方、SMMAは一部の高調波のみを通過させ、残りの高調波を抑制します。
各指標には独自のスペクトルがあります。価格シリーズの取り扱いに使用できます。これをおこなうには、まず元の信号H[]のスペクトルを見つける必要があります。次に、それを項ごとに指標I[]のスペクトルと乗算します。
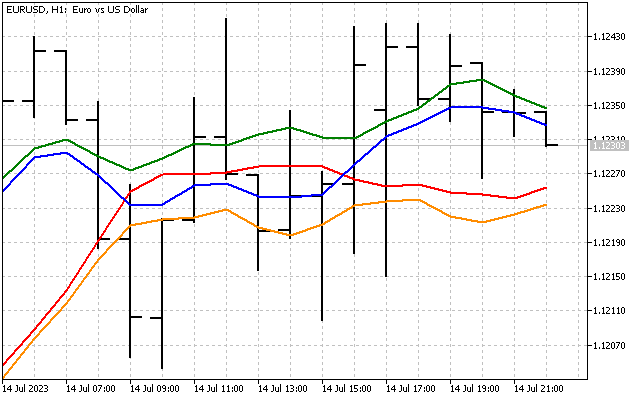
逆ハートレー変換が、得られた結果に適用されます。その結果、周波数領域での信号フィルタリングが得られます。LWMA指標に基づく周波数フィルターの動作は次のように見えます。
ただし、最初に指標のスペクトルを設定し、次にその係数を取得することで、逆の方法を使用することもできます。スペクトル特性が信号のスペクトルに対応する指標を作成してみましょう。
アルゴリズムは以下のようになります。まず、DHTを使用して信号スペクトルを取得します。次に、それを正規化する必要があります。これをおこなうには、すべての高調波値をD=H[0]で除算する必要があります。
正規化後、指標を構築する際にはH[0]=1が必須の条件となることに注意してください。
その後、指標の重み付け係数を提供する逆変換を適用する必要があります。
これらの係数はSMAとあまり変わりません。ただし、このような指標は移動平均と比較してラグが小さいため、市場のダイナミクスをより正確に追跡することが可能になります。
ノイズとカラー
金融時系列を処理する場合、「ノイズ」という用語は、ほとんどの場合、不要な信号の歪みを指します。このようなノイズを除去するには、SMAなどのさまざまなフィルターを使用できます。
ランダムまたは予測不可能な信号もノイズとみなされる場合があります。市場価格の動きをノイズの合計として表すとどうなるでしょうか。これをおこなうには、カラードノイズの概念に目を向ける必要があります。カラードノイズは、異なる周波数範囲で異なるエネルギーを持つノイズです。この名前は、可視光のさまざまな色に由来しています。赤は低周波ノイズ、紫は高周波ノイズです。
価格変動を色付きノイズの合計として表すと、財務時系列を分析する際に興味深い結果が得られることがあります。このアプローチにより、価格変動のさまざまな周波数成分を考慮することができます。
それぞれのカラードノイズには独自の特性があり、f周波数に応じたスペクトル内のエネルギーの分布を反映しています。
ノイズには5つの原色があります。
| pパラメータ | ノイズカラー |
|---|---|
| -2 | 赤 |
| -1 | ピンク |
| 0 | 白 |
| +1 | 青 |
| +2 | バイオレット |
それぞれのノイズは特定の価格変動に関連付けられています。たとえば、レッドノイズは、価格変動の長期的なトレンドやサイクルの存在を示す可能性があります。ホワイトノイズは、市場がフラットな状態にあることを示します。紫色のノイズは、ランダムで予測不可能な価格の動きを示している可能性があります。財務時系列の分析でカラーノイズを使用すると、隠れたパターンや、従来の分析では必ずしも表示されなかったパターンを特定するのに役立ちます。
次に、さまざまなノイズが市場でどのように動作するかを見てみましょう。これには、いくつかの簡単な手順を実行する必要があります。
まず、各高調波のエネルギーを推定できる信号のスペクトルを見つける必要があります。これには、各高調波の値を2乗します。
ここで、pパラメーターを使用してノイズのスケーリング係数の値を推定できます。この係数を使用すると、信号とノイズの合計エネルギーは等しくなります。
この係数がわかれば、EN[]ノイズのエネルギースペクトルを構築できます。
これで、HN[]ノイズスペクトルを見つけることができます。これをおこなうには、エネルギースペクトルの平方根を求める必要があります。
やるべきことはほとんど残されていません。元の信号の高調波と同じように、ノイズスペクトルの高調波に+/-符号を割り当てるだけです。この場合、ノイズと元の信号は同位相になります。
この後、逆ハートレー変換を実行して、価格チャートのノイズ値を取得する必要があります。これは市場におけるレッドノイズの様子です。
しかし、高調波の反対の符号を取ることもできます。この場合、ノイズは元の信号に対して逆位相になります。さらに、厳密に正または負の高調波値を取得することもできます。周波数領域ではこれを許容できます。そうすれば、市場におけるノイズの動きの境界が見えてくるでしょう。
カラーノイズの概念は、市場のダイナミクスを説明するためだけでなく、指標の開発にも使用できます。
これをおこなうには、まず指標のパワーE>0を設定する必要があります。このパラメータは、指標の感度を決定します。この後、すでにおなじみの手順を実行します。まずスケーリング係数を求めます。
その後、HI[]指標のスペクトルを見つけます。HI[0]は1に等しい必要があることを忘れないでください。
必要に応じて、指標スペクトルの高調波に+/-符号を割り当てるだけです。次に、逆ハートレー変換を適用して指標係数を取得する必要があります。これは、さまざまな高調波符号を使用したレッドノイズ指標がどのように見えるかです。
指標を開発するときは、純粋なノイズだけでなく、それらのさまざまな組み合わせも使用できます。たとえば、赤と紫のノイズの合計のスペクトルは次のようになります。
赤ノイズと白ノイズのスペクトルの違いは次のようになります。
Coefficient[]指標係数を受け取った後、それらを正規化する必要があります。これをおこなうには、まずすべての係数の合計を見つける必要があります。
この後、各係数を結果の量で割る必要があります。
リストされている主なノイズに加えて、他のノイズもあります。たとえば、ブラックノイズの定義の1つは、パラメーターp<-2を持つノイズです。別のアプローチを試してみましょう。pノイズパラメータが小数値を取ることができると仮定します。時間の経過とともにどのように変化するかを見てみましょう。
ノイズパラメーターを計算するには、まず信号E[]のエネルギースペクトルを見つける必要があります。この後、4つの係数を計算します。
すべての方程式において、k=1…N-1です。最適なノイズパラメータは、次の式を使用して計算できます。
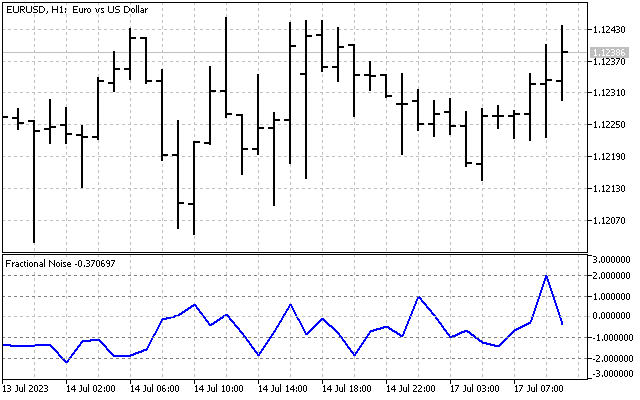
このパラメータは市況によって次のように変化します。
ご覧のとおり、金融時系列分析におけるカラーノイズの使用は、市場のダイナミクスを調査および理解するための有用なツールとなり得ます。このアプローチは、隠れたパターンを明らかにし、価格変動の予測を改善するのに役立ちます。
結論
離散ハートレー変換には、独自の高速変換アルゴリズムがありますが、事前にcas値の配列を割り当てておけば、データの処理速度を大幅に高速化できます。この配列のサイズは(N-1)^2+1に等しい必要があります。ここで、Nは指標期間です。この配列の値は次のように設定されます。
この記事ではまさにこのアプローチを使用しました。
記事には以下の指標が添付されています。
| 銘柄 | 説明 |
|---|---|
| DHT | この指標は、信号高調波の処理能力を示します。
|
| DHTLWMA | この指標は、スペクトル領域でのLWMA指標による価格処理を示します。 |
| Spectrum | 係数が元の信号と同様のスペクトル特性を与える指標 |
| Noise Levels | 指標はカラーノイズのレベルを示します。 ノイズ-ノイズカラー Type-元の信号の位相を変更します。 |
| Noise Indicator | 指標は、選択されたノイズカラーに対応する係数を選択します。 E-ノイズパワー。 |
| Fractional Noise | フラクショナルノイズパラメータを表示する指標。 |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/12984
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
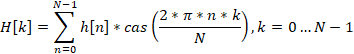
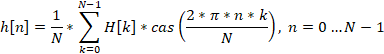
記事をありがとう!
ちょうど昨日、サブサンプルの統計的指標を通じて市場の段階を特定する方法について考えていたところでした。
この方面について、もっと突っ込んだ研究をされたことはありますか?トレンド・フラットの分類は、どれくらいのスピードで(どれくらいのラグで)、どれくらいの誤差でできたのでしょうか?
記事をありがとう!
ちょうど昨日、サブサンプルの統計的指標を通じて市場の段階を特定する方法について考えていたところだったので、記事の中で似たようなアイデアを目にしました。
この方向で何か深い研究をされましたか?トレンド・フラットの分類は、どれくらいのスピードで(どれくらいのラグで)、どれくらいの誤差でできたのでしょうか?
市場のステージを特定するのは、おそらく最も簡単な作業だ。主要シグナルを除いた)価格スペクトルをクラスター分析(コホネンマップ)にかけると、市場ステージが得られます。新しいトレンドの変化や始まりの兆候は、低周波成分の相対的な弱さと高周波高調波の相対的な強さです。しかし残念なことに、トレンドの方向性を見誤ることもある。