MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português 한국어 Français Italiano Türkçe
MQL5での統計確率分布

MQL5での統計確率分布

MetaTrader 5 — 例 | 29 10月 2015, 08:47
1 223 0
Denis Kirichenko
Denis Kirichenko

確率理論全体の基礎は不快の哲学にある。
(Leonid Sukhorukov)

はじめに

その活動の性格によりトレーダーは往々にして確率や無作為性というカテゴリーを扱う必要があります。無作為の対語は「規則性」の概念です。一般の哲学的法則に基づいて、無作為が秩序の中でルールとして成長するのは驚くべきことです。現段階では逆の事柄について述べることはしません。基本的に、無作為－秩序相関関係は重要な関係です。マーケット状況に採り入れられるなら、トレーダーが受け取る収益に直接影響を与えるからです。

本稿では、将来マーケットの規則性を見つけるのに役立つ基本的な理論的インスツルメントを解説していきます。


1. 分布、特質、タイプ

ランダム変数について述べるためには一次元統計の確率分布を必要とします。一定の法則を用いてランダム変数の例を述べます。あらゆる分布法則を適用するにはランダム変数セットが要求されるのです。

なぜ [理論的] 分布を分析するのでしょうか？それにより変数属性値に基づく頻度変化パターンを特定するのが簡単になるからです。また、要求される分布の統計パラメータを取得することができます。

確率分布タイプに関しては、専門の文献によると分布は通常ランダム変数設定タイプにより連続分布および離散分布に分けられます。ただし、別の分類の仕方もあります。たとえば、線分x=x0に対して分布曲線 f(x) の対称性、位置パラメータ、モード数、ランダム変数区間等の基準によるものです。

分布法則を定義する方法はいくつかあります。その中からもっともよく利用されるものを示します。


2. 理論的確率分布

MQL5のコンテクストで統計分布を述べるクラスを作成してみます。それから、MQL5 のコードに適用できるC++ 言語のコード例が専門書に数多く載っていることも付け加えたいと思います。よって、私は一からコードを作成することもしませんでしたし、ときにはよくできた C++ 言語コードを使いました。

もっとも困難でやりがいのあったのは MQL5でサポートされている複数継承がないことでした。複雑なクラス階層を使用しなかったのはそのためです。その著書 Numerical Recipes: The Art of Scientific Computing [2] は関数の多くを借用したもっとも最適な C++ 言語コード源となりました。が、それらはけっこう MQL5のニーズに応じて改善する必要がありました。

2.1.1 標準分布

では従来どおり正規分布から始めます。

ガウス分布とも呼ばれる正規分布は確立密度関数により提供される確率分布です。


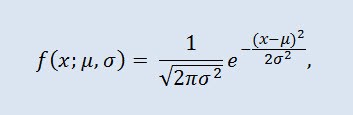
ここでパラメータ μ はランダム変数の平均（期待値）で、分布密度曲線の最大座標を示します。σ² は分散です。


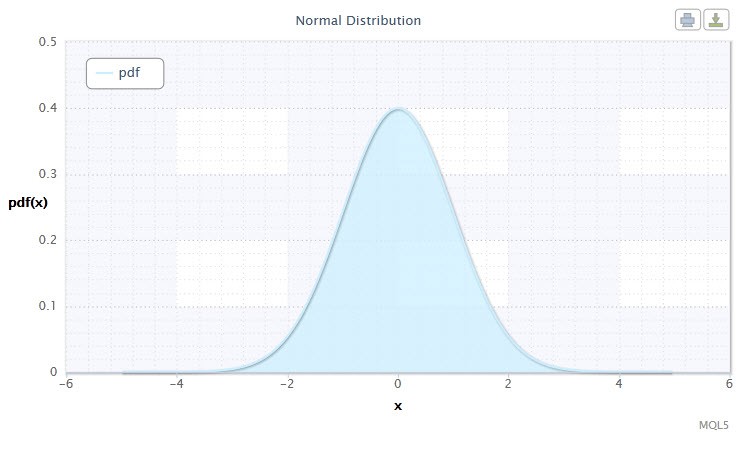
図1　正規分布密度 Nor(0,1)

その表記は以下のフォーマットとなります。X ~ Nor(μ, σ2)、ここで

  • X は正規分布 Norから選択されるランダム変数です。
  • μ は平均パラメータ (-∞ ≤ μ ≤ +∞)
  • σ は分散パラメータ (0<σ)です。

ランダム変数Xの有効範囲：  -∞ ≤ X ≤ +∞

本稿で使用している式は他の資料で提供されているものとは異なるかもしれません。そのような違いは数学的に重要ではありません。それは場合によってはパラメータ化の違いを条件としています。

正規分布は、どれも支配力を持たない非常に多くの無作為な原因の相互作用の結果生じる規則性を反映するため、統計において重要な役割を果たします。また、金融マーケットでは正規分布はほとんど例がないにもかかわらず、それでもなお程度とそれらの異常な性質を判断するために、実験に基づく分布と比較することは重要なことなのです。

正規分布のCNormaldistクラスを以下のように定義します。

//+------------------------------------------------------------------+
//|                Normal Distribution class definition              |
//+------------------------------------------------------------------+
class CNormaldist : CErf // Erf class inheritance
  {
public:
   double            mu, //mean parameter (μ)
   sig;                 //variance parameter (σ)
   //+------------------------------------------------------------------+
   //| CNormaldist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CNormaldist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Normal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return(0.398942280401432678/sig)*exp(-0.5*pow((x-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5*erfc(-0.707106781186547524*(x-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf)                |
   //| quantile function                                                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Normal Distribution!");
      return -1.41421356237309505*sig*inverfc(2.*p)+mu;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };

//+------------------------------------------------------------------+

おわかりのようにCNormaldist クラスはerror functionクラスを定義する基本クラスСErfから派生しています。それはCNormaldist クラスメソッドを計算するのに要求されます。СErf クラスおよび予備クラスerfcc はおおよそ以下のようなものです。

//+------------------------------------------------------------------+
//|                Error Function class definition                   |
//+------------------------------------------------------------------+
class CErf
  {
public:
   int               ncof;    // coefficient array size
   double            cof[28]; // Chebyshev coefficient array
   //+------------------------------------------------------------------+
   //| CErf class constructor                                           |
   //+------------------------------------------------------------------+
   void CErf()
     {
      int Ncof=28;
      double Cof[28]=//Chebyshev coefficients
        {
         -1.3026537197817094,6.4196979235649026e-1,
         1.9476473204185836e-2,-9.561514786808631e-3,-9.46595344482036e-4,
         3.66839497852761e-4,4.2523324806907e-5,-2.0278578112534e-5,
         -1.624290004647e-6,1.303655835580e-6,1.5626441722e-8,-8.5238095915e-8,
         6.529054439e-9,5.059343495e-9,-9.91364156e-10,-2.27365122e-10,
         9.6467911e-11, 2.394038e-12,-6.886027e-12,8.94487e-13, 3.13092e-13,
         -1.12708e-13,3.81e-16,7.106e-15,-1.523e-15,-9.4e-17,1.21e-16,-2.8e-17
        };
      setCErf(Ncof,Cof);
     };
   //+------------------------------------------------------------------+
   //| Set-method for ncof                                              |
   //+------------------------------------------------------------------+
   void setCErf(int Ncof,double &Cof[])
     {
      ncof=Ncof;
      ArrayCopy(cof,Cof);
     };
   //+------------------------------------------------------------------+
   //| CErf class destructor                                            |
   //+------------------------------------------------------------------+
   void ~CErf(){};
   //+------------------------------------------------------------------+
   //| Error function                                                   |
   //+------------------------------------------------------------------+
   double erf(double x)
     {
      if(x>=0.0) return 1.0-erfccheb(x);
      else return erfccheb(-x)-1.0;
     }
   //+------------------------------------------------------------------+
   //| Complementary error function                                     |
   //+------------------------------------------------------------------+
   double erfc(double x)
     {
      if(x>=0.0) return erfccheb(x);
      else return 2.0-erfccheb(-x);
     }
   //+------------------------------------------------------------------+
   //| Chebyshev approximations for the error function                  |
   //+------------------------------------------------------------------+
   double erfccheb(double z)
     {
      int j;
      double t,ty,tmp,d=0.0,dd=0.0;
      if(z<0.) Alert("erfccheb requires nonnegative argument!");
      t=2.0/(2.0+z);
      ty=4.0*t-2.0;
      for(j=ncof-1;j>0;j--)
        {
         tmp=d;
         d=ty*d-dd+cof[j];
         dd=tmp;
        }
      return t*exp(-z*z+0.5*(cof[0]+ty*d)-dd);
     }
   //+------------------------------------------------------------------+
   //| Inverse complementary error function                             |
   //+------------------------------------------------------------------+
   double inverfc(double p)
     {
      double x,err,t,pp;
      if(p >= 2.0) return -100.0;
      if(p <= 0.0) return 100.0;
      pp=(p<1.0)? p : 2.0-p;
      t = sqrt(-2.*log(pp/2.0));
      x = -0.70711*((2.30753+t*0.27061)/(1.0+t*(0.99229+t*0.04481)) - t);
      for(int j=0;j<2;j++)
        {
         err=erfc(x)-pp;
         x+=err/(M_2_SQRTPI*exp(-pow(x,2))-x*err);
        }
      return(p<1.0? x : -x);
     }
   //+------------------------------------------------------------------+
   //| Inverse error function                                           |
   //+------------------------------------------------------------------+
   double inverf(double p)
     {return inverfc(1.0-p);}
  };
//+------------------------------------------------------------------+
double erfcc(const double x)
/* 
 complementary error function erfc(x) with
 a relative error of 1.2 * 10^(-7)               
*/
  {
   double t,z=fabs(x),ans;
   t=2./(2.0+z);
   ans=t*exp(-z*z-1.26551223+t*(1.00002368+t*(0.37409196+t*(0.09678418+
             t*(-0.18628806+t*(0.27886807+t*(-1.13520398+t*(1.48851587+
             t*(-0.82215223+t*0.17087277)))))))));
   return(x>=0.0 ? ans : 2.0-ans);
  }
//+------------------------------------------------------------------+


2.1.2 対数正規分布

ここから対数正規分布を見ていきます。

確率理論における対数正規分布は絶対連続分布の2パラメータ族です。ランダム変数が対数正規分布であれば、その対数は正規の分布を示します。


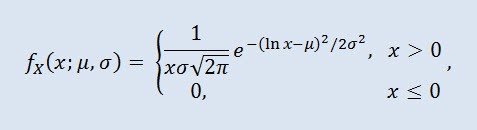
ここでμ は位置パラメータ(0<μ )で、また σ はスケールパラメータ (0<σ)です。


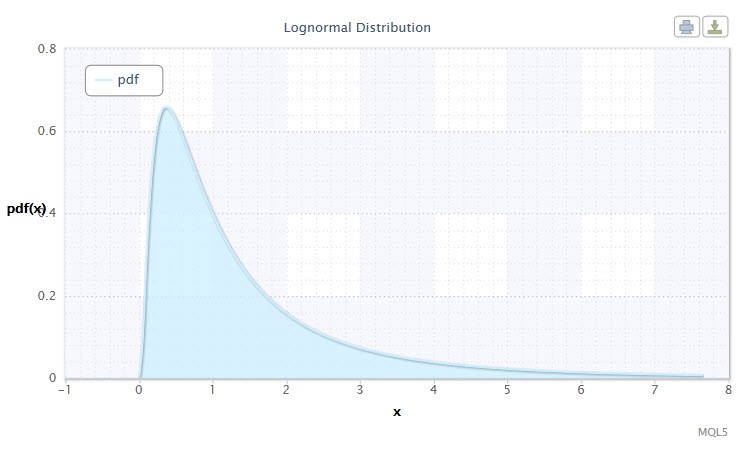
図2　対数正規分布密度  Logn(0,1)

その記述は以下のフォーマットです。X ~ Logn(μ, σ2)、ここで

  • X は対数正規分布 Lognから選択されたランダム変数です。
  • μ 位置パラメータ (0<μ )
  • σ はスケールパラメータ(0<σ)です。

ランダム変数 Xの有効範囲：  0 ≤ X ≤ +∞。

対数正規分布を述べるCLognormaldistクラスを作成 します。コードは以下です。

//+------------------------------------------------------------------+
//|                Lognormal Distribution class definition           |
//+------------------------------------------------------------------+
class CLognormaldist : CErf // Erf class inheritance
  {
public:
   double            mu, //location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CLognormaldist class constructor                                 |
   //+------------------------------------------------------------------+
   void  CLognormaldist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Lognormal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return(0.398942280401432678/(sig*x))*exp(-0.5*pow((log(x)-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return 0.5*erfc(-0.707106781186547524*(log(x)-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf)(quantile)      |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Lognormal Distribution!");
      return exp(-1.41421356237309505*sig*inverfc(2.*p)+mu);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

ごらんのとおり対数正規分布は正規分布とあまり違いはありません。違いはパラメータ x がパラメータ log(x)に置き換わっていることです。 


2.1.3 コーシー分布

確率理論におけるコーシー分布は（物理学でもローレンツ分布またはブライト・ウィグナー分布と呼ばれます。）絶対連続分布族のクラスです。コーシー分布のランダム変数は期待値も分散もない変数の一般的な例です。密度は以下の形式です。


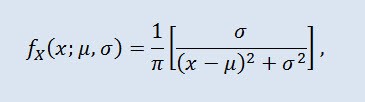
ここで μ は位置パラメータ(-∞ ≤ μ ≤ +∞ )、また σ はスケールパラメータ (0<σ)です。

コーシー分布の記述は 以下のフォーマットです。 X ~ Cau(μ, σ)、 ここで

  • X はコーシー分布 Cauから選択されるランダム変数です。
  • μ は位置パラメータ(-∞ ≤ μ ≤ +∞ )
  • σ はスケールパラメータ(0<σ)です。

ランダム変数Xの有効範囲：  -∞ ≤ X ≤ +∞


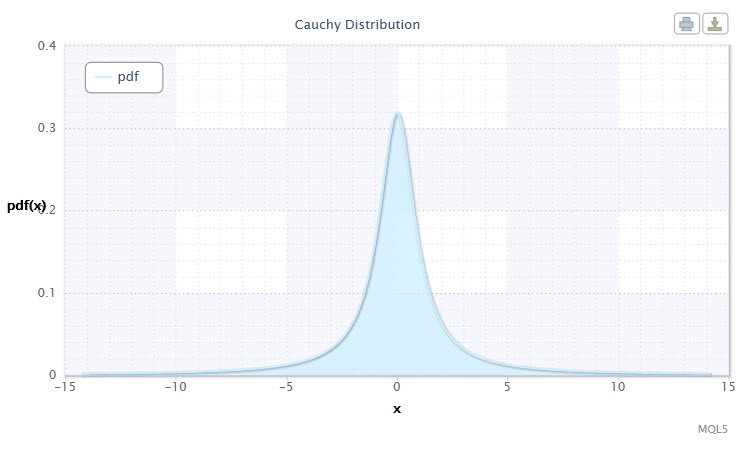
図3　コーシー分布密度Cau(0,1)

CCauchydistクラスの助けを借りてMQL5 fフォーマットで作成されたのが 以下です。

//+------------------------------------------------------------------+
//|                Cauchy Distribution class definition              |
//+------------------------------------------------------------------+
class CCauchydist //
  {
public:
   double            mu,//location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CCauchydist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CCauchydist() 
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Cauchy Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return 0.318309886183790671/(sig*(1.+pow((x-mu)/sig,2)));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5+0.318309886183790671*atan2(x-mu,sig); //todo      
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Cauchy Distribution!");
      return mu+sig*tan(M_PI*(p-0.5));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

ここで注意が必要なのはatan2() 関数が使用されていることです。これは 逆正接の主値をラジアンスで返します。

double atan2(double y,double x)
/*
 Returns the principal value of the arc tangent of y/x,
 expressed in radians. To compute the value, the function
 uses the sign of both arguments to determine the quadrant.
 y - double value representing an y-coordinate.
 x - double value representing an x-coordinate.
*/
  {
   double a;
   if(fabs(x)>fabs(y))
      a=atan(y/x);
   else
     {
      a=atan(x/y); // pi/4 <= a <= pi/4
      if(a<0.)
         a=-1.*M_PI_2-a; //a is negative, so we're adding
      else
         a=M_PI_2-a;
     }
   if(x<0.)
     {
      if(y<0.)
         a=a-M_PI;
      else
         a=a+M_PI;
     }
   return a;
  }


2.1.4 H双曲線正割分布

双曲線正割分布は金融ランク分析を行う方には興味のあるものでしょう。

確率理論および統計では双曲線正割分布は確率密度関数と特定関数が双曲線正割関数に比例する連続確率分布です。密度は式で出されます。


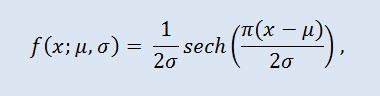
ここで μ は位置パラメータ(-∞ ≤ μ ≤ +∞ )、また σ はスケールパラメータ (0<σ)です。



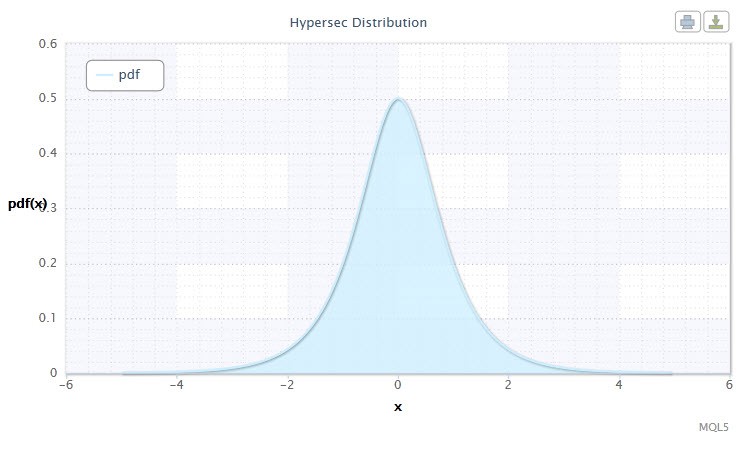
図4　双曲線正割分布 密度HS(0,1)

その notation は以下のフォーマットです。 X ~ HS(μ, σ)、ここで

  • X はランダム変数
  • μ は位置パラメータ(-∞ ≤ μ ≤ +∞ )
  • σ はスケールパラメータ(0<σ)です。

ランダム変数Xの有効範囲：  -∞ ≤ X ≤ +∞

それを CHypersecdistクラスを用いて以下のように記述します。

//+------------------------------------------------------------------+
//|        Hyperbolic Secant Distribution class definition           |
//+------------------------------------------------------------------+
class CHypersecdist //
  {
public:
   double            mu,// location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CHypersecdist class constructor                                 |
   //+------------------------------------------------------------------+
   void  CHypersecdist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Hyperbolic Secant Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return sech((M_PI*(x-mu))/(2*sig))/2*sig;
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 2/M_PI*atan(exp((M_PI*(x-mu)/(2*sig))));
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Hyperbolic Secant Distribution!");
      return(mu+(2.0*sig/M_PI*log(tan(M_PI/2.0*p))));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

この分布名が、双曲線正割関数の確率密度関数 が双曲線正割関数に比例するその関数から名づけられているのはすぐにわかります。

双曲線正割関数 sech は以下です。

//+------------------------------------------------------------------+
//|              Hyperbolic Secant Function                          |
//+------------------------------------------------------------------+
double sech(double x)
// Hyperbolic Secant Function
  {
   return 2/(pow(M_E,x)+pow(M_E,-x));
  }


2.1.5 スチューデントの t 分布

スチューデントの t 分布 は統計において重要な分布です。

確率理論において、チューデントの t 分布はほとんどの場合、絶対連続分布の1パラメータ族です。ただし、分布密度関数から与えられる3パラメータ分布とみなされることもあります。


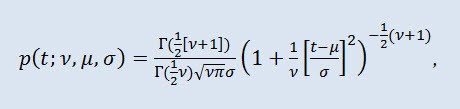
ここで Г は オイラーのガンマ関数、ν は形状パラメータ (ν>0)、 μ は位置パラメータ(-∞ ≤ μ ≤ +∞ )、 σ はスケールパラメータ (0<σ)です。


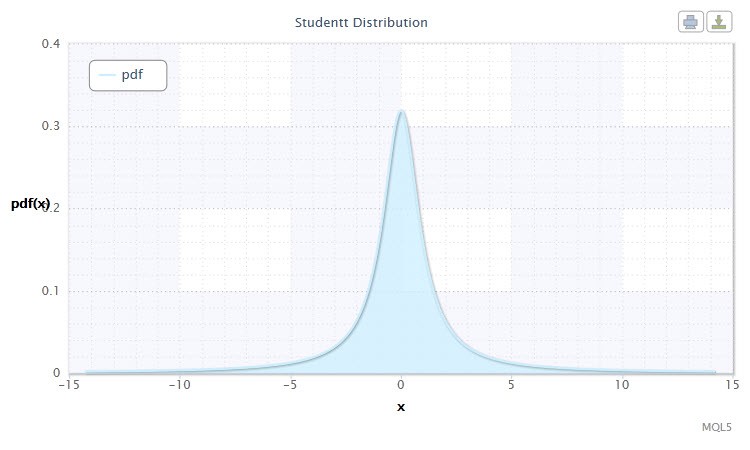
図5　スチューデントの t 分布 密度 Stt(1,0,1)

その 記述は以下のフォーマットです。 t ~ Stt(ν,μ,σ)、ここで

  • t はスチューデントの t 分布 Sttから選択されたランダム変数です。
  • ν は形状パラメータ (ν>0)です。
  • μ は位置パラメータ(-∞ ≤ μ ≤ +∞ )
  • σ はスケールパラメータ(0<σ)です。

ランダム変数Xの有効範囲：  -∞ ≤ X ≤ +∞

よく特に仮説検証において標準t 分布 は μ=0 および σ=1と共に使われます。よってそれはパラメータ νを伴う1パラメータ分布となります。

この分布 は、期待値仮説、回帰関係係数、均一性仮説などを検証するとき、信頼性区間によって、期待値、予想値、その他特性を推定するのに使用されます。

CStudenttdist クラスにより分布を記述します。

//+------------------------------------------------------------------+
//|                Student's t-distribution class definition         |
//+------------------------------------------------------------------+
class CStudenttdist : CBeta // CBeta class inheritance
  {
public:
   int               nu;     // shape parameter (ν)
   double            mu,     // location parameter (μ)
   sig,                     // scale parameter (σ)
   np,                      // 1/2*(ν+1)
   fac;                     // Г(1/2*(ν+1))-Г(1/2*ν)
   //+------------------------------------------------------------------+
   //| CStudenttdist class constructor                                  |
   //+------------------------------------------------------------------+
   void  CStudenttdist()
     {
      int Nu=1;double Mu=0.0,Sig=1.0; //default parameters ν, μ and σ
      setCStudenttdist(Nu,Mu,Sig);
     }
   void setCStudenttdist(int Nu,double Mu,double Sig)
     {
      nu=Nu;
      mu=Mu;
      sig=Sig;
      if(sig<=0. || nu<=0.) Alert("bad sig,nu in Student-t Distribution!");
      np=0.5*(nu+1.);
      fac=gammln(np)-gammln(0.5*nu);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-np*log(1.+pow((x-mu)/sig,2.)/nu)+fac)/(sqrt(M_PI*nu)*sig);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double t)
     {
      double p=0.5*betai(0.5*nu,0.5,nu/(nu+pow((t-mu)/sig,2)));
      if(t>=mu) return 1.-p;
      else return p;
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Student-t Distribution!");
      double x=invbetai(2.*fmin(p,1.-p),0.5*nu,0.5);
      x=sig*sqrt(nu*(1.-x)/x);
      return(p>=0.5? mu+x : mu-x);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
   //+------------------------------------------------------------------+
   //| Two-tailed cumulative distribution function (aa) A(t|ν)          |
   //+------------------------------------------------------------------+
   double aa(double t)
     {
      if(t < 0.) Alert("bad t in Student-t Distribution!");
      return 1.-betai(0.5*nu,0.5,nu/(nu+pow(t,2.)));
     }
   //+------------------------------------------------------------------+
   //| Inverse two-tailed cumulative distribution function (invaa)      |
   //| p=A(t|ν)                                                         |
   //+------------------------------------------------------------------+
   double invaa(double p)
     {
      if(!(p>=0. && p<1.)) Alert("bad p in Student-t Distribution!");
      double x=invbetai(1.-p,0.5*nu,0.5);
      return sqrt(nu*(1.-x)/x);
     }
  };
//+------------------------------------------------------------------+

挙げられているCStudenttdist クラスはCBeta が未完全なベータ関数を記述する基本クラスです。

CBetaクラスは以下です。

//+------------------------------------------------------------------+
//|            Incomplete Beta Function class definition             |
//+------------------------------------------------------------------+
class CBeta : public CGauleg18
  {
private:
   int               Switch;                     //when to use the quadrature method
   double            Eps,Fpmin;
public:
   //+------------------------------------------------------------------+
   //| CBeta class constructor                                          |
   //+------------------------------------------------------------------+
   void CBeta()
     {
      int swi=3000;
      setCBeta(swi,EPS,FPMIN);
     };
   //+------------------------------------------------------------------+
   //| CBeta class set-method                                           |
   //+------------------------------------------------------------------+
   void setCBeta(int swi,double eps,double fpmin)
     {
      Switch=swi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            betai(const double a,const double b,const double x); //incomplete beta function Ix(a,b)
   double            betacf(const double a,const double b,const double x);//continued fraction for incomplete beta function
   double            betaiapprox(double a,double b,double x); //Incomplete beta by quadrature
   double            invbetai(double p,double a,double b);    //Inverse of incomplete beta function
  };

このクラスはまたガウス・ルシャンドル公式など数値統合メソッドに対して係数を提供する基本クラスであるCGauleg18を持ちます。


2.1.6 ロジスティック分布

次にわれわれの調査で考察しようと思うのはロジスティック分布です。

確率理論および統計ではロジスティック分布継続確率分布です。その累積分布関数はロジスティック関数です。形は正規分布ににていますが、尾部が重くなっています。分布密度 

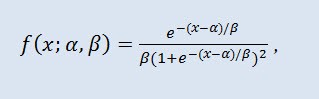
ここでα は位置パラメータ (-∞ ≤ α ≤ +∞ )、β はスケールパラメータ(0<β)です。


図6　ロジスティック 分布 密度 Logi(0,1)

その 記述は以下のフォーマットです。 X ~ Logi(α,β)、ここで

  • X はランダム変数
  • α は位置パラメータ (-∞ ≤ α ≤ +∞ )
  • β はスケールパラメータ(0<β)です。

ランダム変数Xの有効範囲：  -∞ ≤ X ≤ +∞

CLogisticdist クラスは上記分布の実装です。

//+------------------------------------------------------------------+
//|                Logistic Distribution class definition            |
//+------------------------------------------------------------------+
class CLogisticdist
  {
public:
   double            alph,//location parameter (α)
   bet;                   //scale parameter (β)
   //+------------------------------------------------------------------+
   //| CLogisticdist class constructor                                  |
   //+------------------------------------------------------------------+
   void  CLogisticdist() 
     {
      alph=0.0;bet=1.0; //default parameters μ and σ
      if(bet<=0.) Alert("bad bet in Logistic Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-(x-alph)/bet)/(bet*pow(1.+exp(-(x-alph)/bet),2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double et=exp(-1.*fabs(1.81379936423421785*(x-alph)/bet));
      if(x>=alph) return 1./(1.+et);
      else return et/(1.+et);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Logistic Distribution!");
      return alph+0.551328895421792049*bet*log(p/(1.-p));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+


2.1.7 指数分布

ランダム変数の指数分布 についても見ていきます。

ランダム変数X は、密度が以下で与えられた場合、パラメータ λ > 0を伴う指数分布を持ちます。


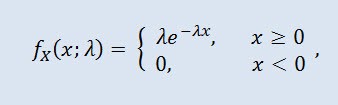
ここで λはスケールパラメータ (λ>0)です。


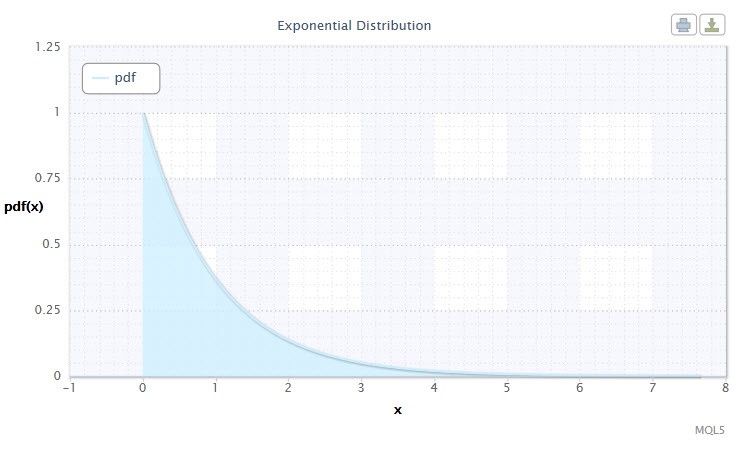
図7　指数 分布密度 Exp(1)

その 記述は以下のフォーマットです。 X ~ Exp(λ)、ここで

  • X はランダム変数
  • λ はスケールパラメータ (λ>0)です。

ランダム変数 Xの有効範囲：  0 ≤ X ≤ +∞。

この分布は特定時刻にひとつずつ起こる一連の出来事を述べるという点で優れた分布です。この分布を用いて、トレーダーは損失取り引きその他を分析することができます。

MQL5 コードではこの分布はCExpondist クラスを用いて記述されます。

//+------------------------------------------------------------------+
//|                Exponential Distribution class definition         |
//+------------------------------------------------------------------+
class CExpondist
  {
public:
   double            lambda;   //scale parameter (λ)
   //+------------------------------------------------------------------+
   //| CExpondist class constructor                                     |
   //+------------------------------------------------------------------+
   void  CExpondist()
     {
      lambda=1.0;              //default parameter λ
      if(lambda<=0.) Alert("bad lambda in Exponential Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Exponential Distribution!");
      return lambda*exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x < 0.) Alert("bad x in Exponential Distribution!");
      return 1.-exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Exponential Distribution!");
      return -log(1.-p)/lambda;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+


2.1.8 ガンマ分布

ガンマ分布を次のランダム変数連続分布として選びました。 

確率理論においてガンマ分布は絶対連続分布の2パラメータ族です。パラメータ α が正数であれば、このガンマ分布は アーラン 分布とも呼ばれます。密度は以下の形式を取ります。

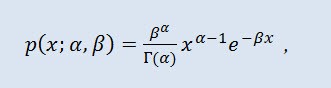
ここで Г は オイラー のガンマ関数、α 形状パラメータ (0<α)、βはスケールパラメータ(0<β)です。


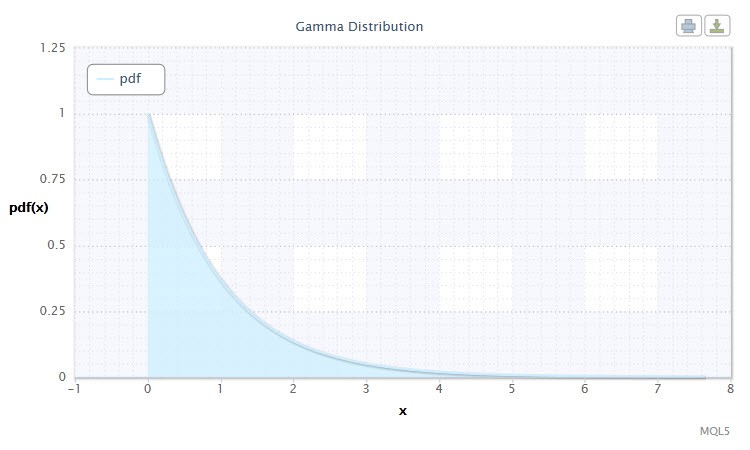
図8　ガンマ 分布密度 Gam(1,1)

その記述は以下のフォーマットです。X ~ Gam(α,β)、ここで

  • X はランダム変数
  • α は形状パラメータ(0<α)
  • β はスケールパラメータ(0<β)です。

ランダム変数 Xの有効範囲：  0 ≤ X ≤ +∞。

CGammadist クラス定義変数ではそれは以下のようなものです。

//+------------------------------------------------------------------+
//|                Gamma Distribution class definition               |
//+------------------------------------------------------------------+
class CGammadist : CGamma // CGamma class inheritance
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous scale parameter  (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| CGammaldist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CGammadist()
     {
      setCGammadist();
     }
   void setCGammadist(double Alph=1.0,double Bet=1.0)//default parameters α and β
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Gamma Distribution!");
      fac=alph*log(bet)-gammln(alph);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0.) Alert("bad x in Gamma Distribution!");
      return exp(-bet*x+(alph-1.)*log(x)+fac);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Gamma Distribution!");
      return gammp(alph,bet*x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Gamma Distribution!");
      return invgammp(p,alph)/bet;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

ガンマ分布クラスは 不完全なガンマ関数を記述するCGamma クラスから派生しています。

CGammaクラスは以下のように定義されます。

//+------------------------------------------------------------------+
//|            Incomplete Gamma Function class definition            |
//+------------------------------------------------------------------+
class CGamma : public CGauleg18
  {
private:
   int               ASWITCH;
   double            Eps,
   Fpmin,
   gln;
public:
   //+------------------------------------------------------------------+
   //| CGamma class constructor                                         |
   //+------------------------------------------------------------------+
   void CGamma()
     {
      int aswi=100;
      setCGamma(aswi,EPS,FPMIN);
     };
   void setCGamma(int aswi,double eps,double fpmin) //CGamma set-method
     {
      ASWITCH=aswi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            gammp(const double a,const double x); //incomplete gamma function
   double            gammq(const double a,const double x); //incomplete gamma function Q(a,x)
   void              gser(double &gamser,double a,double x,double &gln); //incomplete gamma function P(a,x)
   double            gcf(const double a,const double x); //incomplete gamma function Q(a,x)
   double            gammpapprox(double a,double x,int psig); //incomplete gamma by quadrature
   double            invgammp(double p,double a); //inverse of incomplete gamma function
  };
//+------------------------------------------------------------------+

両クラスCGammaおよびCBeta は基本クラスとして CGauleg18 を持ちます。


2.1.9 ベータ分布

ここから  ベータ分布を見ていきます。

確率理論および統計ではベータ分布は絶対連続分布の2パラメータ族です。値が有限区間において定義されるランダム変数を記述するのに使用されます。密度は以下のように定義されます。

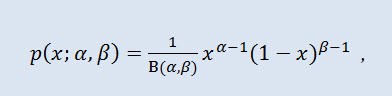
ここで B はベータ関数、 α は第一の形状パラメータ (0<α), βは第二の形状パラメータ(0<β)です。


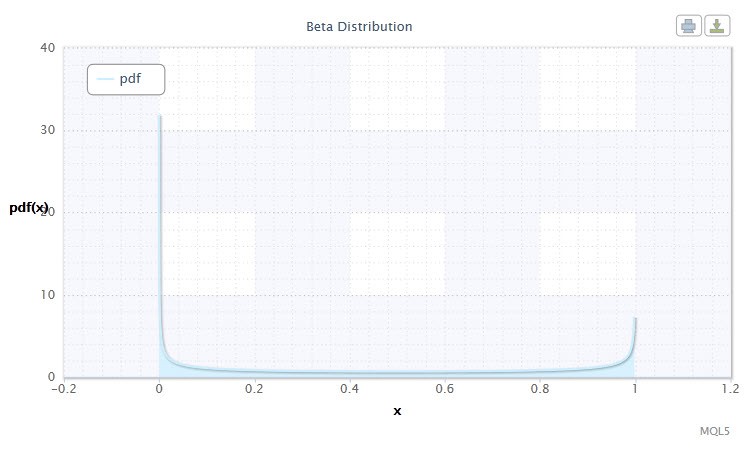
図9　ベータ分布密度 Beta(0.5,0.5)

その記述は以下のフォーマットです。X ~ Beta(α,β)、ここで

  • X はランダム変数
  • α は第一の形状パラメータ (0<α)
  • β は第二の形状パラメータ(0<β)です。

ンダム変数 Xの有効範囲： 0 ≤ X ≤ 1.

CBetadist クラスは以下の方法でこの分布を記述します。

//+------------------------------------------------------------------+
//|                Beta Distribution class definition                |
//+------------------------------------------------------------------+
class CBetadist : CBeta // CBeta class inheritance
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous shape parameter (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| CBetadist class constructor                                      |
   //+------------------------------------------------------------------+
   void  CBetadist()
     {
      setCBetadist();
     }
   void setCBetadist(double Alph=0.5,double Bet=0.5)//default parameters α and β
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Beta Distribution!");
      fac=gammln(alph+bet)-gammln(alph)-gammln(bet);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0. || x>=1.) Alert("bad x in Beta Distribution!");
      return exp((alph-1.)*log(x)+(bet-1.)*log(1.-x)+fac);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0. || x>1.) Alert("bad x in Beta Distribution");
      return betai(alph,bet,x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>1.) Alert("bad p in Beta Distribution!");
      return invbetai(p,alph,bet);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+


2.1.10 ラプラス分布

もう優れた連続分布はラプラス分布 （二重指数分布）です。 

確率理論におけるラプラス分布（ 二重指数分布）は ランダム変数の連続分布で、ここで密度は

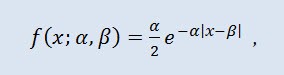
ここでα は位置パラメータ (-∞ ≤ α ≤ +∞ )、β はスケールパラメータ(0<β)です。


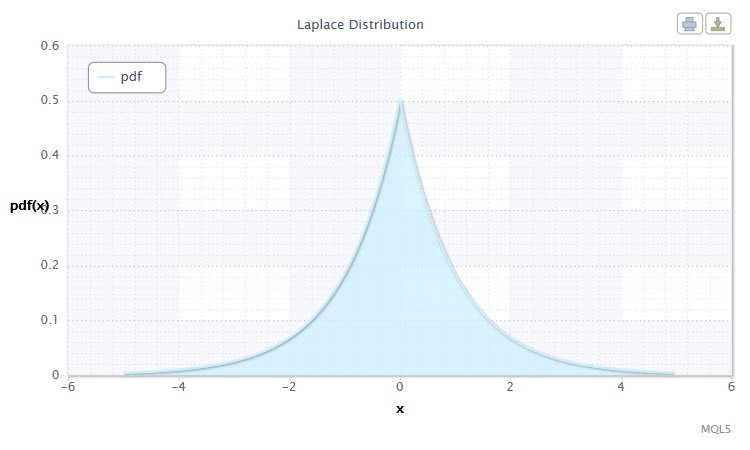
図10　 ラプラス分布密度 Lap(0,1)

その記述は以下のフォーマットです。 X ~ Lap(α,β)、ここで

  • X はランダム変数
  • α は位置パラメータ (-∞ ≤ α ≤ +∞ )
  • β はスケールパラメータ(0<β)です。

ランダム変数Xの有効範囲：  -∞ ≤ X ≤ +∞

CLaplacedist クラスはこの分布を以下のように記述します。

//+------------------------------------------------------------------+
//|                 Laplace Distribution class definition            |
//+------------------------------------------------------------------+
class CLaplacedist
  {
public:
   double            alph;   //location parameter (α)
   double            bet;    //scale parameter (β)
   //+------------------------------------------------------------------+
   //| CLaplacedist class constructor                                   |
   //+------------------------------------------------------------------+
   void  CLaplacedist()
     {
      alph=.0;               //default parameter α
      bet=1.;                //default parameter β
      if(bet<=0.) Alert("bad bet in Laplace Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-fabs((x-alph)/bet))/2*bet;
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double temp;
      if(x<0)
         temp=0.5*exp(-fabs((x-alph)/bet));
      else
         temp=1.-0.5*exp(-fabs((x-alph)/bet));
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      double temp;
      if(p<0. || p>=1.) Alert("bad p in Laplace Distribution!");
      if(p<0.5)
         temp=bet*log(2*p)+alph;
      else
         temp=-1.*(bet*log(2*(1.-p))+alph);
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

MQL5 コード使用で10種類の連続分布に対して10個のクラスを作成しました。それ以外にもいくつか作成されたクラスがあります。それはいわゆる補足で、これは特定の関数およびメソッドに必要だったからです（たとえばCBeta および CGamma）。

それでは分散分布に進み、この分布カテゴリー用のクラスをいくつか作成します。


2.2.1二項分布

二項分布から始めます。

確率理論において二項分布は、個別に無作為な実験を行い、各実験のシーケンスにおける成功確率が等しい成功数の分布です。確率密度は以下の式で計算されます。

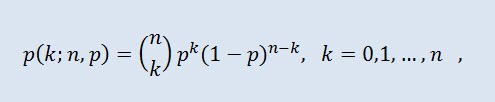
ここで  (n k) は二項係数、 n は試行回数 (0 ≤ n)、 p は成功の確率(0 ≤ p ≤1)です。


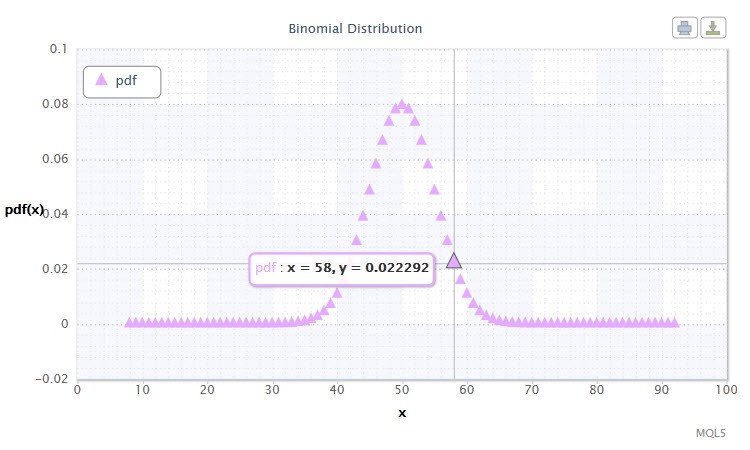
図11　二項 分布 密度 Bin(100,0.5)。

その記述は以下のフォーマットです。 k ~ Bin(n,p)、ここで

  • k はランダム変数
  • n は試行回数 (0 ≤ n)
  • p は成功確率 (0 ≤ p ≤1).

Vランダム変数 Xの有効範囲： 0 or 1.

ランダム変数 Xの有効範囲でなにかがわかりますか？実はこの分布はトレーディングシステムにおいて勝ち取り引き (1) と負け取り引き(0) を分析するのに役立ちます。

以下のようにСBinomialdistクラスを作成します。

//+------------------------------------------------------------------+
//|               Binomial Distribution class definition             |
//+------------------------------------------------------------------+
class CBinomialdist : CBeta // CBeta class inheritance
  {
public:
   int               n;      //number of trials
   double            pe,     //success probability
   fac;                      //factor
   //+------------------------------------------------------------------+
   //| CBinomialdist class constructor                                  |
   //+------------------------------------------------------------------+
   void              CBinomialdist()
     {
      setCBinomialdist();
     }
   void setCBinomialdist(int N=100,double Pe=0.5)//default parameters n and pe
     {
      n=N; pe=Pe;
      if(n<=0 || pe<=0. || pe>=1.) Alert("bad args in Binomial Distribution!");
      fac=gammln(n+1.);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k>n) return 0.;
      return exp(k*log(pe)+(n-k)*log(1.-pe)+fac-gammln(k+1.)-gammln(n-k+1.));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k==0) return 0.;
      if(k>n) return 1.;
      return 1.-betai((double)k,n-k+1.,pe);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int k,kl,ku,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Binomial Distribution!");
      k=fmax(0,fmin(n,(int)(n*pe)));
      if(p<cdf(k))
        {
         do
           {
            k=fmax(k-inc,0);
            inc*=2;
           }
         while(p<cdf(k));
         kl=k; ku=k+inc/2;
           } else {
         do
           {
            k=fmin(k+inc,n+1);
            inc*=2;
           }
         while(p>cdf(k));
         ku=k; kl=k-inc/2;
        }
      while(ku-kl>1)
        {
         k=(kl+ku)/2;
         if(p<cdf(k)) ku=k;
         else kl=k;
        }
      return kl;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(int k)
     {
      return 1.-cdf(k);
     }
  };
//+------------------------------------------------------------------+


2.2.2ポワソン分布

次に考察する分布はポワソン分布です。

ポワソン分布は固定期間に生じるイベント数によって表現されるランダム変数を、これらイベントは固定された平均強度でお互い自立的に起こるという条件でモデル化します。<s2>密度は以下の形式を取ります。</s2>

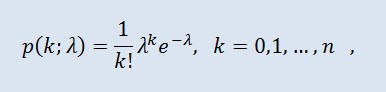
ここで kです!kは乗階、 λ は位置パラメータ (0 < λ)です。


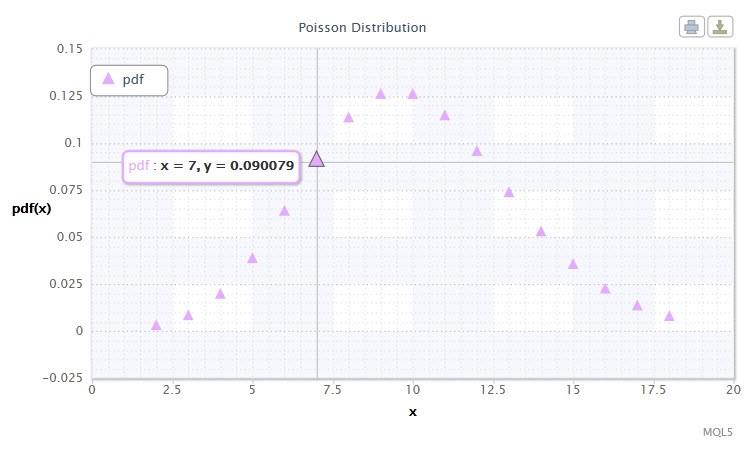
図12　ポワソン 分布密度 Pois(10).

その記述は以下のフォーマットです。k ~ Pois(λ)、ここで

  • k はランダム変数
  • λ は位置パラメータ (0 < λ)です。

ランダム変数 Xの有効範囲：  0 ≤ X ≤ +∞。

ポワソン分布はリスク程度を推測するとき重要な「稀なイベント法則」を記述します。

CPoissondistクラスがこの目的を果たします。

//+------------------------------------------------------------------+
//|               Poisson Distribution class definition              |
//+------------------------------------------------------------------+
class CPoissondist : CGamma // CGamma class inheritance
  {
public:
   double            lambda;   //location parameter (λ)
   //+------------------------------------------------------------------+
   //| CPoissondist class constructor                                   |
   //+------------------------------------------------------------------+
   void CPoissondist()
     {
      lambda=15.;
      if(lambda<=0.) Alert("bad lambda in Poisson Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      return exp(-lambda+n*log(lambda)-gammln(n+1.));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      if(n==0) return 0.;
      return gammq((double)n,lambda);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int n,nl,nu,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Poisson Distribution!");
      if(p<exp(-lambda)) return 0;
      n=(int)fmax(sqrt(lambda),5.);
      if(p<cdf(n))
        {
         do
           {
            n=fmax(n-inc,0);
            inc*=2;
           }
         while(p<cdf(n));
         nl=n; nu=n+inc/2;
           } else {
         do
           {
            n+=inc;
            inc*=2;
           }
         while(p>cdf(n));
         nu=n; nl=n-inc/2;
        }
      while(nu-nl>1)
        {
         n=(nl+nu)/2;
         if(p<cdf(n)) nu=n;
         else nl=n;
        }
      return nl;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(int n)
     {
      return 1.-cdf(n);
     }
  };
//+=====================================================================+

すべての統計分布について一つの記事で考察するのは不可能であり、その必要もないことは明らかです。ユーザーは望むなら、上記の分布一覧を拡げることでしょう。ここで作成した分布はファイルDistribution_class.mqh にあります。


3. 分布グラフの作成

ここからは分布のために作成したクラスが将来の作業でどのように使われるのか見ていこうと思います。

ここで、再びOOPを利用し、ユーザー定義パラメータ分布を処理し、それを『HTML形式でのチャートとグラフ』稿に記載のある方法で画面に表示するCDistributionFigureクラスを作成しました。 

//+------------------------------------------------------------------+
//|           Distribution Figure class definition                   |
//+------------------------------------------------------------------+
class CDistributionFigure
  {
private:
   Dist_type         type;  //distribution type
   Dist_mode         mode;  //distribution mode
   double            x;     //step start
   double            x11;   //left side limit
   double            x12;   //right side limit
   int               d;     //number of points
   double            st;    //step

public:
   double            xAr[]; //array of random variables
   double            p1[];  //array of probabilities
   void              CDistributionFigure();  //constructor 
   void              setDistribution(Dist_type Type,Dist_mode Mode,double X11,double X12,double St); //set-method
   void              calculateDistribution(double nn,double mm,double ss); //distribution parameter calculation
   void              filesave(); //saving distribution parameters
  };
//+------------------------------------------------------------------+

実装オミットこのクラスDist_typeおよびDist_mode にそれぞれ関連したデータメンバtype とmodeを持つことに注意します。 これらタイプは調査した分布の列挙 とそのタイプです。

最後にいくつかの分布についてグラフを作成します。

連続分布にはcontinuousDistribution.mq5 スクリプトを書きました。その主要行は以下です。

//+------------------------------------------------------------------+
//|                     Input variables                              |
//+------------------------------------------------------------------+

input Dist_type dist;  //Distribution Type
input Dist_mode distM; //Distribution Mode
input int nn=1;        //Nu
input double mm=0.,    //Mu
            ss=1.;    //Sigma
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//(Normal #0,Lognormal #1,Cauchy #2,Hypersec #3,Studentt #4,Logistic #5,Exponential #6,Gamma #7,Beta #8 , Laplace #9)
   double Xx1,      //left side limit
          Xx2,     //right side limit          
          st=0.05; //step
   if(dist==0) //Normal
     {
      Xx1=mm-5.0*ss/1.25;
      Xx2=mm+5.0*ss/1.25;
     }
   if(dist==2 || dist==4 || dist==5) //Cauchy,Studentt,Logistic
     {
      Xx1=mm-5.0*ss/0.35;
      Xx2=mm+5.0*ss/0.35;
     }
   else if(dist==1 || dist==6 || dist==7) //Lognormal,Exponential,Gamma
     {
      Xx1=0.001;
      Xx2=7.75;
     }
   else if(dist==8) //Beta
     {
      Xx1=0.0001;
      Xx2=0.9999;
      st=0.001;
     }
   else 
     {
      Xx1=mm-5.0*ss;
      Xx2=mm+5.0*ss;
     }
//---
   CDistributionFigure F;        //creation of the CDistributionFigure class instance 
   F.setDistribution(dist,distM,Xx1,Xx2,st);
   F.calculateDistribution(nn,mm,ss);
   F.filesave();
   string path=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\Distribution_function.htm";
   ShellExecuteW(NULL,"open",path,NULL,NULL,1);
  }
//+------------------------------------------------------------------+

分散分布に対しては、discreteDistribution.mq5 スクリプトを書きました。

標準パラメータを用いてコーシー分布に対してスクリプトを実行し、下のビデオにあるようなグラフを得ました。




おわりに

本稿はランダム変数の理論分布をいくつか紹介し、またそれらをMQL5でコード化しました。私はマーケットトレード自体とトレーディングシステムの動作は確立の基本法則に基づいていると信じています。

そして本稿が興味を持つ読者のみなさんに実用的価値があることを願っています。私としてはこのテーマを拡げ、確率モデル分析で統計確率分布を使用する方法を示す実用的な例を提供していきたいと考えています。


ファイル保存場所

 #  
ファイル
 パス
 内容
 1
  Distribution_class.mqh
  %MetaTrader%\MQL5\Include  分布クラスのギャラリー
 2  DistributionFigure_class.mqh            
 %MetaTrader%\MQL5\Include                           
 分布のグラフィック表示クラス            
 3  continuousDistribution.mq5   %MetaTrader%\MQL5\Scripts  連続分布の作成スクリプト     
 4
  discreteDistribution.mq5
   %MetaTrader%\MQL5\Scripts  分散分布の作成スクリプト          
 5
  dataDist.txt
   %MetaTrader%\MQL5\Files  分布表示データDistribution display data
 6
  Distribution_function.htm
   %MetaTrader%\MQL5\Files  連続分布HTML 形式グラフ         
 7  Distribution_function_discr.htm          
  %MetaTrader%\MQL5\Files  分散分布HTML 形式グラフ                
 8  exporting.js
   %MetaTrader%\MQL5\Files  グラフエクスポート用Javaスクリプト
 9  highcharts.js
   %MetaTrader%\MQL5\Files  Javaスクリプトライブラリ
 10  jquery.min.js   %MetaTrader%\MQL5\Files  Javaスクリプトライブラリ


参考文献

  1. K. Krishnamoorthy. Handbook of Statistical Distributions with Applications, Chapman and Hall/CRC 2006.
  2. W.H. Press, et al. Numerical Recipes: The Art of Scientific Computing, Third Edition, Cambridge University Press: 2007. - 1256 pp.
  3. S.V. Bulashev Statistics for Traders. - M.: Kompania Sputnik +, 2003. - 245 pp.
  4. I. Gaidyshev Data Analysis and Processing: Special Reference Guide - SPb: Piter, 2001. - 752 pp.: ill.
  5. A.I. Kibzun, E.R. Goryainova — Probability Theory and Mathematical Statistics. Basic Course with Examples and Problems
  6. N.Sh. Kremer Probability Theory and Mathematical Statistics. M.: Unity-Dana, 2004. — 573 pp.

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/271

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
直線回帰例によるインディケータスピードアップの3手法 直線回帰例によるインディケータスピードアップの3手法
本稿では、インディケータメソッドの計算アルゴリズムの最適化を取り上げます。みなさんはご自身のニーズにもっとも合うメソッドをお探しのことと思います。本稿では3種類の手法について述べます。その一つはきわめて簡単なものです。次のひとつはしっかりした数学の知識が必要です。そして最後のひとつには多少のウィットが必要です。はここで述べられる手法のほとんどを理解するのにインディケータまたはMetaTrader5 ターミナルのデザイン的特性を利用します。その手法はかなり汎用的で直線回帰計算だけでなくその他のインディケータに対しても使用可能です。
ソースコードのトレーシング デバッギング 構造分析 ソースコードのトレーシング デバッギング 構造分析
実行されたコードのストラクチャーの作成とトレーシングの複雑な問題は、特に困難なく解決することができます。これは、MetaTrader5から可能になりました。これは、MQL5言語の新しい機能である、様々な複雑なデータ型の自動生成やローカルスコープ外に出た際の除去などのおかでです。この記事は、その方法論や、すぐ使えるツールを紹介します。
価格 Correlationの統計データを基にしたシグナルのフィルタリング 価格 Correlationの統計データを基にしたシグナルのフィルタリング
過去の価格変動と将来のトレンドの間に関連はあるのでしょうか？前日の値動き特性が本日繰り返されるのはなぜでしょうか？価格変動予想に統計は有用でしょうか？答えはあり、それはポジティブなものです。もしお疑いならこの記事はそんな方向けです。MQL5のシステムでトレーディングシステム向けの作業フィルター作成方法をお話します。それは価格変動の興味深いパターンを表します。
統計的推定 統計的推定
シーケンスの統計的パラメータの推定はたいへん重要なものです。それはたいていの数学的モデルと手法が異なる前提に基づいているからです。たとえば、分布法則の正常化、分散値、その他パラメータです。よって時系列を分析し推定するとき、主要な統計的パラメータを素早く明確に推定できるシンプルで使い勝手のよいツールが必要です。本稿では、もっともシンプルなランダムシーケンスの統計パラメータとビジュアル分析のメソッドをいくつか取り上げ述べていきます。それにより MQL5 でこれらメソッド、またニュープロットアプリケーションを用いて計算した結果の視覚化メソッドを実装します。