データサイエンスと機械学習（第29回）：AI訓練に最適なFXデータを選ぶための重要なヒント

内容

• はじめに
• 特徴選択とは
• AIモデルに特徴選択が必要な理由
• フィルター法
  相関行列
  統計的検定
  - カイ二乗検定
  - 分散分析検定
• ラッパー法
  再帰的特徴除去(RFE: Recursive feature elimination)
  逐次特徴選択(SFS: Sequential feature selection)
• 埋め込み法
  ラッソ回帰
  決定木ベースの手法
• 次元削減手法
• 結論

はじめに

MetaTrader 5には36種類以上の指標が内蔵されており、相関ストラテジーのデータとして利用できる銘柄ペアも100種類以上存在します。さらに、トレーダーにとって価値のあるニュースなど、さまざまな取引データや情報が豊富にあります。 つまり、トレーダーが手作業で取引を行う際や、取引ロボットを用いてスマートな取引判断をおこなうための人工知能モデルを構築する際に利用できる情報は膨大です。

しかし、私たちが持っている情報の中には、役に立たない情報も含まれていることは常識です。  すべての指標、データ、戦略が、特定の取引銘柄や状況に対して有用であるとは限りません。取引や機械学習モデルの効率性と収益性を最大化するためには、どの情報が適切であるかをどう判断すればよいのでしょうか。そこで、特徴選択の重要性が浮かび上がります。

特徴選択とは

特徴選択とは、モデル構築に用いるために元のデータセットから関連する特徴のサブセットを特定し、選択するプロセスです。このプロセスでは、機械学習モデルに与える最も有用な情報を判断し、あまり重要でない特徴や情報を取り除きます。

特徴選択は、効果的な機械学習モデルを構築するための重要なステップのひとつです。以下に理由を挙げます。

AIモデルに特徴選択が必要な理由

• 次元削減
  
  特徴選択により、無関係な特徴や冗長な特徴を排除することで、モデルがより単純化され、計算コストを削減できます。   
  
  
• パフォーマンスの向上
  
  最も情報量の多い特徴に集中することで、モデルの精度や予測力が向上します。   
  
  
• 解釈可能性の向上
  
  特徴が少ないモデルは、理解しやすく、説明もしやすいことが多いです。   
  
  
• ノイズ除去：ノイズや無関係なデータを排除することで、過剰適合を防ぎ、モデルの安定性を向上させます。
  
  あまり重要でない特徴を取り除くことで、特徴選択は、無関係なデータが多すぎるために起こりがちな過剰適合を防ぐのに役立ちます。   

特徴選択がいかに重要かがわかったところで、データサイエンティストや機械学習の専門家がAIモデルに最適な特徴を見つけるためによく使うさまざまなテクニックを探ってみましょう。

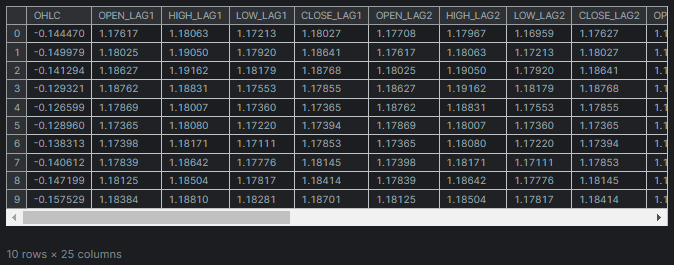
データセットはこの記事（必読）で使用したのと同じで、28の変数があります。

28個の変数のうち、TARGET_OPEN（次のローソク足の始値の値を保持）と TARGET_CLOSE（次のローソク足の終値の値を保持）の列に最も関連性の高い変数を特定し、関連性の低いデータを除外します。

特徴選択の技法や手法は、大きく分けてフィルター法、ラッパー法、埋め込み法の3種類に分類されます。それぞれの手法について、まずは1つずつ詳しく見ていきましょう。

フィルター法

フィルター法は、機械学習モデルやアルゴリズムに依存せず、特徴の評価を行います。この方法には、相関行列の使用や統計的検定の実施が含まれます。

相関行列

相関行列は、異なる変数間の相関係数を示す表です。

相関係数は、2つの変数間の関係の強さと方向を示す統計的尺度であり、範囲は-1から1までです。

1の値は完全な正の相関を示し、一方の変数が増加すると、もう一方の変数も比例して増加します。

0の場合、相関がないことを示し、2つの変数の間に関係がありません。

-1は、完全な負の相関を示し、一方の変数が増加すると、もう一方の変数が比例して減少します。

まずはPythonを使って相関行列を計算してみましょう。

相関行列の計算

# Compute the correlation matrix
corr_matrix = df.corr()

# We generate a mask for the upper triangle
mask = np.triu(np.ones_like(corr_matrix, dtype=bool))
cmap = sns.diverging_palette(220, 10, as_cmap=True) # Custom colormap


plt.figure(figsize=(28, 28)) # 28 columns to fit better 

# Draw the heatmap with the mask and correct aspect ratio
sns.heatmap(corr_matrix, mask=mask, cmap=cmap, vmax=1.0, center=0, annot=True,
            square=True, linewidths=1, cbar_kws={"shrink": .75})

plt.title('Correlation Matrix')
plt.savefig("correlation matrix.png")
plt.show()

出力

行列は膨大すぎて表示しきれませんが、以下は非常に便利な部分の一部です。

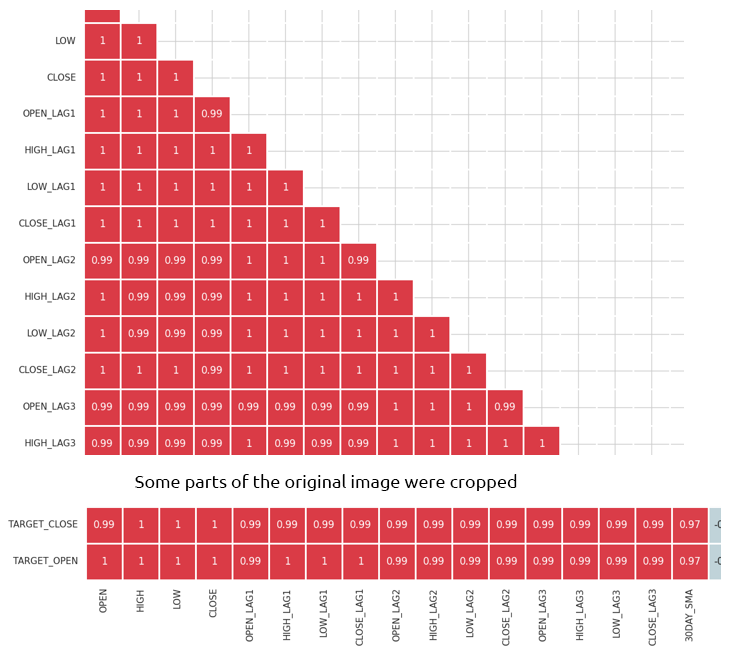
相関性の高い特徴の特定と除去 

高い多重共線性は、2つ以上の特徴が互いに高い相関を持つ場合に発生します。これは、多くの機械学習アルゴリズム、特に線形モデルにおいて問題を引き起こす可能性があります。このような状況は、係数の不安定な推定につながります。

独立変数自体の相関関係

相関性の高い特徴を組み合わせたり取り除いたりすることで、情報をあまり失うことなくモデルを単純化できます。例えば、上記の相関行列の画像では、始値、高値、安値が100%の相関を示しています。さらに、両者の相関は99.0%（最終値は四捨五入）です。これらの変数を取り除き、1つの変数だけにするか、あるいは、これから議論するデータの次元を下げるテクニックを利用するかを決定できます。

独立変数（特徴）と目的変数の相関

目的変数と強い相関を持つ特徴は、一般的に情報量が多く、モデルの予測性能を向上させることができます。

相関係数は数値変数間の線形関係を測定するため、混同行列はDAYOFWEEK、DAYOFYEAR、MONTH のようなデータセットのカテゴリ特徴(Categorical variable)（英語）には直接適用できません。

統計的検定

目的変数と有意な関係を持つ特徴を選択するために、統計的検定を実行することができます。

カイ二乗検定

カイ二乗検定は、分割表において期待されるカウントが観察されたカウントと比較して、2つのカテゴリ変数間に有意な関連があるかどうかを測定する手法です。これは、2つのカテゴリ変数の間に有意な関連があるかどうかを決定するのに役立ちます。

分割表は、変数の度数分布を表示する行列形式の表であり、2つのカテゴリ変数の関係を調べるために使用されます。カイ二乗検定では、予想される度数に対する観察された度数を比較するために、この分割表が利用されます。

カイ二乗検定はカテゴリ変数にのみ適用可能です。

データセットには、DAYOFMONTH、DAYOFWEEK、DAYOFYEAR、MONTHといったいくつかのカテゴリ変数があります。これらの特徴との関係を測定するために、目的変数を作成する必要があります。また、特徴との関係を測定するために、目的変数を作成しなければなりません。

Pythonコード

from sklearn.feature_selection import chi2
from sklearn.feature_selection import SelectKBest

target = []

# Loop through each row in the DataFrame to create the target variable

for i in range(len(df)):
    if df.loc[i, 'TARGET_CLOSE'] > df.loc[i, 'TARGET_OPEN']:
        target.append(1)
    else:
        target.append(0)
        

X = pd.DataFrame({
    'DAYOFMONTH': df['DAYOFMONTH'],
    'DAYOFWEEK': df['DAYOFWEEK'],
    'DAYOFYEAR': df['DAYOFYEAR'],
    'MONTH': df['MONTH']
})


chi2_selector = SelectKBest(chi2, k='all')
chi2_selector.fit(X, target)
chi2_scores = chi2_selector.scores_

# Output scores for each feature

feature_scores = pd.DataFrame({'Feature': X.columns, 'Chi2 Score': chi2_scores})
print(feature_scores)

出力

      Feature  Chi2 Score
0  DAYOFMONTH    0.622628
1   DAYOFWEEK    0.047481
2   DAYOFYEAR   14.618057
3       MONTH    0.489713

上の出力から、DAYOFYEAR が他の変数と比較して、目的変数に最も影響を与える変数であることを示す最高のカイ二乗スコアを持っていることがわかります。これは、データが1日の時間枠から収集されており、各日が1年の特定の日に固有に対応しているため、理にかなっています。データセット中のDAYOFYEAR変数の強い存在は、おそらくその頻度と有意性を高め、目的変数を予測する上で重要な特徴となっています。

ANOVA（Analysis of Variance、分散分析）テスト

は、3つ以上のグループの平均を比較し、少なくとも1つのグループの平均が他のグループと統計的に異なるかどうかを確認するために使用される統計手法です。これは、連続的な特徴とカテゴリカル目的変数との関係の強さを判断するのに役立ちます。

ANOVAは、各グループ内およびグループ間の分散を分析するだけでなく、各グループ内の観測のばらつきや異なるグループの平均間のばらつきも測定します。

この検定では、F統計量を計算します。F統計量は、グループ内分散に対するグループ間分散の比率であり、F統計量が大きいほど、各グループの平均値が異なることを示唆します。

Scikit-learnのf_classifを使って、特徴選択のためのANOVA検定をおこなってみましょう。

Pythonコード

from sklearn.feature_selection import f_classif

# We start by dropping the categorical variables in the dataset

X = df.drop(columns=[
    "DAYOFMONTH",
    "DAYOFWEEK",
    "DAYOFYEAR",
    "MONTH",
    "TARGET_CLOSE",
    "TARGET_OPEN"
])


# Perform ANOVA test

selector = SelectKBest(score_func=f_classif, k='all')
selector.fit(X, target)

# Get the F-scores and p-values
anova_scores = selector.scores_
anova_pvalues = selector.pvalues_

# Create a DataFrame to display results
anova_results = pd.DataFrame({'Feature': X.columns, 'F-Score': anova_scores, 'p-Value': anova_pvalues})
print(anova_results)

出力

            Feature   F-Score   p-Value
0              OPEN  3.483736  0.062268
1              HIGH  3.627995  0.057103
2               LOW  3.400320  0.065480
3             CLOSE  3.666813  0.055792
4         OPEN_LAG1  3.160177  0.075759
5         HIGH_LAG1  3.363306  0.066962
6          LOW_LAG1  3.309483  0.069181
7        CLOSE_LAG1  3.529789  0.060567
8         OPEN_LAG2  3.015757  0.082767
9         HIGH_LAG2  3.034694  0.081810
10         LOW_LAG2  3.259887  0.071295
11       CLOSE_LAG2  3.206956  0.073629
12        OPEN_LAG3  3.236211  0.072329
13        HIGH_LAG3  3.022234  0.082439
14         LOW_LAG3  3.020219  0.082541
15       CLOSE_LAG3  3.075698  0.079777
16        30DAY_SMA  2.665990  0.102829
17      7DAY_STDDEV  0.639071  0.424238
18   DIFF_LAG1_OPEN  1.237127  0.266293
19   DIFF_LAG1_HIGH  0.991862  0.319529
20    DIFF_LAG1_LOW  0.131002  0.717472
21  DIFF_LAG1_CLOSE  0.198001  0.656435

Fスコアが高いほど、その特徴が目的変数と強い関係があることを示します。

有意水準（例えば0.05）未満のP値は統計的に有意とみなされます。

また、最も重要な特徴を特定するために、最高のFスコアまたは最低のP値を持つ特徴を選択し、他の特徴を除外することも可能です。 それでは、上位10の特徴を見てみましょう。

Pythonコード

selector = SelectKBest(score_func=f_classif, k=10)
X_selected = selector.fit_transform(X, target)


# print the selected feature names

selected_features = X.columns[selector.get_support()]
print("Selected Features:", selected_features)

出力

Selected Features: Index(['OPEN', 'HIGH', 'LOW', 'CLOSE', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1',
       'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3'],
      dtype='object')

ラッパー法

ラッパー法では、異なるサブセットや特徴を用いてモデルの性能を評価します。ここでは、再帰的特徴除去(RFE: Recursive Feature Elimination)と逐次的特徴選択(SFS: Sequential Feature Selection)について説明します。

再帰的特徴除去(RFE)

再帰的特徴除去（RFE）は、最も関連性の高い特徴を選択することを目的とした特徴選択手法です。この手法では、より小さな特徴の集合を再帰的に考慮し、モデルを適合させながら、望ましい特徴数に達するまで最も重要でない特徴を削除します。

RFEの仕組み

まず、機械学習モデルを訓練します。この例では、ロジスティック回帰を使用します。

Pythonコード

from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression

# Prepare the target variable, again

y = []

# Loop through each row in the DataFrame to create the target variable
for i in range(len(df)):
    if df.loc[i, 'TARGET_CLOSE'] > df.loc[i, 'TARGET_OPEN']:
        y.append(1)
    else:
        y.append(0)

# Drop future variables from the feature set
X = df.drop(columns=["TARGET_CLOSE", "TARGET_OPEN"])

# Initialize the model
model = LogisticRegression(max_iter=10000)

次に、モデルを指定し、データから選択したい最も影響力のある特徴の数でRFEを初期化します。

# Initialize RFE with the model and number of features to select
rfe = RFE(estimator=model, n_features_to_select=10)

# Fit RFE
rfe.fit(X, y)
selected_features_mask = rfe.support_

最後に、最も重要でない特徴を決定し、それらを排除します。

Pythonコード

# Getting the names of the selected features
feature_names = X.columns
selected_feature_names = feature_names[selected_features_mask]


selected_features = pd.DataFrame({
    "Name": feature_names,
    "Mask": selected_features_mask
})

selected_features.head(-1)

出力

        Name    Mask
0       OPEN    True
1       HIGH    True
2       LOW     True
3       CLOSE   True
4       OPEN_LAG1       False
5       HIGH_LAG1       True
6       LOW_LAG1        True
7       CLOSE_LAG1      True
8       OPEN_LAG2       False
9       HIGH_LAG2       False
10      LOW_LAG2        True
11      CLOSE_LAG2      True
12      OPEN_LAG3       True
13      HIGH_LAG3       False
14      LOW_LAG3        False
15      CLOSE_LAG3      False
16      30DAY_SMA       False
17      7DAY_STDDEV     False
18      DAYOFMONTH      False
19      DAYOFWEEK       False
20      DAYOFYEAR       False
21      MONTH   False
22      DIFF_LAG1_OPEN  False
23      DIFF_LAG1_HIGH  False
24      DIFF_LAG1_LOW   False

Trueの値が割り当てられた特徴はすべて、最も重要な特徴です。それらを取得するには、元のX行列からスライスをおこなえばよいです。

# Filter the dataset to keep only the selected features

X_selected = X.loc[:, selected_features_mask]

#for better readability, we convert this into pandas dataframe

X_selected_df = pd.DataFrame(X_selected, columns=selected_feature_names)

print("Selected Features")
X_selected_df.head()

出力

RFEの利点

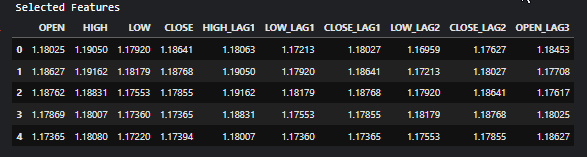
• RFEは、特徴を重要度に基づいてランク付けできる任意のモデルで使用できます。
• 無関係な特徴を排除することで、RFEはモデルの性能を向上させることが可能です。
• 不要な特徴を削除することで、過剰適合を減少させる効果があります。

RFEの欠点

• 大規模なデータセットやニューラルネットワークなどの複雑なモデルに対しては、モデルを何度も再学習させる必要があるため、計算コストが高くなる可能性があります。
• RFEは貪欲なアルゴリズムであり、常に最適な特徴のサブセットを見つけるとは限りません。

逐次特徴選択(SFS)

逐次特徴選択(SFS)は、モデルに対する性能への貢献度に基づいて特徴を追加または削除し、特徴セットを段階的に構築するラッパー法の一種です。SFSには、前向き選択と後向き選択の2つのアプローチがあります。

前向き選択では、最初に空の集合から始まり、特徴の数が所望の数に達するか、特徴を追加してもモデルの性能が向上しないまで、1つずつ特徴を追加していきます。

後向き選択では、前向き選択とは逆のプロセスを辿ります。すべての特徴からスタートし、1つずつ削除していきます。この際、毎回最も重要でない特徴から削除を行い、目的の特徴数に達するまで続けます。

前向き選択

from sklearn.feature_selection import SequentialFeatureSelector

# Create a logistic regression model
model = LogisticRegression(max_iter=10000)

# Create a SequentialFeatureSelector object
sfs = SequentialFeatureSelector(model, n_features_to_select=10, direction='forward')

# Fit the SFS object to the training data
sfs.fit(X, target)

# Get the selected feature indices
selected_features = sfs.get_support(indices=True)
selected_features_names = X.columns[selected_features] # get the feature names

# Print the selected features
print("Selected feature indices:", selected_features)
print("Selected feature names:", selected_feature_names)

出力

Selected feature indices: [ 1  7  8 12 17 19 22 23 24 25]
Selected feature names: Index(['OPEN', 'HIGH', 'LOW', 'CLOSE', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1',
       'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3'],
      dtype='object')

後向き選択

# Create a logistic regression model
model = LogisticRegression(max_iter=10000)

# Create a SequentialFeatureSelector object
sfs = SequentialFeatureSelector(model, n_features_to_select=10, direction='backward')

# Fit the SFS object to the training data
sfs.fit(X, target)

# Get the selected feature indices
selected_features = sfs.get_support(indices=True)
selected_features_names = X.columns[selected_features] # get the feature names

# Print the selected features
print("Selected feature indices:", selected_features)
print("Selected feature names:", selected_feature_names)

出力

Selected feature indices: [ 2  3  7 10 11 12 13 14 15 16]
Selected feature names: Index(['OPEN', 'HIGH', 'LOW', 'CLOSE', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1',
       'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3'],
      dtype='object')

異なるアプローチをとっているにもかかわらず、後向き法も前向き法はどちらも同じ解に収束し、同じ数の特徴量を生成します。

逐次特徴選択の利点

• 理解しやすく、実行しやすいです。
• どんな機械学習アルゴリズムにも使えます。
• 多くの場合、最も関連性の高い特徴を選択することで、モデル性能の向上につながります。

逐次特徴選択の欠点

• 大規模なデータセットや多数の特徴に対しては、計算に時間がかかることがあります。
• 局所的な改善に基づいて判断するため、必ずしも最適な特徴セットを見つけられない可能性があります。

埋め込み法

組み込み法では、モデルの訓練過程において特徴選択を実施します。埋め込み特徴選択のワークフローは、以下のようなステップで構成されます。

1. 機械学習モデルを訓練します
2. 特徴の重要性を導します
3. ランキング上位の予測変数を選択します
   

最も一般的な埋め込み法には、ラッソ回帰や決定木ベースの方法があります。

ラッソ回帰

線形回帰モデルは、特徴空間の線形結合に基づいて結果を予測します。係数は、ターゲットの実測値と予測値の差の二乗を最小化することによって決定されます。正規化には主に3つの手法があります。リッジ回帰(Ridge)、ラッソ回帰(Lasso)、およびエラスティックネット(Elastic Net)です。ラッソ回帰ではL1正則化を用い、係数が指定された定数で縮小されます。これに対し、リッジ回帰ではL2正則化を使用し、係数の二乗に基づいてペナルティを加えます。係数を縮小する目的は、モデルの分散を減少させ、過剰適合を防ぐことです。最適な定数（正則化パラメータ）は、ハイパーパラメータ最適化によって推定する必要があります。

ラッソ正則化の特長は、いくつかの係数を正確にゼロに設定できる点です。これにより、特徴選択が行われ、データから重要でない特徴を安全に除去することができます。

Pythonコード

from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score
from sklearn.preprocessing import MinMaxScaler

y = df["TARGET_CLOSE"]

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# A scaling technique
scaler = MinMaxScaler()

# Initialize and fit the lasso model
lasso = Lasso(alpha=0.001)  # You need tune for the best penalty value

# Train the scaler and transfrom data
X_train = scaler.fit_transform(X_train)

lasso.fit(X_train, y_train)

print(f'Coefficients: {lasso.coef_}') #print coefficients

# Predict on the test set
X_test = scaler.transform(X_test)
y_pred = lasso.predict(X_test)

# Calculate mean squared error
mse = r2_score(y_test, y_pred)
print(f'Lasso regression test accuracy = {mse}')


# select all features with coefficents not equal to zero
selected_features = X.columns[lasso.coef_ != 0]
print(f'Selected Features: {selected_features}')

出力

Coefficients: [ 0.          0.02575516  0.05720178  0.1453415   0.          0.
  0.          0.          0.          0.          0.          0.
  0.          0.          0.          0.          0.0228085  -0.
  0.         -0.          0.          0.          0.          0.
  0.          0.        ]
Lasso regression test accuracy = 0.9894539761500866
Selected Features: Index(['HIGH', 'LOW', 'CLOSE', '30DAY_SMA'], dtype='object')

このモデルは4つの特徴のみを選択したため、98%の精度を示しました。

特徴選択にラッソ回帰を使用する利点

• ラッソは、最も重要な特徴を自動的に選択するため、モデルが単純化され、解釈性が向上します。
• ペナルティ項を追加することで、ラッソは過剰適合のリスクを軽減します。
• ラッソは、無関係な特徴を除去するため、解釈しやすいモデルを生成することができます。

特徴選択にラッソ回帰を使用する欠点

• 特徴量の相関が高い場合、ラッソは不安定な係数推定につながる可能性があります。
• 特徴の数が観測の数を超える場合、ラッソは期待通りに機能しないことがあります。

決定木ベースの手法

決定木アルゴリズムは、データを再帰的に分割することで結果を予測します。各ノードで、アルゴリズムは、不純物の減少を最大化することを目的として、データを分割するための特徴と値を選択します。

決定木における特徴の重要性は、各特徴が木全体を通して達成する不純物の減少の合計によって決定されます。例えば、ある特徴が複数のノードでデータを分割するために使用される場合、その重要度はそれらすべてのノードにおける不純物削減量の合計として計算されます。

ランダムフォレストは、多数の決定木を並行して成長させます。最終的な予測は、各木の予測の平均または多数決によっておこなわれます。ランダムフォレストにおける特徴の重要度は、すべての木における各特徴の平均重要度として評価されます。

XGBoostのような勾配ブースティングマシン(GBM: Gradient boosting machine)は、木を順次構築します。それぞれの木は、前の木の誤差（残差）を修正することを目的としています。GBMでは、特徴の重要度はすべての木にわたる重要度の合計として計算されます。

決定木によって生成された特徴の重要度を分析することで、モデルにとって最も重要な特徴を特定し、選択することができます。

from sklearn.ensemble import RandomForestClassifier

y = []

# Loop through each row in the DataFrame to create the target variable
for i in range(len(df)):
    if df.loc[i, 'TARGET_CLOSE'] > df.loc[i, 'TARGET_OPEN']:
        y.append(1)
    else:
        y.append(0)

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

model = RandomForestClassifier(n_estimators=50, min_samples_split=10, max_depth=5, min_samples_leaf=5)
model.fit(X_train, y_train)

importances = model.feature_importances_

print(importances)

selected_features = importances > 0.04
selected_feature_names = X.columns[selected_features]

print("selected features\n",selected_feature_names)

出力

[0.02691807 0.05334113 0.03780997 0.0563491  0.03162462 0.03486413
 0.02652285 0.0237652  0.03398946 0.02822157 0.01794172 0.02818283
 0.04052433 0.02821834 0.0386661  0.03921218 0.04406372 0.06162133
 0.03103843 0.02206782 0.05104613 0.01700301 0.05191551 0.07251801
 0.0502405  0.05233394]
selected features
 Index(['HIGH', 'CLOSE', 'OPEN_LAG3', '30DAY_SMA', '7DAY_STDDEV', 'DAYOFYEAR',
       'DIFF_LAG1_OPEN', 'DIFF_LAG1_HIGH', 'DIFF_LAG1_LOW', 'DIFF_LAG1_CLOSE'],
      dtype='object')

選択された特徴を急いで使う前に、これらの特徴を選択したランダムフォレスト分類器の精度を測定しなければなりません。テストデータで良好な結果を出したモデルによって選択された特徴を必ず取得す必要があります。

from sklearn.metrics import accuracy_score

test_pred = model.predict(X_test)

print(f"Random forest test accuracy = ",accuracy_score(y_test, test_pred))

特徴選択におけるランダムフォレストの利点

• ランダムフォレストは多数の決定木のアンサンブルを作成するため、単一の決定木と比べて過剰適合のリスクが低くなります。このロバスト性により、特徴の重要度スコアの信頼性が高まります。
• パフォーマンスを大幅に低下させることなく多数の特徴を持つデータセットを管理できるため、高次元空間での特徴選択に適しています。
• 特徴間の複雑な非線形相互作用を捉える能力があり、特徴の重要性をより詳細に理解することができます。

特徴選択におけるランダムフォレストの欠点

• ランダムフォレストの学習は、大規模なデータセットや特徴数が多い場合、計算コストがかかることがあります。 
• 相関のある特徴に対して同じような重要度スコアが割り当てられることがあり、どの特徴が本当に重要なのかを区別するのが難しくなることがあります。
• ランダムフォレストは、連続的な特徴やレベルの多い特徴を、レベルの少ないカテゴリカル特徴よりも優先する傾向があり、これが特徴の重要度スコアに歪みをもたらすことがあります。

次元削減手法

次元削減手法は、特徴選択の手法と組み合わせて使用することができます。主成分分析(PCA)、線形判別分析(LDA)、非負行列因子分解(NMF)、Truncated SVDなどの次元削減手法は、データを低次元空間に変換することを目的としています。

相関行列からわかるように、OPEN、HIGH、LOW、CLOSEの各特徴は高い相関を持っています。PCAによって生成されたこの単一の変数に必要な情報を保持しながら、モデルの特徴を単純化するために、これらの変数を1つにまとめました。線形回帰モデルを用いて、PCAが元のデータよりも次元を下げたデータの精度を保持するのにどれだけ効果的であったかを測定します。

from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression

pca = PCA(n_components=1)

ohlc = pd.DataFrame({
    "OPEN": df["OPEN"],
    "HIGH": df["HIGH"],
    "LOW": df["LOW"],
    "CLOSE": df["CLOSE"]
})

y = df["TARGET_CLOSE"]

# let us use the linear regression model 
model = LinearRegression()

# for OHLC original data 

model.fit(ohlc, y)
preds = model.predict(ohlc)

print("ohlc_original data LR accuracy = ",r2_score(y, preds))

# For data reduced in dimension

ohlc_reduced = pca.fit_transform(ohlc)

print(ohlc_reduced[:10]) # print 10 rows of the reduced data 

model.fit(ohlc_reduced, y)
preds = model.predict(ohlc_reduced)

print("ohlc_reduced data LR accuracy = ",r2_score(y, preds))

出力

ohlc_original data LR accuracy =  0.9937597843724363
[[-0.14447016]
 [-0.14997874]
 [-0.14129409]
 [-0.1293209 ]
 [-0.12659902]
 [-0.12895961]
 [-0.13831287]
 [-0.14061213]
 [-0.14719862]
 [-0.15752861]]
ohlc_reduced data LR accuracy =  0.9921387699876517

どちらのモデルも、約0.99というほぼ同じ精度の値を出しました。1つはオリジナルデータ（4特徴）を使用し、もう1つは次元を縮小したデータ（1特徴）を使用しました。

最後に、OPEN、HIGH、LOW、CLOSEの各特徴を削除し、前の4つの特徴を組み合わせたOHLCという新しい特徴を追加することで、元のデータを修正することができます。

new_df = df.drop(columns=["OPEN", "HIGH", "LOW", "CLOSE"]) #
new_df["OHLC"] = ohlc_reduced

# Reorder the columns to make "ohlc" the first column
cols = ["OHLC"] + [col for col in new_df.columns if col != "OHLC"]
new_df = new_df[cols]

new_df.head(10)

出力

特徴選択における次元削減手法の利点

• 特徴量の数を減らすことで、ノイズや冗長な情報を排除し、機械学習モデルの性能を高めることができます。
• 特徴空間を小さくすることで、次元削減手法は、過剰適合が起こりやすい高次元データを扱う際に、過剰適合を軽減するのに役立ちます。
• これらの手法は、データセットからノイズを除去し、モデルの精度と信頼性を向上させるクリーンなデータに導くことができます。
• 特徴量が少ないモデルは、よりシンプルで解釈しやすくなります。 

特徴選択における次元削減手法の欠点

• 次元削減の結果、重要な情報が失われることが多く、モデルの性能に悪影響を与える可能性があります。
• PCAのような手法では、保持する成分の数を選択する必要があるが、これは簡単ではなく、試行錯誤や交差検証を伴うことがあります。
• 次元削減手法によって作成された新しい特徴は、元の特徴に比べて解釈が難しい場合があります。
• 次元を削減すると、データが過度に単純化され、特徴間の微妙だが重要な関係を見落とすモデルが生まれる可能性があります。

最後に

最も価値のある情報を抽出する方法を理解することは、機械学習モデルを最適化する上で極めて重要です。効果的な特徴選択をおこなうことで、訓練時間を大幅に短縮し、モデルの精度を向上させることができます。これにより、MetaTrader 5におけるAI搭載の取引ロボットの効率が向上します。最も関連性の高い特徴を慎重に選択することで、ライブ取引とストラテジーテストの両方でパフォーマンスを向上させ、最終的に取引アルゴリズムでより良い結果を得ることが可能になります。

ご精読ありがとうございました。

添付ファイルの表

ファイル	説明と使用法
hwww.kaggle.com/code/omegajoctan/feature-selection#Filter-Methodsfeature_selection.ipynb	この記事で説明するすべてのPythonコードは、このJupyterノートブックにあります
Timeseries OHLC.csv	この記事で使用したデータセット

ソース

• A Chi-Square Statistics-Based Feature Selection Method in Text Classification (https://www.researchgate.net/publication/331850396_A_Chi-Square_Statistics_Based_Feature_Selection_Method_in_Text_Classification)
• 特徴選択(https://ja.wikipedia.org/wiki/%E7%89%B9%E5%BE%B4%E9%81%B8%E6%8A%9E)
• 埋め込み法(https://www.blog.trainindata.com/feature-selection-with-embedded-methods/)