しかし、ただ一つ言えることは、これらの指標は独立したものではなく、同じものを相互に置き換えたものであるということだ。一つの指標から他の指標を推測することができ、その計算式は既知である。
ベイズでは何もできない。
ダウンロードしてテスターで実行するだけでも、ちょっと消耗する。この記事には、「教えるにはXを押す」という指示は見当たりませんでした。
また学問のための何か。
また学問のための何か。
大学でファイナンシャル・プランニングを専攻していたとき、確率について勉強しました。
確率=有利な結果の数/結果の総数」という伝統的な「確率の公式」の意味で確率を分析に使ったことはない!
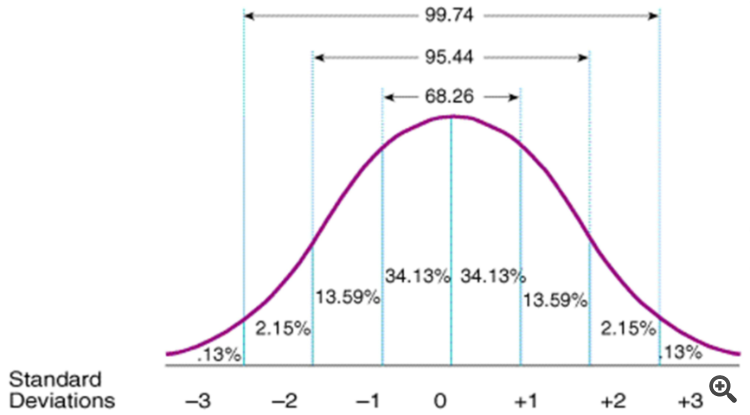
とはいえ、現実的には、標準偏差は、一定期間内のトレードの平均からの乖離(したがって、反転または継続の確率)を提供するという意味で、いずれにせよそういうものだ。(例えば、価格がSD1に近づいている場合、平均に戻る確率は68%、SD2に達している場合は95.5%、SD3に達している場合は99.7%)そのため、標準偏差は、特に標準偏差チャンネルのようなものを使用する場合、取引ポジションが反対方向に向かう可能性が高いタイミングを計る際に非常に便利です。
ですから、伝統的な確率ベースの計算式そのものを直接使うわけではありませんが、私は確率を使っています。
しかし、ANNの訓練や反映におけるニューラルネットワーク分析に関しては、確率の応用が可能であることは確かです!
取引の機会を逃しています。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
新しい記事「データサイエンスと機械学習(第11回):単純ベイズ、取引における確率論」はパブリッシュされました:
確率を利用した取引は綱渡りのようなもので、正確さとバランス、そしてリスクに対する鋭い理解が必要です。取引の世界では、確率がすべてです。確率は、成功と失敗、利益と損失の違いになります。確率の力を活用することで、トレーダーは十分な情報に基づいた意思決定をおこない、リスクを効果的に管理し、経済的目標を達成することができます。つまり、経験豊富な投資家であれ、初心者のトレーダーであれ、確率を理解することは、取引の可能性を引き出す鍵になるのです。この記事では、確率を利用したエキサイティングな取引の世界を探求し、取引ゲームを次のレベルに引き上げる方法を紹介します。
単純ベイズ分類器は、機械学習で分類タスクに使用される乱択アルゴリズムで、利用可能なエビデンスから仮説の確率を計算する、ベイズの定理に基づくものです。この確率的分類器は、シンプルでありながら様々な場面で有効なアルゴリズムで、分類に使用される特徴が互いに独立していることを前提としています。次は例です。身長、足のサイズ、体重、肩幅で人間(男性、女性)を分類する場合、このモデルはこれらの変数をすべて互いに独立したものとして扱い、この場合、足のサイズと身長が人間にとって関係あるとは考えません。
このモデルは、独立変数間のパターンを理解しようとしないので、情報に基づいた取引の意思決定に使用してみるべきだと思います。取引の世界でパターンを完全に理解できる人は誰もいないと思うので、単純ベイズがどのように機能するのか見てみましょう。
作者: Omega J Msigwa