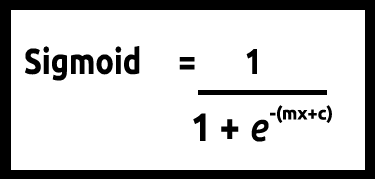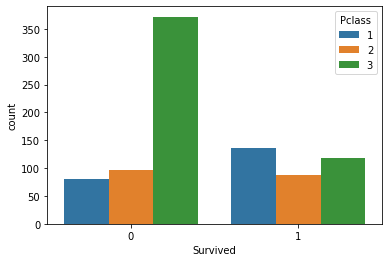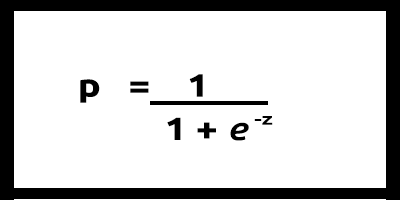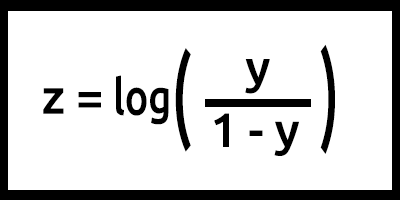
データサイエンスと機械学習（第02回）：ロジスティック回帰

MetaTrader 5 — トレーディングシステム | 4 8月 2022, 17:06

610

Omega J Msigwa

第01回で説明した線形回帰とは異なり、ロジスティック回帰は線形回帰に基づく分類方法です。

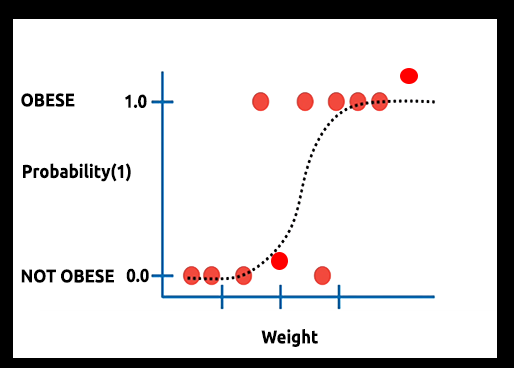
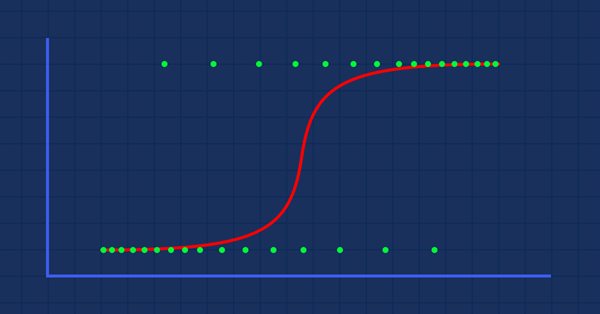
仮説：人が肥満である確率とその体重のグラフを描くとします。

この場合、線形モデルを使用することはできません。別の手法を使用して、この線をシグモイドと呼ばれるS曲線に変換します。

ロジスティック回帰は、カテゴリ型従属変数の結果を予測するために使用されるバイナリ形式で結果を生成するため、結果は次のように離散/カテゴリである必要があります。

0/1
はい/いいえ
True/False
高/低
買/売

作成するライブラリでは、その他の離散値を無視して、バイナリ(0,1)のみに焦点を当てます。

yの値は0～1であると想定されているため、線は0と1でクリップする必要があります。これは、次の式で実現できます。

これでこのグラフが得られます。

線形モデルはロジスティック関数「(sigmoid/p) =1/1+e^t」に渡されます。ここで、tは線形モデルであり、結果は0～1の値です。これは、データポイントがクラスに属する確率を表します。

線形モデルのyを従属として使用する代わりに、その関数は「p」が従属として使用されるように示されます。

p = 1/1+e^-(c+m1x1+m2x2+....+mnxn) 、複数の値の場合

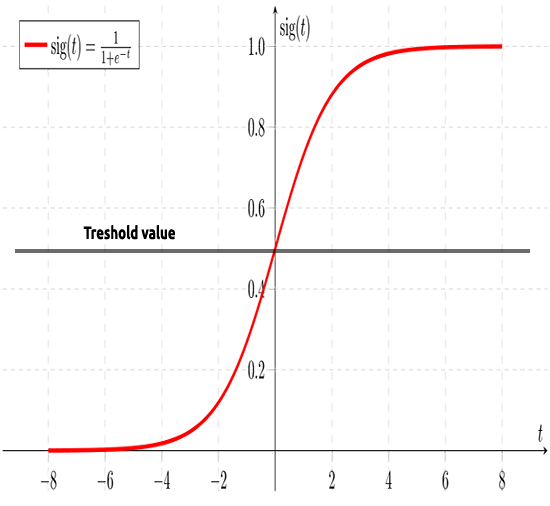
前述のように、シグモイド曲線は無限大の値をバイナリ形式（0または1）の出力に変換することを目的としています。しかし、0.8にデータポイントがある場合、値が0であるか1であるかはどのように判断できるでしょうか。ここで役立つのがしきい値です。

しきい値は勝ち負けの確率を示し、0.5（0と1の中心）にあります。

0.5以上の値は1に丸められるため、勝者と見なされます。0.5未満の値は0に丸められるため、敗者と見なされます。この時点で線形とロジスティック回帰の違いがわかります。

線形回帰vsロジスティック回帰

線形回帰	ロジスティック回帰
連続変数	カテゴリー変数
回帰の問題を解決する	分類の問題を解決する
モデルには直線方程式がある	モデルにはロジスティック方程式がある

コーディング部分とデータを分類するためのアルゴリズムに飛び込む前に、いくつかの手順でデータを理解し、モデルの構築を容易にすることができます。

データの収集と分析
データのクリーニング
精度の確認

01：データの収集と分析

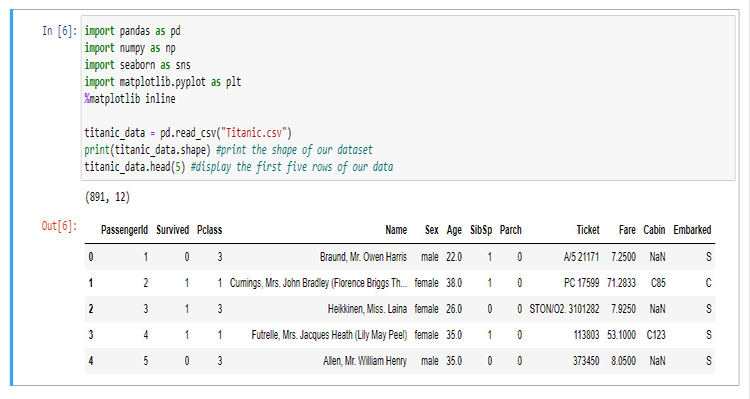
このセクションでは、データを視覚化するためにPythonコードをたくさん書きます。Jupyterノートブックのデータを抽出して視覚化するために使用するライブラリをインポートすることから始めましょう。

ライブラリを構築するために、タイタニックのデータを使用します。氷山にぶつかった後、1912年4月15日に北大西洋で沈んだタイタニック船の事故に関するデータです。ウィキ。すべてのPythonコードとデータセットは、記事の最後にリンクされている私のGitHubにあります。

列は次の略です。

survival - 生存（0=いいえ、1 =はい）
class - 等級（1=1等、2=2等、3=3等）
name - 名前
sex - 性別
age - 年齢
sibsp - 乗船していた兄弟/配偶者の数
parch - 乗船していた親/子供の数
ticket - チケット番号
fare - 旅客運賃
cabin - キャビン
embarked - 乗船港（C=チェルブール、Q=クイーンズタウン、S=サウサンプトン）

データを収集して変数「titanic_data」に保存したので、survival列から始めて、列のデータの視覚化を始めましょう。

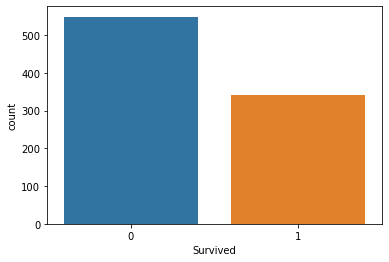
sns.countplot(x="Survived", data = titanic_data)

出力

これは、半数以下の乗客が事故で生き延びたことを示しています。船に乗っていた乗客の約半分が事故を生き延びました。

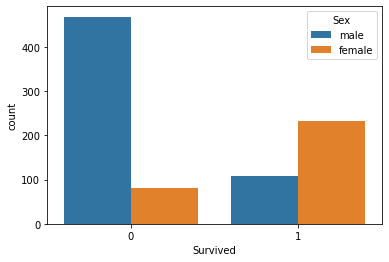
性別による生存数を視覚化しましょう。

sns.countplot(x='Survived', hue='Sex', data=titanic_data)

その日、男性に何が起こったのかはわかりませんが、男性の2倍以上の女性が生き残っています。

等級ごとに生存数を視覚化しましょう。

sns.countplot(x='Survived', hue='Pclass', data=titanic_data)

三等には多くの乗客がいましたが、事故を生き延びた乗客はごくわずかでした。

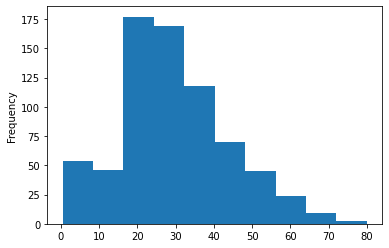
船内にいた乗客の年齢層のヒストグラムをプロットしてみましょう。ここでは、countplotを使用してデータを視覚化することはできません。整理されていないデータセットの年齢のさまざまな値があるためです。

titanic_data['Age'].plot.hist()

出力

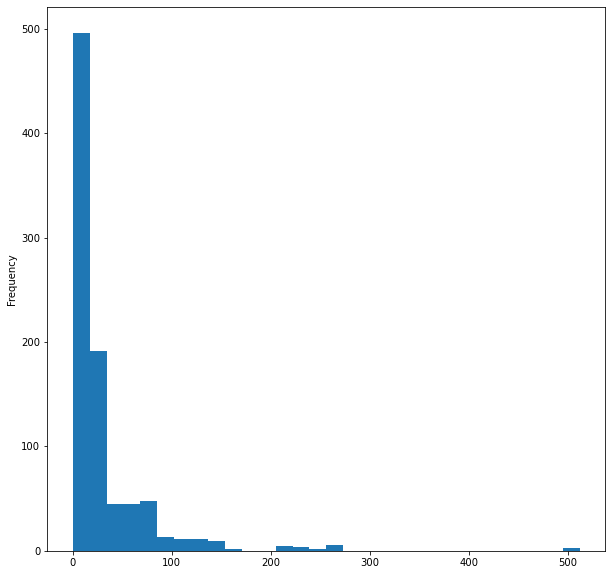
最後に、船の運賃のヒストグラムを視覚化しましょう。

titanic_data['Fare'].plot.hist(bins=30, figsize=(10,10))

データを視覚化するのはこれで終わりですが、12列のうち重要だと思う5列のみを視覚化しました。次に、データをクリーンアップしましょう。

02：データのクリーニング

ここでは、データセット内の不要な列を回避/削除しながら、NaN（欠落）値を削除してデータをクリーンアップします。

ロジスティック回帰を使用するには、double値とinteger値が必要なので、意味のない文字列値を回避する必要があります。この場合、次の列を無視します。

るName列（意味のある情報がない）
Ticketコラム（事故の存続には意味がない）
Cabin列（最初の5行でさえわかるように、欠落している値が多すぎる）
Embarked（無関係）

そのために、WPS officeでCSVファイルを開き、手動で列を削除します。任意のスプレッドシートプログラムを使用できます。

スプレッドシートを使用して列を削除した後、新しいデータを視覚化してみましょう。

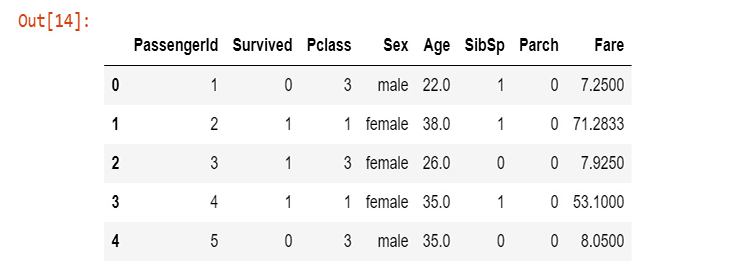
new_data = pd.read_csv(r'C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\titanic.csv')
new_data.head(5)

出力

性別の列に文字列の値があることは言うまでもなく、年齢の列にはまだ値が欠如していますが、データをクリーンアップしました。コードで問題を修正しましょう。男性と女性の文字列をそれぞれ0と1に変換するラベルエンコーダーを作成しましょう。

void CLogisticRegression::LabelEncoder(string &src[],int &EncodeTo[],string members="male,female")
 {
   string MembersArray[];
   ushort separator = StringGetCharacter(m_delimiter,0);
   StringSplit(members,separator,MembersArray); //convert members list to an array
   ArrayResize(EncodeTo,ArraySize(src)); //make the EncodeTo array same size as the source array
   
      int binary=0;
      for(int i=0;i<ArraySize(MembersArray);i++) // loop the members array
        {
           string val = MembersArray[i];
           binary = i; //binary to assign to a member
           int label_counter = 0;
           
           for (int j=0; j<ArraySize(src); j++)
              {
                string source_val = src[j];
                 if (val == source_val)
                   {
                    EncodeTo[j] = binary;
                    label_counter++;
                   }
              } 
           Print(MembersArray[binary]," total =",label_counter," Encoded To = ",binary);
        } 
 }

src[]という名前のソース配列を取得するために、CSVファイルの特定の列からデータを取得して文字列値の配列MembersArray[]に配置する関数もプログラムしました。確認してください。

void CLogisticRegression::GetDatatoArray(int from_column_number, string &toArr[])
 {
  
   int handle  = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI,m_delimiter); 
   int counter=0;
   
   if (handle == INVALID_HANDLE)
      Print(__FUNCTION__," Invalid csv handle err=",GetLastError());
      
    else
     {
       int column = 0, rows=0;
       while (!FileIsEnding(handle))
         {
           string data = FileReadString(handle);
           
           column++;
//---      
           if (column==from_column_number) //if column in the loop is the same as the desired column
              {
                  if (rows>=1) //Avoid the first column which contains the column's header
                    {   
                        counter++;
                        ArrayResize(toArr,counter); 
                        toArr[counter-1]=data;
                    }   
                     
              }
//---
           if (FileIsLineEnding(handle))
             {                     
               rows++;
               column=0;
             }
         }
     }
   FileClose(handle);
 }

testscript.mq5内で、関数を適切に呼び出し、ライブラリを初期化する方法は次のとおりです。

#include "LogisticRegressionLib.mqh";
CLogisticRegression Logreg;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
    Logreg.Init("titanic.csv",",");
     
    
    string Sex[];
    int SexEncoded[];
    Logreg.GetDatatoArray(4,Sex);
    Logreg.LabelEncoder(Sex,SexEncoded,"male,female");
    
    ArrayPrint(SexEncoded);
  }

スクリプトを正常に実行した後、出力が生成されます。

male total =577 Encoded To = 0

female total =314 Encoded To = 1

[ 0] 0 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 0 1 0 1 1 0 0 1 0 0 1 1 0 0 0 0 0 1 1 1 1 0 1 1 0 0 1 0 1 0 0 1 1 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0

[ 75] 0 0 0 0 1 0 0 1 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 1 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 1 1 0 0 1 0 0 0 1 1 1 0 0 0 0 1 0 0

... ... ... ...

[750] 1 0 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 1 1 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 1 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0

[825] 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 0 0 0 1 1 0 1 1 0 0 0 0 1 0 0 1 1 0 0 0 1 1 0 1 0 0 1 0 1 1 0 0

値をエンコードする前に、関数の引数であるmembers="male,female"に注意してください。文字列に最初に表示される値は0としてエンコードされます。男性の列が初めに表示されるため、すべての男性は0にエンコードされ、女性は1にエンコードされます。この関数は2つの値に制限されていません。文字列がデータに意味をなす限り、必要なだけエンコードできます。

欠測値

Age列に注意を払うと、値が欠落していることに気付くでしょう。欠落は、死という主に1つの理由が原因である可能性があります。データセットで個人の年齢を識別できなくなります。特に大規模なデータセットでは時間がかかる場合がありますが、これらのギャップはデータセットを確認することで確認できます。pandasを使用してデータを視覚化するため、すべての列で欠落している行を見つけましょう。

titanic_data.isnull().sum()

出力は次のようになります。

PassengerId 0

Survived 0

Pclass 0

Sex 0

Age 177

SibSp 0

Parch 0

Fare 0

dtype: int64

Age列の891行のうち177行に欠測値（NAN）があります。

次に、値をすべての値の平均に置き換えることにより、列の欠落している値を置き換えます。

void CLogisticRegression::FixMissingValues(double &Arr[])
 {
   int counter=0; double mean=0, total=0;
   for (int i=0; i<ArraySize(Arr); i++) //first step is to find the mean of the non zero values
       {
         if (Arr[i]!=0)
           {
             counter++;
             total += Arr[i];
           }
       }
     mean = total/counter; //all the values divided by their total number
     Print("mean ",MathRound(mean)," before Arr");
     ArrayPrint(Arr);
     
     for (int i=0; i<ArraySize(Arr); i++)
       {
         if (Arr[i]==0)
           {
             Arr[i] = MathRound(mean); //replace zero values in array
           }
       }
     Print("After Arr");
     ArrayPrint(Arr); 
 }

この関数は、ゼロ以外のすべての値の平均を見つけ、配列内のすべてのゼロの値を平均値に置き換えます。

関数を正常に実行した後の出力です。ご覧のとおり、すべてのゼロ値は、タイタニック号の乗客の平均年齢である30.0に置き換えられています。

平均30.0 Before配列

[ 0] 22.0 38.0 26.0 35.0 35.0 0.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 0.0 31.0 0.0 35.0 34.0 15.0 28.0 8.0 38.0 0.0 19.0 0.0 0.0

……………………………………

[840] 20.0 16.0 30.0 34.5 17.0 42.0 0.0 35.0 28.0 0.0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 0.0 41.0 21.0 48.0 0.0 24.0 42.0 27.0 31.0 0.0 4.0

[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 0.0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 0.0 26.0 32.0

After配列

[ 0] 22.0 38.0 26.0 35.0 35.0 30.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 30.0 31.0 30.0 35.0 34.0 15.0 28.0 8.0 38.0 30.0 19.0 30.0 30.0

… … … … … … … … …

[840] 20.0 16.0 30.0 34.5 17.0 42.0 30.0 35.0 28.0 30.0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 30.0 41.0 21.0 48.0 30.0 24.0 42.0 27.0 31.0 30.0 4.0

[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 30.0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 30.0 26.0 32.0

ロジスティック回帰モデルの構築

まず、1つの独立変数と1つの従属変数を持つロジスティック回帰を作成しましょう。その後、問題の完全なソリューションモデルにスケールアップします。

2つの変数SurvivedとAgeに基づいてモデルを構築しましょう。年齢に基づいて、人が生き残ることができる可能性を調べてみましょう。

これまでのところ、ロジスティックモデルの奥深くに線形モデルがあることがわかっています。線形モデルを可能にする関数をコーディングすることから始めましょう。

Coefficient_of_X()およびy_intercept()は新しいものではなく、この連載の最初の記事に基づいて構築されています。これらの関数と線形回帰全般の詳細については、この関数を読むことを検討してください。

double CLogisticRegression::y_intercept()
 {
   // c = y - mx
   return (y_mean-coefficient_of_X()*x_mean);
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CLogisticRegression::coefficient_of_X()
 { 
   double m=0;
//---  
    {
      double x__x=0, y__y=0;
      double numerator=0, denominator=0; 
      
      for (int i=0; i<ArraySize(m_xvalues); i++)
       {
         x__x = m_xvalues[i] - x_mean; //right side of the numerator (x-side)
         y__y = m_yvalues[i] - y_mean; //left side of the numerator  (y-side)
        
         
         numerator += x__x * y__y;  //summation of the product two sides of the numerator
         denominator += MathPow(x__x,2); 
       }
      m = numerator/denominator;
    }
   return (m);
 }

次に、式からロジスティックモデルをプログラムしましょう。

zは対数オッズとも言われます。シグモイドの逆数は、zが1ラベル（例：「生存した」）の確率を0ラベル（例：「生存しなかった」）の確率で割った対数として定義できることを示しているためです。

この場合、y = mx+cです（線形モデルを思い出してください）。

これをコードに変換すると、結果は次のようになります。

     double y_= (m*m_xvalues[i])+c;
     double z = log(y_)-log(1-y_); //log loss
          
     p_hat = 1.0/(MathPow(e,-z)+1);

ここでz値に対して行われたことに注意してください。式はlog(y/1-y)ですが、コードはlog(y_)-log(1-y_);として記述されています。数学の対数の法則から思い出してください。同じ基底の対数を除算すると、指数が減算されます。ご覧ください。.

これは基本的に、数式がプログラムされたときのモデルですがLogisticRegression()関数内では多くのことが行われています。次は、関数内にあるすべてです。

double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7)
 { 
 
   int arrsize = ArraySize(x); //the input array size
   double p_hat =0; //store the probability 
   
//---
  
   int train_size = (int)MathCeil(arrsize*train_size_split);
   int test_size = (int)MathFloor(arrsize*(1-train_size_split));
   
   ArrayCopy(m_xvalues,x,0,0,train_size); 
   ArrayCopy(m_yvalues,y,0,0,train_size); 
   
//---

   y_mean = mean(m_yvalues);
   x_mean = mean(m_xvalues);
   
//   Training our model in the background

   double c = y_intercept(), m = coefficient_of_X(); 


//--- Here comes the logistic regression model
      
      int TrainPredicted[];
      double sigmoid = 0;
      
      ArrayResize(TrainPredicted,train_size); //resize the array to match the train size
      Print("Training starting..., train size=",train_size);
      
      for (int i=0; i<train_size; i++)
        { 
          double y_= (m*m_xvalues[i])+c;
          double z = log(y_)-log(1-y_); //log loss
          
          p_hat = 1.0/(MathPow(e,-z)+1);
          
          double odds_ratio = p_hat/(1-p_hat); 
                    
          TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1  
          
          if (m_debug)
           PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]);
        } 
      
//--- Testing our model 
   if (train_size_split<1.0) //if there is room for testing
      {         
      
         ArrayRemove(m_xvalues,0,train_size); //clear our array
         ArrayRemove(m_yvalues,0,train_size); //clear our array from train data
   
         ArrayCopy(m_xvalues,x,0,train_size,test_size); //new values of x, starts from where the training ended
         ArrayCopy(m_yvalues,y,0,train_size,test_size);  //new values of y, starts from where the testing ended
         
         Print("start testing...., test size=",test_size);
         ArrayResize(Predicted,test_size); //resize the array to match the test size
          
         for (int i=0; i<test_size; i++)
           { 
             double y_= (m*m_xvalues[i])+c;
             double z = log(y_)-log(1-y_); //log loss
             
             p_hat = 1.0/(MathPow(e,-z)+1);
             
             double odds_ratio = p_hat/(1-p_hat); 
             
             TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1  
          
             if (m_debug)  
               PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]);  
           } 
      }

次にTestScript.mq5でモデルを訓練してテストしましょう。

    double Age[];
    Logreg.GetDatatoArray(5,Age);
    Logreg.FixMissingValues(Age); 
    
    double y_survival[];
    int Predicted[];
    Logreg.GetDatatoArray(2,y_survival);
    Logreg.LogisticRegression(Age,y_survival,Predicted);

正常なスクリプト実行の出力は次のようになります。

Training starting..., train size=624

0 Age =22.00 survival_Predicted =0

1 Age =38.00 survival_Predicted =0

... .... ....

622 Age =20.00 survival_Predicted =0

623 Age =21.00 survival_Predicted =0

start testing...., test size=267

0 Age =21.00 survival_Predicted =0

1 Age =61.00 survival_Predicted =1

.... .... ....

265 Age =26.00 survival_Predicted =0

266 Age =32.00 survival_Predicted =0

すばらしいです。モデルは機能しており、少なくともそれから結果を得ることができますが、適切な予測を行っているのでしょうか。

その精度を確認する必要があります。

混同行列

ご存知のとおり、あらゆるモデルが予測を行うことができます。モデルが乗客の生存に関するテストデータからの元の値を使用して作成した予測のCSVファイルを作成しました。ここでも、1は生存を意味し、0は生存しなかったことを意味します。。

次に、ほんの数10列があります。

	元の値	予測値
0	0	0
1	0	1
2	0	1
3	1	0
4	0	0
5	0	0
6	1	1
7	0	1
8	1	0
9	0	0

以下を使用して混同行列を計算します。

TP -真陽性
TN - 真陰性
FP -偽陽性
FN - 偽陰性

さて、これらの値は何でしょうか。

TP（True Positive）

元の値がPositive(1)であり、モデルもPositive(1)を予測する場合です。

TN( True Negative )

元の値がNegative（0）であり、モデルもNegative（0）を予測する場合です。

FP( False Positive )

元の値がNegative（0）であるが、モデルがNegative（1）を予測している場合です。

FN（False Negative）

元の値がPositive（1）であるが、モデルがNegative（0）を予測している場合です。

値がわかったので、例として上記のサンプルの混同行列を計算しましょう。

	元の値	予測値	TP/TN/FP/FN
0	0	0	TN
1	0	1	FP
2	0	1	FP
3	1	0	FN
4	0	0	TN
5	0	0	TN
6	1	1	TP
7	0	1	FP
8	1	0	FN
9	0	0	TN

混同行列は、この式を使用してモデルの精度を計算するために使用できます。

テーブルから：

TN = 4
TP = 1
FN = 2
FP = 3

精度 = 1 + 5 / 4 + 1 + 2 + 3

精度 = 0.5

この場合、精度は50%です。（0.5 * 100％をパーセンテージに変換）

これで、1X1混同行列がどのように機能するかを理解できたので、次にそれをコードに変換し、データセット全体でモデルの精度を分析します。

void CLogisticRegression::ConfusionMatrix(double &y[], int &Predicted_y[], double& accuracy)
 {
    int TP=0, TN=0,  FP=0, FN=0; 
    
    for (int i=0; i<ArraySize(y); i++)
       {
         if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==1)
            TP++;
         if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==0)
            TN++;
         if (Predicted_y[i]==1 && (int)y[i]==0)
            FP++;
         if (Predicted_y[i]==0 && (int)y[i]==1)
            FN++;
       }
     Print("Confusion Matrix \n ","[ ",TN,"  ",FP," ]","\n","  [  ",FN,"  ",TP,"  ] ");
     accuracy = (double)(TN+TP) / (double)(TP+TN+FP+FN);
 }

ここで、LogisticRegression()として知られるクラスのメイン関数に戻りましょう。今回は、モデルの精度を返すdouble関数に変換します。また、Print() メソッドの数を減らします。クラスをデバッグする場合を除いて、毎回値を出力したくないので、それらをifステートメントに追加します。すべての変更は青色で強調表示されています。

double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7)
 { 
 
   double accuracy =0; //Accuracy of our Train/Testmodel
   int arrsize = ArraySize(x); //the input array size
   double p_hat =0; //store the probability 
   
//---
  
   int train_size = (int)MathCeil(arrsize*train_size_split);
   int test_size = (int)MathFloor(arrsize*(1-train_size_split));
   
   ArrayCopy(m_xvalues,x,0,0,train_size); 
   ArrayCopy(m_yvalues,y,0,0,train_size); 
   
//---

   y_mean = mean(m_yvalues);
   x_mean = mean(m_xvalues);
   
//   Training our model in the background

   double c = y_intercept(), m = coefficient_of_X(); 


//--- Here comes the logistic regression model
      
      int TrainPredicted[];
      double sigmoid = 0;
      
      ArrayResize(TrainPredicted,train_size); //resize the array to match the train size
      Print("Training starting..., train size=",train_size);
      
      for (int i=0; i<train_size; i++)
        { 
          double y_= (m*m_xvalues[i])+c;
          double z = log(y_)-log(1-y_); //log loss
          
          p_hat = 1.0/(MathPow(e,-z)+1);
                              
          TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1  
          
          if (m_debug)
           PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]);
        }
      ConfusionMatrix(m_yvalues,TrainPredicted,accuracy); //be careful not to confuse the train predict values arrays
      printf("Train Model Accuracy =%.5f",accuracy);
      
//--- Testing our model 
   if (train_size_split<1.0) //if there is room for testing
      {         
      
         ArrayRemove(m_xvalues,0,train_size); //clear our array
         ArrayRemove(m_yvalues,0,train_size); //clear our array from train data
   
         ArrayCopy(m_xvalues,x,0,train_size,test_size); //new values of x, starts from where the training ended
         ArrayCopy(m_yvalues,y,0,train_size,test_size);  //new values of y, starts from where the testing ended
         
         Print("start testing...., test size=",test_size);
         ArrayResize(Predicted,test_size); //resize the array to match the test size
          
         for (int i=0; i<test_size; i++)
           { 
             double y_= (m*m_xvalues[i])+c;
             double z = log(y_)-log(1-y_); //log loss
             
             p_hat = 1.0/(MathPow(e,-z)+1);
                          
             TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1  
          
             if (m_debug)  
               PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]);  
           }
        ConfusionMatrix(m_yvalues,Predicted,accuracy);
        printf("Testing Model Accuracy =%.5f",accuracy);
      } 
      
    return (accuracy); //Lastly, the testing Accuracy will be returned
 }

スクリプトを正常に実行すると、次のように出力されます。

Training starting..., train size=624

Confusion Matrix

[378 0]

[ 246 0 ]

Train Model Accuracy =0.60577

start testing...., test size=267

Confusion Matrix

[171 0]

[ 96 0 ]

Testing Model Accuracy =0.64045

やりました。モデルがどれだけ優れているかを数値で特定できるようになりましたが、テストデータでの64.045％の精度は （私の意見では） 予測をおこなう際にモデルを使用するには十分ではありません。少なくとも現時点ではロジスティック回帰を使用してデータを分類するのに役立つライブラリがあります。

さらに、主な関数を説明します。

double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7)

入力train_size_split は、データを訓練とテストに分割するためのものです。デフォルトでは、分割は0.7です。つまり、データの70％パーセントが訓練用で残りの30％がテスト用であり、Predicted[]参照配列がテストの予測データを返します。

バイナリクロスエントロピー（別名、損失関数）

平均二乗誤差が線形回帰の誤差関数であるのと同様に、バイナリクロスエントロピーはロジスティック回帰のコスト関数です。

理論

ロジスティック回帰の2つの使用例、つまり実際の出力が0と1の場合にどのように機能するかを見てみましょう。

01:実際の出力値が1の場合

2つの入力サンプルp1=0.4およびp2=0.6のモデルを考えます。p2はp1と比較して1から遠く離れているため、p1はp2よりもペナルティが高くなると予想されます。

数学的な観点から、小さな数の負の対数は大きな数であり、その逆も同様です。

入力にペナルティを課すには、次の式を使用します。

penalty = -log(p)

これらの2つの場合

Penalty = -log(0.4)=0.4、つまり、p1のペナルティは0.4です。
Penalty = -log(0.6)=0.2、つまり、p2のペナルティは0.2です。

02:実際の出力値が0の場合

2つの入力サンプルp1=0.4とp2=0.6のモデル出力を考えます（前の場合と同じ）。 p2は0から遠く離れているため、p1よりもペナルティが高くなると予想されますが、ロジスティックモデルの出力はサンプルが正である確率であることに注意してください。入力確率にペナルティを課すには、次の確率を見つける必要があります。サンプルが負である場合、これは簡単です。

サンプルが負である確率 = 1-サンプルが正である確率

したがって、この場合のペナルティを見つけるには、ペナルティの式は次のようになります。

penalty = -log(1-p)

これらの2つの場合

penalty = -log(1-p) = -log(1-0.4) =0.2、つまり、ペナルティは0.2です。
penalty = -log(1-p) = -log(1-0.6) =0.4、つまり、ペナルティは0.4です。

素晴らしいことに、p2のペナルティはp1よりも大きいです（期待どおりに機能します）。

ここで、モデル出力がpで、真の出力値がyである単一の入力サンプルのペナルティは、次のように計算できます。

if入力サンプルが正y=1:

penalty = -log(p)

else:

penalty = -log(1-p)

上記のif-elseブロックステートメントと同等の1行の方程式は、次のように記述できます。

penalty = -( y*log(p) + (1-y)*log(1-p) )

ここで

y = データセットの実際の値

p = モデルの生の予測確率（丸め前）

この方程式が上記のif-elseステートメントと同等であることを証明しましょう。

01：出力値y=1の場合

penalty = -( 1*log(p) + (1-1)*log(1-p) ) = -log(p)、したがって、証明済み

02：出力値y=0の場合

penalty = -( 0*log(p) + (1-0)* log(1-p) ) = log(1-p)、したがって、証明済み

最後に、N個の入力サンプルの対数損失関数は次のようになります。

対数損失は、予測確率が対応する実際の値/真の値（2項分類の場合は0または1）にどれだけ近いかを示します。予測された確率が実際の値から逸脱するほど、対数損失値は高くなります。

log-lossや他の多くのコスト関数は、モデルがどれだけ優れているかを示す指標として使用できますが、最大の用途は、最急降下法またはその他の最適化アルゴリズムを使用してモデルを最適化する場合です（連載で後に説明します）。

測定することができれば、改善することができます。それがコスト関数の主な目的です。

テストと訓練のデータセットから、対数損失は0.64〜0.68の間にあるように見えますが、これは理想的ではありません（大まかに言えば）。

訓練データセット

Logloss = 0.6858006105398738

テストデータセット

Logloss = 0.6599503403665642

これが、log-loss関数をコードに変換する方法です。

double CLogisticRegression::LogLoss(double &rawpredicted[])
 { 
   double log_loss =0;
   double penalty=0;
   for (int i=0; i<ArraySize(rawpredicted); i++ )
      {   
        penalty += -((m_yvalues[i]*log(rawpredicted[i])) + (1-m_yvalues[i]) * log(1-rawpredicted[i])); //sum all the penalties
         
         if (m_debug)
            printf("penalty =%.5f",penalty); 
      }
    log_loss = penalty/ArraySize(rawpredicted); //all the penalties divided by their total number
    Print("Logloss =",log_loss);
    
    return(log_loss);
 }

生の予測出力を取得するには、ループのメインのテストと訓練に戻り、確率を四捨五入するプロセスの直前にデータを生の予測配列に格納する必要があります。

複数の動的ロジスティック回帰の課題

この記事と前の記事の両方で線形回帰ライブラリとロジスティック回帰ライブラリの両方を構築するときに直面した最大の課題は、追加されるすべてのデータをハードコーディングすることなく、複数のデータ列に使用できる複数の動的回帰関数です。モデルでは、前の記事で同じ名前の2つの関数をハードコーディングしましたが、それらの唯一の違いは、各モデルが処理できるデータの数でした。一方は2つの独立変数を処理でき、もう一方はそれぞれ4つを処理できました。

void   MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); 
void   MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]);

しかし、この方法は不便であり、コーディングの時期尚早のように感じられ、クリーンなコードとDRYのルールに違反します（OOPが達成しようとしている原則を繰り返さないでください）。

*argsおよび**kwargsの助けを借りて多数の関数引数を取ることができる柔軟な関数を備えたPythonとは異なり、MQL5ではこれは私が知っている限り文字列のみを使用して実現できます。これが私たちの出発点だと思います。

void CMultipleLogisticRegression::MLRInit(string x_columns="3,4,5,6,7,8")

入力x_columnsは、ライブラリで使用するすべての独立変数列を表します。これらの列では、列ごとに複数の独立した配列が必要になりますが、配列を動的に作成する方法がないため、配列の使用は失敗します。

複数の CSV ファイルを動的に作成し、それらを配列として使用することはできますが、コンピューターリソースの使用に関しては、配列の使用と比較して、プログラムのコストが高くなります。これは、ファイルを開くために頻繁に使用する while ループは言うまでもなく、複数のデータを処理する場合に特に当てはまります。100% 確信があるわけではないので、間違っている場合は訂正してください。

上記の方法を使用することはできます。

配列を使用する方法を発見しました。すべての列のすべてのデータを1つの配列に格納してから、その単一の配列とは別にデータを使用します。

   int start = 0;
   if (m_debug) //if we are on debug mode print Each Array vs its row
      for (int i=0; i<x_columns_total; i++)
         {
            ArrayCopy(EachXDataArray,m_AllDataArray,0,start,rows_total);
            start += rows_total; 
            
            Print("Array Number =",i," From column number ",m_XColsArray[i]);
            ArrayPrint(EachXDataArray);     
         }

forループ内では、配列内のデータを操作し、すべての列に対して必要な方法でモデルのすべての計算を実行できます。この方法を試しましたが、まだ成功していません。この仮説を説明した理由は、この記事を読んでいるすべての人にこの課題を理解してもらうことです。この複数の動的ロジスティック回帰関数をコーディングする方法についてコメントセクションでご意見をお寄せください。このライブラリを作成するための私の完全な試みはhttps://www.mql5.com/ja/code/38894にあります。

この試みは成功していませんが、希望があり、共有する価値があると思います。

ロジスティック回帰の利点

機能空間でのクラスの分布については想定していないない
複数のクラスに簡単に拡張（多項回帰）
クラス予測の自然な確率論的ビュー
すぐに訓練できる
未知のレコードの分類が非常に高速
多くの単純なデータセットの精度が高い
過剰適合に強い
モデル係数を特徴の重要性の指標として解釈できる

欠点

線形境界を構築する

最後に

この記事はこれですべてです。ロジスティック回帰は、メールをスパムまたはスパムではないとして分類する、手書きを検出するなど、実際のさまざまな分野で使用されています。

特にMetaTrader 5プラットフォームでは、ロジスティック回帰アルゴリズムを使用してタイタニックデータや上記のフィールドを分類するつもりはないことはわかっています。前述のように、データセットはここにリンクされているPythonで達成された出力と比べてライブラリを構築するためだけに使用されました。。次の記事では、ロジスティックモデルを使用して株式市場の暴落を予測する方法を見ていきます。

この記事が長くなりすぎたので、重回帰タスクをすべての読者に宿題として任せます。

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/10626

添付されたファイル |

ZIPをダウンロード

TestScript.mq5 (1.69 KB)

LogisticRegressionLib.mqh (17.79 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。