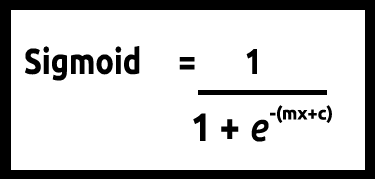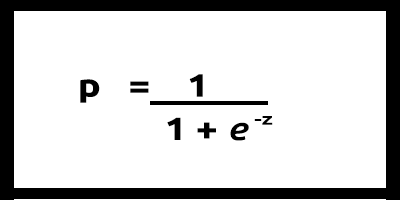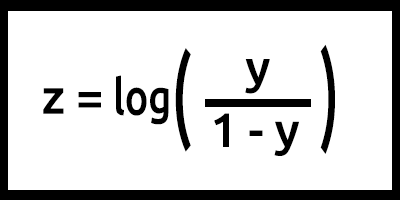
데이터 과학 및 기계 학습(파트 02): 로지스틱 회귀
01부에서 논의한 선형 회귀와 달리 로지스틱 회귀는 선형 회귀를 기반으로 하는 분류 방법입니다.
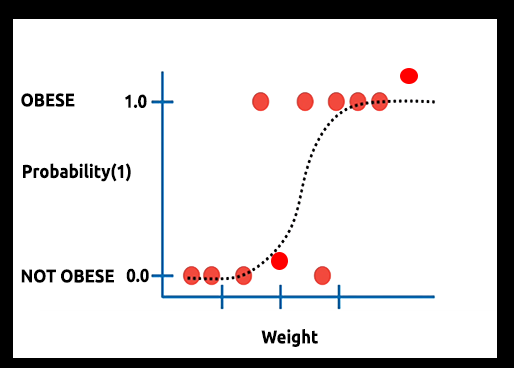
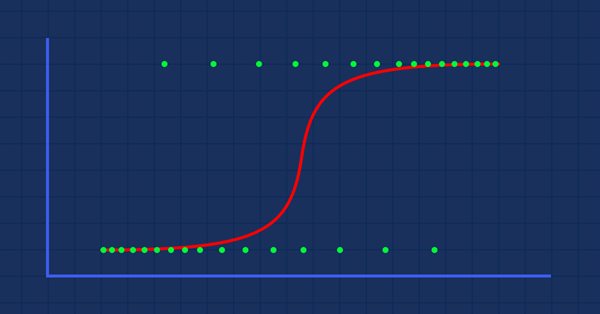
이론: 몸무게에 대해 비만이 될 확률의 그래프를 그린다고 가정해 보겠습니다.
이 경우 선형 모델을 사용할 수 없으며 다른 테크닉을 사용하여 이 선을 S자형으로 알려진 S 곡선으로 변환할 것입니다.
로지스틱 회귀는 범주 종속 변수의 결과를 예측하는 데 사용되는 이진 형식으로 결과를 생성하므로 결과는 다음과 같이 이산/범주여야 합니다:
- 0 또는 1
- 예 또는 아니오
- 참 또는 거짓
- 높음 또는 낮음
- 구매 또는 판매
우리가 만들 라이브러리에서는 다른 이산 값은 무시할 것입니다. 우리는 바이너리 전용(0,1)에 촛점을 맞출 것입니다.
y 값은 0과 1 사이에 있어야 할 것이므로 선은 0과 1에서 잘려야 합니다. 이는 다음 공식을 통해 얻을 수 있습니다:
그러면 다음과 같은 그래프를 얻게 될 것입니다
선형 모델은 로지스틱 함수(sigmoid/p) =1/1+e^t로 전달됩니다. 여기서 t는 0과 1 사이의 값인 선형 모델 결과입니다. 이것은 클래스에 속하는 데이터 포인트의 확률을 나타냅니다.
선형 모델의 y를 종속으로 사용하는 대신 해당 기능은 " p"로 표시되며 종속으로 사용됩니다.
p = 1/1+e^-(c+m1x1+m2x2+....+mnxn) , 여러 값의 경우
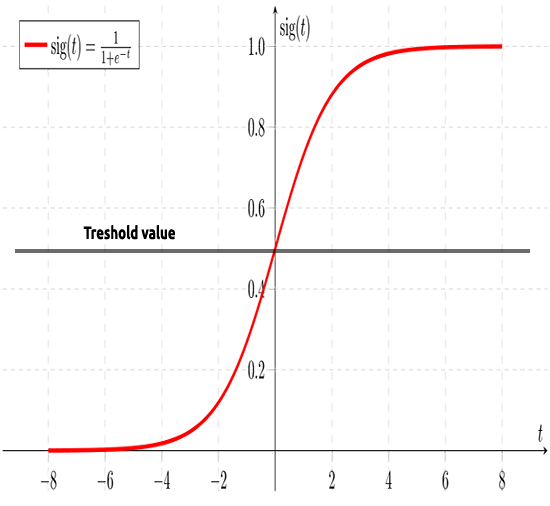
앞서 말했듯이 시그모이드 곡선은 무한대 값을 이진 형식의 출력(0 또는 1)으로 변환하는 것을 목표로 합니다. 그러나 0.8에 데이터 포인트가 있는 경우 값이 0인지 1인지 어떻게 결정할 수 있을까요? 이 부분이 임계값이 작용할 부분입니다.
임계값은 이기거나 지는 확률을 나타내며 0.5(0과 1의 중심)에 있습니다.
0.5보다 크거나 같은 값은 1로 반올림되어 승자로 간주되는 반면 0.5 미만의 값은 0으로 반올림되어 이 시점에서 패자로 간주됩니다. 이제 선형과 로지스틱회귀의 차이입니다.
선형 대 로지스틱 회귀
| 선형 | 로지스틱 회귀 |
|---|---|
| 연속변수 | 범주형 변수 |
| 회귀 문제 해결 | 분류 문제 해결 |
| 모델에는 직선 방정식이 있습니다. | 모델에는 로지스틱 방정식이 있습니다. |
코딩 부분과 데이터 분류 알고리즘 부분에 대해 알아보기 전에 몇 가지 단계를 통하면 데이터를 이해하고 모델을 더 쉽게 구축하는 법을 알 수 있습니다.
- 데이터 수집 및 분석
- 데이터 정리
- 정확도 확인
01: 데이터 수집 및 분석
이 섹션에서는 데이터를 시각화하기 위해 상당량의 파이썬 코드를 작성할 것입니다. 그럼 Jupyter 노트북에서 데이터를 추출하고 시각화하는 데 사용할 라이브러리를 가져오는 것부터 시작하겠습니다.
도서관 건립을 위해 타이타닉 데이터를 사용하겠습니다. 데이터는 1912년 4월 15일 북대서양에서 빙산과 충돌하여 침몰한 타이타닉 선박 사고에 대한 데이터입니다, Wikipedia. 모든 파이썬 코드와 데이터 세트는 기사 끝에 링크된 저의 GitHub에서 찾을 수 있습니다.
데이터 시각화 라이브러리 가져오기
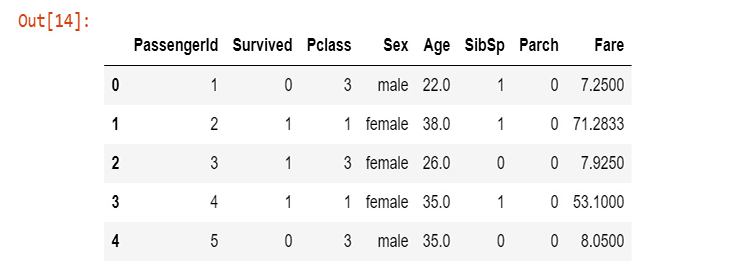
열은 다음을 나타냅니다.
생존 - 생존(0 = 아니오, 1 = 예)
클래스 - 승객 클래스(1 = 1등급, 2 = 2등급, 3 = 3등급)
이름 - 이름
성별 - 성별
나이 - 나이
sibsp - 탑승한 형제/배우자의 수
parch - 탑승한 부모/자녀 수
티켓 - 티켓 번호
운임 - 여객 운임
cabin - Cabin
embarked - 승선항(C = Cherbourg, Q = Queenstown, S = Southampton)
이제 데이터를 수집하고 변수 titanic_data에 저장했으므로 생존 열부터 시작하여 열 데이터의 시각화를 시작하겠습니다.
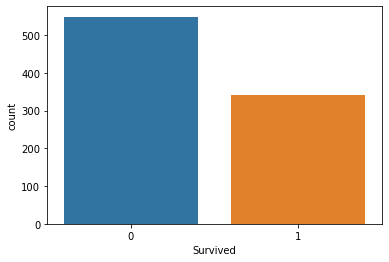
sns.countplot(x="Survived", data = titanic_data)
출력
이것은 소수의 승객이 사고에서 살아남았다는 것을 말해줍니다. 배에 타고 있던 승객의 약 절반이 사고에서 살아남았습니다.
성별에 따른 생존자의 수를 시각화해 봅시다
sns.countplot(x='Survived', hue='Sex', data=titanic_data)
성별에 따른 따른 타이타닉 생존
이유를 모르겠지만 그날 여성은 남성보다 2배 이상 생존했습니다.
성별에 따른 생존자의 수를 시각화해 보겠습니다.
sns.countplot(x='Survived', hue='Pclass', data=titanic_data)
성별에 따른 따른 타이타닉 생존
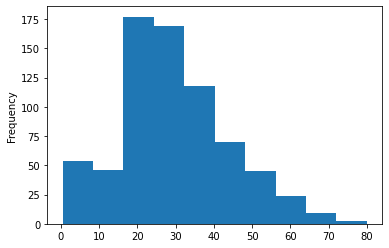
배에 탑승한 승객 연령 그룹의 히스토그램을 나타내 보겠습니다. 여기서는Count-plots를 사용하여 데이터를 시각화할 수 없습니다. 왜냐하면 여러 다른 데이터 세트의 연령 값이 정리되지 않았기 때문입니다.
titanic_data['Age'].plot.hist()출력:
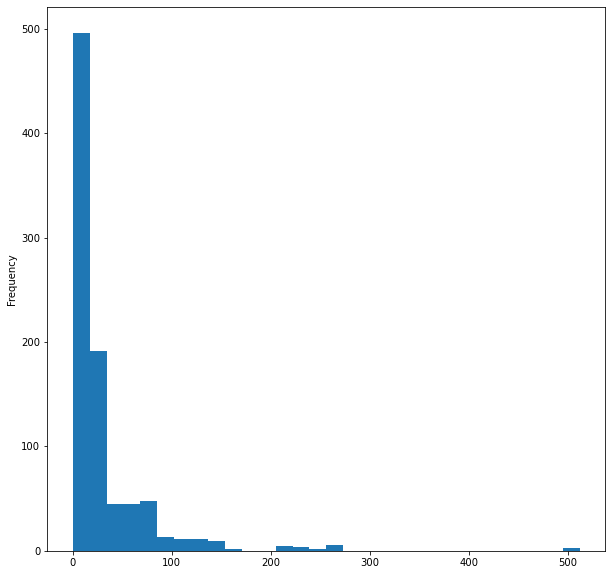
마지막으로 배의 운임의 히스토그램을 시각화해 봅시다.
titanic_data['Fare'].plot.hist(bins=30, figsize=(10,10))
12개의 열 중 5개의 열만 시각화했지만 중요한 열이라고 생각해 시각화 한 것입니다. 이제 데이터를 정리하겠습니다.
02: 데이터 정리
여기서 우리는 데이터 세트에서 불필요한 열을 피해 제거하면서 NaN(누락) 값을 제거하여 데이터를 정리합니다.
로지스틱 회귀를 사용하면 double 및 integer 값이 필요하므로 의미 없는 문자열 값을 피해야 합니다. 다음 열은 무시합니다:
- 이름 열(의미 있는 정보가 없음)
- 티켓 칼럼(사고에 따른 생존과 관련 없음)
- Cabin 열(없는 값이 너무 많으며 처음 5개 행에서도 표시됨)
- 승선(저는 이것도 관련이 없다고 생각합니다)
그렇게 하려면WPS office에서 CSV 파일을 열고 열을 수동으로 제거합니다. 여러분은 여러분이 원하는 스프레드시트 프로그램을 사용해도 됩니다.
스프레드시트를 사용하여 열을 제거한 후 새 데이터를 시각화해 보겠습니다.
new_data = pd.read_csv(r'C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\titanic.csv') new_data.head(5)
출력:
성별 열에 문자열 값이 있고 나이 열에 여전히 누락된 값이 있기는 하나 이제 데이터를 정리했습니다. 코드를 통해 문제를 해결해 보겠습니다. 남성과 여성 문자열을 각각 0과 1로 변환하는 label encoder를 만들어 보겠습니다.
void CLogisticRegression::LabelEncoder(string &src[],int &EncodeTo[],string members="male,female") { string MembersArray[]; ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(members,separator,MembersArray); //convert members list to an array ArrayResize(EncodeTo,ArraySize(src)); //make the EncodeTo array same size as the source array int binary=0; for(int i=0;i<ArraySize(MembersArray);i++) // loop the members array { string val = MembersArray[i]; binary = i; //binary to assign to a member int label_counter = 0; for (int j=0; j<ArraySize(src); j++) { string source_val = src[j]; if (val == source_val) { EncodeTo[j] = binary; label_counter++; } } Print(MembersArray[binary]," total =",label_counter," Encoded To = ",binary); } }
src[]라는 이름의 소스 배열을 얻으려면 CSV 파일의 특정 열에서 데이터를 가져오는 함수를 프로그래밍한 다음 이를 문자열 값 MembersArray[]배열에 넣습니다.
void CLogisticRegression::GetDatatoArray(int from_column_number, string &toArr[]) { int handle = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI,m_delimiter); int counter=0; if (handle == INVALID_HANDLE) Print(__FUNCTION__," Invalid csv handle err=",GetLastError()); else { int column = 0, rows=0; while (!FileIsEnding(handle)) { string data = FileReadString(handle); column++; //--- if (column==from_column_number) //if column in the loop is the same as the desired column { if (rows>=1) //Avoid the first column which contains the column's header { counter++; ArrayResize(toArr,counter); toArr[counter-1]=data; } } //--- if (FileIsLineEnding(handle)) { rows++; column=0; } } } FileClose(handle); }
testscript.mq5 내부에서 함수를 올바르게 호출하고 라이브러리를 초기화하는 방법은 다음과 같습니다.
#include "LogisticRegressionLib.mqh"; CLogisticRegression Logreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- Logreg.Init("titanic.csv",","); string Sex[]; int SexEncoded[]; Logreg.GetDatatoArray(4,Sex); Logreg.LabelEncoder(Sex,SexEncoded,"male,female"); ArrayPrint(SexEncoded); }
스크립트를 성공적으로 실행한 후 프린트 된 출력
남성 총 = 577 인코딩 됨 = 0
남성 총 = 314 인코딩 됨 = 1
[ 0] 0 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 0 1 0 1 1 0 0 1 0 0 1 1 0 0 0 0 0 1 1 1 1 0 0 1 1 0 1 0 1 0 0 1 1 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0
[ 75] 0 0 0 0 1 0 0 1 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 1 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 1 1 0 0 1 0 0 0 1 1 1 0 0 0 0 1 0 0
... ... ... ...
... ... ... ...
[750] 1 0 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 1 1 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 1 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0
[825] 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 0 0 0 1 1 0 1 1 0 0 0 0 1 0 0 1 1 0 0 0 1 1 0 1 0 0 1 0 1 1 0 0
값을 인코딩하기 전에 함수 인수의 Members="male,female"에 주의를 기울기 바랍니다. 문자열에 나타나는 첫 번째 값은 0으로 인코딩 됩니다. 남성 열은 첫번째로 나타나므로 모든 남성은 0으로 모든 여성은 1로 인코딩됩니다. 이 기능은 두 값에 제한되지 않지만 문자열이 데이터에 의미가 있는 한 원하는 만큼 인코딩할 수 있습니다.
누락값
연령 열에 주의를 기울이면 누락된 값이 있음을 알 수 있을 것입니다. 누락된 값은 주로 한 가지 이유 때문일 수 있습니다... 사망 입니다. 우리가 가진 데이터 세트에서 개인의 연령을 식별하는 것이 불가능합니다. 데이터를 시각화하기 위해 pandas를 사용하고 있기 때문에 특히 큰 데이터 세트에서 시간이 많이 소요될 수 있는 데이터 세트를 살펴봄으로써 이러한 격차를 없애고 모든 열에서 누락된 행을 찾아보겠습니다.
titanic_data.isnull().sum()
출력은 다음과 같을 것입니다:
PassengerId 0
Survived 0
Pclass 0
Sex 0
Age 177
SibSp 0
Parch 0
Fare 0
dtype: int64
연령 열의 891개 행 중 177개 행에 누락값(NAN)이 있습니다.
이제 열의 누락된 값을 모든 값의 평균으로 바꿀 것입니다.
void CLogisticRegression::FixMissingValues(double &Arr[]) { int counter=0; double mean=0, total=0; for (int i=0; i<ArraySize(Arr); i++) //first step is to find the mean of the non zero values { if (Arr[i]!=0) { counter++; total += Arr[i]; } } mean = total/counter; //all the values divided by their total number Print("mean ",MathRound(mean)," before Arr"); ArrayPrint(Arr); for (int i=0; i<ArraySize(Arr); i++) { if (Arr[i]==0) { Arr[i] = MathRound(mean); //replace zero values in array } } Print("After Arr"); ArrayPrint(Arr); }
이 함수는 0이 아닌 모든 값의 평균을 찾은 다음 배열의 모든 0의 값을 평균 값으로 대체합니다.
함수를 성공적으로 실행한 후의 출력을 해 보면 볼 수 있듯이 모든 0 값은 타이타닉에 탑승한 승객의 평균 연령인30.0으로 대체되었습니다.
Arr 전 mean 30.0
[ 0] 22.0 38.0 26.0 35.0 35.0 0.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 0.0 31.0 0.0 35.0 34.0 15.0 28.0 8.0 38.0 0.0 19.0 0.0 0.0
… … … … … … … … …
[840] 20.0 16.0 30.0 34.5 17.0 42.0 0.0 35.0 28.0 0.0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 0.0 41.0 21.0 48.0 0.0 24.0 42.0 27.0 31.0 0.0 4.0
[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 0.0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 0.0 26.0 32.0
arr 이후
[ 0] 22.0 38.0 26.0 35.0 35.0 30.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 30.0 31.0 30.0 35.0 34.0 15.0 28.0 8.0 38.0 30.0 19.0 30.0 30.0
… … … … … … … … …
[840] 20.0 16.0 30.0 34.5 17.0 42.0 30.0 35.0 28.0 30.0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 30.0 41.0 21.0 48.0 30.0 24.0 42.0 27.0 31.0 30.0 4.0
[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 30.0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 30.0 26.0 32.0
로지스틱 회귀 모델 만들기
먼저 하나의 독립 변수와 하나의 종속 변수가 있는 로지스틱 회귀를 만들어 보겠습니다. 그런 다음 나중에 문제에 대한 전체 솔루션 모델로 확장할 것입니다.
생존 대 나이 두 변수에 대한 모델을 구축해 보겠습니다. 나이를 기준으로 한 사람이 생존할 수 있는 가능성이 어떠한지 알아보겠습니다.
우리는 로지스틱 모델 내부 깊숙이 선형 모델이 있다는 것을 알게 되었습니다. 선형 모델을 가능하게 하는 함수를 코딩하는 것으로부터 시작하겠습니다.
Coefficient_of_X()및y_intercept() 이 함수는 새로운 것이 아닙니다. 이 시리즈의 첫 번째 기사를 기반으로 작성했습니다. 이러한 함수와 선형 회귀에 대한 자세한 내용은 이 기사를 읽어보십시오.
double CLogisticRegression::y_intercept() { // c = y - mx return (y_mean-coefficient_of_X()*x_mean); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CLogisticRegression::coefficient_of_X() { double m=0; //--- { double x__x=0, y__y=0; double numerator=0, denominator=0; for (int i=0; i<ArraySize(m_xvalues); i++) { x__x = m_xvalues[i] - x_mean; //right side of the numerator (x-side) y__y = m_yvalues[i] - y_mean; //left side of the numerator (y-side) numerator += x__x * y__y; //summation of the product two sides of the numerator denominator += MathPow(x__x,2); } m = numerator/denominator; } return (m); }
이제 공식에서 로지스틱 모델을 프로그래밍해 보겠습니다.
z는 로그 확률이라고도 합니다. 시그모이드의 역함수는 z가 1레이블(예: "생존")의 확률을0레이블(예: "살아남지 않음")의 확률로 나눈 로그로 정의될 수 있다고 명시하기 때문입니다.
이 경우 y = mx+c(선형 모델에서 기억하실 겁니다).
이것을 코드로 바꾸면 결과는,
double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1);
여기서 z값에 대해 수행된 작업에 주의하십시오. 공식은log(y/1-y) 이지만 코드는log(y_)-log(1-y_)로 작성됩니다. 수학의 로그 법칙을 기억하세요!! 지수의 뺄셈과 동일한 기본 결과의 로그 나누기, 읽어보기.
기본적으로 이것은 공식이 프로그래밍될 때 우리의 모델이지만 LogisticRegression() 함수 내부에서 많은 일이 일어나고 있습니다. 함수 내부에 있는 모든 것은 다음과 같습니다.
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7) { int arrsize = ArraySize(x); //the input array size double p_hat =0; //store the probability //--- int train_size = (int)MathCeil(arrsize*train_size_split); int test_size = (int)MathFloor(arrsize*(1-train_size_split)); ArrayCopy(m_xvalues,x,0,0,train_size); ArrayCopy(m_yvalues,y,0,0,train_size); //--- y_mean = mean(m_yvalues); x_mean = mean(m_xvalues); // Training our model in the background double c = y_intercept(), m = coefficient_of_X(); //--- Here comes the logistic regression model int TrainPredicted[]; double sigmoid = 0; ArrayResize(TrainPredicted,train_size); //resize the array to match the train size Print("Training starting..., train size=",train_size); for (int i=0; i<train_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); double odds_ratio = p_hat/(1-p_hat); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]); } //--- Testing our model if (train_size_split<1.0) //if there is room for testing { ArrayRemove(m_xvalues,0,train_size); //clear our array ArrayRemove(m_yvalues,0,train_size); //clear our array from train data ArrayCopy(m_xvalues,x,0,train_size,test_size); //new values of x, starts from where the training ended ArrayCopy(m_yvalues,y,0,train_size,test_size); //new values of y, starts from where the testing ended Print("start testing...., test size=",test_size); ArrayResize(Predicted,test_size); //resize the array to match the test size for (int i=0; i<test_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); double odds_ratio = p_hat/(1-p_hat); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]); } }
이제 TestScript.mq5에서 모델을 훈련하고 테스트해 보겠습니다.
double Age[]; Logreg.GetDatatoArray(5,Age); Logreg.FixMissingValues(Age); double y_survival[]; int Predicted[]; Logreg.GetDatatoArray(2,y_survival); Logreg.LogisticRegression(Age,y_survival,Predicted);
스크립트 실행이 성공적이면 출력은 다음과 같습니다:
훈련 시작 중..., 훈련 크기=624
0 나이 =22.00 생존_예측 =0
1 나이 =38.00 생존_예측 =0
... .... ....
622 나이 =20.00 생존_예측 =0
623 나이 =21.00 생존_예측 =0
테스트 시작...., 테스트 크기=267
0 나이 =21.00 생존_예측 =0
1 나이 =61.00 생존_예측 =1
.... .... ....
265 나이 =26.00 생존_예측 =0
266 나이 =32.00 생존_예측 =0
좋습니다. 우리의 모델은 이제 작동하고 있으며 모델로부터 결과를 얻을 수는 있지만 모델은 좋은 예측을 하고 있을까요?
정확성을 확인해야 합니다.
혼동 행렬(Confusion Matrix)
우리 모두 알고 있듯이 좋은 모델이던 나쁜 모델이던 예측을 할 수 있습니다. 저는 우리의 모델이 승객의 생존에 대한 테스트 데이터의 원래 값을 편향되게 한 예측에 대해 CSV 파일을 만들었습니다. 1은 생존을 의미하고 0은 그렇지 않음을 의미합니다.
다음은 10개 열입니다:
| 원래 | 예측 | |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 2 | 0 | 1 |
| 3 | 1 | 0 |
| 4 | 0 | 0 |
| 5 | 0 | 0 |
| 6 | 1 | 1 |
| 7 | 0 | 1 |
| 8 | 1 | 0 |
| 9 | 0 | 0 |
다음을 사용하여 혼동 행렬을 계산합니다:
- TP - True Positive
- TN - True Negative
- FP - False Positive
- FN - False Negative
이 값들은 무엇일까요?
TP(True Positive)
원래 값이 양수(1)이고 모델도 양수(1)를 예측하는 경우입니다.
TN(True Negative)
원래 값이 음수(0)이고 모델도 음수(0)를 예측하는 경우입니다.
FP(False Positive)
원래 값이 음수(0)이지만 모델이 양수(1)를 예측하는 경우입니다.
FN(False Negative)
원래 값이 양수(1)이지만 모델이 음수(0)를 예측하는 경우입니다.
이제 값에 대해 알았으므로 위의 샘플에 대한 혼동 행렬을 예제로 계산해 보겠습니다.
| 원래 | 예측 | TP/TN/FP/FN | |
|---|---|---|---|
| 0 | 0 | 0 | TN |
| 1 | 0 | 1 | FP |
| 2 | 0 | 1 | FP |
| 3 | 1 | 0 | FN |
| 4 | 0 | 0 | TN |
| 5 | 0 | 0 | TN |
| 6 | 1 | 1 | TP |
| 7 | 0 | 1 | FP |
| 8 | 1 | 0 | FN |
| 9 | 0 | 0 | TN |
혼동 행렬은 이 공식을 사용하여 모델의 정확도를 계산하는 데 사용할 수 있습니다.
우리 테이블에서:
- TN = 4
- TP = 1
- FN = 2
- FP = 3
정확도 = 1 + 5 / 4 + 1 + 2 + 3
정확도 = 0.5
이 경우 정확도는 50%입니다. (0.5*100%를 백분율로 변환)
이제 1X1 혼동 행렬이 작동하는 방식을 알게 되었을 것입니다. 이제 코드로 변환하고 전체 데이터 세트에서 모델의 정확도를 분석할 시간입니다.
void CLogisticRegression::ConfusionMatrix(double &y[], int &Predicted_y[], double& accuracy) { int TP=0, TN=0, FP=0, FN=0; for (int i=0; i<ArraySize(y); i++) { if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==1) TP++; if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==0) TN++; if (Predicted_y[i]==1 && (int)y[i]==0) FP++; if (Predicted_y[i]==0 && (int)y[i]==1) FN++; } Print("Confusion Matrix \n ","[ ",TN," ",FP," ]","\n"," [ ",FN," ",TP," ] "); accuracy = (double)(TN+TP) / (double)(TP+TN+FP+FN); }
LogisticRegression()으로 알려진 클래스의 Main Function으로 돌아가서 이번에는 모델의 정확도를 반환하는 이중 함수로 변환하고Print()메서드의 수도 줄일 것입니다. 그러나 이들을 if 문에 추가하십시오. 클래스를 디버그하고 싶지 않다면 매번 값을 인쇄하고 싶지 않을 것이기 때문입니다. 모든 변경 사항은 파란색으로 강조 표시됩니다:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7) { double accuracy =0; //Accuracy of our Train/Testmodel int arrsize = ArraySize(x); //the input array size double p_hat =0; //store the probability //--- int train_size = (int)MathCeil(arrsize*train_size_split); int test_size = (int)MathFloor(arrsize*(1-train_size_split)); ArrayCopy(m_xvalues,x,0,0,train_size); ArrayCopy(m_yvalues,y,0,0,train_size); //--- y_mean = mean(m_yvalues); x_mean = mean(m_xvalues); // Training our model in the background double c = y_intercept(), m = coefficient_of_X(); //--- Here comes the logistic regression model int TrainPredicted[]; double sigmoid = 0; ArrayResize(TrainPredicted,train_size); //resize the array to match the train size Print("Training starting..., train size=",train_size); for (int i=0; i<train_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]); } ConfusionMatrix(m_yvalues,TrainPredicted,accuracy); //be careful not to confuse the train predict values arrays printf("Train Model Accuracy =%.5f",accuracy); //--- Testing our model if (train_size_split<1.0) //if there is room for testing { ArrayRemove(m_xvalues,0,train_size); //clear our array ArrayRemove(m_yvalues,0,train_size); //clear our array from train data ArrayCopy(m_xvalues,x,0,train_size,test_size); //new values of x, starts from where the training ended ArrayCopy(m_yvalues,y,0,train_size,test_size); //new values of y, starts from where the testing ended Print("start testing...., test size=",test_size); ArrayResize(Predicted,test_size); //resize the array to match the test size for (int i=0; i<test_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]); } ConfusionMatrix(m_yvalues,Predicted,accuracy); printf("Testing Model Accuracy =%.5f",accuracy); } return (accuracy); //Lastly, the testing Accuracy will be returned }
스크립트의 실행이 성공적이면 다음이 출력됩니다.
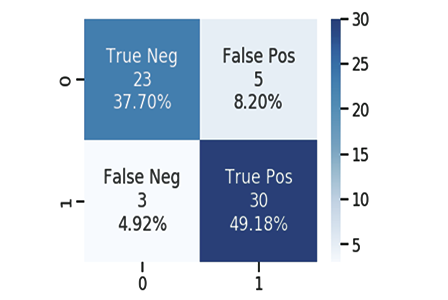
훈련 시작 중..., 훈련 크기=624
혼동 행렬(Confusion Matrix)
[ 378 0 ]
[ 246 0 ]
훈련 모델 정확도 = 0.60577
테스트 시작...., 테스트 크기=267
혼동 행렬(Confusion Matrix)
[ 171 0 ]
[ 96 0 ]
테스트 모델 정확도 = 0.64045
만세! 우리는 이제 숫자를 통해 우리의 모델이 얼마나 좋은지 확인할 수 있습니다. 테스트 데이터에 대한 64.045%의 정확도는 적어도 현재로서는(내 의견으로는)예측을 하는 데 모델을 사용하기에 충분하지 않습니다. 우리에게는 로지스틱 회귀를 사용하여 데이터를 분류하는 데 도움이 될 수 있는 라이브러리가 있습니다.
이외 주요 함수에 대한 설명:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7)
입력 train_size_split은 데이터를 훈련 및 테스트로 분할하기 위한 것입니다. 기본적으로 분할은 0.7입니다. 즉 데이터의 70%는 훈련용이고 나머지 30%는 테스트용이며Predicted[]참조 배열은 테스트 예측 데이터를 반환할 것입니다.
손실 함수라고도도 알려진 이진 교차 엔트로피(Binary Cross Entropy)
평균 제곱 오차가 선형 회귀의 오류 함수인 것처럼 이진 교차 엔트로피는 로지스틱 회귀의 비용 함수입니다.
이론:
로지스틱 회귀의 두 가지 사용 사례, 즉 실제 출력이 0 & 1일 때 어떻게 작동하는지 봅시다.
01: 실제 출력 값이 1일 때
두 개의 입력 샘플 p1 = 0.4 및 p2 = 0.6에 대한 모델을 생각해 보십시오. p1은 p1에 비해 1과 거리가 멀기 때문에 p2보다 더 패널티를 받아야 할 것으로 예상됩니다.
수학적 관점에서 작은 숫자의 음의 로그는 큰 숫자이고 그 반대의 경우도 마찬가지입니다.
입력에 패널티를 주기 위해 다음 공식을 사용합니다.
penalty = -log(p)
이 두 가지 경우에
- Penalty = -log(0.4)=0.4 즉, p1의 패널티는 0.4입니다.
- Penalty = -log(0.6)=0.2 즉, p2의 패널티는 0.2입니다.
02: 실제 출력 값이 0일 때
두 개의 입력 샘플, p1 = 0.4 및 p2= 0.6에 대한 모델 출력을 생각해 보십시오.(이전의 경우와 동일). p2는 0과 거리가 멀기 때문에 p1보다 더 많은 패널티를 받아야 할 것으로 예상되지만 로지스틱 모델의 출력은 샘플이 양수일 확률이라는 점을 명심하십시오. 입력 확률에 패널티를 주기 위해 샘플이 음수가 되는 확률이 필요합니다, 그건 쉽습니다. 여기 공식이 있습니다
샘플이 음수일 확률 = 1-샘플이 양수일 확률
따라서 이 경우 패널티를 구하려면 패널티 공식은 다음과 같습니다.
penalty = -log(1-p)
이 두 가지 경우에
- penalty = -log(1-p) = -log(1-0.4) =0.2 패널티는 0.2
- penalty = -log(1-p) = -log(1-0.6) =0.4 패널티는 0.4
p2의 패널티는 p1보다 큽니다(예상대로 작동합니다) 멋집니다!
이제 모델 출력이 p이고 실제의 출력 값이 y인 단일 입력 샘플에 대한 패널티는 다음과 같이 계산할 수 있습니다.
입력 샘플이 양수인 경우y=1:
penalty = -log(p)
그렇지 않으면:
penalty = -log(1-p)
위의 if-else 블록 문과 동일한 한 줄 방정식은 다음과 같이 작성할 수 있습니다.
penalty = -( y*log(p) + (1-y)*log(1-p) )
설명
y = 데이터세트의 실제 값
p = 모델의 원시 예측 확률(반올림 전)
이 방정식이 위의 if-else 문과 동일함을 증명해 봅시다.
01: 출력 값 y = 1일 때
penalty = -( 1*log(p) + (1-1)*log(1-p) ) = -log(p) 이렇게 증명됩니다
02: 출력 값 y = 0일 때
penalty = -( 0*log(p) + (1-0)* log(1-p) ) = log(1-p) 이렇게 증명됩니다
마지막으로 N 입력 샘플에 대한 로그 손실 함수는 다음과 같습니다.
로그 손실은 예측 확률이 해당 실제/참 값(이진 분류의 경우 0 또는 1)에 얼마나 가까운지를 나타냅니다. 예측 확률이 실제 값과 다를수록 로그 손실 값이 높아집니다.
로그 손실 및 기타 여러 비용 함수는 모델이 얼마나 좋은지에 대한 메트릭으로 사용할 수 있지만 가장 큰 용도는 gradient descent 또는 기타 최적화 알고리즘을 사용하여 최상의 매개변수에 대해 모델을 최적화할 때입니다(추후의 시리즈에서 논의할 것입니다).
만약 여러분이 측정할 수 있는 것이 있다면 그것을 개선할 수 있습니다. 이것이 비용 함수의 주요 목적입니다.
테스트 및 교육 데이터 세트에서 로그 손실이 0.64 - 0.68 사이에 있는 것으로 나타났으며 이는 이상적이지 않습니다(대략적으로 말하면).
훈련 데이터 세트
Logloss =0.6858006105398738
테스트 데이터 세트
Logloss =0.6599503403665642
로그 손실 함수를 코드로 변환하는 방법은 다음과 같습니다.
double CLogisticRegression::LogLoss(double &rawpredicted[]) { double log_loss =0; double penalty=0; for (int i=0; i<ArraySize(rawpredicted); i++ ) { penalty += -((m_yvalues[i]*log(rawpredicted[i])) + (1-m_yvalues[i]) * log(1-rawpredicted[i])); //sum all the penalties if (m_debug) printf("penalty =%.5f",penalty); } log_loss = penalty/ArraySize(rawpredicted); //all the penalties divided by their total number Print("Logloss =",log_loss); return(log_loss); }
원시 예측 출력을 얻으려면 루프를 위해 기본 테스트 및 훈련으로 돌아가서 확률을 반올림하는 프로세스 직전에 원시 예측 배열에 데이터를 저장해야 합니다.
다중 동적 로지스틱 회귀 문제
이 기사와 이전 기사에서 선형 및 로지스틱 회귀 라이브러리를 모두 구축할 때 직면한 가장 큰 문제는 우리의 모델에 추가되는 모든 데이터에 대해 하드 코딩하지 않고도 여러 데이터 열에 사용할 수 있는 다중 동적 회귀 함수입니다. 우리 모델은 이전 기사에서 동일한 이름의 두 함수를 하드코딩 했습니다. 둘 사이의 유일한 차이점은 각 모델이 작업할 수 있는 데이터의 수였습니다. 하나는 2개의 독립 변수로 작업할 수 있었고 다른 하나는 각각 4개를 사용할 수 있었습니다.
void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]);
그러나 이 방법은 불편하고 미숙한 코딩처럼 보이며 깨끗한 코드 및 DRY의 규칙을 위반합니다(OOP가 우리가 목표를 달성하는 것을 돕는다는 식의 원칙을 반복하지 마십시오).
*args 및 **kwargs의 도움으로 많은 수의 기능적인 인수를 취할 수 있는 유연한 함수를 가진 파이썬과 달리 MQL5에서는 문자열만 사용하여 이를 달성할 수 있습니다. 제가 생각하는 한 이것이 우리의 출발점이라고 생각합니다.
void CMultipleLogisticRegression::MLRInit(string x_columns="3,4,5,6,7,8")
input x_columns는 우리가 라이브러리에서 사용할 모든 독립 변수 열을 나타냅니다. 이러한 열은 각 열에 대해 여러 개의 독립 배열이 필요하지만 배열을 동적으로 생성할 수 있는 방법이 없으므로 배열 사용이 실패합니다.
여러 CSV 파일을 동적으로 생성하여 배열로 사용할 수는 있지만 배열 사용에 비해 컴퓨터 리소스의 사용과 관련하여 특히 여러 데이터를 처리할 때 프로그램 비용이 더 많이 듭니다. 파일을 여는 데 자주 사용하는 루프는 전체 프로세스를 느리게 합니다. 제가 100% 확신할 수는 없으므로 틀렸다면 수정해 주세요.
우리는 여전히 언급된 방법을 사용할 수 있지만.
배열을 사용하는 방법을 찾았습니다. 모든 열의 모든 데이터를 하나의 배열에 저장한 다음 해당 단일 배열과 별도로 데이터를 사용할 것입니다.
int start = 0; if (m_debug) //if we are on debug mode print Each Array vs its row for (int i=0; i<x_columns_total; i++) { ArrayCopy(EachXDataArray,m_AllDataArray,0,start,rows_total); start += rows_total; Print("Array Number =",i," From column number ",m_XColsArray[i]); ArrayPrint(EachXDataArray); }
for 루프 내에서 배열의 데이터를 조작하고 모든 열에 대해 원하는 방식으로 모델에 대한 모든 계산을 수행할 수 있습니다. 저는 이 방법을 시도했었는데 아직 성공적이지 않았습니다. 제가 이 가설을 설명한 이유는 이 기사를 읽는 모든 사람이 이러한 도전을 이해할 수 있으면 하는 바램 때문입니다. 다중 동적 로지스틱 회귀 함수를 코딩하는 방법에 대해 기사의 의견 섹션에서 여러분들의 모든 의견을 환영합니다. 이 라이브러리를 만들려는 전체 시도는https://www.mql5.com/ko/code/38894에서 찾을 수 있습니다.
비록 이 시도는 실패했지만 희망이 있고 공유할 가치가 있다고 생각합니다.
로지스틱 회귀의 장점
- 피쳐 공간에서 클래스의 분포에 대해 가정하지 않음
- 여러 클래스로 쉽게 확장(다항 회귀)
- 클래스 예측의 자연스러운 확률론적 관점
- 빠른 훈련
- 알려지지 않은 기록을 매우 빠르게 분류
- 많은 양의 간단한 데이터 세트에 대한 우수한 정확도
- 과적합에 강함
- 모델 계수를 기능 중요도의 지표로 해석할 수 있음
단점
- 선형 경계를 구성
마침말
이상입니다. 로지스틱 회귀는 이메일을 스팸 혹은 스팸이 아닌 이메일로 분류, 손글씨 감지 및 훨씬 더 흥미로운 많은 것들 등 실생활의 여러 분야에서 사용됩니다.
저는 우리가 엄청난 양의 데이터나 위의 언급된 필드를 분류하기 위해 로지스틱 회귀 알고리즘을 사용하지 않을 것이라고 생각합니다. 특히 MetaTrader 5 플랫폼과 관련해서는 앞서 설명했듯이 데이터 세트는 라이브러리를 구축하기 위해 사용되었으며 여기 링크된 python에서 얻은 출력과 비교하고자 한 것입니다. - >https://github.com/MegaJoctan/LogisticRegression-MQL5-and-python. 다음 기사에서는 로지스틱 모델을 사용하여 주식 시장 붕괴를 예측하는 방법에 대해 살펴보겠습니다.
이 기사가 너무 길어졌기 때문에 다중 회귀 작업은 모든 독자에게 숙제로 남겨둡니다.
MetaQuotes 소프트웨어 사를 통해 영어가 번역됨
원본 기고글: https://www.mql5.com/en/articles/10626
경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.
이 글은 사이트 사용자가 작성했으며 개인의 견해를 반영합니다. Metaquotes Ltd는 제시된 정보의 정확성 또는 설명 된 솔루션, 전략 또는 권장 사항의 사용으로 인한 결과에 대해 책임을 지지 않습니다.
 이동 평균으로 할 수 있는 것
이동 평균으로 할 수 있는 것
 스토캐스틱으로 거래 시스템 설계 하는 방법 알아보기
스토캐스틱으로 거래 시스템 설계 하는 방법 알아보기
 ADX 기반의 트레이딩 시스템을 설계하는 방법 알아보기
ADX 기반의 트레이딩 시스템을 설계하는 방법 알아보기
 데이터 과학 및 기계 학습(파트 01): 선형 회귀
데이터 과학 및 기계 학습(파트 01): 선형 회귀