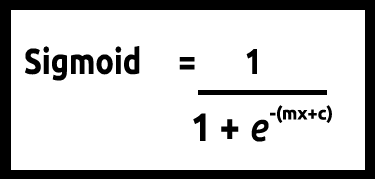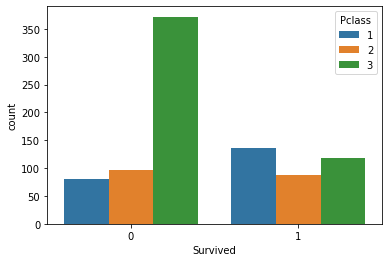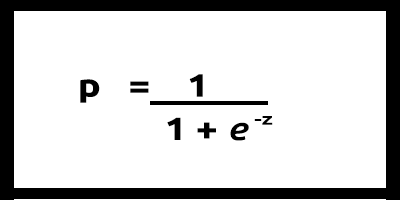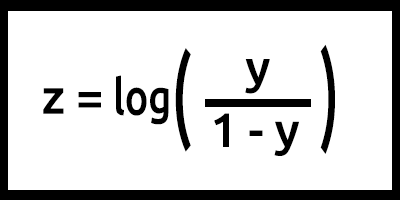
Veri Bilimi ve Makine Öğrenimi (Bölüm 02): Lojistik Regresyon
İlk bölümde lineer regresyondan bahsetmiştik, bu bölümde de lineer regresyona dayalı bir sınıflandırma yöntemi olan lojistik regresyon hakkında konuşacağız.
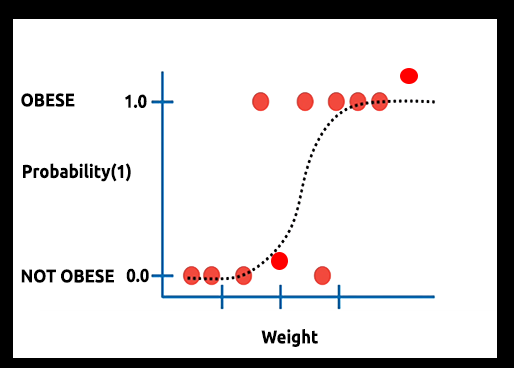
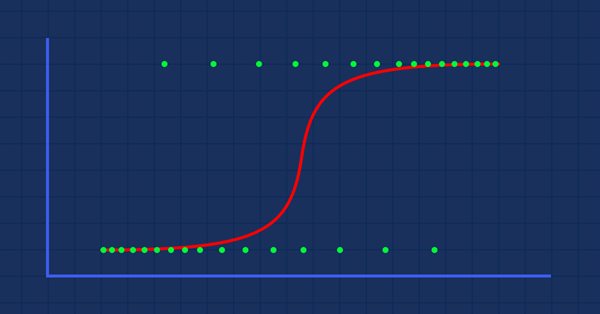
Teori: Bir kişinin obez olma olasılığı ile kilosu arasındaki ilişkiyi bir grafik olarak çizdiğimizi varsayalım.
Bu durumda bir lineer model kullanamayız, bu çizgiyi sigmoid olarak bilinen bir S-eğrisine dönüştürmek için farklı bir teknik kullanacağız.
Lojistik regresyon, kategorik bağımlı değişkenin çıktısını öngörmek için kullanılan ikili formatta sonuçlar ürettiğinden, çıktı ayrık/kategorik olmalıdır, örneğin:
- 0 veya 1
- Evet veya hayır
- Doğru veya yanlış
- Yükseliş veya düşüş
- Alış veya satış
Oluşturacağımız kütüphanede, diğer ayrık değerleri göz ardı edeceğiz. Odağımız sadece (0,1) olacaktır.
y değerlerimizin 0 ile 1 arasında olması gerektiğinden, çizgimizin de 0 ve 1'de kırpılması gerekir. Bu, aşağıdaki formül aracılığıyla elde edilebilir:
Bu da bize şu grafiği verecektir:
Burada, lineer model bir lojistik fonksiyona (sigmoid veya p = 1/(1+et)) dönüştürüldü, formülde t, lineer modeldir ve sonuç ise 0 ile 1 arasında olur. Bu, veri noktasının sınıfa ait olma olasılığını temsil eder.
Bir lineer modelin y'sini bağımlı olarak kullanmak yerine, onun fonksiyonu, yani "p" bağımlı olarak kullanılır.
p = 1/(1+e-(c+m1x1+m2x2+....+mnxn)), birden fazla değer olduğunda
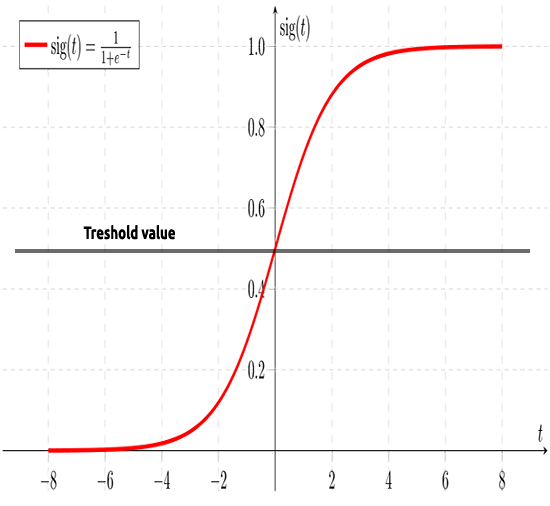
Daha önce de belirttiğim gibi, sigmoid eğrisi sonsuz değerleri ikili formatta sonuca (0 veya 1) dönüştürmeyi amaçlar. Peki ya 0,8'de bulunan bir veri noktası varsa, değerin sıfır mı yoksa bir mi olduğuna nasıl karar verilir? Bunu yapmak için eşik değerleri kullanacağız.
Eşik, kazanma veya kaybetme olasılığını gösterir, 0,5'te (0 ve 1'in ortasında) bulunur.
0,5'ten eşit veya büyük herhangi bir değer bire yuvarlanır ve dolayısıyla kazanan olarak kabul edilir, 0,5'in altındaki herhangi bir değer de 0'a yuvarlanır ve dolayısıyla kaybeden olarak kabul edilir. Şimdi lineer ve lojistik regresyon arasındaki farkın ne olduğunu görelim.
Lineer ve Lojistik Regresyon
| Lineer regresyon | Lojistik Regresyon |
|---|---|
| Sürekli değişken | Kategorik değişken |
| Regresyon problemlerini çözer | Sınıflandırma problemlerini çözer |
| Model düz bir denkleme sahiptir | Model lojistik bir denkleme sahiptir |
Veri sınıflandırma kodlarına ve algoritmalarına geçmeden önce, verileri anlamaya ve model oluşturmayı kolaylaştırmaya yardımcı olacak birkaç adımı inceleyelim:
- Verileri toplama ve analiz etme
- Verileri temizleme
- Doğruluk kontrolü
01: Verileri Toplama ve Analiz Etme
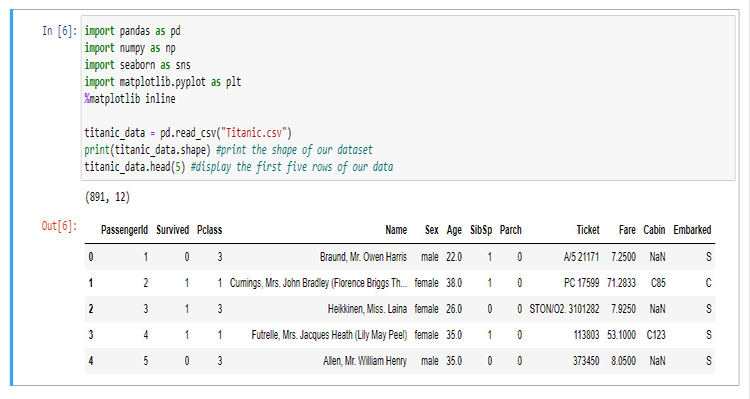
Bu bölümde, verilerimizi görselleştirmek için çok miktarda Python kodu yazacağız. Öncelikle, Jupyter Notebook’taki verileri ayıklamak ve görselleştirmek için kullanacağımız kütüphaneleri içe aktararak başlayalım.
Kütüphanemizi oluşturmak için, 15 Nisan 1912'de Kuzey Atlantik Okyanusu'nda bir buz dağına çarptıktan sonra batan Titanik'e ilişkin verileri kullanacağız (Titanik’e aşina değilseniz, ayrıntılar için Wikipedia'ya bakabilirsiniz). Tüm Python kodları ve veri kümesi makalenin sonunda linki sunulmuş olan GitHub'ımdan bulunabilir.
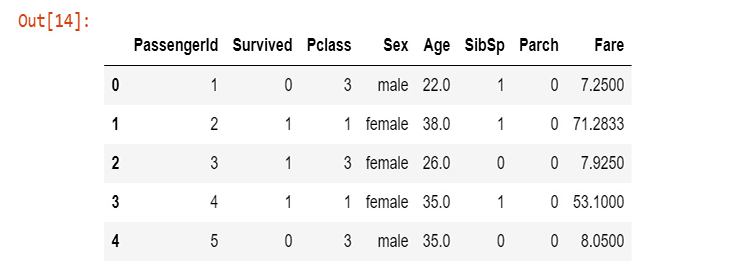
Sütunların ne anlama geldiği aşağıda açıklanmaktadır:
Survived - Hayatta kalma (0 = Hayır; 1 = Evet)
Pclass - Yolcu sınıfı (1 = 1.; 2 = 2.; 3 = 3.)
Name - Ad
Sex - Cinsiyet
Age - Yaş
SibSp - Gemideki kardeş/eş sayısı
Parch - Gemideki ebeveyn/çocuk sayısı
Ticket - Bilet numarası
Fare - Yolcu ücreti
Cabin - Kamara
Embarked - Gemiye biniş limanı (C = Cherbourg; Q = Queenstown; S = Southampton)
Artık verilerimizi topladığımıza ve titanic_data değişkenine kaydettiğimize göre, hayatta kalma sütunundan başlayarak verileri sütunlar halinde görselleştirmeye başlayalım.
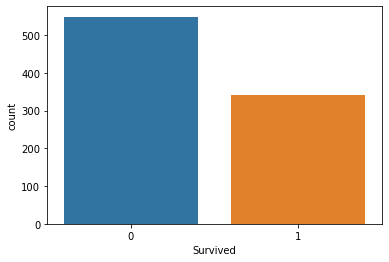
sns.countplot(x="Survived", data = titanic_data)
Çıktı:
Bu, gemideki yolcuların azınlığının kazadan sağ kurtulduğunu ortaya koyuyor. Yolcuların yaklaşık 3’te 2’sinin hayatını kaybettiği görülüyor.
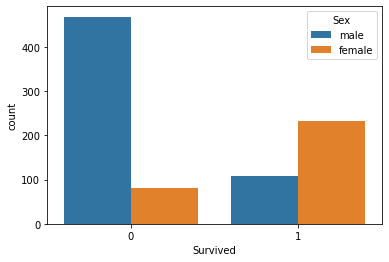
Cinsiyete göre hayatta kalma sayısını görselleştirelim:
sns.countplot(x='Survived', hue='Sex', data=titanic_data)
O gün erkeklere ne oldu bilmiyorum ama hayatta kalanlardan kadınların sayısı erkeklerin yaklaşık iki katıdır.
Şimdi yolcu sınıflarına göre hayatta kalanların sayısını görselleştirelim:
sns.countplot(x='Survived', hue='Pclass', data=titanic_data)
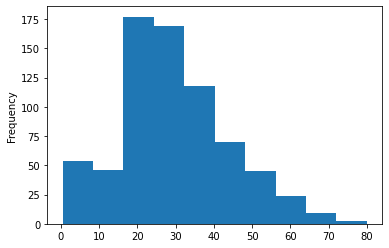
Gemide bulunan yolcuların yaş gruplarının histogramını oluşturalım, burada verilerimizi görselleştirmek için count-plot’u kullanamayız çünkü veri kümemizde organize olmayan birçok farklı yaş değeri mevcuttur.
titanic_data['Age'].plot.hist()Çıktı:
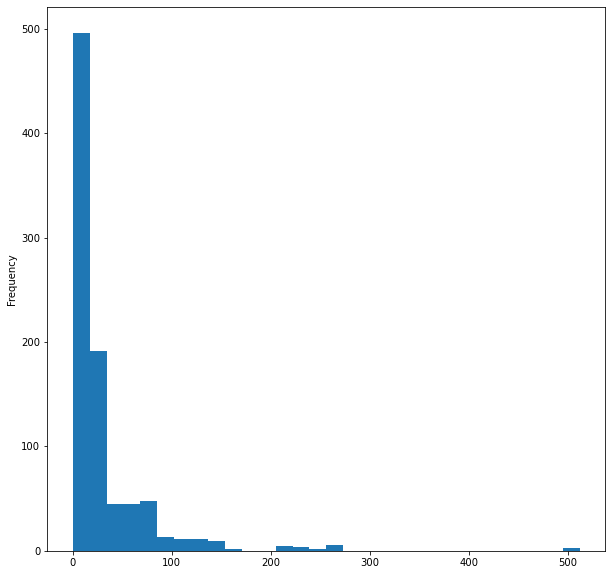
Son olarak da, gemideki yolcu ücretlerinin histogramını görselleştirelim:
titanic_data['Fare'].plot.hist(bins=30, figsize=(10,10))
Verileri görselleştirme için bu kadar. Burada, 12 sütundan sadece 5’ini görselleştirdik çünkü bunların en önemli sütunlar olduğunu düşünüyorum. Şimdi verilerimizi temizleyelim.
02: Verileri Temizleme
Burada, veri kümesindeki gereksiz sütunları kaldırarak verilerimizi temizleyeceğiz.
Lojistik regresyonu kullanırken double ve int tipi değerlere sahip olmamız gerekir, dolayısıyla anlamlı olmayan string tipi değerlerden kaçınmalıyız, bu yüzden bizim durumumuzda aşağıdaki sütunları yok sayacağız:
- Name sütunu (anlamlı bir bilgi içermiyor)
- Ticket sütunu (hayatta kalma için hiçbir anlam ifade etmiyor)
- Cabin sütunu (çok fazla NaN (eksik) değer var, ilk 5 satır bile bunu gösteriyor)
- Embarked sütunu (bence önemli değil)
Bunu yapmak için CSV dosyasını WPS Office’te açacağım ve sütunları manuel olarak kaldıracağım, siz de istediğiniz herhangi bir hesap tablosu programını kullanabilirsiniz.
Sütunları kaldırdıktan sonra yeni verileri görselleştirelim.
new_data = pd.read_csv(r'C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\titanic.csv') new_data.head(5)
Çıktı:
Artık temizlenmiş verilere sahibiz, ancak yaş sütununda hala eksik değerlerimiz var ve cinsiyet sütununda da string tipi değerlere sahibiz. Bu sorunları bazı kodlar aracılığıyla çözelim. male ve female string değerlerini sırasıyla 0 ve 1'e dönüştürmek için bir etiket kodlayıcı oluşturalım.
void CLogisticRegression::LabelEncoder(string &src[],int &EncodeTo[],string members="male,female") { string MembersArray[]; ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(members,separator,MembersArray); //convert members list to an array ArrayResize(EncodeTo,ArraySize(src)); //make the EncodeTo array same size as the source array int binary=0; for(int i=0;i<ArraySize(MembersArray);i++) // loop the members array { string val = MembersArray[i]; binary = i; //binary to assign to a member int label_counter = 0; for (int j=0; j<ArraySize(src); j++) { string source_val = src[j]; if (val == source_val) { EncodeTo[j] = binary; label_counter++; } } Print(MembersArray[binary]," total =",label_counter," Encoded To = ",binary); } }
src[] adlı kaynak diziyi elde etmek adına, CSV dosyasındaki belirli bir sütundan verileri almak ve ardından onu MembersArray[] string değerleri dizisine yerleştirmek için bir fonksiyon programladım, işte burada:
void CLogisticRegression::GetDatatoArray(int from_column_number, string &toArr[]) { int handle = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI,m_delimiter); int counter=0; if (handle == INVALID_HANDLE) Print(__FUNCTION__," Invalid csv handle err=",GetLastError()); else { int column = 0, rows=0; while (!FileIsEnding(handle)) { string data = FileReadString(handle); column++; //--- if (column==from_column_number) //if column in the loop is the same as the desired column { if (rows>=1) //Avoid the first column which contains the column's header { counter++; ArrayResize(toArr,counter); toArr[counter-1]=data; } } //--- if (FileIsLineEnding(handle)) { rows++; column=0; } } } FileClose(handle); }
testscript.mq5 dosyamızın içerisinde, şu şekilde fonksiyonlar düzgün bir şekilde çağrılır ve kütüphane başlatılır:
#include "LogisticRegressionLib.mqh"; CLogisticRegression Logreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- Logreg.Init("titanic.csv",","); string Sex[]; int SexEncoded[]; Logreg.GetDatatoArray(4,Sex); Logreg.LabelEncoder(Sex,SexEncoded,"male,female"); ArrayPrint(SexEncoded); }
Komut dosyası başarıyla çalıştırıldıktan sonra aşağıdaki çıktı yazdırılacaktır:
male total =577 Encoded To = 0
female total =314 Encoded To = 1
[ 0] 0 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 0 1 0 1 1 0 0 1 0 0 1 1 0 0 0 0 0 1 1 1 1 0 1 1 0 0 1 0 1 0 0 1 1 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0
[ 75] 0 0 0 0 1 0 0 1 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 1 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 1 1 0 0 1 0 0 0 1 1 1 0 0 0 0 1 0 0
... ... ... ...
... ... ... ...
[750] 1 0 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 1 1 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 1 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0
[825] 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 0 0 0 1 1 0 1 1 0 0 0 0 1 0 0 1 1 0 0 0 1 1 0 1 0 0 1 0 1 1 0 0
Değerleri kodlamadan önce, fonksiyon argümanlarındaki members="male,female" ifadesine dikkat edin. Buradaki ilk değer 0 olarak kodlanacaktır. Bizim durumumuzda, erkek sütunu önce gelmektedir, dolayısıyla erkekler 0'a, kadınlar da 1'e kodlanacaktır. Bu fonksiyon iki değerle sınırlı değildir, bir anlam ifade ettiği sürece istediğiniz kadar değer kodlayabilirsiniz.
Eksik değerler
Yaş sütununa dikkat ederseniz eksik değerler olduğunu fark edeceksiniz. Veri kümemizdeki eksik değerlerin başlıca nedeni ölüm olabilir. Bu, kişinin yaşını belirlemeyi imkansız hale getirir. Bu boşluklar veri kümesi incelenerek belirlenebilir. Ancak bu özellikle büyük veri kümelerinde uzun zaman alıcı olabilir. Verilerimizi görselleştirmek için Pandas’ı kullandığımıza göre, tüm sütunlardaki eksik satırları da orada bulalım.
titanic_data.isnull().sum()
Çıktı şu şekilde olacaktır:
PassengerId 0
Survived 0
Pclass 0
Sex 0
Age 177
SibSp 0
Parch 0
Fare 0
dtype: int64
Age sütunumuzdaki 891 satırdan 177'sinde eksik değer (NaN) bulunmaktadır.
Şimdi, sütunumuzdaki eksik değerleri tüm değerlerin ortalaması ile değiştirerek yerine koyacağız.
void CLogisticRegression::FixMissingValues(double &Arr[]) { int counter=0; double mean=0, total=0; for (int i=0; i<ArraySize(Arr); i++) //first step is to find the mean of the non zero values { if (Arr[i]!=0) { counter++; total += Arr[i]; } } mean = total/counter; //all the values divided by their total number Print("mean ",MathRound(mean)," before Arr"); ArrayPrint(Arr); for (int i=0; i<ArraySize(Arr); i++) { if (Arr[i]==0) { Arr[i] = MathRound(mean); //replace zero values in array } } Print("After Arr"); ArrayPrint(Arr); }
Bu fonksiyon, sıfır olmayan tüm değerlerin ortalamasını bulur ve ardından dizideki tüm sıfır değerlerini ortalama değerle değiştirir.
Aşağıda fonksiyonu başarıyla çalıştırdıktan sonraki çıktıyı görebilirsiniz. Gördüğünüz gibi, tüm sıfır değerleri Titanik'teki yolcuların ortalama yaşı olan 30.0 ile değiştirildi.
mean 30.0 before Arr
[ 0] 22.0 38.0 26.0 35.0 35.0 0.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 0.0 31.0 0.0 35.0 34.0 15.0 28.0 8.0 38.0 0.0 19.0 0.0 0.0
… … … … … … … … …
[840] 20.0 16.0 30.0 34.5 17.0 42.0 0.0 35.0 28.0 0.0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 0.0 41.0 21.0 48.0 0.0 24.0 42.0 27.0 31.0 0.0 4.0
[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 0.0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 0.0 26.0 32.0
After Arr
[ 0] 22.0 38.0 26.0 35.0 35.0 30.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 30.0 31.0 30.0 35.0 34.0 15.0 28.0 8.0 38.0 30.0 19.0 30.0 30.0
… … … … … … … … …
[840] 20.0 16.0 30.0 34.5 17.0 42.0 30.0 35.0 28.0 30.0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 30.0 41.0 21.0 48.0 30.0 24.0 42.0 27.0 31.0 30.0 4.0
[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 30.0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 30.0 26.0 32.0
Lojistik Regresyon Modeli Oluşturma
İlk olarak, bir bağımsız değişken ve bir bağımlı değişkene sahip olacağımız lojistik regresyonumuzu oluşturalım. Devamında ihtiyacımız için olan tam çözüm modele ilerleyeceğiz.
Modeli Survived ve Age değişkenleri üzerine kuralım. Bir kişinin yaşına bağlı olarak hayatta kalma şansının ne olduğunu bulalım.
Şimdiye kadar öğrendiklerimizden, bir lojistik modelin derinliklerinde bir lineer model olduğunu biliyoruz. Dolayısıyla, bir lineer modeli mümkün kılan fonksiyonları kodlayarak başlayalım.
Coefficient_of_X() ve y_intercept(), yeni fonksiyonlar değildir. Bu makale serisinin ilk bölümünde onlarla çalıştık. Bu fonksiyonlar ve genel olarak lineer regresyon hakkında daha fazla bilgi için ilgili makaleyi okumanızı tavsiye ederim.
double CLogisticRegression::y_intercept() { // c = y - mx return (y_mean-coefficient_of_X()*x_mean); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CLogisticRegression::coefficient_of_X() { double m=0; //--- { double x__x=0, y__y=0; double numerator=0, denominator=0; for (int i=0; i<ArraySize(m_xvalues); i++) { x__x = m_xvalues[i] - x_mean; //right side of the numerator (x-side) y__y = m_yvalues[i] - y_mean; //left side of the numerator (y-side) numerator += x__x * y__y; //summation of the product two sides of the numerator denominator += MathPow(x__x,2); } m = numerator/denominator; } return (m); }
Şimdi, formülü kullanarak lojistik modeli programlayalım.
z'nin aynı zamanda log odds olarak da ifade edildiğini unutmayın. Çünkü sigmoidin tersi, z'nin 1 etiketinin (örneğin, "Hayatta kaldı") olasılığının 0 etiketinin olasılığına (örneğin, "Hayatta kalamadı") bölünmesinin logaritması olarak tanımlanabileceğini belirtir:
Burada, y = mx+c (lineer modelden hatırlayın).
Bunu koda dönüştürdüğümüzde sonuç şöyle olacaktır:
double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1);
Burada z değerine ne yapıldığına dikkat edin. Formül log(y/1-y) şeklindedir, ancak kod log(y_)-log(1-y_); şeklinde yazılmıştır. Matematikteki logaritma yasalarını hatırlayın! Aynı tabana sahip logaritmaların bölünmesi üslerin çıkarılmasıyla sonuçlanır, bu konuda daha fazla bu bilgi için burayı okuyabilirsiniz.
Formül programlandığında, temel olarak modelimiz budur, ancak LogisticRegression() fonksiyonumuzun içerisinde de çok şey oluyor, işte fonksiyonun içerisindeki her şey:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7) { int arrsize = ArraySize(x); //the input array size double p_hat =0; //store the probability //--- int train_size = (int)MathCeil(arrsize*train_size_split); int test_size = (int)MathFloor(arrsize*(1-train_size_split)); ArrayCopy(m_xvalues,x,0,0,train_size); ArrayCopy(m_yvalues,y,0,0,train_size); //--- y_mean = mean(m_yvalues); x_mean = mean(m_xvalues); // Training our model in the background double c = y_intercept(), m = coefficient_of_X(); //--- Here comes the logistic regression model int TrainPredicted[]; double sigmoid = 0; ArrayResize(TrainPredicted,train_size); //resize the array to match the train size Print("Training starting..., train size=",train_size); for (int i=0; i<train_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); double odds_ratio = p_hat/(1-p_hat); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]); } //--- Testing our model if (train_size_split<1.0) //if there is room for testing { ArrayRemove(m_xvalues,0,train_size); //clear our array ArrayRemove(m_yvalues,0,train_size); //clear our array from train data ArrayCopy(m_xvalues,x,0,train_size,test_size); //new values of x, starts from where the training ended ArrayCopy(m_yvalues,y,0,train_size,test_size); //new values of y, starts from where the testing ended Print("start testing...., test size=",test_size); ArrayResize(Predicted,test_size); //resize the array to match the test size for (int i=0; i<test_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); double odds_ratio = p_hat/(1-p_hat); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]); } }
Şimdi modelimizi TestScript.mq5’te eğitelim ve test edelim.
double Age[]; Logreg.GetDatatoArray(5,Age); Logreg.FixMissingValues(Age); double y_survival[]; int Predicted[]; Logreg.GetDatatoArray(2,y_survival); Logreg.LogisticRegression(Age,y_survival,Predicted);
Başarılı bir kod çalışmasının çıktısı şöyle olacaktır:
Training starting..., train size=624
0 Age =22.00 survival_Predicted =0
1 Age =38.00 survival_Predicted =0
... .... ....
622 Age =20.00 survival_Predicted =0
623 Age =21.00 survival_Predicted =0
start testing...., test size=267
0 Age =21.00 survival_Predicted =0
1 Age =61.00 survival_Predicted =1
.... .... ....
265 Age =26.00 survival_Predicted =0
266 Age =32.00 survival_Predicted =0
Harika. Artık modelimiz çalışıyor ve en azından ondan sonuçlar elde edebiliyoruz, ancak modelimiz iyi öngörüler yapıyor mu?
Doğruluğunu kontrol etmemiz gerekiyor.
Hata Matrisi
Hepimizin bildiği gibi, iyi ya da kötü her model öngörüler yapabilir. Modelimizin yolcuların hayatta kalmasına ilişkin test sonucunda yaptığı öngörüleri ve orijinal değerleri yan yana getirerek bir CSV dosyası oluşturdum. Burada, yine 1 hayatta kaldı, 0 hayatta kalamadı anlamına gelir.
İşte bazıları:
| Orijinal | Öngörülen | |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 2 | 0 | 1 |
| 3 | 1 | 0 |
| 4 | 0 | 0 |
| 5 | 0 | 0 |
| 6 | 1 | 1 |
| 7 | 0 | 1 |
| 8 | 1 | 0 |
| 9 | 0 | 0 |
Aşağıdakileri kullanarak hata matrisini hesaplıyoruz:
- TP - True Positive, gerçek pozitif
- TN - True Negative, gerçek negatif
- FP - False Positive, yanlış pozitif
- FN - False Negative, yanlış negatif
Peki bu değerler ne anlama geliyor?
TP (Gerçek pozitif)
Orijinal değer pozitif (1) olduğunda ve model de pozitif (1) öngördüğünde
TN (Gerçek negatif )
Orijinal değer negatif (0) olduğunda ve model de negatif (0) öngördüğünde
FP (Yanlış pozitif)
Orijinal değer negatif (0) olduğunda, ancak model pozitif (1) öngördüğünde
FN (Yanlış negatif)
Orijinal değer pozitif (1) olduğunda, ancak model negatif (0) öngördüğünde
Şimdi yukarıdaki örnek için hata matrisini hesaplayalım.
| Orijinal | Öngörülen | TP/TN/FP/FN | |
|---|---|---|---|
| 0 | 0 | 0 | TN |
| 1 | 0 | 1 | FP |
| 2 | 0 | 1 | FP |
| 3 | 1 | 0 | FN |
| 4 | 0 | 0 | TN |
| 5 | 0 | 0 | TN |
| 6 | 1 | 1 | TP |
| 7 | 0 | 1 | FP |
| 8 | 1 | 0 | FN |
| 9 | 0 | 0 | TN |
Hata matrisi, aşağıdaki formül kullanarak modelimizin doğruluğunu hesaplamak için kullanılabilir.
Tablomuzdan:
- TN = 4
- TP = 1
- FN = 2
- FP = 3
Doğruluk = (1+5)/(4+1+2+3)
Doğruluk = %0,5
Bu durumda doğruluğumuz %50'dir (0,5*%100).
1X1 hata matrisinin nasıl çalıştığını anladık. Bunu koda dönüştürmenin ve modelimizin doğruluğunu tüm veri kümesi üzerinde analiz etmenin zamanı geldi.
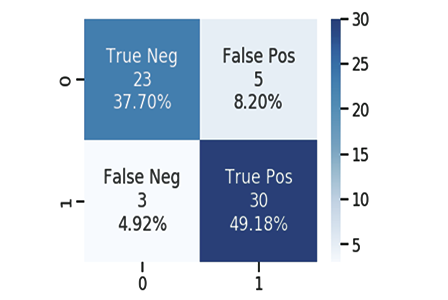
void CLogisticRegression::ConfusionMatrix(double &y[], int &Predicted_y[], double& accuracy) { int TP=0, TN=0, FP=0, FN=0; for (int i=0; i<ArraySize(y); i++) { if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==1) TP++; if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==0) TN++; if (Predicted_y[i]==1 && (int)y[i]==0) FP++; if (Predicted_y[i]==0 && (int)y[i]==1) FN++; } Print("Confusion Matrix \n ","[ ",TN," ",FP," ]","\n"," [ ",FN," ",TP," ] "); accuracy = (double)(TN+TP) / (double)(TP+TN+FP+FN); }
Şimdi sınıfımızdaki ana fonksiyona dönelim - LogisticRegression(). Bu sefer onu modelin doğruluğunu geri döndüren bir double fonksiyona dönüştüreceğiz. Ayrıca Print() metotlarının sayısını azaltmak istiyorum, onları if ifadesine ekleyeceğim. Aslında her seferinde değerleri yazdırmamıza gerek yok (tabii ki sınıfımızda hata ayıklamak istemiyorsak). Tüm değişiklikler mavi renkle vurgulanmıştır:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7) { double accuracy =0; //Accuracy of our Train/Testmodel int arrsize = ArraySize(x); //the input array size double p_hat =0; //store the probability //--- int train_size = (int)MathCeil(arrsize*train_size_split); int test_size = (int)MathFloor(arrsize*(1-train_size_split)); ArrayCopy(m_xvalues,x,0,0,train_size); ArrayCopy(m_yvalues,y,0,0,train_size); //--- y_mean = mean(m_yvalues); x_mean = mean(m_xvalues); // Training our model in the background double c = y_intercept(), m = coefficient_of_X(); //--- Here comes the logistic regression model int TrainPredicted[]; double sigmoid = 0; ArrayResize(TrainPredicted,train_size); //resize the array to match the train size Print("Training starting..., train size=",train_size); for (int i=0; i<train_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]); } ConfusionMatrix(m_yvalues,TrainPredicted,accuracy); //be careful not to confuse the train predict values arrays printf("Train Model Accuracy =%.5f",accuracy); //--- Testing our model if (train_size_split<1.0) //if there is room for testing { ArrayRemove(m_xvalues,0,train_size); //clear our array ArrayRemove(m_yvalues,0,train_size); //clear our array from train data ArrayCopy(m_xvalues,x,0,train_size,test_size); //new values of x, starts from where the training ended ArrayCopy(m_yvalues,y,0,train_size,test_size); //new values of y, starts from where the testing ended Print("start testing...., test size=",test_size); ArrayResize(Predicted,test_size); //resize the array to match the test size for (int i=0; i<test_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]); } ConfusionMatrix(m_yvalues,Predicted,accuracy); printf("Testing Model Accuracy =%.5f",accuracy); } return (accuracy); //Lastly, the testing Accuracy will be returned }
Başarıyla çalıştırıldığında şu çıktıyı verecektir:
Training starting..., train size=624
Confusion Matrix
[ 378 0 ]
[ 246 0 ]
Train Model Accuracy =0.60577
start testing...., test size=267
Confusion Matrix
[ 171 0 ]
[ 96 0 ]
Testing Model Accuracy =0.64045
Yaşasın! Artık modelimizin ne kadar iyi olduğunu sayılarla belirleyebiliyoruz. Test verilerindeki %64,045'lik doğruluk, modeli öngörülerde kullanmak adına yeterince iyi değil (benim görüşüme göre). En azından şimdilik, lojistik regresyon kullanarak verileri sınıflandırmamıza yardımcı olabilecek bir kütüphanemiz var.
Aşağıda ana fonksiyonun açıklaması yer almaktadır:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7)
train_size_split girdisi, verileri eğitim ve test olarak bölmek içindir. Varsayılan olarak, veriler 0,7 şeklinde bölünür; bu, verilerin %70'inin eğitim için, kalan %30'unun ise test amaçlı olacağı anlamına gelir. Predicted[] referans dizisi, öngörülen verileri geri döndürür.
İkili Çapraz Entropi (Kayıp Fonksiyonu)
Ortalama karesel hatanın lineer regresyon için hata fonksiyonu olması gibi, ikili çapraz entropi de lojistik regresyon için maliyet fonksiyonudur.
Teori:
Lojistik regresyon için iki kullanım durumunda, gerçek çıktı 0 ve 1 olduğunda nasıl çalıştığını görelim.
01: Gerçek çıktı değeri 1 olduğunda
Modeli p1=0,4 ve p2=0,6 olmak üzere iki girdi örneği için ele alalım. p1'in p2'den daha fazla cezalandırılması beklenir çünkü p1, p2'ye kıyasla 1'den daha uzaktır.
Matematiksel açıdan bakıldığında, küçük bir sayının negatif logaritması büyük bir sayıdır ve bunun tersi de geçerlidir.
Girdileri cezalandırmak için aşağıdaki formülü kullanacağız:
Ceza = -log(p)
İlgili iki durumda,
- Ceza=-log(0.4)=0.4 yani p1 üzerindeki ceza 0.4'tür.
- Ceza=-log(0.6)=0.2 yani p2 üzerindeki ceza 0.2'dir.
02: Gerçek çıktı değeri 0 olduğunda
Modeli p1=0,4 ve p2=0,6 olmak üzere iki girdi örneği için ele alalım (önceki durumda olduğu gibi). 0'dan daha uzak olduğu için p2'nin p1'den daha fazla cezalandırılması beklenir. Ancak, lojistik modelin çıktısının örneğin pozitif olma olasılığı olduğunu unutmayın. Girdi olasılıklarını cezalandırmak için örneğin negatif olma olasılığını bulmamız gerekir. Bu çok kolaydır, işte formül:
Örneğin negatif olma olasılığı = 1 - örneğin pozitif olma olasılığı
Dolayısıyla, bu durumda cezayı bulmak için formül şöyle olacaktır:
Ceza = -log(1-p)
İlgili iki durumda,
- Ceza=-log(1-p)=-log(1-0.4)=0.2 yani ceza 0.2'dir.
- Ceza=-log(1-p)=-log(1-0.6)=0.4 yani ceza 0.4'tür.
p2 üzerindeki ceza p1 üzerindeki cezadan daha büyük (beklendiği gibi çalışıyor), çok iyi!
Böylece, gerçek çıktı değerinin y olduğu, model çıktısı p olan tek bir girdi örneği için ceza aşağıdaki gibi hesaplanabilir:
if çıktı değeri y=1:
Ceza = -log(p)
else:
Ceza = -log(1-p)
Yukarıdaki if-else blok ifadesine eşdeğer tek satırlık bir denklem şu şekilde yazılabilir:
Ceza = -(y*log(p) + (1-y)*log(1-p))
Burada:
y = veri kümemizdeki gerçek değerler
p = modelin ham öngörülen olasılığı (yuvarlamadan önce)
Bu denklemin yukarıdaki if-else ifadesine eşdeğer olduğunu kanıtlayalım.
01: Çıktı değeri y=1 olduğunda
Ceza = -(1*log(p) + (1-1)*log(1-p)) = -log(p) dolayısıyla kanıtlandı
02: Çıktı değeri y=0 olduğunda
Ceza = -(0*log(p) + (1-0)* log(1-p)) = log(1-p) dolayısıyla kanıtlandı
Böylece, N girdi örneği için kayıp fonksiyonu (log loss) aşağıdaki gibi görünür:
Kayıp fonksiyonu, öngörülen olasılığın karşılık gelen gerçek değere (ikili sınıflandırma durumunda 0 veya 1) ne kadar yakın olduğunu gösterir. Öngörülen olasılık gerçek değerden ne kadar uzaklaşırsa, kayıp fonksiyonu değeri de o kadar yüksek olur.
Kayıp fonksiyonu vb. gibi maliyet fonksiyonları, modelin ne kadar iyi olduğuna dair bir metrik olarak kullanılabilir. Bununla birlikte, maliyet fonksiyonları en fazla şekilde, gradyan azalmayı veya diğer optimizasyon algoritmalarını kullanarak en iyi parametreler için modeli optimize ederken kullanılır (bunu daha sonraki bir makale serisinde inceleyeceğiz, takipte kalın).
Eğer ölçebiliyorsak, iyileştirebiliriz. Maliyet fonksiyonlarının temel amacı da budur.
Test ve eğitim veri kümemizden, kayıp fonksiyonumuz 0,64 - 0,68 arasında olduğu görülmektedir ki bu ideal değildir (kabaca konuşursak).
training dataset
Logloss =0.6858006105398738
testing dataset
Logloss =0.6599503403665642
Kayıp fonksiyonumuzu şu şekilde koda dönüştürebiliriz:
double CLogisticRegression::LogLoss(double &rawpredicted[]) { double log_loss =0; double penalty=0; for (int i=0; i<ArraySize(rawpredicted); i++ ) { penalty += -((m_yvalues[i]*log(rawpredicted[i])) + (1-m_yvalues[i]) * log(1-rawpredicted[i])); //sum all the penalties if (m_debug) printf("penalty =%.5f",penalty); } log_loss = penalty/ArraySize(rawpredicted); //all the penalties divided by their total number Print("Logloss =",log_loss); return(log_loss); }
Öngörülen ham çıktıyı elde etmek için, ana test ve eğitim döngülerine geri dönmemiz ve olasılıkları yuvarlama işleminden hemen önce verileri ham öngörülen dizisine depolamamız gerekir.
Çoklu Dinamik Lojistik Regresyon Zorluğu
Hem önceki makalede hem de bu makalede hem lineer hem de lojistik regresyon kütüphanelerini oluştururken karşılaştığım en büyük zorluk, modele eklenen her veri için kodlama yapmak zorunda kalmamamızı sağlayacak, birden fazla veri sütunu için kullanabileceğimiz çoklu dinamik regresyon fonksiyonlarıydı. Bir önceki makalede aynı isimli iki fonksiyon kodlamıştım. Aralarındaki tek fark, her bir modelin çalışabileceği veri sayısıydı; aşağıda gösterildiği şekilde sırasıyla biri iki bağımsız değişkenle, diğeri ise dört bağımsız değişkenle çalışabiliyordu:
void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]);
Ancak, bu yöntem elverişsizdir ve ayrıca temiz kod ve DRY (kendini tekrar etme) kurallarını ihlal eder.
*args ve **kwargs yardımıyla çok sayıda işlevsel argüman alabilen esnek fonksiyonlara sahip Python'ın aksine, MQL5'te bu, bildiğim kadarıyla yalnızca dizge kullanılarak gerçekleştirilebilir. Başlangıç noktamızın burası olduğuna inanıyorum.
void CMultipleLogisticRegression::MLRInit(string x_columns="3,4,5,6,7,8")
x_columns girdisi, kütüphanemizde kullanacağımız tüm bağımsız değişken sütunlarını temsil eder. Bu, her bir sütun için ayrı bir diziye sahip olmamızı gerektirir. Ancak, dinamik olarak diziler oluşturmamızın bir yolu yoktur, bu nedenle dizilerin kullanımı burada başarısız olur.
Dinamik olarak CSV dosyaları oluşturabilir ve bunları diziler olarak kullanabiliriz, ancak bu, bilgisayar kaynaklarının kullanımı açısından programlarımızı dizilerin kullanımına kıyasla daha pahalı hale getirecektir. Özellikle çok fazla veriyle çalışırken, dosyaları açmak için sıklıkla kullanacağımız while döngülerinden bahsetmiyorum bile, tüm süreci yavaşlatacaktır. Ancak bundan %100 emin değilim, bu yüzden yanılıyorsam beni düzeltin.
Yine de bahsedilen yol kullanılabilir.
Ve dizileri kullanmanın bir yolunu keşfettim, tüm sütunlardaki tüm verileri tek bir dizide depolayacağız ve ardından verileri bu tek diziden ayrı ayrı kullanacağız.
int start = 0; if (m_debug) //if we are on debug mode print Each Array vs its row for (int i=0; i<x_columns_total; i++) { ArrayCopy(EachXDataArray,m_AllDataArray,0,start,rows_total); start += rows_total; Print("Array Number =",i," From column number ",m_XColsArray[i]); ArrayPrint(EachXDataArray); }
For döngüsü içerisinde, dizilerdeki verileri manipüle edebilir ve model için tüm hesaplamaları tüm sütunlar için istediğimiz şekilde gerçekleştirebiliriz. Bu yöntemi denedim ancak hala başarılı olamadım. Bu hipotez hakkında konuşmamın nedeni, bu makaleyi okuyan herkesin bu zorluğu anlamasını sağlamaktır. Nasıl çoklu dinamik lojistik regresyon fonksiyonu kodlayabileceğimize dair tüm görüşlerinizi yorum bölümlerinde bekliyorum. Bu kütüphaneyi oluşturma girişimimin tamamını şu linkten bulabilirsiniz: https://www.mql5.com/tr/code/38894.
Bu girişim başarısız oldu ancak umutları var, bu yüzden paylaşmaya değer olduğuna inanıyorum.
Lojistik Regresyonun Avantajları
- Sınıfın özellik uzayında dağılımına ilişkin varsayımda bulunmaz.
- Birden çok sınıfa kolayca genişletilebilir (multinominal regresyon).
- Sınıf öngörülerinin doğal olasılıksal görünümü.
- Eğitimi hızlı.
- Bilinmeyen kayıtları sınıflandırmada çok hızlı.
- Birçok basit veri kümesi için iyi doğruluk.
- Aşırı uyuma karşı dirençli.
- Model katsayılarını özellik öneminin bir göstergesi olarak yorumlayabilir.
Dezavantajlar
- Lineer sınırlar oluşturur.
Son Düşünceler
Bu makale için hepsi bu kadar. Lojistik regresyon, gerçek hayatta, e-postaları spam ve spam değil olarak sınıflandırmak, el yazısını tespit etmek vb. gibi birçok alanda kullanılmaktadır.
Elbette MetaTrader 5 platformunda Titanik verilerini veya bahsedilen alanlardan herhangi birini sınıflandırmak için lojistik regresyon algoritmalarını kullanmayacağımızı biliyorum. Daha önce de belirtildiği gibi, veri kümesi, linkte sunulan Python'daki çıktıya kıyasla sadece kütüphaneyi oluşturmak için kullanıldı: https://github.com/MegaJoctan/LogisticRegression-MQL5-and-python. Bir sonraki makalede, borsa düşüşlerini öngörmek için lojistik modelleri nasıl kullanabileceğimizi göreceğiz.
Bu makale halihazırda çok uzun olduğu için çoklu regresyon görevini tüm okuyuculara ev ödevi olarak bırakıyorum.
MetaQuotes Ltd tarafından İngilizceden çevrilmiştir.
Orijinal makale: https://www.mql5.com/en/articles/10626
Uyarı: Bu materyallerin tüm hakları MetaQuotes Ltd.'a aittir. Bu materyallerin tamamen veya kısmen kopyalanması veya yeniden yazdırılması yasaktır.
Bu makale sitenin bir kullanıcısı tarafından yazılmıştır ve kendi kişisel görüşlerini yansıtmaktadır. MetaQuotes Ltd, sunulan bilgilerin doğruluğundan veya açıklanan çözümlerin, stratejilerin veya tavsiyelerin kullanımından kaynaklanan herhangi bir sonuçtan sorumlu değildir.
 ADX göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?
ADX göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?
 Hareketli ortalamalar ile neler yapılabilir?
Hareketli ortalamalar ile neler yapılabilir?
 ATR göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?
ATR göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?
 Veri Bilimi ve Makine Öğrenimi (Bölüm 01): Lineer Regresyon
Veri Bilimi ve Makine Öğrenimi (Bölüm 01): Lineer Regresyon
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz