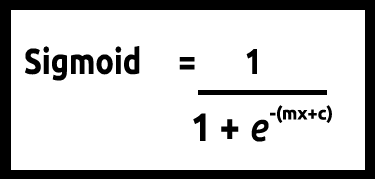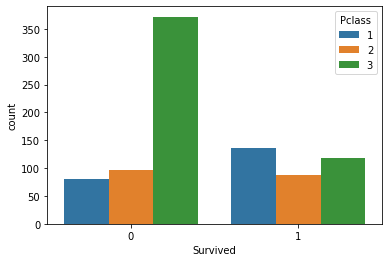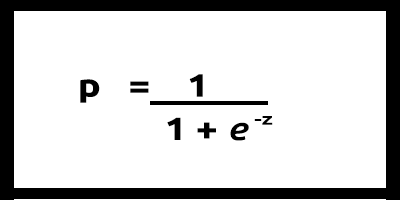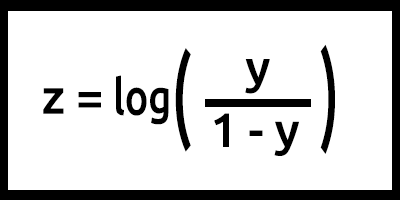
Scienza dei Dati e Apprendimento Automatico (Parte 02): Regressione Logistica
342
0
A differenza della Regressione Lineare di cui abbiamo discusso nella parte 01, la Regressione Logistica è un metodo di classificazione basato sulla regressione lineare.
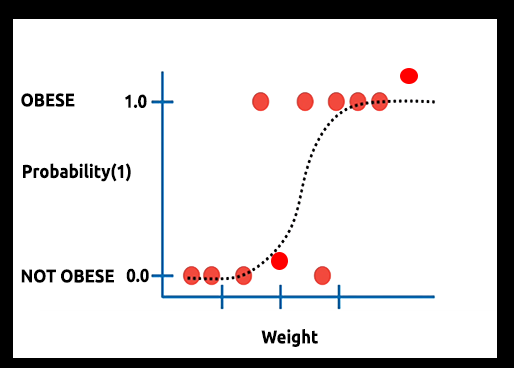
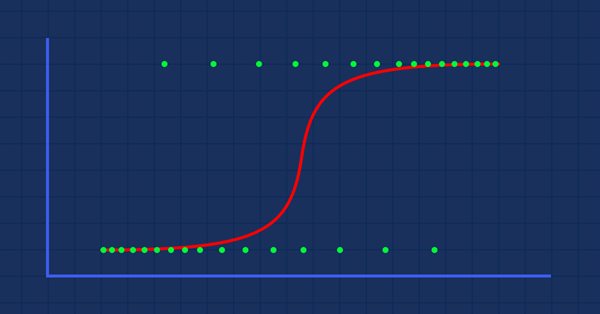
Teoria: Supponiamo di tracciare un grafico della probabilità che qualcuno sia obeso rispetto al suo peso.
In questo caso, non possiamo utilizzare un modello lineare, utilizzeremo un'altra tecnica per trasformare questa linea in una curva a S nota come Sigmoidea.
Poiché la Regressione Logistica produce risultati in un formato binario che viene utilizzato per prevedere il risultato della variabile dipendente categoriale, così il risultato dovrebbe essere discreto/categoriale come:
- 0 o 1
- Si o No
- Vero o Falso
- Alto o Basso
- Compra o Vendi
Nella nostra libreria che creeremo, ignoreremo altri valori discreti. Il nostro focus sarà solo sul binario (0,1).
Poiché i nostri valori di y dovrebbero essere compresi tra 0 e 1, la nostra linea deve essere ritagliata tra 0 e 1. Questo può essere ottenuto attraverso la formula:
Che ci darà questo grafico
Il modello lineare viene passato a una funzione logistica (sigmoid/p) =1/1+e^t dove t è il risultato del modello lineare il cui valore è tra 0 e 1. Questo rappresenta la probabilità che un punto dati appartenga a una classe.
Invece di utilizzare y di un modello lineare come dipendente, la sua funzione viene mostrata come " p" e utilizzata come dipendente
p = 1/1+e^-(c+m1x1+m2x2+....+mnxn) ,in caso di valori multipli.
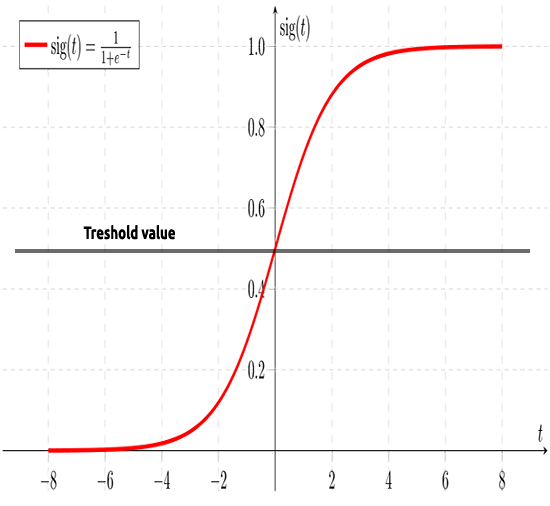
Come detto in precedenza, la curva sigmoidea mira a convertire i valori di infinito in output in formato binario (0 o 1). Ma cosa succede se ho un punto dati situato a 0,8, come si può decidere che il valore è zero o uno? È qui che entrano in gioco i valori di soglia.
La soglia indica la probabilità di vincere o perdere, si trova a 0,5 (centro di 0 e 1).
Qualsiasi valore maggiore o uguale a 0,5 verrà arrotondato a uno, quindi considerato vincente, mentre qualsiasi valore inferiore a 0,5 verrà arrotondato a 0 quindi considerato perdente a questo punto, è tempo di vedere la differenza tra regressione lineare e logistica .
Regressione Lineare vs Logistica
| Lineare | Regressione logistica |
|---|---|
| Variabile continua | Variabile categoriale |
| Risolve i problemi di regressione | Risolve i problemi di classificazione |
| Il modello ha un'equazione lineare | Il modello ha un'equazione logistica |
Prima di approfondire la parte di codifica e gli algoritmi per classificare i dati, diversi passaggi potrebbero aiutarci a comprendere i dati e semplificarci la costruzione del nostro modello:
- Raccolta e Analisi dei Dati
- Pulizia dei propri dati
- Verifica della precisione
01:Raccolta e Analisi dei Dati
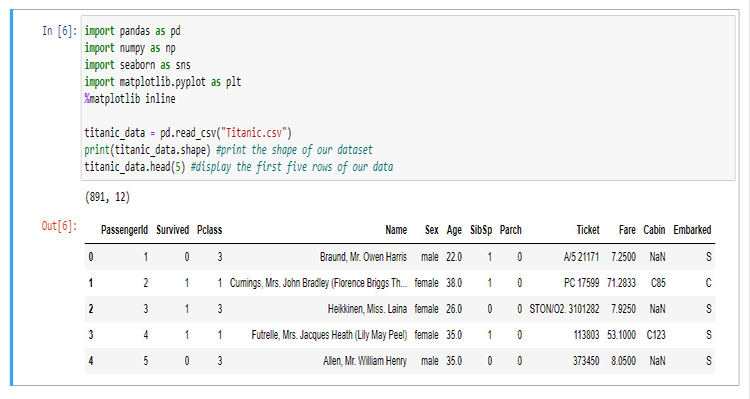
In questa sezione, scriveremo molto codice Python per visualizzare i nostri dati. Iniziamo importando le librerie che utilizzeremo per estrarre e visualizzare i dati nel notebook Jupyter.
Per costruire la nostra biblioteca, utilizzeremo i dati di titanic, per chi non li conoscesse, sono i dati sull'incidente della nave titanic che affondò nell'Oceano Atlantico del nord il 15 aprile 1912 dopo aver colpito un iceberg, Wikipedia. Tutti i codici Python e il dataset si trovano sul mio GitHub linkato alla fine dell'articolo.
Le colonne rappresentano
sopravvivenza - Sopravvivenza (0 = No; 1 = Sì)
classe - Classe Passeggeri (1 = 1st; 2 = 2nd; 3 = 3rd)
nome - Nome
sesso - Sesso
età - Età
sibsp - Numero di fratelli/coniugi a bordo
parch - Numero di genitori/figli a bordo
biglietto - Numero biglietto
tariffa - Tariffa Passeggero
cabina - Cabina
imbarcato - Porto di imbarco (C = Cherbourg; Q = Queenstown; S = Southampton)
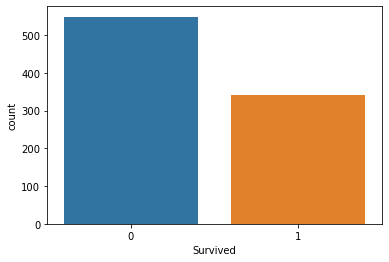
Ora che i nostri dati sono stati raccolti e archiviati in una variabile titanic_data, iniziamo a visualizzare i dati in colonne, a partire dalla colonna di sopravvivenza.
sns.countplot(x="Survived", data = titanic_data)
in uscita
Questo ci dice che la minoranza di passeggeri è sopravvissuta all'incidente, circa la metà dei passeggeri che erano sulla nave è sopravvissuta all'incidente.
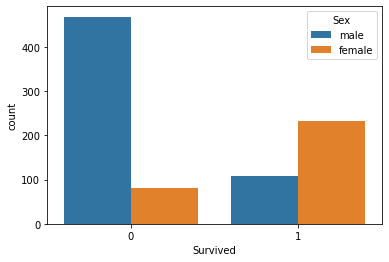
Visualizziamo il numero di sopravvivenza in base al sesso
sns.countplot(x='Survived', hue='Sex', data=titanic_data)
Non so cosa sia successo ai maschi quel giorno, ma le femmine sono sopravvissute più del doppio dei maschi
Visualizziamo ora il numero di sopravissuti in base ai gruppi delle classi
sns.countplot(x='Survived', hue='Pclass', data=titanic_data)
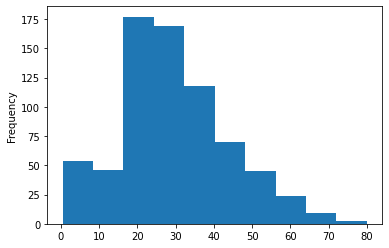
Tracciamo l'istogramma dei gruppi di età dei passeggeri che erano sulla nave, qui non possiamo usare il Count-plots per visualizzare i nostri dati poiché ci sono tanti valori differenti di età nel nostro set di dati che non sono organizzati.
titanic_data['Age'].plot.hist()Output:
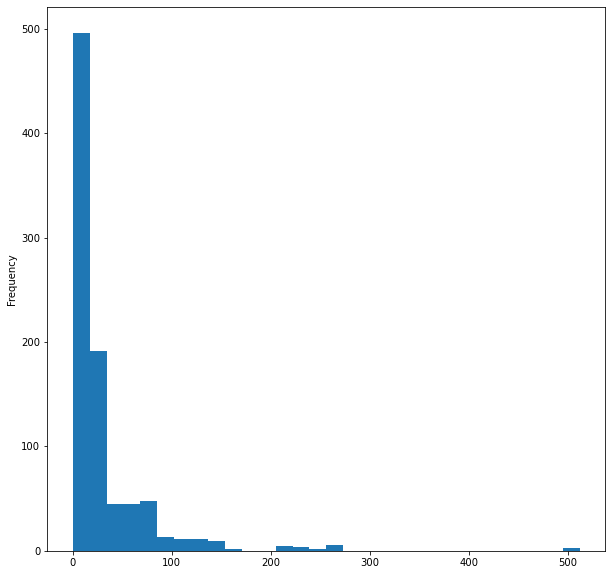
Infine, visualizziamo l'istogramma della tariffa della nave
titanic_data['Fare'].plot.hist(bins=30, figsize=(10,10))
Questo è tutto per visualizzare i dati anche se abbiamo visualizzato solo 5 colonne su 12 perché penso che quelle siano colonne importanti, ora ripuliamo i nostri dati.
02: Pulizia dei nostri Dati
Qui puliamo i nostri dati rimuovendo i valori NaN (mancanti) evitando/rimuovendo le colonne non necessarie nel set di dati.
Usando la regressione logistica devi avere valori di tipo double e interi, quindi devi evitare valori di stringa non significativi in questo caso ignoreremo le seguenti colonne:
- Colonna del nome (non ha informazioni significative)
- Colonna biglietto (non ha alcun senso per la sopravvivenza all'incidente)
- Colonna cabina (ha troppi valori mancanti, anche le prime 5 righe lo mostrano)
- Imbarcato (penso sia irrilevante)
Per farlo, aprirò il file CSV in WPS office e rimuoverò manualmente le colonne, puoi utilizzare qualsiasi programma per fogli di calcolo di tua scelta.
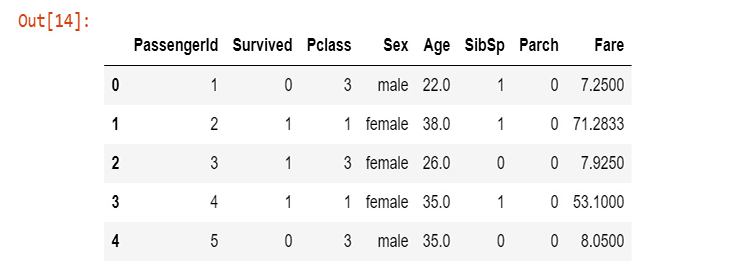
Dopo aver rimosso le colonne utilizzando un foglio di calcolo, visualizziamo i nuovi dati.
new_data = pd.read_csv(r'C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\titanic.csv') new_data.head(5)
Output:
Ora abbiamo pulito i dati anche se abbiamo ancora valori mancanti nella colonna dell'età per non parlare dei valori della stringa nella colonna del sesso. Risolviamo il problema tramite del codice. Creiamo un codificatore di etichette per convertire la stringa maschio e femmina rispettivamente in 0 e 1.
void CLogisticRegression::LabelEncoder(string &src[],int &EncodeTo[],string members="male,female") { string MembersArray[]; ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(members,separator,MembersArray); //convert members list to an array ArrayResize(EncodeTo,ArraySize(src)); //make the EncodeTo array same size as the source array int binary=0; for(int i=0;i<ArraySize(MembersArray);i++) // loop the members array { string val = MembersArray[i]; binary = i; //binary to assign to a member int label_counter = 0; for (int j=0; j<ArraySize(src); j++) { string source_val = src[j]; if (val == source_val) { EncodeTo[j] = binary; label_counter++; } } Print(MembersArray[binary]," total =",label_counter," Encoded To = ",binary); } }
Per ottenere l'array di origine denominato src[] ho anche programmato una funzione per ottenere dati da una colonna specifica in un file CSV, quindi li ho inseriti in un array con valori di tipo stringa MembersArray[], dai un'occhiata:
void CLogisticRegression::GetDatatoArray(int from_column_number, string &toArr[]) { int handle = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI,m_delimiter); int counter=0; if (handle == INVALID_HANDLE) Print(__FUNCTION__," Invalid csv handle err=",GetLastError()); else { int column = 0, rows=0; while (!FileIsEnding(handle)) { string data = FileReadString(handle); column++; //--- if (column==from_column_number) //if column in the loop is the same as the desired column { if (rows>=1) //Avoid the first column which contains the column's header { counter++; ArrayResize(toArr,counter); toArr[counter-1]=data; } } //--- if (FileIsLineEnding(handle)) { rows++; column=0; } } } FileClose(handle); }
Dentro il nostro testscript.mq5, ecco come chiamare correttamente le funzioni e Inizializzare la Libreria:
#include "LogisticRegressionLib.mqh"; CLogisticRegression Logreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- Logreg.Init("titanic.csv",","); string Sex[]; int SexEncoded[]; Logreg.GetDatatoArray(4,Sex); Logreg.LabelEncoder(Sex,SexEncoded,"male,female"); ArrayPrint(SexEncoded); }
Output stampato, dopo aver eseguito correttamente lo script,
totale maschi =577 codificato in = 0
totale femmine =314 Codificato in =1
[ 0] 0 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 0 1 0 1 1 0 0 1 0 0 1 1 0 0 0 0 0 1 1 1 1 0 1 1 0 0 1 0 1 0 0 1 1 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0
[ 75] 0 0 0 0 1 0 0 1 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 1 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 1 1 0 0 1 0 0 0 1 1 1 0 0 0 0 1 0 0
... ... ... ...
... ... ... ...
[750] 1 0 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 1 1 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 1 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0
[825] 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 0 0 0 1 1 0 1 1 0 0 0 0 1 0 0 1 1 0 0 0 1 1 0 1 0 0 1 0 1 1 0 0
Prima di codificare i tuoi valori, presta attenzione ai members="male,female" sull'argomento della tua funzione, il primo valore che apparirà sulla tua stringa sarà codificato come 0, come puoi vedere appare prima la colonna maschile, quindi tutti i maschi saranno codificati su 0 le femmine saranno codificate su 1. Tuttavia, questa funzione non è limitata a due valori, puoi codificarne quante ne vuoi purché la stringa abbia un senso per i tuoi dati.
Valori mancanti
Se presti attenzione alla colonna Età noterai che ci sono valori mancanti, i valori mancanti potrebbero essere principalmente dovuti ad un motivo ... la morte del nostro set di dati, rendendo impossibile identificare l'età di un individuo, puoi identificare queste mancanze guardando il set di dati considerando che potrebbe richiedere molto tempo soprattutto su set di dati di grandi dimensioni, visto l'utilizzo di pandas per la visualizzazione dei nostri dati, scopriamo le righe mancanti in tutte le colonne
titanic_data.isnull().sum()
L'output sarà:
PassengerId 0
Survived 0
Pclass 0
Sex 0
Age 177
SibSp 0
Parch 0
Fare 0
dtype: int64
Su 891, 177 righe nella nostra colonna Età hanno valori mancanti (NAN).
Ora, sostituiremo i valori mancanti nella nostra colonna rimpiazzandoli con la media di tutti i valori.
void CLogisticRegression::FixMissingValues(double &Arr[]) { int counter=0; double mean=0, total=0; for (int i=0; i<ArraySize(Arr); i++) //first step is to find the mean of the non zero values { if (Arr[i]!=0) { counter++; total += Arr[i]; } } mean = total/counter; //all the values divided by their total number Print("mean ",MathRound(mean)," before Arr"); ArrayPrint(Arr); for (int i=0; i<ArraySize(Arr); i++) { if (Arr[i]==0) { Arr[i] = MathRound(mean); //replace zero values in array } } Print("After Arr"); ArrayPrint(Arr); }
Questa funzione trova la media di tutti i valori diversi da zero, quindi sostituisce tutti i valori zero nell'array con il valore medio.
L'output dopo aver eseguito correttamente la funzione, come puoi vedere tutti i valori zero sono stati sostituiti con 30.0 che era l'età media dei passeggeri del titanic.
Significa 30.0 prima di Arr
[ 0] 22.0 38.0 26.0 35.0 35.0 0.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 0.0 31.0 0.0 35.0 34.0 15.0 28.0 8.0 38.0 0.0 19.0 0.0 0.0
… … … … … … … … …
[840] 20.0 16.0 30.0 34.5 17.0 42.0 0.0 35.0 28.0 0.0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 0.0 41.0 21.0 48.0 0.0 24.0 42.0 27.0 31.0 0.0 4.0
[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 0.0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 0.0 26.0 32.0
Dopo Arr
[ 0] 22.0 38.0 26.0 35.0 35.0 30.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 30.0 31.0 30.0 35.0 34.0 15.0 28.0 8.0 38.0 30.0 19.0 30.0 30.0
… … … … … … … … …
[840] 20.0 16.0 30.0 34.5 17.0 42.0 30.0 35.0 28.0 30.0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 30.0 41.0 21.0 48.0 30.0 24.0 42.0 27.0 31.0 30.0 4.0
[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 30.0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 30.0 26.0 32.0
Costruzione del Modello di Regressione Logistica
Per prima cosa, costruiamo la nostra regressione logistica in cui avremo una variabile indipendente e una variabile dipendente. Quindi arriveremo ad un modello di soluzione completa per il nostro problema in seguito.
Costruiamo il modello su due variabili Survived Versus Age, troveremo quali erano le possibilità che una persona potesse sopravvivere in base alla propria Età.
Finora, sappiamo che alla base di un modello logistico c'è un modello lineare. Iniziamo codificando le funzioni che rendono possibile un modello lineare.
Coefficient_of_X() e y_intercept() queste funzioni non sono nuove, le costruiamo in base al primo articolo di questa serie, prendi in considerazione di leggerlo per ulteriori informazioni su queste funzioni e sulla regressione lineare in generale.
double CLogisticRegression::y_intercept() { // c = y - mx return (y_mean-coefficient_of_X()*x_mean); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CLogisticRegression::coefficient_of_X() { double m=0; //--- { double x__x=0, y__y=0; double numerator=0, denominator=0; for (int i=0; i<ArraySize(m_xvalues); i++) { x__x = m_xvalues[i] - x_mean; //right side of the numerator (x-side) y__y = m_yvalues[i] - y_mean; //left side of the numerator (y-side) numerator += x__x * y__y; //summation of the product two sides of the numerator denominator += MathPow(x__x,2); } m = numerator/denominator; } return (m); }
Ora programmiamo il modello logistico dalla formula.
Tieni presente che z viene chiamato anche log-odds perché l'inverso del sigmoide afferma che z può essere definito come il log della probabilità dell'etichetta 1 (ad es. "Sopravvissuto") diviso per la probabilità dell'etichetta 0 (ad es. , "non sopravvissuto"):
In questo caso y = mx+c (ricorda dal modello lineare).
Trasformandolo in codice il risultato sarà,
double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1);
Presta attenzione a ciò che è stato fatto qui sul valore z la formula è log(y/1-y), ma il codice è scritto come log(y_ )-log(1-y_); Ricorda dalle Regole dei Logaritmi in matematica!! La divisione dei logaritmi con la stessa base risulta dalla sottrazione degli esponenti, leggi.
Questo è fondamentalmente il nostro modello quando la formula è programmata, ma c'è molto da fare all'interno della nostra funzione LogisticRegression() , ecco tutto ciò che è all'interno della funzione:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7) { int arrsize = ArraySize(x); //the input array size double p_hat =0; //store the probability //--- int train_size = (int)MathCeil(arrsize*train_size_split); int test_size = (int)MathFloor(arrsize*(1-train_size_split)); ArrayCopy(m_xvalues,x,0,0,train_size); ArrayCopy(m_yvalues,y,0,0,train_size); //--- y_mean = mean(m_yvalues); x_mean = mean(m_xvalues); // Training our model in the background double c = y_intercept(), m = coefficient_of_X(); //--- Here comes the logistic regression model int TrainPredicted[]; double sigmoid = 0; ArrayResize(TrainPredicted,train_size); //resize the array to match the train size Print("Training starting..., train size=",train_size); for (int i=0; i<train_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); double odds_ratio = p_hat/(1-p_hat); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]); } //--- Testing our model if (train_size_split<1.0) //if there is room for testing { ArrayRemove(m_xvalues,0,train_size); //clear our array ArrayRemove(m_yvalues,0,train_size); //clear our array from train data ArrayCopy(m_xvalues,x,0,train_size,test_size); //new values of x, starts from where the training ended ArrayCopy(m_yvalues,y,0,train_size,test_size); //new values of y, starts from where the testing ended Print("start testing...., test size=",test_size); ArrayResize(Predicted,test_size); //resize the array to match the test size for (int i=0; i<test_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); double odds_ratio = p_hat/(1-p_hat); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]); } }
Ora, formiamo e testiamo il nostro modello nel nostro TestScript.mq5
double Age[]; Logreg.GetDatatoArray(5,Age); Logreg.FixMissingValues(Age); double y_survival[]; int Predicted[]; Logreg.GetDatatoArray(2,y_survival); Logreg.LogisticRegression(Age,y_survival,Predicted);
L'output di uno script eseguito correttamente sarà:
Inizio formazione..., dimensione della formazione=624
0 Age =22.00 survival_Predicted =0
1 Age =38.00 survival_Predicted =0
... .... ....
622 Age =20.00 survival_Predicted =0
623 Age =21.00 survival_Predicted =0
Inizio formazione..., dimensione della formazione=267
0 Age =21.00 survival_Predicted =0
1 Age =61.00 survival_Predicted =1
.... .... ....
265 Age =26.00 survival_Predicted =0
266 Age =32.00 survival_Predicted =0
Bene. Il nostro modello è ora funzionante e possiamo almeno ottenere i risultati da esso, ma il modello sta facendo buone previsioni?
Dobbiamo verificarne la precisione.
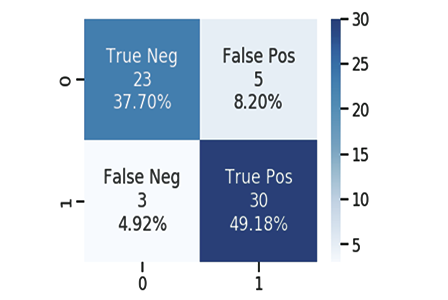
La Matrice di Confusione
Come tutti sappiamo, ogni modello buono o cattivo può fare previsioni, ho creato un file CSV per le previsioni che il nostro modello da un lato ha fatto con i valori originali dei test dei dati sulla sopravvivenza dei passeggeri, ancora una volta 1 significa sopravvissuto, 0 significa non sopravvissuto.
Qui sono solo scarse 10 colonne:
| Originale | Previsione | |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 2 | 0 | 1 |
| 3 | 1 | 0 |
| 4 | 0 | 0 |
| 5 | 0 | 0 |
| 6 | 1 | 1 |
| 7 | 0 | 1 |
| 8 | 1 | 0 |
| 9 | 0 | 0 |
Calcoliamo la matrice di confusione utilizzando:
- TP - Vero Positivo
- TN - Vero Negativo
- FP - Falso Positivo
- FN - Falso Negativo
Ora, cosa sono questi valori?
TP (Vero Positivo)
È quando il valore Originale è Positivo (1) e il tuo modello prevede anch'esso Positivo (1)
TN (Vero Negativo)
È quando il valore Originale è Negativo (0) e il tuo modello prevede anch'esso Negativo (0)
FP (Falso Positivo)
E' quando il valore originale è Negativo (0), ma il tuo modello prevede Positivo (1)
FN (Falso Negativo)
È quando il valore originale è Positivo (1) ma il tuo modello prevede Negativo (0)
Ora che conosci i valori, calcoliamo la matrice di confusione per il campione sopra come esempio
| Originale | Previsione | TP/TN/FP/FN | |
|---|---|---|---|
| 0 | 0 | 0 | TN |
| 1 | 0 | 1 | FP |
| 2 | 0 | 1 | FP |
| 3 | 1 | 0 | FN |
| 4 | 0 | 0 | TN |
| 5 | 0 | 0 | TN |
| 6 | 1 | 1 | TP |
| 7 | 0 | 1 | FP |
| 8 | 1 | 0 | FN |
| 9 | 0 | 0 | TN |
La matrice di confusione può essere utilizzata per calcolare l'Accuratezza del nostro modello utilizzando questa formula.
Dalla nostra tabella:
- TN = 4
- TP = 1
- FN = 2
- FP = 3
Accuratezza = 1 + 5 / 4 + 1 + 2 + 3
Accuratezza = 0,5
In questo caso la nostra precisione è del 50% .( 0,5*100% convertendolo in percentuale)
Ora, che hai capito come funziona la matrice di confusione 1X1. È ora di convertirlo in codice e analizzare l'accuratezza del nostro modello sull'intero set di dati
void CLogisticRegression::ConfusionMatrix(double &y[], int &Predicted_y[], double& accuracy) { int TP=0, TN=0, FP=0, FN=0; for (int i=0; i<ArraySize(y); i++) { if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==1) TP++; if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==0) TN++; if (Predicted_y[i]==1 && (int)y[i]==0) FP++; if (Predicted_y[i]==0 && (int)y[i]==1) FN++; } Print("Confusion Matrix \n ","[ ",TN," ",FP," ]","\n"," [ ",FN," ",TP," ] "); accuracy = (double)(TN+TP) / (double)(TP+TN+FP+FN); }
Ora torniamo alla nostra Funzione Principale nella nostra classe nota come LogisticRegression(), questa volta la trasformeremo in una doppia funzione che restituisce l'accuratezza del modello, ridurrò anche il numero di funzioni Print() ma li aggiungo a un'istruzione if poiché non vogliamo stampare i valori ogni volta a meno che non desideriamo eseguire il debug della nostra classe. Tutte le modifiche sono evidenziate in blu:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7) { double accuracy =0; //Accuracy of our Train/Testmodel int arrsize = ArraySize(x); //the input array size double p_hat =0; //store the probability //--- int train_size = (int)MathCeil(arrsize*train_size_split); int test_size = (int)MathFloor(arrsize*(1-train_size_split)); ArrayCopy(m_xvalues,x,0,0,train_size); ArrayCopy(m_yvalues,y,0,0,train_size); //--- y_mean = mean(m_yvalues); x_mean = mean(m_xvalues); // Training our model in the background double c = y_intercept(), m = coefficient_of_X(); //--- Here comes the logistic regression model int TrainPredicted[]; double sigmoid = 0; ArrayResize(TrainPredicted,train_size); //resize the array to match the train size Print("Training starting..., train size=",train_size); for (int i=0; i<train_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]); } ConfusionMatrix(m_yvalues,TrainPredicted,accuracy); //be careful not to confuse the train predict values arrays printf("Train Model Accuracy =%.5f",accuracy); //--- Testing our model if (train_size_split<1.0) //if there is room for testing { ArrayRemove(m_xvalues,0,train_size); //clear our array ArrayRemove(m_yvalues,0,train_size); //clear our array from train data ArrayCopy(m_xvalues,x,0,train_size,test_size); //new values of x, starts from where the training ended ArrayCopy(m_yvalues,y,0,train_size,test_size); //new values of y, starts from where the testing ended Print("start testing...., test size=",test_size); ArrayResize(Predicted,test_size); //resize the array to match the test size for (int i=0; i<test_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]); } ConfusionMatrix(m_yvalues,Predicted,accuracy); printf("Testing Model Accuracy =%.5f",accuracy); } return (accuracy); //Lastly, the testing Accuracy will be returned }
L'esecuzione corretta dello script produrrà quanto segue:
Inizio formazione..., dimensione della formazione=624
Matrice di Confusione
[ 378 0 ]
[ 246 0 ]
Accuratezza Modello di Prova = 0.60577
Inizio formazione..., dimensione della formazione=267
Matrice di Confusione
[ 171 0 ]
[ 96 0 ]
Accuratezza del Modello Test= 0.64045
Evviva! Ora siamo in grado di identificare quanto sia buono il nostro modello attraverso i numeri, sebbene l'accuratezza del 64,045% sui dati del test non sia abbastanza buona per utilizzare il modello per fare previsioni (secondo me) almeno per ora, abbiamo una libreria che potrebbe aiutarci a classificare i dati usando la regressione logistica.
Ulteriori spiegazioni sulla funzione principale:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7)
L'input train_size_split serve per suddividere i dati in training e testing per impostazione predefinita la suddivisione è 0,7, il che significa che il 70% percento dei dati sarà per il training mentre il restante 30% sarà per scopi di test, l'array di riferimento Predicted[] restituirà i dati previsti del test.
Binary Cross Entropy nota come Loss Function
Proprio come l'Errore Quadratico medio è la funzione di errore per la regressione lineare, la Binary cross-entropy è la funzione di costo per la regressione logistica.
Teoria:
Vediamo come funziona usandolo in due casi per la regressione logistica, ovvero: quando l'output effettivo è 0 & 1
01: Quando il valore dell'output attuale è 1
Considera il modello per due campioni di input p1 = 0,4 e p2 = 0,6. Ci si aspetta che p1 venga penalizzato più di p2 perché è più lontano da 1 rispetto a p1.
Da un punto di vista matematico, il logaritmo negativo di un numero piccolo è un numero grande e viceversa.
Per penalizzare gli input useremo la formula
penalità = -log(p)
In questi due casi
- Penalità = -log(0.4)=0.4 cioè la penalità su p1 è 0,4
- Penalità = -log(0.6)=0.2 cioè la penalità su p2 è 0,2
02: Quando il valore dell'output attuale è 0
Considera l'output del modello per due campioni di input, p1 = 0,4 e p2= 0,6 (come nel caso precedente). Ci si aspetta che p2 debba essere penalizzato più di p1 perché è più lontano da 0 ma, tieni presente che l'output del modello logistico è la probabilità che un campione sia positivo, penalizzare le probabilità di input di cui abbiamo bisogno per trovare la probabilità che un campione sia negativo, è facile ecco la formula
Probabilità che un campione sia negativo = 1-probabilità che un campione sia positivo
Quindi, per trovare la penalità in questo caso la formula della penalità sarà
penalità = -log(1-p)
In questi due casi
- Penalità = -log(1-p) = -log(1-0.4) =0.2 cioè la penalità è 0.2
- Penalità = -log(1-p) = -log(1-0.6) =0.4 cioè la penalità è 0.4
La penalità su p2 è maggiore che su p1 (funziona come previsto) cool!
Ora la penalità per un singolo campione di input il cui output del modello è p e il vero valore di output è y può essere calcolata come segue.
se il campione di input è positivo y=1:
penalità = -log(p)
altrimenti:
penalità = -log(1-p)
Un'equazione a riga singola equivalente alla precedente istruzione del blocco se-altrimenti può essere scritta come
penalità = -( y*log(p) + (1-y)*log(1-p) )
dove
y = valore attuale nella nostra serie di dati
p = probabilità stimata grezza del modello (prima dell'arrotondamento)
Dimostriamo che questa equazione è equivalente alla precedente affermazione se-altrimenti
01: quando il valore di output di y = 1
penalita = -( 1*log(p) + (1-1)*log(1-p) ) = -log(p) quindi provato
02: quando il valore di output di y = 0
penalità = -( 0*log(p) + (1-0)* log(1-p) ) = log(1-p) quindi provato
Infine, la funzione log loss per N campioni di input sembra
Log-loss è indicativo di quanto è vicina la probabilità di previsione al valore effettivo/vero corrispondente (0 o 1 nel caso di classificazione binaria). Più la probabilità prevista diverge dal valore effettivo, maggiore è il valore della log-loss.
Le funzioni di costo come log-loss e molte altre possono essere utilizzate come metrica su quanto è buono il modello, ma l'uso più grande è quando si ottimizza il modello per i parametri migliori usando la discesa del gradiente o altri algoritmi di ottimizzazione(ne parleremo nelle serie successive rimanete sintonizzati).
Se puoi misurarlo, puoi migliorarlo. Questo è lo scopo principale delle funzioni di costo.
dal nostro set di dati di test e addestramento sembra che la nostra log-loss sia compresa tra 0,64 e 0,68, il che non è l'ideale (in parole povere).
set di dati di formazione
Logloss =0.6858006105398738
set di dati del test
Logloss =0.6599503403665642
Ecco come possiamo convertire la nostra funzione log-loss in codice
double CLogisticRegression::LogLoss(double &rawpredicted[]) { double log_loss =0; double penalty=0; for (int i=0; i<ArraySize(rawpredicted); i++ ) { penalty += -((m_yvalues[i]*log(rawpredicted[i])) + (1-m_yvalues[i]) * log(1-rawpredicted[i])); //sum all the penalties if (m_debug) printf("penalty =%.5f",penalty); } log_loss = penalty/ArraySize(rawpredicted); //all the penalties divided by their total number Print("Logloss =",log_loss); return(log_loss); }
Per ottenere l'output previsto grezzo, è necessario tornare al test principale e all'addestramento per i loop e archiviare i dati nell'array previsto grezzo subito prima del processo di arrotondamento delle probabilità.
Sfida di Regressione Logistica Dinamica Multipla
La sfida più grande che ho dovuto affrontare durante la creazione di librerie di regressione sia lineare che logistica in entrambi gli articoli sia questo che il precedente, sono le molteplici funzioni di regressione dinamica in cui potremmo usarle per più colonne di dati senza dover programmare le cose per ogni dato che viene aggiunto al nostro modello, nell'articolo precedente ho codificato due funzioni con lo stesso nome l'unica differenza tra loro era il numero di dati con cui ogni modello poteva lavorare, uno era in grado di lavorare con due variabili indipendenti l'altro con quattro, rispettivamente:
void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]);
Ma questo metodo è scomodo e sembra un modo precipitoso di codificare le cose e viola le regole del codice pulito e DRY (non ripeterti i principi che OOP sta cercando di aiutarci a raggiungere).
A differenza di Python con funzioni flessibili che potrebbero richiedere un gran numero di argomenti funzionali con l'aiuto di *args e **kwargs, in MQL5 questo potrebbe essere ottenuto usando solo la stringa per quanto posso pensare, credo questo sia il nostro punto di partenza.
void CMultipleLogisticRegression::MLRInit(string x_columns="3,4,5,6,7,8")
L'input x_columns rappresenta tutte le colonne delle variabili indipendenti che useremo nella nostra libreria, queste colonne richiederanno di avere più array indipendenti per ciascuna delle colonne ma non c'è modo di creare array dinamicamente, quindi l'uso degli array qui fallisce.
Possiamo creare più file CSV in modo dinamico e usarli come array, di sicuro questo renderà i nostri programmi più costosi quando si tratta di utilizzare le risorse del computer rispetto all'uso di array, specialmente quando si tratta di dati multipli per non parlare dei cicli while che useremo frequentemente per aprire i file rallenteranno l'intero processo, non sono sicuro al 100% quindi correggimi se sbaglio.
Anche se possiamo ancora usare il modo menzionato.
Ho scoperto la strada da seguire per utilizzare gli array, memorizzeremo tutti i dati di tutte le colonne in un array, quindi utilizzeremo i dati separatamente da un singolo array.
int start = 0; if (m_debug) //if we are on debug mode print Each Array vs its row for (int i=0; i<x_columns_total; i++) { ArrayCopy(EachXDataArray,m_AllDataArray,0,start,rows_total); start += rows_total; Print("Array Number =",i," From column number ",m_XColsArray[i]); ArrayPrint(EachXDataArray); }
All'interno del ciclo for, possiamo manipolare i dati negli array ed eseguire tutti i calcoli per il modello nel modo desiderato per tutte le colonne, ho provato questo metodo ma ho ancora fallito nel tentativo,il motivo per cui ho spiegato questa ipotesi è per far capire a tutti coloro che leggono questo articolo questa sfida e accolgo con favore tutte le tue opinioni nelle sezioni dei commenti su come possiamo codificare questa funzione di regressione logistica dinamica multipla il mio tentativo di creare questa libreria si trova a questo link https:// www.mql5.com/it/code/38894.
Questo tentativo non ha avuto successo ma ha delle speranze e credo valga la pena condividerle.
Vantaggi della Regressione Logistica
- Non presuppone per quanto riguarda la distribuzione della classe nelle caratteristiche di spazio
- Facilmente estendibile a più classi (regressione multinomiale)
- Naturale visione probabilistica delle previsioni di classe
- Veloce da addestrare
- Molto veloce nella classificazione dei record sconosciuti
- Buona precisione per molti set di dati semplici
- Resistente all'overfitting
- Può interpretare i coefficienti del modello come un indicatore con caratteristiche importanti
Svantaggi
- Costruisce confini lineari
Pensieri finali
Questo è tutto per questo articolo, la regressione logistica viene utilizzata in più campi nella vita reale come la classificazione delle e-mail come spam e non spam, il rilevamento della scrittura a mano e molte altre cose interessanti.
So che non useremo algoritmi di regressione logistica per classificare i dati titanici o nessuno dei campi citati, tuttavia, specialmente nella piattaforma MetaTrader 5, come detto in precedenza, il set di dati è stato utilizzato solo per costruire la libreria rispetto all'output ottenuto in Python linkato qui > https://github.com/MegaJoctan/LogisticRegression-MQL5-and-python. Nel prossimo articolo vedremo come possiamo utilizzare i modelli logistici per prevedere il crollo del mercato azionario.
Poiché questo articolo è diventato troppo lungo, lascio il compito di regressione multipla come compito a tutti i lettori.
Tradotto dall’inglese da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/en/articles/10626
Impara a progettare un sistema di trading tramite ADX
Scienza dei Dati e Apprendimento Automatico (Parte 01): Regressione Lineare
Imparare come progettare un sistema di trading con ATR
Cosa è possibile fare con le Medie Mobili
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso