Brute-Force-Ansatz zur Mustersuche (Teil II): Immersion

Einführung

Ich habe beschlossen, das Thema fortzusetzen, das wir im vorherigen Artikel begonnen haben. Diesmal werden wir eine eingehende Analyse von Währungspaaren unter Verwendung der modifizierten Anwendungsversion durchführen. Ich möchte dem Nutzer Aleksey Vyazmikin für seinen Beitrag zur Projektentwicklung danken. Seine Ratschläge waren in technischer Hinsicht sehr nützlich und haben die weitere Entwicklung vorangetrieben. Ich werde diese Arbeit im nächsten Artikel fortsetzen und weitere interessante Daten und Ergebnisse liefern. Ich glaube, dass es sehr wichtig ist, die Effektivität der Analyse eines bestimmten Währungspaares im globalen Maßstab zu zeigen, sowie den Unterschied in der Analyse von Zeitintervallen mit maximaler und minimaler Dauer zu demonstrieren. Da meine Zeit- und Rechenressourcen begrenzt sind, konnte ich nur wenige Währungspaare mit nur einem Zeitrahmen abdecken. Für die erste Bekanntschaft mit globalen Mustern scheint dies jedoch ausreichend zu sein. Bei der Analyse der Daten werde ich zusätzlich die Daten aus dem vorherigen Artikel verwenden.

Warum ist dieses Thema so interessant?

Sehr oft bedeuten alle Ideen für die MetaTrader 4 und MetaTrader 5 Expert Advisor Programmierer unzählige Zeilen Code, unzählige Tests, Optimierungen, Hin- und Her-Tests. In den meisten Fällen bekommen wir nicht das, was wir wollen. Manche Programmierer langweilen sich bei diesem Spezifikum. Der Prozess des Forschens und Suchens wird zur Routine. Wenn die Arbeit keine moralische Befriedigung und kein Geld bringt, dann ist es sehr wahrscheinlich, dass man aufgibt. Genau das ist mir passiert. Ich beschloss, mich von der Routine zu verabschieden und mit der Automatisierung von Handlungen zu beginnen, die erfolgreich von einer Maschine ausgeführt werden können. Die Maschine hat keine Emotionen und sie ist ein idealer Arbeiter, im Gegensatz zu mir. Natürlich hat die Maschine kein so weitreichendes Denken wie ein Mensch, aber sie verfügt über eine Menge Rechenressourcen und kann einige Prozesse einfacher und schneller umsetzen. Ich hatte die Wahl, eine eigene, entwicklungsfähige neuronale Netzwerkarchitektur zu schreiben oder mit dem einfachsten Ansatz zur Lösung des Problems zu beginnen. Ich entschied mich für den letzteren Ansatz. Trotz seiner Einfachheit bietet das Projekt Raum für Kreativität und Interesse, im Gegensatz zur einfachen Programmierung von MQL-Produkten. Es ist eine gute Idee, an einer universellen Vorlage zu arbeiten und diese durch schrittweises Hinzufügen der erforderlichen Funktionalität weiterzuentwickeln. Wir können mit einer einfachen Vorlage beginnen und dann neue Vorlagen für ein bestimmtes Funktionsprinzip erstellen. So können wir uns von der langweiligen Routine befreien und in unserer Entwicklung vorankommen. Tja, Faulheit ist der Vater des Fortschritts.

Neue Version des Brute-Force-Programms und eine Liste der Änderungen

Es gab nur eine Änderung im Programm, die in einem roten Rahmen dargestellt ist. Diese Einstellung wurde von der zweiten Registerkarte übernommen, wo sie sich am besten bewährt hat. Der Grund für die Aufnahme dieser Einstellung ist, dass sie einen sehr starken Einfluss auf die Qualität der Endergebnisse hat. Während der Analyse, auf der ersten Registerkarte, wurden alle Ergebnisse zunächst nach Qualität sortiert. Als Qualitätskriterium wurde der Gewinnfaktor oder die erwartete Auszahlung in Punkten verwendet. Aber das Programm erlaubte uns nicht die Bewertung der Graphenform. Ich habe den Linearitätsfaktor (Ähnlichkeit mit einer Geraden) als Formkriterium verwendet, was uns die visuelle Überprüfung jeder Option erspart. Hier können wir zu dem Schluss kommen, dass geradere und glattere Graphen eher eine hochwertige Variante auf der zweiten Registerkarte ergeben. Außerdem haben solche Graphen eine geringere Anzahl von Varianten, die durch einen Filter auf der zweiten Registerkarte verworfen werden. Für die Berechnung dieses Wertes ist ein zweiter Durchlauf erforderlich. Wenn dieser Filter aktiv ist, ist die Brute-Force-Geschwindigkeit etwa 2 mal langsamer. Aber es ist nicht die Geschwindigkeit, die für uns wichtig ist, sondern die Gesamtzahl der erhaltenen primären Ergebnisse, da deren Qualität die weitere Leistung beeinflusst.

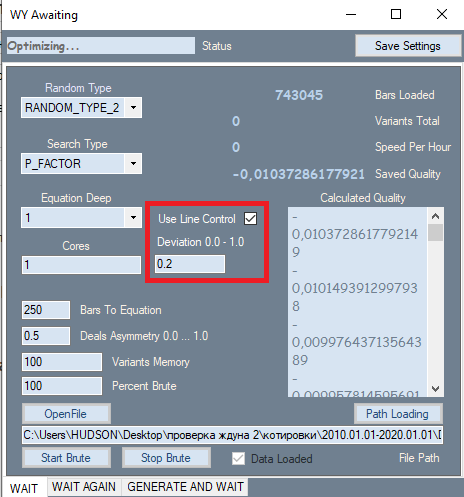
Neben dem eingeführten Filter hat sich auch das Polynom selbst geändert. Jetzt akzeptiert das Polynom nicht nur Close[i]-Open[i] bestimmter Balken als Argumente, sondern auch die folgenden Werte:

• Close[i]-Open[i]
• High[i]-Open[i]
• Low[i]-Close[i]
• Low[i]-Open[i]
• High[i]-Close[i]

Jetzt beinhaltet die Formel alle Preisdaten eines bestimmten Balkens, anders als die vorherige Version des Programms. Dadurch wird die Komplexität des Polynoms stark erhöht, was zu einer Verringerung der Brute-Force-Geschwindigkeit führt. Aber jetzt können wir bessere und effizientere Marktformeln auswählen, vorausgesetzt, es sind genügend Rechenressourcen vorhanden. Natürlich könnten wir auch andere Variablen mit diesen Daten erstellen. Aber wenn diese Werte im Polynom verwendet werden, erhält man diejenigen Werte, die z. B. eine lineare Kombination der obigen Werte sein können: 

• C1*(High[i]-Close[i]) + C2*(Low[i]-Close[i]) = NewQuant
• if  C1 = 1 and C2 = -1
• NewQuant = (High[i]-Close[i]) - (Low[i]-Close[i]) =  High[i]-Low[i]
• in den anderen Fällen
• NewQuant = (C1-C3)*(High[i]-Close[i])+(C2+C3)*(Low[i]-Close[i])  +  C3*((High[i]-Close[i]) - (Low[i]-Close[i])) = (C1-C3)*(High[i]-Close[i])+(C2-C3)*(Low[i]-Close[i]) +  C3*(High[i]-Low[i])

Mit anderen Worten: Mit Hilfe einer Linearkombination von Variablen, die wiederum aus Linearkombinationen anderer Variablen bestehen, können wir neue Variablen zusammensetzen, ohne sie überhaupt in die Grundformel aufzunehmen. Es ist besser zu versuchen, die Variablen, die aus anderen gebildet werden können, die bereits in der Formel vorhanden sind, nicht aufzunehmen. Sie werden bei der Auswahl der Koeffizienten erscheinen, abhängig von den Werten der Koeffizienten selbst.

Als Ergebnis wird das neue Polynom viel komplizierter sein:

• Y = Sum(0,NC-1)( C[i]*Variant of product(x[1]^p[1]*x[2]^p[2]...*x[N]^p[N]) )
  
• Sum(0,N)(p[i])=MaxPowOfPolinom
• NC - die Gesamtzahl der Terme im Polynom, die gleich der Anzahl der ausgewählten Koeffizienten ist,
  

wobei x[i] Argumente sind, die das Polynom annimmt, und p[i] der Grad ist, auf den das Argument erhöht wird. Der Gesamtgrad aller konstituierenden Faktoren sollte die erlaubte Anzahl für unser Polynom nicht überschreiten, da kein Computer mit solch komplexen Expansionen umgehen kann. Ich verwende fast immer Grad 1 oder 2 oder 3, wenn die Anzahl der Balken für die Formel minimal ist. Wie auch immer, die Verwendung höherer Grade ist ineffektiv, selbst auf den Servern. Es gibt nicht genug Rechenleistung.

Nachfolgend sind die Argumentationsmöglichkeiten aufgeführt. Die Endsumme umfasst alle möglichen Kombinationen von Produkten:

1. x[i] =Close[i]-Open[i]
2. x[i] =High[i]-Open[i]
3. x[i] =Low[i]-Close[i]
4. x[i] =High[i]-Open[i]
5. x[i] =High[i]-Close[i]

Ich möchte auch klären, warum wir alle diese Aktionen mit dem Polynom durchführen. Der Punkt ist, dass jedes System letztlich auf einen Satz von Bedingungen hinausläuft. Es kann eine oder mehrere Bedingungen geben, was keine Rolle spielt, denn Bedingungen sind eine logische Funktion. Ein Satz von Bedingungen kann letztendlich in einen booleschen Ausdruck umgewandelt werden, der entweder wahr oder falsch zurückgibt. Ein solches Signal kann nur als Ja oder Nein interpretiert werden. Es ist aber nicht möglich, zu bestimmen, wie stark das Signal ist oder das Signal anzupassen. Wenn Sie mehrere Indikatoren als Signale verwenden, können Sie die Parameter dieser Indikatoren separat anpassen, was zu einer Änderung des endgültigen logischen Ausdrucks oder zu einer Änderung des Signals führt, was sich schließlich auf den Handel auswirkt. Aber ich denke, dass dies extrem unpraktisch ist, denn wenn man den einen oder anderen Parameter eines bestimmten Indikators ändert, weiß man nicht, wie sich das auf den Handel auswirkt.

Die Hauptidee hinter diesem Ansatz war Einfachheit und Effizienz. Warum gerade dieser Ansatz? Er hat mehrere Vorteile:

• Einzigartigkeit der optimierten Funktion
• Abhängigkeit der Signalstärke von dem Funktionswert
• Einfache Bedienung
• Der einzige optimierbare Parameter ist der Polynomwert

Das Wichtigste ist, dass wir die Anzahl der Bedingungen und deren Typ nicht auswählen müssen. Das liegt daran, dass wir ursprünglich die Idee akzeptieren, dass wir, anstatt nach einer unendlichen Menge von Bedingungen zu suchen, alle diese Bedingungen auf eine einzige Funktion reduzieren können, die entweder eine positive oder negative Bruchzahl ausgibt. Je nachdem, wie zuverlässig die eine oder andere Funktion ist, kann sie ein stärkeres Signal im Modulus benötigen. In einigen Formeln kann dies Skalierbarkeit bieten. Skalierbarkeit bedeutet hier die Fähigkeit, ein Signal zu verstärken, wenn die Anzahl der Geschäfte abnimmt.

Im Allgemeinen führen meine Untersuchungen, wie auch die vieler anderer Personen, zu einer einzigen Schlussfolgerung. Ein Versuch, das Einstiegssignal zu verstärken, führt unweigerlich zu einer Abnahme der Anzahl der Geschäfte in einem bestimmten Zeitraum. Mit anderen Worten, für jede Funktion, die eine Zufallskomponente hat, haben einige Punkte immer ein vorhersehbareres Ergebnis als andere Punkte. Wenn unsere Funktion effizient genug ist, dann kann sie mit steigenden Anforderungen an das von dieser Funktion gelieferte Signal ein bestimmtes Level an Vorhersagbarkeit erreichen. Natürlich gilt das nicht für jede Funktion, die unsere Primärbedingungen erfüllt. Aber je strenger die primären Bedingungen sind, desto höher ist die erwartete Ausbeute derjenigen Formelvarianten, die wir mit dem Brute-Force-Ansatz finden können. Dies gilt auch für Gradient Boosting sowie für andere Methoden der Mustersuche, einschließlich neuronaler Netze.

Vieles hängt von der Datenstichprobe ab. Je kleiner die Stichprobe ist, desto größer ist die Chance, ein zufälliges Ergebnis zu erhalten. Ein zufälliges Ergebnis ist hier ein Ergebnis, das entweder nicht funktioniert oder extrem ineffektiv arbeitet, wenn man das endgültige System auf die globale Historie des Symbols, auf dem das Muster gesucht wurde, testet.

Wir werden versuchen, die Frage zu beantworten, wie die zukünftige Qualität des endgültigen Handelssystems von der Größe des analysierten Datenbereichs und dem Arbeitsaufwand, der für das Finden dieses Systems erforderlich ist, abhängt. Zunächst wollen wir die Formel für die mathematische Erwartung der Anzahl der gefundenen Strategien über einen festen Zeitraum definieren:

• Mn(t) = W(t,F)*Ef(T,N,L)
• Mn -  mathematisch erwartete Anzahl der gefundenen Strategien, die unsere Anforderungen erfüllen
• W(t,F) = F*t - die resultierende Anzahl der geprüften Varianten pro Zeiteinheit
• Ef(T,N,L) = ? - die Brute-Force-Effizienz, die von der Intervalllänge, dem Quotentyp, der geforderten Anzahl der geschlossenen Ordnungen und dem geforderten Linearitätsfaktor abhängt, wenn er bei der Brute-Force berücksichtigt wird (dieser Wert ist gleich der Wahrscheinlichkeit, dass die Ergebnisse der aktuellen Variante die notwendigen und ausreichenden Werte annehmen werden)
  
• N - die minimal zulässige Anzahl der Positionen, die für unseren Test ausreichen würde
• L - der maximal zulässige Linearitätsfaktor (als ein zusätzliches Kontrollkriterium)
• F - die Brute-Force-Häufigkeit der Strategievarianten

Es ist äußerst schwierig, die Form der Ef-Funktion zu bestimmen, aber wir können grob abschätzen, wie sie aussehen wird und welche Eigenschaften sie hat:

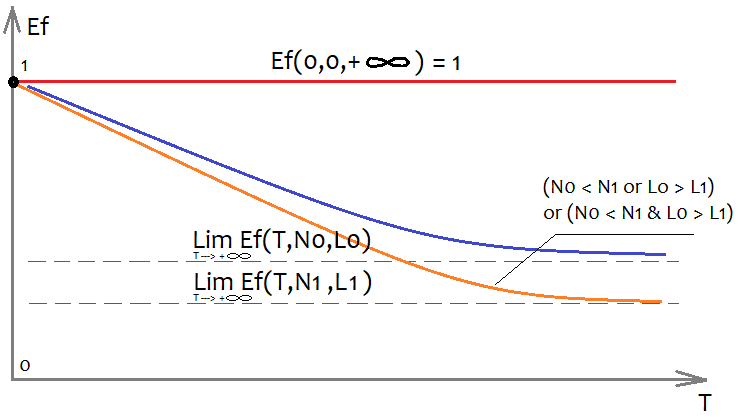
Um eine mehrdimensionale Funktion auf einer Ebene darstellen zu können, ist es notwendig, alle ihre Argumente mit einigen Zahlen zu fixieren, außer einem Argument, durch das der Graph selbst gebildet wird. Besonders interessant ist die Variable T, die die Dauer der analysierten Probe in der Zeit bezeichnet, vorausgesetzt wir analysieren einen Zeitrahmen. Wenn wir diese Annahme verwerfen, dann können wir den Stichprobenumfang als T nehmen - dies wird das Aussehen des Graphen nicht verändern. Natürlich sind wir daran interessiert, wie sich die verbleibenden 2 Argumente auf das Aussehen des Graphen auswirken werden.Wenn wir uns erinnern, wie die Funktion mit einem Quantisierungsfehler aussieht Dies ist in der Abbildung dargestellt. Je mehr Ordnungen wir in der endgültigen Version haben wollen, desto weniger Systeme werden wir finden, die unsere Anforderungen erfüllen, einfach weil es viel einfacher ist, ein System mit weniger Ordnungen zu finden. Dasselbe gilt für den Linearitätsfaktor (Abweichung von einer Geraden), allerdings ist hier der bessere Linearitätsfaktor der kleinere (tendiert gegen Null).

Wenn wir das Konzept der Systemqualität nicht fixieren (weil dieser Wert sowohl ein Gewinnfaktor als auch eine mathematische Erwartung sein kann), dann können wir auch das Konzept der maximalen Qualität des gefundenen Systems einführen. Wir können auf ähnliche Weise beschreiben, wovon sie abhängt:

• Mq=Mq(T,N,S)
• S - die gewählte Formelkonfiguration

Mit anderen Worten, die höchstmögliche Qualität der Strategie hängt direkt von der Effektivität unserer Formel ab, sowie von unseren Anforderungen und der Komplexität des Intervalls. Gleichzeitig gehen wir immer noch davon aus, dass der Beginn des Bereichs fest ist und jede Variation des Trainingsstartpunkts einzigartig ist und einzigartige Startparameter ergibt. Mit anderen Worten, wenn wir einen anderen Startzeitpunkt für den Trainingsbereich wählen, erhalten wir unterschiedliche Effizienzwerte und andere Parameter, sowie die endgültige Qualität der erhaltenen Systeme.

Wir können auch zu dem Verständnis kommen, dass jeder Qualitätstyp seinen Maximalwert hat, z. B. ist der Maximalwert des Gewinnfaktors unendlich, aber ich mag dieses Maß nicht für die Analyse verwenden, weil sein Maximalwert nicht begrenzt ist, und somit werden grafische Modelle mit dem PF schwieriger zu verstehen sein. Daher verwende ich P_FACTOR, mein eigenes Analogon von PF. Er liegt im Bereich [-1,1].

• P_FACTOR=(Profit-Loss)/(Profit+Loss)

Sein Maximum ist gleich 1, und daher ist es bequemer, mit ihm zu arbeiten. Hier ist die Funktion, die das Maximum dieses Wertes in Abhängigkeit von T (ausgewählter Bereich und seine Stichprobe) beschreibt.

• Mx=Mx(T)

Wenn der Parameter oder das Qualitätskriterium P_FACTOR ist, dann ist Mx(T)=1. Die Funktionsform kann unbekannt sein, aber es ist bekannt, dass Mx'(T) > 0 im gesamten positiven Teil der T-Achse ist. Das bedeutet, dass der Wert an jedem Punkt positiv ist, und somit das Chart die ganze Zeit über ansteigt.

Für den Gewinnfaktor sieht das wie folgt aus:

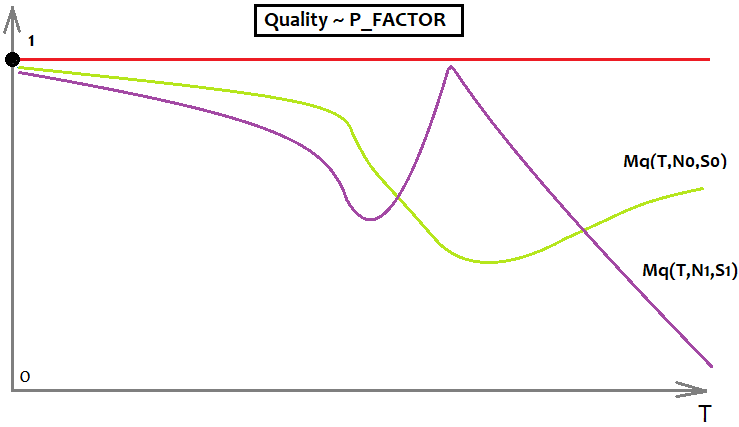
Dieses Beispiel hat eine Obergrenze des PF und zwei Diagramme, die zwei verschiedene Formeln mit unterschiedlichen Anforderungen zeigen. Auf dem Graphen ist die Formel mit der Kalkfarbe besser, weil sie weniger anfällig für Qualitätsschwund ist, wenn "T" gegen unendlich tendiert.

Für die mathematische Erwartung sieht dies wie folgt aus:

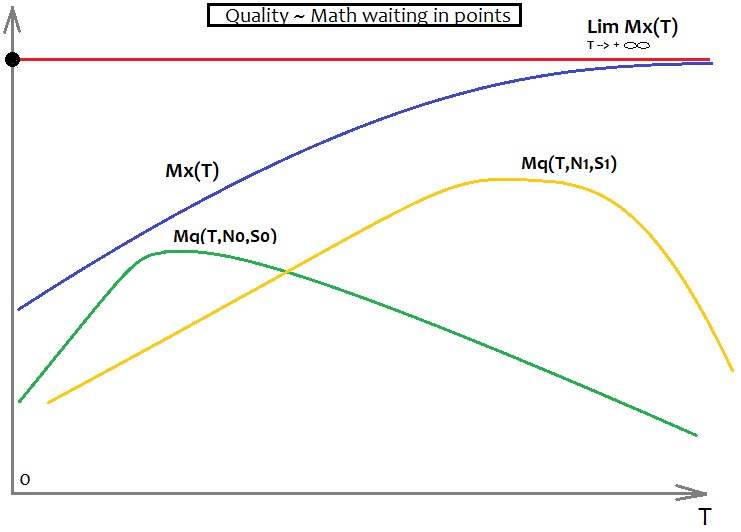
Hier haben wir wieder zwei Varianten für zwei verschiedene Formeln mit unterschiedlichen Anforderungen. Zusätzlich haben wir hier Mx(T), das als Asymptote dient - Mq(T,N,S) kann diese Barriere nicht überwinden. Das ideale Mq(T,N,S) wird mit dem Mx(T)-Diagramm übereinstimmen und bedeutet, dass wir den heiligen Gral gefunden haben. Natürlich wird das in der Realität nie passieren. Ich glaube jedoch, dass dies für das richtige Verständnis des Marktes sehr wichtig ist, wenn Sie ihn wirklich verstehen wollen.

Im Forex, wie auch in jedem anderen Finanzmarkt, ist es am korrektesten und genauesten, nur mit den Konzepten der Wahrscheinlichkeitstheorie zu arbeiten. Hier sind einige der wichtigsten mathematischen Analyseregeln für den Forex-Markt:

• Fast alle Größen sind nicht fix und werden durch ihre mathematischen Erwartungen ersetzt.
• Die mathematischen Erwartungen von Werten aus einer größeren Stichprobe tendieren zu dem Ergebnis aus einer globalen Stichprobe.
• Häufiger Wahrscheinlichkeiten verwenden.

Die Zuverlässigkeit des Datensegments ist nur eine Stichprobenrate. Je größer die Stichprobe, je umfangreicher der Eingabedatensatz, desto gerechter die endgültige Formel. Tatsache ist, dass, wenn die Stichprobe gegen unendlich tendiert, wird das Endergebnis zu einem festen Grenzwert tendieren.

Vorlagenänderungen

Da die Logik verbessert wurde, müssen wir die Funktionen in der Vorlage ändern, um einen ordnungsgemäßen Betrieb zu gewährleisten. Sie müssen in der Lage sein, neue Parameter zu empfangen. Die Implementierung dieser Funktionen ist sowohl im Programm als auch im Code der Vorlage identisch. Die ursprünglichen Funktionen wurden entwickelt, um mit einem Wert zu arbeiten, während wir jetzt 4 weitere davon haben, also müssen wir die Funktionen überarbeiten. In erster Linie sollen diese Änderungen für eine höhere Qualität der Formeln sorgen. Je mehr Daten in einer Formel verwendet werden, desto höher sind ihre Suchmöglichkeiten.

Beim Schreiben dieses Artikels habe ich einen Fehler in meinem Code gefunden: Kombinationen von Faktoren können sich wiederholen, während die Reihenfolge dieser Faktoren aufgrund der Eigenheiten der Funktion, die ein mehrdimensionales Polynom implementiert, chaotisch ist. Diese Funktion baut einen Aufrufbaum auf, aber sie kann die Permutationen der Elemente nicht kontrollieren. Dies kann auf zwei Arten vermieden werden:

1. Wir können alle möglichen Permutationen von Faktoren kontrollieren
2. Die Anzahl der doppelten Faktoren in einer Formel kompensieren, indem der Gesamtkoeffizient durch ihre Anzahl geteilt wird

Ich habe mich für die zweite Möglichkeit entschieden. Der Nachteil dieses Ansatzes ist, dass der durchschnittliche Koeffizient gegen 0,5 tendieren wird. Zumindest werden die Faktoren nicht unbrauchbar sein. Für diesen Artikel habe ich ein Polynom vom Grad 1 verwendet, das vom Fehler nicht betroffen ist. Wir können leicht die Anzahl der Kombinationen für einen Multiplikator mit einem festen Gesamtgrad berechnen:

• Comb=n!/(n-k)!
• n ist die Anzahl der möglichen unabhängigen Multiplikatoren
• k ist der Gesamtgrad des letzten Terms

Nachfolgend finden Sie die Implementierung dieser Formel im Code:

double Combinations(int k,int n)
   {
   int i1=1;
   int i2=1;
   for ( int i=n; i<n-k; i-- ) i1*=i;
   for ( int i=n-k; i>1; i-- ) i2*=i;
   return double(i1/i2);
   }

Hier sehen Sie, wie sich die Hauptfunktion des endgültigen Polynoms geändert hat. Die Änderungen beziehen sich auf das eindimensionale Polynom-Chart, da wir jetzt nicht mehr von einem Balken-Parameter abhängen, sondern von fünf. Natürlich gibt es 4 Anfangsarrays. Aber die Preisdaten können nicht einfach als Daten verwendet werden, sie müssen in einige flexiblere Werte transformiert werden. Wir verwenden die Differenz zwischen benachbarten Preisen, wobei benachbarte Preise sowohl Eröffnungs- als auch Schlusskurse der Balken sein können.

double Val;
int iterator;
double PolinomTrade()//Polynomial for trading
   {
   Val=0;
   iterator=0;
   if ( DeepBruteX <= 1 )
      {
      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(Close[i+1]-Open[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(High[i+1]-Open[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(Open[i+1]-Low[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(High[i+1]-Close[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(Close[i+1]-Low[i+1])/Point;
         iterator++;
         }

      return Val;   
      }
   else
      {
      CalcDeep(C1,CNum,DeepBruteX);
      return ValStart;
      }
   }


///Fractal calculation of numbers
double ValW;//the number where everything is multiplied (and then added to ValStart)
uint NumC;//the current number for the coefficient
double ValStart;//the number where to add everything
void Deep(double &Ci0[],int Nums,int deepC,int deepStart,double Val0=1.0)//intermediary fractal
   {
   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(Close[i+1]-Open[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(Close[i+1]-Open[i+1])*Val0/Point;
         NumC++;
         }
      } 
      
   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(High[i+1]-Open[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(High[i+1]-Open[i+1])*Val0/Point;
         NumC++;
         }
      }

   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(Open[i+1]-Low[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(Open[i+1]-Low[i+1])*Val0/Point;
         NumC++;
         }
      }

   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(High[i+1]-Close[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(High[i+1]-Close[i+1])*Val0/Point;
         NumC++;
         }
      }

   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(Close[i+1]-Low[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(Close[i+1]-Low[i+1])*Val0/Point;
         NumC++;
         }
      }
   }
   
void CalcDeep(double &Ci0[],int Nums,int deepC=1)
   {
   NumC=0;
   ValStart=0.0;
   for ( int i=0; i<deepC; i++ ) Deep(Ci0,Nums,i+1,i+1);
   }

Einige kleinere Änderungen betreffen die Funktion, die die Größe des Arrays der Koeffizienten berechnet.> Die Schleife ist jetzt 5 mal länger:

int NumCAll=0;//size of the array of coefficients
void DeepN(int Nums,int deepC=1)//intermediate fractal
   {
   for ( int i=0; i<Nums*5; i++ )
      {
      if (deepC > 1) DeepN(Nums,deepC-1);
      else NumCAll++;
      }
   }

void CalcDeepN(int Nums,int deepC=1)
   {
   NumCAll=0;
   for ( int i=0; i<deepC; i++ ) DeepN(Nums,i+1);
   }  

Alle diese Funktionen werden benötigt, um das endgültige Polynom zu implementieren. OOP ist hier überflüssig, und es ist besser, ähnliche Funktionen zu verwenden, um einen Aufrufbaum aufzubauen, insbesondere für Formeln, die nicht explizit geschrieben werden können (z. B. mehrdimensionale Expansionen). Es ist ziemlich schwierig, ihre Logik zu verstehen, aber es ist möglich. Analoge dieser Funktionen sind innerhalb des C#-Programms implementiert. Leider haben die beigefügten EAs diesen Code nicht, sondern sie verwenden intern die vorherige Version. Sie ist recht effizient, wenn auch etwas unbeholfen. Das Programm befindet sich noch im Prototypenstadium und wird später noch verbessert und vervollständigt werden. Bisher ist das Programm nicht für die Analyse von globalen Mustern auf normalen PCs geeignet. Es gibt noch eine Menge kleiner Fehler auf der Seite des Programms, und ich entdecke immer wieder Fehler und behebe sie. So wachsen die Fähigkeiten des Programms ständig und nähern sich dem gewünschten Zustand.

Analysieren gefundener Muster

Da meine Computerkapazitäten und auch die Zeit begrenzt sind, musste ich die Datenmenge begrenzen. Trotzdem denke ich, dass sie für einige Schlussfolgerungen ausreichend ist. Insbesondere musste ich nur H1 Charts für die Analyse der globalen Muster verwenden, sowie die Analysezeit begrenzen. Alle Tests werden in MetaTrader 4 durchgeführt. Die Sache ist die, dass die mathematische Erwartung der gefundenen Muster nahe am Level des Spreads liegt, und in MetaTrader 5 wendet der Tester einen Spread an, der nicht kleiner als der historisch registrierte Wert ist, auch wenn wir die Option nutzerdefinierte Testsymbol-Einstellungen verwenden. Der Wert wird auf der Grundlage der realen Tickdaten des aktuellen Brokers und des Spreads im ausgewählten Bereich angepasst. Dadurch wird verhindert, dass zu optimistische Testergebnisse generiert werden. Ich wollte den Einfluss dieses Mechanismus ausschalten und entschied mich für den MetaTrader 4. 

Ich werde mit globalen Mustern beginnen. Ihre mathematische Erwartung lag bei etwa 8 Punkten. Das liegt daran, dass wir 50 Kerzen für die Formel verwendet haben und etwa 200.000 Varianten im ersten Tab für jedes Währungspaar geprüft haben, während wir nur 1 Kern verwendet haben. Es wäre einfacher mit einer besseren Maschine. Die nächste Version des Programms wird weniger abhängig von der Rechenleistung sein. Hier möchte ich mich nicht auf die resultierende Rechenleistung in Punkten konzentrieren, sondern darauf, wie sich die Leistung in Zukunft auf die EA-Performance auswirken wird.

Lassen Sie uns mit EURUSD H1 beginnen. Der Test wurde im Intervall 2010.01.01-2020.01.01 durchgeführt. Der Zweck war, ein globales Muster zu finden:

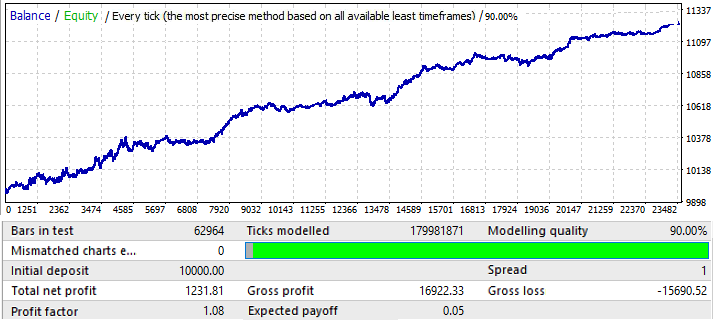
Die Ergebnisse sind nicht sehr attraktiv, und das ist alles, was wir in dem gegebenen Zeitintervall aus dem Paar herausquetschen konnten. Wir können ein globales Muster identifizieren, obwohl es nicht so klar ist. Ich habe 50 Kerzen in der Formel für Brute Force verwendet. Das Ergebnis ist nicht so gut, wie wir es erwarten könnten, aber es ist notwendig. Sie werden weiter sehen, wofür. Lassen Sie uns das gleiche Segment in der Vorwärtszeitraum 2020.01.01-2020.11.01 testen, um seine zukünftige Performance zu verstehen:

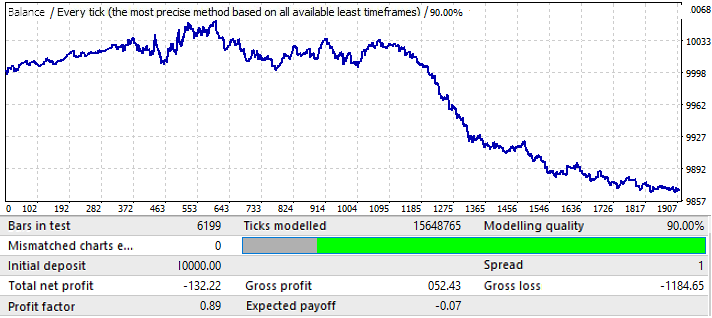
Das Ergebnis ist durchaus nachvollziehbar. Diese Analyse erwies sich als unzureichend für den Versuch, von der Musterfortsetzung zu profitieren. Generell, wenn wir globale Muster analysieren, dann sollte das Ziel sein, ein Muster zu finden, das mindestens noch einige Jahre lang funktioniert, sonst ist eine solche Analyse völlig nutzlos. Zu Beginn des Charts funktioniert das Muster weiterhin, aber nach sechs Monaten ist es invertiert. Eine solche Analyse kann also für den Handel für mehrere Monate ausreichen, vorausgesetzt, wir schaffen es, ausreichend gute Parameter für den Anfangstest zu finden. In diesem Fall wurde die Analyse durch den Wert P_Factor durchgeführt. Dieser Parameter ist ähnlich dem Profit Factor, aber er nimmt Werte im Bereich von [0...1] an. 1 - 100% des Gewinns. In der ersten Registerkarte lag der höchste Wert dieses Parameters bei 0,029. Der Durchschnittswert aller gefundenen Varianten lag bei etwa 0,02.

Der nächste EURCHF Chart:

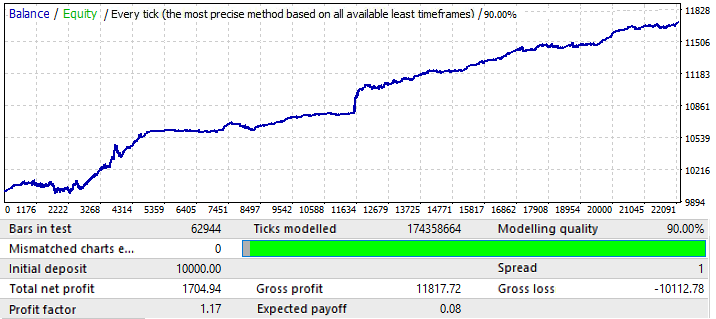
Das maximale Ergebnis für die Chart-Varianten auf der ersten Registerkarte lag bei etwa 0,057. Der Grad der Vorhersagbarkeit ist 2-mal höher als der des vorherigen Charts, was auch den endgültigen Profitfaktor beeinflusst hat, der tatsächlich 0,09 höher ist als der des vorherigen Charts. Lassen Sie uns sehen, ob die Verbesserung der globalen Indikatoren die Vorwärtsperiode beeinflusst hat:

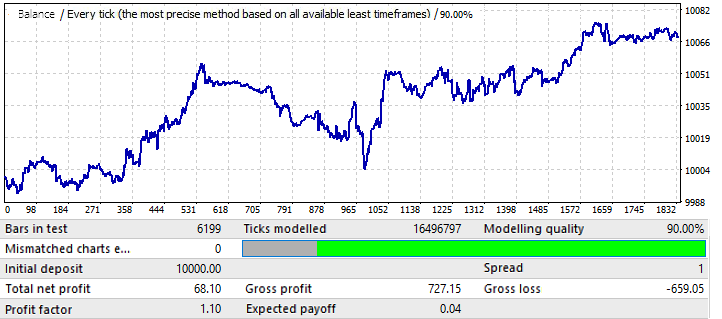
Wie Sie sehen können, setzt sich das Muster das ganze Jahr über fort. Es ist nicht sehr gleichmäßig, und der Gewinnfaktor ist niedriger. Wir können jedoch einige vorläufige Schlussfolgerungen ziehen. Eigentlich ist der PF niedriger, weil der globale Test ziemlich große Bereiche mit starkem Saldowachstum hatte, was den resultierenden Gewinnfaktor erhöhte. Ich bin sicher, dass das Ergebnis bei den nächsten Tests fast das gleiche sein wird. Die vorläufige Schlussfolgerung ist, dass eine Verbesserung der Qualität und des Aussehens des Charts seine Leistung in der Zukunft beeinflusst. Also, wir haben dieses Ergebnis erhalten, indem wir unsere Einstellungen auf dieses spezielle Währungspaar angewendet haben. Der Grund für die Wellen im Chart ist im globalen Test zu sehen, wo die Gleichgewichtsschwankungen in den letzten Jahren stark zugenommen haben. Die Wellen sind also nur eine Fortsetzung dieser Schwankungen.

Weiter geht es mit dem USDJPY Chart:

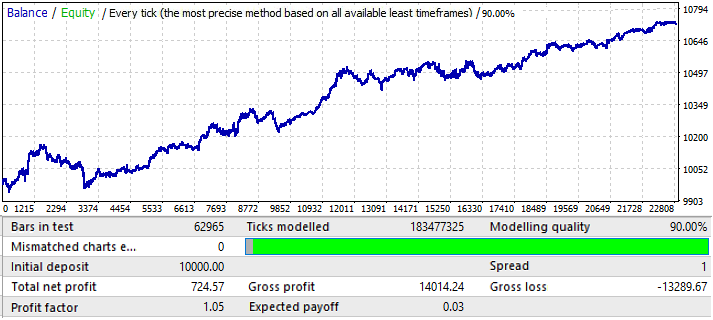
Dies ist der schlechteste Chart. Lassen Sie uns die Vorwärtsperiode überprüfen:

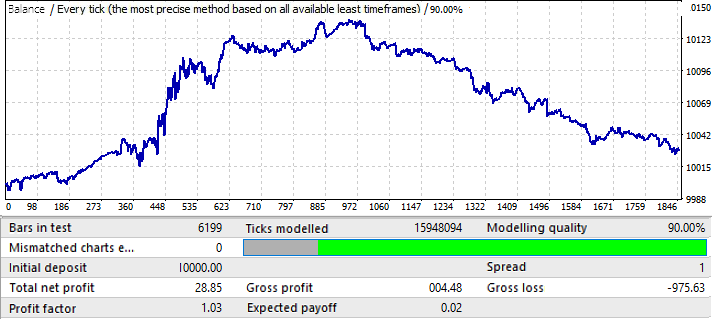
Scheint sich in einer positiven Zone zu befinden, aber seine zweite Hälfte ist der des ersten Charts (EURUSD H1) sehr ähnlich, der auch mit einer Aufwärtsbewegung begann, sich dann umkehrte und eine fast gerade Abwärtsbewegung hatte. Die Schlussfolgerungen sind hier also die gleichen. Die Qualität des Endergebnisses ist nicht hoch genug. Nichtsdestotrotz könnten wir ein paar Monate profitablen Handels mit diesem Muster erwarten, vorausgesetzt die mathematische Erwartung und der Gewinnfaktor sind gut genug.

Der letzte Chart, USDCHF:

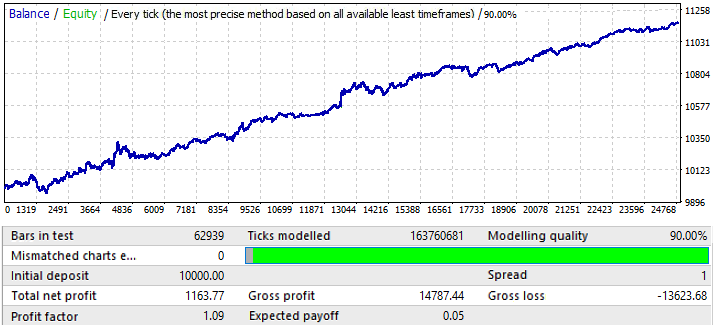
Er ist nicht sehr beeindruckend. Lassen Sie uns einen Blick auf die Vorwärtsperiode werfen:

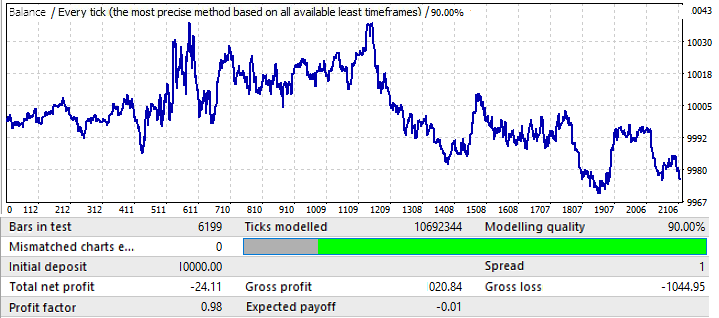
Scheint ähnlich zu sein wie andere Charts, außer EURCHF. Seine Performance ist bis Mitte des Jahres gut, dann kommt es zu einer Umkehr und einer Musterumkehr.

Wir können die folgenden vorläufigen Schlussfolgerungen ziehen:

1. Offensichtlich war EURCHF der beste Chart
2. EURCHF war besser als alle anderen Paare sowohl in der Trainingsperiode als auch im Vorwärtstest
3. In allen Charts außer EURCHF bleibt das Muster bis zur Mitte des Jahres erhalten

Basierend auf dem oben Gesagten können wir die Schlussfolgerung ziehen, dass die Qualität der Ergebnisse in der Trainingsperiode einen direkten Einfluss auf die Performance in der Vorwärtsperiode hat. Eine Erhöhung des Gewinnfaktors des Endergebnisses kann darauf hinweisen, dass das Ergebnis viel weniger zufällig ist als das der anderen Charts. Dies wiederum kann darauf hinweisen, dass wir ein globales Muster gefunden haben. Auf den Devisenmarkt angewandt, können wir sagen, dass "in einem Muster ein Anteil von allen Mustern steckt". Je stärker die Testwerte sind, desto höher ist der Anteil.

Jetzt werde ich versuchen, die Stichprobengröße zu ändern. Lassen Sie uns 1 Jahr verwenden. 2017.01.01-2018.01.01 EURJPY H1. Lassen Sie uns sehen, wie sich das Muster einen Monat in der Zukunft verhält:

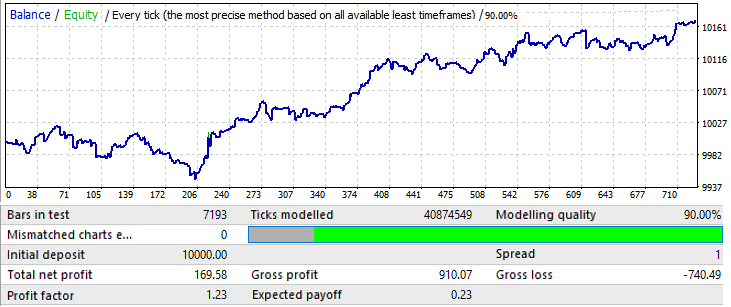
Der Chart sieht nicht sehr gut aus, aber der resultierende Gewinnfaktor und die mathematische Erwartung sind höher als die der 10-Jahres-Variante. Die Stichprobe ist 12-mal kleiner als bei den Ausgangsvarianten, dennoch sollten diese Daten nicht ignoriert werden.

Die Vorwärtsperiode beträgt ein Monat: 2018.01.01-2018.02.01:

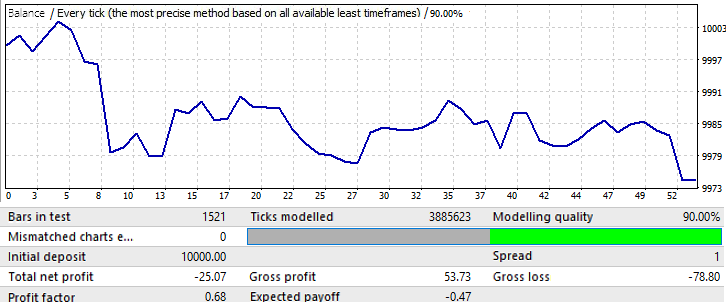
Dies ist nur ein Beispiel, um die weitere Argumentation zu verdeutlichen. Hier kehrt sich das Muster fast sofort um. Leider konnte ich nicht mehr Daten zur Verfügung stellen. Die Berechnungen und die Einrichtung der Software nehmen viel Zeit in Anspruch. Trotzdem sollten diese Informationen für die erste Analyse ausreichen.

Analyse der Daten

Nachdem wir die Expert Advisors getestet haben, können wir einige Schlussfolgerungen ziehen:

• Expert Advisors, die globale Muster ausnutzen und die in der Lage sind, über einen längeren Zeitraum zu operieren, können mit einer einfachen Zahlenbrutalität erstellt werden.
• Die Dauer der zukünftigen Operation hängt direkt von der Größe der Datenprobe ab.
• Die Dauer des Betriebs hängt direkt von der Testqualität im Trainingsbereich ab.
• Beim Testen für die Zukunft bleibt die Funktionsfähigkeit von globalen Mustern auf allen Charts mindestens 2-3 Monate erhalten.
• Die Wahrscheinlichkeit, ein Muster zu finden, das mindestens noch ein paar Jahre funktioniert, steigt, wenn die Qualität des Endergebnisses im Brute-Force-Bereich gegen 100 % tendiert.
• Wenn wir nach globalen Mustern suchen, funktionieren verschiedene Einstellungen für verschiedene Währungspaare unterschiedlich.

Bei lokalen Mustern, wie z. B. einem Monat, ist die Situation hier völlig anders. In meinem vorherigen Artikel habe ich lokale Muster analysiert, aber ich habe die neuen Funktionen, die in der Programmversion eingeführt wurden, nicht verwendet. Alle Verbesserungen erlauben ein besseres Verständnis derselben Fragen. Was die lokalen Muster betrifft:

• Spielen Sie immer den Musterwechsel.
• Martingale kann verwendet werden, indem man vorsichtig.

Je größer also das Muster ist, desto länger wird es seine zukünftige Funktionsfähigkeit behalten. Und umgekehrt, je kleiner das Sample, desto schneller wird das Muster in der Zukunft invertieren (natürlich unter der Voraussetzung, dass es keine Vorwärtsoptimierung gibt, die ich übrigens plane, später hinzuzufügen). Die Musterinversion bei einem kurzen Intervall ist garantiert. Basierend auf diesen Schlussfolgerungen gibt es zwei mögliche Handelsarten:

1. Ausnutzung von globalen Mustern,
2. Ausnutzung von lokalen Mustern.

Im ersten Fall gilt: Je größer der Trainingsbereich, desto länger wird das Muster funktionieren. Es ist jedoch immer noch besser, alle 2 bis 3 Monate nach neuen Formeln zu suchen. Bei lokalen Mustern sollte die Suche jede Woche durchgeführt werden, solange der Markt eingefroren ist. Die Qualität der Ergebnisse wird nicht hoch sein, aber Sie brauchen sich keine Sorgen um das Ergebnis zu machen - zumindest werden Sie in der Lage sein, etwas Gewinn zu erzielen.

Jetzt werde ich versuchen, alle Daten zusammenzufassen, die ich als Ergebnis meiner Forschung über die Muster verschiedener Skalen erhalten habe. Dazu werde ich eine Funktion einführen, die die erwartete Auszahlung (mathematische Erwartung) einer bestimmten Bestellung widerspiegelt, sowie eine Funktion, die den Gewinnfaktor widerspiegelt. Sie können beliebige andere Funktionen hinzufügen, die weniger wichtige Metriken charakterisieren. Der Ereignisraum oder eine Zufallsvariable werden alle möglichen Varianten von Ereignisentwicklungen in der Zukunft sein. Jetzt wissen wir nur das Folgende:

• Es gibt unzählige mögliche Entwicklungen für den "F"-ten Balken in der Zukunft (unabhängig davon, ob eine Order darauf eröffnet wird oder nicht).
• Für alle Varianten der zukünftigen Entwicklung, bei denen eine Order auf einem bestimmten Balken eröffnet wird, wird diese Order eine erwartete Auszahlung in Punkten und einen Gewinnfaktor haben (stellen Sie sich vor, Sie führen einen Test auf einem Balken durch, nur die folgenden Balken sind für jede Order immer unterschiedlich).
• Alle diese Größen werden für jede Formel unterschiedlich sein.
• Für Abschnitte mit unterschiedlichen zukünftigen Anfangsdaten (der Anfang der Zukunft ist das Ende des Trainingsabschnitts) und unterschiedlichen Trainingsabschnittsdauern (was unterschiedlichen Anfangsdaten des Trainingsabschnitts entspricht), werden die gesuchten Endparameter eindeutige Werte annehmen.

Alle diese Aussagen können in mathematische Formeln umgewandelt werden. Hier sind die Formeln:

• MF=MF(T,I,F,S,R) — mathematische Erwartung der Aufträge auf einem bestimmten Balken in der Zukunft.
• PF=PF(T,I,F,S,R) — Gewinnfaktor der Aufträge auf einem bestimmten Balken in der Zukunft. 
• T — die Dauer des Trainingsabschnitts (in diesem Fall ist es der Stichprobenumfang oder die Anzahl der Balken).
• I — das Datum des Endes des Trainingsabschnitts.
• F — die Nummer des Balkens in der Zukunft, beginnend mit dem Datum des Trainingsendes.
• S — ein eindeutiges Polynom oder ein Algorithmus (wenn das Muster manuell oder durch einen anderen EA gefunden wird).
• R — die Ergebnisse, die mit einem bestimmten Polynom oder einer Strategie erzielt wurden (die Qualität der Signaloptimierung); sie beinhalten die Anzahl der Trades im Trainingszeitraum und die gewünschten Metriken, wie die mathematische Erwartung, den Gewinnfaktor und andere Parameter.

Basierend auf den Daten, die durch Brute-Force auf verschiedenen Instrumenten und verschiedenen Daten erhalten wurden, kann ich die oben genannten Funktionen in einem Chart zeichnen ("F" wird als Argument verwendet):

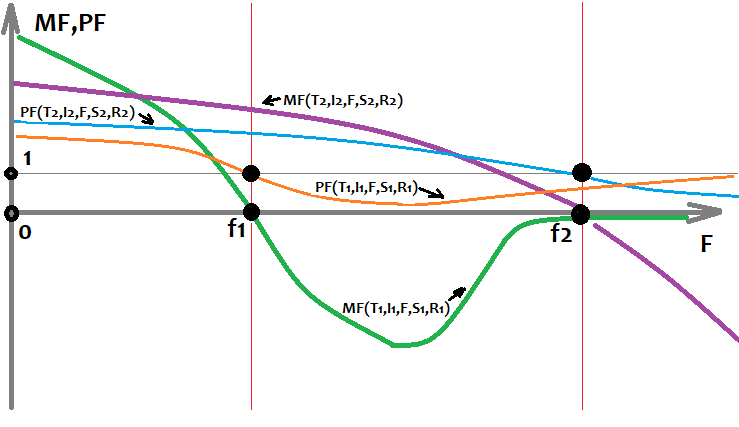
Dieser Chart zeigt 2 einzigartige Varianten von Strategien, die in verschiedenen Segmenten mit unterschiedlichen Einstellungen trainiert wurden und unterschiedliche Ergebnisse erzielten. Es gibt unzählige solcher Varianten, aber sie alle haben eine unterschiedliche Dauer und Qualität des ursprünglichen Musters. Es folgt immer eine Musterinversion. Nur bei sehr starken Mustern mag diese Regel nicht funktionieren. Aber selbst für diese besteht immer das Risiko, dass sich der Chart umkehrt, vielleicht in 5 Jahren, aber er wird sich umkehren. Die stabilsten Formeln werden diejenigen sein, die aus der größten Stichprobe gefunden werden. Wenn die Formeln manuell gefunden werden und aus einer Theorie stammen, dann können solche Formeln in der Zukunft unbegrenzt funktionieren. Wir haben jedoch keine solchen Garantien, wenn wir Brute-Force- oder andere maschinelle Lernmethoden verwenden. Alles, was wir haben, ist eine Schätzung der Betriebszeit, die nur auf der Grundlage statistischer Daten vorgenommen werden kann. Diese Analyse ist mit meinem Programm möglich, kann aber aufgrund der begrenzten Zeit und Rechenleistung nicht von einer Person durchgeführt werden.

Wie ist Тext?

Die Analyse von globalen Mustern hat gezeigt, dass die Leistung eines gewöhnlichen Computers für eine tiefe und qualitativ hochwertige Analyse von großen Stichproben, z. B. 10 Jahre oder mehr, nicht ausreicht. Auf jeden Fall sollten sehr große Stichproben analysiert werden, um qualitativ hochwertige Suchergebnisse zu gewährleisten. Wenn wir das Programm ein paar Monate lang auf einem Hochleistungsserver laufen lassen, können wir vielleicht ein oder zwei gute Varianten finden. Daher müssen wir die Effizienz zusammen mit einer Erhöhung der Brute-Force-Geschwindigkeit verbessern. Die mögliche Weiterentwicklung des Programms sieht folgendermaßen aus:

1. Hinzufügen der Fähigkeit, feste Server-Zeitfenster zu analysieren.
2. Hinzufügen der Fähigkeit, die Analyse an festen Wochentagen durchzuführen.
3. Hinzufügen der Fähigkeit, zufällige Zeitfenster zu generieren.
4. Hinzufügen der Fähigkeit, eine Reihe von erlaubten Wochentagen für den Handel zufällig zu generieren.
5. Verbesserung der zweiten Stufe der Analyse (Registerkarte "Optimierung"), insbesondere die Implementierung von Multicore-Berechnungen und die Korrektur von Fehlern des Optimierers.

Diese Änderungen sollten sowohl die Arbeitsgeschwindigkeit des Programms als auch die Variabilität und Qualität der gefundenen Optionen deutlich erhöhen. Sie sollten auch ein komfortables Toolkit für die Marktanalyse bereitstellen.

Schlussfolgerungen

Ich hoffe, dieser Artikel ist für Sie nützlich. Es scheint mir, dass das Thema der globalen Muster im Artikel sehr wichtig ist. Allerdings war es für mich extrem schwierig, dies zu tun, weil die Möglichkeiten des Programms für diese Art der Analyse noch nicht ausreichen. Dies wäre einfacher, wenn ich Zugriff auf 30 Kerne hätte. Um die Qualität der Analyse zu verbessern, müssten wir viel mehr Zeit aufwenden.

Hoffentlich wird es in Zukunft möglich sein, auf mehr Rechenleistung zuzugreifen. Wir werden im nächsten Artikel damit fortfahren. Ich habe in diesem Artikel auch einige mathematische Grundlagen für das allgemeine Verständnis bereitgestellt, die sowohl bei der Verwendung des Programms als auch bei der manuellen Suche nach Mustern und deren Optimierung nützlich sein werden.

Das allgemeine Ideal dieses Artikels war es, Informationen für diejenigen bereitzustellen, die es noch nicht geschafft haben, selbst diese kleinen Ergebnisse manuell zu erzielen. Er sollte helfen, die Grundlagen der Ideen zu verstehen, die bei der Entwicklung von Robotern verwendet werden.

Es scheint mir nicht so wichtig zu sein, wie man ein Muster findet, manuell oder mit Hilfe einer Software. Wenn ein Muster einige profitable Ergebnisse liefert, können wir es als ein funktionierendes Muster betrachten. Einige Musterparameter geben uns einige Vorhersagen. Das kann eine Vorhersage für die nahe Zukunft sein, aber es kann immer noch genug sein, um zu verdienen.Es gibt vielleicht halbherzige Maßnahmen, aber nichts kann garantiert werden. Wenn Sie jedoch ein Muster gefunden haben, bedeutet das nicht, dass dasselbe Muster auch in der Zukunft funktionieren wird. Um es zu überprüfen, benötigen Sie eine sehr große Stichprobe mit sehr guten Handelsergebnissen während der gesamten Stichprobe und mit einer ausreichenden Anzahl von Orders in Anbetracht der Stichprobengröße. Neben dem Finden eines Musters gibt es ein weiteres Problem - die Einschätzung seiner möglichen zukünftigen Wirkungszeit. Diese Frage ist meiner Meinung nach fundamental. Was hat es für einen Sinn, ein Muster zu finden, wenn wir nicht wissen, wie lange und wie gut es funktionieren wird. Jeder kann mein Programm benutzen. Es ist im Anhang des Artikels verfügbar. Für spezifische Setup-Fragen senden Sie mir eine PM.