模式搜索的暴力方法（第二部分）：深入

介绍

我决定继续我们在上一篇文章中开始的话题。这次我们将使用修改后的应用程序版本对货币对进行深入分析。我要感谢用户 Aleksey Vyazmikin 对项目开发的贡献,他的建议在技术上非常有用，并推动了进一步的开发。我将在下一篇文章中继续这项工作，并将提供更有趣的数据和结果。我认为，在全局范围内展示对特定货币对的分析的有效性，以及展示对最长和最短持续时间间隔的分析的差异，是非常重要的。因为我的时间和计算资源是有限的，所以我只能在一个时间范围内涵盖几个货币对。然而，对于第一次了解全局模式的人来说，这似乎已经足够了。在分析数据时，我将另外使用上一篇文章中的数据。

为什么这个主题这么有趣？

通常，MetaTrader 4 和 MetaTrader 5 EA 交易程序员的所有想法都意味着无数的代码行、无数的测试、优化、前后测试。在大多数情况下，我们得不到我们想要的。有些程序员对这个特定的问题感到厌烦。研究和搜索的过程变成了一个常规。如果工作不能给你带来任何道德上的满足感和金钱，那么你很可能会退出，我就是这样。我决定告别常规，开始自动化机器可以成功执行的操作。这台机器没有感情，它是一个理想的工人，不像我。当然，机器不像人那样思维开阔，但它拥有大量的计算资源，可以更轻松、更快地实现一些过程。我有一个选择，开始写我自己的神经网络架构能够进化，或开始用最简单的方法来解决问题。我决定采用后一种方法。尽管它很简单，但与MQL产品的简单编程相比，该项目为创造力和兴趣提供了空间。使用通用模板并通过逐步添加必要的功能对其进行进一步开发是一个好主意。我们可以从一个简单的模板开始，然后为特定的工作原理创建新的模板。这样，我们就可以摆脱枯燥的日常工作，而继续我们的开发。懒惰是进步之父。

暴力程序的新版本和更改列表

程序中只有一个更改，显示在红色框中。这个设置取自第二个选项卡，在那里它显示了它的最佳状态。添加此设置的原因是它对最终结果的质量有很大的影响。在分析期间，在第一个选项卡上，所有结果最初都按质量排序。利润因素或以点数表示的预期收益被用作质量标准。但是程序不允许我们对图形形状进行评估。我使用了线性因子（与直线的相似性）作为形状标准，这样我们就不需要目视检查每个选项。在这里，我们可以得出这样的结论：更直和更平滑的图更有可能在第二个选项卡上给出高质量的方案。同样，这样的图上结果数量会减少，这些结果将被第二个选项卡上的过滤器丢弃。计算此值需要第二次过程，如果此过滤器被激活，则暴力计算速度大约慢2倍。但对我们来说，重要的不是速度，而是获得的主要结果的总数，因为它们的质量影响着进一步的成效。

除了引入过滤器外，多项式本身也发生了变化。现在多项式不仅接受特定柱的 Close[i]-Open[i] 值作为参数，还接受以下值：

• Close[i]-Open[i]
• High[i]-Open[i]
• Low[i]-Close[i]
• Low[i]-Open[i]
• High[i]-Close[i]

现在这个公式包含了一个特定柱的所有价格数据，这与以前版本的程序不同。这大大增加了多项式的复杂性，从而导致暴力计算速度的下降。但现在只要有足够的计算资源，我们就可以选择更好、更有效的市场公式。当然，我们可以用这些数据创建其他变量。但在多项式中使用这些值时，可以获得上述值的线性组合，例如： 

• C1*(High[i]-Close[i]) + C2*(Low[i]-Close[i]) = NewQuant
• if  C1 = 1 and C2 = -1
• NewQuant = (High[i]-Close[i]) - (Low[i]-Close[i]) =  High[i]-Low[i]
• 其它情况下
• NewQuant = (C1-C3)*(High[i]-Close[i])+(C2+C3)*(Low[i]-Close[i])  +  C3*((High[i]-Close[i]) - (Low[i]-Close[i])) = (C1-C3)*(High[i]-Close[i])+(C2-C3)*(Low[i]-Close[i]) +  C3*(High[i]-Low[i])

换言之，使用变量的线性组合，而这些变量又由其他变量的线性组合组成，我们甚至可以在基本公式中不包含新变量。最好不要包含那些可以由公式中已经存在的其他变量形成的变量。它们将出现在系数的选择过程中，具体取决于系数本身的值。

因此，新的多项式将更加复杂：

• Y = Sum(0,NC-1)( C[i]*Variant of product(x[1]^p[1]*x[2]^p[2]...*x[N]^p[N]) )
  
• Sum(0,N)(p[i])=MaxPowOfPolinom
• NC - 多项式中项的总数，等于所选系数的个数
  

其中x[i]是多项式采用的参数，p[i]是参数的阶数。所有组成因子的总次数不应超过多项式允许的次数，因为没有计算机能处理这种复杂的展开式。当公式的柱数最小时，我几乎总是使用1次、2次或3次。无论如何，使用更高的次数是无效的，即使在服务器上，也没有足够的计算能力。

下面是参数选项。最终总和包括所有可能的组合：

1. x[i] =Close[i]-Open[i]
2. x[i] =High[i]-Open[i]
3. x[i] =Low[i]-Close[i]
4. x[i] =High[i]-Open[i]
5. x[i] =High[i]-Close[i]

我还要解释为什么我们用多项式来执行所有这些操作。关键是任何系统最终都会归结为一组条件。可以有一个或几个条件，这无关紧要，因为条件是一个逻辑函数。一组条件最终可以转换为返回true或false的布尔表达式。这样的信号只能解释为是或否，但无法确定信号有多强，也无法调整信号。如果使用多个指标作为信号，可以分别调整这些指标的参数，这将导致最终逻辑表达式发生变化或信号发生变化，最终影响交易。但我认为这是非常不方便的，因为通过改变一个特定指标的一个或另一个参数，我们将不知道这将如何影响交易。

这种方法的主要思想是简单和高效。为什么要这样做？它有几个优点：

• 优化函数的唯一性
• 信号强度与函数值的关系
• 易用性
• 唯一可优化的参数是多项式值

最重要的是我们不需要选择条件的数量和类型。这是因为我们最初接受这样一种观点，即不需要寻找一组无限的条件，我们可以将所有这些条件简化为一个函数，输出一个正分数或负分数。根据一个或另一个函数的可靠性，它可能需要一个更强大的模信号。在某些公式中，这可能提供可伸缩性。这里的可伸缩性意味着当交易数量减少时放大信号的能力。

总的来说，我的研究和其他许多人的研究一样，只能得出一个结论。试图强化进入信号，必然导致固定时间内交易数量的减少。换言之，对于任何具有随机分量的函数，某些点总是比其他点具有更可预测的结果。如果我们的功能足够有效，那么它可以达到一定的可预测性水平，对该功能提供的信号的要求也会越来越高。当然，这不是对所有满足我们基本条件的函数都是正确的。但是，初始条件越严格，这些公式变量的期望收益就越高，我们可以用暴力方法找到。这也适用于梯度增强，以及其他模式搜索方法，包括神经网络。

很大程度上取决于数据样本，样本越小，得到随机结果的几率就越大。这里的随机结果要么不起作用，要么在搜索模式的交易品种的全局历史上测试最终系统时效果非常差。

我们将试图回答这样一个问题：最终交易系统的未来质量如何取决于所分析数据区域的大小以及找到该系统所需的精力数量。首先，让我们定义一段固定时间内发现的策略数量的数学期望公式：

• Mn(t) = W(t,F)*Ef(T,N,L)
• Mn -  数学上期望的满足我们要求的策略数目
• W(t,F) = F*t - 每单位时间内检查的变体的结果数
• Ef(T,N,L) = ? - 暴力效率，取决于间隔长度、报价类型、所需的关闭订单数和所需的线性系数（如果在暴力期间考虑到这一点）（该值等于当前变量的结果采用必要和充分值的概率）
  
• N - 我们测试所允许的最小交易数量
• L - 最大允许线性系数（作为附加控制标准）
• F - 策略变量暴力频率

很难确定Ef函数的形式，但我们可以粗略估计它的外观和特性：

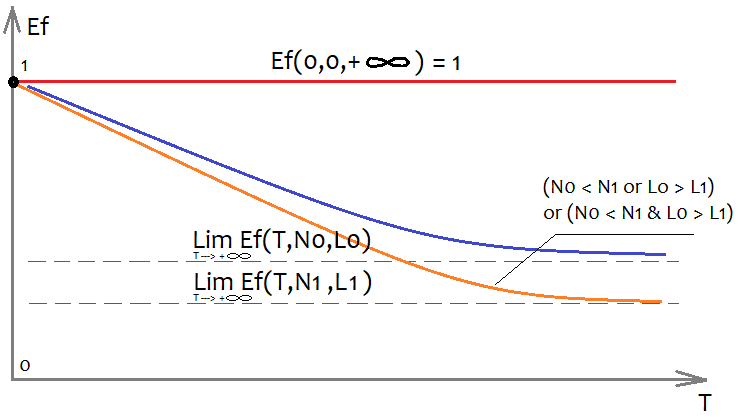
为了能够在一个平面上显示一个多维函数，必须用一些数字来固定它的所有参数，除了一个参数之外，这个参数是用来建立图形本身的。特别有趣的是T变量，它表示分析样本的持续时间，只要我们分析一个时间段。如果我们放弃这个假设，那么我们可以将样本大小作为T-这不会改变图的外观。当然，我们感兴趣的是剩下的两个参数将如何影响图的外观,如图所示。我们希望最终版本中的订单越多，满足我们需求的系统就越少，这仅仅是因为找到订单较少的系统要容易得多。对于线性系数（偏离直线）也是如此，但是这里的线性系数越小越好（趋于零）。

如果我们不固定系统质量的概念（因为这个值既可以是利润因子，也可以是数学期望），那么我们还可以引入所发现系统的最大质量的概念。我们可以类似地描述它依赖于什么：

• Mq=Mq(T,N,S)
• S - 选定的公式配置

换句话说，策略的最高可能质量直接取决于我们公式的有效性，以及我们的要求和时间间隔的复杂性。同时，我们仍然假设区域的起始点是固定的，训练起始点的每一个变化都是唯一的，并且给出了唯一的起始参数。也就是说，通过为训练区域选择不同的起始日期，我们将得到不同的效率值和其他参数，以及最终得到的系统质量。

我们还可以理解，每种质量都有其最大值，例如，利润因素的最大质量是无穷大的，但我不喜欢用这个指标来分析，因为它的最大值是不受限制的，因此带有PF的图形模型将更难理解。因此，我使用P_FACTOR，我自己的模拟PF。它的取值范围是 [-1,1].

• P_FACTOR=(Profit-Loss)/(Profit+Loss)

它的最大值等于1，因此使用起来更方便。这是一个函数，它描述了这个值的最大值取决于T（所选区域及其样本）。

• Mx=Mx(T)

如果参数或者质量标准是 P_FACTOR, 则 Mx(T)=1. 函数形式可能未知，但已知 Mx'（T）>0 贯穿于T轴的整个正部分。这意味着该值在任何点都是正的，因此图表一直在增加。

利润因子如下：

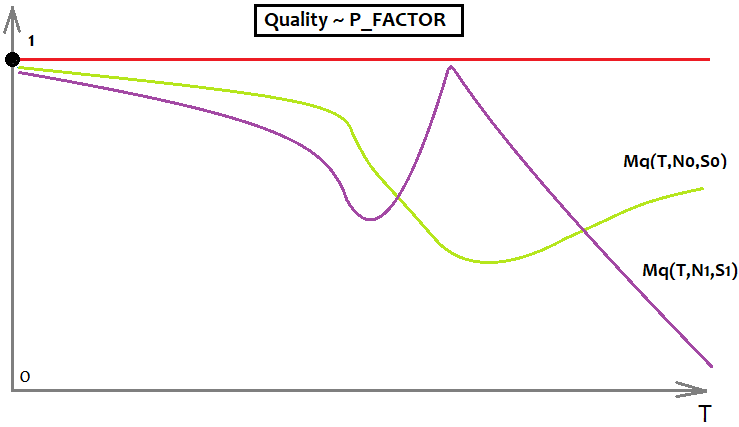
这个例子有一个PF的上限，两个图显示了两个不同的公式和不同的要求。在图表上，浅绿色的公式更好，因为它不太容易在“T”趋于无穷大时质量下降。

数学期望如下所示：

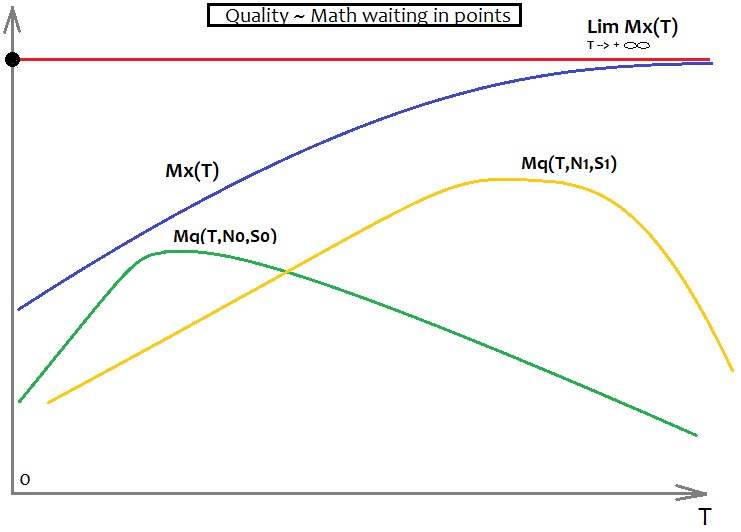
在这里，我们有两个不同的要求，两个不同的公式的变化。此外，我们这里有Mx（T）作为渐近线-Mq（T，N，S）不能克服这个障碍。理想的Mq（T，N，S）将匹配Mx（T）图，这意味着我们已经找到了圣杯。当然，这在现实中永远不会发生。不过，我相信这对于正确认识市场是非常重要的，如果你真的想了解的话。

在外汇市场，如同在任何其他金融市场，它是最正确和准确的操作只有与概率论的概念。以下是外汇市场的一些主要数学分析规则：

• 几乎所有的量都不是固定的，而是由它们的数学期望所代替。
• 大样本的数学期望值倾向于全局样本的结果
• 更频繁地使用概率

数据段的可靠性只是一个采样率。样本越大，输入的数据集就越广泛，最终的公式就越公平。事实上，当样本趋于无穷大时，最终结果将趋于一个固定的极限值。

模板变更

由于逻辑已经改进，我们需要修改模板中的函数以确保正确的运行，它们需要能够接收新的参数。这些函数的实现在程序和模板代码中都是相同的。原来的函数是用开发用于处理1个数值，而现在我们又有4个，所以我们需要修改函数。首先，这些变化应该提供更高质量的公式。公式中使用的数据越多，其搜索能力就越高。

在撰写本文时，我发现代码中存在一个缺陷：因子的组合可以重复，而由于实现多维多项式的函数的特殊性，这些因子的顺序是混乱的。这个函数建立了一个调用树，但是它不能控制元素的排列。这可以通过两种方式避免：

1. 我们可以控制所有可能的因素排列
2. 用总系数除以公式中重复因子的个数，以补偿公式中重复因子的个数

我决定使用第二种选择。这种方法的缺点是平均系数趋于0.5。至少，这些因素不会是无用的。在本文中，我使用了一个不受误差影响的1次多项式。我们可以很容易地计算固定总次数的乘法器的组合数：

• Comb=n!/(n-k)!
• n 是可能的独立乘数的数目
• k 是最后的总次数

下面是这个公式在代码中的实现：

double Combinations(int k,int n)
   {
   int i1=1;
   int i2=1;
   for ( int i=n; i<n-k; i-- ) i1*=i;
   for ( int i=n-k; i>1; i-- ) i2*=i;
   return double(i1/i2);
   }

下面是最后一个多项式的主函数是如何变化的。这些变化与一维多项式图有关，因为现在我们不依赖于一个柱形参数，而是依赖于其中的五个。当然，有4个初始数组。但价格数据不能仅仅用作数据，而需要将其转换为一些更灵活的值。我们使用相邻价格之间的差异，而相邻价格可以是柱的开盘价和收盘价。

double Val;
int iterator;
double PolinomTrade()//Polynomial for trading
   {
   Val=0;
   iterator=0;
   if ( DeepBruteX <= 1 )
      {
      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(Close[i+1]-Open[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(High[i+1]-Open[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(Open[i+1]-Low[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(High[i+1]-Close[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(Close[i+1]-Low[i+1])/Point;
         iterator++;
         }

      return Val;   
      }
   else
      {
      CalcDeep(C1,CNum,DeepBruteX);
      return ValStart;
      }
   }


///Fractal calculation of numbers
double ValW;//the number where everything is multiplied (and then added to ValStart)
uint NumC;//the current number for the coefficient
double ValStart;//the number where to add everything
void Deep(double &Ci0[],int Nums,int deepC,int deepStart,double Val0=1.0)//intermediary fractal
   {
   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(Close[i+1]-Open[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(Close[i+1]-Open[i+1])*Val0/Point;
         NumC++;
         }
      } 
      
   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(High[i+1]-Open[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(High[i+1]-Open[i+1])*Val0/Point;
         NumC++;
         }
      }

   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(Open[i+1]-Low[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(Open[i+1]-Low[i+1])*Val0/Point;
         NumC++;
         }
      }

   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(High[i+1]-Close[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(High[i+1]-Close[i+1])*Val0/Point;
         NumC++;
         }
      }

   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(Close[i+1]-Low[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(Close[i+1]-Low[i+1])*Val0/Point;
         NumC++;
         }
      }
   }
   
void CalcDeep(double &Ci0[],int Nums,int deepC=1)
   {
   NumC=0;
   ValStart=0.0;
   for ( int i=0; i<deepC; i++ ) Deep(Ci0,Nums,i+1,i+1);
   }

一些小的变化涉及到计算系数数组大小的函数。现在循环的长度是原来的5倍：

int NumCAll=0;//size of the array of coefficients
void DeepN(int Nums,int deepC=1)//intermediate fractal
   {
   for ( int i=0; i<Nums*5; i++ )
      {
      if (deepC > 1) DeepN(Nums,deepC-1);
      else NumCAll++;
      }
   }

void CalcDeepN(int Nums,int deepC=1)
   {
   NumCAll=0;
   for ( int i=0; i<deepC; i++ ) DeepN(Nums,i+1);
   }  

要实现最终的多项式，所有这些函数都是需要的。OOP在这里是多余的，最好使用类似的函数来构建调用树，特别是对于不能显式编写的公式（如多维扩展）。很难理解它们的逻辑，但这是可能的。这些函数的模拟在C#程序中实现。不幸的是，所附的EA没有此代码，但它们在内部使用以前的版本。这是相当有效的，虽然相当笨拙。该程序尚处于原型阶段，将在以后加以改进和完成。到目前为止，这个程序还不适合在普通PC机上分析全局模式，我的程序仍然有很多小缺陷，我不断发现错误并修复它们。这样，程序功能就能不断增长，接近所需状态。

分析找到的模式

由于我的计算能力和时间有限，我不得不限制数据量。不管怎样，我认为得出一些结论就足够了。特别是，我必须只使用H1图表来分析全局模式，并限制分析时间。所有测试将在 MetaTrader 4 中执行。问题是，找到的模式的数学期望值接近于点差水平，在 MetaTrader 5 中，测试器应用的点差不小于历史记录值，即使我们使用选项自定义测试交易品种设置。该值将根据当前经纪商的实际交易数据和选定区域的点差进行调整。这样可以防止产生过于乐观的测试结果。我想消除这种机制的影响，决定使用 MetaTrader 4。 

我将从全局模式开始，他们的数学期望值在8个点左右。这是因为我们在公式中使用了50个烛形，在每个货币对的第一个选项卡中检查了大约200000个变体，而只使用了1个内核。有更好的机器会更容易。下一个版本的程序将减少对计算能力的依赖。在这里，我不想把重点放在最终的数学期望上，而是放在性能如何影响未来的EA性能上。

让我们从 EURUSD H1 开始，测试时间间隔为2010.01.01-2020.01.01。其目的是寻找一种全局模式：

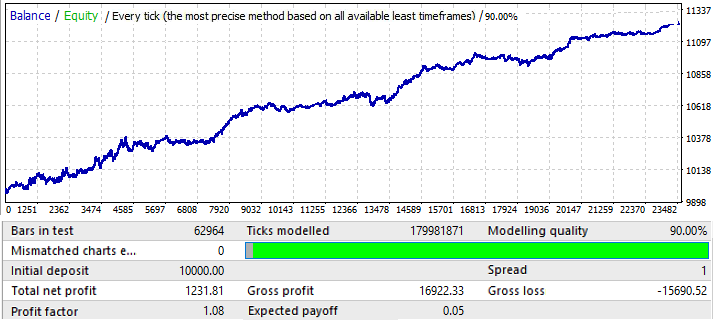
结果不是很吸引人，这就是我们在给定的时间间隔内设法挤出的结果。我们可以确定一个全局模式，尽管还不太清楚。我用了50个烛形来使用暴力算法，结果不如我们预期的好，但这是必要的，你会看到更多的原因。让我们在 2020.01.01-2020.11.01 测试同一段时间，以了解其未来表现：

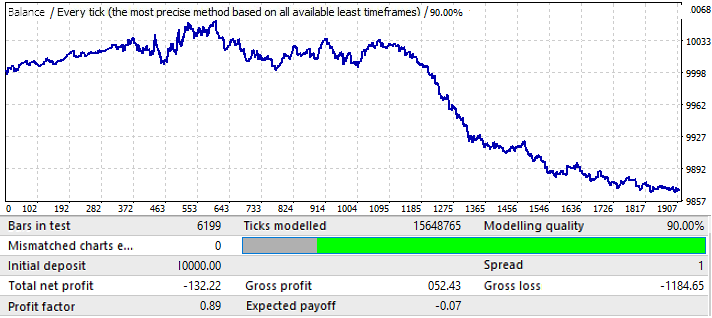
结果是可以理解的。这种分析结果不足以从模式延续中获利。一般来说，如果我们分析全局模式，那么目的应该是找到一个至少还能工作几年的模式，否则这样的分析是完全无用的。在图表开始的时候，这种模式仍然有效，但在六个月之后，它就反转了。因此，如果我们能够找到足够好的初始测试参数，这样的分析可能足够交易几个月。在这种情况下，分析是通过 P_Factor 的值进行的，此参数类似于利润系数，但取值范围为[0…1]。利润的 1 - 100% 。在第一个选项卡中，此参数的最大值约为0.029。所有发现的变体的平均值约为0.02。

下一个 EURCHF 图表:

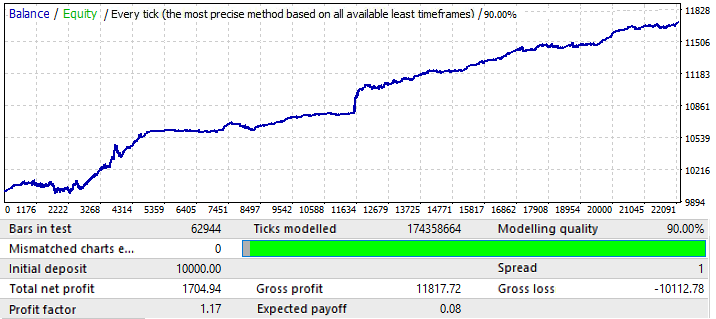
第一个选项卡上图表变量的最大结果约为0.057。它的可预测性比上一张图高出2倍，这也影响了最终利润系数，实际比上一张图高出0.09。让我们看看全局指标的改善是否影响到未来时期：

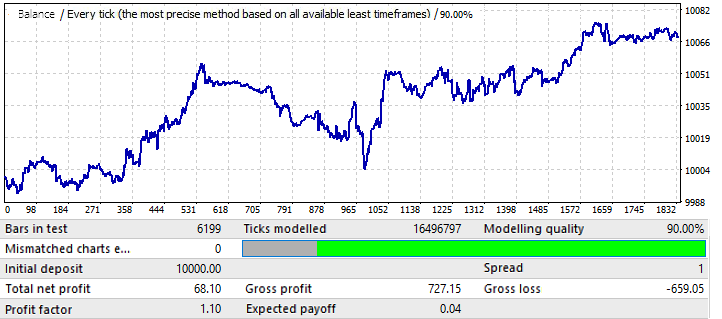
如你所见，这种模式贯穿全年，不太均匀，利润因子较低。然而，我们可以得出一些初步的结论。事实上，PF较低是因为全局测试有相当大的区域的急剧余额增长，这增加了由此产生的利润因子。我敢肯定，如果我们再测试后面几年，结果会差不多。初步结论是，图表质量和外观的改善将影响其未来的性能。所以，我们通过将我们的设置应用于这个特定的货币对得到了这个结果。图表上出现波动的原因可以从全局测试中看出，在全局测试中，余额的波动近年来大大增加。所以，波动只是这些波动的延续。

转到 USDJPY 图表:

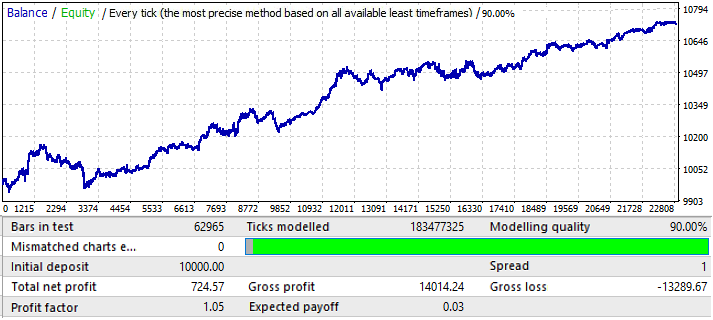
这是最差的图表。让我们查看一下未来时间段:

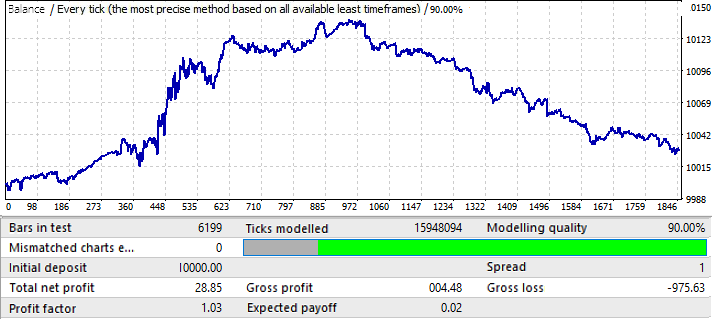
看起来是在一个正向的区域，但它的后半部分是非常类似的第一张图表（EURUSD H1），这也开始了向上运动，然后逆转，几乎直线向下运动。所以，这里的结论是一样的，最终结果质量不够高。不过，如果数学预期和利润因素足够好的话，我们可以预计用这种模式进行几个月的可以获利的交易。

最后一个图表, USDCHF:

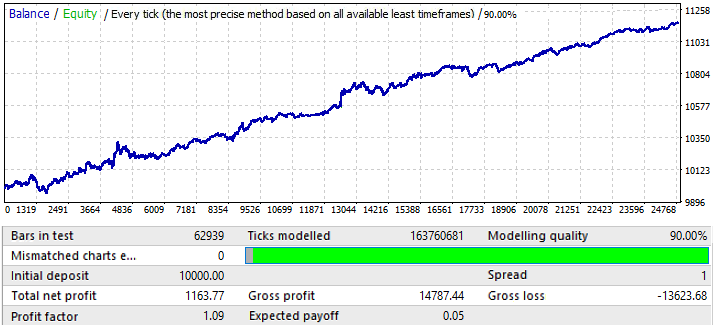
它没有什么特别的，让我们来看看未来时期：

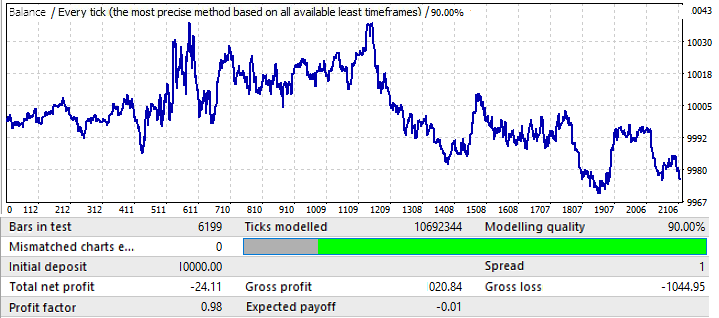
似乎与其他图表相似，除了 EURCHF。它的表现一直好到年中，然后出现反转和模式反转。

我们可以得出以下初步结论：

1. 显然，EURCHF 是最好的图表
2. 无论是在训练期还是在前向测试中，EURCHF 都优于其他所有的货币对
3. 在除 EURCHF 以外的所有图表中，这一模式一直保持到年中

基于以上分析，我们可以得出结论：训练阶段的质量成绩直接影响着未来期的表现。最终结果利润系数的增加表明，结果的随机性比其他图表要小得多。这反过来又表明我们已经找到了一个全局模式。应用于外汇市场，我们可以说“任何一种模式中都有一种模式的一部分”，测试值越强，份额越高。

现在我将尝试更改样本大小，让我们用一年。2017.01.01-2018.01.01 EURJPY H1. 让我们看看未来一个月的模式表现如何：

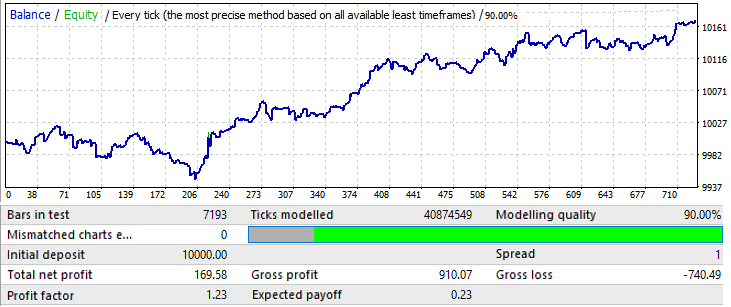
这张图表看起来不太好，但由此产生的利润系数和数学预期高于10年期变量。样本比初始变量小12倍，但是不应忽略此数据。

未来期为一个月：2018.01.01-2018.02.01：

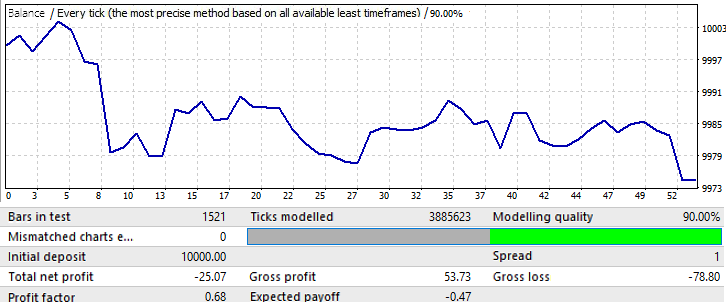
这只是一个例子，使进一步的推理更清楚。在这里，模式几乎立即逆转，不幸的是，我不能提供更多的数据。计算和软件安装需要很多时间。不管怎样，这些信息应该足以进行第一次分析。

数据分析

通过对专家顾问的测试，我们可以得出以下结论：

• EA交易，利用全局模式，并能够在相当长的时间内运作，可以创建一个简单的数字暴力算法
• 未来有效的持续时间直接取决于数据样本的大小
• 有效运行时间的长短直接取决于训练区的测试质量
• 在进行远期测试时，所有图表上全局模式的有效性至少保持2-3个月
• 当暴力计算部分最终结果的质量趋于100%时，找到一个至少还能工作几年的模式的可能性就会增加
• 当我们搜索全局模式时，不同的设置对不同的货币对起着不同的作用

至于局部的模式，比如一个月，这里的情况完全不同。在上一篇文章中，我分析了局部模式，但没有使用程序版本中引入的新函数。任何改进都可以更好地理解相同的问题。对于局部模式:

• 模式一直在改变
• 可以小心地使用马丁格尔

因此，样本越大，它保留未来可操作性的时间就越长。反之亦然，样本越小，模式在未来反转的速度就越快（当然，前提是没有正向优化，顺便提一下，我计划稍后添加）。短期内模式肯定会反转。根据这些结论，有两种可能的交易类型：

1. 利用全局模式
2. 利用局部模式

在第一种情况下，训练区域越大，模式工作的时间就越长。但是，最好每2到3个月搜索一次新的公式。至于局部模式，应该在市场冻结时每周进行搜索。结果的质量不会很高，但你不必担心结果-至少你可以赚取一些利润。

现在，我将尝试总结我在不同尺度模式研究中获得的所有数据。为此，我将引入一个反映特定订单预期收益（数学期望）的函数，以及一个反映利润因子的函数。您可以添加任何其他具有不太重要度量特征的函数。事件空间或随机变量都是未来事件发展的可能变量。现在我们只知道以下几点：

• 未来“F”柱有无数可能的发展（无论是否有订单打开）
• 对于未来开发的所有选项，其中订单在特定柱上打开，此订单将具有以点数和利润系数表示的预期收益（假设您在一个柱上进行测试，对于每个订单，只有以下柱始终不同）
• 每个公式的所有这些量都是不同的
• 对于具有不同未来开始日期（未来的开始是训练部分的结束）和不同训练部分持续时间（相当于训练部分的不同开始日期）的部分，最终寻求的参数将采用唯一的值

所有这些陈述都可以转化成数学公式。这里就是公式:

• MF=MF(T,I,F,S,R) — 未来特定柱上订单的数学期望。
• PF=PF(T,I,F,S,R)  — 未来特定柱上订单的利润因子。 
• T  — 训练部分的持续时间（在这种情况下是样本大小或柱数）。
• I  — 训练部分结束的日期。
• F  — 未来柱的编号，从训练结束日期开始。
• S  — 一个唯一的多项式或一个算法（如果模式是手动或由另一个EA发现的）。
• R  — 使用特定多项式或策略（信号优化的质量）获得的结果；它们包括训练周期上的交易次数和所需的度量，如数学期望、利润因子和其他参数。

根据暴力算法在不同工具和不同日期上获得的数据，我可以在图表上画出上述函数（“F”用作参数）：

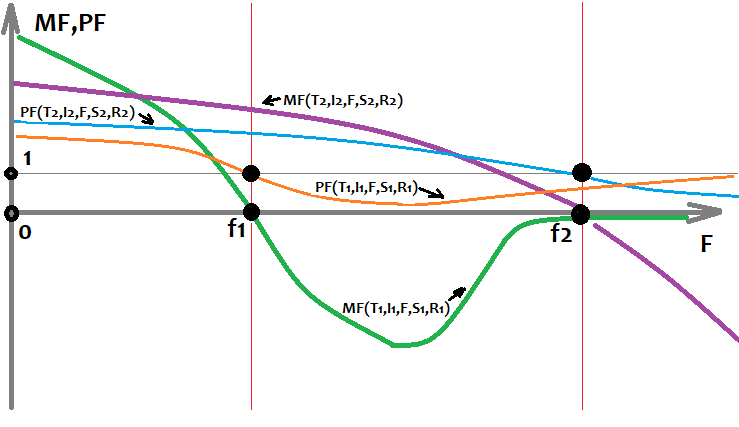
这张图表显示了两种独特的策略变化，它们在不同的领域使用不同的设置进行训练，并取得了不同的结果。有无数这样的选择，但它们都有不同的时间和最初模式的质量。这总是伴随着模式反转。这个规则可能不适用于非常强的模式。但即使是对它们来说，图表也总是有可能反转，也许5年后，但它会反转。最稳定的公式将是从最大样本中找到的公式。如果这些公式是人工找到的，并且来源于某种理论，那么将来这些公式就可以无限期地工作。然而，在使用暴力或其他机器学习方法时，我们没有这样的保证。我们所掌握的只是对运行时间的估计，这只能根据统计数据来确定。这个分析可以通过我的程序实现，但是由于时间和计算能力的限制，不能由一个人来实现。

下一步怎样做?

对全局模式的分析表明，普通计算机的能力不足以对大样本进行深入和高质量的分析，比如长达10年甚至更长的时间。无论如何，为了保证高质量的搜索结果，应该对非常大的样本进行分析。也许如果我们在高性能服务器上运行这个程序几个月，就能找到一两个好的变体。因此，我们需要在提高暴力算法速度的同时提高效率。对程序的进一步开发可能如下：

1. 添加分析固定服务器时间窗口的功能。
2. 添加在一周的固定日期执行分析的功能。
3. 添加随机生成时间窗口的功能。
4. 添加随机生成一周中允许交易的天数数组的功能。
5. 改进分析的第二阶段（优化选项卡），特别是多核计算的实现和优化器错误的纠正。

这些变化将极大地提高程序运行速度和所发现选项的可变性和质量。它们还应为市场分析提供方便的工具。

结论

我希望这篇文章对你有用。在我看来，本文中关于全局模式的主题非常重要。然而，这对我来说是非常困难的，因为程序的能力仍然不足以进行这种分析。如果我有30个核心，这会更容易。为了提高分析质量，我们需要花费更多的时间。

希望将来有可能获得更高的计算能力。我们将在下一篇文章中继续。在本文中，我还提供了一些用于一般理解的数学知识，在使用该程序时，以及在手动搜索模式和优化模式时，这些知识将非常有用。

这篇文章的总的理想是为那些还没有成功地手动实现这些小结果的人提供信息。它应该有助于理解开发机器人时使用的基本思想。

在我看来，你如何找到一个模式，手动或使用一些软件似乎并不那么重要。如果一个模式有一些获利的结果，我们可以认为它是一个可行的模式。一些模式参数给了我们一些预测，这可能是一个不久的将来的预测，但它仍然可以赚足够的钱。然而，如果你已经找到了一个模式，并不意味着同样的模式在将来也会起作用。要检查它，你将需要一个非常大的样品非常好的交易结果，整个样品和足够数量的订单考虑到样品的大小。除了找到一个模式，还有另一个问题——估计未来可能的运行时间。在我看来，这个问题很重要。如果我们不了解模式的工作时间和效果，那么找到一个模式有什么意义呢。任何人都可以使用我的程序，可在文章附件中找到。对于具体设置问题可以给我发私信。