パターン検索への総当たり攻撃アプローチ(第II部): イマージョン

はじめに

前の記事で始めたトピックを続けることにしました。今回は、変更されたアプリケーションバージョンを使用して通貨ペアの詳細な分析を行います。プロジェクト開発に貢献していただいたユーザのAleksey Vyazmikinさんに感謝します。彼のアドバイスは技術的に非常に役立つもので、さらなる発展の後押しとなりました。次の記事ではこの作業を続け、より興味深いデータと結果を提供します。特定の通貨ペアの分析の有効性をグローバルな規模で示すこと、および最大期間と最小期間の時間間隔の分析の違いを示すことは非常に重要であると私は信じています。私の時間とコンピューティングリソースは限られているため、1つの時間枠で少数の通貨ペアしかカバーできませんでした。ただし、グローバルパターンの初心者にとってはこれで十分なようです。データを分析するときは、前の記事のデータも使用します。

このトピックがとても興味深い理由

MetaTrader4およびMetaTrader5エキスパートアドバイザープログラマーのすべてのアイデアは、無数のコード行、無数のテスト、最適化、バックテストとフォワードテストを暗示していることがよくあります。ほとんどの場合、望むものは手に入りません。一部のプログラマーは、この仕様に飽きてしまいます。調査と検索のプロセスは日常業務に変わります。仕事が道徳的な満足とお金をもたらさない場合、やめる可能性が非常に高いです。これが私に起こったことです。私はルーチンに別れを告げ、マシンで正常に実行できるアクションの自動化を開始することにしました。機械には感情がなく、私とは異なり、理想的な労働者です。もちろん、マシンは人ほど広い視野を持っていませんが、多くのコンピューティングリソースを備えており、一部のプロセスをより簡単かつ迅速に実装できます。進化することができる独自のニューラルネットワークアーキテクチャを書き始めるか、問題を解決するための最も簡単なアプローチから始めるかを選択しました。私は後者のアプローチを使用することにしました。その単純さにもかかわらず、このプロジェクトは、MQL製品の単純なプログラミングとは対照的に、創造性と興味の余地を与えます。汎用テンプレートで作業し、必要な機能を徐々に追加してさらに開発することをお勧めします。単純なテンプレートから始めて、特定の動作原理のために新しいテンプレートを作成できます。結果として、退屈なルーチンを取り除いて開発を進めることができます。まあ、怠惰は進歩の父です。

総当たり攻撃プログラムの新バージョンと変更点のリスト

プログラムに変更があったのは1つだけで、赤い枠で示されています。この設定は、最高の状態を示している2番目のタブから取得されます。この設定を追加する理由は、最終結果の品質に非常に強い影響を与えるためです。分析中、最初のタブで、すべての結果は当初、品質で並び替えられました。利益率またはポイントでのペイオフ期待値が品質基準として使用されました。しかし、プログラムではグラフの形状を評価することはできませんでした。形状基準として直線性係数(直線との類似性)を使用したため、各オプションを視覚的に確認する必要がありません。ここで、よりまっすぐで滑らかなグラフは、2番目のタブに高品質のバリアントを与える可能性が高いという結論に達することができます。また、このようなグラフでは、2番目のタブのフィルターによって破棄されるバリアントの数が減ります。この値を計算するには、2回目のパスが必要です。このフィルターがアクティブな場合、総当たり攻撃の速度は約2倍遅くなります。しかし、私たちにとって重要なのは速度ではなく、得られた主要な結果の総数です。それらの品質がさらなるパフォーマンスに影響を与えるためです。

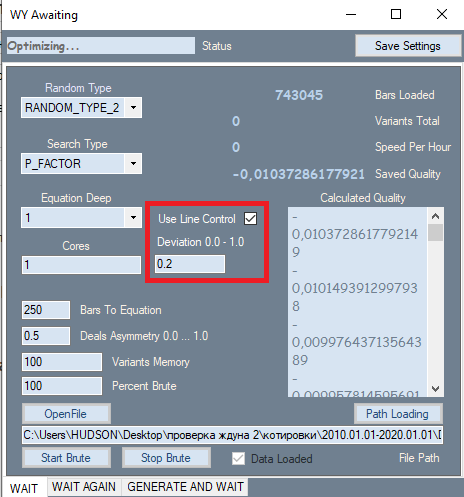
導入されたフィルターに加えて、多項式自体が変更されました。多項式は特定のバーのClose[i]-Open[i]値だけでなく、次の値も受け入れるようになっています。

• Close[i]-Open[i]
• High[i]-Open[i]
• Low[i]-Close[i]
• Low[i]-Open[i]
• High[i]-Close[i]

以前のバージョンのプログラムとは異なり、数式には特定のバーのすべての価格データが含まれるようになりました。これにより、多項式の複雑さが大幅に増加し、総当たり攻撃の速度が低下します。しかし、十分なコンピューティングリソースがあれば、より適切で効率的な市場の公式を選択できます。もちろん、これらのデータを使用して他の変数を作成することもできます。ただし、これらの値を多項式で使用すると、上記の値を線形結合できる値が得られます。次に例を示します。 

• C1*(High[i]-Close[i]) + C2*(Low[i]-Close[i]) = NewQuant
• C1 = 1およびC2 = -1の場合
• NewQuant = (High[i]-Close[i]) - (Low[i]-Close[i]) =  High[i]-Low[i]
• その他の場合
• NewQuant = (C1-C3)*(High[i]-Close[i])+(C2+C3)*(Low[i]-Close[i])  +  C3*((High[i]-Close[i]) - (Low[i]-Close[i])) = (C1-C3)*(High[i]-Close[i])+(C2-C3)*(Low[i]-Close[i]) +  C3*(High[i]-Low[i])

つまり、他の変数の線形結合で構成される変数の線形結合を使用すると、基本式に含めなくても新しい変数を作成できます。式にすでに存在する他の変数から形成される可能性のある変数を含めないようにすることをお勧めします。それらは、係数自体の値に応じて、係数の選択中に表示されます。

その結果、新しい多項式ははるかに複雑になります。

• Y = Sum(0,NC-1)( C[i]*Variant of product(x[1]^p[1]*x[2]^p[2]...*x[N]^p[N]) )
  
• Sum(0,N)(p[i])=MaxPowOfPolinom
• NC - 多項式の項の総数(選択された係数の数に等しい)
  

ここで、x[i]は多項式が取る引数であり、p[i]は引数が発生する度合いです。このような複雑な展開を処理できるコンピューターはないため、すべての構成要素の合計次数は、多項式の許容数を超えてはなりません。数式のバーの数が最小限の場合、私はほとんどの場合次数1、2、3のいずれかを使用します。とにかく、サーバ上ででも、より高い次数の使用は効果がありません。十分な計算能力がありません。

以下は引数オプションです。最終的な合計には、製品のすべての可能な組み合わせが含まれます。

1. x[i] =Close[i]-Open[i]
2. x[i] =High[i]-Open[i]
3. x[i] =Low[i]-Close[i]
4. x[i] =High[i]-Open[i]
5. x[i] =High[i]-Close[i]

また、これらすべてのアクションを多項式で実行する理由を明らかにしたいと思います。重要なのは、システムというのは最終的に一連の条件だということです。条件は論理関数であるため、1つまたは複数の条件が存在する可能性がありますが、これは問題ではありません。一連の条件は、最終的にtrueまたはfalseのいずれかを返すブール式に変換できます。このようなシグナルは、「はい」または「いいえ」としてのみ解釈できますが、シグナルの強さを判断したりシグナルを調整したりすることは不可能です。複数のインディケーターをシグナルとして使用する場合、これらのインディケーターのパラメータは個別に調整できるため、最終的な論理式やシグナルが変更されて、最終的に取引に影響します。しかし、これは非常に不便だと思います。特定のインディケーターのパラメータの変更が取引にどのように影響するかがわからないためです。

このアプローチの背後にある主なアイデアは、シンプルさと効率でした。なぜこのアプローチなのかというと、これにはいくつかの利点があるからです。

• 最適化された機能の独自性
• シグナル強度の関数値への依存性
• 使いやすさ
• 最適化可能な唯一のパラメータは多項式値である

最も重要なことは、条件の数とそのタイプを選択する必要がないということです。これは、条件の無限のセットを探す代わりに、これらすべての条件を、正または負のいずれかの分数を出力する単一の関数に減らすことができるという考えを元々受け入れているためです。異なる関数の信頼性によっては、モジュラスでより強いシグナルが必要になる場合があります。一部の式では、これによりスケーラビリティが提供される場合があります。ここでのスケーラビリティとは、取引数が減少したときにシグナルを増幅する能力を意味します。

一般的に言って、私の研究は、他の多くの人々の研究と同様に、単一の結論につながります。エントリシグナルを強化しようとすると、必然的に一定期間の取引数が減少します。言い換えると、ランダムなコンポーネントを持つ関数の場合、一部のポイントは常に他のポイントよりも予測可能な結果をもたらします。関数が十分に効率的である場合、この関数によって提供されるシグナルの要件を増やすことで、特定の予測可能性レベルを達成できます。もちろん、これは主要な条件を満たすすべての関数に当てはまるわけではありませんが、一次条件が厳しくなるほど、総当たり攻撃アプローチを使用して見つけることができるこれらの数式バリアントのペイオフ期待値が高くなります。これは、勾配ブースティングだけでなく、ニューラルネットワークを含む他のパターン検索方法にも当てはまります。

データ標本への依存は大きいです。標本が小さいほど、ランダムな結果が得られる可能性が高くなります。ここでのランダムな結果とは、パターンが検索された銘柄のグローバル履歴で最終システムをテストするときに、機能しないか、非常に効果的に機能しない結果です。

最終的な取引システムの将来の品質が、分析されたデータ領域のサイズとこのシステムを見つけるために必要な労力の量にどのように依存するかという質問に答えてみましょう。まず、一定期間に見つかった戦略数の数学的期待値を表す式を定義します。

• Mn(t) = W(t,F)*Ef(T,N,L)
• Mn - 要件を満たす戦略数の数学的期待値
• W(t,F) = F*t - チェックされたバリアントの単位時間あたりの結果数
• Ef(T,N,L) = ? - 総当たり攻撃の効率。これは、間隔の長さ、相場タイプ、必要な注文決済数、および総当たり攻撃中に考慮される場合に必要な線形性係数に依存します(この値は、現在のバリアントの結果が必要十分な値をとる確率に等しくなります)
  
• N - テストに十分な最小許容取引数
• L - 最大許容直線性係数(追加の制御基準として)
• F - 戦略バリアントでの総当たり攻撃の頻度

Ef関数の形式を決定することは非常に困難ですが、それがどのように見えるか、そしてどのような特性を持っているかは大まかに見積もることができます。

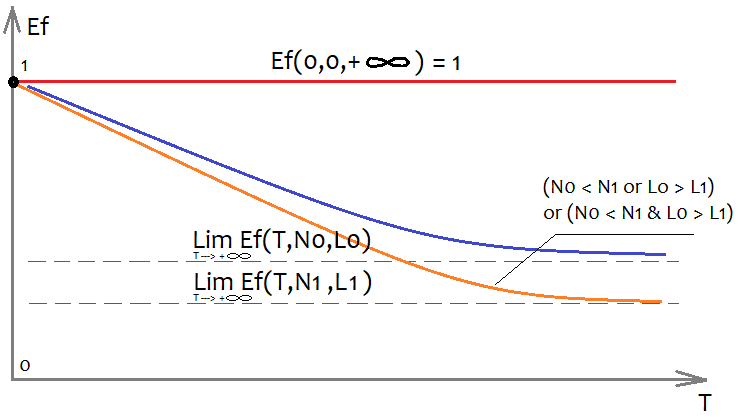
平面上で多次元関数を表示できるようにするには、グラフ自体を作成する1つの引数を除いて、すべての引数を何らかの数値で固定する必要があります。特に興味深いのは、1つの時間枠を分析する場合に、分析された標本の期間を時間で表すT変数です。この仮定を破棄すると、標本サイズをTと見なすことができます。グラフの外観は変わりません。当然、残りの2つの引数がグラフの外観にどのように影響するかに関心があるので、これを図に示します。最終バージョンで必要な注文が多いほど、要件を満たすシステムが少なくなります。これは、注文が少ないシステムを見つけるのがはるかに簡単だからです。線形性係数(直線からの偏差)についても同じことが言えますが、ここでは、線形性係数は小さいほど(ゼロに近い)より優れています。

システム品質の概念を修正しない場合(この値は利益要因と数学的期待値の両方になる可能性があるため)、見つかったシステムの最大品質の概念を導入することもできます。同様に、それが何に依存するかを説明することができます。

• Mq=Mq(T,N,S)
• S - 選択した式の構成

言い換えれば、戦略の可能な限り最高の品質は、式の有効性、および要件と間隔の複雑さに直接依存します。同時に、エリアの開始は固定されており、トレーニング開始点の各バリエーションは一意であり、一意の開始パラメータを提供すると想定します。つまり、トレーニングエリアに異なる開始日を選択することで、異なる効率値やその他のパラメータ、および取得したシステムの最終的な品質を取得できます。

また、品質の種類ごとに最大値があることも理解できます。たとえば、利益率の最大品質は無限大ですが、最大値が制限されていないため、PFを使用したグラフィカルモデルは理解しにくくなるため、私はこの測定値を分析に使用することは好みません。 したがって、私はPFの独自のアナログであるP_FACTORを使用します。これは[-1,1]の範囲にあります。

• P_FACTOR=(Profit-Loss)/(Profit+Loss)

その最大値は1に等しいため、作業がより便利です。以下は、T(選択された領域とその標本)に応じたこの値の最大値を表す関数です。

• Mx=Mx(T)

パラメータまたは品質基準がP_FACTORの場合、Mx(T)=1です。関数形式は不明な場合がありますが、T軸の正の部分全体でMx'(T) > 0であることがわかっています。値が任意の時点で正であるため、これはグラフが常に増加していることを意味します。

利益要因については次のようになります。

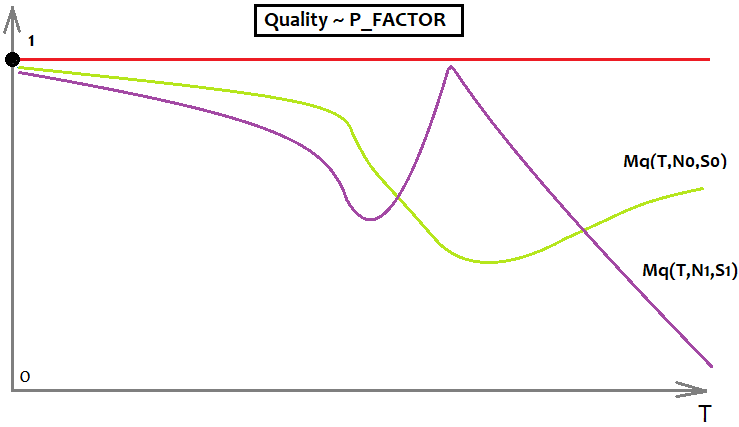
この例には、PFの上限と、要件が異なる2つの異なる式を示す2つのグラフがあります。グラフでは、「T」が無限大になるにつれて品質が低下する傾向が少ないため、ライムカラーの式の方が優れています。

数学的期待値については次のようになります。

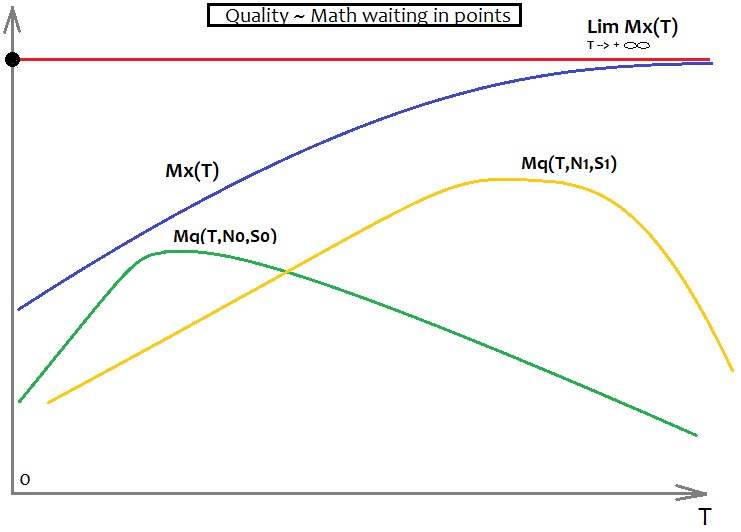
ここでも、要件が異なる2つの異なる式の2つのバリアントがあります。さらに、ここに漸近線として機能するMx(T)があります- Mq(T,N,S)はこの障壁を克服できません。理想的なMq(T,N,S)はMx(T)グラフと一致し、聖杯を見つけたことを意味します。もちろん、これは実際には決して起こりません。しかし、本当に市場を理解したいのであれば、これは理解のために非常に重要だと思います。

外国為替では、他の金融市場と同様に、確率論の概念のみで操作することが最も正しく正確です。外国為替市場の主な数学的分析ルールのいくつかを次に示します。

• ほとんどすべての量は固定されておらず、数学的期待に置き換えられている
• より大きな標本からの値の数学的期待は、グローバル標本からの結果になる傾向がある
• より頻繁に確率を使用する

データセグメントの信頼性は標本レートのみです。標本が大きいほど、入力データセットが広範になり、最終的な式がより公平になります。事実、標本は無限大になる傾向があるため、最終結果は固定された制限値になる傾向があります。

テンプレートの変更

ロジックが改善されたため、適切に動作するようにテンプレートの関数を変更する必要があります。新しいパラメータを受信できる必要があります。これらの関数の実装は、プログラムとテンプレートコードの両方で同じです。元の関数は1つの値で機能するように開発されましたが、現在値は4つあるため、関数を修正する必要があります。まず第一に、これらの変更はより高品質の数式を提供するはずです。数式で使用されるデータが多いほど、検索機能は高くなります。

この記事を書いているときに、コードに欠陥が見つかりました。多次元多項式を実装する関数の特殊性のために、これらの因子の順序は混沌としているのに、因子の組み合わせを繰り返すことができます。この関数は呼び出しツリーを構築しますが、要素の順列を制御することはできません。これは、次の2つの方法で回避できます。

1. 因子のすべての可能な順列を制御する
2. 合計係数をそれらの数で割ることにより、数式内の重複する要素の数を補正する

私は2番目のオプションを使用することにしました。このアプローチの欠点は、平均係数が0.5になる傾向があることです。少なくとも、因子は役に立たないでしょう。この記事では、エラーの影響を受けない次数1の多項式を使用しました。合計次数が固定された乗数の組み合わせの数は簡単に計算できます。

• Comb=n!/(n-k)!
• nは可能な独立した乗数の数
• kは最終項の合計度

以下は、コードでのこの式の実装です。

double Combinations(int k,int n)
   {
   int i1=1;
   int i2=1;
   for ( int i=n; i<n-k; i-- ) i1*=i;
   for ( int i=n-k; i>1; i-- ) i2*=i;
   return double(i1/i2);
   }

これが最終多項式の主な関数がどのように変化したかです。変更は1次元多項式チャートに関連しています。これは、1つではなく5つのパラメータに依存するようになったためです。もちろん、4つの初期配列があります。ただし、価格データを単なるデータとして使用することはできませんが、より柔軟な値に変換する必要があります。隣接する価格の差を使用しますが、隣接する価格はバーの開始と終了の両方になり得ます。

double Val;
int iterator;
double PolinomTrade()//Polynomial for trading
   {
   Val=0;
   iterator=0;
   if ( DeepBruteX <= 1 )
      {
      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(Close[i+1]-Open[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(High[i+1]-Open[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(Open[i+1]-Low[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(High[i+1]-Close[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(Close[i+1]-Low[i+1])/Point;
         iterator++;
         }

      return Val;   
      }
   else
      {
      CalcDeep(C1,CNum,DeepBruteX);
      return ValStart;
      }
   }


///Fractal calculation of numbers
double ValW;//the number where everything is multiplied (and then added to ValStart)
uint NumC;//the current number for the coefficient
double ValStart;//the number where to add everything
void Deep(double &Ci0[],int Nums,int deepC,int deepStart,double Val0=1.0)//intermediary fractal
   {
   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(Close[i+1]-Open[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(Close[i+1]-Open[i+1])*Val0/Point;
         NumC++;
         }
      } 
      
   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(High[i+1]-Open[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(High[i+1]-Open[i+1])*Val0/Point;
         NumC++;
         }
      }

   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(Open[i+1]-Low[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(Open[i+1]-Low[i+1])*Val0/Point;
         NumC++;
         }
      }

   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(High[i+1]-Close[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(High[i+1]-Close[i+1])*Val0/Point;
         NumC++;
         }
      }

   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(Close[i+1]-Low[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(Close[i+1]-Low[i+1])*Val0/Point;
         NumC++;
         }
      }
   }
   
void CalcDeep(double &Ci0[],int Nums,int deepC=1)
   {
   NumC=0;
   ValStart=0.0;
   for ( int i=0; i<deepC; i++ ) Deep(Ci0,Nums,i+1,i+1);
   }

いくつかの小さな変更は、係数の配列のサイズを計算する関数に関係しています。これで、ループは5倍長くなります。

int NumCAll=0;//size of the array of coefficients
void DeepN(int Nums,int deepC=1)//intermediate fractal
   {
   for ( int i=0; i<Nums*5; i++ )
      {
      if (deepC > 1) DeepN(Nums,deepC-1);
      else NumCAll++;
      }
   }

void CalcDeepN(int Nums,int deepC=1)
   {
   NumCAll=0;
   for ( int i=0; i<deepC; i++ ) DeepN(Nums,i+1);
   }  

これらの関数はすべて、最終的な多項式を実装するために必要です。ここではOOPは冗長であり、特に明示的に記述できない式(多次元展開など)の場合は、同様の関数を使用して呼び出しツリーを構築することをお勧めします。それらの論理を理解することはかなり難しいですが可能です。これらの関数と同様なものはC#プログラム内に実装されています。残念ながら、添付されたEAにはこのコードがありませんが、内部で以前のバージョンを使用しています。かなり不器用ですが、非常に効率的です。プログラムはまだプロトタイプ段階にあり、後で改善されて完了する予定です。これまでのところ、このプログラムは通常のPCでのグローバルパターンの分析には適していません。プログラムの側面にはまだ多くの小さな欠陥があり、私はエラーを見つけて修正し続けています。そのため、プログラムの機能は絶えず成長し、目的の状態に近づきます。

見つかったパターンの分析

私の計算能力と時間は限られているので、データの量を制限しなければなりませんでした。とにかく、結論にはそれで十分だと思います。特に、グローバルパターンの分析にH1チャートのみを使用し、分析時間を制限する必要がありました。すべてのテストはMetaTrader4で実行されます。重要なのは、見つかったパターンの数学的期待値がスプレッドレベルに近いことです。MetaTrader5では、オプションカスタムテスト銘柄設定を使用している場合でも、テスターは過去に登録された値以上のスプレッドを適用します。値は現在の証券会社からの実際のティックデータと選択したエリアのスプレッドに基づいて調整され、楽観的すぎるテスト結果が生成されるのを防ぎます。このメカニズムの影響を取り除きたいと思い、MetaTrader4を使用することにしました。 

グローバルパターンから始めます。数学的期待は約8ポイントでした。これは、数式に50本のローソク足を使用し、1つのコアのみを使用しながら、各通貨ペアの最初のタブで約20万のバリアントをチェックしたためです。より良い機械があればもっと簡単でしょう。プログラムの次のバージョンの計算能力への依存度はより低くなります。ここでは、結果として得られる数学期待値ではなく、パフォーマンスが将来のEAのパフォーマンスにどのように影響するかに焦点を当てたいと思います。

EURUSDH1から始めましょう。テストは2010.01.01～2020.01.01の間隔で実行されました。その目的は、グローバルパターンを見つけることでした。

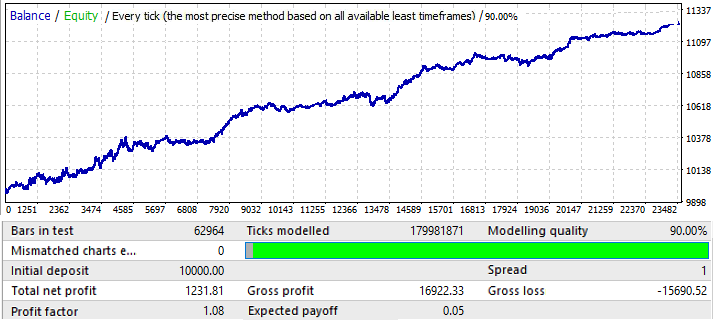
結果はあまり魅力的ではなく、これが、指定された時間間隔でペアから絞り出すことができたすべてです。それほど明確ではありませんが、グローバルパターンを特定できます。私は総当たり攻撃の式で50本のローソク足を使用しました。結果は私たちが期待したほど良くはありませんが、それは必要です。理由は後で分かります。将来のパフォーマンスを理解するために、将来の期間2020.01.01〜2020.11.01で同じセグメントをテストしてみましょう。

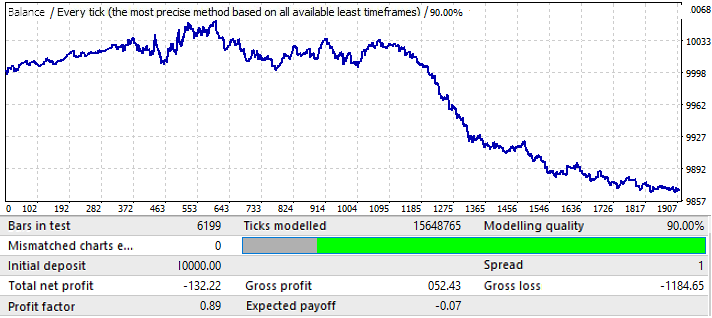
結果は非常にわかりやすいです。この分析は、パターンの継続から利益を得ようとするのに不十分であることが判明しました。一般に、グローバルパターンを分析する場合、目的は少なくともあと数年は機能するパターンを見つけることです。さもないと、そのような分析はまったく役に立ちません。チャートの最初ではパターンは機能し続けますが、6か月後には反転します。したがって、最初のテストで十分なパラメータを見つけることができれば、このような分析で数か月の取引に十分である可能性があります。この場合、分析はP_Factor値によって実行されました。このパラメータはProfitFactorに似ていますが、[0 ... 1]の範囲の値を取ります。利益の1～100％です。最初のタブでは、このパラメータの最大値は約0.029でした。見つかったすべてのバリアントの平均値は約0.02でした。

次はEURCHFチャートです。

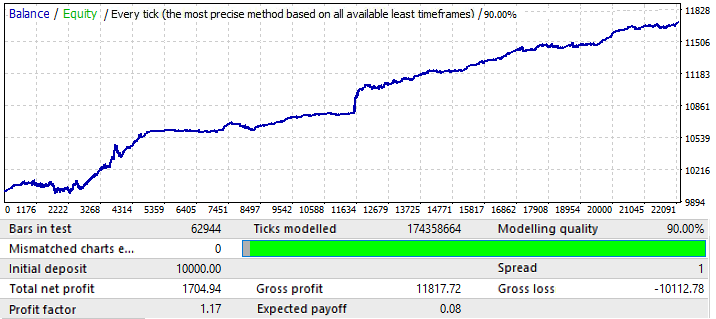
最初のタブのチャートバリアントの最大結果は約0.057でした。その予測可能性の程度は前のチャートの2倍であり、これは最終的な利益率にも影響を及ぼしました。これは実際には前のチャートより0.09高くなっています。グローバル指標の改善が将来の期間に影響を与えたかどうかを見てみましょう。

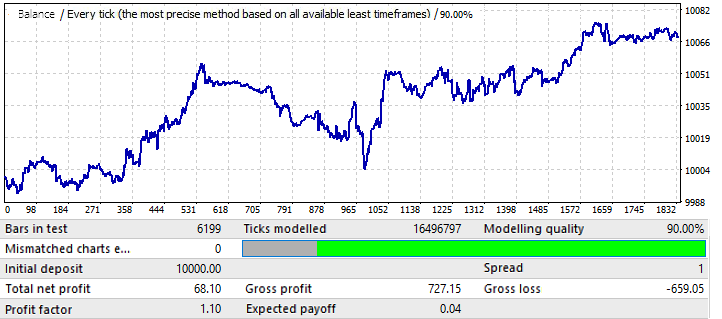
ご覧のとおり、このパターンは年間を通じて継続しています。それはあまり均一ではなく、利益率はより低くなりますが、いくつかの予備的な結論を引き出すことができます。実際、グローバルテストではバランスが急激に増加する領域が非常に大きく、結果として利益率が増加したため、PFは低くなっています。次の何年かテストしても、結果はほぼ同じになると確信しています。予備的な結論は、チャートの品質と外観の改善が将来のパフォーマンスに影響を与えたということです。この特定の通貨ペアに設定を適用することで、この結果が得られました。チャートの波の理由は、バランスの変動が近年大幅に増加しているグローバルテストで見ることができます。波はこれらの変動の単なる継続です。

USDJPYチャートに移ります。

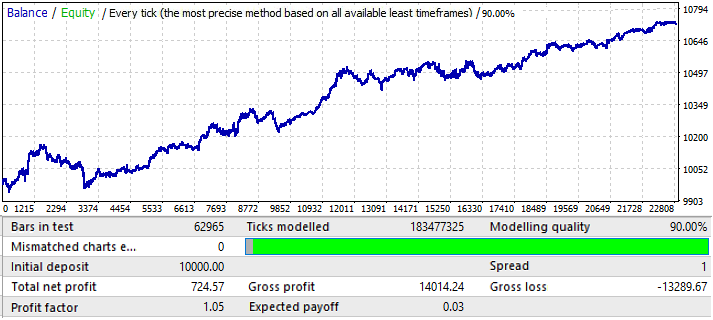
これは最悪のチャートです。フォワード期間を確認しましょう。

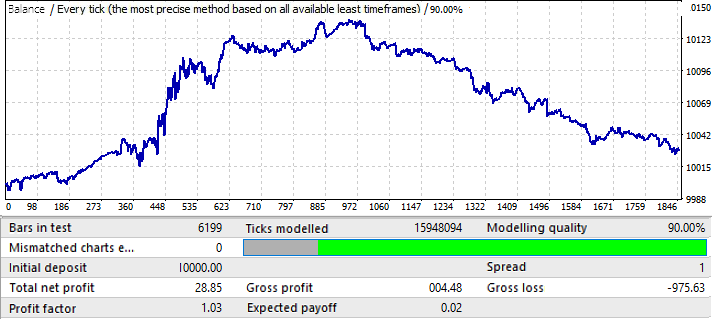
ポジティブゾーンにあるように見えますが、後半は最初のチャート(EURUSD H1)と非常によく似ており、上向きの動きで始まってその後反転してほぼ真っ直ぐ下向きの動きをしました。結論はここでも同じです。最終結果の品質は十分に高くありません。それでも、数学的期待値と利益率が十分であれば、このパターンで数か月の収益性の高い取引を期待できます。

最後のチャートはUSDCHFです。

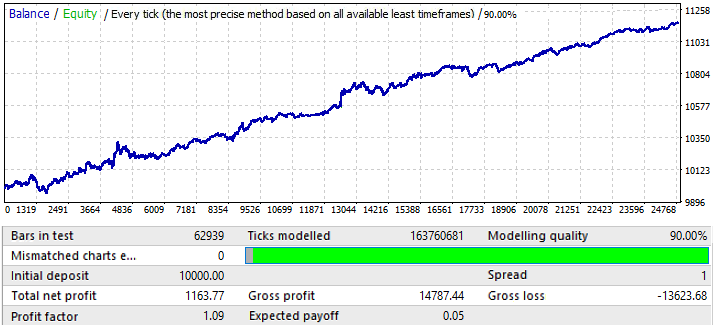
これは、あまり印象的ではありません。フォワード期間を見てみましょう。

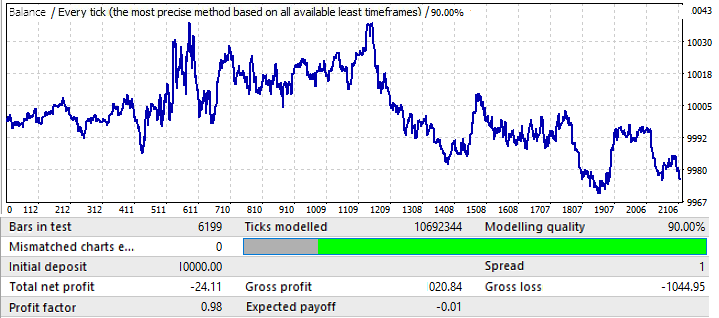
EURCHFを除いて、他のチャートと同様のようです。そのパフォーマンスは年の半ばまで良好であり、その後、反転とパターン反転があります。

以下の予備的な結論を導き出すことができます。

1. EURCHFが断然最高のチャートだった
2. EURCHFはトレーニング期間とフォワードテストの両方で他のすべてのペアよりも優れていた
3. EURCHFを除くすべてのチャートで、パターンは年の半ばまで保持される

上記に基づいて、トレーニング期間の品質結果がフォワード期間のパフォーマンスに直接影響するという結論を下すことができます。最終結果の利益率の増加は、結果が他のチャートよりもはるかにランダムでないことを示している可能性があります。これは、グローバルパターンが見つかったことを示している可能性があります。外国為替市場に当てはめると、「どのパターンでもパターンのシェアがある」と言えます。テスト値が強いほど、シェアは高くなります。

次に、標本サイズを変更してみます。1年を使いましょう。2017.01.01-2018.01.01 EURJPY H1. 1か月先のパターンがどのように動作するかを見てみましょう。

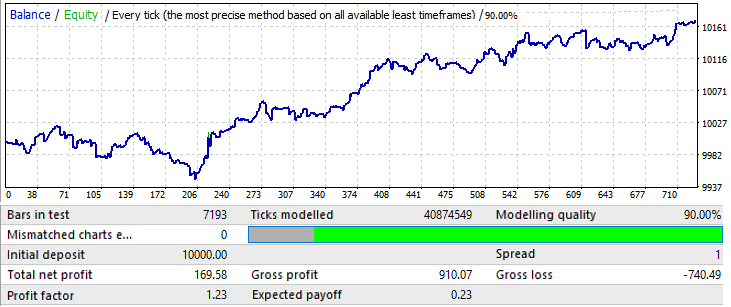
チャートはあまり良く見えませんが、結果として得られる利益係数と数学的期待値は、10年のバリアントのものよりも高くなっています。標本は最初のバリアントの12分の1です。このデータは無視しないでください。

フォワード期間は1か月です(2018.01.01～2018.02.01)。

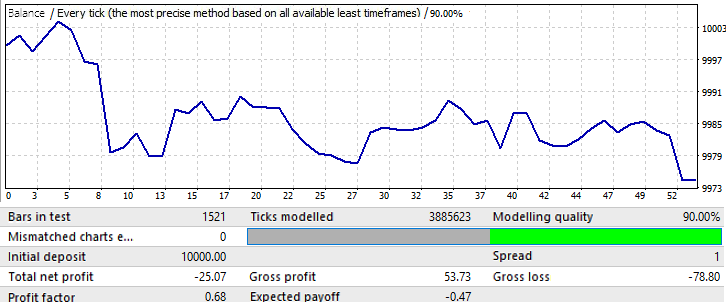
これは、さらに推論を明確にするための単なる例です。ここでは、パターンはほぼ即座に逆転します。残念ながら、これ以上のデータを提供できませんでした。計算とソフトウェアのセットアップには多くの時間がかかります。とにかく、この情報は最初の分析には十分なはずです。

データ分析

エキスパートアドバイザーをテストした後で、いくつかの結論を出すことができます。

• グローバルパターンを活用して非常に長期間作動できるエキスパートアドバイザーは、単純な総当たり攻撃を使用して作成できる
• 将来の操作の期間は、データ標本のサイズに直接依存する
• 操作の期間は、トレーニングエリアのテスト品質に直接依存する
• フォワード期間をテストする場合、すべてのチャートのグローバルパターンの操作性は少なくとも2〜3か月のままである
• 総当たり攻撃セクションでの最終結果の品質が100％に徐々に向かう場合、少なくともあと数年は機能するパターンを見つける可能性が高くなる
• グローバルパターンを検索する場合、異なる設定は異なる通貨ペアに対して異なる働きをする

月などのローカルなパターンについては、ここでは状況がまったく異なります。前回の記事では、ローカルパターンを分析しましたが、プログラムバージョンで導入された新機能は使用しませんでした。改善すれば、同じ質問をよりよく理解できます。ローカルパターンの場合:

• 常にパターン変更を再生する
• マーチンゲールは慎重に使用できる

したがって、標本が大きいほど、将来の操作性が長く維持されます。逆に、標本が小さいほど、将来のパターンの反転が速くなります(もちろん、前方最適化がない場合です。後でこれを追加する予定です)。間隔が短い場合のパターン反転が保証されます。これらの結論に基づいて、2つの可能な取引タイプがあります。

1. グローバルパターンの活用
2. ローカルパターンの活用

最初のケースでは、トレーニングエリアが大きいほど、パターンが長く機能しますが、2〜3か月ごとに新しい数式を検索することをお勧めします。ローカルパターンについては、市場が凍結している間、毎週検索を実行する必要があります。結果の品質は高くありませんが、結果について心配する必要はありません。少なくとも、ある程度の利益を得ることができます。

ここで、さまざまなスケールのパターンを調査した結果得られたすべてのデータを要約してみます。そのために、特定の注文のペイオフ期待値(数学的期待値)を反映する関数と、利益率を反映する関数を紹介します。重要度の低い指標を特徴付ける他の関数を追加できます。イベントのスペースまたは確率変数は、将来のイベント開発のすべての可能なバリアントになります。今わかっているのは次のことだけです。

• 将来的には「F」番目のバーの開発の可能性は無数にある(注文が開かれているかどうかに関係なく)
• 注文が特定のバーで開かれる将来の開発のすべてのオプションについて、この注文はポイントと利益係数でペイオフ期待値を持つ(1つのバーでテストを実行していると想像してください、次のバーだけが常に注文ごとに異なります)
• これらの量はすべて、式ごとに異なる
• 異なる将来の開始日(将来の始まりはトレーニングセクションの終わりです)と異なるトレーニングセクション期間(トレーニングセクションの異なる開始日に相当)を持つセクションの場合、最終的に求められるパラメーターは一意の値を取る

これらのステートメントはすべて数式に変換できます。式は次のとおりです。

• MF=MF(T,I,F,S,R) - 将来の特定のバーでの注文の数学的期待値
• PF=PF(T,I,F,S,R) - 将来の特定のバーでの注文の利益率 
• T - トレーニングセクションの期間(この場合、標本サイズまたはバーの数)
• I - トレーニングセクションの終了日
• F - トレーニングの終了日から始まる将来のバー番号
• S - 一意の多項式またはアルゴリズム(パターンが手動または別のEAによって検出された場合)
• R — 特定の多項式または戦略を使用して達成された結果(シグナル最適化の品質)。トレーニング期間中の取引数と、数学的期待値、利益率、その他のパラメータなどの望ましい指標が含まれる。

さまざまな商品と日付で総当たり攻撃で得られたデータに基づいて、上記の関数をチャートに描くことができます(「F」は引数として使用されます)。

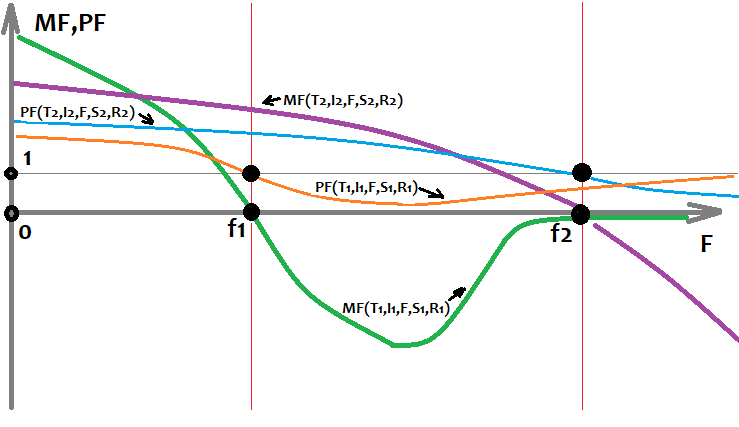
このチャートは、異なる設定を使用して異なるセグメントでトレーニングされ、異なる結果を達成した戦略の2つの一意のバリアントを示しています。そのようなオプションは無数にありますが、すべて元のパターンの期間と品質が異なります。これには常にパターン反転が続きます。このルールは、非常に強いパターンに対してのみ機能するとは限りません。しかし、それらにとってさえ、チャートが逆転するリスクがあります。5年以内かもしれませんが、それは逆転します。最も安定した式は、最大の標本から見つかった式になります。数式が手動で検出され、何らかの理論に基づいている場合、そのような数式は将来無期限に機能する可能性があります。ただし、総当たり攻撃法やその他の機械学習方法を使用する場合、そのような保証はありません。持っているのは操作時間の見積りだけで、これは統計データに基づいてのみ行うことができます。この分析は私のプログラムを使用することで可能ですが、時間と計算能力が限られているため、1人で実行することはできません。

次の段階

グローバルパターンの分析によって、通常のコンピュータの能力は、10年以上のような大きな標本の深くて高品質の分析には十分ではないことがわかります。とにかく、高品質の検索結果を保証するためには非常に大きな標本を分析する必要があります。おそらく、高性能サーバで2か月間プログラムを実行すれば、1つまたは2つの優れたバリアントを見つけることができます。したがって、総当たり攻撃の速度を増加するとともに効率を改善する必要があります。プログラムの可能なさらなる開発は次のとおりです。

1. 固定サーバーの時間枠を分析する機能の追加
2. 固定された曜日に分析を実行する機能の追加
3. 時間枠をランダムに生成する機能の追加
4. 取引に許可された曜日の配列をランダムに生成する機能の追加
5. 分析の第2段階([最適化]タブ)の改善、特にマルチコア計算の実装とオプティマイザーエラーの修正

これらの変更により、プログラムの動作速度と、見つかったオプションの変動性と品質の両方が大幅に向上するはずです。また、市場分析のための便利なツールキットを提供することになるはずです。

終わりに

この記事がお役に立てば幸いです。この記事のグローバルパターンのトピックは非常に重要であるように思われます。しかし、この種の分析にはプログラムの機能がまだ十分ではないため、これを行うことは非常に困難でした。30コアにアクセスできれば、これはもっと簡単なはずです。分析の質を向上させるには、もっと多くの時間を費やす必要があります。

うまくいけば、将来的には増加した計算能力にアクセスできるようになるでしょう。次の記事に続きます。また、この記事では、一般的な理解のためにいくらかの数学を提示しました。これは、プログラムを使用するときや、パターンを手動で検索して最適化するときに役立ちます。

この記事の一般的な理想は、これらの小さな結果も手動で達成することにまだ成功していない人々に情報を提供することでした。ロボットを開発するときに使用される基本的なアイデアの基礎を理解するのに役立つはずです。

手動で、またはソフトウェアを使用して、パターンを見つける方法はそれほど重要ではないようです。パターンに有益な結果が得られれば、それは機能するパターンと見なすことができます。いくつかのパターンパラメータは私たちにいくつかの予測を与えます。これは近い将来の予測かもしれませんが、それでも稼ぐには十分です。ただし、パターンを見つけたとしても、同じパターンが将来機能するという意味ではありません。それをチェックするには、サンプル全体で非常に良好な取引結果があり、サンプルサイズを考慮して十分な数の注文がある非常に大きなサンプルが必要になります。パターンを見つけることとは別に、別の問題があります-それが可能な将来の操作時間を見積もることです。私の意見では、この質問は基本的なものです。パターンがどのくらいの期間、どれだけうまく機能するかがわからなければ、パターンを見つける意義がありません。プログラムはご自由にお使いください。記事の添付ファイルで入手できます。特定の設定に関する質問については、メールしてください。