
Optimización paralela con el método de enjambre de partículas (Particle Swarm Optimization)
Como ya sabemos, MetaTrader 5 permite optimizar estrategias comerciales con la ayuda de un simulador incorporado que se basa en dos algoritmos: la iteración directa de los parámetros de entrada y el algoritmo genético, AG. La optimización genética es una de las variedades de los algoritmos evolutivos que ofrecen una aceleración significativa de los procesos. Además, los resultados del AG pueden depender en gran medida tanto de la tarea en cuestión como de los matices de la implementación específica del AG, en particular, la que ofrece el simulador. Por eso, muchos tráders que, por un motivo u otro, no se adaptan a la funcionalidad estándar, tratan de crear sus propios optimizadores para MetaTrader. En este caso, además, los posibles modos de optimización rápida no se limitan a la genética. Aparte del AG, son ampliamente conocidos los métodos como "el recocido simulado" y "el método de enjambre de partículas".
En el presente artículo, implementaremos el algoritmo de enjambre de partículas (Particle Swarm Optimization, PSO) e intentaremos incorporarlo al simulador de MetaTrader para el inicio paralelo en los agentes locales disponibles. La función de optimización objetivo será el indicador comercial del asesor que el usuario seleccione.
El método de enjambre de partículas (PSO)
Desde un punto de vista algorítmico, el método de PSO es relativamente sencillo. La idea principal consiste en generar un conjunto de "partículas" virtuales en el espacio de los parámetros de entrada del asesor experto. Después, las partículas se mueven y modifican su velocidad dependiendo de las métricas comerciales del asesor experto en los puntos correspondientes en el espacio. El proceso se repite en multitud de ocasiones, hasta que las métricas dejen de mejorar. A continuación, mostramos el pseudocódigo del algoritmo:

Particle Swarm Optimization Pseudo-Code
Según este, cada partícula tiene la posición, velocidad y memoria actuales de su "mejor" punto en el pasado. Entendemos por "mejor" el punto (el conjunto de parámetros de entrada del experto) donde se ha conseguido el mejor valor de la función objetivo para esta partícula. Vamos a describir esto en una clase.
class Particle { public: double position[]; // current point double best[]; // best point known to the particle double velocity[]; // current speed double positionValue; // EA performance in current point double bestValue; // EA performance in the best point int group; Particle(const int params) { ArrayResize(position, params); ArrayResize(best, params); ArrayResize(velocity, params); bestValue = -DBL_MAX; group = -1; } };
El tamaño total de las matrices es igual a la dimensión del espacio de optimización, es decir, al número de parámetros optimizables del asesor (pasados al constructor). Como la optimización presupone, por defecto, que cuanto mayor sea el valor de la función objetivo, mejor será el valor de la función objetivo, vamos a inicializar el campo bestValue con el número mínimo posible -DBL_MAX. Como criterio de valoración del experto, suele intervenir una de las métricas comerciales (el beneficio, la rentabilidad, el ratio de Sharpe, etcétera). Si realizamos la optimización utilizando un parámetro cuyos valores inferiores se consideran más convenientes (por ejemplo la reducción), podremos realizar las transformaciones adecuadas para maximizar los valores opuestos.
Las matrices y variables se han hecho públicas para simplificar el acceso y su código de recálculo. Respetando estrictamente los principios de la POO, deberíamos ocultar estas utilizando el modificador private y describir los métodos de lectura y modificación.
Aparte de las partículas individuales, el algoritmo trabaja con las llamadas "topologías" o subconjuntos de partículas. Estos se pueden crear según principios diferentes. En nuestro caso, usaremos la "topología de grupo social". Este grupo guarda la información sobre la mejor posición entre todas sus partículas.
class Group { private: double result; // best EA performance in the group public: double optimum[]; // best known position in the group Group(const int params) { ArrayResize(optimum, params); ArrayInitialize(optimum, 0); result = -DBL_MAX; } void assign(const double x) { result = x; } double getResult() const { return result; } bool isAssigned() { return result != -DBL_MAX; } };
La pertenencia de una partícula a un grupo se establece usando el número de grupo en el campo group en la clase Particle (ver arriba).
Ahora, vamos a proceder a codificar el propio algoritmo de enjambre de partículas como una clase separada. Comenzaremos con las matrices de partículas y grupos.
class Swarm { private: Particle *particles[]; Group *groups[]; int _size; // number of particles int _globals; // number of groups int _params; // number of parameters to optimize
Tenemos que especificar para cada parámetro un intervalo con los valores en los que se realizará la optimización, y también el incremento (salto).
double highs[]; double lows[]; double steps[];
Asimismo, tenemos que guardar el conjunto óptimo de parámetros en algún lugar.
double solution[];
Como la clase tendrá varios constructores distintos, vamos a describir un método de inicialización unificado.
void init(const int size, const int globals, const int params, const double &max[], const double &min[], const double &step[]) { _size = size; _globals = globals; _params = params; ArrayCopy(highs, max); ArrayCopy(lows, min); ArrayCopy(steps, inc); ArrayResize(solution, _params); ArrayResize(particles, _size); for(int i = 0; i < _size; i++) // loop through particles { particles[i] = new Particle(_params); ///do ///{ for(int p = 0; p < _params; p++) // loop through all dimesions { // random placement particles[i].position[p] = (MathRand() * 1.0 / 32767) * (highs[p] - lows[p]) + lows[p]; // adjust it according to step granularity if(steps[p] != 0) { particles[i].position[p] = ((int)MathRound((particles[i].position[p] - lows[p]) / steps[p])) * steps[p] + lows[p]; } // the only position is the best so far particles[i].best[p] = particles[i].position[p]; // random speed particles[i].velocity[p] = (MathRand() * 1.0 / 32767) * 2 * (highs[p] - lows[p]) - (highs[p] - lows[p]); } ///} ///while(index.add(crc64(particles[i].position)) && !IsStopped()); } ArrayResize(groups, _globals); for(int i = 0; i < _globals; i++) { groups[i] = new Group(_params); } for(int i = 0; i < _size; i++) { // random group membership particles[i].group = (_globals > 1) ? (int)MathMin(MathRand() * 1.0 / 32767 * _globals, _globals - 1) : 0; } }
Todas las matrices se distribuyen según la dimensión establecida y se llenan con los datos transmitidos. La posición inicial de las partículas, así como su velocidad y su pertenencia al grupo, son determinadas de forma aleatoria. Hay algo importante comentado en el código anterior. Volveremos a ello un poco después.
Debemos tener en cuenta que la versión clásica del algoritmo de enjambre de partículas se usa para optimizar funciones definidas en coordenadas continuas. No obstante, los parámetros del asesor generalmente se ponen a prueba con un cierto salto. Por ejemplo, una media móvil estándar no puede tener un periodo de 11,5. Por ello, además de un intervalo de valores aceptables para todas las dimensiones, debemos establecer el salto usado para redondear las posiciones de las partículas. Lo haremos no solo en la fase de inicialización, sino también en los cálculos durante la optimización.
Ahora, vamos a implementar un par de constructores usando init.
#define AUTO_SIZE_FACTOR 5 public: Swarm(const int params, const double &max[], const double &min[], const double &step[]) { init(params * AUTO_SIZE_FACTOR, (int)MathSqrt(params * AUTO_SIZE_FACTOR), params, max, min, step); } Swarm(const int size, const int globals, const int params, const double &max[], const double &min[], const double &step[]) { init(size, globals, params, max, min, step); }
El primero usa una conocida regla empírica para calcular el tamaño del enjambre y el número de grupos utilizando como base el número de parámetros. La constante AUTO_SIZE_FACTOR, igual por defecto a 5, se puede modificar como deseemos. El segundo nos permite definir todos los valores de forma explícita.
El destructor libera la memoria asignada.
~Swarm()
{
for(int i = 0; i < _size; i++)
{
delete particles[i];
}
for(int i = 0; i < _globals; i++)
{
delete groups[i];
}
}
Y ahora, ha llegado el momento de escribir el método principal de la clase que ejecuta directamente la optimización.
double optimize(Functor &f, const int cycles, const double inertia = 0.8, const double selfBoost = 0.4, const double groupBoost = 0.4)
El primer parámetro Functor &f es particularmente interesante. Resulta obvio que, durante el proceso de optimización, llamaremos a un asesor experto para varios parámetros de entrada y, como respuesta, recibiremos un número estimado (beneficio, rentabilidad u otra característica). El enjambre no sabe nada sobre el experto, y no debería saberlo. Su única misión consiste en encontrar el óptimo de una función objetivo desconocida con un conjunto aleatorio de argumentos numéricos. Por consiguiente, debemos implicar una interfaz abstracta, en nuestro caso, la clase Functor.
class Functor { public: virtual double calculate(const double &vector[]) = 0; };
El único método toma en la entrada una matriz de parámetros y retorna un número (todos los tipos son double). En el futuro, el asesor deberá implementar de alguna forma una clase derivada de Functor y calcular la variable necesaria dentro del método de cálculo. Por eso, el primer parámetro del método "optimize" recibirá el objeto con la función de retorno de llamada ofrecida por el robot comercial.
El segundo parámetro del método "optimize" será el número máximo de ciclos para que se ejecute el algoritmo. Los próximos 3 parámetros indican los coeficientes de PSO, a saber: "inertia", para mantener la velocidad de la partícula (la velocidad generalmente disminuye con los valores inferiores a 1); y "selfBoost" y "groupBoost", que definen la sensibilidad de una partícula al ajustar su dirección a las posiciones más conocidas en la historia de la propia partícula/grupo.
Una vez hemos analizado todos los parámetros, vamos a proceder al estudio del algoritmo. De una manera un tanto simplificada, los ciclos de optimización reproducen casi por completo el pseudocódigo.
double optimize(Functor &f, const int cycles, const double inertia = 0.8, const double selfBoost = 0.4, const double groupBoost = 0.4) { double result = -DBL_MAX; ArrayInitialize(solution, 0); for(int c = 0; c < cycles && !IsStopped(); c++) // predefined number of cycles { for(int i = 0; i < _size && !IsStopped(); i++) // loop through all particles { for(int p = 0; p < _params; p++) // update particle position and speed { double r1 = MathRand() * 1.0 / 32767; double rg = MathRand() * 1.0 / 32767; particles[i].velocity[p] = inertia * particles[i].velocity[p] + selfBoost * r1 * (particles[i].best[p] - particles[i].position[p]) + groupBoost * rg * (groups[particles[i].group].optimum[p] - particles[i].position[p]); particles[i].position[p] = particles[i].position[p] + particles[i].velocity[p]; // make sure to keep the particle inside the boundaries of parameter space if(particles[i].position[p] < lows[p]) particles[i].position[p] = lows[p]; else if(particles[i].position[p] > highs[p]) particles[i].position[p] = highs[p]; // respect step size if(steps[p] != 0) { particles[i].position[p] = ((int)MathRound((particles[i].position[p] - lows[p]) / steps[p])) * steps[p] + lows[p]; } } // get the function value for the particle i particles[i].positionValue = f.calculate(particles[i].position); // update the particle's best value and position (if improvement is found) if(particles[i].positionValue > particles[i].bestValue) { particles[i].bestValue = particles[i].positionValue; ArrayCopy(particles[i].best, particles[i].position); } // update the group's best value and position (if improvement is found) if(particles[i].positionValue > groups[particles[i].group].getResult()) { groups[particles[i].group].assign(particles[i].positionValue); ArrayCopy(groups[particles[i].group].optimum, particles[i].position); // update the global maximum value and solution (if improvement is found) if(particles[i].positionValue > result) { result = particles[i].positionValue; ArrayCopy(solution, particles[i].position); } } } } return result; }
El método retorna el valor máximo hallado de la función objetivo. El otro método está reservado para la lectura de las coordenadas (conjunto de parámetros).
bool getSolution(double &result[]) { ArrayCopy(result, solution); return !IsStopped(); }
En esencia, este es prácticamente todo el algoritmo. Pero, no en vano, antes hemos dicho que hay algunas simplificaciones en el código. En primer lugar, debemos analizar el siguiente matiz.
Un mundo discreto sin repeticiones
Para recalcular dinámicamente conjuntos de parámetros, el functor se llama muchas veces, pero no hay garantía de que el algoritmo no llegue varias veces al mismo punto, especialmente considerando la discreción a lo largo de los ejes. Para evitar esta situación, debemos identificar de alguna forma los puntos ya calculados, y después omitirlos.
Los parámetros son solo números, una secuencia de bytes. La técnica más popular para comprobar la unicidad de los datos es utilizar un hash. Podemos considerar que la forma más popular de obtener un hash es la CRC. La CRC es un número de control (generalmente un número entero, de varios bits) que se genera usando datos como base, de tal forma que la coincidencia de dos números característicos de dos conjuntos de datos implique con una alta probabilidad de que los conjuntos sean idénticos. Cuantos más bits haya en la CRC, mayor será la probabilidad de coincidencia (hasta casi del 100%). Una CRC de 64 bits probablemente baste para nuestra tarea, pero, de ser necesario, podemos ampliar o cambiar a otra función hash. La implementación del cálculo de CRC se puede migrar fácilmente de C a MQL. Una de las posibles variantes está disponible en el archivo crc64.mqh, adjunto a continuación. La principal función de trabajo tiene el siguiente prototipo.
ulong crc64(ulong crc, const uchar &s[], int l);
Esta toma la CRC del bloque de datos anterior (si hay varios; para un bloque deberemos establecer 0), una matriz de bytes y cuántos elementos del mismo procesar. La función retorna una CRC de 64 bits.
Necesitamos suministrar a la entrada de esta función un conjunto de parámetros, pero no se puede hacer directamente, ya que cada parámetro es del tipo double. Para transformarlo en una matriz de bytes, utilizaremos la biblioteca TypeToBytes.mqh (el archivo se adjunta al artículo, pero es mejor usar la versión más actual del código base).
Tras activar esta biblioteca, podemos crear una función "de envoltorio" para calcular CRC64 partiendo de una matriz de parámetros:
#include <TypeToBytes.mqh> #include <crc64.mqh> template<typename T> ulong crc64(const T &array[]) { ulong crc = 0; int len = ArraySize(array); for(int i = 0; i < len; i++) { crc = crc64(crc, _R(array[i]).Bytes, sizeof(T)); } return crc; }
Pero entonces, nos surgen las siguientes preguntas: ¿dónde guardaremos los hashes y cómo verificaremos su singularidad? Aquí, la mejor opción será un árbol binario. Se trata de una estructura de datos que posibilita operaciones rápidas para añadir nuevos valores y comprobar la existencia de los ya añadidos. La velocidad se consigue gracias a una propiedad especial del árbol llamada equilibrio. En otras palabras, el árbol debe estar equilibrado (mantenerse en un estado de equilibrio constante) para garantizar la máxima velocidad de operaciones en mismo. Por fortuna, el hecho de que los hashes se guarden en el árbol nos resulta beneficioso. Vamos a recordar la definición de hash.
Una función hash (algoritmo de generación de hashes) genera para cualquier dato de entrada un valor de salida distribuido uniformemente. Como resultado, la adición de un hash a un árbol binario posibilita estadísticamente un estado casi equilibrado para el mismo y, por consiguiente, redunda en una alta efectividad.
Un árbol binario supone una colección de nodos; cada uno de ellos contiene un cierto valor y dos referencias opcionales al llamado nodo derecho e izquierdo. El valor del nodo izquierdo es siempre inferior al valor del nodo principal; el valor en el nodo derecho es siempre superior al del nodo padre. El árbol se rellena desde la raíz, comparando un nuevo valor con los valores de los nodos. Si el nuevo valor es igual al valor de la raíz (u otro nodo), se retorna el signo de la existencia del valor en el árbol. Si el nuevo valor es inferior al valor en el nodo, nos desplazaremos al nodo izquierdo según la referencia y procesaremos su subárbol de manera similar. Si el nuevo valor es superior al valor en el nodo, seguiremos el subárbol derecho. Si alguna de las referencias es nula (significará que no hay más ramas), la búsqueda se completará sin resultados. Por eso, deberemos crear un nuevo nodo con un nuevo valor, en lugar de una referencia nula.
Para implementar esta lógica, hemos creado un par de clases de plantilla: TreeNode y BinaryTree. Ofrecemos sus códigos completos en el archivo de encabezado adjunto.
template<typename T> class TreeNode { private: TreeNode *left; TreeNode *right; T value; public: TreeNode(T t): value(t) {} // adds new value into subtrees and returns false or // returns true if t exists as value of this node or in subtrees bool add(T t); ~TreeNode(); TreeNode *getLeft(void) const; TreeNode *getRight(void) const; T getValue(void) const; }; template<typename T> class BinaryTree { private: TreeNode<T> *root; public: bool add(T t); ~BinaryTree(); };
El método add retorna true si el valor ya se encuentra en el árbol, y false si no se encontraba allí antes, pero se acaba de añadir. La eliminación de una raíz en el destructor del árbol automáticamente redunda en eliminación de todos los nodos secundarios.
La clase de árbol implementada es una de las variantes más simples; hay árboles más avanzados, por lo que, si así lo desea, podrá incorporarlos por sí mismo.
Vamos a añadir BinaryTree a la clase Swarm.
class Swarm { private: BinaryTree<ulong> index;
En el método de optimización, necesitamos mejorar los sitios donde desplazamos las partículas a nuevas posiciones.
double optimize(Functor &f, const int cycles, const double inertia = 0.8, const double selfBoost = 0.4, const double groupBoost = 0.4) { // ... double next[]; ArrayResize(next, _params); for(int c = 0; c < cycles && !IsStopped(); c++) { int skipped = 0; for(int i = 0; i < _size && !IsStopped(); i++) { // new placement of particles using temporary array next for(int p = 0; p < _params; p++) { double r1 = MathRand() * 1.0 / 32767; double rg = MathRand() * 1.0 / 32767; particles[i].velocity[p] = inertia * particles[i].velocity[p] + selfBoost * r1 * (particles[i].best[p] - particles[i].position[p]) + groupBoost * rg * (groups[particles[i].group].optimum[p] - particles[i].position[p]); next[p] = particles[i].position[p] + particles[i].velocity[p]; if(next[p] < lows[p]) next[p] = lows[p]; else if(next[p] > highs[p]) next[p] = highs[p]; if(steps[p] != 0) { next[p] = ((int)MathRound(next[p] / steps[p])) * steps[p]; } } // check if the tree contains this parameter set and add it if not if(index.Add(crc64(next))) { skipped++; continue; } // apply new position to the particle ArrayCopy(particles[i].position, next); particles[i].positionValue = f.calculate(particles[i].position); // ... } Print("Cycle ", c, " done, skipped ", skipped, " of ", _size, " / ", result); if(skipped == _size) break; // full coverage }
A continuación, añadiremos la matriz auxiliar next, donde irán primero las nuevas coordenadas generadas. A continuación, calculamos la CRC para ellas y comprobamos la unicidad de este valor. Si aún no hemos encontrado la nueva posición, añadimos esta al árbol, la copiamos en la partícula correspondiente y realizamos todos los cálculos necesarios para ella. Si la posición ya se halla en el árbol (es decir, el functor ya ha sido calculado para él), esta iteración se omitirá.
Probando la funcionalidad básica
Todo lo anteriormente analizado constituye la base mínima imprescindible para ejecutar las primeras pruebas. Vamos a utilizar el script testpso.mq5 para asegurarnos de que la optimización realmente funcione. El archivo de encabezado ParticleSwarmParallel.mqh utilizado en este script no solo contiene las clases ya conocidas, sino también otras mejoras que analizaremos a continuación.
Las pruebas están diseñadas en el estilo de la POO, lo cual nos permite configurar nuestras funciones objetivo favoritas. La clase básica para las pruebas es BaseFunctor.
class BaseFunctor: public Functor { protected: const int params; double max[], min[], steps[]; public: BaseFunctor(const int p): params(p) // number of parameters { ArrayResize(max, params); ArrayResize(min, params); ArrayResize(steps, params); ArrayInitialize(steps, 0); PSOTests::register(&this); } virtual void test(const int loop) // worker method { Swarm swarm(params, max, min, steps); swarm.optimize(this, loop); double result[]; swarm.getSolution(result); for(int i = 0; i < params; i++) { Print(i, " ", result[i]); } } };
Todos los objetos de las clases derivadas se registrarán automáticamente en el momento de la creación usando el método register en la clase PSOTests.
class PSOTests { static BaseFunctor *testCases[]; public: static void register(BaseFunctor *f) { int n = ArraySize(testCases); ArrayResize(testCases, n + 1); testCases[n] = f; } static void run(const int loop = 100) { for(int i = 0; i < ArraySize(testCases); i++) { testCases[i].test(loop); } } };
En sí mismas, las pruebas (optimización) se ejecutan con el método run, que llama a test para todos los objetos registrados.
Existen muchas funciones objetivo de prueba populares. Entre ellas, en concreto, están "rosenbrock", "griewank" y "sphere", que están programados en el script. Por ejemplo, para la "esfera", podemos establecer el alcance de búsqueda y el método calculate de la siguiente forma.
class Sphere: public BaseFunctor { public: Sphere(): BaseFunctor(3) // expected global minimum (0, 0, 0) { for(int i = 0; i < params; i++) { max[i] = 100; min[i] = -100; } } virtual void test(const int loop) { Print("Optimizing " + typename(this)); BaseFunctor::test(loop); } virtual double calculate(const double &vec[]) { int dim = ArraySize(vec); double sum = 0; for(int i = 0; i < dim; i++) sum += pow(vec[i], 2); return -sum; // negative for maximization } };
No olvidemos que las funciones de referencia estándar presuponen la minimización, al tiempo que implementamos un algoritmo basado en la maximización (porque nuestro objetivo es buscar el máximo rendimiento del asesor). Por ello, el resultado del cálculo se usará con un signo menos. Además, aquí no utilizaremos un salto discreto y, por consiguiente, las funciones serán continuas.
void OnStart()
{
PSOTests::Sphere sphere;
PSOTests::Griewank griewank;
PSOTests::Rosenbrock rosenbrock;
PSOTests::run();
}
Al ejecutar el script, podemos ver que en el log se muestran los valores de las coordenadas próximos a la solución exacta (extremo). Como las partículas se inicializan de forma aleatoria, cada inicio generará valores ligeramente distintos. La precisión de la solución dependerá de los parámetros de entrada del algoritmo.
Optimizing PSOTests::Sphere PSO[3] created: 15/3 PSO Processing... Cycle 0 done, skipped 0 of 15 / -1279.167775306995 Cycle 10 done, skipped 0 of 15 / -231.4807406906516 Cycle 20 done, skipped 0 of 15 / -4.269510657558273 Cycle 30 done, skipped 0 of 15 / -1.931949742316357 Cycle 40 done, skipped 0 of 15 / -0.06018744740061506 Cycle 50 done, skipped 0 of 15 / -0.009498109984732127 Cycle 60 done, skipped 0 of 15 / -0.002058433538555499 Cycle 70 done, skipped 0 of 15 / -0.0001494176502579518 Cycle 80 done, skipped 0 of 15 / -4.141817579039349e-05 Cycle 90 done, skipped 0 of 15 / -1.90930142126799e-05 Cycle 99 done, skipped 0 of 15 / -8.161728746514931e-07 PSO Finished 1500 of 1500 planned calculations: true 0 -0.000594423827318461 1 -0.000484001094843528 2 0.000478096358862763 Optimizing PSOTests::Griewank PSO[2] created: 10/3 PSO Processing... Cycle 0 done, skipped 0 of 10 / -26.96927938978973 Cycle 10 done, skipped 0 of 10 / -0.939220906325796 Cycle 20 done, skipped 0 of 10 / -0.3074442362962919 Cycle 30 done, skipped 0 of 10 / -0.121905607345751 Cycle 40 done, skipped 0 of 10 / -0.03294107382891465 Cycle 50 done, skipped 0 of 10 / -0.02138355984774098 Cycle 60 done, skipped 0 of 10 / -0.01060479828529859 Cycle 70 done, skipped 0 of 10 / -0.009728742850384609 Cycle 80 done, skipped 0 of 10 / -0.008640623678293768 Cycle 90 done, skipped 0 of 10 / -0.008578769833161193 Cycle 99 done, skipped 0 of 10 / -0.008578769833161193 PSO Finished 996 of 1000 planned calculations: true 0 3.188612982502877 1 -4.435728146291838 Optimizing PSOTests::Rosenbrock PSO[2] created: 10/3 PSO Processing... Cycle 0 done, skipped 0 of 10 / -19.05855349617553 Cycle 10 done, skipped 1 of 10 / -0.4255148824156119 Cycle 20 done, skipped 0 of 10 / -0.1935391314277153 Cycle 30 done, skipped 0 of 10 / -0.006468452482022688 Cycle 40 done, skipped 0 of 10 / -0.001031992354315317 Cycle 50 done, skipped 0 of 10 / -0.00101322411502283 Cycle 60 done, skipped 0 of 10 / -0.0008800704421316765 Cycle 70 done, skipped 0 of 10 / -0.0005593151578155307 Cycle 80 done, skipped 0 of 10 / -0.0005516786893301249 Cycle 90 done, skipped 0 of 10 / -0.0005473814163781119 Cycle 99 done, skipped 0 of 10 / -7.255520122486163e-06 PSO Finished 982 of 1000 planned calculations: true 0 1.001858172119364 1 1.003524791491219
Debemos considerar que el tamaño del enjambre y el número de grupos (escritos en el registro en líneas como PSO[N] created: X/G, donde N es la dimensión del espacio, X es el número de partículas y G es el número de grupos) se seleccionan automáticamente según las reglas generales programadas de acuerdo con los datos de entrada.
Pasando a un mundo paralelo
La primera prueba ha resultado buena. No obstante, tiene un pequeño "pero": el ciclo de recuento de partículas se efectúa en un solo flujo, mientras que el terminal permite usar todos los núcleos del procesador. Nuestro objetivo final consiste en escribir un motor de optimización de PSO que pueda integrarse en los asesores para la optimización multiproceso en el simulador de MetaTrader y, por consiguiente, ofrecer una alternativa al algoritmo genético estándar.
No podemos paralelizar los cálculos transfiriendo mecánicamente el algoritmo dentro de un asesor en lugar de un script. Para ello, deberíamos modificar el algoritmo.
Si observamos el código existente dentro de la tarea plantada, los cálculos paralelos parecen requerir la selección de grupos de partículas. Cada grupo se puede procesar de forma independiente respecto a los demás. Dentro de cada grupo, se realiza un ciclo completo el número indicado de veces.
Para evitar la modificación del núcleo de la clase Swarm, utilizaremos una solución simple: en lugar de varios grupos dentro de una clase, crearemos varias instancias de clase; en cada una de ellas, el número de grupos será degenerado, es decir, igual a uno. Además, necesitaremos completar un código que permita a las instancias intercambiar información, ya que cada una de ellas se ejecutará en su propio agente de simulación.
Primero, vamos a mejorar la inicialización de objetos con un nuevo método.
Swarm(const int size, const int globals, const int params, const double &max[], const double &min[], const double &step[]) { if(MQLInfoInteger(MQL_OPTIMIZATION)) { init(size == 0 ? params * AUTO_SIZE_FACTOR : size, 1, params, max, min, step); } ...
Partiendo del signo de funcionamiento del programa en el modo de optimización, establecemos el número de grupos en 1. El tamaño por defecto del enjambre es determinado por una regla general (a menos que se especifique explícitamente un valor distinto de 0 en el parámetro de tamaño).
En el controlador de eventos OnTester, el asesor puede recibir el resultado del mini-enjambre (que consta de un solo grupo) utilizando la función getSolution y enviarlo en un frame al terminal. Aquel puede analizar las pasadas y seleccionar la mejor. Es mejor hacer que el número de enjambres/grupos paralelos sea al menos igual al número de núcleos, pero también puede ser mayor (sería conveniente mantener la multiplicidad del número de núcleos). Obviamente, cuanto mayor sea la dimensión del espacio de búsqueda óptimo, más grupos se necesitarán, pero para las pruebas simples basta con limitarse al número de núcleos.
El intercambio de datos entre las instancias es necesario para poder calcular el espacio sin puntos repetidos. Como recordaremos, en cada objeto la lista de puntos procesados se guarda en el árbol binario index. Por analogía con los resultados, podríamos enviarla al terminal dentro de un frame, pero el hipotético registro combinado de estas listas no se podría enviar de retorno a los agentes. Por desgracia, la arquitectura del simulador admite el reenvío controlado de datos durante la optimización solo desde los agentes al terminal, pero no al contrario. Desde el terminal, las tareas se distribuyen a los agentes en un formato cerrado.
Por consiguiente, hemos decidido limitarnos a los agentes locales y guardar los índices de cada grupo en archivos en una carpeta compartida (FILE_COMMON). Con este enfoque, cada agente escribirá su propio índice y tendrá la posibilidad de leer los índices de todos las demás pasadas en cualquier momento, y después añadirlas a su propio índice. En concreto, esto tendrá sentido al inicializar una pasada.
En MQL, los cambios en un archivo escrito solo pueden ser leídos por otros procesos después de que dicho archivo sea cerrado. Las banderas FILE_SHARE_READ, FILE_SHARE_WRITE y la función FileFlush no son aquí de ayuda.
La compatibilidad con la escritura de índices se implementa con el conocido patrón de "visitante".
template<typename T> class Visitor { public: virtual void visit(TreeNode<T> *node) = 0; };
Su interfaz minimalista declara que vamos a efectuar alguna operación aleatoria en el nodo del árbol transmitido. Para trabajar con los archivos, hemos creado una implementación heredera específica: Exporter. El valor interno de cada nodo se guarda en el archivo en una línea aparte, en el orden de iteración por todo el árbol según las referencias.
template<typename T> class Exporter: public Visitor<T> { private: int file; uint level; public: Exporter(const string name): level(0) { file = FileOpen(name, FILE_READ | FILE_WRITE | FILE_CSV | FILE_ANSI | FILE_SHARE_READ| FILE_SHARE_WRITE | FILE_COMMON, ','); } ~Exporter() { FileClose(file); } virtual void visit(TreeNode<T> *node) override { #ifdef PSO_DEBUG_BINTREE if(node.getLeft()) visit(node.getLeft()); FileWrite(file, node.getValue()); if(node.getRight()) visit(node.getRight()); #else const T v = node.getValue(); FileWrite(file, v); level++; if((level | (uint)v) % 2 == 0) { if(node.getLeft()) visit(node.getLeft()); if(node.getRight()) visit(node.getRight()); } else { if(node.getRight()) visit(node.getRight()); if(node.getLeft()) visit(node.getLeft()); } level--; #endif } };
El método de iteración ordenada del árbol, que parece ser el más lógico, solo se puede usar con fines depurativos, si necesitamos conseguir líneas ordenadas dentro de los archivos para efectuar una comparación contextual. Este método está rodeado por la directiva de compilación condicional PSO_DEBUG_BINTREE y está desactivado por defecto. En la práctica, el equilibrio estadístico del árbol se puede garantizar mediante la adición de valores aleatorios distribuidos uniformemente y guardados en el árbol (hashes). Si los elementos del árbol se almacenan de forma ordenada, su posterior carga desde el archivo dará como resultado la configuración más lenta y menos óptima (una rama larga, en la práctica, una lista). Para evitarlo, en la etapa de almacenamiento del árbol, introduciremos una cierta incertidumbre respecto a la secuencia en la que se procesarán los nodos.
Con la ayuda de la clase Explorer, resulta muy sencillo añadir a la clase BinaryTree un método especial que guarda el árbol en el "visitante" transmitido.
template<typename T> class BinaryTree { ... void visit(Visitor<T> *visitor) { visitor.visit(root); } };
Para iniciar una operación, también se requiere un nuevo método en la clase Swarm.
void exportIndex(const int id) { const string name = sharedName(id); Exporter<ulong> exporter(name); index.visit(&exporter); }
El parámetro id es el número de salto único (también conocido como número de grupo); de acuerdo precisamente con este parámetro configuraremos la optimización en el simulador. Tiene sentido llamar al método exportIndex justo después de procesar los dos métodos swarm: optimize y getSolution. De esto se encarga el código de llamada, porque puede que no siempre sea necesario: nuestro primer ejemplo "paralelo" (ver a continuación) funcionará sin él. Por definición, si el número de grupos es igual al número de núcleos, no tendrán tiempo de intercambiar información, ya que se iniciarán en paralelo y la lectura del archivo dentro del ciclo resulta ineficaz.
La función auxiliar sharedName, que ya mencionamos dentro de exportIndex, nos permitirá crear un nombre único basado en el número del grupo, el nombre del experto y la carpeta del terminal.
#define PPSO_FILE_PREFIX "PPSO-" string sharedName(const int id, const string prefix = PPSO_FILE_PREFIX, const string ext = ".csv") { ushort array[]; StringToShortArray(TerminalInfoString(TERMINAL_PATH), array); const string program = MQLInfoString(MQL_PROGRAM_NAME) + "-"; if(id != -1) { return prefix + program + StringFormat("%08I64X-%04d", crc64(array), id) + ext; } return prefix + program + StringFormat("%08I64X-*", crc64(array)) + ext; }
Si transmitimos a la función un identificador igual a -1, esta creará una máscara para buscar todos los archivos de esta instancia del terminal. Esto se usa al eliminar archivos temporales antiguos (de la anterior optimización de este asesor experto), así como al leer los índices de los flujos paralelos. Así es cómo se hace en líneas generales.
bool restoreIndex() { string name; const string filter = sharedName(-1); // use wildcards to merge multiple indices for all cores long h = FileFindFirst(filter, name, FILE_COMMON); if(h != INVALID_HANDLE) { do { FileReader reader(name, FILE_COMMON); reader.read(this); } while(FileFindNext(h, name)); FileFindClose(h); } return true; }
Cada archivo localizado se transmite a la nueva clase FileReader para su procesamiento. Este se ocupa de abrir el archivo en el modo lectura y cargar secuencialmente todas las líneas, transfiriéndolas de forma inmediata a la interfaz de Feed.
class Feed { public: virtual bool feed(const int dump) = 0; }; class FileReader { protected: int dump; public: FileReader(const string name, const int flags = 0) { dump = FileOpen(name, FILE_READ | FILE_CSV | FILE_SHARE_READ | FILE_SHARE_WRITE | FILE_ANSI | flags, ','); } virtual bool isReady() const { return dump != INVALID_HANDLE; } virtual bool read(Feed &pass) { if(!isReady()) return false; while(!FileIsEnding(dump)) { if(!pass.feed(dump)) { return false; } } return true; } };
Como el lector podrá adivinar, la interfaz de Feed debe implementarse en el propio enjambre, porque se transmite dentro de FileReader.
class Swarm: public Feed { private: ... int _read; int _unique; int _restored; BinaryTree<ulong> merge; public: ... virtual bool feed(const int dump) override { const ulong value = (ulong)FileReadString(dump); _read++; if(!index.add(value)) _restored++; // just added into the tree else if(!merge.add(value)) _unique++; // was already indexed, hitting _unique in total return true; } ...
Usando las variables _read, _unique y _restored, el método calcula el número total de elementos leídos (de todos los archivos), el número de elementos añadidos al índice y el número de elementos que no han sido añadidos (que ya se encuentran en el índice). Como los grupos trabajan de forma independiente, los índices de distintos grupos pueden tener duplicados.
Estas estadísticas son importantes al determinar el momento en que el espacio de búsqueda se encuentra completamente explorado o está cerca de ser completamente explorado. En este caso, el número de _unique se acerca al número de posibles combinaciones de parámetros.
A medida que aumenta la cantidad de pasadas completadas, en los índices locales se cargarán más y más puntos únicos de la historia conjunta. Después de la siguiente ejecución de calculate, el índice se rellenará con nuevos puntos comprobados y el tamaño de los archivos guardados aumentará constantemente. Paulatinamemte, comenzarán a prevalecer los elementos superpuestos en los archivos. Esto demandará algunos costes adicionales, que, no obstante, resultarán inferiores al recálculo de la actividad comercial del asesor. Esto provocará que los ciclos de PSO se aceleren con el procesamiento de cada uno de los grupos posteriores (tareas del simulador), a medida que el procesamiento se aproxime a la cobertura total del espacio de optimización.
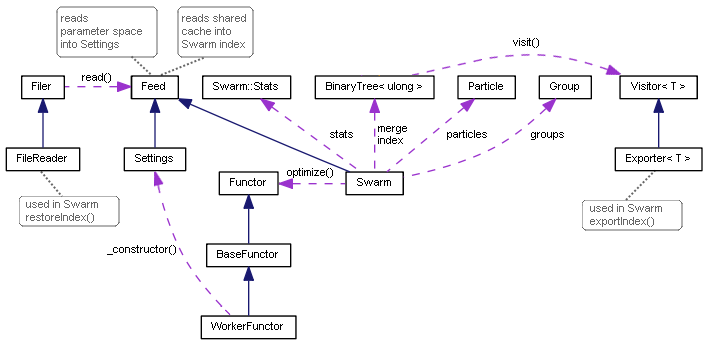
Diagrama con las clases de la Particle Swarm Optimization
Simulación de cálculos paralelos
Para poner a prueba el rendimiento del algoritmo en varios subprocesos, vamos a transformar el script anterior en el asesor experto PPSO.mq5. Este se ejecutará en el modo de cálculo matemático, ya que el entorno comercial aún no es necesario.
El conjunto de funciones objetivo de prueba permanecerá inalterado, y las clases que las implementan prácticamente no se modificarán. La selección de una prueba en particular se efectuará en las variables de entrada.
enum TEST { Sphere, Griewank, Rosenbrock }; sinput int Cycles = 100; sinput TEST TestCase = Sphere; sinput int SwarmSize = 0; input int GroupCount = 0;
Aquí también podemos indicar el número de ciclos, el tamaño del enjambre y el número de grupos. Todo ello se usa en la implementación del functor, en concreto, en el constructor Swarm. Los valores establecidos en cero por defecto indican, como antes, que se ajustan automáticamente en función de la dimensión del problema.
class BaseFunctor: public Functor { protected: const int params; double max[], min[], steps[]; double optimum; double result[]; public: ... virtual void test() { Swarm swarm(SwarmSize, GroupCount, params, max, min, steps); optimum = swarm.optimize(this, Cycles); swarm.getSolution(result); } double getSolution(double &output[]) const { ArrayCopy(output, result); return optimum; } };
Todos los cálculos se inician desde el manejador OnTester. El parámetro GroupCount (con la ayuda del cual se organizarán las iteraciones del simulador) se utiliza como un aleatorizador para que las instancias en diferentes subprocesos contengan diferentes partículas. Dependiendo del parámetro TestCase, se crea uno u otro functor de prueba. A continuación, llamamos al método functor.test(), después de lo cual, podemos leer los resultados utilizando functor.getSolution() y enviarlos en un frame al terminal.
double OnTester() { MathSrand(GroupCount); // reproducable randomization BaseFunctor *functor = NULL; switch(TestCase) { case Sphere: functor = new PSOTests::Sphere(); break; case Griewank: functor = new PSOTests::Griewank(); break; case Rosenbrock: functor = new PSOTests::Rosenbrock(); break; } functor.test(); double output[]; double result = functor.getSolution(output); if(MQLInfoInteger(MQL_OPTIMIZATION)) { FrameAdd("PSO", 0xC0DE, result, output); } else { Print("Solution: ", result); for(int i = 0; i < ArraySize(output); i++) { Print(i, " ", output[i]); } } delete functor; return result; }
En el propio terminal, funciona un conjunto de funciones OnTesterInit, OnTesterPass, OnTesterDeinit, que reúne frames, determinando de paso la mejor solución entre los enviados.
int passcount = 0; double best = -DBL_MAX; double location[]; void OnTesterPass() { ulong pass; string name; long id; double r; double data[]; while(FrameNext(pass, name, id, r, data)) { // compare r with all other passes results if(r > best) { best = r; ArrayCopy(location, data); } Print(passcount, " ", id); const int n = ArraySize(data); ArrayResize(data, n + 1); data[n] = r; ArrayPrint(data, 12); passcount++; } } void OnTesterDeinit() { Print("Solution: ", best); ArrayPrint(location); }
En el log se escriben el contador de pasadas, su número ordinal (puede resultar distinto en tareas complejas, cuando un flujo supera a otro debido a diferencias en los datos), el valor de la función objetivo y los parámetros correspondientes. La decisión final se muestra en OnTesterDeinit.
También haremos posible que el asesor experto se pueda iniciar no solo en el simulador, sino también en un gráfico normal. En este caso, el algoritmo de PSO operará en el modo estándar de un solo subproceso.
int OnInit() { if(!MQLInfoInteger(MQL_TESTER)) { EventSetTimer(1); } return INIT_SUCCEEDED; } void OnTimer() { EventKillTimer(); OnTester(); }
Veamos cómo funciona esto. Seleccionamos valores concretos para los parámetros de entrada:
- Cycles — 100;
- TestCase — Griewank;
- SwarmSize — 100;
- GroupCount — 10;
Al colocar el experto en el gráfico, veremos más o menos el siguiente log.
Successive PSO of Griewank PSO[2] created: 100/10 PSO Processing... Cycle 0 done, skipped 0 of 100 / -1.000317162069485 Cycle 10 done, skipped 0 of 100 / -0.2784790501384311 Cycle 20 done, skipped 0 of 100 / -0.1879188508394087 Cycle 30 done, skipped 0 of 100 / -0.06938172138150922 Cycle 40 done, skipped 0 of 100 / -0.04958694402304631 Cycle 50 done, skipped 0 of 100 / -0.0045818974357138 Cycle 60 done, skipped 0 of 100 / -0.0045818974357138 Cycle 70 done, skipped 0 of 100 / -0.002161613760466419 Cycle 80 done, skipped 0 of 100 / -0.0008991629607246754 Cycle 90 done, skipped 0 of 100 / -1.620636881582982e-05 Cycle 99 done, skipped 0 of 100 / -1.342285474092986e-05 PSO Finished 9948 of 10000 planned calculations: true Solution: -1.342285474092986e-05 0 0.004966759354110293 1 0.002079707592422949
Como los ejemplos de prueba se calculan rápidamente (en uno o dos segundos), no tiene sentido medir el tiempo. Esto se añadirá posteriormente para las tareas comerciales reales.
Ahora, seleccionamos el asesor en el simulador, elegimos "Cálculos matemáticos" en la lista de "Modelado" y dejamos los parámetros anteriores para el asesor, salvo GroupCount. La optimización se realizará según este parámetro. Por consiguiente, estableceremos los valores iniciales y finales, digamos 0 y 3, con un salto de 1, para producir 4 grupos (igual al número de núcleos). El tamaño de todos los grupos será de 100 (SwarmSize, el enjambre completo). Con un número de núcleos de procesador suficiente (si todos los grupos trabajan en paralelo en los agentes), esto no debería afectar al rendimiento, pero sí que incrementará la precisión de la solución usando comprobaciones adicionales del espacio de optimización. Podemos obtener el siguiente registro:
Parallel PSO of Griewank -12.550070232909 -0.002332638407 -0.039510275469 -3.139749741924 4.438437934965 -0.007396077598 3.139620588383 4.438298282495 -0.007396126543 0.000374731767 -0.000072178955 -0.000000071551 Solution: -7.1550806279852e-08 (after 4 passes) 0.00037 -0.00007
De esta forma, nos hemos asegurado de que la modificación paralela del algoritmo PSO esté disponible en el simulador en el modo de optimización. No obstante, de momento, solo ha sido una prueba que usa "cálculos matemáticos". Ha llegado la hora de adaptar la PSO para optimizar los asesores expertos en un entorno comercial.
Virtualización y optimización del experto (API MQL4 en MetaTrader 5)
Para optimizar los asesores expertos que usan el motor PSO, necesitamos implementar funciones que puedan simular el comercio en la historia utilizando como base un conjunto de parámetros de entrada, y también calcular las estadísticas.
Esto genera un dilema que confrontan muchos desarrolladores de aplicaciones al escribir su propio optimizador por encima y/o en lugar del estándar. ¿Cómo posibilitar un entorno comercial que incluya, en primer lugar, cotizaciones, pero también el estado de la cuenta y el archivo de operaciones? Si utilizamos el modo de cálculos matemáticos, deberemos prepararnos de alguna manera, y luego transmitir los datos requeridos al asesor experto (a los agentes). En este caso, deberemos desarrollar una capa intermedia para la API, capaz de emular "de forma transparente" muchas funciones comerciales; esto permitiría al asesor experto operar de forma similar al modo en línea habitual.
Para evitar esto, hemos decidido usar una solución de comercio virtual ya existente, creada totalmente en MQL, utilizando estructuras de datos históricas estándar, en concreto, ticks y barras. Nos referimos a la biblioteca Virtual (autor fxsaber). Esta permite calcular una pasada virtual de un asesor experto sobre la historia disponible tanto en línea (por ejemplo, para la autooptimización periódica en un gráfico), como en el simulador. En el último caso, podemos utilizar cualquier modo de tick habitual ("Todos los ticks", "Cada tick basado en ticks reales") o incluso "OHLC en M1" para realizar una valoración rápida pero más ajustada del sistema (solo tiene 4 ticks por minuto).
Después de incluir el archivo de encabezado Virtual.mqh (se descarga con las dependencias necesarias) en el código del asesor, podemos organizar fácilmente un test virtual utilizando las siguientes líneas:
MqlTick _ticks[]; // global array ... // copy/collect ticks[] VIRTUAL::Tester(_ticks, OnTick /*, TesterStatistics(STAT_INITIAL_DEPOSIT)*/ ); Print(VIRTUAL::ToString(INT_MAX)); // output virtual trades in the log const double result = TesterStatistics(STAT_PROFIT); // get required performance meter VIRTUAL::ResetTickets(); // optional VIRTUAL::Delete(); // optional
El método estático VIRTUAL::Tester se encarga de todo el trabajo. Debemos transmitir al mismo una matriz previamente rellenada con los ticks del periodo histórico y el nivel de detalle deseados, el puntero a la función OnTick (también resultará conveniente un manejador estándar, si la lógica para cambiar de comercio en línea a virtual está integrada en él), y también el depósito inicial (esto es opcional; si no se indica, tomaremos el balance actual de la cuenta). Si colocamos el fragmento anterior en el manejador de OnTester (como lo haremos nosotros), podremos transmitir el depósito inicial del simulador. Podemos averiguar el resultado del comercio virtual llamando a la conocida función TesterStatistics, que, tras incluir la biblioteca, resulta en realidad "bloqueada", como muchas otras funciones de la API de MQL (si el lector lo desea, podrá consultar el código fuente). Esta "superposición" es lo suficientemente inteligente como para delegar las llamadas de la función original del núcleo hacia donde se dirige el comercio real. Debemos tener en cuenta que no todas las métricas estándar de TesterStatistics se calculan en la biblioteca para el comercio virtual.
Una característica de la biblioteca es que está basada en la API comercial de MetaTrader 4. En otras palabras, se puede aplicar solo a asesores que usen funciones "antiguas" en su código, aunque están escritas en MQL5. Funcionan en el entorno MetaTrader 5 gracias a otra popular biblioteca del mismo autor: MT4Orders.
Como "conejillo de indias", actuará la modificación del asesor experto ExprBot.mq5 que se presentó originalmente en el artículo Cálculo de expresiones matemáticas (Parte 2). Precisamente esta se ha implementado usando MT4Orders. Una nueva versión, denominada ExprBotPSO.mq5, se adjunta a este artículo.
El asesor experto usa un motor de análisis para calcular las señales comerciales basadas en expresiones. Aclararemos la utilidad de esto para nosotros un poco más tarde. Vamos a dejar la estrategia comercial igual: el cruzamiento de dos medias móviles, considerando el umbral de divergencia especificado. Recordemos cómo se veían las configuraciones junto con las expresiones para las señales; no necesitan mucha explicación, ya que hablan por sí mismas:
input string SignalBuy = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) > 1 + Threshold"; input string SignalSell = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) < 1 - Threshold"; input string Variables = "Threshold=0.001"; input int Fast = 10; input int Slow = 21;
Si el lector tiene alguna pregunta sobre cómo se sustituyen las variables de entrada por expresiones y cómo se integran las funciones de la EMA incorporadas con el indicador correspondiente, le recomendamos leer el artículo mencionado. El nuevo robot usa los mismos principios. Vamos a mejorarlo ligeramente.
Tenga en cuenta que el motor de análisis ha sido actualizado a la versión v1.1, y también está incluido. Su versión antigua, si ha sido descargada con anterioridad, no funcionará.
Además de los parámetros de entrada para las señales, que analizaremos más tarde, el asesor dispone de parámetros para gestionar las pruebas virtuales y el algoritmo de PSO.
- VirtualTester — bandera que permite la simulación y/u optimización virtuales; el valor predeterminado es false, lo que indica un funcionamiento normal.
- Estimator — variable mediante la cual se realiza la optimización; por defecto, STAT_PROFIT.
- InternalOptimization — marca que activa la optimización en el modo virtual; el valor predeterminado es false, lo que indica el comercio virtual de un solo salto. True inicia la optimización interna mediante el método PSO.
- PSO_Enable — activar/desactivar PSO;
- PSO_Cycles — número de ciclos de recálculo de PSO en cada pasada; cuanto mayor sea el valor, mejor será la calidad de búsqueda de PSO, pero la pasada única se ejecutará durante más tiempo, y sin feedback (muestra en el log).
- PSO_SwarmSize — tamaño del enjambre; por defecto es 0, lo que indica una selección empírica automática basada en el número de parámetros.
- PSO_GroupCount — número de grupos; es un parámetro que se puede incrementar para organizar varias pasadas: partiendo de un valor 0 hasta el número de núcleos/agentes, luego se puede aumentar.
- PSO_RandomSeed — aleatorizador; se le añade el número de grupo en cada grupo, por lo que todos se inicializan de manera diferente.
En el modo VirtualTester, el asesor recopila los ticks en OnTick en una matriz. A continuación, en OnTester, la biblioteca virtual opera utilizando esta matriz, llamando al propio manejador OnTick con una bandera de conjunto especial que permite la ejecución del código con operaciones virtuales.
Entonces, para cada valor de PSO_GroupCount incrementado en un agente aparte, se realiza un ciclo de PSO_Cycles de recálculos de enjambre con un tamaño de partículas PSO_SwarmSize. En total, conseguimos una comprobación de PSO_GroupCount * PSO_Cycles * PSO_SwarmSize = N puntos en el espacio de optimización. Cada punto es una pasada virtual del sistema comercial.
Para alcanzar los mejores resultados, necesitaremos encontrar los parámetros de PSO correctos usando el método de ensayo y error. Estableciendo el número total de pruebas N, podemos variar los componentes. Debido a los aciertos aleatorios en los mismos puntos (recordemos que se almacenan en un árbol binario, en un enjambre), el número final de pruebas será inferior a N.
El intercambio de datos entre agentes tiene lugar solo en el momento del envío de la siguiente tarea. Las tareas ejecutadas en paralelo aún no ven los resultados entre sí, y también pueden calcular varias coordenadas idénticas con cierta probabilidad.
Obviamente, hemos añadido clases functor al asesor experto ExprBotPSO, que en general son similares a las que hemos visto en los ejemplos anteriores. Concretamente, el método test (como era de esperar) crea una instancia del enjambre, realiza la optimización con ella y guarda los resultados en variables miembro (optimum, result[]).
class BaseFunctor: public Functor { ... public: virtual bool test(void) { Swarm swarm(PSO_SwarmSize, PSO_GroupCount, params, max, min, steps); if(MQLInfoInteger(MQL_OPTIMIZATION)) { if(!swarm.restoreIndex()) return false; } optimum = swarm.optimize(this, PSO_Cycles); swarm.getSolution(result); if(MQLInfoInteger(MQL_OPTIMIZATION)) { swarm.exportIndex(PSO_GroupCount); } return true; } };
No obstante, esta es la primera vez que vemos cómo se usan los métodos restoreIndex y exportIndex descritos en las secciones anteriores. Las tareas de optimización para un asesor experto generalmente necesitan de un gran número de cálculos (parámetros y grupos, y cada grupo, una pasada del simulador), por lo que los agentes necesitarán intercambiar información.
La prueba virtual de un asesor experto se realiza en el método de cálculo según el esquema declarado. Pero en la inicialización del espacio de optimización, participa una nueva clase, Settings.
class WorkerFunctor: public BaseFunctor { string names[]; public: WorkerFunctor(const Settings &s): BaseFunctor(s.size()) { s.getNames(names); for(int i = 0; i < params; i++) { max[i] = s.get<double>(i, SET_COLUMN_STOP); min[i] = s.get<double>(i, SET_COLUMN_START); steps[i] = s.get<double>(i, SET_COLUMN_STEP); } } virtual double calculate(const double &vec[]) { VIRTUAL::Tester(_ticks, OnTick, TesterStatistics(STAT_INITIAL_DEPOSIT)); VIRTUAL::ResetTickets(); const double r = TesterStatistics(Estimator); VIRTUAL::Delete(); return r; } };
El caso es que, para iniciar una optimización, el usuario deberá configurar los parámetros de entrada del asesor de la forma habitual. No obstante, el algoritmo del enjambre utiliza el simulador solo para paralelizar tareas (incrementando el número del grupo). Por ello, el asesor debería poder leer los ajustes de los parámetros de optimización, guardar estos en un archivo auxiliar transmitido a cada agente, restablecer dichas configuraciones en el simulador y asignar la optimización según el número de grupo. La clase Settings se encargará de leer los ajustes desde un archivo auxiliar. El archivo es "EA_name.mq5.csv"; deberemos incluirlo mediante una directiva.
#define PPSO_SHARED_SETTINGS __FILE__ + ".csv" #property tester_file PPSO_SHARED_SETTINGS
Ofrecemos al lector familiarizarse con la clase Settings de forma independiente. La clase lee un archivo CSV línea por línea, asumiendo que las siguientes columnas se encuentran presentes:
#define MAX_COLUMN 4 #define SET_COLUMN_NAME 0 #define SET_COLUMN_START 1 #define SET_COLUMN_STEP 2 #define SET_COLUMN_STOP 3
Todas ellas se recuerdan en matrices internas y están disponibles a través de métodos get según el nombre o el número. El método isVoid() retorna el signo de ausencia de configuraciones (el archivo no se ha podido leer, está vacío o en un formato incorrecto).
Las configuraciones se escriben en un archivo en el manejador OnTesterInit (ver más abajo).
Recomendamos crear inmediatamente de forma manual el archivo vacío "expert_name.mq5.csv" en la carpeta MQL5/Files. De no hacer esto, tendremos problemas para ejecutar la optimización la primera vez.
Por desgracia, en el primer inicio, el simulador, aunque crea este archivo de forma automática, no lo envía a los agentes, por lo que la inicialización del asesor experto en ellos termina con el error INIT_PARAMETERS_INCORRECT. Reiniciarlo tampoco nos servirá para enviarlo, ya que el simulador, aparentemente, guarda en la caché la información sobre los recursos conectados y no considera el archivo como aparecido hasta que el usuario selecciona el experto en la lista desplegable de la configuración del simulador. Solo después de ello, este archivo comenzará a actualizarse normalmente y será enviado a los agentes. Así, resulta más fácil crearlo a mano previamente.
string header[]; void OnTesterInit() { int h = FileOpen(PPSO_SHARED_SETTINGS, FILE_ANSI|FILE_WRITE|FILE_CSV, ','); if(h == INVALID_HANDLE) { Print("FileSave error: ", GetLastError()); } MqlParam parameters[]; string names[]; EXPERT::Parameters(0, parameters, names); for(int i = 0; i < ArraySize(names); i++) { if(ResetOptimizableParam<double>(names[i], h)) { const int n = ArraySize(header); ArrayResize(header, n + 1); header[n] = names[i]; } } FileClose(h); // 5008 bool enabled; long value, start, step, stop; if(ParameterGetRange("PSO_GroupCount", enabled, value, start, step, stop)) { if(!enabled) { const int cores = TerminalInfoInteger(TERMINAL_CPU_CORES); Print("PSO_GroupCount is set to default (number of cores): ", cores); ParameterSetRange("PSO_GroupCount", true, 0, 1, 1, cores); } } // remove CRC indices from previous optimization runs Swarm::removeIndex(); }
La función adicional ResetOptimizableParam se usa para buscar los parámetros para los que el indicador de optimización está activado, y también para restablecer dichos indicadores. Asimismo, en OnTesterInit, recordamos los nombres de estos parámetros usando la biblioteca Expert (autor fxsaber), que permite mostrar los resultados de una forma visualmente más clara. No obstante, necesitábamos la biblioteca básicamente porque los nombres debeían conocerse de antemano para así poder llamar a las funciones estándar ParameterGetRange/ParameterSetRange, pero la API MQL no nos permite obtener la lista de parámetros. Esto hará también que el código sea más universal y, por consiguiente, que podamos incluir este código en cualquier asesor sin modificaciones especiales.
template<typename T> bool ResetOptimizableParam(const string name, const int h) { bool enabled; T value, start, step, stop; if(ParameterGetRange(name, enabled, value, start, step, stop)) { // disable all native optimization except for PSO-related params // preserve original settings in the file h if((StringFind(name, "PSO_") != 0) && enabled) { ParameterSetRange(name, false, value, start, step, stop); FileWrite(h, name, start, step, stop); // 5007 return true; } } return false; }
En el manejador OnInit, ejecutado ya en el agente, los ajustes se leen en el objeto global Settings de la forma siguiente:
Settings settings; int OnInit() { ... FileReader f(PPSO_SHARED_SETTINGS); if(f.isReady() && f.read(settings)) { const int n = settings.size(); Print("Got settings: ", n); } else { if(MQLInfoInteger(MQL_OPTIMIZATION)) { Print("FileLoad error: ", GetLastError()); return INIT_PARAMETERS_INCORRECT; } else { Print("WARNING! Virtual optimization inside single pass - slowest mode, debugging only"); } } ... }
Como veremos posteriormente, este objeto se transmite al objeto WorkerFunctor creado en el controlador OnTester, dentro del cual se efectúan todos los cálculos y la optimización. Antes de iniciar los cálculos, deberemos recopilar los ticks. Esto se consigue en el manejador OnTick.
bool OnTesterCalled = false; void OnTick() { if(VirtualTester && !OnTesterCalled) { MqlTick _tick; SymbolInfoTick(_Symbol, _tick); const int n = ArraySize(_ticks); ArrayResize(_ticks, n + 1, n / 2); _ticks[n] = _tick; return; // skip all time scope and collect ticks } ... // trading goes on here }
¿Por qué se hace de esta forma, y no llamando a la función CopyTicksRange directamente en OnTester? En primer lugar, esta función solo opera en los modos de ticks, y es deseable tener soporte para el modo OHLC M1 rápido (4 ticks por minuto). En segundo lugar, en el modo de generación de ticks, por algún motivo, el tamaño de la matriz retornada se ve limitado a 131072 (no existe tal restricción cuando se trabaja con ticks reales).
La variable OnTesterCalled es inicialmente igual a false y, por consiguiente, se recopila la historia de ticks. OnTesterCalled se establece como true posteriormente (como su nombre indica) en OnTester, antes de iniciar la PSO. A continuación, el objeto Swarm comenzará a calcular el functor en un ciclo, en el que, como vimos anteriormente, se llama a VIRTUAL::Tester con una referencia al propio OnTick. Solo que, en esta ocasión, OnTesterCalled será igual a true, y el control no se transferirá al bloque de ensamblaje de ticks, sino al bloque con la lógica comercial. Hablaremos de ello a continuación. En el futuro, a medida que se desarrolle la biblioteca de PSO, es posible que aparezcan mecanismos que simplifiquen la integración en los asesores expertos existentes al reemplazar el manejador OnTick en el archivo de encabezado de la biblioteca.
Y ahora, vamos a hablar del propio OnTester (de forma simplificada).
double OnTester() { if(VirtualTester) { OnTesterCalled = true; // MQL API implies some limitations for CopyTicksRange function, so ticks are collected in OnTick const int size = ArraySize(_ticks); PrintFormat("Ticks size=%d error=%d", size, GetLastError()); if(size <= 0) return 0; if(settings.isVoid() || !InternalOptimization) // fallback to a single virtual test without PSO { VIRTUAL::Tester(_ticks, OnTick, TesterStatistics(STAT_INITIAL_DEPOSIT)); Print(VIRTUAL::ToString(INT_MAX)); Print("Trades: ", VIRTUAL::VirtualOrdersHistoryTotal()); return TesterStatistics(Estimator); } settings.print(); const int n = settings.size(); if(PSO_Enable) { MathSrand(PSO_GroupCount + PSO_RandomSeed); // reproducable randomization WorkerFunctor worker(settings); Swarm::Stats stats; if(worker.test(&stats)) { double output[]; double result = worker.getSolution(output); if(MQLInfoInteger(MQL_OPTIMIZATION)) { FrameAdd(StringFormat("PSO%d/%d", stats.done, stats.planned), PSO_GroupCount, result, output); } ArrayResize(output, n + 1); output[n] = result; ArrayPrint(output); return result; } } ... return 0; } return TesterStatistics(Estimator); }
El código anterior muestra la creación del functor WorkerFunctor utilizando el conjunto de parámetros del objeto settings, así como el inicio de un enjambre usando su método test. Los resultados conseguidos se envían en un frame al terminal, donde son recibidos en OnTesterPass.
El manejador OnTesterPass es similar al del asesor de prueba de PPSO, salvo que los datos recibidos en los frames no se imprimen en el log, sino en un archivo CSV titulado PPSO-nombre-del-experto-fecha_hora.
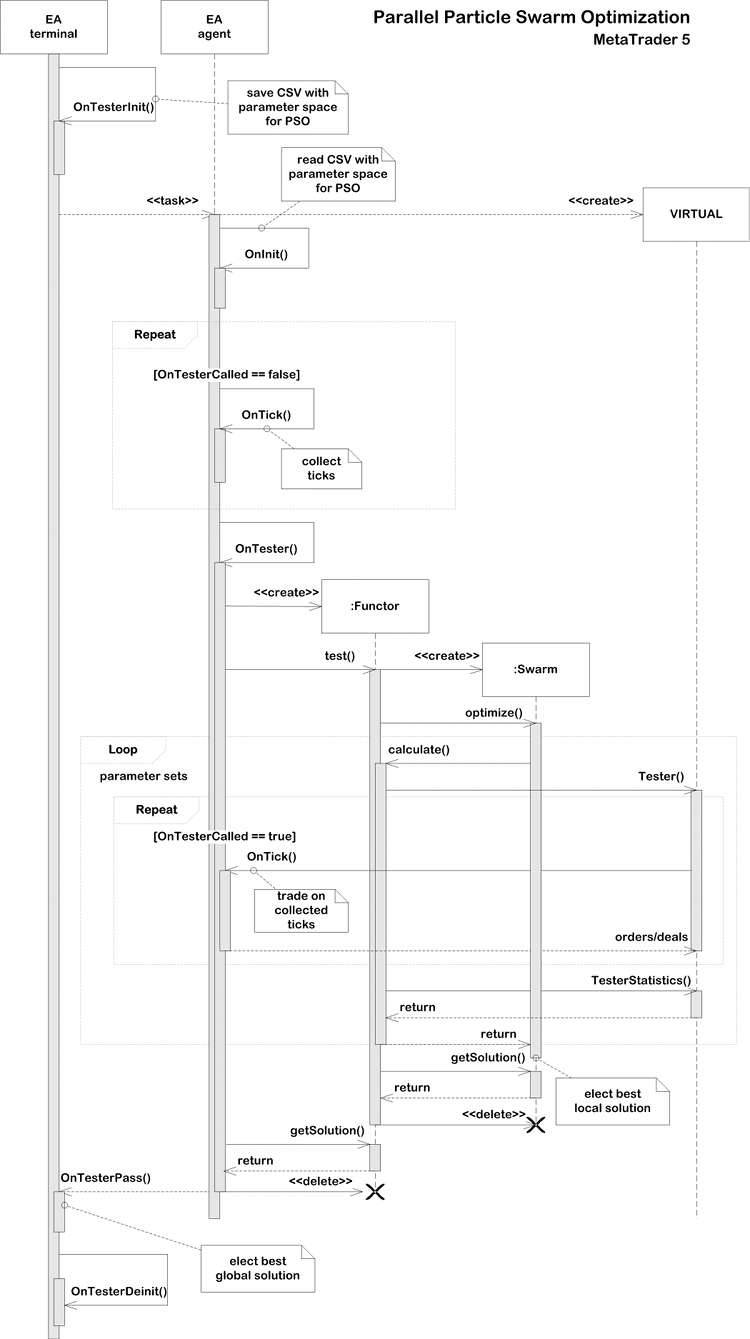
Diagrama secuencial de la Parallel Particle Swarm Optimization
Vamos a retornar finalmente a la estrategia comercial. Resulta casi la misma que se utilizó en el artículo Cálculo de expresiones matemáticas (Parte 2). No obstante, necesitaremos algunos ajustes para permitir el comercio virtual. Las fórmulas de las señales anteriores calculan los indicadores EMA según los precios de apertura en la barra cero:
input string SignalBuy = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) > 1 + Threshold"; input string SignalSell = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) < 1 - Threshold";
Ahora, deberán leerse desde las barras históricas (porque los cálculos se realizan desde OnTester al final de la pasada). El número de la barra "actual" en el pasado se puede determinar fácilmente: la biblioteca virtual anula la función de sistema TimeCurrent y, por consiguiente, se puede escribir en OnTick lo siguiente:
const int bar = iBarShift(_Symbol, PERIOD_CURRENT, TimeCurrent());
El número de barra actual debe añadirse con un nombre adecuado al recuadro de expresiones de la variable, por ejemplo, "Bar"; a continuación, podemos reescribir las fórmulas de la señal de la siguiente manera:
input string SignalBuy = "EMA_OPEN_{Fast}(Bar)/EMA_OPEN_{Slow}(Bar) > 1 + Threshold"; input string SignalSell = "EMA_OPEN_{Fast}(Bar)/EMA_OPEN_{Slow}(Bar) < 1 - Threshold";
La versión actualizada de los parsers dispone de la llamada intermedia del nuevo método with (también en OnTick) al cambiar la variable (número de barra) y calcular la fórmula con este valor:
const int bar = iBarShift(_Symbol, PERIOD_CURRENT, TimeCurrent()); // NEW bool buy = p1.with("Bar", bar).resolve(); // WAS: bool buy = p1.resolve(); bool sell = p2.with("Bar", bar).resolve(); // WAS: bool sell = p2.resolve();
A continuación, el código comercial de OnTick no tiene cambios.
No obstante, las correcciones necesarias no terminan aquí.
Las fórmulas actuales usan los periodos de EMA fijos establecidos en la configuración y se convierten en variables dentro de las expresiones. No obstante, los periodos deben modificarse durante la optimización, lo cual implica usar diferentes instancias de los indicadores. El problema es que la optimización virtual con ajuste de parámetros por enjambre se realiza dentro del salto del simulador, al final, en la función OnTester. Y allí ya es demasiado tarde para crear los identificadores de los indicadores.
El problema mencionado tiene carácter global para cualquier optimización virtual, y hay para el mismo 3 soluciones más obvias:
- no usar indicadores en absoluto; inicialmente, los sistemas comerciales sin indicadores tendrían ventaja aquí;
- considerar los indicadores de una manera especial, de forma independiente dentro del asesor; muchos tráders hacen precisamente eso, porque resulta la forma más rápida, incluso en comparación con los indicadores estándar; eso sí, también es la más laboriosa;
- crear de antemano un conjunto de indicadores para todas las combinaciones de parámetros de la configuración; esto necesita de muchos recursos y puede requerir limitar el rango de parámetros;
El último método deja una cuestión abierta referente a los sistemas encargados de calcular las señales tick a tick. El caso es que todas las barras de la historia virtual ya están cerradas y los indicadores ya están construidos. En otras palabras, solo están disponibles las señales de barra. Si, según dicha historia, "ejecutamos" el sistema sin control de apertura de barras, dará muchas menos transacciones y estas serán de menor calidad que los ticks no virtuales.
En nuestro asesor experto, el comercio se efectúa por barras, por lo que esto no supone un problema. Este también es el caso de algunos ejemplos de los asesores expertos proporcionados con MetaTrader 5, pero debemos prestar atención a cómo se detecta el evento de una nueva apertura de barra. El método para controlar un único volumen de ticks no resulta adecuado para la historia virtual, porque todas las barras ya están llenas de ticks. Por consiguiente, recomendamos definir una nueva barra comparando su hora con la anterior.
Para resolver el problema descrito, hemos ampliado el motor de expresiones de una tercera forma. Además de las funciones de los indicadores MA individuales (MAIndicatorFunc), hemos creado funciones MA de abanico (MultiMAIndicatorFunc, ver Indicators.mqh). Su nombre debe comenzar con el prefijo "M_" y contener el periodo mínimo, el salto del periodo y el periodo máximo, por ejemplo:
input string SignalBuy = "M_EMA_OPEN_9_6_27(Fast,Bar)/M_EMA_OPEN_9_6_27(Slow,Bar) > 1 + T"; input string SignalSell = "M_EMA_OPEN_9_6_27(Fast,Bar)/M_EMA_OPEN_9_6_27(Slow,Bar) < 1 - T";
El método de cálculo y el tipo de precio se indican en el nombre, igual que antes. Aquí, se prescribe crear en las señales un abanico de EMA al precio OPEN con periodos de 9 a 27 (incluidos), con un salto de 6.
Otra innovación en la biblioteca de expresiones es un conjunto de variables que ofrecen acceso a las estadísticas comerciales de TesterStatistics (ver TesterStats.mqh). Usando como base este conjunto, podemos añadir la variable de entrada Formula al asesor, lo cual permite establecer el valor objetivo como una expresión arbitraria. Cuando hemos rellenado esta variable, se ignora Estimator. Concretamente, en lugar de STAT_PROFIT_FACTOR (que no está definido para pérdidas cero), podemos ajustar un indicador "más suave" con una fórmula similar a Estimator: "(GROSSPROFIT-(1/(TRADES+1)))/-(GROSSLOSS-1/(TRADES+1))".
Ahora, ya está todo listo para efectuar la optimización comercial virtual usando el método PSO.
Realizando pruebas prácticas
Vamos a preparar el simulador. Debemos usar una optimización lenta, es decir, una iteración completa de todos los parámetros. En nuestro caso, no será lenta, porque solo se modifica el número de grupo en cada ejecución, mientras que la iteración selectiva de los parámetros del asesor correrá a cargo de un enjambre dentro de su ciclo. La genética no se puede usar por tres motivos. Primero, no garantiza que se calculen todas las combinaciones de parámetros (en nuestro caso, un número determinado de grupos). En segundo lugar, debido a su naturaleza específica, se "desplazará" paulatinamente hacia los parámetros que han producido un resultado más atractivo, sin considerar el hecho de que no haya dependencia entre el número de grupo y su éxito, porque el número de grupo es solo un aleatorizador de la estructura de datos de PSO. En tercer lugar, el número de grupo no suele ser lo suficientemente grande como para usar un enfoque genético.
La optimización se efectúa según el máximo del criterio personalizado.
Primero, optimizamos el asesor experto de la forma estándar con la biblioteca virtual desactivada (archivo ExprBotPSO-standard-optimization.set). El número de combinaciones de parámetros para la optimización es pequeño para fines demostrativos. Los parámetros Fast y Slow varían de 9 a 45 con un salto de 6; el parámetro T, de 0 a 0,01, con un salto de 0,0025.
EURUSD, H1, intervalo desde principios de 2020, usando ticks reales. Se pueden obtener los siguientes resultados:
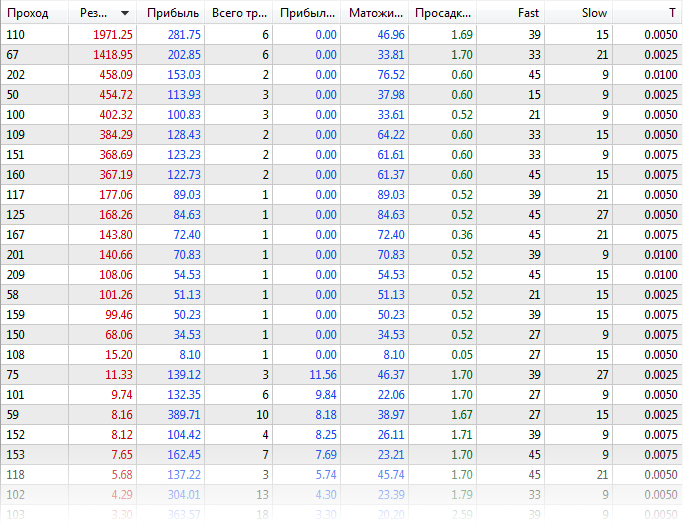
Recuadro de resultados de la optimización estándar
Veamos en el log cuánto tiempo han tardado dos agentes: casi 21 minutos.
Experts optimization frame expert ExprBotPSO (EURUSD,H1) processing started Tester Experts\ExprBotPSO.ex5 on EURUSD,H1 from 2020.01.01 00:00 to 2020.08.01 00:00 Tester complete optimization started ... Core 2 connected Core 1 connected Core 2 authorized (agent build 2572) Core 1 authorized (agent build 2572) ... Tester optimization finished, total passes 245 Statistics optimization done in 20 minutes 55 seconds Statistics shortest pass 0:00:05.691, longest pass 0:00:23.114, average pass 0:00:10.206
Ahora, vamos a optimizar el asesor experto con comercio virtual y la PSO activada (ExprBotPSO-virtual-pso-optimization.set). El número de grupos es igual a 4 y se determina iterando el parámetro PSO_GroupCount de 0 a 3. Otros parámetros operativos para los que se activa la optimización se desactivarán forzosamente en la optimización estándar, pero se transmitirán a los agentes en archivos CSV para realizar la optimización virtual interna mediante el algoritmo de PSO.
En la simulación, dejamos el modo de ticks reales, pero también era posible usar la generación u OHLC M1 para los cálculos rápidos. Los cálculos matemáticos no funcionarán, ya que recopilamos los ticks en el simulador para el comercio virtual.
En el log del simulador, veremos más o menos lo que sigue:
Tester input parameter 'Fast' set to: enable=false, value=9, start=9, step=6, stop=45 Tester input parameter 'Slow' set to: enable=false, value=21, start=9, step=6, stop=45 Tester input parameter 'T' set to: enable=false, value=0, start=0, step=0.0025, stop=0.01 Experts optimization frame expert ExprBotPSO (EURUSD,H1) processing started Tester Experts\ExprBotPSO.ex5 on EURUSD,H1 from 2020.01.01 00:00 to 2020.08.01 00:00 Tester complete optimization started ... Core 1 connected Core 2 connected Core 2 authorized (agent build 2572) Core 1 authorized (agent build 2572) ... Tester optimization finished, total passes 4 Statistics optimization done in 4 minutes 00 seconds Statistics shortest pass 0:01:27.723, longest pass 0:02:24.841, average pass 0:01:56.597 Statistics 4 frames (784 bytes total, 196 bytes per frame) received
Cada 'pass' es ahora un paquete de optimizaciones virtuales, por lo que se ha vuelto más largo. Pero su número total es inferior, y el tiempo total se reduce significativamente: solo 4 minutos.
En los logs del terminal, recibimos los mensajes de los frames (muestran las mejores métricas de cada grupo). No obstante, los resultados comerciales reales y virtuales son ligeramente distintos.
22:22:52.261 ExprBotPSO (EURUSD,H1) 2 tmp-files deleted 22:25:07.981 ExprBotPSO (EURUSD,H1) 0 PSO75/1500 0 1974.400000000025 22:25:23.348 ExprBotPSO (EURUSD,H1) 2 PSO84/1500 2 402.6000000000062 22:26:51.165 ExprBotPSO (EURUSD,H1) 3 PSO70/1500 3 455.000000000003 22:26:52.451 ExprBotPSO (EURUSD,H1) 1 PSO79/1500 1 458.3000000000047 22:26:52.466 ExprBotPSO (EURUSD,H1) Solution: 1974.400000000025 22:26:52.466 ExprBotPSO (EURUSD,H1) 39.00000 15.00000 0.00500
Conviene notar que los resultados no coincidirán exactamente (incluso si tuviéramos una estrategia libre de indicadores tick a tick), porque el simulador tiene características comerciales específicas que no se pueden repetir en la biblioteca MQL. Éstas son solo algunas de ellas:
- las órdenes límite se pueden activar de maneras diferentes cerca del precio de mercado.
- el margen no se calcula o no se calcula con precisión;
- la comisión no se calcula automáticamente (limitación de API MQL), pero se puede programar mediante parámetros de entrada adicionales;
- el registro de órdenes y transacciones en el modo de compensación puede diferir;
- solo se admite el símbolo actual;
Para más información sobre la biblioteca virtual, consulte la documentación y los debates correspondientes.
A modo de depuración, y también para comprender el funcionamiento del enjambre, el asesor de prueba admite el modo de optimización virtual en un núcleo dentro de una ejecución de prueba normal. Podrá ver un ejemplo de configuración en el archivo ExprBotPSO-virtual-internal-optimization-single-pass.set, adjunto a continuación. No se olvide de desactivar la optimización en el simulador.
Los resultados intermedios se describen con detalle en el log del simulador. En cada ciclo, la posición y el valor de la función objetivo de cada partícula se obtienen de los PSO_Cycles establecidos. Si la partícula entra en las coordenadas ya marcadas, el cálculo se omitirá.
Ticks size=15060113 error=0
[,0] [,1] [,2] [,3]
[0,] "Fast" "9" "6" "45"
[1,] "Slow" "9" "6" "45"
[2,] "T" "0" "0.0025" "0.01"
PSO[3] created: 15/3
PSO Processing...
Fast:9.0, Slow:33.0, T:0.0025, 1.31285
Fast:21.0, Slow:21.0, T:0.0025, -1.0
Fast:15.0, Slow:33.0, T:0.0075, -1.0
Fast:27.0, Slow:39.0, T:0.0025, 0.07673
Fast:9.0, Slow:9.0, T:0.005, -1.0
Fast:33.0, Slow:21.0, T:0.01, -1.0
Fast:39.0, Slow:45.0, T:0.0025, -1.0
Fast:15.0, Slow:15.0, T:0.0025, -1.0
Fast:33.0, Slow:21.0, T:0.0, 0.32895
Fast:33.0, Slow:39.0, T:0.0075, -1.0
Fast:33.0, Slow:15.0, T:0.005, 384.5
Fast:15.0, Slow:27.0, T:0.0, 2.44486
Fast:39.0, Slow:27.0, T:0.0025, 11.41199
Fast:9.0, Slow:15.0, T:0.0, 1.08838
Fast:33.0, Slow:27.0, T:0.0075, -1.0
Cycle 0 done, skipped 0 of 15 / 384.5000000000009
...
Fast:45.0, Slow:9.0, T:0.0025, 0.86209
Fast:21.0, Slow:15.0, T:0.005, -1.0
Cycle 15 done, skipped 13 of 15 / 402.6000000000062
Fast:21.0, Slow:15.0, T:0.0025, 101.4
Cycle 16 done, skipped 14 of 15 / 402.6000000000062
Fast:27.0, Slow:15.0, T:0.0025, 8.18754
Fast:39.0, Slow:15.0, T:0.005, 1974.40002
Cycle 17 done, skipped 13 of 15 / 1974.400000000025
Fast:45.0, Slow:9.0, T:0.005, 1.00344
Cycle 18 done, skipped 14 of 15 / 1974.400000000025
Cycle 19 done, skipped 15 of 15 / 1974.400000000025
PSO Finished 89 of 1500 planned calculations: true
39.00000 15.00000 0.00500 1974.40000
final balance 10000.00 USD
OnTester result 1974.400000000025
Como el espacio de optimización es pequeño, ha resultado completamente cubierto por el ciclo 19. Obviamente, esto no sucederá con problemas reales con millones de combinaciones. Para ellos, resulta muy importante seleccionar la combinación correcta de PSO_Cycles, PSO_SwarmSize, PSO_GroupCount, mediante ensayo y error.
No olvide que con la PSO, se ejecuta internamente una pasada del simulador por cada PSO_GroupCount hasta las pasadas PSO_Cycles*PSO_SwarmSize individuales virtuales, por lo que la indicación de progreso será mucho más lenta de lo habitual.
Muchos tráders intentan obtener los mejores resultados de la optimización genética incorporada ejecutándola muchas veces seguidas; esto recopila varias pruebas debido a la inicialización aleatoria y, después de varias ejecuciones, existe la posibilidad de encontrar progreso. En el caso de la PSO, PSO_GroupCount actúa como un análogo del inicio múltiple de la genética. El número de pasadas individuales, que en genética puede llegar a 10000, debe distribuirse en la PSO entre los dos componentes del producto PSO_Cycles*PSO_SwarmSize, por ejemplo, 100*100. PSO_Cycles es un análogo de las generaciones en genética, y PSO_SwarmSize es el tamaño de la población.
Virtualización de expertos en API MQL5
Hasta ahora, hemos analizado un ejemplo de un asesor experto escrito usando la API comercial de MQL4. Esto se debe a las particularidades de implementación de la biblioteca Virtual. Al mismo tiempo, nos gustaría aplicar la PSO para un asesor con las "nuevas" funciones de API MQL5. Para ello, hemos desarrollado una capa experimental intermedia para redireccionar las llamadas de la API de MQL5 a la API de MQL4. Está diseñada como un archivo MT5Bridge.mqh que necesita de la biblioteca Virtual y/o MT4Orders para su funcionamiento.
#include <fxsaber/Virtual/Virtual.mqh> #include <MT5Bridge.mqh> #include <Expert\Expert.mqh> #include <Expert\Signal\SignalMA.mqh> #include <Expert\Trailing\TrailingParabolicSAR.mqh> #include <Expert\Money\MoneySizeOptimized.mqh> ...
Después de añadir Virtual y MT5Bridge al inicio del código, antes de otros #include, la llamada a las funciones de la API de MQL5 pasa por las funciones "puente" redefinidas desde las cuales se llaman las funciones "virtuales" de la API de MQL4. Como resultado, podemos probar y optimizar el asesor experto de forma virtual. En particular, podemos organizar la optimización de la PSO de la misma forma que se ha hecho en ExprBotPSO. Deberemos escribir (copiar parcialmente) un functor y los controladores para el simulador. Pero lo más laborioso puede ser la adaptación de la generación de señales a partir de indicadores para los parámetros de variable.
El estado experimental de MT5Bridge.mqh implica que su funcionalidad no ha sido ampliamente probada. Esta es una investigación del tipo Proof Of the Concept. Use el código fuente para depurar y corregir errores.
Conclusión
Hemos analizado el algoritmo de Particle Swarm Optimization y lo hemos implementado en MQL con soporte para multiflujo usando los agentes del simulador. La existencia de configuraciones de PSO abiertas permite una mayor flexibilidad en la regulación del proceso, en comparación con el uso de la optimización genética incorporada. Además de la configuración ofrecida en los parámetros de entrada, tiene sentido probar otros coeficientes adaptables que hemos usado como argumentos para el método optimize con valores por defecto: inertia(0.8), selfBoost(0.4), groupBoost(0.4). Esto hará más flexible el algoritmo, pero dificultará la selección de la configuración para una tarea específica. La biblioteca de PSO que adjuntamos a continuación se puede utilizar en el modo de cálculos matemáticos (si usted tiene su propio mecanismo de cotizaciones, indicadores y transacciones virtuales), así como en los modos de barra y ticks, utilizando las clases de emulación del comercio de terceros listas para usar, como por ejemplo, Virtual.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/8321
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Redes neuronales: así de sencillo (Parte 2): Entrenamiento y prueba de la red
Redes neuronales: así de sencillo (Parte 2): Entrenamiento y prueba de la red
 Símbolo personalizados: fundamentos de uso en la práctica
Símbolo personalizados: fundamentos de uso en la práctica
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Con la directiva tester_file, ¿se reenviará este archivo al Agente durante un cambio de paquete de trabajo?
En caso afirmativo, es posible cambiar el contenido de este archivo durante la optimización.
Puede cambiar el contenido, pero no tendrá ningún efecto - parece que la información se almacena en caché en algún lugar durante el inicio de la optimización. Al menos era así antes.
¿Cuál es la forma más rápida de cargar grandes cantidades de datos en cada pasada?
Para agentes locales probablemente sea la más rápida a través de un directorio compartido. Para agentes distribuidos no hay muchas opciones.
Hay pocas opciones para los distribuidos.
Incrustar en la fuente ZIP(MqlTick[]).
Incrustar en la fuente ZIP(MqlTick[]).
¿En qué se diferenciará de tester_file o, más concretamente, de resource? Lo más probable es que el tiempo de acceso será diferente, pero insignificante.
¿En qué se diferenciará de tester_file o, más concretamente, de resource? Lo más probable es que el tiempo de acceso sea diferente, pero insignificante.
No se sentará en una caja de arena y dependerá de la velocidad de FileLoad. Usted debe medirlo, en general.