
Las Tablas Electrónicas en MQL5
Introducción
Generalmente, las tablas electrónicas hacen referencia a los procesadores de tablas (aplicaciones que almacenan y procesan los datos), como EXCEL. Aunque el código que se muestra en el artículo no es tan potente, se puede utilizar como base para una implementación completa de un procesador de tablas. No tengo por objetivo crear MS Excel utilizando MQL5, pero quiero implementar una clase para trabajar con datos de diferentes tipos en una matriz bidimensional.
Y aunque la clase que he implementado no se puede comparar por su rendimiento a una matriz bidimensional de un solo tipo de datos (con acceso directo a los datos), parecía una clase práctica para utilizarla. Además, esta clase se puede considerar tanto una implementación de la clase Variant en C++, como un caso particular de una tabla simplificada en una columna.
Para los impaciente y para los que no quieren analizar el algoritmo de implementación, comenzaré describiendo la clase de CTable de los métodos disponibles.
1. Descripción de los Métodos de la Clase
Al principio, consideremos los métodos disponibles de la clase con una descripción más detallada de su objetivo y principios de uso.
1.1. FirstResize
Diseño de la tabla, descripción de las clases de columnas, TYPE[] - matriz de tipo ENUM_DATATYPE que determina el tamaño de la fila y los tipos de celdas.
void FirstResize(const ENUM_DATATYPE &TYPE[]);
Prácticamente, este método es una construcción adicional que tiene un parámetro. Esto es práctico por dos razones: primero, resuelve el problema del envío de un parámetro dentro del constructor; segundo, proporciona la posibilidad de pasar un objeto como un parámetro, y entonces realizar la división necesaria de la matriz. Esta característica permite utilizar la clase como clase Variant en C++.
Las peculiaridades de la implementación incluyen el hecho de que a pesar de que la función ajusta la primera dimensión y el tipo de datos de las columnas, no requiere que se especifique el tamaño de la primera dimensión como parámetro. Este parámetro se toma del tamaño de la matriz enviada TYPE.
1.2. SecondResize
Cambia el número de filas a 'j'.
void SecondResize(int j);
La función ajusta un tamaño especificado para todas las matrices de la segunda dimensión. Así, podemos decir que agrega filas a la tabla.
1.3. FirstSize
El método devuelve el tamaño de la primera dimensión (longitud de fila).
int FirstSize();
1.4. SecondSize
El método devuelve el tamaño de la segunda dimensión (longitud de fila).
int SecondSize();
1.5. PruningTable
Establece un nuevo tamaño para la primera dimensión; el cambio es posible en el tamaño del principio.
void PruningTable(int count);
Prácticamente, la función no cambia la longitud de la fila; sólo reescribe el valor de una variable, que es responsable de almacenar el valor de la longitud de la fila. La clase contiene otra variable que almacena el verdadero tamaño de la memoria asignada, que se establece en la división inicial de la tabla. Dentro de los valores de esta variable, es posible el cambio virtual de tamaño de la primera dimensión. La función sirve para cortar una parte no deseada al copiar de una tabla a otra.
1.6. CopyTable
Método para copiar de una tabla a otra la longitud entera de la segunda dimensión:
void CopyTable(CTable *sor);
La función copia de una tabla a otra. Comienza al recibir la tabla. Se puede usar como una construcción adicional. La estructura interna de las variantes de ordenamiento no se copia. De la tabla inicial, sólo se copian el tamaño, los tipos de columnas y los datos. La función acepta la referencia del objeto copiado del tipo CTable como un parámetro, que pasa por la función GetPointer.
Al copiar de una tabla a otra, se crea una nueva tabla creada según la muestra "sor".
void CopyTable(CTable *sor,int sec_beg,int sec_end);
Hacer caso omiso de la función descrita arriba con los parámetros adicionales: sec_beg; punto de partida de la copia de la tabla inicial, sec_end; punto final de la copia (por favor, no lo confunda con la cantidad de datos copiados). Ambos parámetros se refieren a la segunda dimensión. Los datos se añadirán al principio de la tabla receptora. El tamaño de la tabla receptora se ajusta como sec_end-sec_beg+1.
1.7. TypeTable
Devuelve el valor type_table (de tipo ENUM_DATATYPE) de la columna 'i'.
ENUM_DATATYPE TypeTable(int i)
1.8. Change
El método Change() lleva a cabo el intercambio de columnas.
bool Change(int &sor0,int &sor1);
Como se ha mencionado anteriormente, el método cambia las columnas (funciona con la primera dimensión). Dado que en realidad la información no se mueve, la velocidad de funcionamiento de la función no se ve afectada por el tamaño de la segunda dimensión.
1.9. Insert
El método Insert, inserta una columna en una posición especificada.
bool Insert(int rec,int sor);
La función es la misma que la que hemos descrito anteriormente, excepto que se desarrolla tirando o empujando de otras columnas dependiendo donde se deba mover la columna especificada. El parámetro "rec" especifica dónde se pondrá la columna, "sor" especifica de dónde se moverá.
1.10. Variant/VariantCopy
Después tenemos tres funciones de la serie "variant". La memorización de las variantes de procesamiento de la tabla se implementa en la clase.
Las variantes recuerdan a un cuaderno. Por ejemplo, si realiza el ordenamiento por la tercera columna y no quiere reajustar los datos durante el siguiente proceso, debe cambiar la variante. Para conseguir acceso a la variante anterior del proceso, llame a la función "variant". Si el siguiente proceso se debe basar en el resultado del anterior, debe copiar las variantes. Una variante con el número 0 está establecida por defecto.
Crear una variante (si no hay tal variante, se creará, así como todas las variantes perdidas hasta "ind") y conseguir la variante activa. El método "variantcopy" copia la variante "sor" en la variante "rec".
void variant(int ind); int variant(); void variantcopy(int rec,int sor);
El método de la variant(ind int) cambia la variante seleccionada. Realiza la asignación automática de memoria. Si el parámetro especificado es menor que el anteriormente especificado, la memoria se reasigna.
El método variantcopy permite copiar la variante "sor" en la variante "rec". La función se crea para ordenar las variantes. Aumenta automáticamente el número de variantes si la variante "rec" no existe; también cambia a la variante que acaba de copiar.
1.11. SortTwoDimArray
El método de SortTwoDimArray ordena una tabla junto a la fila seleccionada "i".
void SortTwoDimArray(int i,int beg,int end,bool mode=false);
La función de ordenamiento de una tabla por una columna especificada. Parámetro: i - columna, beg - punto de partida del ordenamiento, end - punto final del ordenamiento (incluido), mode - variable booleana que determina la dirección del ordenamiento. Si mode=true, significa que los valores aumentan junto con los índices ("false" es el valor por defecto, ya que los índices aumentan de arriba a abajo de la tabla).
1.12. QuickSearch
El método realiza una búsqueda rápida de posición de un elemento de la matriz por el valor equivalente al modelo del elemento (element).
int QuickSearch(int i,long element,int beg,int end,bool mode=false);
1.13. SearchFirst
Busca el primer elemento igual a un modelo en una matriz ordenada. Devuelve el índice del primer valor que es igual al modelo "element". Es necesario especificar el tipo de ordenamiento realizado anteriormente en este rango (si no hay tal elemento, devuelve -1).
int SearchFirst(int i,long element,int beg,int end,bool mode=false);
1.14. SearchLast
Busca el último elemento igual a un modelo en una matriz ordenada.
int SearchLast(int i,long element,int beg,int end,bool mode=false);
1.15. SearchGreat
Busca el elemento más cercano superior a un modelo en una matriz ordenada.
int SearchGreat(int i,long element,int beg,int end,bool mode=false);
1.16. SearchLess
Busca el elemento más cercano inferior a un modelo en una matriz ordenada.
int SearchLess(int i,long element,int beg,int end,bool mode=false);
1.17. Set/Get
Las funciones Set y Get tienen el tipo void; son sobreescritas por cuatro tipos de datos con los que funciona la tabla. Las funciones reconocen el tipo de datos, y entonces si el parámetro "value" no corresponde al tipo de columna, en lugar de asignarlo se muestra un aviso. La única excepción es el tipo string. Si el parámetro de entrada es el del tipo string, se convertirá en el tipo de columna. Esta excepción se hace para el más conveniente envío de datos cuando no haya posibilidad de establecer una variable que acepte el valor de la celda.
Los métodos para ajustar valores (i - índice de la primera dimensión, j - índice de la segunda dimensión).
void Set(int i,int j,long value); // setting value of the i-th row and j-th column void Set(int i,int j,double value); // setting value of the i-th row and j-th columns void Set(int i,int j,datetime value);// setting value of the i-th row and j-tj column void Set(int i,int j,string value); // setting value of the i-th row and j-th column
Los métodos para obtener valores (i - índice de la primera dimensión, j - índice de la segunda dimensión).
//--- getting value void Get(int i,int j,long &recipient); // getting value of the i-th row and j-th column void Get(int i,int j,double &recipient); // getting value of the i-th row and j-th column void Get(int i,int j,datetime &recipient); // getting value of the i-th row and j-th column void Get(int i,int j,string &recipient); // getting value of the i-th row and j-th column
1.19. sGet
Consigue un valor de tipo string de la columna "j" y de la fila "i".
string sGet(int i,int j); // return value of the i-th row and j-th column
La única función de las series Get que devuelve el valor a través del operador "return" en vez de una variable paramétrica. Devuelve un valor de tipo string independientemente del tipo de columna.
1.20. StringDigits
Cuando los tipos se convierten al tipo "string", podemos utilizar una precisión establecida por las funciones:
void StringDigits(int i,int digits);
para ajustar la precisión de "double" y
int StringDigits(int i);
Para ajustar una precisión de visualización de segundos en "datetime"; se envía a cualquier valor que no sea igual a -1. El valor especificado se memoriza para la columna, por lo que no es necesario indicarlo cada vez que se muestre la información. Podemos ajustar una precisión para muchas veces, ya que la información está almacenada en los tipos originales y se transforma a la precisión específica sólo durante la salida. Los valores de precisión no son memorizados cuando se copia, así, al copiar una tabla en una nueva, la precisión de las columnas de la nueva tabla corresponderá a la precisión predefinida.
1.21. Un ejemplo del uso:
#include <Table.mqh> ENUM_DATATYPE TYPE[7]= {TYPE_LONG,TYPE_LONG,TYPE_STRING,TYPE_DATETIME,TYPE_STRING,TYPE_STRING,TYPE_DOUBLE}; // 0 1 2 3 4 5 6 //7 void OnStart() { CTable table,table1; table.FirstResize(TYPE); // dividing table, determining column types table.SecondResize(5); // change the number of rows table.Set(6,0,"321.012324568"); // assigning data to the 6-th column, 0 row table.Insert(2,6); // insert 6-th column in the 2-nd position table.PruningTable(3); // cut the table to 3 columns table.StringDigits(2,5); // set precision of 5 digits after the decimal point Print("table ",table.sGet(2,0)); // print the cell located in the 2-nd column, 0 row table1.CopyTable(GetPointer(table)); // copy the entire table 'table' to the 'table1' table table1.StringDigits(2,8); // set 8-digit precision Print("table1 ",table1.sGet(2,0)); // print the cell located in the 2-nd column, 0 row of the 'table1' table. }
El resultado de la operación se escribe en el contenido de la celda (2;0). Como probablemente ha observado, la precisión de los datos copiados no excede la precisión de la tabla inicial.
2011.02.09 14:18:37 Table Script (EURUSD,H1) table1 321.01232000 2011.02.09 14:18:37 Table Script (EURUSD,H1) table 321.01232
Ahora vamos a pasar a la descripción del propio algoritmo.
2. Elegir un Modelo
Hay dos formas de organizar la información: el esquema de columnas conectadas (implementado en este artículo) y su alternativa en forma de filas conectadas se muestran a continuación.
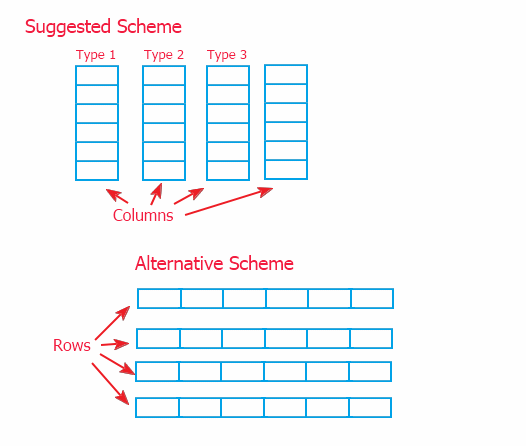
Debido a la referencia a la información a través de un intermediario (descrito en la p. 2), no hay gran diferencia de implementación del rango superior. Pero he escogido el modelo de columnas, ya que permite implementar el método de los datos en el rango inferior, en los objetos que almacenan los datos. Y el esquema alterno requeriría ignorar los métodos para trabajar con información en la clase superior de CTable. Y esto puede complicar la mejora de la clase, en caso de que sea necesaria.
En ese momento, se puede utilizar cada uno de los esquemas. El sistema sugerido permite mover los datos rápidamente, y el alternativo permite agregar datos más rápido (porque la información a menudo se añade línea a línea en una tabla) y consiguiendo filas.
Hay también otra manera de arreglar una tabla - como una matriz de estructuras. Y aunque es el más fácil de aplicar, tiene una desventaja significativa. La estructura debe ser descrita por un programador. Por tanto, se pierde la posibilidad de ajustar los atributos de la tabla a través de parámetros personalizados (sin cambiar el código fuente).
3. Unir datos en una matriz dinámica
Para tener una posibilidad de unir tipos diferentes de datos en una matriz dinámica única, debemos resolver el problema de asignar tipos diferentes a las celdas de la matriz. Este problema ya está resuelto en las listas conectadas de la librería estándar. Mis primeros desarrollos se basaron en la librería estándar de las clases. Pero durante el desarrollo del proyecto, parecía que debía hacer muchos cambios en la clase base CObject.
Por eso me decidí a desarrollar mi propia clase. Para los que no estudiaron la librería estándar, voy a explicar cómo se resolvió el problema descrito arriba. Para resolver el problema, necesita utilizar el mecanismo de herencia.
class CBase { public: CBase(){Print(__FUNCTION__);}; ~CBase(){Print(__FUNCTION__);}; virtual void set(int sor){}; virtual void set(double sor){}; virtual int get(int k){return(0);}; virtual double get(double k){return(0);}; }; //+------------------------------------------------------------------+ class CA: public CBase { private: int temp; public: CA(){Print(__FUNCTION__);}; ~CA(){Print(__FUNCTION__);}; void set(int sor){temp=sor;}; int get(int k){return(temp);}; }; //+------------------------------------------------------------------+ class CB: public CBase { private: double temp; public: CB(){Print(__FUNCTION__);}; ~CB(){Print(__FUNCTION__);}; void set(double sor){temp=sor;}; double get(double k){return(temp);}; }; //+------------------------------------------------------------------+ void OnStart() { CBase *a; CBase *b; a=new CA(); b=new CB(); a.set(15); b.set(13.3); Print("a=",a.get(0)," b=",b.get(0.)); delete a; delete b; }
Visualmente, el mecanismo de herencia se puede mostrar como un peine:
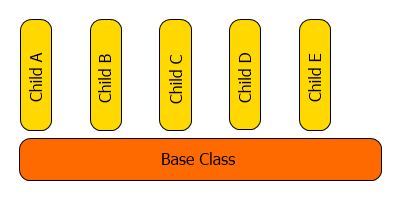
Si se declara la creación de un objeto dinámico de la clase, significa que se llamará al constructor de la clase base. Esta propiedad exacta hace que sea posible crear un objeto en dos pasos. Como las funciones virtuales de la clase base se sobreescriben, conseguimos la posibilidad de llamar a la función con diferentes tipos de parámetros de las clases derivadas.
¿Por qué la simple sobreescritura no es suficiente? El asunto es que las funciones ejecutadas son inmensas, tanto que si describimos sus cuerpos en la clase base (sin utilizar la herencia), luego la función no usada con el código completo del cuerpo se crearía para cada objeto en la clave binaria. Y cuando se usa el mecanismo de herencia, se crean funciones vacías, que ocupan mucha menos memoria que las funciones de código completo.
4. Operaciones con matrices
La segunda, y razón principal que me hizo rechazar el uso de las clases estándar, está relacionada con los datos. Utilizo referencias indirectas para las celdas de matriz a través de una matriz de índices en lugar de referirme a los índices de las celdas. Con ello se estipula una velocidad inferior de trabajo que cuando se usa en referencia directa a través de una variable. El tema es que la variable que indica que un índice funciona más rápido que una celda de la matriz, se debe encontrar en la memoria, al principio.
Analicemos lo que es la diferencia fundamental de ordenar una matriz unidimensional y una matriz multidimensional. Antes de ordenar, una matriz unidimensional tiene posiciones aleatorias de elementos, y después del ordenamiento los elementos están ordenados. Al ordenar una matriz bidimensional, no necesitamos ordenar la matriz entera, sino que sólo se ordena una de sus columnas. Todas las filas deben cambiar su posición manteniendo su estructura.
Las mismas filas de aquí son las estructuras consolidadas que contienen datos de diferentes tipos. Para solucionar este problema, necesitamos ordenar los datos en una matriz seleccionada y salvar la estructura de los índices iniciales. De esta manera, si sabemos qué fila contenía la celda, podemos mostrar la fila entera. Así, al ordenar una matriz bidimensional, debemos conseguir la matriz de índices de la matriz ordenada sin cambiar la estructura de datos.
Por ejemplo:
before sorting by the 2-nd column 4 2 3 1 5 3 3 3 6 after sorting 1 5 3 3 3 6 4 2 3 Initial array looks as following: a[0][0]= 4; a[0][1]= 2; a[0][2]= 3; a[1][0]= 1; a[1][1]= 5; a[1][2]= 3; a[2][0]= 3; a[2][1]= 3; a[2][2]= 6; And the array of indexes of sorting by the 2-nd column looks as: r[0]=1; r[1]=2; r[2]=0; Sorted values are returned according to the following scheme: a[r[0]][0]-> 1; a[r[0]][1]-> 5; a[r[0]][2]-> 3; a[r[1]][0]-> 3; a[r[1]][1]-> 3; a[r[1]][2]-> 6; a[r[2]][0]-> 4; a[r[2]][1]-> 2; a[r[2]][2]-> 3;
Así, tenemos una posibilidad de ordenar la información por símbolos, fechas de apertura de posición, beneficios, etc.
Muchos algoritmos de ordenamiento ya están desarrollados. La mejor variante para este desarrollo será el algoritmo de la ordenación estable.
El algoritmo de ordenamiento rápido(Quick Sorting), que se usa en las clases estándar, se refiere a los algoritmos de ordenamiento inestables. Por eso no nos conviene en su implementación clásica. Pero aún después de traer el ordenamiento rápido a una forma estable (y es una copia adicional de datos y un ordenamiento de matrices de índices), el ordenamiento rápido parece ser más rápido que la burbuja de ordenamiento (uno de los algoritmos más rápidos de ordenamiento fijo). El algoritmo es muy rápido, pero utiliza la recurrencia.
Este es el motivo por el que uso el ordenamiento de burbuja bidireccional (Cocktail Sort) cuando trabajo con matrices del tipo string (requiere mucha más memoria de pila).
5. Disposición de una matriz bidimensional
Y el último tema que quiero tratar es la disposición de una matriz bidimensional dinámica. Para tal disposición es suficiente hacer un envoltorio como una clase para una matriz unidimensional y llamar al objeto matriz a través de la matriz de punteros. Es decir, tenemos que crear una matriz de matrices.
class CarrayInt { public: ~CarrayInt(){}; int array[]; }; //+------------------------------------------------------------------+ class CTwoarrayInt { public: ~CTwoarrayInt(){}; CarrayInt array[]; }; //+------------------------------------------------------------------+ void OnStart() { CTwoarrayInt two; two.array[0].array[0]; }
6. Estructura del Programa
El código de la clase CTable fue escrito utilizando plantillas descritas en el artículo Usos de las Pseudo-Plantillas como Alternativa de las Plantillas C++. Por el hecho de utilizar las plantillas, podría escribir este código tan grande rápidamente. Por eso no describiré el código entero en detalle; además, la mayoría de las partes del código de los algoritmos son una modificación de las clases estándar.
Voy a mostrar solamente la estructura general de la clase y algunas de sus características interesantes de funciones que aclaran varios puntos importantes.
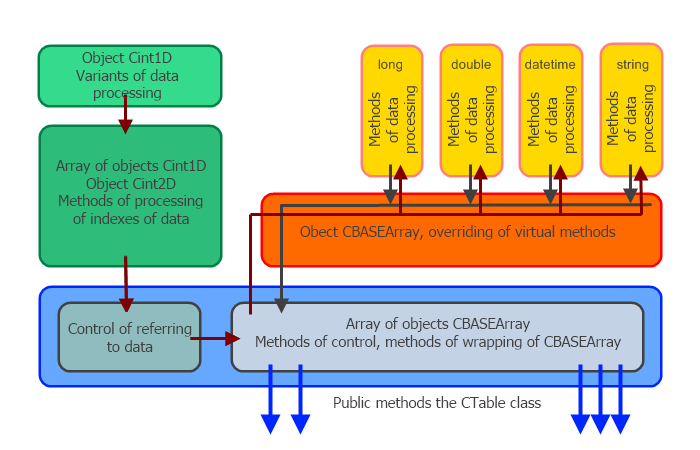
La parte derecha del diagrama de bloques está ocupada principalmente por los métodos sobreescritos situados en las clases derivadas CLONGArray, CDOUBLEArray, CDATETIMEArray y CSTRINGArray. Cada uno de ellos (en la sección privada) contiene una matriz del tipo correspondiente. Esas matrices exactas se utilizan con todos los trucos de acceso a la información. Los nombres de los métodos de las clases enumerados arriba son iguales a los nombres de los métodos públicos.
La clase base CBASEArray se rellena mediante métodos virtuales sobreescritos y es necesaria sólo para la declaración de la matriz dinámica de objetos CBASEArray en la sección privada de la clase CTable. La matriz de punteros CBASEArray está declarada como una matriz dinámica de objetos dinámicos. La construcción final de objetos y la elección del ejemplo necesario se lleva a cabo en la función FirstResize(). También se puede hacer en la función CopyTable(), porque se llama FirstResize() en su cuerpo.
La clase CTable también realiza la coordinación de métodos de procesamiento de datos (situados en las instancias de la clase CTable) y el objeto de controlar los índices de la clase Cint2D. La completa coordinación está envuelta en los métodos públicos sobreescritos.
Las partes repetidas de la sobreescritura en la clase CTable se reemplazan con definiciones para evitar producir líneas muy largas:
#define _CHECK0_ Print(__FUNCTION__+"("+(string)i+","+(string)j+")");return; #define _CHECK_ Print(__FUNCTION__+"("+(string)i+")");return(-1); #define _FIRST_ first_data[aic[i]] #define _PARAM0_ array_index.Ind(j),value #define _PARAM1_ array_index.Ind(j),recipient #define _PARAM2_ element,beg,end,array_index,mode
Por lo tanto, la parte de una forma más compacta:
int QuickSearch(int i,long element,int beg,int end,bool mode=false){if(!check_type(i,TYPE_LONG)){_CHECK_}return(_FIRST_.QuickSearch(_PARAM2_));};
será reemplazada con la línea siguiente mediante el preprocesador:
int QuickSearch(int i,long element,int beg,int end,bool mode=false){if(!check_type(i,TYPE_LONG)){Print(__FUNCTION__+"("+(string)i+")");return(-1);} return(first_data[aic[i]].QuickSearch(element,beg,end,array_index,mode));};
En el ejemplo de arriba, está claro cómo se llama a los métodos de procesamiento de datos (la parte dentro de "return").
Ya he mencionado que la clase CTable no realiza el movimiento físico de datos durante el procesamiento; sólo cambia el valor en el objeto de los índices. Para dar a los métodos de procesamiento de datos una posibilidad de interactuar con el objeto de los índices, se les envía a todas las funciones de procesamiento así como al parámetro array_index.
El objeto array_index almacena la relación de la posición de los elementos de la segunda dimensión. La indexación de la primera dimensión es responsabilidad de la matriz dinámica aic[] que está declarada en la zona privada de la clase de CTable. Proporciona una posibilidad de cambiar la posición de las columnas (por supuesto, no físicamente, pero a través de los índices).
Por ejemplo, al realizar la operación Change(), sólo dos celdas de memoria, que contienen los índices de las columnas, cambian de sitio. Aunque visualmente parece que se mueven de dos columnas. Las funciones de la clase de la Tabla C están bastante bien descritas en la documentación (en algún lugar incluso línea a línea).
Ahora, vamos a pasar a las funciones de las clases heredadas de CBASEArray. Realmente, los algoritmos de estas clases son los algoritmos tomados de las clases estándar. Cogí los nombres estándar para tener una idea de los mismos. La modificación consiste en la devolución indirecta de los valores que usan una matriz de los índices a diferencia de los algoritmos estándar donde se devuelven los valores directamente.
En primer lugar, la modificación se hizo con el ordenamiento rápido. Ya que el algoritmo es de la categoría de los inestables, antes de comenzar el ordenamiento, debemos hacer una copia de los datos, que se pasarán al algoritmo. También añadí la modificación simultánea del objeto de los índices según el modelo de cambio de los datos.
void CLONGArray::QuickSort(long &m_data[],Cint2D &index,int beg,int end,bool mode=0)
Aquí está la parte del ordenamiento del código:
... if(i<=j) { t=m_data[i]; it=index.Ind(i); m_data[i++]=m_data[j]; index.Ind(i-1,index.Ind(j)); m_data[j]=t; index.Ind(j,it); if(j==0) break; else j--; } ...
No hay ninguna instancia de la clase Cint2D en el algoritmo original. Cambios similares se han hecho a otros algoritmos estándar. No voy a describir las plantillas de todos los códigos. Si alguien quiere perfeccionar el código, puede hacer una plantilla del código real reemplazando los tipos reales con la plantilla.
Para escribir las plantillas, usé los códigos de la clase que funciona con el tipo long. En tales algoritmos económicos, los desarrolladores tratan de evitar el uso innecesario de enteros si hay una posibilidad de utilizar int. Es por eso que una variable de tipo long es sin duda un parámetro sobreescrito. Se reemplazan con "templat" cuando se usan las plantillas.
Conclusión
Espero que este artículo sea una buena ayuda para los programadores principiantes cuando estudien el enfoque orientado a objetos, y facilite el trabajo con las informaciones. La clase CTable puede convertirse en una clase base para muchas aplicaciones complejas. Los métodos descritos en el artículo pueden llegar a ser una base para el desarrollo de una clase inmensa de soluciones, ya que implementan un enfoque general para trabajar con los datos.
Además de esto, el artículo demuestra que no tiene fundamento abusar de MQL5. ¿Quería el tipo Variant? Se implementa aquí por medio de MQL5. Por eso, no hay necesidad de cambiar los estándares y debilitar la seguridad del lenguaje. ¡Buena suerte!
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/228
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 MQL5 Wizard: Cómo crear un módulo de gestión de riesgo y dinero
MQL5 Wizard: Cómo crear un módulo de gestión de riesgo y dinero
 MQL5 Wizard: Cómo crear un módulo de señales de trading
MQL5 Wizard: Cómo crear un módulo de señales de trading
 MQL5 Wizard: Cómo crear un módulo de Trailing de posiciones abiertas
MQL5 Wizard: Cómo crear un módulo de Trailing de posiciones abiertas
 Análisis de los gráficos mediante métodos econométricos
Análisis de los gráficos mediante métodos econométricos
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Nikolay, tengo una pregunta.
¿Es posible escribir una tabla de MT5 a Excel en esta forma?
Me interesan esos 2 nombres de macro columnas ("Datos absolutos" y "Datos relativos"), que están resaltados en color. Combinan 3 celdas cada una.
Tal vez quiero mucho de MQL5 en términos de formato de celdas de Excel. Pero y si :-)))
¿Qué significado físico le das a las palabras "combinar 3 celdas"?
En principio se puede, pero sin las 2 filas superiores, los tipos de datos se resumen por columnas, de modo que en una columna para meter cadena y doble no va a funcionar, pero se puede hacer cuando se imprime. O refinar la clase para que contenga cadenas mayúsculas formateadas por separado de la tabla.
La forma más sencilla es crear dos tablas y fusionarlas.
¿Qué significado físico le das a las palabras "combinar 3 células"?
Esto es lo que tenemos ahora:
Lo que me gustaría haber traído ya ....
Se publica un nuevo artículo Tablas electrónicas en MQL5:
Autor: Николай