Electronic Tables in MQL5

Introduction

Usually, electronic tables refer to table processors (applications that store and process data), such as EXCEL. Though the code shown in the article is not so powerful, it can be used as a base class for a full-featured implementation of a table processor. I don't have a purpose to create MS Excel using MQL5, but I want to implement a class for operating with data of different types in a two-dimensional array.

And though the class implemented by me cannot be compared by its performance to a two-dimensional array of single-type data (with direct access to data), the class appeared to be convenient for use. In addition, this class can be considered as an implementation of the Variant class in C++, as a particular case of a table degenerated to one column.

For impatient ones and for the ones who doesn't want to analyze the algorithm of implementation, I'm going to start describing the CTable class from the available methods.

1. Description of the Class Methods

At first, let's consider the available methods of the class with more detailed description of their purpose and principles of using.

1.1. FirstResize

Table layout, description of column types, TYPE[] - array of the ENUM_DATATYPE type that determines row size and types of cells.

void  FirstResize(const ENUM_DATATYPE &TYPE[]);

Practically, this method is an additional constructor that has a parameter. This is convenient for two reasons: first, it solves the problem of passing of a parameter inside the constructor; second, it gives a possibility to pass an object as a parameter, and then perform the necessary division of the array. This feature allows using the class as the Variant class in C++.

The peculiarities of implementation include the fact that despite the function sets the first dimension and the type of data of columns, it doesn't require specifying a size of the first dimension as the parameter. This parameter is taken from the size of the passed array TYPE.

1.2. SecondResize

Changes the number of rows to 'j'.

void  SecondResize(int j);

The function sets a specified size for all arrays of the second dimension. Thus, we can say that it adds rows to a table.

1.3. FirstSize

The method returns the size of the first dimension (length of row).

int   FirstSize();

1.4. SecondSize

The method returns the size of the second dimension (length of column).

int   SecondSize();

1.5. PruningTable

It sets a new size for the first dimension; the change is possible within the start size.

void   PruningTable(int count);

Practically, the function doesn't change the length of row; it only rewrites value of a variable, which is responsible for storing the value of row length. The class contains another variable that stores the actual size of allocated memory, which is set at the initial division of a table. Within the values of this variable, the virtual change of size of the first dimension is possible. The function is meant to cut off an unwanted part when copying one table to another.

1.6. CopyTable

The method of copying one table to another on the entire length of the second dimension:

void   CopyTable(CTable *sor);

The function copies one table to another. It starts the initialization of the receiving table. It can be used as an additional constructor. The internal structure of variants of sorting is not copied. Only size, types of columns and data are copied from the initial table. The function accepts the reference of the copied object of the CTable type as a parameter, which is passed by the GetPointer function. 

Copying of one table to another, a new table is created according to the 'sor' sample.

void   CopyTable(CTable *sor,int sec_beg,int sec_end);

Overriding of the function described above with the additional parameters: sec_beg - starting point of copying the initial table, sec_end - end point of copying (please, don't confuse with the amount of copied data). Both parameters refer to the second dimension. Data will be added to the beginning of the recipient table. Size of the receiving table is set as sec_end-sec_beg+1.

1.7. TypeTable

Returns the type_table value (of the ENUM_DATATYPE type) of the 'i' column.

ENUM_DATATYPE  TypeTable(int i)

1.8. Change

The Change() method performs swapping of columns.

bool   Change(int &sor0,int &sor1);

As is mentioned above, the method swaps columns (works with the first dimension). Since the information is not moved actually, the speed of operation of the function is not affected by the size of the second dimension.

1.9. Insert

The Insert method inserts a column in a specified position.

bool   Insert(int rec,int sor);

The function is the same as the one described above, except it performs pulling or pushing of other columns depending on where the specified column should be moved. The parameter 'rec' specifies where the column will be moved, 'sor' specifies from where it will be moved. 

1.10. Variant/VariantCopy

Then come three functions of the 'variant' series. Memorizing of the variants of table processing is implemented in the class.

The variants remind of a notebook. For example, if you perform sorting by the third column and you don't want to reset data during the next processing, you should switch the variant. To access the previous variant of processing, call the 'variant' function. If the next processing should be based on the result of the previous one, you should copy the variants. On default, one variant with the number 0 is set up.

Setting up of a variant (if there is no such variant, it will be created as well as all the missing variants up to 'ind') and getting the active variant. The 'variantcopy' method copies the 'sor' variant to the 'rec' variant.

void   variant(int ind);
int    variant(); 
void   variantcopy(int rec,int sor);

The variant(int ind) method switches the selected variant. Performs automatic allocation of memory. If the specified parameter is less than the previously specified one, the memory is not reallocated.

The variantcopy method allows copying the 'sor' variant to the 'rec' variant. The function is created for arranging the variants. It automatically increases the number of variants if the 'rec' variant doesn't exist; also it switches to the newly copied variant.

1.11. SortTwoDimArray

The SortTwoDimArray method sorts a table by the selected row 'i'.

void   SortTwoDimArray(int i,int beg,int end,bool mode=false);

The function of sorting of a table by a specified column. Parameter: i - column, beg - starting point of sorting, end - end point of sorting (inclusive), mode - boolean variable that determines direction of sorting. If mode=true, it means that values increase together with indexes ('false' is the default value, because indexes increase from top to bottom of the table).

1.12. QuickSearch

The method performs a quick search of position of an element in the array by the value equal to the 'element' pattern.

int   QuickSearch(int i,long element,int beg,int end,bool mode=false);

1.13. SearchFirst

Searches for the first element that is equal to a pattern in a sorted array. Returns the index of the first value that is equal to the 'element' pattern. It's necessary to specify the type of sorting performed earlier at this range (if there is no such element, it returns -1).

int  SearchFirst(int i,long element,int beg,int end,bool mode=false);

1.14. SearchLast

Searches for the last element that is equal to a pattern in a sorted array.

int   SearchLast(int i,long element,int beg,int end,bool mode=false);

1.15. SearchGreat

Searches for the closest element that is greater than a pattern in a sorted array.

int   SearchGreat(int i,long element,int beg,int end,bool mode=false);

1.16. SearchLess

Searches for the closest element that is less than a pattern in a sorted array.

int  SearchLess(int i,long element,int beg,int end,bool mode=false);

1.17. Set/Get

The Set and Get functions have the void type; they are overridden by four types of data the table works with. The functions recognize the data type, and then if the 'value' parameter doesn't correspond to the column type, a warning is printed instead of assigning. The only exception is the string type. If the input parameter is of the string type, it will be casted to the column type. This exception is made for more convenient transmission of information when there is no possibility of setting a variable that would accept the value of cell.

The methods of setting values (i - index of the first dimension, j - index of the second dimension).

void   Set(int i,int j,long     value); // setting value of the i-th row and j-th column
void   Set(int i,int j,double   value); // setting value of the i-th row and j-th columns
void   Set(int i,int j,datetime value);// setting value of the i-th row and j-tj column
void   Set(int i,int j,string   value); // setting value of the i-th row and j-th column 

Methods of getting values (i - index of the first dimension, j- index of the second dimension).

   //--- getting value
void   Get(int i,int j,long     &recipient); // getting value of the i-th row and j-th column
void   Get(int i,int j,double   &recipient); // getting value of the i-th row and j-th column
void   Get(int i,int j,datetime &recipient); // getting value of the i-th row and j-th column
void   Get(int i,int j,string   &recipient); // getting value of the i-th row and j-th column

1.19. sGet

Gets a value of string type from the 'j' column and 'i' row.

string sGet(int i,int j); // return value of the i-th row and j-th column 

The only function of the Get series that returns the value through the 'return' operator instead of a parametric variable. Returns a value of the string type regardless of the column type.

1.20. StringDigits

When types are casted to 'string', you can use a precision set by the functions:

void  StringDigits(int i,int digits);

to set precision of 'double' and

int   StringDigits(int i);

to set a precision of displaying of seconds in 'datetime'; any value that is not equal to -1 is passed. Specified value is memorized for the column, so you don't need to indicate it each time when displaying information. You can set a precision for many times, since the information is stored in original types and is transformed to the specified precision only during the output. The values of precision are not memorized at copying, thus, when copying a table to a new table the precision of columns of the new table will correspond to the default precision.

1.21. An example of using:

#include <Table.mqh>  
ENUM_DATATYPE TYPE[7]=
  {TYPE_LONG,TYPE_LONG,TYPE_STRING,TYPE_DATETIME,TYPE_STRING,TYPE_STRING,TYPE_DOUBLE};
//     0          1          2            3              4            5            6   //7 
void OnStart()
  {
   CTable table,table1;
   table.FirstResize(TYPE);             // dividing table, determining column types   
   table.SecondResize(5);               // change the number of rows    

   table.Set(6,0,"321.012324568");        // assigning data to the 6-th column, 0 row
   table.Insert(2,6);                   // insert 6-th column in the 2-nd position
   table.PruningTable(3);               // cut the table to 3 columns
   table.StringDigits(2,5);             // set precision of 5 digits after the decimal point
   Print("table ",table.sGet(2,0));       // print the cell located in the 2-nd column, 0 row  

   table1.CopyTable(GetPointer(table));  // copy the entire table 'table' to the 'table1' table
   table1.StringDigits(2,8);            // set 8-digit precision
   Print("table1 ",table1.sGet(2,0));     // print the cell located in the 2-nd column, 0 row of the 'table1' table.  
  }

The result of operation is printing of content of the cell (2;0). As you probably noticed, the precision of copied data doesn't exceed the precision of the initial table.

2011.02.09 14:18:37     Table Script (EURUSD,H1)        table1 321.01232000
2011.02.09 14:18:37     Table Script (EURUSD,H1)        table 321.01232

Now let's move to the description of the algorithm itself.

2. Choosing a Model

There are two ways of organization of information: the scheme of connected columns (implemented in this article) and its alternative in the form of connected rows are shown below.

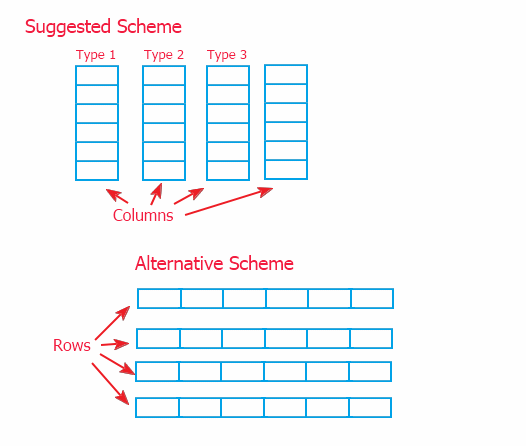
Because of referring to information through an intermediary (described in p. 2), there is no big difference of implementation of the upper scope. But I've chosen the model of columns, since it allows implementing method of data on the low scope, in the objects that store the data. And the alternate scheme would require overriding of methods for working with information in the upper class CTable. And this can complicate enhancing of the class, in case it's necessary.

At that, each of the schemes can be used. The suggested scheme allows quick moving of data, and the alternate one allows more quick adding of data (because information is more often added to a table line by line) and getting of rows.

There is also another way of arranging a table - as an array of structures. And though it's the easiest one to implement, it has a significant disadvantage. The structure must be described by a programmer. Thus, we lose a possibility of setting attributes of the table through via custom parameters (without changing the source code).

3. Uniting Data in a Dynamic Array

To have a possibility of uniting different types of data in a single dynamic array, we need to solve the problem of assigning different types to the array cells. This problem is already solved in connected lists of the standard library. My first developments were based on the standard library of classes. But during the development of project, it appeared that I need to make many changes in the base class CObject.

That's why I decided to develop my own class. For the ones who didn't study the standard library, I'm going to explain, how the problem described above is solved. To solve the problem you need to use the mechanism of inheritance.

class CBase
  {
public:
                     CBase(){Print(__FUNCTION__);};                    
                    ~CBase(){Print(__FUNCTION__);};
   virtual void       set(int sor){};
   virtual void       set(double sor){};
   virtual int        get(int k){return(0);};
   virtual double     get(double k){return(0);};
  };
//+------------------------------------------------------------------+
class CA: public CBase
  {
private:
   int              temp;
public:
                     CA(){Print(__FUNCTION__);};  
                    ~CA(){Print(__FUNCTION__);};
   void              set(int sor){temp=sor;};
   int               get(int k){return(temp);};
  };
//+------------------------------------------------------------------+
class CB: public CBase
  {
private:
   double            temp;
public:
                    CB(){Print(__FUNCTION__);};  
                   ~CB(){Print(__FUNCTION__);};
   void             set(double sor){temp=sor;};   
   double           get(double k){return(temp);};
  };  
//+------------------------------------------------------------------+
void OnStart()
  {
   CBase *a;   CBase *b;  
   a=new CA(); b=new CB(); 
   a.set(15);  b.set(13.3);
   Print("a=",a.get(0)," b=",b.get(0.));
   delete a;
   delete b;
  }

Visually, the mechanism of inheritance can be shown as a comb:

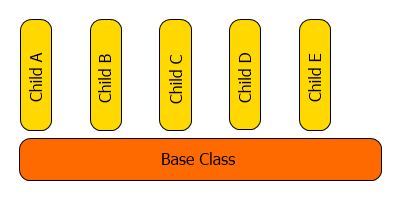
If creation of a dynamic object of the class is declared, it means that the constructor of the base class will be called. This exact property makes it possible to create an object in two steps. As virtual functions of the base class are overridden, we get the possibility of calling the function with different types of parameters from the derived classes.

Why is the simple overriding not enough? The matter is the executed functions are huge, so if we described their bodies in the base class (without using the inheritance), then unused function with the full code of the body would be created for each object in the binary code. And when using the mechanism of inheritance, empty functions, which occupy much less memory than the functions filled with code, are created.

4. Operations with Arrays

Second and the main cornerstone, that made me refuse from using the standard classes, is referring to data. I use indirect referring to array cells through an intermediary array of indexes instead of referring by the indexes of cells. It stipulates a lower speed of working than when using direct referring through a variable. The matter is the variable that indicates an index works faster than an array cell, which needs to be found in the memory, at first.

Let's analyze what is the fundamental difference of sorting a unidimensional and a multidimensional array. Before sorting, a unidimensional array has random positions of elements, and after sorting the elements are arranged. When sorting a two-dimensional array, we don't need the entire array to be sorted, but only one of its columns the sorting is performed by. All rows must change their position keeping their structure.

The rows themselves here are the bound structures that contain data of different types. To solve such problem, we need both to sort data in a selected array and save the structure of initial indexes. In this way, if we know, which row contained the cell, we can display the whole row. Thus, when sorting a two-dimensional array, we need to get the array of indexes of the sorted array without changing the structure of data.

For example:

before sorting by the 2-nd column
4 2 3
1 5 3
3 3 6
after sorting
1 5 3
3 3 6
4 2 3
Initial array looks as following:
a[0][0]= 4; a[0][1]= 2; a[0][2]= 3;
a[1][0]= 1; a[1][1]= 5; a[1][2]= 3;
a[2][0]= 3; a[2][1]= 3; a[2][2]= 6;
And the array of indexes of sorting by the 2-nd column looks as:
r[0]=1;
r[1]=2;
r[2]=0;
Sorted values are returned according to the following scheme:
a[r[0]][0]-> 1; a[r[0]][1]-> 5; a[r[0]][2]-> 3;
a[r[1]][0]-> 3; a[r[1]][1]-> 3; a[r[1]][2]-> 6;
a[r[2]][0]-> 4; a[r[2]][1]-> 2; a[r[2]][2]-> 3;

Thus, we have a possibility of sorting information by symbol, date of opening of position, profit, etc.

A lot of algorithms of sorting are already developed. The best variant for this development will be the algorithm of stable sorting.

The Quick Sorting algorithm, which is used in the standard classes, refers to the algorithms of unstable sorting. That's why it doesn't suit us in its classic implementation. But even after bringing the quick sorting to a stable form (and it is an additional copying of data and sorting of arrays of indexes), the quick sorting appears to be quicker than the bubble sorting (one of the fastest algorithms of stable sorting). The algorithm is very quick, but it uses recursion.

That's the reason why I use Cocktail sort when working with arrays of the string type (it requires much more stack memory).

5. Arrangement of a Two-Dimensional Array

And the last question I want to discuss is the arrangement of a dynamic two-dimensional array. For such arrangement it's enough to make a wrapping as a class for a unidimensional array and call the object-array through the array of pointers. In other words, we need to create and array of arrays.

class CarrayInt
  {
public:
                    ~CarrayInt(){};
   int               array[];
  };
//+------------------------------------------------------------------+
class CTwoarrayInt
  {
public:
                    ~CTwoarrayInt(){};
   CarrayInt         array[];
  };
//+------------------------------------------------------------------+
void OnStart()
  {
   CTwoarrayInt two;
   two.array[0].array[0];
  }

6. Structure of the Program

Code of the CTable class was written using templates described in the Using Pseudo-Templates as Alternative of С++ Templates article. Just because of using templates, I could write such big code so quickly. That's why I'm not going to describe the entire code in details; moreover, the most part of the code of the algorithms is a modification of the standard classes.

I'm just going to show the general structure of the class and some of its interesting features of functions that clarify several important points.

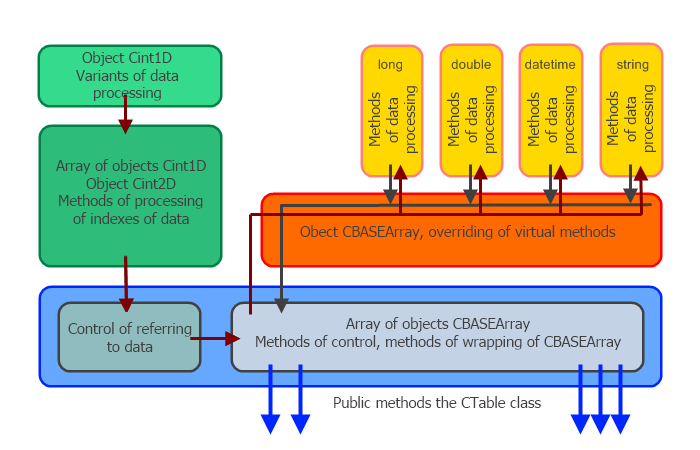
The right part of the block diagram is mainly occupied by the overridden methods located in the derived classes CLONGArray, CDOUBLEArray, CDATETIMEArray and CSTRINGArray. Each of them (in the private section) contains an array of the corresponding type. Those exact arrays are used for all the tricks of access to information. The names of methods of classes listed above are the same as of the public methods.

The base class CBASEArray is filled with overriding of virtual methods and is necessary only for declaration of the dynamic array of objects CBASEArray in the private section of the CTable class. The array of pointers CBASEArray is declared as a dynamic array of dynamic objects. Final construction of objects and choosing of the necessary instance is performed in the FirstResize() function. It also can be done in the CopyTable() function, because it calls FirstResize() in its body.

The CTable class also performs the coordination of methods of data processing (located in the instances of the CTable class) and the object of controlling the indexes of the Cint2D class. The entire coordination is wrapped in the overridden public methods. 

Frequently repeated parts of overriding in the CTable class are replaced with definitions to avoid producing very long lines:

#define _CHECK0_ Print(__FUNCTION__+"("+(string)i+","+(string)j+")");return;
#define _CHECK_ Print(__FUNCTION__+"("+(string)i+")");return(-1);
#define _FIRST_ first_data[aic[i]]
#define _PARAM0_ array_index.Ind(j),value
#define _PARAM1_ array_index.Ind(j),recipient
#define _PARAM2_ element,beg,end,array_index,mode

Thus, the part of a more compact form:

int QuickSearch(int i,long element,int beg,int end,bool mode=false){if(!check_type(i,TYPE_LONG)){_CHECK_}return(_FIRST_.QuickSearch(_PARAM2_));};

will be replaced with the following line by the preprocessor:

int QuickSearch(int i,long element,int beg,int end,bool mode=false){if(!check_type(i,TYPE_LONG)){Print(__FUNCTION__+"("+(string)i+")");return(-1);} return(first_data[aic[i]].QuickSearch(element,beg,end,array_index,mode));};

In the example above, it is clear how the methods of data processing are called (the part inside 'return').

I've already mentioned that the CTable class doesn't perform the physical moving of data during processing; it just changes the value in the object of indexes. To give the methods of data processing a possibility of interacting with the object of indexes, it is passed to all the functions of processing as the array_index parameter.

The array_index object stores the positional relationship of elements of the second dimension. Indexation of the first dimension is the responsibility of the aic[] dynamic array that is declared in the private zone of the CTable class. It gives a possibility of changing the position of columns (of course, not physically, but via indexes).

For example, when performing the Change() operation, only two memory cells, which contain the indexes of columns, change their places. Though visually it looks like moving of two columns. Functions of the CTable class are pretty well described in the documentation (somewhere even line by line).

Now, let's move to the functions of classes inherited from CBASEArray. Actually, the algorithms of these classes are the algorithms taken from the standard classes. I took the standard names to have a notion about them. The modification consists in indirect returning of values using an array of indexes as distinct from the standard algorithms where values are returned directly.

First of all, the modification was made to the Quick sorting. Since the algorithm is from the category of unstable ones, before starting the sorting, we need to make a copy of data, which will be passed to the algorithm. I also added the synchronous modification of the object of indexes according to the pattern of changing the data.

void CLONGArray::QuickSort(long &m_data[],Cint2D &index,int beg,int end,bool mode=0)

Here is the part of the code sorting:

...
            if(i<=j)
              {
               t=m_data[i];            it=index.Ind(i);
               m_data[i++]=m_data[j];  index.Ind(i-1,index.Ind(j));
               m_data[j]=t;            index.Ind(j,it);
               if(j==0) break;
               else     j--;
              }
...

There is no instance of the Cint2D class in the original algorithm. Similar changes are made to the other standard algorithms. I'm not going to describe the templates of all the codes. If anyone wants to improve the code, they can make a template from the real code by replacing the real types with the template.

For writing templates, I used the codes of the class that works with the long type. In such economic algorithms, developers try to avoid unnecessary using of integers if there is a possibility to use int. That's why a variable of the long type is most probably an overridden parameter. They are to be replaced with 'templat' when using the templates.

Conclusion

I hope this article will be a good help for novice programmers when studying the object-oriented approach, and will make working with information easier. The CTable class may become a base class for many complex applications. The methods described in the article may become a basis of development of a huge class of solutions, since they implement a general approach to working with data.

In addition to it, the article proves that abusing MQL5 is groundless. You wanted the Variant type? Here it is implemented by means of MQL5. At that, there is no need to change the standards and weaken the security of the language. Good luck!