Del básico al intermedio: Punto flotante

Introducción

El contenido expuesto aquí tiene un propósito puramente didáctico. En ningún caso debe considerarse una aplicación final, cuyo objetivo no sea el estudio de los conceptos mostrados aquí.

En el artículo anterior, «Del básico al intermedio: Definiciones (II)», hablamos de lo importantes que son las macros y de cómo podemos hacer un buen uso de ellas, esto con el objetivo de hacer nuestro código aún más legible.

Pues bien, con base en todo lo que ya se ha visto hasta ahora, ya tenemos material suficiente y también medios adecuados para explicar una cosa: cómo funcionan los números de punto flotante. Sé que muchos creen que valores del tipo double o del tipo float son la mejor elección en diversas situaciones. Sin embargo, existe un problema con este tipo de número que pocas personas, si no casi nadie fuera del círculo de la programación, realmente comprende.

Y como este tipo de número es muy utilizado aquí en MQL5, por esta razón, ya que trabajamos con información donde el punto flotante es casi un consenso, es necesario entender muy bien cómo este tipo de valor es procesado por la CPU.

¿Y por qué estoy diciendo esto? Es claro que los números con valores fraccionados, como por ejemplo 2.5, siempre se entienden muy bien, ya que nadie va a confundir este tipo de valor con cualquier otro. Pero, mi querido lector, cuando se trata de computación, las cosas no son así. Los números en punto flotante son, de hecho, algo bastante útil en diversas situaciones. Sin embargo, no deben ser considerados o entendidos de la misma forma que los números enteros.

Básicamente, muchos de ustedes deben estar acostumbrados a lidiar con punto flotante en dos tipos de notación: la científica, donde escribimos los valores como, por ejemplo, 1-e2, y la más común, que es la aritmética, donde escribimos los valores como 0.01. Ambos valores son iguales en magnitud, pero escritos de forma diferente. Así como también existe la forma fraccionaria de escribir este mismo valor, que sería 1/100.

Nota que, en todos los casos, estamos hablando del mismo valor. Pero a pesar de ello, los distintos programas o lenguajes de programación manejan estos valores de forma diferente.

Un poco de historia

Al inicio de la computación, los números de punto flotante, tal como se conocen actualmente, no existían —o, mejor dicho, no existía una forma estandarizada de manejarlos. Cada programador, cada sistema operativo o incluso cada programa trataba este tipo de número de manera muy particular y personal.

Durante los años entre 1960 y 1970, no existía una forma de que un programa se comunicara con otro hasta el punto de compartir y agilizar la factorización de tales valores. Solo imagina: en pleno inicio de la era espacial, donde tales números serían de suma importancia, NO ERA POSIBLE calcular valores de punto flotante en los ordenadores de la época. Y, cuando tal posibilidad existía, no era posible dividir la tarea entre más ordenadores con el fin de efectuar los cálculos de forma más rápida.

Entonces, IBM, que era quien tenía casi la totalidad del mercado, comenzó a proponer una forma de representar este tipo de valor. Pero el mercado no siempre acepta lo que se le propone. Así que otros fabricantes crearon sus propias maneras de representar tales valores. Era un verdadero CAOS. Hasta que, en un momento dado, el Instituto de Ingenieros Eléctricos y Electrónicos (IEEE) comenzó a poner orden en la casa, estableciendo así lo que se conoce como el estándar IEEE 754. Al final de este artículo, en las referencias, dejaré algunos enlaces para quien tenga interés en profundizar en el tema.

El primer estándar establecido fue el IEEE 754-1985, como una forma de intentar resolver toda esta cuestión. Hoy en día ya utilizamos un estándar mucho más actual, pero todo está basado en aquel patrón establecido inicialmente.

Un detalle importante: a pesar de existir este estándar, con el fin de normalizar y permitir una factorización distribuida, existen casos en los que este estándar no se utiliza, y la computación —o, mejor dicho, la factorización— se realiza siguiendo otros criterios, que no veremos aquí, ya que se salen completamente del tema. Esto se debe a que MQL5 hace uso, al igual que diversos otros lenguajes, de este mismo estándar IEEE 754.

Al principio, la CPU no conseguía manejar este tipo de cálculo, por lo que existía una CPU que era conocida, en aquella época, como FPU, únicamente para este objetivo. Esta FPU se compraba por separado, ya que su costo no siempre justificaba su utilización. Un ejemplo de FPU sería el 80387. Y sí, no lo escribí mal. El modelo, de hecho, se parece mucho al conocido 80386, popularmente llamado 386. Pero esto era más una cuestión de marketing de Intel, para diferenciar la CPU, que sería el 80386, de la FPU, que sería el 80387. El ordenador podía trabajar solo con la CPU, pero no únicamente con la FPU, ya que esta estaba diseñada solo para realizar los cálculos de punto flotante.

Bien, pero ¿cuál es el problema del punto flotante? ¿Por qué un artículo solo para hablar de esto? El motivo es que, sin entender cómo funciona el punto flotante, puedes terminar cometiendo una serie de errores. No debido a una programación deficiente, sino por imaginar que los cálculos realizados deben tomarse al pie de la letra, cuando, en realidad, el simple hecho de utilizar el estándar IEEE 754 genera un error potencial en el valor final que estaría siendo calculado.

Esto puede parecer un absurdo, ya que los ordenadores son máquinas que siempre deberían presentarnos valores precisos. Decir que existe un error en el resultado de una operación no parece algo tangible, ni mucho menos aceptable. Dado que el objetivo es operar en el mercado de capitales usando tales datos, y, si nuestros cálculos están equivocados, podríamos estar perdiendo dinero, incluso cuando todo indica que deberíamos estar ganando. Y es precisamente por esta razón que este artículo es importante.

Hay una serie de cosas relacionadas con el punto flotante que, para lo que vamos a hacer, no tienen mucha relevancia. Pero hay una cosa que sí es muy importante y que marca toda la diferencia, que es el redondeo.

Sé que muchos dicen, o incluso se jactan diciendo: 

Pero yo no hago redondeo en mis cálculos. Son siempre exactos y precisos.

Pero es precisamente esta idea la que, a mi entender, demuestra una completa y total falta de comprensión sobre programación, que lleva a las personas a imaginar algo, cuando, en realidad, las cosas no son como parecen. El redondeo no necesita ser hecho por el programador. Simplemente existe, independientemente de que el programador quiera o no realizarlo. Por eso, es importante que veas las referencias que dejaré al final del artículo, ya que esta cuestión del punto flotante no es algo que pueda explicarse en un simple artículo. Recuerda: hay profesionales trabajando en esto desde los inicios de la computación.

Lo que vamos ver aquí es otro tipo de cosa, mucho más simple y enfocada precisamente en entender qué es un double o float, ya que todos los demás tipos son mucho más simples y fueron explicados en los artículos anteriores.

Representación de un punto flotante

Bien, aquí vamos a hablar del tipo realmente utilizado en MQL5. En este tipo, básicamente seguimos lo que propone el IEEE 754, teniendo dos formatos —o, mejor dicho, dos precisiones diferentes. Y sí, lo correcto, cuando hablamos de punto flotante, es decir “precisión” y no “formato” ni “número de bits involucrados”. Pero, para que no resulte demasiado confuso —ya que, por sí sola, puede ser serlo para muchos— aquí vamos a utilizar el término “número de bits” únicamente para permitir una mejor comprensión por parte de la gran mayoría, además de hacer más sencilla la explicación que se va a dar. Pues creo que no estoy hablando con ingenieros o personas de ese calibre, con un amplio y vasto conocimiento en electrónica o desarrollo de chips, sino con personas interesadas y sedientas de conocimiento sobre programación en MQL5.

Pues bien, para comenzar, vamos a ver un código muy simple. Sin embargo, aunque sea simple, para poder entenderlo es necesario que hayas asimilado el conocimiento presente en los artículos anteriores. Así que, vamos a ello.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define typeFloating float
05. //+----------------+
06. void OnStart(void)
07. {
08.     union un_1
09.     {
10.         typeFloating v;
11.         uchar arr[sizeof(typeFloating)];
12.     }info;
13. 
14.     info.v = 741;
15. 
16.     PrintFormat("Floating point value: [ %f ] Hexadecimal representation: [ %s ]", info.v, ArrayToHexadecimal(info.arr));
17. }
18. //+------------------------------------------------------------------+
19. string ArrayToHexadecimal(const uchar &arr[])
20. {
21.     const string szChars = "0123456789ABCDEF";
22.     string sz = "0x";
23. 
24.     for (uchar c = 0; c < (uchar)arr.Size(); c++)
25.         sz = StringFormat("%s%c%c", sz, szChars[(uchar)((arr[c] >> 4) & 0xF)], szChars[(uchar)(arr[c] & 0xF)]);
26. 
27.     return sz;
28. }
29. //+------------------------------------------------------------------+

Código 01

Bien, mi querido lector, este código es muy interesante, además de ser bastante curioso y divertido de experimentar con él. A pesar de todo, aquí estamos haciendo solo la primera parte de lo que realmente queremos e haremos.

Presta atención: en la línea cuatro, indicamos qué tipo de valor estaremos usando como punto flotante. Podemos decir que queremos el tipo double o float. La diferencia entre uno y otro es precisamente la precisión que cada uno nos permite obtener. Pero, antes de entrar en esos detalles, vamos a entender qué está haciendo este código.

Muy bien, hecha la declaración del tipo, podemos usar una unión para crear una forma de leer la memoria. Para esto, usamos la línea ocho. Ya dentro de la unión, usamos la línea 10 para crear una variable y la línea 11 para un array compartido. Este tipo de cosas ya se han visto y explicado en artículos anteriores. Revisa los mismos para más detalles, en caso de que no estés entendiendo lo que está ocurriendo aquí y cuál es el propósito de la creación de esta unión.

Ya la línea más importante aquí para nosotros es precisamente la línea 14, pues en ella declaramos el valor que queremos visualizar. Y la línea 16 solo nos proporcionará la forma de mostrar el contenido de la memoria, como es nuestro deseo actual, ya que queremos entender cómo un valor en punto flotante está representado en la memoria hasta el punto de que el ordenador consiga comprenderlo.

Muy bien, al ejecutarse, este código 01 nos presentará el resultado mostrado en la imagen de abajo.

Imagen 01

Hum... ¿Qué cosa extraña es esta que estamos viendo como representación hexadecimal? Bien, mi querido lector, esta es la forma en que el ordenador, usando la norma IEEE 754, interpreta un valor en punto flotante. Un detalle importante: este valor se está escribiendo como un valor que sigue el modelo Little Endian. Más adelante, hablaremos más sobre qué representa este modelo. Pero, por ahora, solo necesitas entender lo siguiente: este valor hexadecimal está escrito al revés, y debe leerse de derecha a izquierda.

Bien, de todas formas, tal vez no lo estés creyendo. Así que podemos usar otro programa solo para dejar esto claro. Vamos a utilizar un editor hexadecimal. HxD es un editor simple y gratuito. Si escribes los valores mostrados en el campo hexadecimal de la imagen 01, los seleccionas y ves qué valor está siendo representado allí, encontrarás una imagen parecida a la que se muestra más abajo.

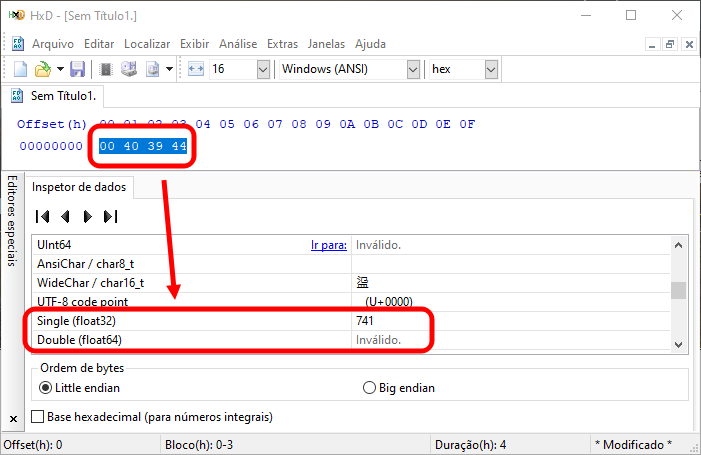
Imagen 02

Observa que, de hecho, tenemos el valor esperado que puede ser visualizado allí. Sin embargo, a mí, en particular, me gusta usar una extensión de mi plataforma de desarrollo para ver este tipo de cosa —esto para evitar tener varios programas instalados en la máquina. Aunque HxD no necesita ser instalado. De cualquier forma, lo que podemos ver está mostrado en la siguiente imagen.

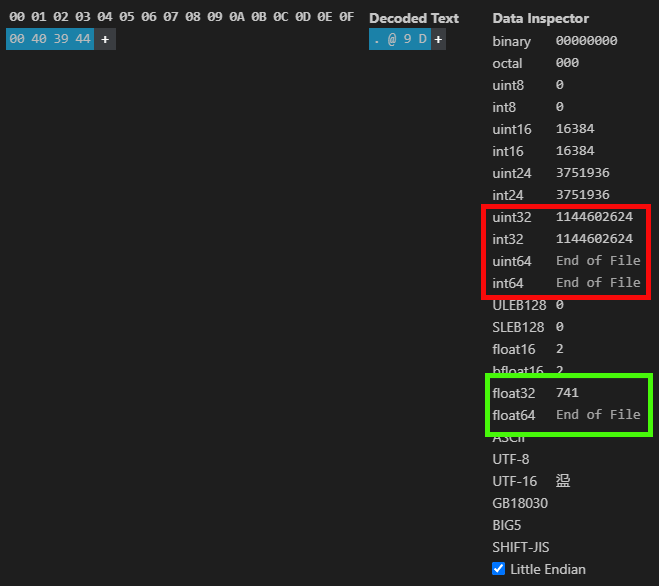
Imagen 03

Este tipo de información que estás viendo aquí también puede verse tanto en MetaTrader 5 como en HxD. Pero quiero que observes lo que estoy mostrando en esta imagen 03. Nota que un mismo valor en punto flotante representa otro valor en entero. Pero ¿por qué es esto? El motivo es que, para el ordenador, da igual si es entero u otro tipo cualquiera —para él, no hace diferencia. Sin embargo, para nosotros, y para el compilador, un tipo u otro puede hacer que recibamos una respuesta plausible o una completamente extraña.

Pero este caso que vimos en este código 01 es un ejemplo simple. Vamos a cambiar el código 01 por un ejemplo un poco diferente. Este se ve justo abajo.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. // #define Floating_64Bits
05. //+----------------+
06. #ifdef Floating_64Bits
07.     #define typeFloating double
08. #else
09.     #define typeFloating float
10. #endif
11. //+----------------+
12. void OnStart(void)
13. {
14.     union un_1
15.     {
16.         typeFloating v;
17. #ifdef Floating_64Bits
18.         ulong integer;
19. #else
20.         uint integer;
21. #endif
22.         uchar arr[sizeof(typeFloating)];
23.     }info;
24. 
25.     info.v = 42.25;
26. 
27.     PrintFormat("Using a type with %d bits\nFloating point value: [ %f ]\nHexadecimal representation: [ %s ]\nDecimal representation: [ %I64u ]",
28. #ifdef Floating_64Bits
29.         64,
30. #else
31.         32,
32. #endif
33.         info.v, ArrayToHexadecimal(info.arr), info.integer);
34. }
35. //+------------------------------------------------------------------+
36. string ArrayToHexadecimal(const uchar &arr[])
37. {
38.     const string szChars = "0123456789ABCDEF";
39.     string sz = "0x";
40. 
41.     for (uchar c = 0; c < (uchar)arr.Size(); c++)
42.         sz = StringFormat("%s%c%c", sz, szChars[(uchar)((arr[c] >> 4) & 0xF)], szChars[(uchar)(arr[c] & 0xF)]);
43. 
44.     return sz;
45. }
46. //+------------------------------------------------------------------+

Código 02

Muy bien, este código 02 parece ser más complicado. Sin embargo, es tan simple como el código 01, solo que en él tenemos la oportunidad de decir algunas cosas extras sobre cómo se nos presentará el punto flotante. Esto porque, gracias a la línea cuatro, podemos seleccionar si queremos usar un tipo con precisión simple o precisión doble. Pero, al ejecutarse el código, como se muestra arriba, obtendremos como respuesta lo que se ve a continuación.

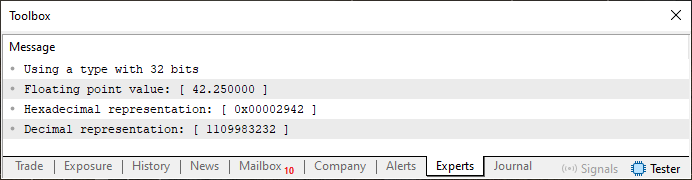
Imagen 04

Y, de la misma forma que vimos antes, al usar los valores informados y vistos en la imagen 04, obtenemos el resultado que se ve en la siguiente imagen.

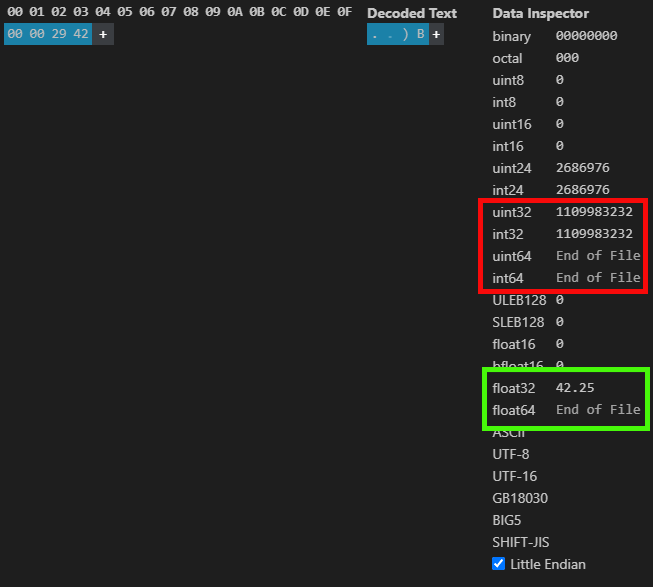
Imagen 05

Es decir, de hecho, algo está ocurriendo aquí. Pero ¿cómo funciona este sistema IEEE 754? Bien, mi querido lector, para explicar esto necesitamos recurrir a una visualización más interna del propio sistema. Trataré de no complicar demasiado las cosas, ya que eso acabaría por destruir cualquier intento de explicar y de que tú comprendas lo que ocurre aquí. Pero, básicamente —y actualmente— tenemos dos formatos IEEE 754: uno para precisión simple, donde usamos 32 bits, y otro para precisión doble, donde usamos 64 bits. La diferencia entre uno y otro no está en que uno sea más exacto que el otro; la diferencia está en el rango que podemos utilizar. Por eso, el término “precisión” muchas veces resulta algo engañoso. Así que prefiero no utilizar ese término, a pesar de ser el término correcto.

En la imagen justo abajo, puedes observar los dos tipos que son definidos por el estándar.

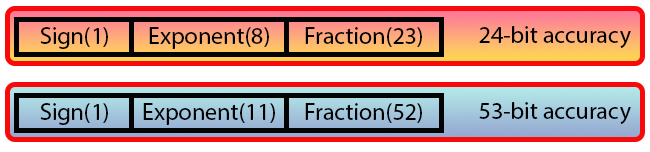
Imagen 06

Pero espera un poco... ¿No dijiste que usamos 32 bits para un tipo y 64 para otro? Pero aquí parece que estamos utilizando algo que no tiene mucho sentido. ¿Qué son todos estos datos y valores que podemos ver en la imagen 06? Bien, esta es la forma en que un valor en punto flotante es representado por la norma IEEE 754. Aquí, cada uno de los valores que puedes observar son BITS. Nota que tenemos unidades con un ancho diferente al usual visto hasta aquí. Sin embargo, esto no nos impide entender tal sistema. Aunque el mismo sería más sencillo de explicar si se usara C o C++. Esto porque, en MQL5, no tenemos medios de nombrar bit a bit —cosa que sí se puede hacer en C o C++. Sin embargo, podemos usar macros y definiciones para acercarnos a lo que se haría en C o C++.

Entonces, voy a intentar explicar esto aún en este artículo. Si no es posible, haré otro artículo para permitir una explicación adecuada. No quiero explicar la cosa de manera superficial. Quiero que tú, mi querido lector, comprendas qué tipo de problema existe cuando usamos punto flotante en nuestros códigos. Pues veo a mucha gente afirmar y creer que podemos calcular cosas que, en realidad, no podemos. Porque existe un pequeño desvío entre el resultado esperado y el resultado calculado, generando así problemas cuando no estamos debidamente preparados para ellos.

Vamos a comenzar entendiendo lo siguiente: si tú sumas la cantidad de bits mostrados en la imagen 06, notarás que el primer formato contiene 32 bits y el segundo, 64 bits. Aquí empiezan las preguntas. Entonces, para simplificar, vamos a enfocarnos en solo uno de los formatos, ya que la diferencia entre uno y otro tiene que ver con el valor usado en el ajuste. Pero hablaremos de eso más adelante.

El bit que, en la imagen 06, aparece como Sign es el bit de signo. Es decir, es el que indica si un valor es negativo o positivo, tal como sucede en los tipos enteros, donde el bit más a la izquierda nos indica si el valor es negativo o positivo.

Bien, siguiendo este bit Sign, tenemos ocho bits con el nombre de Exponent. Este valor genera un bias de 127, que codifica el exponente. En el caso de una precisión doble, tenemos once bits, que generan un bias de 1023. Observa que, a pesar del nombre “precisión doble”, el bias es mucho mayor.

Pero la parte que de hecho nos interesa es la que viene justo después, que es el campo Fraction. Este campo es el que genera la precisión del valor que será representado. Nota que, en el caso de 32 bits, tenemos 23 bits en este campo, lo que nos da una precisión de 24 bits. Y, en el caso de la precisión doble, tenemos 52 bits en este campo, lo que nos da una precisión de 53 bits. Nuevamente, el valor es más del doble que el anterior y, por esta razón, una vez más, este término “precisión doble” resulta algo engañoso.

Pero, si profundizas en esta cuestión de los números en punto flotante, verás que este campo que aquí llamamos Fraction es conocido como mantisa, siendo esta la parte interesante en la creación de valores en punto flotante.

Hay una serie de cosas involucradas aquí, pero, para hacer las cosas agradables —ya que muchos pueden acabar desanimándose al ver ciertos detalles implicados—, vamos a un ejemplo práctico. En el código 01, usamos, en la línea 14, el valor 741 y lo transformamos en un valor de punto flotante. En este caso, un valor de 32 bits, es decir, precisión simple. Así, podemos usar el modelo en naranja de la imagen 06. Quiero que procures enfocarte en lo que será mostrado para entender este modelo simple primero.

Bien, para empezar, necesitamos transformar este valor 741 en binario. Para hacer esto, podemos usar diversos medios. Sin embargo, lo que muchos consideran más simple es justamente usar la división por dos. Un detalle: si no sabes cómo convertir un número en binario, no te preocupes, ya que este primer valor es más simple. Será fácil entender cómo hacerlo. En la imagen 07, vista justo abajo, vemos cómo se hace esto.

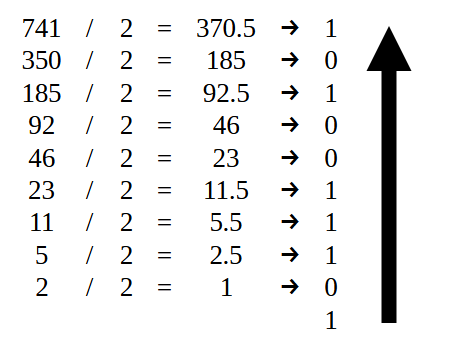
Imagen 07

Una vez hechas las divisiones, tenemos, al final, una serie de ceros y unos. Pero, para que el valor sea escrito correctamente, necesitamos escribirlo conforme se muestra con la flecha. Con esto, obtenemos lo que se ve en la imagen de abajo.

Imagen 08

Bien, esa es la primera parte: lograr llegar a esta imagen 08. Una vez hecho esto, podemos pasar a la segunda fase, que es precisamente transformar este valor binario en un valor de punto flotante. Ahora, presta atención, porque este es el caso más simple que existe. Sin embargo, necesita ser muy bien entendido para poder comprender casos más complicados.

Necesitamos crear nuestra mantisa, es decir, la parte fraccionaria. Para hacer esto, debemos desplazar la coma —que está en el extremo derecho— de forma implícita hacia la izquierda. Esto, de manera que tengamos solo un bit con valor igual a uno a la izquierda. Esto generará lo que se ve en la imagen de abajo.

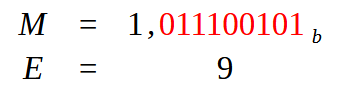
Imagen 09

Ahora observa lo siguiente: M es lo que sería nuestra mantisa, o sea, la parte fraccionaria del punto flotante. E sería nuestro exponente. Pero ¿de dónde surge este valor igual a nueve? Bien, surge del hecho de que tenemos nueve valores en rojo en la mantisa. Pero este valor nueve aún necesita ser trabajado. Y aquí es donde surge la tercera fase de la transformación. Pues, dependiendo de la elección que hagamos, trabajaremos este valor nueve de una forma u otra, generando así valores diferentes. Esto, para representar el punto flotante en términos de información hexadecimal.

Pero, antes de ver qué haremos con este valor nueve, vamos a entender cómo se crea la parte fraccionaria del punto flotante.

¿Recuerdas que tenemos 23 bits para un valor de precisión simple y 52 bits para un valor de precisión doble? ¿Pero que la precisión era de 24 bits para la precisión simple y 53 para la precisión doble? Pues bien, aquel uno que puedes observar en negro en la imagen 09 es precisamente el bit extra que aparece aquí. Es decir, NO ESTÁ PRESENTE, pero está implícito en el campo Fraction. Con esto, tenemos el campo Fraction creado de la siguiente manera:

Imagen 10

La cantidad de ceros en verde en esta imagen 10 depende de la cantidad de bits en el campo Fraction. Pero habrá tantos ceros como sean necesarios para completar todo el resto del campo. Así, ya tenemos la parte fraccionaria del valor en punto flotante. Nos falta la parte del exponente. Como el valor es positivo, tenemos que el campo Sign será igual a cero. Para crear la parte del exponente, necesitamos ver el tipo de precisión que estamos utilizando. Si se trata de una precisión simple, sumaremos el valor E, visto en la imagen 09 —que, en este caso, es nueve— con el valor del bias, que en este caso sería 127. Con esto, obtenemos el valor de 136. Esta operación se muestra en la imagen justo abajo.

Imagen 11

Ahora, finalmente, podemos construir el valor de precisión simple para representar 741 en formato de punto flotante. Este valor se muestra justo abajo.

Imagen 12

Separando estos bits de la imagen 12, con el fin de construir la representación en hexadecimal, tenemos lo que se ve en la imagen 13, justo a continuación.

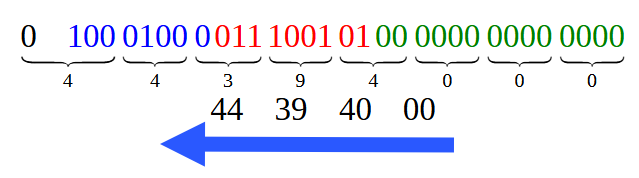
Imagen 13

Observa que cada uno de estos valores en hexadecimal, vistos en esta imagen 13, son los mismos que podemos visualizar en la imagen 01. Sin embargo, debes recordar leerlos conforme a la indicación de la flecha, esto por un detalle que veremos en otro artículo futuro. Esto se debe a un detalle que veremos en un próximo artículo. Bien, este es el caso más simple de todos. Sin embargo, en este artículo vimos otro caso un poco más complicado —si es que podemos decirlo así— que es el caso visto en el código 02, donde tenemos, de hecho, un valor con punto decimal. Y, en esta situación, ¿cómo deberíamos proceder?

Bien, mi querido lector, cuando tenemos un punto decimal siendo utilizado en el valor numérico, la cosa es un poco diferente —pero no tanto. La verdad es que, en este caso, necesitamos dividir lo que sería la etapa de conversión a binario en dos partes: una para la parte a la izquierda del punto decimal y otra para la parte a la derecha del punto decimal. arece complicado, ¿no es así? Pero, en la práctica, es bastante simple y directo, basta con que prestes atención a lo que estás haciendo.

Para comenzar, la parte que esté a la IZQUIERDA del punto decimal deberá hacerse como en la imagen 07. Es decir, debemos usar solo el valor 42, como se ve justo abajo.

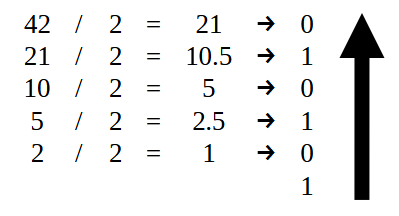
Imagen 14

Ya la parte que esté a la DERECHA del punto decimal deberá hacerse conforme puede verse en la imagen 15. Es decir, el 0.25 —ahora vamos a convertir a binario la parte decimal del valor que está en el código 02.

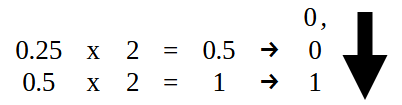
Imagen 15

Esto resulta en lo que es la representación justo debajo del valor 42.25 en binario.

Imagen 16

Presta mucha, pero mucha atención al hecho de que, en esta imagen 16, YA TENEMOS UNA COMA indicada allí. Esto cambiará ligeramente lo que se hará en los próximos pasos —básicamente, lo que sería el paso visto en la imagen 09, donde buscamos el valor de la mantisa y del exponente. Como aquí, en la imagen 16, ya tenemos una coma indicada, todo lo que necesitamos es desplazarla de forma que podamos tener solo —y únicamente— un único bit con el valor uno en el extremo izquierdo. De la misma forma que ocurrió en la imagen 09. Con esto, tenemos el siguiente resultado, visto en la imagen justo a continuación.

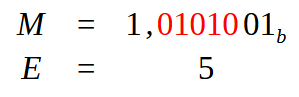
Imagen 17

Observa que, aquí en la imagen 17, los valores en rojo son exactamente los que fue necesario desplazar para lograr llevar la coma a la posición correcta. Con esto, tenemos que el valor de ajuste para el exponente será igual a cinco. Así como también ya tenemos el valor de la mantisa, que se utiliza para generar la parte del campo Fraction. Entonces, calculando el valor para una precisión simple, tenemos lo que se muestra justo abajo.

Imagen 18

Observa que el valor hexadecimal que fue encontrado es exactamente el valor mostrado en la imagen 04. Recordando, por supuesto, que necesitas leerlo siguiendo la flecha, en grupos de dos en dos. De acuerdo, pero ¿tendríamos el mismo resultado si se utilizara la precisión doble? Es decir, si hiciéramos que la línea cuatro del código 02 no fuera un comentario, de modo que esa directiva se utilizara, estaríamos usando 64 bits en lugar de 32 bits, utilizando así la precisión doble en el sistema.

Entonces, en ese caso, ¿tendríamos el mismo dato que vemos en la imagen 18? Bien, sería más o menos eso, mi querido lector. En realidad, la parte fraccionaria se mantendría —claro que necesitaríamos añadir más ceros para completar los demás bits y así llenar los 52 bits que la parte fraccionaria exigiría en este caso. Sin embargo, la parte del exponente sería bastante diferente. Esto se debe al hecho de que, en lugar de utilizar 127 para ajustar el exponente, necesitaríamos utilizar el valor de 1023. Así, la única parte que sería visiblemente modificada en la imagen 18 es precisamente la parte mostrada en azul. Para dejar esto más claro, observa en la imagen de abajo cómo sería la representación del valor en el caso de que usáramos la precisión doble.

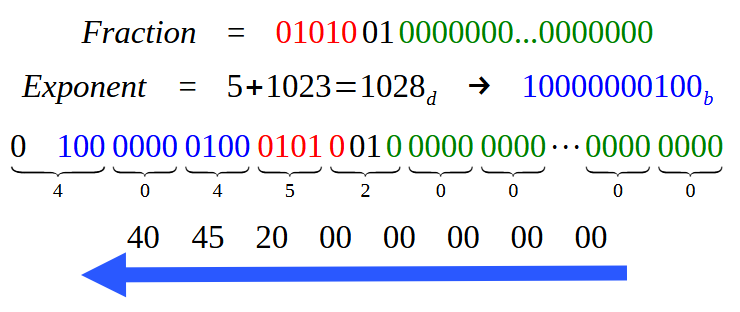
Imagen 19

Y, para comprobar si está o no correcta esta nuestra estimación, ejecutamos el código 02 con el cambio propuesto, y el resultado es el que se muestra a continuación.

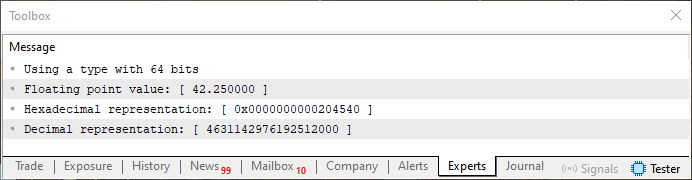
Imagen 20

Consideraciones finales

En este artículo, que es solo una breve introducción a lo que serían los puntos flotantes, vimos cómo se representa un punto flotante dentro de la memoria y cómo podemos trabajar con este tipo de valor. Sé que, en este momento, puedes estar algo confundido respecto a varias cosas sobre puntos flotantes, mi querido lector. No es para menos. Yo mismo, al principio, tardé algún tiempo en lograr comprender cómo se creaba este tipo de dato, pero principalmente cómo efectuar cálculos usando tales informaciones. Aunque no es mi objetivo principal aquí, quién sabe, en un futuro momento, pueda explicar cómo ocurren los cálculos usando puntos flotantes. Pues es algo, de hecho, muy interesante —aún más utilizando el estándar IEEE 754.

Claro que existen otros formatos y maneras de representar números que contienen punto decimal. Sin embargo, como MQL5, al igual que diversos otros lenguajes de programación, hace uso de lo que se ha visto aquí en este artículo, es conveniente que procures entender y estudiar con calma este tipo de dato. Ya que este, muchas veces, no representa exactamente el valor que estamos calculando. Y te sugiero que veas las referencias que estoy incluyendo y busques estudiar cómo se realiza el redondeo para valores en punto flotante, pues existen reglas para ello, y no se hace de cualquier manera.

No obstante, esto queda como algo que cada uno deberá procurar saber. Ya que, con base en lo que se ha mostrado aquí, ya podremos trabajar con este tipo de valor. Dado que estas partes extras —como saber cómo se hace el redondeo y qué valores pueden o no ser representados aquí— son algo necesario solo para quien realmente desea una buena precisión y exactitud en los valores utilizados en sus aplicaciones. Cosa que, aquí, no será de hecho necesaria.

Referencias:

• 754
• Trabajo con modelos ONNX en formatos float16 y float8