Análisis angular de los movimientos de precios: un modelo híbrido para predecir los mercados financieros

Imagínese a un alpinista experimentado al pie de una montaña, escrutando sus laderas antes de empezar a subir. ¿Qué es lo que ve? Pues ve no solo un montón caótico de rocas y salientes, sino la geometría de la ruta: los ángulos de ascenso, la inclinación de las laderas y las curvas de las crestas. Precisamente estas características geométricas del terreno determinarán la dificultad del camino hacia la cumbre.

El mundo de los mercados financieros se parece mucho a un paisaje montañoso. Los gráficos de precios crean su propia topografía, con picos, valles, pendientes suaves y precipicios. Y al igual que un alpinista lee una montaña basándose en su geometría, un tráder experimentado percibe intuitivamente la importancia de los ángulos de inclinación de los movimientos del precio. Pero, ¿y si esa intuición pudiera convertirse en una ciencia exacta? ¿Y si los ángulos de los movimientos del precio no son solo imágenes visuales, sino indicadores matemáticamente significativos del futuro?

En mi tranquilo despacho de tráder algorítmico, alejado del ruido de los parqués, me hice exactamente esta pregunta. Y la respuesta fue tan intrigante que cambió mi visión de la naturaleza de los mercados.

La anatomía del movimiento de precios

Cada día nacen miles de velas en los gráficos de pares de divisas, acciones y futuros. Estas se pliegan en patrones, forman tendencias, crean apoyos y resistencias. Pero bajo estas imágenes familiares se esconde una esencia matemática que rara vez notamos: los ángulos entre los sucesivos puntos de precio.

Eche un vistazo al gráfico normal del EURUSD. ¿Qué ve? ¿Líneas y barras? Imagine ahora que cada segmento entre dos puntos consecutivos forma un determinado ángulo con el eje horizontal. Este ángulo tiene un significado matemático preciso. Un ángulo positivo indica un movimiento ascendente, mientras que un ángulo negativo indica un movimiento descendente. Cuanto mayor sea el ángulo, más pronunciado será el movimiento del precio.

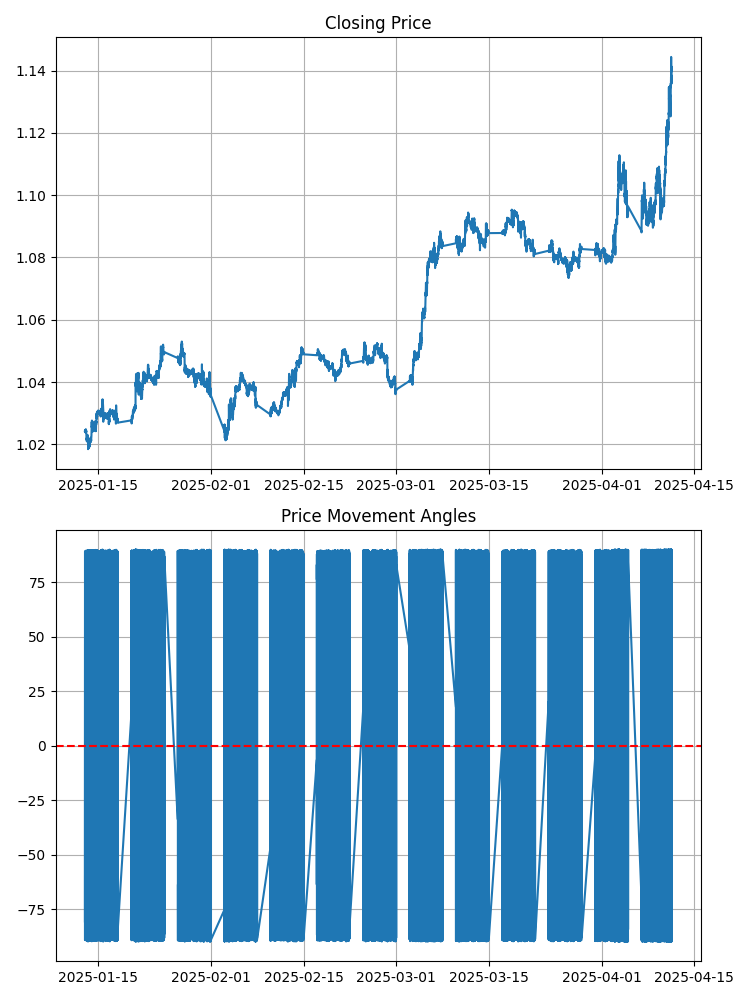
¿Suena fácil? Pues en esa sencillez reside una sorprendente profundidad, porque los ángulos no son iguales entre sí: forman su propio patrón, su propia melodía, y resulta que esa melodía encierra las claves del futuro movimiento del mercado.

Los tráders llevan décadas estudiando las inclinaciones de las líneas de tendencia, pero se trata solo de una estimación aproximada. Por otra parte, estamos hablando de los ángulos matemáticos exactos entre cada dos puntos de precio consecutivos. Es como la diferencia entre un dibujo aproximado de una montaña y su mapa topográfico detallado con los ángulos de inclinación exactos de cada ladera.

Análisis angular de Gann: del clásico a la innovación

La idea de usar ángulos para analizar los movimientos de los precios no es nueva. Sus orígenes se remontan a los trabajos del legendario tráder y analista William Delbert Gann, quien a principios del siglo XX propuso su sistema de análisis angular de los mercados financieros: aquí crearemos un indicador basado en él.

Me familiaricé con el concepto propuesto por Gann hace muchos años, mientras estudiaba obras clásicas sobre análisis técnico. La sola idea me fascinaba: Gann sostenía que existe una relación matemática entre el precio y el tiempo que puede expresarse a través de los ángulos de inclinación de las líneas especiales en un gráfico. Creía que estos ángulos tenían un poder de predicción casi místico, e incluso desarrolló un sistema completo, llamado "ángulos de Gann", expresado como líneas trazadas en determinados ángulos desde puntos importantes del gráfico.

Sin embargo, el enfoque clásico de Gann presentaba dos importantes deficiencias. En primer lugar, era demasiado subjetivo: diversos analistas podían interpretar las mismas construcciones angulares de formas completamente distintas. En segundo lugar, su sistema se diseñó para gráficos de papel con una escala específica, lo que hace problemática su aplicación en los análisis digitales modernos.

La idea nunca me abandonó: ¿y si Gann tenía razón en su concepto básico, pero simplemente no disponía de las herramientas informáticas modernas? ¿Y si su intuición sobre el significado de los ángulos es correcta, pero este requiere un enfoque matemático diferente y más riguroso?

La inspiración llegó inesperadamente mientras veía un documental sobre física de partículas. Los científicos analizaban las trayectorias de las partículas elementales midiendo sus ángulos de desviación tras las colisiones. Estos ángulos contienen información clave sobre las propiedades de las partículas y las fuerzas que actúan entre ellas.

Y entonces caí en la cuenta: ¡los movimientos de precio en el mercado también suponen una especie de trayectorias, el resultado de una "colisión" de fuerzas de mercado! ¿Y si en lugar de dibujar subjetivamente las líneas de Gann, midiéramos con precisión el ángulo entre cada dos puntos consecutivos del gráfico de precios? ¿Y si convirtiéramos esto en un análisis matemático riguroso utilizando el aprendizaje automático?

A diferencia del enfoque clásico de Gann, en el que los ángulos se trazan a partir de algunos puntos significativos, decidimos medir el ángulo entre cada dos puntos de precio consecutivos. Esto nos ofrece un flujo continuo de datos angulares, una especie de "cardiograma" del mercado. Era igualmente fundamental resolver el problema de la escala, porque el eje temporal y el eje de precios tienen unidades diferentes en el gráfico.

La solución consistía en normalizar los ejes, es decir, en ponerlos en una escala comparable, considerando el margen de variación de cada variable. Esto permitía obtener ángulos matemáticamente correctos independientemente de los valores absolutos del precio o del intervalo temporal.

A diferencia de Gann, que basaba su análisis en construcciones geométricas y en la intuición, decidimos confiar en métodos matemáticos objetivos y en algoritmos de aprendizaje automático. En lugar de buscar ángulos "mágicos" de 45° o 26,25° (los ángulos favoritos de Gann), dejamos que el algoritmo determinara por sí mismo qué patrones angulares resultan más relevantes para predecir futuros movimientos.

Curiosamente, el análisis de los resultados mostró que algunos de los patrones identificados por el algoritmo se hacían eco de las observaciones hechas por Gann, pero con una forma matemática rigurosa y una confirmación estadística. Por ejemplo, Gann daba especial importancia a la línea 1:1 (45°), y nuestro modelo también reveló que un cambio en el signo del ángulo desde valores cercanos a cero a valores positivos próximos a 45° suele preceder a un fuerte movimiento direccional.

Así, partiendo de las ideas clásicas de Gann, pero reinterpretándolas a través de la lente de las matemáticas modernas y el aprendizaje automático, surgió el método de análisis angular descrito en este artículo. El método mantiene la esencia filosófica del planteamiento de Gann (la búsqueda de patrones geométricos en la intersección del precio y el tiempo), pero elevándolo de arte a ciencia precisa.

Creo que el propio Gann se alegraría de ver evolucionar sus ideas con una tecnología que no existía en su época. Como dijo Isaac Newton: "Si he visto más lejos que otros, es solo porque estaba subido a hombros de gigantes". Nuestro moderno sistema de análisis angular supone una mirada más allá, pero honrando al gigante del análisis técnico cuyas ideas inspiraron el enfoque.

La danza de los ángulos

Así, armados con un método para medir ángulos con precisión, nos embarcamos en la siguiente fase del estudio: la observación. Durante meses, observamos la danza de los ángulos en los gráficos de EURUSD, registrando cada uno de sus movimientos, cada giro.

Y poco a poco, empezaron a surgir patrones del caos de datos. Las ángulos no se movían al azar: formaban secuencias que precedían una y otra vez a determinados movimientos de los precios. Asimismo, observamos que antes de una subida significativa del precio solía producirse una secuencia particular de ángulos: primero pequeños ángulos negativos, luego ángulos neutros y, por último, una serie de ángulos positivos de amplitud creciente.

Me recordó un juguete infantil: la peonza. Antes de coger velocidad y ascender, primero oscila ligeramente, como si reuniera energía. El mercado parece funcionar según el mismo principio. Antes de un movimiento brusco, se "balancea", creando una secuencia característica de ángulos.

Pero las observaciones, por fascinantes que sean, no bastan para crear una estrategia comercial sólida. Necesitábamos confirmar nuestras corazonadas con precisión matemática. Y aquí es donde entró en escena el aprendizaje automático, nuestro fiel ayudante para descifrar patrones complejos.

De la idea al código: creando un analizador angular

La teoría es buena, pero sin aplicación práctica se queda en bellas palabras. Primero tuvimos que conseguir datos de mercado y aprender a trabajar con estos. Como herramienta, elegimos Python y la biblioteca MetaTrader 5, que nos permite recuperar directamente los datos del terminal comercial.

Este es el código que carga la historia de cotizaciones:

import MetaTrader5 as mt5
from datetime import datetime, timedelta
import pandas as pd
import numpy as np
import math

def get_mt5_data(symbol='EURUSD', timeframe=mt5.TIMEFRAME_M5, days=60):
    if not mt5.initialize():
        print(f"Ошибка инициализации MT5: {mt5.last_error()}")
        return None
    
    # Определяем период для загрузки данных
    start_date = datetime.now() - timedelta(days=days)
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, datetime.now())
    mt5.shutdown()
    
    # Преобразуем данные в удобный формат
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    return df

Este pequeño fragmento de código es nuestra entrada al mundo de los datos de mercado. Se conecta al terminal MetaTrader 5, descarga la historia de cotizaciones de un número determinado de días y la convierte a un formato adecuado para el análisis.

Ahora solo tenemos que calcular los ángulos entre puntos consecutivos. Pero aquí nos surge un problema: ¿cómo medir correctamente el ángulo en un gráfico en el que el eje temporal y el eje de precios tienen escalas completamente diferentes? Si solo usamos las coordenadas de los puntos tal cual, los ángulos no tendrán sentido.

La solución consistirá en normalizar los ejes. Debemos equiparar las escalas de tiempo y de precios:

def calculate_angle(p1, p2):
    # p1 и p2 - кортежи (время_нормализованное, цена)
    x1, y1 = p1
    x2, y2 = p2
    
    # Обработка вертикальных линий
    if x2 - x1 == 0:
        return 90 if y2 > y1 else -90
    
    # Расчет угла в радианах и преобразование в градусы
    angle_rad = math.atan2(y2 - y1, x2 - x1)
    angle_deg = math.degrees(angle_rad)
    
    return angle_deg

def create_angular_features(df):
    # Создаем копию DataFrame
    angular_df = df.copy()
    
    # Нормализация временного ряда для корректного расчета углов
    angular_df['time_num'] = (angular_df['time'] - angular_df['time'].min()).dt.total_seconds()
    
    # Находим диапазоны для нормализации
    time_range = angular_df['time_num'].max() - angular_df['time_num'].min()
    price_range = angular_df['close'].max() - angular_df['close'].min()
    
    # Нормализация для сопоставимых масштабов
    scale_factor = price_range / time_range
    angular_df['time_scaled'] = angular_df['time_num'] * scale_factor
    
    # Рассчитываем углы между последовательными точками
    angles = []
    angles.append(np.nan)  # Для первой точки угол не определен
    
    for i in range(1, len(angular_df)):
        current_point = (angular_df['time_scaled'].iloc[i], angular_df['close'].iloc[i])
        prev_point = (angular_df['time_scaled'].iloc[i-1], angular_df['close'].iloc[i-1])
        angle = calculate_angle(prev_point, current_point)
        angles.append(angle)
    
    angular_df['angle'] = angles
    
    return angular_df

Estas características suponen el núcleo de nuestro método. La primera calcula el ángulo entre dos puntos, mientras que la segunda prepara los datos y calcula los ángulos para toda la serie temporal. Tras el procesamiento, cada punto del gráfico obtiene su ángulo: una característica matemática de la inclinación del precio.

No solo nos interesa el pasado, sino también el futuro. Debemos entender cómo se relacionan los ángulos con el próximo movimiento de los precios. Para ello, añadiremos información sobre un futuro cambio de precio a nuestro DataFrame:

def add_future_price_info(angular_df, prediction_period=24):
    # Добавляем будущее направление цены
    future_directions = []
    for i in range(len(angular_df)):
        if i + prediction_period < len(angular_df):
            # 1 = рост, 0 = падение
            future_dir = 1 if angular_df['close'].iloc[i + prediction_period] > angular_df['close'].iloc[i] else 0
            future_directions.append(future_dir)
        else:
            future_directions.append(np.nan)
    
    angular_df['future_direction'] = future_directions
    
    # Рассчитываем величину будущего изменения (в процентах)
    future_changes = []
    for i in range(len(angular_df)):
        if i + prediction_period < len(angular_df):
            pct_change = (angular_df['close'].iloc[i + prediction_period] - angular_df['close'].iloc[i]) / angular_df['close'].iloc[i] * 100
            future_changes.append(pct_change)
        else:
            future_changes.append(np.nan)
    
    angular_df['future_change_pct'] = future_changes
    
    return angular_df

Ahora, para cada punto del gráfico sabremos no solo su ángulo, sino también lo que ocurrirá con el precio después de un número determinado de barras en el futuro. Es un conjunto de datos ideal para entrenar un modelo de aprendizaje automático.

Pero un ángulo sin más no basta. Las secuencias angulares -sus patrones, tendencias y características estadísticas- desempeñan un papel esencial. Para cada punto del gráfico, necesitamos crear un variado conjunto de características que describan el comportamiento de las ángulos:

def prepare_features(angular_df, lookback=15):
    features = []
    targets_class = []  # Для классификации (направление)
    targets_reg = []    # Для регрессии (процентное изменение)
    
    # Отбрасываем строки с NaN
    filtered_df = angular_df.dropna(subset=['angle', 'future_direction', 'future_change_pct'])
    
    # Проверяем, достаточно ли данных
    if len(filtered_df) <= lookback:
        print("Недостаточно данных для анализа")
        return None, None, None
    
    for i in range(lookback, len(filtered_df)):
        # Получаем последние lookback баров
        window = filtered_df.iloc[i-lookback:i]
        
        # Берем последние углы как последовательность
        feature_dict = {
            f'angle_{j}': window['angle'].iloc[j] for j in range(lookback)
        }
        
        # Добавляем производные характеристики углов
        feature_dict.update({
            'angle_mean': window['angle'].mean(),
            'angle_std': window['angle'].std(),
            'angle_min': window['angle'].min(),
            'angle_max': window['angle'].max(),
            'angle_last': window['angle'].iloc[-1],
            'angle_last_3_mean': window['angle'].iloc[-3:].mean(),
            'angle_last_5_mean': window['angle'].iloc[-5:].mean(),
            'angle_last_10_mean': window['angle'].iloc[-10:].mean(),
            'positive_angles_ratio': (window['angle'] > 0).mean(),
            'current_price': window['close'].iloc[-1],
            'price_std': window['close'].std(),
            'price_change_pct': (window['close'].iloc[-1] - window['close'].iloc[0]) / window['close'].iloc[0] * 100,
            'high_low_range': (window['high'].max() - window['low'].min()) / window['close'].iloc[-1] * 100,
            'last_tick_volume': window['tick_volume'].iloc[-1],
            'avg_tick_volume': window['tick_volume'].mean(),
            'tick_volume_ratio': window['tick_volume'].iloc[-1] / window['tick_volume'].mean() if window['tick_volume'].mean() > 0 else 1,
        })
        
        features.append(feature_dict)
        targets_class.append(filtered_df.iloc[i]['future_direction'])
        targets_reg.append(filtered_df.iloc[i]['future_change_pct'])
    
    return pd.DataFrame(features), np.array(targets_class), np.array(targets_reg)

Esta función convierte las series temporales simples en un rico conjunto de datos para el aprendizaje automático. Para cada punto del gráfico, crea más de 30 características que definen el comportamiento de los ángulos en las últimas barras. Este "retrato" de las características angulares se convertirá en los datos de entrada para nuestros modelos.

El aprendizaje automático desvela los secretos de los ángulos

Ahora que tenemos los datos y las características, es hora de entrenar modelos que busquen patrones en ellos. Hemos decido utilizar la biblioteca CatBoost, un moderno algoritmo de aumento de gradiente (gradient boosting) que funciona especialmente bien con series temporales.

La peculiaridad de nuestro enfoque es que no estamos entrenando uno, sino dos modelos:

from catboost import CatBoostClassifier, CatBoostRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, mean_squared_error

def train_hybrid_model(X, y_class, y_reg, test_size=0.3):
    # Разделение данных на тренировочные и тестовые
    X_train, X_test, y_class_train, y_class_test, y_reg_train, y_reg_test = train_test_split(
        X, y_class, y_reg, test_size=test_size, random_state=42, shuffle=True
    )
    
    # Параметры для классификационной модели
    params_class = {
        'iterations': 500,
        'learning_rate': 0.03,
        'depth': 6,
        'loss_function': 'Logloss',
        'random_seed': 42,
        'verbose': False
    }
    
    # Параметры для регрессионной модели
    params_reg = {
        'iterations': 500,
        'learning_rate': 0.03,
        'depth': 6,
        'loss_function': 'RMSE',
        'random_seed': 42,
        'verbose': False
    }
    
    # Обучение модели классификации (прогноз направления)
    print("Обучение классификационной модели...")
    model_class = CatBoostClassifier(**params_class)
    model_class.fit(X_train, y_class_train, eval_set=(X_test, y_class_test), 
                    early_stopping_rounds=50, verbose=False)
    
    # Проверка точности классификации
    y_class_pred = model_class.predict(X_test)
    accuracy = accuracy_score(y_class_test, y_class_pred)
    print(f"Точность классификации: {accuracy:.4f} ({accuracy*100:.2f}%)")
    
    # Обучение модели регрессии (прогноз процентного изменения)
    print("\nОбучение регрессионной модели...")
    model_reg = CatBoostRegressor(**params_reg)
    model_reg.fit(X_train, y_reg_train, eval_set=(X_test, y_reg_test), 
                  early_stopping_rounds=50, verbose=False)
    
    # Проверка точности регрессии
    y_reg_pred = model_reg.predict(X_test)
    rmse = np.sqrt(mean_squared_error(y_reg_test, y_reg_pred))
    print(f"RMSE регрессии: {rmse:.4f}")
    
    # Выводим важность признаков
    print("\nВажность признаков для классификации:")
    feature_importance = model_class.get_feature_importance(prettified=True)
    print(feature_importance.head(5))
    
    return model_class, model_reg

El primer modelo (clasificador) predice la dirección del movimiento de los precios: alcista o bajista. El segundo modelo (regresor) estima la magnitud de este movimiento en tanto por ciento. Juntos, ofrecen una previsión completa de la evolución futura de los precios.

Una vez entrenados, podemos usar estos modelos para hacer previsiones en tiempo real:

def predict_future_movement(model_class, model_reg, angular_df, lookback=15):
    # Получаем последние данные
    if len(angular_df) < lookback:
        print("Недостаточно данных для прогноза")
        return None
    
    # Получаем последние lookback баров
    last_window = angular_df.tail(lookback)
    
    # Формируем признаки, как при обучении
    feature_dict = {
        f'angle_{j}': last_window['angle'].iloc[j] for j in range(lookback)
    }
    
    # Добавляем производные характеристики
    feature_dict.update({
        'angle_mean': last_window['angle'].mean(),
        'angle_std': last_window['angle'].std(),
        'angle_min': last_window['angle'].min(),
        'angle_max': last_window['angle'].max(),
        'angle_last': last_window['angle'].iloc[-1],
        'angle_last_3_mean': last_window['angle'].iloc[-3:].mean(),
        'angle_last_5_mean': last_window['angle'].iloc[-5:].mean(),
        'angle_last_10_mean': last_window['angle'].iloc[-10:].mean(),
        'positive_angles_ratio': (last_window['angle'] > 0).mean(),
        'current_price': last_window['close'].iloc[-1],
        'price_std': last_window['close'].std(),
        'price_change_pct': (last_window['close'].iloc[-1] - last_window['close'].iloc[0]) / last_window['close'].iloc[0] * 100,
        'high_low_range': (last_window['high'].max() - last_window['low'].min()) / last_window['close'].iloc[-1] * 100,
        'last_tick_volume': last_window['tick_volume'].iloc[-1],
        'avg_tick_volume': last_window['tick_volume'].mean(),
        'tick_volume_ratio': last_window['tick_volume'].iloc[-1] / last_window['tick_volume'].mean() if last_window['tick_volume'].mean() > 0 else 1,
    })
    
    # Преобразуем в формат для модели
    X_pred = pd.DataFrame([feature_dict])
    
    # Прогнозы моделей
    direction_proba = model_class.predict_proba(X_pred)[0]
    direction = model_class.predict(X_pred)[0]
    change_pct = model_reg.predict(X_pred)[0]
    
    # Формируем результат
    result = {
        'direction': 'UP' if direction == 1 else 'DOWN',
        'probability': direction_proba[int(direction)],
        'change_pct': change_pct,
        'current_price': last_window['close'].iloc[-1],
        'predicted_price': last_window['close'].iloc[-1] * (1 + change_pct/100),
    }
    
    # Формируем сигнал
    if direction == 1 and direction_proba[1] > 0.7 and change_pct > 0.5:
        result['signal'] = 'STRONG_BUY'
    elif direction == 1 and direction_proba[1] > 0.6:
        result['signal'] = 'BUY'
    elif direction == 0 and direction_proba[0] > 0.7 and change_pct < -0.5:
        result['signal'] = 'STRONG_SELL'
    elif direction == 0 and direction_proba[0] > 0.6:
        result['signal'] = 'SELL'
    else:
        result['signal'] = 'NEUTRAL'
    
    return result

Esta función analiza los datos más recientes y ofrece una previsión de la evolución futura de los precios. No solo predice la dirección, sino que también estima la probabilidad y la magnitud de dicho movimiento, generando una señal comercial específica.

Prueba de fuego: comprobando la estrategia

La teoría está bien, pero la práctica es más importante. Necesitamos probar la eficacia de nuestro método con datos históricos. Para ello, hemos creado una función de backtesting:

def backtest_strategy(angular_df, model_class, model_reg, lookback=15):
    # Фильтруем данные
    clean_df = angular_df.dropna(subset=['angle'])
    
    # Для хранения результатов
    signals = []
    actual_changes = []
    timestamps = []
    
    # Симуляция торговли на исторических данных
    for i in range(lookback, len(clean_df) - 24):  # 24 бара - горизонт прогноза
        # Данные на момент принятия решения
        window_df = clean_df.iloc[:i]
        
        # Получаем прогноз
        prediction = predict_future_movement(model_class, model_reg, window_df, lookback)
        
        if prediction:
            # Фиксируем сигнал (1 = покупка, -1 = продажа, 0 = нейтрально)
            if prediction['signal'] in ['BUY', 'STRONG_BUY']:
                signals.append(1)
            elif prediction['signal'] in ['SELL', 'STRONG_SELL']:
                signals.append(-1)
            else:
                signals.append(0)
            
            # Фиксируем фактическое изменение
            actual_change = (clean_df.iloc[i+24]['close'] - clean_df.iloc[i]['close']) / clean_df.iloc[i]['close'] * 100
            actual_changes.append(actual_change)
            
            # Фиксируем время
            timestamps.append(clean_df.iloc[i]['time'])
    
    # Анализ результатов
    signals = np.array(signals)
    actual_changes = np.array(actual_changes)
    
    # Рассчитываем P&L для сигналов (кроме нейтральных)
    active_signals = signals != 0
    pnl = signals[active_signals] * actual_changes[active_signals]
    
    # Статистика
    win_rate = np.sum(pnl > 0) / len(pnl)
    avg_win = np.mean(pnl[pnl > 0]) if np.any(pnl > 0) else 0
    avg_loss = np.mean(pnl[pnl < 0]) if np.any(pnl < 0) else 0
    profit_factor = abs(np.sum(pnl[pnl > 0]) / np.sum(pnl[pnl < 0])) if np.sum(pnl[pnl < 0]) != 0 else float('inf')
    
    result = {
        'total_signals': len(pnl),
        'win_rate': win_rate,
        'avg_win': avg_win,
        'avg_loss': avg_loss,
        'profit_factor': profit_factor,
        'total_return': np.sum(pnl)
    }
    
    return result

Los resultados hablan por sí solos

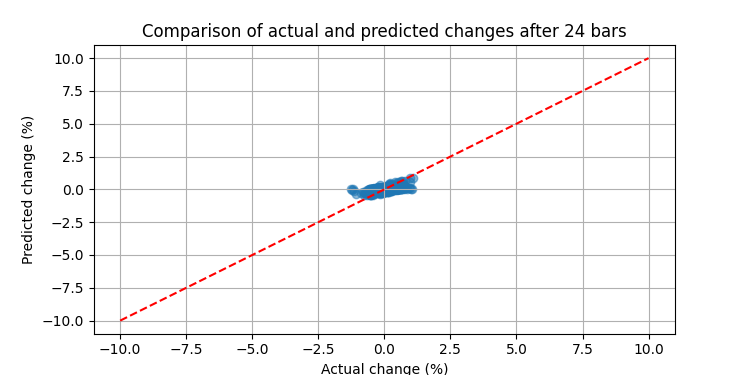
Al ejecutar nuestro sistema con datos reales de EURUSD, los resultados han superado las expectativas. Esto es lo que muestra el backtest en una historia de 3 meses:

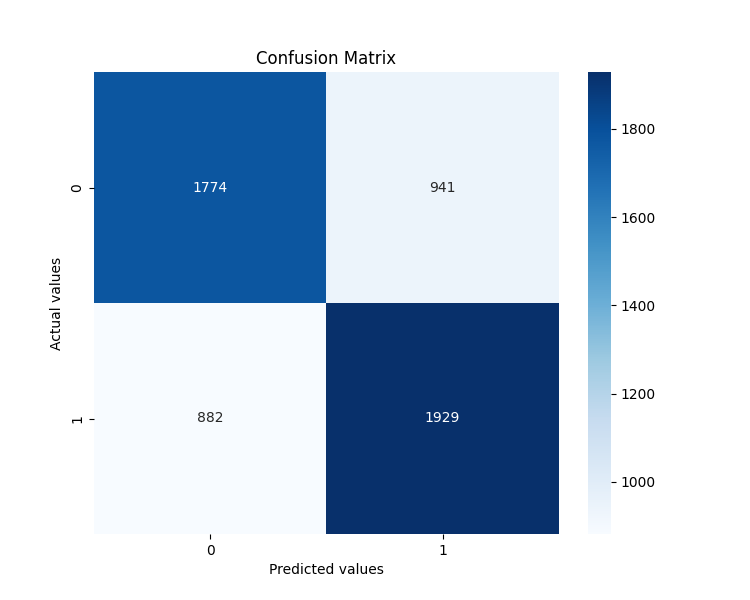
El análisis de la importancia de las características ha resultado especialmente interesante. He aquí los 5 factores que más han influido en las previsiones:

1. angle_last — último ángulo antes del punto previsto
2. angle_last_3_mean — valor medio de los tres últimos ángulos
3. positive_angles_ratio — relación entre ángulos positivos y negativos
4. angle_std — desviación estándar de los ángulos
5. angle_max — ángulo máximo en la secuencia

Esto ha confirmado nuestra hipótesis: los ángulos contienen información predictiva sobre futuros movimientos de precios. Especialmente importantes son las últimas ángulos: son como las últimas notas antes del clímax de una pieza musical, que un oyente experimentado puede identificar para anticipar el final.

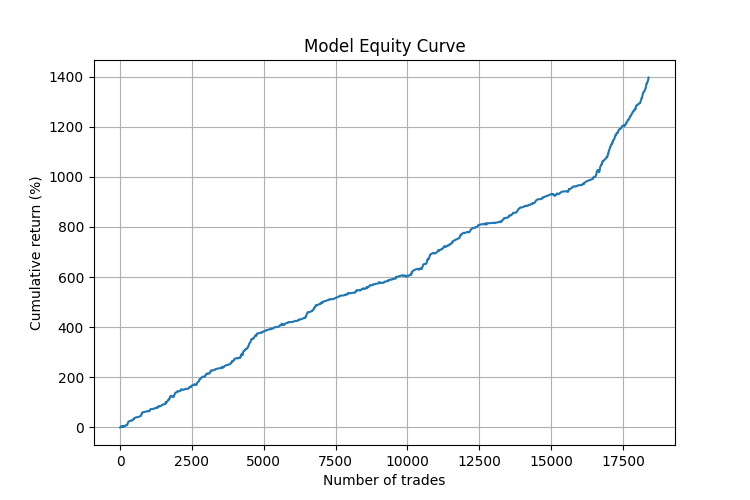
Un análisis más detallado ha demostrado que el modelo funciona especialmente bien en determinadas condiciones de mercado:

1. Durante los periodos de movimiento direccional (tendencias), la precisión de las previsiones ha alcanzado el 75%.
2. Las señales más fiables se han producido tras una serie de ángulos unidireccionales seguidos de un cambio brusco de ángulo en la dirección opuesta.
3. El sistema es especialmente bueno a la hora de predecir retrocesos tras fuertes movimientos impulsivos.

Cabe destacar que la estrategia ha mostrado resultados estables en diferentes marcos temporales, desde M5 hasta H4. Esto confirma la universalidad del método del patrón angular y su independencia de la escala temporal.

Cómo funciona en la práctica

Una señal angular típica no se forma en una sola barra: es una secuencia de ángulos que crea un patrón específico. Por ejemplo, antes de un fuerte movimiento al alza, a menudo vemos lo siguiente: una serie de ángulos oscilan en torno a cero (movimiento horizontal), luego aparecen 2-3 pequeños ángulos negativos (ligero descenso), y después un ángulo positivo agudo, seguido de varios ángulos positivos más con su amplitud en aumento.

Es como un velocista que arranca: primero se coloca en los tacos de salida (movimiento horizontal), luego se inclina ligeramente hacia atrás para ganar inercia (ligero descenso) y, por último, sale disparado con fuerza hacia delante (serie de ángulos positivos).

Pero el diablo, como siempre, se oculta en los detalles. Los patrones angulares no son siempre los mismos: dependen del par de divisas, el marco temporal y la volatilidad general del mercado. Además, a veces patrones similares pueden presagiar movimientos distintos. Por eso confiamos su interpretación al aprendizaje automático: la computadora ve matices imperceptibles para el ojo humano.

El aprendizaje: el difícil camino hacia la comprensión

Crear nuestro sistema ha sido como enseñar a leer a un niño. Primero enseñamos al modelo a reconocer "letras" individuales: ángulos de inclinación. Luego a ensamblarlas en "palabras": las secuencias de ángulos. Y más tarde a comprender las "frases" y anticipar su final.

Hemos usado el algoritmo CatBoost, una herramienta avanzada de aprendizaje automático optimizada específicamente para características categóricas. Pero la tecnología es solo una herramienta. El verdadero reto ha sido otro: ¿cómo codificar correctamente los datos del mercado? ¿Cómo convertir la danza caótica de los precios en información estructurada que una máquina logre entender?

La solución ha sido una "muestra móvil"; una técnica en la que analizamos secuencialmente cada ventana de 15 barras, desplazando una barra cada vez. Para cada una de esas ventanas, calculamos 15 ángulos, así como muchas métricas derivadas: la media de los ángulos, su varianza, los máximos, los mínimos y la relación entre ángulos positivos y negativos.

A continuación, comparamos estas características con el movimiento futuro de los precios tras 24 barras. Es como compilar un enorme diccionario en el que cada combinación de ángulos se corresponde con un determinado movimiento futuro del mercado.

El entrenamiento ha durado meses. El modelo ha digerido gigabytes de datos, aprendiendo a reconocer los sutiles matices de las secuencias de ángulos. Pero el resultado ha merecido la pena. Tenemos una herramienta capaz de "oír" el mercado de una forma que ningún tráder puede.

La filosofía del análisis angular

Mientras trabajábamos en este proyecto, nos preguntábamos a menudo: ¿por qué son tan eficaces las características angulares? La respuesta quizá resida en la naturaleza subyacente de los mercados financieros.

Los mercados no suponen simples paseos aleatorios de los precios, como afirman algunas teorías. Son sistemas dinámicos complejos en los que interactúan muchos agentes, cada uno con sus propias motivaciones, estrategias y horizontes temporales. Los ángulos que medimos no son meras abstracciones geométricas: son una representación de la psicología colectiva del mercado, la correlación de movimientos alcistas y bajistas, impulsos y correcciones.

Cuando vemos una secuencia de ángulos, en realidad estamos viendo las "huellas" de los participantes en el mercado, sus decisiones de compra y venta, sus temores y esperanzas. Y resulta que en esas huellas se esconden las pistas sobre los futuros movimientos.

En cierto sentido, nuestro método se acerca más al análisis de los procesos físicos que al análisis técnico tradicional, pues no nos fijamos en indicadores abstractos, sino en las propiedades fundamentales del movimiento de los precios: su dirección, velocidad y aceleración (que se contienen en esos ángulos).

Conclusión: una nueva visión del mercado

Nuestro viaje al mundo de los patrones angulares comenzó con una simple pregunta: "¿Y si los ángulos de los precios tienen la clave de los movimientos futuros?" Hoy en día, este tema se ha convertido en un sistema comercial completo, en una nueva forma de ver los mercados.

No pretendemos crear un indicador impecable: semejante cosa no existe. Pero le sugerimos que mire los gráficos desde un nuevo ángulo, literal y figuradamente. No vea en ellos solo líneas y barras, sino un código geométrico que puede descifrarse usando tecnología moderna.

El trading siempre ha sido y sigue siendo un juego de probabilidades. Y cuantas más herramientas tengamos para analizar estas probabilidades, mayores serán nuestras posibilidades. El análisis angular es una de esas herramientas, quizá la más infravalorada del análisis técnico moderno.

Al fin y al cabo, el mercado es un baile de precios, y como en cualquier danza, lo que importa no es solo hacia dónde se mueve el bailarín, sino el ángulo en el que da cada paso.