機械学習に基づく平均回帰戦略の作成

MetaTrader 5 — トレーディング | YYYY年02月DD日, 16:53

削除済み

はじめに

本記事では、機械学習を使った取引システムを構築するための、もう1つの独自のアプローチを提案します。前回の記事では、クラスタリングを因果推論の問題に応用する方法についてすでに考察しました。今回の記事では、クラスタリングを使って金融時系列データをいくつかのモードに分割し、それぞれのモードに固有の特性を持たせたうえで、取引システムを構築してテストします。

さらに、平均回帰戦略のための例のラベル付け方法をいくつか確認し、EUR/GBP通貨ペアでテストします。この通貨ペアはレンジ相場（持ち合い）であるとされるため、これらの戦略を十分に適用できます。

この記事を通して、Pythonでさまざまな機械学習モデルを学習させ、それらをMetaTrader 5取引ターミナル用の取引システムに変換する方法を学ぶことができます。

必要なパッケージの準備

モデルの学習はPythonでおこなうので、以下のパッケージがインストールされていることを確認してください。

import math
import pandas as pd
import pickle
from datetime import datetime
from catboost import CatBoostClassifier

from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans

from bots.botlibs.labeling_lib import *
from bots.botlibs.tester_lib import tester
from bots.botlibs.export_lib import export_model_to_ONNX

最後の3つのモジュールは私が作成したもので、記事の最後に添付しています。それぞれ、Scipy、Numpy、Sklearn、Numbaなどの他のパッケージをインポートする場合があります。これらもあらかじめインストールしておく必要があります。これらのパッケージは広く知られており、一般に公開されているため、インストールに問題はないはずです。

クリーンなPython環境を使用する場合、以下のパッケージをインストールしてください。

pip install numpy
pip install pandas
pip install scipy
pip install scikit-learn
pip install catboost
pip install numba

また、記事の最後に添付したライブラリを使う場合、開発環境や配置場所によっては絶対インポートパスを使用する必要があるかもしれません。

このコードは、Pythonインタープリターや特定のパッケージのバージョンに大きく依存しないよう設計されていますが、可能であれば最新の安定版を使用することをお勧めします。

平均回帰戦略のためのラベル付け方法

これまでの記事でどのようにラベル付けをおこなっていたかを振り返ってみましょう。以前は、ループを作成し、各取引の期間をランダムに設定していました。たとえば1〜15バーの間で期間を決め、その期間内に仮想の取引を開始してから、市場が上昇したか下降したかに応じて、買いまたは売りのラベルを付けていました。この関数は特徴量とラベルを持つDataFrameを返し、データセットはすでに機械学習モデルの学習に使える形で準備されていました。

def get_labels(dataset, markup, min = 1, max = 15) -> pd.DataFrame:
    labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        curr_pr = dataset['close'].iloc[i]
        future_pr = dataset['close'].iloc[i + rand]

        if (future_pr + markup) < curr_pr:
            labels.append(1.0)
        elif (future_pr - markup) > curr_pr:
            labels.append(0.0)
        else:
            labels.append(2.0)
        
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(
        dataset[dataset.labels == 2.0].index)
    return dataset

しかし、このラベル付け方法には大きな欠点があります。それはランダムであることです。この方法では、機械学習モデルがどのパターンを学習すべきかという指針が与えられません。そのため、ラベル付けおよび学習の結果も大部分がランダムになります。この問題を解決するために、複数回の総当たり的な学習をおこなったり、アルゴリズムの構造を複雑にしたりしましたが、それでもラベル自体の意味は依然として乏しいままでした。ランダムサンプリングのため、一部のモデルだけがOOS（アウトオブサンプル）テストに合格しました。

そこで本記事では、元の時系列データをフィルタリングすることでラベル付けをおこなう新しいアプローチを提案します。以下に、このラベル付け方法を例を使って説明します。

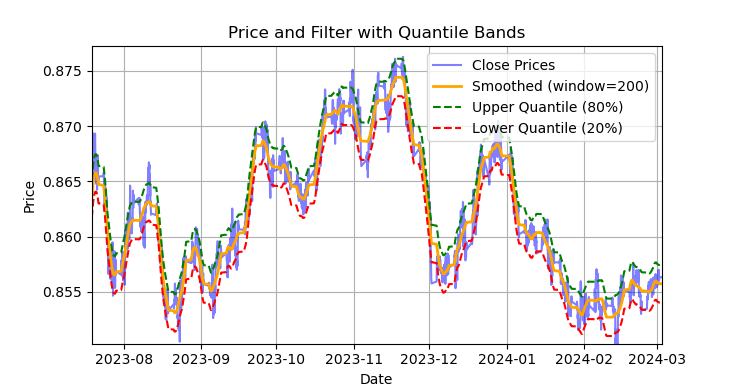
図1：Savitzky-Golayフィルタとバンド（分位数）によるラベル付け

図1は、Savitzky-Golayフィルタで平滑化した線と、20％および80％分位バンドを示しています。ボリンジャーバンドに似ていますが、Savitzky-Golayフィルタは価格に対する遅れがほとんど生じない点が大きな違いです。この性質により、価格を滑らかにしつつ、残差の「ノイズ（フィルタ値からの偏差）を平均回帰戦略の開発に利用できます。上バンドと下バンドを価格が横切ると、売買のシグナルが形成されます。価格が上バンドを越えれば売りシグナル、下バンドを越えれば買いシグナルです。

Savitzky-Golayフィルタは、データを滑らかにし、ピークやトレンドなど重要な特徴を保持しながらノイズを抑えるデジタルフィルタです。1964年にAbraham SavitzkyとMarcel J. E. Golayによって提案され、信号処理やデータ分析で広く使用されています。

このフィルタは、データを低次（2次～4次）の多項式で局所的に近似することで、最小二乗法で計算します。各データ点について近傍（ウィンドウ）を選択し、その範囲内のデータを多項式で近似した後、ウィンドウ中央の値を多項式による近似値で置き換えます。これにより、信号の形を保ちながらノイズを平滑化できます。

以下のコードで、フィルタを構築し、可視化することができます。

def plot_close_filter_quantiles(dataset, rolling=200, quantiles=[0.2, 0.8], polyorder=3):
    # Calculate smoothed prices
    smoothed = savgol_filter(dataset['close'], 
                            window_length=rolling, 
                            polyorder=polyorder)
    
    # Calculate difference between prices and filter
    lvl = dataset['close'] - smoothed
    
    # Get quantile values
    q_low, q_high = lvl.quantile(quantiles).tolist()
    
    # Calculate bands based on quantiles
    upper_band = smoothed + q_high  # Upper band
    lower_band = smoothed + q_low   # Lower band
    
    # Create plot
    plt.figure(figsize=(14, 7))
    plt.plot(dataset.index, dataset['close'], label='Close Prices', color='blue', alpha=0.5)
    plt.plot(dataset.index, smoothed, label=f'Smoothed (window={rolling})', color='orange', linewidth=2)
    plt.plot(dataset.index, upper_band, label=f'Upper Quantile ({quantiles[1]*100:.0f}%)', 
             color='green', linestyle='--')
    plt.plot(dataset.index, lower_band, label=f'Lower Quantile ({quantiles[0]*100:.0f}%)', 
             color='red', linestyle='--')
    
    # Configure display
    plt.title('Price and Filter with Quantile Bands')
    plt.xlabel('Date')
    plt.ylabel('Price')
    plt.legend()
    plt.grid(True)
    plt.show()

注意点として、このフィルタは非定常時系列をオンラインで処理する場合には不向きです。最新の値が再計算によって変化する可能性があるためです。しかし、既存データ上で取引にラベルを付けるには非常に適しています。

次に、Savitzky-Golayフィルタを用いて学習用データのラベル付けをおこなうコードを作成します。このラベル付け関数は、他の類似関数とともにlabeling_lib.pyモジュールに格納され、プロジェクトにインポートして使用します。

@njit
def calculate_labels_filter(close, lvl, q):
    labels = np.empty(len(close), dtype=np.float64)
    for i in range(len(close)):
        curr_lvl = lvl[i]

        if curr_lvl > q[1]:
            labels[i] = 1.0
        elif curr_lvl < q[0]:
            labels[i] = 0.0
        else:
            labels[i] = 2.0
    return labels

def get_labels_filter(dataset, rolling=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame:
    """
    Generates labels for a financial dataset based on price deviation from a Savitzky-Golay filter.

    This function applies a Savitzky-Golay filter to the closing prices to generate a smoothed
    price trend. It then calculates trading signals (buy/sell) based on the deviation of the 
    actual price from this smoothed trend. Buy signals are generated when the price is 
    significantly below the smoothed trend, anticipating a potential price reversal. 

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        rolling (int, optional): Window size for the Savitzky-Golay filter. Defaults to 200.
        quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55].
        polyorder (int, optional): Polynomial order for the Savitzky-Golay filter. Defaults to 3.

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (no signal) are removed.
                       - Rows with missing values (NaN) are removed.
                       - The temporary 'lvl' column is removed. 
    """

    # Calculate smoothed prices using the Savitzky-Golay filter
    smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling, polyorder=polyorder)
    
    # Calculate the difference between the actual closing prices and the smoothed prices
    diff = dataset['close'] - smoothed_prices
    dataset['lvl'] = diff  # Add the difference as a new column 'lvl' to the DataFrame
    
    # Remove any rows with NaN values 
    dataset = dataset.dropna()
    
    # Calculate the quantiles of the 'lvl' column (price deviation)
    q = dataset['lvl'].quantile(quantiles).to_list() 

    # Extract the closing prices and the calculated 'lvl' values as NumPy arrays
    close = dataset['close'].values
    lvl = dataset['lvl'].values
    
    # Calculate buy/sell labels using the 'calculate_labels_filter' function 
    labels = calculate_labels_filter(close, lvl, q) 

    # Trim the dataset to match the length of the calculated labels
    dataset = dataset.iloc[:len(labels)].copy()
    
    # Add the calculated labels as a new 'labels' column to the DataFrame
    dataset['labels'] = labels
    
    # Remove any rows with NaN values
    dataset = dataset.dropna()
    
    # Remove rows where the 'labels' column has a value of 2.0 (no signals)
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index)
    
    # Return the modified DataFrame with the 'lvl' column removed
    return dataset.drop(columns=['lvl'])

ラベル付けを高速化するために、前回の記事で説明したNumbaパッケージを使用します。

get_labels_filter()関数は、価格とそこから構築された特徴量を含む元のデータセット、フィルタの近似ウィンドウの長さ、下分位および上分位の境界値、多項式の次数を入力として受け取ります。この関数の出力は、元のデータセットに買いと売りのラベルを追加することです。このデータセットは、そのまま学習用データセットとして使用できます。

価格履歴ループは、calc_labels_filterという別の関数で実装されており、Numbaパッケージを用いて計算負荷の高い処理を効率化しています。

このタイプのラベル付けには以下の特徴があります。

すべてのマークされた取引が利益になるわけではありません。バンドを越えた後の価格変動が必ずしも逆方向に進むとは限らないため、買いまたは売りとして誤ってラベル付けされる場合があります。
しかし、この欠点は理論的にはラベル付けが均一かつ非ランダムである点で補われます。そのため、誤ってラベル付けされた例も学習誤差やシステム全体の誤差として扱うことができ、結果的に過学習を抑える効果が期待できます。

取引ラベル付けロジックの詳細な説明は以下に記載されています。

calculate_labels_filter関数

入力データ

close：終値の配列
lvl：平滑化トレンドからの価格偏差の配列
q：シグナルゾーンを定義する分位値の配列

以下がロジックです。

1. 初期化：closeと同じ長さの空のlabels配列を作成し、シグナルを格納します。

2. 価格のループ処理：各終値[i]と対応するレベル[i]偏差について：

売りシグナル：lvl[i]が上分位q[1]を超える場合、価格は平滑化トレンドより大幅に上にあるため、売りシグナルと判断する(labels[i] = 1.0)
買いシグナル：lvl[i]が下分位q[0]未満の場合、価格は平滑化トレンドより大幅に下にあるため、買いシグナルと判断する(labels[i] = 0.0)
シグナルなし：その他（偏差が分位値の間）はシグナルなしとする(labels[i] = 2.0)

3. 結果を返す：シグナル付きのlabels配列を返します。

get_labels_filter関数

入力データ

dataset：close列（終値）を含む金融データのDataFrame
rolling：Savitzky-Golayフィルタの平滑化ウィンドウサイズ
quantiles：シグナルゾーンを決定する分位値
polyorder：Savitzky-Golay平滑化の多項式次数

以下がロジックです。

1. 価格の平滑化

dataset['close']にSavitzky-Golayフィルタを適用し、smoothed_pricesを計算する

2. 偏差の計算

実際の終値と平滑化価格の差分diffを計算する
結果をDataFrameにlvl列として追加する

3. 欠損値の削除

NaNが含まれる行をDataFrameから削除する

4. 分位数の計算

lvl列の分位値を計算し、シグナルゾーンを決定する

5. シグナルの計算

calculate_labels_filter関数を呼び出し、終値、偏差、分位値を渡す
シグナル付きのlabels配列を取得する

6. DataFrameの処理

DataFrameをlabels配列の長さに切り詰める
labels配列を新しいlabels列としてDataFrameに追加する
labelsが2.0（シグナルなし）の行を削除する
一時列lvlを削除する

7. 結果を返す：labels列に買い・売りシグナルを含む修正済みDataFrameを返す

上記のラベル付け方法を標準として考えます。これにより、平均回帰戦略のラベル付けの基本原則が示されます。これは実際に使用できる実用的な方法です。また、複数のフィルタに対応したり、平均からの偏差の分散が変動する場合に対応するように一般化および修正することも可能です。以下に、そのような変更を実装したget_labels_multiple_filters関数を示します。

@njit
def calc_labels_multiple_filters(close, lvls, qs):
    labels = np.empty(len(close), dtype=np.float64)
    for i in range(len(close)):
        label_found = False
        
        for j in range(len(lvls)):
            curr_lvl = lvls[j][i]
            curr_q_low = qs[j][0][i]
            curr_q_high = qs[j][1][i]
            
            if curr_lvl > curr_q_high:
                labels[i] = 1.0
                label_found = True
                break
            elif curr_lvl < curr_q_low:
                labels[i] = 0.0
                label_found = True
                break
                
        if not label_found:
            labels[i] = 2.0
            
    return labels

def get_labels_multiple_filters(dataset, 
                              rolling_periods=[200, 400, 600], 
                              quantiles=[.45, .55], 
                              window=100,
                              polyorder=3) -> pd.DataFrame:
    """
    Generates trading signals (buy/sell) based on price deviation from multiple 
    smoothed price trends calculated using a Savitzky-Golay filter with different
    rolling periods and rolling quantiles. 

    This function applies a Savitzky-Golay filter to the closing prices for each 
    specified 'rolling_period'. It then calculates the price deviation from these
    smoothed trends and determines dynamic "reversion zones" using rolling quantiles.
    Buy signals are generated when the price is within these reversion zones 
    across multiple timeframes.

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        rolling_periods (list, optional): List of rolling window sizes for the Savitzky-Golay filter. 
                                           Defaults to [200, 400, 600].
        quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.05, .95].
        window (int, optional): Window size for calculating rolling quantiles. Defaults to 100.
        polyorder (int, optional): Polynomial order for the Savitzky-Golay filter. Defaults to 3.

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (no signal) are removed.
                       - Rows with missing values (NaN) are removed. 
    """
    
    # Create a copy of the dataset to avoid modifying the original
    dataset = dataset.copy()
    
    # Lists to store price deviation levels and quantiles for each rolling period
    all_levels = []
    all_quantiles = []
    
    # Calculate smoothed price trends and rolling quantiles for each rolling period
    for rolling in rolling_periods:
        # Calculate smoothed prices using the Savitzky-Golay filter
        smoothed_prices = savgol_filter(dataset['close'].values, 
                                      window_length=rolling, 
                                      polyorder=polyorder)
        # Calculate the price deviation from the smoothed prices
        diff = dataset['close'] - smoothed_prices
        
        # Create a temporary DataFrame to calculate rolling quantiles
        temp_df = pd.DataFrame({'diff': diff})
        
        # Calculate rolling quantiles for the price deviation
        q_low = temp_df['diff'].rolling(window=window).quantile(quantiles[0])
        q_high = temp_df['diff'].rolling(window=window).quantile(quantiles[1])
        
        # Store the price deviation and quantiles for the current rolling period
        all_levels.append(diff)
        all_quantiles.append([q_low.values, q_high.values])
    
    # Convert lists to NumPy arrays for faster calculations (potentially using Numba)
    lvls_array = np.array(all_levels)
    qs_array = np.array(all_quantiles)
    
    # Calculate buy/sell labels using the 'calc_labels_multiple_filters' function 
    labels = calc_labels_multiple_filters(dataset['close'].values, lvls_array, qs_array)
    
    # Add the calculated labels to the DataFrame
    dataset['labels'] = labels
    
    # Remove rows with NaN values and no signals (labels == 2.0)
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index)
    
    # Return the DataFrame with the new 'labels' column
    return dataset

この関数は、Savitzky-Golayフィルタに対して無制限の平滑化パラメータを受け取ることができます。異なる期間を持つ複数のフィルタを使ってラベル付けをおこなうため、これは追加の利点をもたらします。シグナルを形成するためには、分位値の境界の距離で平均からの偏差が少なくとも1つのフィルタで発生すれば十分です。

これにより、取引のラベル付けに階層構造を構築することが可能になります。たとえば、まずハイパスフィルタの条件を確認し、次にミッドパスフィルタ、最後にローパスフィルタを確認します。ローパスフィルタのシグナルはより信頼性が高いと考えられるため、ローパスフィルタでシグナルが発生した場合は、それ以前のシグナルは上書きされます。しかし、ローパスフィルタがシグナルを生成しない場合は、取引は依然として以前のフィルタからのシグナルに基づいてラベル付けされます。これにより、ラベル付けされた例の数を増やすことができ、入力閾値（分位点）を高く設定することも可能になります。なぜなら、フィルタのセットのいずれかで少なくとも1つのシグナルが発生する可能性が高まるからです。

分位値の計算は、現在、設定可能な期間を持つスライディングウィンドウ方式でおこなわれます。これにより、平均からの偏差の分散が変動する場合にも対応でき、より正確なシグナルを得ることができます。

最後に、非対称取引の場合を考えることもできます。これは、価格分布が歪んでいるため、買い注文と売り注文のラベル付けに異なる平滑化期間のフィルタが必要になる場合を想定しています。このアプローチは、get_labels_filter_bidirectional関数で実装されています。

@njit
def calc_labels_bidirectional(close, lvl1, lvl2, q1, q2):
    labels = np.empty(len(close), dtype=np.float64)
    for i in range(len(close)):
        curr_lvl1 = lvl1[i]
        curr_lvl2 = lvl2[i]

        if curr_lvl1 > q1[1]:
            labels[i] = 1.0
        elif curr_lvl2 < q2[0]:
            labels[i] = 0.0
        else:
            labels[i] = 2.0
    return labels

def get_labels_filter_bidirectional(dataset, rolling1=200, rolling2=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame:
    """
    Generates trading labels based on price deviation from two Savitzky-Golay filters applied
    in opposite directions (forward and reversed) to the closing price data.

    This function calculates trading signals (buy/sell) based on the price's 
    position relative to smoothed price trends generated by two Savitzky-Golay filters 
    with potentially different window sizes (`rolling1`, `rolling2`). 

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        rolling1 (int, optional): Window size for the first Savitzky-Golay filter. Defaults to 200.
        rolling2 (int, optional): Window size for the second Savitzky-Golay filter. Defaults to 200.
        quantiles (list, optional): Quantiles to define the "reversion zones". Defaults to [.45, .55].
        polyorder (int, optional): Polynomial order for both Savitzky-Golay filters. Defaults to 3.

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (no signal) are removed.
                       - Rows with missing values (NaN) are removed.
                       - Temporary 'lvl1' and 'lvl2' columns are removed.
    """

    # Apply the first Savitzky-Golay filter (forward direction)
    smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling1, polyorder=polyorder)
    
    # Apply the second Savitzky-Golay filter (could be in reverse direction if rolling2 is negative)
    smoothed_prices2 = savgol_filter(dataset['close'].values, window_length=rolling2, polyorder=polyorder)

    # Calculate price deviations from both smoothed price series
    diff1 = dataset['close'] - smoothed_prices
    diff2 = dataset['close'] - smoothed_prices2

    # Add price deviations as new columns to the DataFrame
    dataset['lvl1'] = diff1
    dataset['lvl2'] = diff2
    
    # Remove rows with NaN values 
    dataset = dataset.dropna()

    # Calculate quantiles for the "reversion zones" for both price deviation series
    q1 = dataset['lvl1'].quantile(quantiles).to_list()
    q2 = dataset['lvl2'].quantile(quantiles).to_list()

    # Extract relevant data for label calculation
    close = dataset['close'].values
    lvl1 = dataset['lvl1'].values
    lvl2 = dataset['lvl2'].values
    
    # Calculate buy/sell labels using the 'calc_labels_bidirectional' function
    labels = calc_labels_bidirectional(close, lvl1, lvl2, q1, q2)

    # Process the dataset and labels
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index) # Remove bad signals (if any)
    
    # Return the DataFrame with temporary columns removed
    return dataset.drop(columns=['lvl1', 'lvl2'])

この関数は、売り取引と買い取引に対応する平滑化期間として、rolling1とrolling2を受け取ります。これらのパラメータを変化させることで、新しいデータに対するラベル付けや汎化能力を向上させることを試みることができます。たとえば、通貨ペアが上昇トレンドにあり、買い取引を優先的におこないたい場合、売り取引をラベル付けするためのrolling1ウィンドウの長さを長くすると、売り取引は少なくなるか、非常に強いトレンド反転のタイミングでのみ発生するようになります。買い取引については、rolling2ウィンドウの長さを短くすることで、売り取引よりも多くの買い取引が発生するようになります。

利益のある取引に制限を設けたラベル付けとフィルタ選択

前述の通り、提案した取引シグナルでは、ラベル付けされたものの明らかに利益が出ない取引が存在する場合があります。これはバグではなく、むしろ意図された特徴です。

利益のある取引のみをラベル付けするようにチェックを追加することも可能です。これは、資産曲線を大きなドローダウンのない理想的な直線に近づけたい場合に有用です。

また、これまで単一のSavitzky-Golayフィルタのみを使用してきましたが、単純移動平均やスプラインをフィルタとして追加することで、多様性を高めたいと考えています。

ここでは、このような取引サンプル生成方法の選択肢を見ていきます。基礎として、利益制限およびフィルタ選択を考慮したget_labels_mean_reversion関数を使用します。

@njit
def calculate_labels_mean_reversion(close, lvl, markup, min_l, max_l, q):
    labels = np.empty(len(close) - max_l, dtype=np.float64)
    for i in range(len(close) - max_l):
        rand = random.randint(min_l, max_l)
        curr_pr = close[i]
        curr_lvl = lvl[i]
        future_pr = close[i + rand]

        if curr_lvl > q[1] and (future_pr + markup) < curr_pr:
            labels[i] = 1.0
        elif curr_lvl < q[0] and (future_pr - markup) > curr_pr:
            labels[i] = 0.0
        else:
            labels[i] = 2.0
    return labels

def get_labels_mean_reversion(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=0) -> pd.DataFrame:
    """
    Generates labels for a financial dataset based on mean reversion principles.

    This function calculates trading signals (buy/sell) based on the deviation of
    the price from a chosen moving average or smoothing method. It identifies
    potential buy opportunities when the price deviates significantly below its 
    smoothed trend, anticipating a reversion to the mean.

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        markup (float): The percentage markup used to determine buy signals.
        min_l (int, optional): Minimum number of consecutive days the markup must hold. Defaults to 1.
        max_l (int, optional): Maximum number of consecutive days the markup is considered. Defaults to 15.
        rolling (float, optional): Rolling window size for smoothing/averaging. 
                                     If method='spline', this controls the spline smoothing factor.
                                     Defaults to 0.5.
        quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55].
        method (str, optional): Method for calculating the price deviation:
                                 - 'mean': Deviation from the rolling mean.
                                 - 'spline': Deviation from a smoothed spline.
                                 - 'savgol': Deviation from a Savitzky-Golay filter.
                                 Defaults to 'spline'.
        shift (int, optional): Shift the smoothed price data forward (positive) or backward (negative).
                                 Useful for creating a lag/lead effect. Defaults to 0.

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (no signal) are removed.
                       - Rows with missing values (NaN) are removed.
                       - The temporary 'lvl' column is removed. 
    """

    # Calculate the price deviation ('lvl') based on the chosen method
    if method == 'mean':
        dataset['lvl'] = (dataset['close'] - dataset['close'].rolling(rolling).mean())
    elif method == 'spline':
        x = np.array(range(dataset.shape[0]))
        y = dataset['close'].values
        spl = UnivariateSpline(x, y, k=3, s=rolling) 
        yHat = spl(np.linspace(min(x), max(x), num=x.shape[0]))
        yHat_shifted = np.roll(yHat, shift=shift) # Apply the shift
        dataset['lvl'] = dataset['close'] - yHat_shifted
        dataset = dataset.dropna()  # Remove NaN values potentially introduced by spline/shift
    elif method == 'savgol':
        smoothed_prices = savgol_filter(dataset['close'].values, window_length=int(rolling), polyorder=3)
        dataset['lvl'] = dataset['close'] - smoothed_prices

    dataset = dataset.dropna()  # Remove NaN values before proceeding
    q = dataset['lvl'].quantile(quantiles).to_list()  # Calculate quantiles for the 'reversion zone'

    # Prepare data for label calculation
    close = dataset['close'].values
    lvl = dataset['lvl'].values
    
    # Calculate buy/sell labels 
    labels = calculate_labels_mean_reversion(close, lvl, markup, min_l, max_l, q) 

    # Process the dataset and labels
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index)  # Remove sell signals (if any)
    return dataset.drop(columns=['lvl'])  # Remove the temporary 'lvl' column

このセクションの冒頭で説明され、前回の記事でも使用したget_labels関数のコードを利用して、取引の収益性を確認し、基礎としました。この原則に従い、フィルタを用いたラベル付けを通過した取引が選択されます。指定されたステップ数先まで利益が出る取引のみが選ばれ、それ以外は2.0としてマークされ、その後データセットから削除されます。また、2つの新しいフィルタとして、移動平均とスプラインを追加しました。

単純移動平均は取引で広く知られていますが、スプラインの構築方法は誰もが知っているわけではないため、説明が必要です。

スプラインは、関数を近似するための柔軟なツールです。関数全体に対して1つの複雑な多項式を構築する代わりに、スプラインは定義域を複数の区間に分割し、それぞれの区間で別々の多項式を構築します。これらの多項式は区間の境界で滑らかに結合され、連続的で滑らかな曲線を作り出します。

スプラインにはさまざまな種類がありますが、構築の原理は共通しています。

定義域の分割：関数が定義されている元の区間を、ノードと呼ばれる点によって複数の部分区間に分割します。
多項式の次数の選択：各部分区間で使用する多項式の次数を決定します。
多項式の構築：各部分区間において、選択した次数の多項式を構築し、その区間内のデータ点を通過するようにします。
滑らかさの確保：区間の境界でスプラインが滑らかになるように、多項式の係数を選択します。通常は、隣接する多項式の値およびその導関数がノードにおいて一致するようにします。

スプラインは、金融時系列分析において以下の用途に有用です。

データ補間および平滑化：スプラインを用いることで、データ内のノイズを平滑化し、観測値が欠損している点における時系列の値を推定できます。
トレンドのシミュレーション：スプラインは、短期的な変動から分離した長期トレンドをモデル化するために使用できます。
予測：特定の種類のスプラインは、時系列の将来値の予測に使用できます。
導関数の推定：スプラインを用いることで、時系列の導関数を推定でき、価格の変化率の分析に役立ちます。

本記事では、Savitzky-Golayフィルタを使用した場合と同様に、スプラインおよび移動平均を用いて時系列を平滑化します。各フィルタごとにラベル付けを実行し、その結果を比較して、状況に応じて最適な方法を選択します。

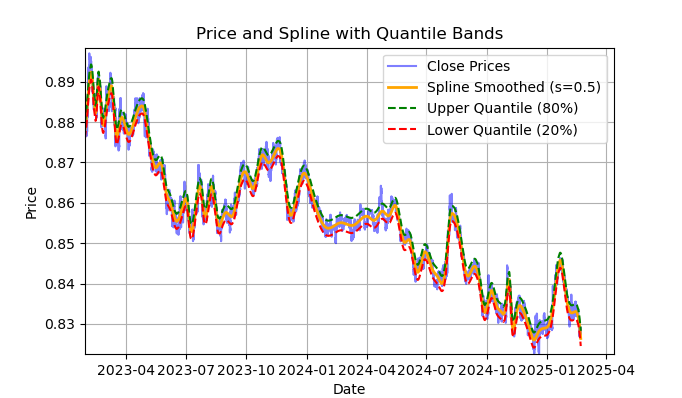
図2：スプラインフィルタとバンド（分位数）によるフィルタリング

図2は、スプラインフィルタの平滑化ラインと、20分位および80分位のバンドを示しています。スプラインフィルタとSavitzky-Golayフィルタの主な違いは、平滑化係数sおよび多項式の次数に応じて、区分的な線形または非線形関数を用いて系列を平滑化する点です。平滑化係数sは0.1〜1の範囲で設定するのが適切であり、多項式の次数は通常1〜3の範囲で設定します。これらのパラメータを変更することで、得られる平滑化結果の違いを視覚的に評価できます。コードでは多項式の次数k=3に固定していますが、変更することも可能です。

スプラインの構築および視覚的評価のためのコードは以下のとおりです。

import pandas as pd
from scipy.interpolate import UnivariateSpline
import matplotlib.pyplot as plt

def plot_close_filter_quantiles(dataset, rolling=200, quantiles=[0.2, 0.8]):
    """
    Plots close prices with spline smoothing and quantile bands.

    Args:
        dataset (pd.DataFrame): DataFrame with 'close' column and datetime index.
        rolling (int, optional): Rolling window size for spline smoothing. 
                                  Defaults to 200.
        quantiles (list, optional): Quantiles for band calculation. 
                                     Defaults to [0.2, 0.8].
        s (float, optional): Smoothing factor for UnivariateSpline. 
                             Adjusts the spline stiffness. Defaults to 1000.
    """
    
    # Create spline smoothing
    # Convert datetime index to numerical values (Unix timestamps)
    numerical_index = pd.to_numeric(dataset.index)
    
    # Create spline smoothing using the numerical index
    spline = UnivariateSpline(numerical_index, dataset['close'], k=3, s=rolling)  
    smoothed = spline(numerical_index)
    
    # Calculate difference between prices and filter
    lvl = dataset['close'] - smoothed
    
    # Get quantile values
    q_low, q_high = lvl.quantile(quantiles).tolist()
    
    # Calculate bands based on quantiles
    upper_band = smoothed + q_high
    lower_band = smoothed + q_low
    
    # Create plot
    plt.figure(figsize=(14, 7))
    plt.plot(dataset.index, dataset['close'], label='Close Prices', color='blue', alpha=0.5)
    plt.plot(dataset.index, smoothed, label=f'Spline Smoothed (s={rolling})', color='orange', linewidth=2)
    plt.plot(dataset.index, upper_band, label=f'Upper Quantile ({quantiles[1]*100:.0f}%)', 
             color='green', linestyle='--')
    plt.plot(dataset.index, lower_band, label=f'Lower Quantile ({quantiles[0]*100:.0f}%)', 
             color='red', linestyle='--')
    
    # Configure display
    plt.title('Price and Spline with Quantile Bands')
    plt.xlabel('Date')
    plt.ylabel('Price')
    plt.legend()
    plt.grid(True)
    plt.show()

取引ラベル付けコードを完全に理解するために、calculate_labels_mean_reversion関数の詳細な説明を以下に示します。

calculate_labels_mean_reversion関数

入力データ

close：終値の配列
lvl：平滑化系列からの価格乖離の配列
markup：パーセント指定
min_l：条件を検証する最小ローソク足数
max_l：条件を検証する最大ローソク足数
q：シグナルゾーンを定義する分位点の配列

以下がロジックです。

1. 初期化：シグナルを格納するための空のlabels配列を「len(close) - max_l」の長さで作成します。将来価格を参照するため、長さを短縮しています。

2. 価格のループ処理：インデックスiを0から「len(close) - max_l - 1」まで変化させ、各close[i]について処理します。

randとしてmin_lからmax_lの範囲でランダムな整数を定義します。
curr_prとして現在価格、curr_lvlとして現在の乖離、future_prとしてrand本先の将来価格を取得します。
売りシグナル：curr_lvlが上位分位点q[1]を上回り、かつmarkupを考慮したfuture_prが現在価格を下回る場合、labels[i]を1.0に設定します。
買いシグナル：curr_lvlが下位分位点q[0]を下回り、かつmarkupを差し引いたfuture_prが現在価格を上回る場合、labels[i]を0.0に設定します。
シグナルなし：その他の場合はlabels[i]を2.0に設定します。

3. 結果を返す：シグナル付きのlabels配列を返します。

get_labels_mean_reversion関数

入力データ

データセット：close列を含む金融データのDataFrame
markup：パーセント指定
min_l：条件を検証する最小ローソク足数
max_l：条件を検証する最大ローソク足数
rolling：平滑化パラメータ（ウィンドウサイズまたは比率）
quantiles：シグナルゾーンを決定する分位値
method：平滑化法（mean、spline、savgol）
shift：滑化系列のシフト量

以下がロジックです。

1. 乖離の計算：選択されたmethodに応じて、終値closeの平滑化系列からの乖離lvlを計算します。

mean：移動平均からの乖離
spline：スプライン平滑化曲線からの乖離
savgol：平滑化されたSavitzky-Golayフィルタからの乖離

2. 欠損値の削除datasetからNaNを含む行を削除します。

3. 分位数の計算lvlの乖離値に対して分位点qを計算します。

4. データの準備datasetからclose配列およびlvl配列を抽出します。

5. シグナルの計算

準備したデータを用いてcalculate_labels_mean_reversion関数を呼び出し、シグナルを格納したlabels配列を取得します。

6. DataFrameの処理

datasetをlabelsの長さに合わせて切り詰めます。
labelsを新しいlabels列としてdatasetに追加します。
datasetからNaNを含む行を削除します。
labelsが2.0（シグナルなし）の行を削除する
lvl列を削除します。

7. 結果を返す：labels列に買い・売りシグナルを含む修正済みdatasetのみを返します。

バリエーションとして、単一のフィルタではなく、異なる期間を持つ複数のフィルタに対して条件を検証する同様のサンプル生成方法を実装します。すべてのフィルタにおいて条件が満たされ、かつ方向（買いまたは売り）が一致し、さらに将来n本先までの期間で取引が利益となる場合のみ、ラベル付け条件を満たすものとします。それ以外の場合は無視し、学習サンプルから除外します。

@njit
def calculate_labels_mean_reversion_multi(close_data, lvl_data, q, markup, min_l, max_l, windows):
    labels = []
    for i in range(len(close_data) - max_l):
        rand = random.randint(min_l, max_l)
        curr_pr = close_data[i]
        future_pr = close_data[i + rand]

        buy_condition = True
        sell_condition = True
        qq = 0
        for rolling in windows:
            curr_lvl = lvl_data[i, qq]            
            if not (curr_lvl >= q[qq][1]):
                sell_condition = False
            if not (curr_lvl <= q[qq][0]):
                buy_condition = False
            qq+=1
    
        if sell_condition and (future_pr + markup) < curr_pr:
            labels.append(1.0)
        elif buy_condition and (future_pr - markup) > curr_pr:
            labels.append(0.0)
        else:
            labels.append(2.0)
    return labels

def get_labels_mean_reversion_multi(dataset, markup, min_l=1, max_l=15, windows=[0.2, 0.3, 0.5], quantiles=[.45, .55]):
    """
    Generates labels for a financial dataset based on mean reversion 
    principles using multiple smoothing windows.

    This function calculates trading signals (buy/sell) based on the deviation 
    of the price from smoothed price trends calculated using multiple spline 
    smoothing factors (windows). It identifies potential buy opportunities when 
    the price deviates significantly below its smoothed trends across multiple
    timeframes.

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        markup (float): The percentage markup used to determine buy signals.
        min_l (int, optional): Minimum number of consecutive days the markup must hold. Defaults to 1.
        max_l (int, optional): Maximum number of consecutive days the markup is considered. Defaults to 15.
        windows (list, optional): List of smoothing factors (rolling window equivalents) 
                                   for spline calculations. Defaults to [0.2, 0.3, 0.5].
        quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55].

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (sell signal) are removed.
                       - Rows with missing values (NaN) are removed. 
    """

    q = []  # Initialize an empty list to store quantiles for each window
    lvl_data = np.empty((dataset.shape[0], len(windows)))  # Initialize a 2D array to store price deviation data

    # Calculate price deviation from smoothed trends for each window
    for i, rolling in enumerate(windows):
        x = np.array(range(dataset.shape[0]))  # Create an array of x-values (time index)
        y = dataset['close'].values  # Extract closing prices
        spl = UnivariateSpline(x, y, k=3, s=rolling)  # Create a spline smoothing function
        yHat = spl(np.linspace(min(x), max(x), num=x.shape[0]))  # Generate smoothed price data
        lvl_data[:, i] = dataset['close'] - yHat  # Calculate price deviation from smoothed prices
        q.append(np.quantile(lvl_data[:, i], quantiles).tolist())  # Calculate and store quantiles

    dataset = dataset.dropna()  # Remove NaN values before proceeding

    close_data = dataset['close'].values  # Extract closing prices 

    # Calculate buy/hold labels using multiple price deviation series
    labels = calculate_labels_mean_reversion_multi(close_data, lvl_data, q, markup, min_l, max_l, windows)

    # Process the dataset and labels
    dataset = dataset.iloc[:len(labels)].copy()  # Trim the dataset to match label length
    dataset['labels'] = labels  # Add the calculated labels as a new column
    dataset = dataset.dropna()  # Remove rows with NaN values
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index)  # Remove sell signals (if any)
    
    return dataset

最後に、平均回帰取引のための別のラベル付け関数を実装します。この関数では、分位点を観測期間全体に対して計算するのではなく、指定した期間のスライディングウィンドウ内で計算します。これにより、価格が平均から乖離する際のボラティリティの変動による影響を平滑化できます。

@njit
def calculate_labels_mean_reversion_v(close_data, lvl_data, volatility_group, quantile_groups, markup, min_l, max_l):
    labels = []
    for i in range(len(close_data) - max_l):
        rand = random.randint(min_l, max_l)
        curr_pr = close_data[i]
        curr_lvl = lvl_data[i]
        curr_vol_group = volatility_group[i]
        future_pr = close_data[i + rand]

        q = quantile_groups[curr_vol_group]

        if curr_lvl > q[1] and (future_pr + markup) < curr_pr:
            labels.append(1.0)
        elif curr_lvl < q[0] and (future_pr - markup) > curr_pr:
            labels.append(0.0)
        else:
            labels.append(2.0)
    return labels

def get_labels_mean_reversion_v(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=1, volatility_window=20) -> pd.DataFrame:
    """
    Generates trading labels based on mean reversion principles, incorporating
    volatility-based adjustments to identify buy opportunities.

    This function calculates trading signals (buy/sell), taking into account the 
    volatility of the asset. It groups the data into volatility bands and calculates 
    quantiles for each band. This allows for more dynamic "reversion zones" that 
    adjust to changing market conditions.

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        markup (float): The percentage markup used to determine buy signals.
        min_l (int, optional): Minimum number of consecutive days the markup must hold. Defaults to 1.
        max_l (int, optional): Maximum number of consecutive days the markup is considered. Defaults to 15.
        rolling (float, optional): Rolling window size or spline smoothing factor (see 'method'). 
                                     Defaults to 0.5.
        quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55].
        method (str, optional): Method for calculating the price deviation:
                                 - 'mean': Deviation from the rolling mean.
                                 - 'spline': Deviation from a smoothed spline.
                                 - 'savgol': Deviation from a Savitzky-Golay filter.
                                 Defaults to 'spline'.
        shift (int, optional): Shift the smoothed price data (lag/lead effect). Defaults to 1.
        volatility_window (int, optional): Window size for calculating volatility. Defaults to 20.

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (no signal) are removed.
                       - Rows with missing values (NaN) are removed.
                       - Temporary 'lvl', 'volatility', 'volatility_group' columns are removed.
    """

    # Calculate Volatility
    dataset['volatility'] = dataset['close'].pct_change().rolling(window=volatility_window).std()
    
    # Divide into 20 groups by volatility 
    dataset['volatility_group'] = pd.qcut(dataset['volatility'], q=20, labels=False)
    
    # Calculate price deviation ('lvl') based on the chosen method
    if method == 'mean':
        dataset['lvl'] = (dataset['close'] - dataset['close'].rolling(rolling).mean())
    elif method == 'spline':
        x = np.array(range(dataset.shape[0]))
        y = dataset['close'].values
        spl = UnivariateSpline(x, y, k=3, s=rolling)
        yHat = spl(np.linspace(min(x), max(x), num=x.shape[0]))
        yHat_shifted = np.roll(yHat, shift=shift) # Apply the shift 
        dataset['lvl'] = dataset['close'] - yHat_shifted
        dataset = dataset.dropna() 
    elif method == 'savgol':
        smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling, polyorder=5)
        dataset['lvl'] = dataset['close'] - smoothed_prices

    dataset = dataset.dropna()
    
    # Calculate quantiles for each volatility group
    quantile_groups = {}
    for group in range(20):
        group_data = dataset[dataset['volatility_group'] == group]['lvl']
        quantile_groups[group] = group_data.quantile(quantiles).to_list()
    
    # Prepare data for label calculation (potentially using Numba)
    close_data = dataset['close'].values
    lvl_data = dataset['lvl'].values
    volatility_group = dataset['volatility_group'].values

    # Calculate buy/sell labels 
    labels = calculate_labels_mean_reversion_v(close_data, lvl_data, volatility_group, quantile_groups, markup, min_l, max_l)
    
    # Process dataset and labels
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index) # Remove sell signals
    
    # Remove temporary columns and return
    return dataset.drop(columns=['lvl', 'volatility', 'volatility_group'])

これで、実験に使用できる複数の取引シグナルが揃いました。各アプローチは組み合わせることができ、さらに新しい手法を作成することも可能です。

上記で説明した取引サンプル生成方法の一覧を、labeling_lib.pyライブラリから以下に示します。これらを基に、市場パターンへの理解度や最終的に実現したい戦略に応じて、既存のサンプル生成方法を修正したり、新しいサンプル生成方法を作成したりできます。なお、このモジュールには他にもカスタム取引サンプル生成方法が含まれていますが、それらは平均回帰戦略には関連しないため、本記事では説明していません。

# FILTERING BASED LABELING W/O RESTRICTIONS
def get_labels_filter(dataset, rolling=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame
def get_labels_multiple_filters(dataset, rolling_periods=[200, 400, 600], quantiles=[.45, .55], window=100, polyorder=3) -> pd.DataFrame
def get_labels_filter_bidirectional(dataset, rolling1=200, rolling2=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame:

# MEAN REVERSION WITH RESTRICTIONS BASED LABELING
def get_labels_mean_reversion(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=0) -> pd.DataFrame
def get_labels_mean_reversion_multi(dataset, markup, min_l=1, max_l=15, windows=[0.2, 0.3, 0.5], quantiles=[.45, .55]) -> pd.DataFrame
def get_labels_mean_reversion_v(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=1, volatility_window=20) -> pd.DataFrame:

いよいよ記事の後半に進みます。ここでは市場モードのクラスタリングを取り上げ、その後、平均回帰アプローチと組み合わせて取引システムを構築します。

何をクラスタ化するのか、そしてなぜそれが必要なのか

クラスタリングをおこなう前に、そもそもなぜそれが必要なのかを明確にする必要があります。トレンド、レンジ、高ボラティリティ期間、低ボラティリティ期間、さまざまなパターンや特徴を含む価格チャートを想像してみてください。価格チャートは一様なものではなく、常に同じパターンが存在しているわけではありません。むしろ、時期によって異なるパターンが出現し、別の期間では消滅することもあると言えます。

クラスタリングを用いることで、元の時系列を特定の特徴に基づいて複数の状態に分割し、それぞれの状態が類似した観測値を表すようにできます。これにより、より均質で類似したデータに対して学習をおこなえるため、取引システムの構築が容易になる可能性があります。少なくとも、そのように考えることができます。当然ながら、この場合取引システムは全期間の履歴データで動作するのではなく、与えられたクラスタに属する値のみから構成される、時間的に分散した選択的な部分データ上で動作することになります。

クラスタリング後は、選択されたサンプルのみにラベル付け（固有のクラスラベルの付与）をおこない、最終モデルを構築します。クラスタが類似した観測値からなる均質なデータを含んでいれば、そのラベル付けもより一貫性のあるものとなり、結果として予測可能性が高まります。複数のクラスタを取得し、それぞれを個別にラベル付けしたうえで、各クラスタのデータに対して機械学習モデルを学習させ、学習データおよびテストデータで評価できます。モデルが十分に学習し、新しいデータに対して汎化および予測できるクラスタが見つかれば、取引システム構築の課題は実質的に完了したと言えます。

市場モードを特定するための金融時系列クラスタリング

このセクションを読む前に、前回の記事で説明した各種クラスタリングアルゴリズムについて確認しておくとよいでしょう。そこでは、さまざまなクラスタリング手法の比較表およびテスト結果も示されています。本記事では、最も高速かつ効率的である従来型のk-meansクラスタリングアルゴリズムを採用します。

get_features関数による特徴量生成の段階では、クラスタリングに使用する特徴量がデータセット内に含まれるようにしておく必要があります。ここでは、まず3つの基本的なオプションから始めることを提案します。市場レジームを適切に表現できると考える他の特徴量があれば、自由に追加してください。その場合は、特徴量生成関数に計算処理を追加し、名称に「meta_feature」を含める必要があります。これにより、後段でメイン特徴量と区別できます。

def get_features(data: pd.DataFrame) -> pd.DataFrame:
    pFixed = data.copy()
    pFixedC = data.copy()
    count = 0

    for i in hyper_params['periods']:
        pFixed[str(count)] = pFixedC.rolling(i).mean()
        count += 1
    
    for i in hyper_params['periods_meta']:
        pFixed[str(count)+'meta_feature'] = pFixedC.rolling(i).skew()
        count += 1

    # for i in hyper_params['periods_meta']:
    #     pFixed[str(count)+'meta_feature'] = pFixedC.rolling(i).std()
    #     count += 1

    # for i in hyper_params['periods_meta']:
    #     pFixed[str(count)+'meta_feature'] = pFixedC - pFixedC.rolling(i).mean()
    #     count += 1

    return pFixed.dropna()

最初のループでは、periodsリストに指定されたすべての特徴量を計算します。これらは、売買方向を予測するメインの機械学習モデルの学習に使用される主要特徴量です。この例では、異なる期間の単純移動平均を使用しています。

2番目のループでは、periods_metaリストに指定された特徴量を計算します。これらが市場レジームのクラスタリングに使用される特徴量です。デフォルトでは、スライディングウィンドウ内の価格の歪度に基づいてクラスタリングをおこないます。コメントアウトされている部分は、スライディングウィンドウ内の標準偏差、または価格増分に基づく特徴量計算に対応しています。特徴量の選択は経験的におこない、さまざまな組み合わせを試します。実験の結果、歪度に基づく（すなわち非対称性に基づく）クラスタリングはデータを良好に分離できることが確認されています。そのため、本記事ではこの手法を使用します。

歪度（または非対称性）とは、データ分布がその平均値に対してどの程度対称でないかを示す特性です。歪度は、分布が対称形（たとえば正規分布）からどの程度逸脱しているかを測定します。歪度は歪度係数によって定量化されます。歪度に基づくクラスタリングを用いることで、分布特性が類似したデータ群を識別でき、市場モードの特定に役立ちます。たとえば、正の歪度は、稀ではあるが強い価格急騰が発生する期間（例：危機時）を示す可能性があり、負の歪度は、より滑らかな価格変動が続く期間を示す可能性があります。

特徴量の生成が完了した後、最終データセットはクラスタリングを実行する関数に渡されます。この関数は、新たにclusters列を追加し、各サンプルに対応するクラスタ番号を格納します。

def clustering(dataset, n_clusters: int) -> pd.DataFrame:
    data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy()
    meta_X = data.loc[:, data.columns.str.contains('meta_feature')]
    data['clusters'] = KMeans(n_clusters=n_clusters).fit(meta_X).labels_
    return data

「先読み」を防ぐため、アルゴリズム設定で指定された日付の前後でデータを切り詰め、モデル学習に使用されるデータのみでクラスタリングを実行します。また、クラスタリングに使用する特徴量は、列名に「meta_feature」を含むもののみを選択しています。

アルゴリズムのハイパーパラメータはすべて辞書に格納されており、このデータを用いて特徴量生成や学習期間の選択などをおこないます。

hyper_params = {
    'symbol': 'EURGBP_H1',
    'export_path': '/Users/dmitrievsky/Library/Containers/com.isaacmarovitz.Whisky/Bottles/54CFA88F-36A3-47F7-915A-D09B24E89192/drive_c/Program Files/MetaTrader 5/MQL5/Include/Mean reversion/',
    # 'export_path': '/Users/dmitrievsky/Library/Containers/com.isaacmarovitz.Whisky/Bottles/54CFA88F-36A3-47F7-915A-D09B24E89192/drive_c/Program Files (x86)/RoboForex MT4 Terminal/MQL4/Include/',
    'model_number': 0,
    'markup': 0.00010,
    'stop_loss':  0.02000,
    'take_profit': 0.00200,
    'periods': [i for i in range(5, 300, 30)],
    'periods_meta': [10],
    'backward': datetime(2000, 1, 1),
    'forward': datetime(2021, 1, 1),
    'n_clusters': 10,
    'rolling': 200,
}

銘柄の価格データが格納されているファイル名
学習済みモデルをMetaTrader5ターミナルの#includeディレクトリへエクスポートするパス
複数モデルをエクスポートする場合に区別するためのモデルID
平均スプレッドおよび手数料を考慮したマークアップ（ポイント単位）。取引ラベルの精度向上や履歴テストに使用
高速カスタムテスターがサポートするストップロス
テイクプロフィット
主要特徴量を計算する期間リスト。リスト内の各要素が個別の特徴量に対応。要素数が多いほど特徴量も増加
クラスタリングに使用する特徴量の期間リスト
モデル学習開始日
モデル学習終了日
データを分割するクラスタ数（市場モード数）
フィルタ平滑化のためのスライディングウィンドウパラメータ

ここまで整理したら、次は全体を統合してメインのモデル学習ループを確認し、前処理および学習の各ステージを順に解析していきます。

# LEARNING LOOP
dataset = get_features(get_prices())
models = []
for i in range(1):
    data = clustering(dataset, n_clusters=hyper_params['n_clusters'])
    sorted_clusters = data['clusters'].unique()
    sorted_clusters.sort()
    for clust in sorted_clusters:
        clustered_data = data[data['clusters'] == clust].copy()
        if len(clustered_data) < 500:
            print('too few samples: {}'.format(len(clustered_data)))
            continue
    
        clustered_data = get_labels_filter(clustered_data, 
                                           rolling=hyper_params['rolling'],
                                           quantiles=[0.45, 0.55],
                                           polyorder=3
                                            )

        print(f'Iteration: {i}, Cluster: {clust}')
        clustered_data = clustered_data.drop(['close', 'clusters'], axis=1)

        meta_data = data.copy()
        meta_data['clusters'] = meta_data['clusters'].apply(lambda x: 1 if x == clust else 0)
        models.append(fit_final_models(clustered_data, meta_data.drop(['close'], axis=1)))

まず、価格と特徴量を含むデータセットを作成します。特徴量の生成方法は前述の通りです。次に、学習済みモデルを格納するためのmodelsリストを作成します。その後、ループ内で何回学習をおこなうかを指定します。デフォルトは1回です。複数モデルを学習させたい場合は、range()の引数で指定します。

その後、元のデータセットをクラスタリングし、各サンプルにクラスタ番号を割り当てます。ハイパーパラメータでn_clusters=10を指定した場合、この値が関数に渡され、10クラスタへの分割がおこなわれます。実験の結果、10クラスタが市場モードの最適数であることが確認されていますが、もちろんこの値を調整して試すことも可能です。

次に、最終的なクラスタ数を確定させ、クラスタ番号を昇順にソートします。そして各クラスタ番号に対して、対応する行だけをデータセットから抽出します。観測数が少ないクラスタは学習に不向きなため、少なくとも500サンプル以上あることを確認します。

その後、選択されたクラスタに対して取引ラベル付け関数を呼び出します。この例では、記事の最初で紹介したget_labels_filter関数を使用しています。取引にラベルが付けられた後、データは2つのデータセットに分割されます。1つ目はメイン特徴量とラベルを含むデータセット、2つ目はクラスタリングに使用したmeta特徴量とラベル0と1を含むデータセットです。ラベル1は対象クラスタに属するデータ、ラベル0はそれ以外のクラスタに属するデータを意味します。これは、取引システムが特定の市場モードでのみ取引をおこなうようにするためです。

こうして、1つ目のモデルは取引方向を予測し、2つ目のモデルは取引をおこなうべきタイミングかどうかを予測します。

次に、2つの最終モデルを受け取りCatBoostアルゴリズムで学習させるfit_final_models関数の内容を見ていきます。

def fit_final_models(clustered, meta) -> list:
    # features for model\meta models. We learn main model only on filtered labels 
    X, X_meta = clustered[clustered.columns[:-1]], meta[meta.columns[:-1]]
    X = X.loc[:, ~X.columns.str.contains('meta_feature')]
    X_meta = X_meta.loc[:, X_meta.columns.str.contains('meta_feature')]
    
    # labels for model\meta models
    y = clustered['labels']
    y_meta = meta['clusters']
    
    y = y.astype('int16')
    y_meta = y_meta.astype('int16')

    # train\test split
    train_X, test_X, train_y, test_y = train_test_split(
        X, y, train_size=0.7, test_size=0.3, shuffle=True)
    
    train_X_m, test_X_m, train_y_m, test_y_m = train_test_split(
        X_meta, y_meta, train_size=0.7, test_size=0.3, shuffle=True)


    # learn main model with train and validation subsets
    model = CatBoostClassifier(iterations=1000,
                               custom_loss=['Accuracy'],
                               eval_metric='Accuracy',
                               verbose=False,
                               use_best_model=False,
                               task_type='CPU',
                               thread_count=-1)
    model.fit(train_X, train_y, eval_set=(test_X, test_y),
              early_stopping_rounds=30, plot=False)
    
    # learn meta model with train and validation subsets
    meta_model = CatBoostClassifier(iterations=500,
                                    custom_loss=['F1'],
                                    eval_metric='F1',
                                    verbose=False,
                                    use_best_model=True,
                                    task_type='CPU',
                                    thread_count=-1)
    meta_model.fit(train_X_m, train_y_m, eval_set=(test_X_m, test_y_m),
              early_stopping_rounds=25, plot=False)

    
    R2 = test_model([model, meta_model], hyper_params['stop_loss'], hyper_params['take_profit'])
    if math.isnan(R2):
        R2 = -1.0
        print('R2 is fixed to -1.0')
    print('R2: ' + str(R2))

    return [R2, model, meta_model]

学習ステージ

1. データの準備

入力されたclusteredおよびmetaのDataFrameから、特徴量（X、X_meta）とラベル（y、y_meta）を抽出します。
ラベルのデータ型をint16に変換します。これはモデルをONNX形式に変換する際に必要です。
train_test_splitを用いて、学習用とテスト用にデータを分割します。

2. メインモデルの学習

指定されたハイパーパラメータでCatBoostClassifierオブジェクトを作成します。
モデルは（train_X、train_y）を用いて学習し、（test_X、test_y）で検証をおこない、早期終了を設定します。

3. メタモデルの学習

メタモデル用にCatBoostClassifierオブジェクトを作成し、指定されたハイパーパラメータを使用します。
このメタモデルもメインモデルと同様に、対応する学習データとテストデータを用いて学習します。

4. モデル評価

学習済みモデル（model、meta_model）はstop_lossおよびtake_profitパラメータとともにtest_model関数に渡され、、性能が評価されます。
返されるR²の値は、モデルの性能指標を表します。

5. R²を処理して結果を返す

R²がNaNの場合は、-1.0に置き換えられます。
R²の値は画面に表示されます。
関数は、R²と学習済みモデル（model、meta_model）を含むリストを返します。

クラスタごとに出力されるのは、最終的な可視テストおよびMetaTrader 5ターミナルへのエクスポートに使用できる2つの学習済み分類モデルです。学習の各反復では、ハイパーパラメータで指定されたクラスタ数と同じ数のモデルペアが作成されることに注意してください。この数にイテレーション回数を掛けることで、生成される総モデルペア数を把握できます。たとえば、クラスタ数が10、反復数が10の場合、出力されるモデルペアは100組となります。ただし、最小サンプル数条件を満たさなかったクラスタは除外されます。

モデルの学習とテスト、アルゴリズムの検証

アルゴリズムをより便利に使用するためには、Pythonのインタラクティブ環境で1行ずつ実行することを推奨します。こうすることで、ハイパーパラメータを変更したり、さまざまなサンプル生成方法を試したりすることが容易になります。また、コード全体を.ipynb形式に変換し、ノートパソコン上でIPythonから実行することも可能です。スクリプト全体を実行する場合でも、パラメータをカスタマイズするために編集が必要になります。

各ラベル付け関数は、10回のイテレーションを実行してテストすることをお勧めします。他のパラメータは、添付のスクリプトで指定されたものと同じにします。

学習ループを開始すると、各クラスタごとの各反復における学習結果が表示されます。

R2: 0.9815970951474068
Iteration: 9, Cluster: 5
R2: 0.9914890771969395
Iteration: 9, Cluster: 6
R2: 0.9450681335265942
Iteration: 9, Cluster: 7
R2: 0.9631330369697314
Iteration: 9, Cluster: 8
R2: 0.9680380185183347
Iteration: 9, Cluster: 9
R2: 0.8203651933893291

その後、すべての結果をR²の昇順でソートし、最も良いモデルを選択できます。また、テスター上で資産曲線(balance curve)を視覚的に確認することも可能です。

models.sort(key=lambda x: x[0])
test_model(models[-1][1:], hyper_params['stop_loss'], hyper_params['take_profit'], plt=True)

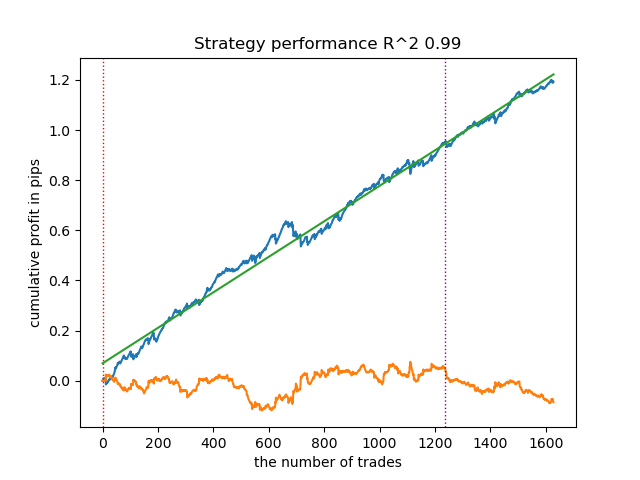
ここで強調されているのは、リストの末尾から1番目のモデル（すなわち最も高いR²を持つモデル）がテストされるという意味です。2番目に高いモデルをテストしたい場合は「-2」に設定する、というように続きます。テスターは、資産曲線（青色）と通貨ペアグラフ（橙色）、および学習期間と新規データを区切る垂直線を表示します。すべてのモデルは2010年初めから2021年初めまでのデータで学習されており、これはハイパーパラメータで指定されています。学習およびテスト期間は任意に変更可能です。本記事での全モデルのテスト期間は、2021年初めから2025年初めまでとなっています。

異なる取引サンプル生成方法のテスト

get_labels_filter(dataset, rolling=200, quantiles=[.45, .55], polyorder=3)

以下はget_labels_filterマーカーの最良結果です。

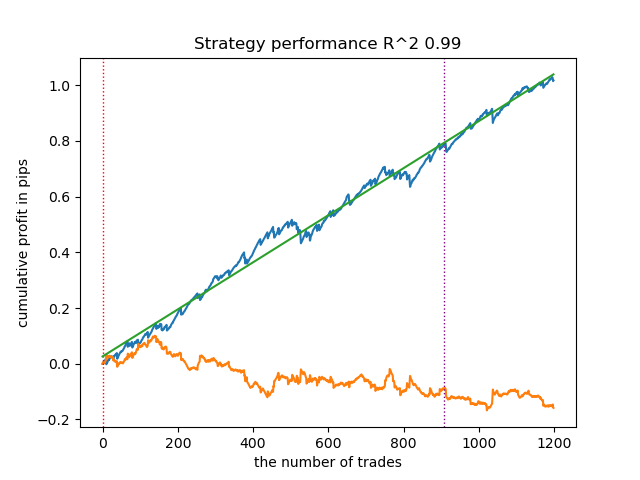
基本的なマーカーは取引のラベル付けをうまくおこない、すべてのモデルが新規データ上でも利益を出すことができました。次に、残りのマーカーについても同様にテストし、結果を確認します。

get_labels_multiple_filters(dataset,rolling_periods=[50,100,200],quantiles=[.45,.55],window=100,polyorder=3)

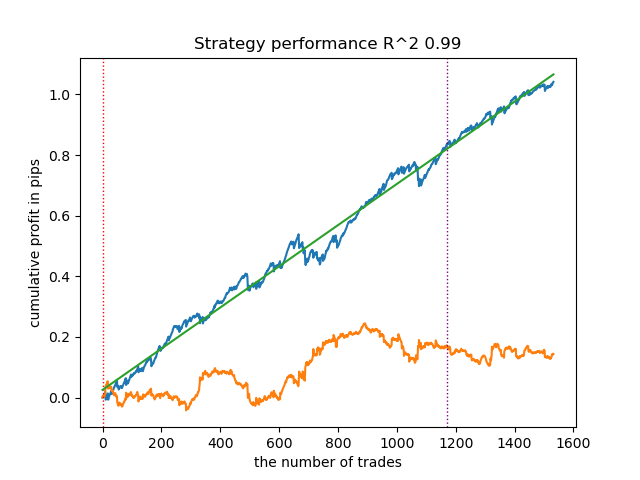
このマーカーのデータで学習したモデルは、ベースラインに比べて取引数が増加することがよくあります。ここでは設定を細かく調整していません。記事が長くなりすぎるためです。

get_labels_filter_bidirectional(dataset, rolling1=50, rolling2=200, quantiles=[.45, .55], polyorder=3)

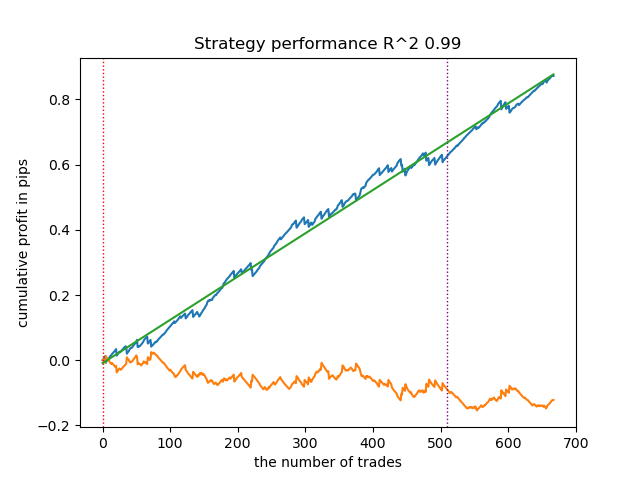
この非対称マーカーも、新規データ上で効率的であることが確認されました。買いと売りで平滑化パラメータを別々に設定することで、最適な結果が得られます。

次に、利益が確定する取引のみを対象とする制約付きマーカーに移ります。前述のマーカーは学習期間中でも滑らかな資産曲線を提供しませんが、全体のパターンは捉えています。ここで、学習データセットから負け取引を除外した場合の変化を見てみましょう。

get_labels_mean_reversion(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=0)

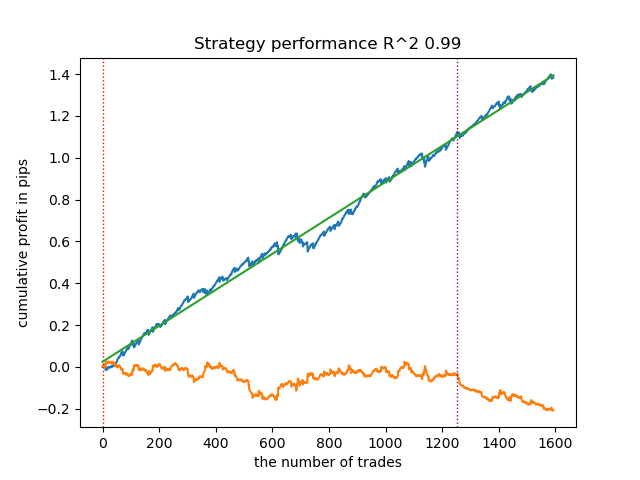
このマーカーは、スプラインをフィルタとして使用し、固定の平滑化係数0.5でテストしました。記事ではSavitzky-Golayフィルタや単純移動平均でのテストは示していません。しかし、取引の利益制約を設けることで、より滑らかなバランス曲線を得られることが確認できます。

get_labels_mean_reversion_multi(dataset, markup, min_l=1, max_l=15, windows=[0.2, 0.3, 0.5], quantiles=[.45, .55])

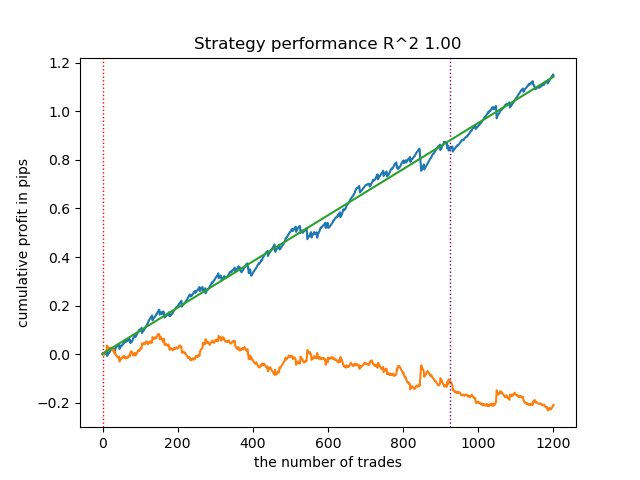
このサンプル生成方法も高品質なサンプルを提供できるため、モデルは新規データ上でも引き続き利益を出すことが可能です。

get_labels_mean_reversion_v(dataset, markup, min_l=1, max_l=15, rolling=0.2, quantiles=[.45, .55], method='spline', shift=0, volatility_window=20)

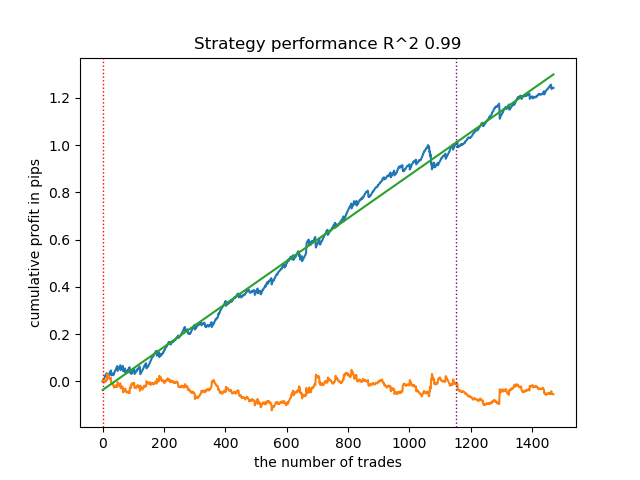
このアルゴリズムも、十分に許容できるラベル付けと、良好なモデル出力を示すことができます。

取引シグナルに関する結論

どこから始めればよいかわからず、全体が複雑に感じられる場合は、まずは許容できる結果を出せる最も基本的なサンプル生成方法を使用してください。
すぐにきれいなグラフが得られなくても、取引のラベル付けやモデル学習にはランダム要素が含まれていることを覚えておいてください。アルゴリズムを数回再実行するだけで改善する場合があります。
基本設定のサンプル生成方法であれば、いずれも許容できる結果を出すことが可能です。より精密な調整をおこなう場合は、そのうちの1つに絞り、パラメータの選定を開始してください。

クラスタリングに関する結論

バックグラウンドでは、クラスタリングを用いずにサンプル生成方法のみでテストした場合や、サンプル生成方法を使わずにクラスタリングだけでテストした場合も複数回検証しました。その結果、これらのアルゴリズムは単独で使用するよりも、組み合わせて使用した方が効果的であることがわかりました。
クラスタリングに用いる特徴量を増やしすぎる必要はありません。特徴量が多すぎるとモデルが複雑になり、新しいデータに対する汎化性能が低下します。
最適なクラスタ数は5～10程度です。クラスタ数が少なすぎると汎化能力が低く、新しいデータでの結果が悪化します。一方、クラスタ数が多すぎると、取引数が大幅に減少します。

コード内で使用したい取引シグナルのコメントを外して有効化してください。

# LEARNING LOOP
dataset = get_features(get_prices())
models = []
for i in range(10):
    data = clustering(dataset, n_clusters=hyper_params['n_clusters'])
    sorted_clusters = data['clusters'].unique()
    sorted_clusters.sort()
    for clust in sorted_clusters:
        clustered_data = data[data['clusters'] == clust].copy()
        if len(clustered_data) < 500:
            print('too few samples: {}'.format(len(clustered_data)))
            continue
    
        clustered_data = get_labels_filter(clustered_data, 
                                           rolling=hyper_params['rolling'],
                                           quantiles=[0.45, 0.55],
                                           polyorder=3
                                            )
        # clustered_data = get_labels_multiple_filters(clustered_data, 
        #                                              rolling_periods=[50, 100, 200], 
        #                                              quantiles=[.45, .55], 
        #                                              window=100, 
        #                                              polyorder=3)
        # clustered_data = get_labels_filter_bidirectional(clustered_data, 
        #                                                  rolling1=50, 
        #                                                  rolling2=200, 
        #                                                  quantiles=[.45, .55], 
        #                                                  polyorder=3)
        # clustered_data = get_labels_mean_reversion(clustered_data,
        #                                             markup = hyper_params['markup'],
        #                                             min_l=1, max_l=15, 
        #                                             rolling=0.5, 
        #                                             quantiles=[.45, .55], 
        #                                             method='spline', shift=0)
        # clustered_data = get_labels_mean_reversion_multi(clustered_data, 
        #                                                  markup = hyper_params['markup'], 
        #                                                  min_l=1, max_l=15, 
        #                                                  windows=[0.2, 0.3, 0.5], 
        #                                                  quantiles=[.45, .55])
        # clustered_data = get_labels_mean_reversion_v(clustered_data,
        #                                             markup = hyper_params['markup'],
        #                                             min_l=1, max_l=15, 
        #                                             rolling=0.2, 
        #                                             quantiles=[.45, .55], 
        #                                             method='spline', 
        #                                             shift=0, 
        #                                             volatility_window=100)

        print(f'Iteration: {i}, Cluster: {clust}')
        clustered_data = clustered_data.drop(['close', 'clusters'], axis=1)

        meta_data = data.copy()
        meta_data['clusters'] = meta_data['clusters'].apply(lambda x: 1 if x == clust else 0)
        models.append(fit_final_models(clustered_data, meta_data.drop(['close'], axis=1)))

# TESTING & EXPORT
models.sort(key=lambda x: x[0])
test_model(models[-1][1:], hyper_params['stop_loss'], hyper_params['take_profit'], plt=True)

MetaTrader 5での学習済みモデルのエクスポート

学習済みモデルとヘッダファイルをONNX形式でエクスポートする手順は、ほぼ最終段階です。添付のexport_lib.pyモジュールにはexport_model_to_ONNX(**kwargs)関数が含まれており、これがモデル保存とヘッダファイル生成の役割を担います。詳しく見てみましょう。

def export_model_to_ONNX(**kwargs):
    model = kwargs.get('model')
    symbol = kwargs.get('symbol')
    periods = kwargs.get('periods')
    periods_meta = kwargs.get('periods_meta')
    model_number = kwargs.get('model_number')
    export_path = kwargs.get('export_path')

    model[1].save_model(
    export_path +'catmodel ' + symbol + ' ' + str(model_number) +'.onnx',
    format="onnx",
    export_parameters={
        'onnx_domain': 'ai.catboost',
        'onnx_model_version': 1,
        'onnx_doc_string': 'main model',
        'onnx_graph_name': 'CatBoostModel_main'
    },
    pool=None)

    model[2].save_model(
    export_path + 'catmodel_m ' + symbol + ' ' + str(model_number) +'.onnx',
    format="onnx",
    export_parameters={
        'onnx_domain': 'ai.catboost',
        'onnx_model_version': 1,
        'onnx_doc_string': 'meta model',
        'onnx_graph_name': 'CatBoostModel_meta'
    },
    pool=None)
    
    code = '#include <Math\Stat\Math.mqh>'
    code += '\n'
    code += '#resource "catmodel '+ symbol + ' '+str(model_number)+'.onnx" as uchar ExtModel_' + symbol + '_' + str(model_number) + '[]'
    code += '\n'
    code += '#resource "catmodel_m '+ symbol + ' '+str(model_number)+'.onnx" as uchar ExtModel2_' + symbol + '_' + str(model_number) + '[]'
    code += '\n\n'
    code += 'int Periods' + symbol + '_' + str(model_number) + '[' + str(len(periods)) + \
        '] = {' + ','.join(map(str, periods)) + '};'
    code += '\n'
    code += 'int Periods_m' + symbol + '_' + str(model_number) + '[' + str(len(periods_meta)) + \
        '] = {' + ','.join(map(str, periods_meta)) + '};'
    code += '\n\n'

    # get features
    code += 'void fill_arays' + symbol + '_' + str(model_number) + '( double &features[]) {\n'
    code += '   double pr[], ret[];\n'
    code += '   ArrayResize(ret, 1);\n'
    code += '   for(int i=ArraySize(Periods'+ symbol + '_' + str(model_number) + ')-1; i>=0; i--) {\n'
    code += '       CopyClose(NULL,PERIOD_H1,1,Periods' + symbol + '_' + str(model_number) + '[i],pr);\n'
    code += '       ret[0] = MathMean(pr);\n'
    code += '       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
    code += '   ArraySetAsSeries(features, true);\n'
    code += '}\n\n'

    # get features
    code += 'void fill_arays_m' + symbol + '_' + str(model_number) + '( double &features[]) {\n'
    code += '   double pr[], ret[];\n'
    code += '   ArrayResize(ret, 1);\n'
    code += '   for(int i=ArraySize(Periods_m' + symbol + '_' + str(model_number) + ')-1; i>=0; i--) {\n'
    code += '       CopyClose(NULL,PERIOD_H1,1,Periods_m' + symbol + '_' + str(model_number) + '[i],pr);\n'
    code += '       ret[0] = MathSkewness(pr);\n'
    code += '       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
    code += '   ArraySetAsSeries(features, true);\n'
    code += '}\n\n'

    file = open(export_path + str(symbol) + ' ONNX include' + ' ' + str(model_number) + '.mqh', "w")
    file.write(code)

    file.close()
    print('The file ' + 'ONNX include' + '.mqh ' + 'has been written to disk')

関数が受け取る代表的な引数は以下の通りです。

model = models[-1]：学習済みモデル2つを格納したリスト。テスター同様、インデックス「-1」はR²が最も高いモデルに対応、「-2」は2番目に高いモデルに対応します。視覚的に良いモデルを選んだ場合、そのインデックスを使用してエクスポートします。
symbol = hyper_params['symbol']：ハイパーパラメータで指定された銘柄名（例：EURGBP_H1）。異なる銘柄用のモデルを区別するためにエクスポート時に付与されます。
periods = hyper_params['periods']：メインモデルの特徴量期間リスト
periods_meta = hyper_params['periods_meta']：追加モデルの特徴量の期間リストで、現在の市場モードを判定するために使用
model_number = hyper_params['model_number']：複数のモデルをエクスポートする場合に、上書きを避けるためのモデル番号。モデル名に付与されます。
export_path = hyper_params['export_path']：多ーミナルのincludeフォルダまたはそのサブディレクトリにファイルを保存するためのパス

この関数は、メインモデルとメタモデルの両方を.onnx形式で保存し、さらにこれらのモデルを呼び出し、特徴量を計算するためのヘッダファイルを生成します。特徴量の計算はターミナル内で直接おこなわれるため、Pythonスクリプトでの計算と完全に同一であることを確認する必要があります。コードを見ると、fill_arrays関数はメインモデル用に移動平均を計算し、fill_arrays_m関数はメタモデル用に価格の歪度を計算しています。Pythonスクリプトで特徴量を変更した場合は、この関数内またはヘッダファイル内での計算も同様に変更する必要があります。

関数を呼び出してモデルをディスクに保存する例は以下の通りです。

export_model_to_ONNX(model = models[-1],
                     symbol = hyper_params['symbol'],
                     periods = hyper_params['periods'],
                     periods_meta = hyper_params['periods_meta'],
                     model_number = hyper_params['model_number'],
                     export_path = hyper_params['export_path'])

ONNXモデルを使用して取引を実行する自動売買ボットの構築

カスタムテスターを使用して、視覚的に良好なモデルを学習し、選択したと仮定します。

次に、ターミナル内でエクスポート関数を呼び出します。

モデルをエクスポートすると、MetaTrader 5ターミナルのinclude/mean reversion/フォルダ（私の場合は他のモデルと混同しないようサブディレクトリを使用）に3つのファイルが作成されます。

catmodel EURGBP_H1 0.onnx：売買シグナルを提供するメインモデル
catmodel_m EURGBP_H1 0.onnx：取引の許可・禁止を判断する追加モデル（メタモデル）
EURGBP_H1 ONNX include 0.mqh：これらのモデルをインポートし、特徴量を計算するヘッダファイル

ONNXモデル名は常に「catmodel」で始まり、CatBoostモデルであることを示しています。その後に銘柄名と時間足が続きます。追加モデルは「_m」接尾辞が付き、メタモデルであることを示します。ヘッダファイル名は常に取引銘柄で始まり、エクスポート時に指定したモデル番号で終わるため、必要がなければ新しいモデルで既存モデルが上書きされることはありません。

次に、.mqhファイルの内容を見てみましょう。

#include <Math\Stat\Math.mqh>
#resource "catmodel EURGBP_H1 0.onnx" as uchar ExtModel_EURGBP_H1_0[]
#resource "catmodel_m EURGBP_H1 0.onnx" as uchar ExtModel2_EURGBP_H1_0[]

int PeriodsEURGBP_H1_0[10] = {5,35,65,95,125,155,185,215,245,275};
int Periods_mEURGBP_H1_0[1] = {10};

void fill_araysEURGBP_H1_0( double &features[]) {
   double pr[], ret[];
   ArrayResize(ret, 1);
   for(int i=ArraySize(PeriodsEURGBP_H1_0)-1; i>=0; i--) {
       CopyClose(NULL,PERIOD_H1,1,PeriodsEURGBP_H1_0[i],pr);
       ret[0] = MathMean(pr);
       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }
   ArraySetAsSeries(features, true);
}

void fill_arays_mEURGBP_H1_0( double &features[]) {
   double pr[], ret[];
   ArrayResize(ret, 1);
   for(int i=ArraySize(Periods_mEURGBP_H1_0)-1; i>=0; i--) {
       CopyClose(NULL,PERIOD_H1,1,Periods_mEURGBP_H1_0[i],pr);
       ret[0] = MathSkewness(pr);
       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }
   ArraySetAsSeries(features, true);
}

まず、平均値や歪度の計算に必要な数学計算ライブラリが接続されます。必要に応じて、特徴量の計算方法を変更する際には、分布の他のモーメントやその他の数学的計算にも利用可能です。次に、売買シグナルを生成するために使用する2つのONNXモデルをリソースとして読み込みます。その後、特徴量を計算するための期間配列が宣言されます。これがメインモデルおよびメタモデルへの入力データとなります。

残りの2つの関数は、これらの配列に特徴量の値を格納します。ここで注意してほしいのは、これらのファイルはPythonスクリプトからモデルをエクスポートした際に自動生成されるため、毎回ゼロから書く必要はないということです。取引用EAに接続するだけで十分です。これは、たとえば一定期間後にモデルを再学習したい場合に非常に便利です。新しいモデルをターミナルにエクスポートすれば既存のモデルは上書きされ、EAのコードに手を加えることなくボットを再コンパイルするだけで済みます。コードの量自体は最初は圧倒されるかもしれませんが、実際の操作はスクリプトを実行してボットをコンパイルするだけで済み、わずか数分で完了します。

次に、このヘッダファイルを接続してONNXモデルを初期化する取引用EAを作成する必要があります。

#include <Mean reversion/EURGBP_H1 ONNX include 0.mqh>
#include <Trade\Trade.mqh>
#include <Trade\AccountInfo.mqh>
#property strict
#property copyright "Copyright 2025, Dmitrievsky max."
#property link      "https://www.mql5.com/ru/users/dmitrievsky"
#property version   "1.0"

CTrade mytrade;
CPositionInfo myposition;

input bool Allow_Buy = true;           //Allow BUY
input bool Allow_Sell = true;          //Allow SELL
double main_threshold = 0.5;
double meta_threshold = 0.5;
sinput double   MaximumRisk=0.001;     //Progressive lot coefficient
sinput double   ManualLot=0.01;        //Fixed lot, set 0 if progressive
sinput ulong    OrderMagic = 57633493; //Orders magic
input int max_orders = 3;              //Max positions number
input int orders_time_delay = 5;       //Time delay between positions
input int max_spread = 20;             //Max spread
input int stoploss = 2000;             //Stop loss
input int takeprofit = 200;            //Take profit
input string comment = "mean reversion bot";

static datetime last_time = 0;
#define Ask SymbolInfoDouble(_Symbol, SYMBOL_ASK)
#define Bid SymbolInfoDouble(_Symbol, SYMBOL_BID)


const long  ExtInputShape [] = {1, ArraySize(PeriodsEURGBP_H1_0)};
const long  ExtInputShape2 [] = {1, ArraySize(Periods_mEURGBP_H1_0)};
long     ExtHandle = INVALID_HANDLE, ExtHandle2 = INVALID_HANDLE;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   mytrade.SetExpertMagicNumber(OrderMagic);

   ExtHandle = OnnxCreateFromBuffer(ExtModel_EURGBP_H1_0, ONNX_DEFAULT);
   ExtHandle2 = OnnxCreateFromBuffer(ExtModel2_EURGBP_H1_0, ONNX_DEFAULT);

   if(ExtHandle == INVALID_HANDLE || ExtHandle2 == INVALID_HANDLE)
     {
      Print("OnnxCreateFromBuffer error ", GetLastError());
      return(INIT_FAILED);
     }

   if(!OnnxSetInputShape(ExtHandle, 0, ExtInputShape))
     {
      Print("OnnxSetInputShape 1 failed, error ", GetLastError());
      OnnxRelease(ExtHandle);
      return(-1);
     }

   if(!OnnxSetInputShape(ExtHandle2, 0, ExtInputShape2))
     {
      Print("OnnxSetInputShape 2 failed, error ", GetLastError());
      OnnxRelease(ExtHandle2);
      return(-1);
     }

   const long output_shape[] = {1};
   if(!OnnxSetOutputShape(ExtHandle, 0, output_shape))
     {
      Print("OnnxSetOutputShape 1 error ", GetLastError());
      return(INIT_FAILED);
     }
   if(!OnnxSetOutputShape(ExtHandle2, 0, output_shape))
     {
      Print("OnnxSetOutputShape 2 error ", GetLastError());
      return(INIT_FAILED);
     }

   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   OnnxRelease(ExtHandle);
   OnnxRelease(ExtHandle2);
  }

最も重要なのは、各モデルの入力配列の次元を正しく初期化することです。これは、特徴量計算用の期間値が格納されているヘッダファイル内の配列のサイズと同じに設定します。特徴量の数は期間値の数と一致します。

両モデルの出力次元は、いずれも1に設定されます。

const long  ExtInputShape [] = {1, ArraySize(PeriodsEURGBP_H1_0)};
const long  ExtInputShape2 [] = {1, ArraySize(Periods_mEURGBP_H1_0)};

次に、モデルに対してハンドルを割り当てます。

ExtHandle = OnnxCreateFromBuffer(ExtModel_EURGBP_H1_0, ONNX_DEFAULT);
ExtHandle2 = OnnxCreateFromBuffer(ExtModel2_EURGBP_H1_0, ONNX_DEFAULT);

そして、ボットの初期化関数内で、入力と出力の次元を正しく設定します。

if(!OnnxSetInputShape(ExtHandle, 0, ExtInputShape))
     {
      Print("OnnxSetInputShape 1 failed, error ", GetLastError());
      OnnxRelease(ExtHandle);
      return(-1);
     }

if(!OnnxSetInputShape(ExtHandle2, 0, ExtInputShape2))
     {
      Print("OnnxSetInputShape 2 failed, error ", GetLastError());
      OnnxRelease(ExtHandle2);
      return(-1);
     }

ボットをチャートから削除すると、モデルも同時に削除されます。

ボットは計算を高速化するために、各新しいローソク足の始値で取引をおこないます。次に、モデルからどのようにシグナルを取得するかを確認する必要があります。

void OnTick()
  {
   if(!isNewBar())
      return;

   double features[], features_m[];
   fill_araysEURGBP_H1_0(features);
   fill_arays_mEURGBP_H1_0(features_m);

   double f[ArraySize(PeriodsEURGBP_H1_0)], f_m[ArraySize(Periods_mEURGBP_H1_0)];

   for(int i = 0; i < ArraySize(PeriodsEURGBP_H1_0); i++)
     {
      f[i] = features[i];
     }

   for(int i = 0; i < ArraySize(Periods_mEURGBP_H1_0); i++)
     {
      f_m[i] = features_m[i];
     }

   static vector out(1), out_meta(1);

   struct output
     {
      long           label[];
      float          proba[];
     };

   output out2[], out2_meta[];
   
   OnnxRun(ExtHandle, ONNX_DEBUG_LOGS, f, out, out2);
   OnnxRun(ExtHandle2, ONNX_DEBUG_LOGS, f_m, out_meta, out2_meta);

   double sig = out2[0].proba[1];
   double meta_sig = out2_meta[0].proba[1];

ONNXモデルからシグナルを取得する手順は以下の通りです。

featuresおよびfeatures_m配列を作成します。
これらの配列に、対応するfill_arrays関数を使って特徴量の値を格納します。
配列内の要素の順序は、モデルが受け取るべき順序とは逆になっているため、fおよびf_m配列を作成し、データを正しい順序に書き換えます。
モデルに出力ベクトルの次元を伝えるためのoutおよびout_metaベクトルを作成します。
予測された0/1ラベルおよび確率を受け取るための出力構造を作成します。シグナル計算には確率が使用されます。
シグナルを受け取るために、out2およびout2_metaという出力構造のインスタンスを作成します。
モデルを起動し、特徴量と出力次元を渡します。モデルは予測値を返します。
構造体のインスタンスから予測（確率）を抽出します。

最後に、取得したシグナルに基づきポジションを建てるロジックを考慮します。決済のシグナルは逆のロジックで動作します。

// OPEN POSITIONS BY SIGNALS
   if((Ask-Bid < max_spread*_Point) && meta_sig > meta_threshold &&
      AllowTrade(OrderMagic))
      if(countOrders(OrderMagic) < max_orders &&
         CheckMoneyForTrade(_Symbol, LotsOptimized(), ORDER_TYPE_BUY))
        {
         double l = LotsOptimized();
         if(sig < 1-main_threshold && Allow_Buy)
           {
            int res = -1;
            do
              {
               double stop = Bid - stoploss * _Point;
               double take = Ask + takeprofit * _Point;
               res = mytrade.PositionOpen(_Symbol, ORDER_TYPE_BUY, l, Ask, stop, take, comment);
               Sleep(50);
              }
            while(res == -1);
           }
         else
           {
            if(sig > main_threshold && Allow_Sell)
              {
               int res = -1;
               do
                 {
                  double stop = Ask + stoploss * _Point;
                  double take = Bid - takeprofit * _Point;
                  res = mytrade.PositionOpen(_Symbol, ORDER_TYPE_SELL, l, Bid, stop, take, comment);
                  Sleep(50);
                 }
               while(res == -1);
              }
           }
        }

まず、2つ目のモデルのシグナルを確認します。確率が0.5より大きければ、ポジションを建てることが許可されます（市場が必要なモードにあることを意味します）。次に、買いまたは売りの可能性を予測するメインモデルに対して条件を確認します。確率が0.5未満であれば買い、0.5より大きければ売りを示します。条件に応じて取引が開始されます。

これでボットをコンパイルし、ストラテジーテスターでテストする準備が整いました。

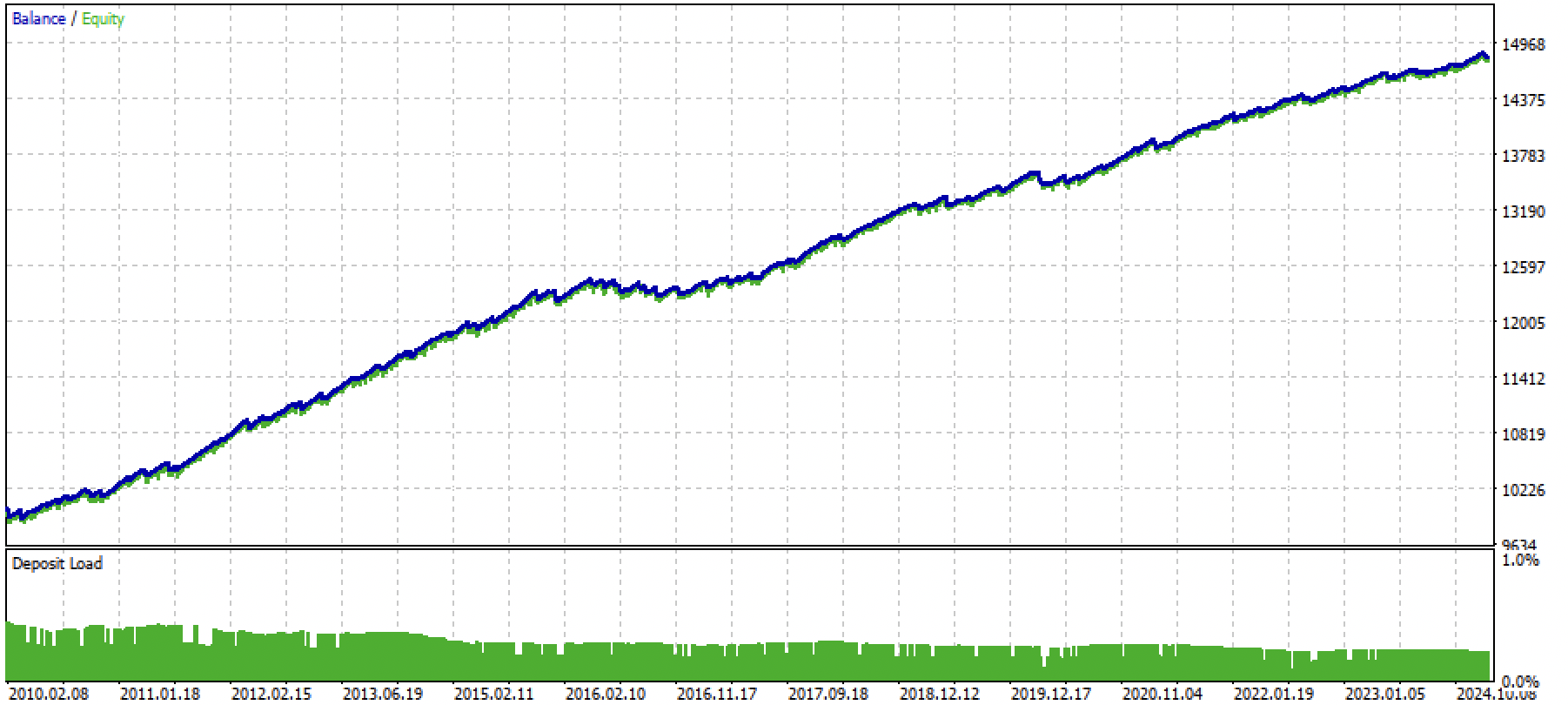
図3：平均回帰戦略を用いた学習済みモデルのテスト

結論

本記事では、機械学習を用いた平均回帰戦略の開発に関わるすべてのステップを示しました。取引のラベル付け、市場モードの識別、モデルの学習、そして完全な自動売買ボットの作成までを含む、包括的なアプローチを解説しています。

記事内には、独自に実験をおこなうために必要なすべてのコードが含まれています。

Python files.zipには、Python環境での開発用のファイルが含まれています。

ファイル名	説明
mean reversion.py	モデル学習用のメインスクリプト
labeling_lib.py	取引シグナル用モジュール
tester_lib.py	機械学習ベースのカスタムストラテジーテスター
export_lib.py	MetaTrader 5ターミナルへONNX形式でモデルをエクスポートするライブラリ
EURGBP_H1.csv	MetaTrader 5ターミナルからエクスポートしたレートデータ

MQL5 files.zipには、MetaTrader 5ターミナル用のファイルが含まれています。

ファイル名	説明
mean reversion.ex5	記事で作成したボットのコンパイル済みファイル
mean reversion.mq5	記事で使用したボットのソースコード
folder Include//Mean reversion	ONNXモデルおよびボット接続用ヘッダファイル

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16457

添付されたファイル |

ZIPをダウンロード

Python_files.zip (1503.93 KB)

MQL5_files.zip (449.31 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

最後のコメント | ディスカッションに移動 (91)

Vladimir Levchenko | 3 7月 2025 において 10:48

Maxim Dmitrievsky #:

確認したところ、すべてうまくいった。記事の学習済みモデルのファイルと、上記の更新されたボットを添付します。

記事にデモモデルが添付されているので、その後再トレーニングするのが望ましい。pythonスクリプトが理解できたら。

はい、このリリースではボット自体はコンパイルされ、正しく動作します。しかし、モデルの再トレーニングが必要です。そして一般的に、私が理解しているように、それは定期的に行われるべきです。
私はpythonを理解しつつありますが、まだすべてを理解しているわけではありません。ノートパソコンでRutopのメインリリースを起動し、現在のバージョンにアップデートした。必要なパッケージ（pandas, numba, numpy, catboost, scipy, scikit-learn）を全てインストールした。引用符をダウンロードした。MT5のメインカタログのFilesフォルダに、quotesのファイルとすべてのスクリプトを入れた。モデル・トレーニング・スクリプトのコードにパスを書きました。
MetaEditoreでスクリプトコードを修正した。そこからスクリプトを実行しようとしました。プロセスはエラーでクラッシュします（pythonのbotsパッケージが見つからず、他のパッケージのインストールスキームに従ってインストールしようとしてもエラーで終わります）。pythonコンソールからスクリプトを実行しても同じエラーが発生します。
このトピックをどの方向に掘り下げるべきかアドバイスいただけますか？

削除済み | 3 7月 2025 において 12:07

Vladimir Levchenko #:

はい、このリリースではボット自体はコンパイルされ、正しく動作します。しかし、モデルの再学習が必要です。そして一般的に、私が理解しているように、それは定期的に行われるべきです。
私はpythonを理解しつつありますが、今のところすべてがうまくいっているわけではありません。ノートパソコンでRutopのメインリリースを起動し、現在のバージョンにアップデートしました。必要なパッケージ(pandas, numba, numpy, catboost, scipy, scikit-learn)を全てインストールした。引用符をダウンロードした。MT5のメインカタログのFilesフォルダに、quotesのファイルとすべてのスクリプトを入れた。モデルトレーニングスクリプトのコードにパスを書きました。
MetaEditoreでスクリプトコードを修正した。そこからスクリプトを実行しようとしました。プロセスはエラーでクラッシュします（pythonのbotsパッケージが見つからず、他のパッケージのインストールスキームに従ってインストールしようとしてもエラーで終わります）。pythonコンソールからスクリプトを実行しても同じエラーが発生します。
このトピックをどのような方向に掘り下げるべきかアドバイスいただけますか？

Bots は記事のモジュールがあるルートディレクトリ(フォルダ)です。もしスクリプトがモジュール(追加ファイル)をインポートするときにそれらを見ないなら、ファイルへのフルパスを書いてください。

もしくは、これらのファイルをメインスクリプトと同じフォルダに放り込んで、代わりにこれをやってください：

Было
from bots.botlibs.labeling_lib import get_labels
from bots.botlibs.tester_lib import test_model
from bots.botlibs.export_lib import export_model_to_ONNX

Стало
from labeling_lib import get_labels
from tester_lib import test_model
from export_lib import export_model_to_ONNX

PythonをインストールしたときにPYTHONPATHが設定されていないと、このようなことが起こります。Pythonのインストール時にPYTHONPATHが設定されていない場合、このようなことが起こる可能性があります。つまり、Pythonはディスク上のファイルを見ません。

あるいは、インターネット上のモジュールのインポートに関する基本的なコースを読んでください。

Vladimir Levchenko | 7 7月 2025 において 15:49

Maxim Dmitrievsky #:

Bots は、記事のモジュールが置かれるルートディレクトリ(フォルダ)です。モジュール（追加ファイル）をインポートするときに、スクリプトがそれらを見ない場合は、ファイルへのフルパスを書いてください。

あるいは、これらのファイルをメインスクリプトと同じフォルダに放り込んで、代わりにこうしてください：

これは Python をインストールしたときに PYTHONPATH が設定されていなかった場合に起こる可能性があります。Pythonのインストール時にPYTHONPATHが設定されていない場合、このようなことが起こる可能性があります。つまり、pythonはディスク上のファイルを見ません。

あるいはインターネットでモジュールのインポートに関する基本的なコースを読んでください。

ごきげんよう、マキシム。ありがとう。ほぼすべて解決しました。最後の質問です。
トレーニングモデル用のメインスクリプトにコメント行（154-182）があります。私の理解では、これらは代替ディールサンプラー（マークアップ）です。しかし、試すことができません。マークアップのどれかがコメントアウトされておらず（条件付きで、154-158行目）、オリジナルのものがコメントアウトされている場合（149-153行目）、スクリプトが開始されません。
原因は何でしょうか？

ありがとうございます。）

削除済み | 7 7月 2025 において 16:41

Vladimir Levchenko #:

こんにちは、マキシム。ありがとう。ほぼすべて解決しました。最後の質問です。
モデルをトレーニングするためのメインスクリプトにコメント行（154-182）があります。私の理解では、これらは代替ディールサンプラー（マークアップ）です。しかし、試すことができません。マークアップのどれかがコメント解除され（条件付きで154-158行目）、オリジナルのものがコメントされると（149-153行目）、スクリプトが起動しません。
原因は何でしょうか、どこを見ればよいでしょうか？

ありがとうございます。）

Python インタプリタが何を書いたかのログが必要です。

Alexey Klenov | 13 10月 2025 において 14:13

Vladimir Levchenko #:

ありがとうございます。）

コメントされていないテキストが同じ行にあるか確認してください。

以下のスクリーンショットのように、下線があってはいけません。

MQL5での戦略の可視化：基準チャートに最適化結果をレイアウトする

本記事では、最適化プロセスを可視化する例を示し、4つの最適化基準ごとに上位3つのパスを表示します。また、その3つのうち1つを選択し、表やチャートでデータを表示できる機能も提供します。

市場シミュレーション（第10回）：ソケット(IV)

本記事では、MetaTrader 5を管理するためにExcelを活用する方法を、興味深い形で解説していきます。そのために、組み込みVBAを使わずに済むよう、Excelアドインを使用します。アドインが何を意味するのか分からない場合、本記事でExcelで直接Pythonをプログラミングする方法を学ぶことができます。

エラー 146 (「トレードコンテキストビジー」) と、その対処方法

この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。

取引におけるニューラルネットワーク：ハイブリッドグラフシーケンスモデル（最終部）

引き続き、異なるアーキテクチャの利点を統合し、高い分析精度と計算リソースの効率的な配分を実現するハイブリッドグラフシーケンスモデル(GSM++)を検討します。これらのモデルは、隠れたパターンを効果的に識別し、市場ノイズの影響を低減して予測精度を向上させます。