
Redes neuronales en el trading: Integración de la teoría del caos en la previsión de series temporales (Final)
Introducción
Seguimos construyendo nuestra propia visión de los planteamientos propuestos por los autores del framework Attraos. En el artículo anterior conocimos los aspectos teóricos del framework. Recordemos que usa los principios de la teoría del caos para resolver problemas de previsión de series temporales.
La arquitectura del framework Attraos es un complejo sistema multicomponente que combina técnicas de análisis no lineal, aprendizaje automático y optimización computacional. El uso de la reconstrucción del espacio de fases (Phase Space Reconstruction — PSR) permite a Attraos modelizar procesos dinámicos ocultos y considerar las relaciones no lineales entre las distintas variables del mercado. Esto permite identificar patrones coherentes en los datos del mercado y usarlos para mejorar la calidad de la previsión de los próximos movimientos de precios.
Una de las principales características de Attraos es la unidad de memoria dinámica de resolución múltiple (Multi-Resolution Dynamic Memory Unit — MDMU), que permite al modelo conservar patrones históricos del movimiento de los precios y adaptarse a las cambiantes condiciones del mercado. Esto resulta especialmente importante para los mercados financieros, donde las pautas pueden repetirse en distintos intervalos de tiempo con diferente amplitud e intensidad. El modelo se adapta dinámicamente a la estructura cambiante de los mercados financieros, ofreciendo previsiones más precisas en distintos horizontes temporales.
La aplicación de una estrategia de evolución local en el dominio de la frecuencia permite adaptarse a las condiciones cambiantes del mercado amplificando las diferencias de los atractores. Esto ayuda al modelo a minimizar los errores y controlar las desviaciones del atractor, garantizando pronósticos estables y muy precisos.
A continuación le mostramos la visualización del framework Attraos realizada por el autor.
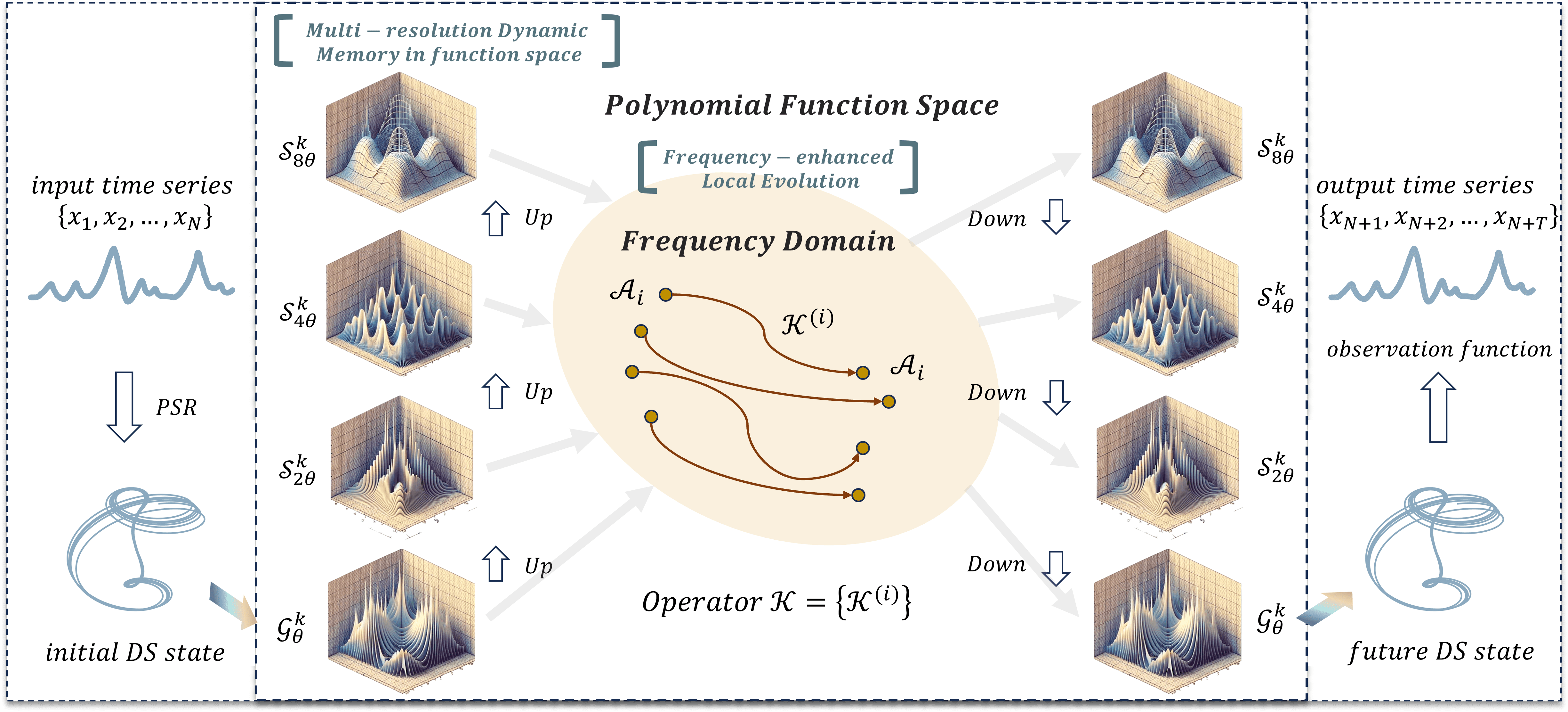
En la parte práctica del artículo anterior implementamos los componentes básicos en el lado del programa OpenCL. Y hoy crearemos los objetos en el programa principal.
Construimos un objeto Attraos
El algoritmo Attraos comienza con el módulo PSR, que transforma las series temporales analizadas en un espacio de fases considerando un desfase temporal concreto. Este proceso representa una etapa clave del preprocesamiento de datos que nos permite identificar dependencias ocultas, la estructura de las series temporales y posibles patrones latentes en la dinámica.
Una serie temporal multivariante suele representarse como una matriz en la que cada fila contiene los parámetros del sistema analizado en un punto temporal t. Sin embargo, en nuestro caso, los datos se almacenan en búferes unidimensionales y su representación matricial tiene carácter condicional. En este caso, la estructura de datos se organiza de tal manera que el búfer almacene secuencialmente los valores de los vectores que describen el estado del sistema en un punto temporal. El tamaño de dicho vector se especifica usando el parámetro window. Por consiguiente, para crear subsecuencias con cierto desfase temporal, basta con aumentar proporcionalmente el valor del parámetro window y, en consecuencia, reducir la longitud de la secuencia. Así, el proceso de transformación de las series temporales en espacio de fases no requiere recursos informáticos adicionales y se realiza únicamente usando la elección de la arquitectura del modelo.
Construiremos todas las operaciones posteriores del framework dentro del objeto CNeuronAttraos, cuya estructura mostramos a continuación.
class CNeuronAttraos : public CNeuronBaseOCL { protected: CNeuronBaseOCL cOne; CNeuronBaseOCL cX_norm; CNeuronConvOCL cA; CNeuronConvOCL cX_proj; CNeuronBaseOCL cDelta; CNeuronBaseOCL cB; CNeuronBaseOCL cC; CNeuronConvOCL cD; CNeuronBaseOCL cH; CNeuronConvOCL cDelta_proj; CNeuronBaseOCL cDeltaA; CNeuronBaseOCL cDeltaB; CNeuronBaseOCL cDeltaBX; CNeuronBaseOCL cDeltaH; CNeuronBaseOCL cHS; //--- virtual bool PScan(void); virtual bool PScanCalcGradient(void); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronAttraos(void) {}; ~CNeuronAttraos(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronAttraos; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
En la estructura presentada de la nueva clase, además del conjunto estándar de métodos virtuales redefinidos, vemos un número bastante grande de objetos internos. Cumplen diferentes funciones y hacen posible la interacción entre los elementos de la clase. El uso de objetos internos ayuda a organizar el código de forma más eficaz. Cada uno es responsable de una parte distinta del trabajo, lo cual hace que el sistema sea modular y fácil de modificar. Conforme vayamos implementando los métodos del nuevo objeto, veremos con más detalle la funcionalidad de cada uno de los componentes internos. Esto nos permitirá comprender su finalidad y apreciar su papel en la estructura general.
Todos los objetos internos se declararán estáticamente, lo cual eliminará la necesidad de crearlos y eliminarlos dinámicamente. Gracias a ello, el constructor y el destructor de la clase permanecerán vacíos, ya que la gestión de la memoria de estos objetos se efectuará automáticamente, mientras que la inicialización de todos los objetos declarados y heredados se realizará en el método Init. En los parámetros de este método obtendremos las constantes que nos permitirán definir inequívocamente la arquitectura del objeto creado. Creo que en este caso usted no tendrá ninguna duda sobre la estructura de los parámetros.
bool CNeuronAttraos::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false; SetActivationFunction(None);
En el cuerpo del método, como es habitual, llamaremos directamente al método homónimo de la clase padre, en cuyo cuerpo ya están organizados los puntos de control mínimos necesarios y el proceso de inicialización de las interfaces heredadas.
Aquí también desactivaremos explícitamente la función de activación para nuestro objeto, ya que todos los procesos se realizarán utilizando objetos internos, mientras que las interfaces heredadas solo servirán para intercambiar datos a nivel global.
Una vez ejecutadas con éxito las operaciones del método de la clase padre, inicializaremos los objetos declarados. Aquí primero inicializaremos los objetos de las dos matrices de parámetros entrenados:
- A — matriz de transición de estados;
- D — matriz de enlaces residuales con los datos de origen.
Como estas matrices se multiplicarán por matrices completas que contienen todos los elementos de la secuencia analizada, tenemos que repetir inmediatamente sus valores por el número de elementos de la secuencia. Esto evitará operaciones de copiado adicionales y optimizará la propagación inversa del gradiente de error.
Al igual que antes, utilizaremos un pequeño modelo de dos capas consecutivas para organizar los parámetros entrenados. La primera capa contendrá un valor fijo, mientras que la segunda generará el tensor requerido multiplicando los parámetros internos entrenados por un número fijo de la primera capa. Este enfoque nos permitirá utilizar algoritmos de capas neuronales ya existentes para el entrenamiento de parámetros sin crear funciones adicionales. Para minimizar el número de parámetros entrenados de la segunda capa, normalmente solo se utilizará un elemento en la primera capa.
Sin embargo, en este caso, necesitaremos obtener un tensor con valores repetidos a la salida de la segunda capa. Para ello, repetiremos los valores fijos de la primera capa un número determinado de veces. Como segunda capa utilizaremos una capa de convolución con un número de filtros igual al número de parámetros entrenados. Fijaremos el tamaño de la ventana y el paso de convolución en 1 para que cada elemento del tensor en la salida dependa de un solo valor inicial.
int index = 0; if(!cOne.Init(0, index, OpenCL, units_count, optimization, iBatch)) return false; if(!cOne.getOutput().Fill(1)) return false; cOne.SetActivationFunction(None); //--- index++; if(!cA.Init(0, index, OpenCL, 1, 1, window * window_key, units_count, 1, optimization, iBatch)) return false; cA.SetActivationFunction(MinusSoftPlus); CBufferFloat *w = cA.GetWeightsConv(); if(!w || !w.Fill(0)) return false;
Como en este caso la primera capa no tiene parámetros entrenables, podemos utilizarla para generar también la segunda matriz de parámetros entrenables. Por consiguiente, solo inicializaremos el segundo objeto para generar los parámetros entrenados necesarios.
index++; if(!cD.Init(0, index, OpenCL, 1, 1, window, units_count, 1, optimization, iBatch)) return false; cD.SetActivationFunction(None); w = cD.GetWeightsConv(); if(!w || !w.Fill(1)) return false;
Tenga en cuenta que al inicializar los objetos, rellenaremos las matrices de parámetros entrenados con valores fijos. Esto es algo distinto al enfoque general de rellenar los parámetros entrenados con valores aleatorios. La inicialización fija resulta pertinente en situaciones en las que el modelo debe conservar ciertas propiedades en las primeras fases del entrenamiento, o las condiciones iniciales tienen una influencia significativa en la distribución final de los parámetros. En este caso, evitará fluctuaciones bruscas al principio y facilitará una adaptación más suave del modelo a los datos.
Los demás parámetros del modelo de espacio de estados los crearemos como dependientes de los datos de origen, lo cual nos permitirá adaptarlos a las peculiaridades de la secuencia analizada. Para generarlos, utilizaremos una capa convolucional que generará los valores de todas las entidades del modelo a la vez. Este enfoque garantizará un procesamiento eficaz de los datos, ya que la convolución se realizará en paralelo en toda la secuencia, lo cual acelerará considerablemente los cálculos.
No obstante, antes de generar los parámetros del modelo de espacio de estados, primero normalizaremos los datos de origen. La normalización eliminará la influencia de las diferencias en la escala de los valores originales, lo que hará que el proceso de optimización resulte más suave y predecible.
//--- index++; if(!cX_norm.Init(0, index, OpenCL, window * units_count, optimization, iBatch)) return false; cX_norm.SetActivationFunction(None); index++; if(!cX_proj.Init(0, index, OpenCL, window, window, 4 * window_key, units_count, 1, optimization, iBatch)) return false; cX_proj.SetActivationFunction(None);
A continuación tendremos que dividir los parámetros generados del modelo en entidades separadas. Y para almacenar los datos, crearemos objetos adicionales cuyo nombre indicará la entidad de los datos registrados.
index++; if(!cDelta.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cDelta.SetActivationFunction(None); index++; if(!cB.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cB.SetActivationFunction(None); index++; if(!cC.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cC.SetActivationFunction(None); index++; if(!cH.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cH.SetActivationFunction(None);
El siguiente paso consistirá en inicializar el objeto responsable de generar los parámetros de decaimiento exponencial de los estados ocultos. Este componente desempeñará un papel clave en el control de la dinámica de la información transmitida a través de la secuencia, regulando el grado en que se retienen o atenúan los estados pasados.
index++; if(!cDelta_proj.Init(0, index, OpenCL, window_key, window_key, window, units_count, 1, optimization, iBatch)) return false; cDelta_proj.SetActivationFunction(SoftPlus);
El uso de SoftPlus como función de activación garantizará que solo haya valores positivos en la salida.
A continuación, inicializaremos algunos objetos más para almacenar los resultados intermedios de los cálculos. Todos serán del mismo tamaño.
index++; if(!cDeltaA.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaA.SetActivationFunction(None); index++; if(!cDeltaB.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaB.SetActivationFunction(None); index++; if(!cDeltaBX.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaBX.SetActivationFunction(None); index++; if(!cDeltaH.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaH.SetActivationFunction(None); index++; if(!cHS.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cHS.SetActivationFunction(None); //--- return true; }
Y finalizaremos el método de inicialización devolviendo el resultado lógico de las operaciones al programa que realiza la llamada.
Tenga en cuenta que no hemos almacenado los parámetros de arquitectura en variables locales separadas en este objeto. Como parte de esta implementación, hemos decidido no crear variables adicionales que almacenen permanentemente valores almacenados en objetos internos. En su lugar, planeamos usar variables locales que rellenaremos al principio de los métodos de pasada directa e inversa.
Una vez finalizado el trabajo de inicialización del objeto, construiremos el algoritmo de pasada directa, que organizamos en el método feedForward. En los parámetros de este método obtendremos el puntero al objeto de los datos de origen.
bool CNeuronAttraos::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- uint window = cX_proj.GetWindow(); uint window_key = cX_proj.GetFilters() / 4; uint units = cD.GetUnits();
En el cuerpo del método primero cargaremos desde los objetos internos los parámetros de los datos de origen que no guardamos en la fase de inicialización. Y luego generaremos los tensores de los parámetros entrenados del modelo.
if(!cA.FeedForward(cOne.AsObject())) // (Units, Window, WindowKey) return false; if(!cD.FeedForward(cOne.AsObject())) // (Units, Window)) return false;
En el siguiente paso, normalizaremos los datos de origen y generaremos parámetros de modelo sensibles al contexto.
if(!NeuronOCL || !SumAndNormilize(NeuronOCL.getOutput(), NeuronOCL.getOutput(), cX_norm.getOutput(), window, true, 0, 0, 0, 0.5f)) return false; if(!cX_proj.FeedForward(cX_norm.AsObject())) // (Units, 4*WindowKey) return false;
Después, los dividiremos en entidades separadas.
if(!DeConcat(cDelta.getOutput(), cB.getOutput(), cC.getOutput(), cH.getOutput(), cX_proj.getOutput(), window_key, window_key, window_key, window_key, units)) // 4*(Units, WindowKey) return false;
Y generaremos los parámetros del paso temporal adaptativo.
if(!cDelta_proj.FeedForward(cDelta.AsObject())) // (Units, Window) return false;
Con esto finalizará la fase preparatoria, y pasaremos a la construcción del algoritmo MDMU, que se encargará de modelizar la dinámica de las series temporales. El estado del modelo se actualizará usando una ecuación recurrente:
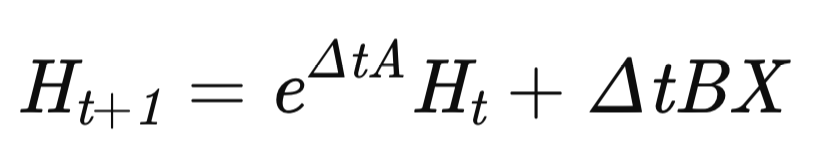
donde Δt es el paso temporal adaptativo.
Primero calcularemos el valor exponencial en el primer sumando. Solo que sustituiremos la función de exponente por SoftPlus, que tiene algunas ventajas.
if(!DiagMatMul(cDelta_proj.getOutput(), cA.getOutput(), cDeltaA.getOutput(), window, window_key, units, SoftPlus)) // (Units, Window, WindowKey) return false;
SoftPlus crece más despacio que un exponente, lo cual reducirá el riesgo de un aumento brusco de la matriz de transiciones. De este modo, los gradientes cambiarán suavemente y el entrenamiento se volverá más estable.
El exponente cambiará la dinámica fuertemente para pequeños cambios en Δ. SoftPlus suavizará los cambios, lo cual reducirá la probabilidad de saltos bruscos en los estados ocultos.
Con datos ruidosos, SoftPlus reducirá el impacto de las emisiones. Su crecimiento estará limitado por una función logarítmica. Esto hará que el modelo sea más estable.
A continuación, calcularemos los valores del segundo sumando mediante la multiplicación matricial sucesiva.
if(!MatMul(cDelta_proj.getOutput(), cB.getOutput(), cDeltaB.getOutput(), window, 1, window_key, units)) // (Units, Window, WindowKey) return false; if(!DiagMatMul(cX_norm.getOutput(), cDeltaB.getOutput(), cDeltaBX.getOutput(), window, window_key, units, None)) // (Units, Window, WindowKey) return false;
Y ajustaremos la matriz del controlador dinámico de cambios de estados ocultos por la tasa de cambio del estado oculto.
if(!MatMul(cDelta_proj.getOutput(), cH.getOutput(), cDeltaH.getOutput(), window, 1, window_key, units)) // (Units, Window, WindowKey) return false;
Tras preparar todos los datos necesarios, corregiremos los estados ocultos del sistema utilizando el algoritmo de escaneo paralelo que implementamos en el último artículo en el lado OpenCL. En este caso, bastará con llamar al método-envoltorio del kernel PScan.
if(!PScan()) return false;
El método de llamada al kernel se basará en un algoritmo estándar, así que no nos detendremos en su consideración detallada en el marco de este artículo. El código completo del método anterior se encuentra en el archivo adjunto al artículo (en el archivo NeuroNet.cl).
A continuación, nos quedará generar el estado predictivo del sistema analizado. Para ello, multiplicaremos la matriz de estados ocultos actualizada por la matriz de proyección de estados ocultos.
if(!MatMul(cHS.getOutput(), cC.getOutput(), Output, window, window_key, 1, units)) // (Units, Window, 1) return false;
Luego multiplicaremos los datos básicos normalizados por los coeficientes de vinculación directa.
if(!ElementMult(cD.getOutput(), cX_norm.getOutput(), PrevOutput)) // (Units, Window)) return false;
Y sumaremos los resultados de las dos operaciones.
if(!SumAndNormilize(Output, PrevOutput, Output, window, false, 0, 0, 0, 1)) // (Units, Window)) return false;
Además, añadiremos los datos de origen obtenidos creando una línea troncal de enlaces residuales.
if(!SumAndNormilize(Output, NeuronOCL.getOutput(), Output, window, false, 0, 0, 0, 1)) // (Units, Window)) return false; //--- return true; }
Este enfoque nos permite combinar información sobre estados latentes y dependencias a corto plazo en los datos de origen.
Con esto concluimos el algoritmo de pasada directa de nuestra visión del framework Attraos. Después devolveremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.
A continuación, pasaremos a construir los algoritmos de pasada inversa para nuestro objeto. Para los propósitos de este artículo, consideraremos el método calcInputGradients para distribuir los gradientes de error. En los parámetros del método, como antes, obtendremos un puntero al objeto de datos de origen. Solo que esta vez tendremos que pasarle el tamaño del error, según la influencia de los datos de entrada en el resultado final del modelo.
bool CNeuronAttraos::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
En el cuerpo del método comprobaremos directamente la relevancia del puntero recibido, porque solo podremos pasar los datos a un objeto válido. De lo contrario, todas las operaciones posteriores carecerán de sentido.
A continuación, como en el método de pasada directa, almacenaremos los parámetros de los datos de origen en variables locales.
uint window = cX_proj.GetWindow(); uint window_key = cX_proj.GetFilters() / 4; uint units = cD.GetUnits();
Luego distribuiremos el gradiente de error desde el nivel de resultados a los flujos de información correspondientes. Recordemos que en la pasada directa, involucraremos 3 flujos de información de transferencia de datos:
- el modelo de espacio de estados;
- los enlaces directos con el coeficiente;
- los enlaces residuales.
En primer lugar, distribuiremos el gradiente de error entre los coeficientes de enlace directo y los datos de origen normalizados.
if(!ElementMultGrad(cD.getOutput(), cD.getGradient(), cX_norm.getOutput(), cX_norm.getPrevOutput(), Gradient, cD.Activation(), None)) // (Units, Window)) return false;
A continuación, pasaremos los datos al segundo flujo de datos, donde distribuiremos el gradiente de error entre los estados ocultos del sistema y sus coeficientes de proyección.
if(!MatMulGrad(cHS.getOutput(), cHS.getGradient(), cC.getOutput(), cC.getGradient(), Gradient, window, window_key, 1, units)) // (Units, Window, 1) return false;
Si es necesario, corregiremos los resultados obtenidos mediante las derivadas de las funciones de activación correspondientes.
if(cHS.Activation() != None) { if(!DeActivation(cHS.getOutput(), cHS.getGradient(), cHS.getGradient(), cHS.Activation())) return false; } if(cC.Activation() != None) { if(!DeActivation(cC.getOutput(), cC.getGradient(), cC.getGradient(), cC.Activation())) return false; }
A continuación, distribuiremos el gradiente de error a través del módulo de escaneo paralelo, llamando al método-envoltorio del kernel correspondiente.
if(!PScanCalcGradient()) return false;
Los valores resultantes se distribuirán entre las entidades correspondientes. Primero pasaremos el gradiente de error en los estados ocultos y los parámetros de paso temporal adaptativo.
if(!MatMulGrad(cDelta_proj.getOutput(), cDelta_proj.getGradient(), cH.getOutput(), cH.getGradient(), cDeltaH.getGradient(), window, 1, window_key, units)) // (Units, Window, WindowKey) return false;
Y luego haremos descender el gradiente de error al nivel de los datos de origen normalizados.
if(!DiagMatMulGrad(cX_norm.getOutput(), cX_norm.getGradient(), cDeltaB.getOutput(), cDeltaB.getGradient(), cDeltaBX.getGradient(), window, window_key, units)) // (Units, Window, WindowKey) return false; if(!SumAndNormilize(cX_norm.getGradient(), cX_norm.getPrevOutput(), cX_norm.getPrevOutput(), window, false, 0, 0, 0, 1)) return false;
Aquí cabe señalar que hemos transmitido previamente los valores del gradiente de error al objeto de datos de origen normalizados. Por ello, en esta fase resumiremos los datos de los dos flujos de información.
Aquí distribuiremos el gradiente de error entre los coeficientes de la influencia de los datos de origen sobre el estado oculto y los parámetros del paso temporal adaptativo.
if(!MatMulGrad(cDelta_proj.getOutput(), cDelta_proj.getPrevOutput(), cB.getOutput(), cB.getGradient(), cDeltaB.getGradient(), window, 1, window_key, units)) // (Units, Window, WindowKey) return false; if(!SumAndNormilize(cDelta_proj.getGradient(), cDelta_proj.getPrevOutput(), cDelta_proj.getGradient(), window, false, 0, 0, 0, 1)) return false;
Lugo sumaremos los datos en el nivel de parámetros del paso temporal adaptativo con los valores acumulados anteriormente.
A continuación tendremos que bajar el gradiente de error hasta el nivel de la matriz de evolución del estado oculto, pero antes corregiremos los valores obtenidos mediante la derivada de la función de activación.
if(!DeActivation(cDeltaA.getOutput(), cDeltaA.getGradient(), cDeltaA.getGradient(), SoftPlus)) return false;
Y después, distribuiremos los valores entre las entidades.
if(!DiagMatMulGrad(cDelta_proj.getOutput(), cDelta_proj.getPrevOutput(), cA.getOutput(), cA.getGradient(), cDeltaA.getGradient(), window, window_key, units)) // (Units, Window, WindowKey) return false; if(!SumAndNormilize(cDelta_proj.getGradient(), cDelta_proj.getPrevOutput(), cDelta_proj.getGradient(), window, false, 0, 0, 0, 1)) return false;
En esta fase, volvemos a sumar los valores del gradiente de error en el nivel del parámetro del paso temporal adaptativo. Pero esta vez, este será el último flujo de información en esta dirección. Y ahora corregiremos los valores acumulados mediante la derivada de la función de activación correspondiente.
if(cDelta_proj.Activation() != None) { if(!DeActivation(cDelta_proj.getOutput(), cDelta_proj.getGradient(), cDelta_proj.getGradient(), cDelta_proj.Activation())) return false; }
A continuación, reduciremos el gradiente de error al nivel de los pasos temporales adaptativos.
if(!cDelta.calcHiddenGradients(cDelta_proj.AsObject())) return false;
Así obtendremos los gradientes de error a nivel de todas las entidades dependientes del contexto. Luego ensamblaremos el valor obtenido en un único tensor.
if(!Concat(cDelta.getGradient(), cB.getGradient(), cC.getGradient(), cH.getGradient(), cX_proj.getGradient(), window_key, window_key, window_key, window_key, units)) // 4*(Units, WindowKey) return false;
A continuación, reduciremos el gradiente de error al nivel de los datos de origen normalizados.
if(!cX_norm.calcHiddenGradients(cX_proj.AsObject())) return false; if(!SumAndNormilize(cX_norm.getGradient(), cX_norm.getPrevOutput(), cX_norm.getGradient(), window, false, 0, 0, 0, 1)) return false;
Recordemos que ya hemos pasado dos veces el gradiente de error al objeto de datos de origen normalizados. Por lo tanto, los datos obtenidos en esta fase se añadirán a los valores acumulados anteriormente.
Aquí también añadiremos los valores a lo largo de la línea troncal de enlaces residuales, tras lo cual, transferiremos los valores acumulados al nivel de datos de origen, corrigiéndolos previamente mediante la derivada de la función de activación correspondiente.
if(!SumAndNormilize(cX_norm.getGradient(), Gradient, cX_norm.getGradient(), window, false, 0, 0, 0, 1)) return false; if(!DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), cX_norm.getGradient(), NeuronOCL.Activation())) return false; //--- return true; }
Con esto completaremos el método de distribución del gradiente de error y retornaremos el resultado lógico al programa que realiza la llamada.
Le sugiero que se familiarice con el método updateInputWeights de actualización de los parámetros del modelo. En él, solo llamaremos a los métodos homónimos de los cuatro objetos internos que contienen los parámetros a entrenar.
Y aquí nos gustaría decir unas palabras sobre los algoritmos de los métodos de guardado y restablecimiento de objetos. Nuestra nueva clase contiene bastantes objetos internos, pero solo 4 de ellos contienen parámetros entrenables. Por ello, al realizar el guardado, solo tendremos que escribir la información sobre estos objetos internos en el disco.
bool CNeuronAttraos::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false; //--- if(!cA.Save(file_handle)) return false; if(!cD.Save(file_handle)) return false; if(!cX_proj.Save(file_handle)) return false; if(!cDelta_proj.Save(file_handle)) return false; //--- return true; }
Pero la cuestión se plantea a la hora de restablecer la operatividad del objeto. En el método Load, primero cargaremos los datos guardados previamente en el disco.
bool CNeuronAttraos::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false; //--- if(!LoadInsideLayer(file_handle, cA.AsObject())) return false; if(!LoadInsideLayer(file_handle, cD.AsObject())) return false; if(!LoadInsideLayer(file_handle, cX_proj.AsObject())) return false; if(!LoadInsideLayer(file_handle, cDelta_proj.AsObject())) return false;
A continuación, escribiremos los parámetros de la arquitectura del objeto en variables locales.
uint window = cX_proj.GetWindow(); uint window_key = cX_proj.GetFilters() / 4; uint units_count = cD.GetUnits();
El algoritmo posterior repetirá el proceso de inicialización de los objetos de almacenamiento temporal de datos.
if(!cOne.Init(0, 0, OpenCL, units_count, optimization, iBatch)) return false; if(!cOne.getOutput().Fill(1)) return false; cOne.SetActivationFunction(None); int index = 3; if(!cX_norm.Init(0, index, OpenCL, window * units_count, optimization, iBatch)) return false; cX_norm.SetActivationFunction(None); index += 2; if(!cDelta.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cDelta.SetActivationFunction(None); index++; if(!cB.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cB.SetActivationFunction(None); index++; if(!cC.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cC.SetActivationFunction(None); index++; if(!cH.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cH.SetActivationFunction(None); index += 2; if(!cDeltaA.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaA.SetActivationFunction(None); index++; if(!cDeltaB.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaB.SetActivationFunction(None); index++; if(!cDeltaBX.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaBX.SetActivationFunction(None); index++; if(!cDeltaH.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaH.SetActivationFunction(None); index++; if(!cHS.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cHS.SetActivationFunction(None); //--- return true; }
Este enfoque permite optimizar el proceso de almacenamiento de datos y restablecimiento de objetos, así como el uso del espacio en disco.
Con esto concluiremos la revisión de algoritmos para construir el framework Attraos utilizando herramientas MQL5. El código completo de la clase CNeuronAttraos y todos sus métodos se encuentran en el archivo adjunto.
Arquitectura del modelo
Tras implementar los algoritmos del framework Attraos, describiremos la arquitectura de los modelos entrenados. En este experimento, entrenaremos dos modelos utilizando enfoques de aprendizaje multitarea. La arquitectura de ambos modelos se presenta en el método CreateDescriptions. En los parámetros del método obtenemos punteros a 2 arrays dinámicos a los que debemos transmitir la descripción de la arquitectura de los modelos.
bool CreateDescriptions(CArrayObj *&actor, CArrayObj *&probability) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!probability) { probability = new CArrayObj(); if(!probability) return false; }
En el cuerpo del método comprobaremos inmediatamente la relevancia de los punteros recibidos y, si es necesario, crearemos nuevas instancias de objetos.
En primer lugar, describiremos la arquitectura del actor que utilizará los enfoques del framework Attraos implementados anteriormente. Como viene siendo habitual, el modelo comenzará con una capa de datos de origen totalmente conectada, seguida de una capa de normalización de datos por lotes. Este enfoque nos permitirá introducir en el modelo los datos de origen brutos recibidos del terminal. Al mismo tiempo, su procesamiento primario en forma de normalización ya se realizará mediante el modelo.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
A continuación, utilizaremos la primera capa de la arquitectura Attraos. En este caso, utilizaremos un desfase de 5 pasos para transformar los datos de origen en un espacio de fases, lo que se corresponde con 5 minutos en un marco temporal de minutos.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronAttraos; descr.window = BarDescr*5; // 5 min descr.count = HistoryBars/5; // 24 descr.window_out = 256; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Para la siguiente capa, aumentaremos el paso de tiempo a 15 elementos.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronAttraos; descr.window = BarDescr*15; // 15 min descr.count = HistoryBars/15; // 8 descr.window_out = 256; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Y en el tercero, hasta 30.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronAttraos; descr.window = BarDescr*30; // 30 min descr.count = HistoryBars/30; // 4 descr.window_out = 256; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Nótese aquí que en la salida de cada objeto CNeuronAttraos, obtendremos un resultado en la dimensionalidad de los datos de origen. Por lo tanto, la siguiente capa de convolución reducirá la dimensionalidad del tensor en un factor de 3,
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count=descr.count = HistoryBars/3; descr.window = BarDescr*3; descr.step = descr.window; int prev_window=descr.window_out = BarDescr; descr.activation = SoftPlus; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
seguido de una cabeza de decisión de 3 capas consecutivas totalmente conectadas.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 512; descr.batch = 1e4; descr.activation = TANH; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 256; descr.activation = TANH; descr.batch = 1e4; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NActions; descr.activation = SoftPlus; descr.batch = 1e4; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Luego normalizaremos el resultado obtenido.
//--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Y añadiremos un bloque de gestión de riesgos.
//--- layer 10 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMacroHFTvsRiskManager; //--- Windows { int temp[] = {3, 15, NActions, AccountDescr}; //Window, Stack Size, N Actions, Account Description if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } descr.count = 10; descr.window_out = 16; descr.step = 4; // Heads descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 11 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = NActions / 3; descr.window = 3; descr.step = 3; descr.window_out = 3; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
El modelo de probabilidades de dirección del próximo movimiento se ha heredado completamente de trabajos anteriores sin modificaciones, así que no vamos a describirlo en el marco de este artículo. En el anexo figura una descripción completa de la arquitectura de los modelos entrenados. Allí también encontrará el código completo de los programas de entrenamiento de modelos y de interacción con el entorno, que también han sido trasladados de artículos anteriores sin cambios.
Simulación
A lo largo de los dos artículos, hemos realizado una importante labor de adaptación y desarrollo de las ideas de los autores del framework Attraos. Y ahora nos acercamos a una de las etapas clave: comprobar el rendimiento y la eficacia de los métodos aplicados con datos históricos reales. Este proceso resulta crucial para evaluar la viabilidad del modelo y su capacidad para identificar patrones, proporcionando resultados coherentes en diferentes condiciones de mercado.
Para entrenar el modelo, hemos utilizado una muestra que incluye cotizaciones históricas del par de divisas EURUSD en el marco temporal M1 para todo el año 2024. Todos los parámetros de los indicadores analizados permanecerán ajustados por defecto, sin optimización adicional. Este enfoque eliminará la influencia de factores externos, como el ajuste de los parámetros a datos históricos específicos, y se centrará únicamente en la calidad fundamental del rendimiento del modelo. Debemos señalar que el uso de parámetros indicadores invariables también nos permitirá evaluar la capacidad del modelo para adaptarse a la dinámica real del mercado sin necesidad de intervenciones y reajustes constantes.
Como antes, el entrenamiento del modelo se realizará en 2 etapas. En la primera etapa, fijaremos el tamaño del paquete de entrenamiento en 1, lo que nos permitirá utilizar un estado completamente aleatorio de la muestra de entrenamiento en cada iteración del proceso de aprendizaje. Esto nos permitirá maximizar el rendimiento del modelo en su nuevo estado. Sin embargo, esto no bastará para formar correctamente a la unidad de gestión de riesgos. Por lo tanto, en la segunda etapa, aumentaremos el tamaño del paquete a 60, lo que nos permitirá ajustar el rendimiento del modelo y la unidad de gestión de riesgos en 60 estados del entorno consecutivos. Si se utiliza el marco temporal de minutos, esto se corresponde con una hora.
Los datos de enero-febrero de 2025 se utilizarán para probar el modelo entrenado. Hemos elegido este periodo para poner a prueba de forma rigurosa la capacidad del modelo para funcionar con datos nuevos, nunca antes vistos. Al mismo tiempo, todos los demás parámetros del experimento han permanecido inalterados, lo que garantiza la pureza del experimento, la reproducibilidad de los resultados y la corrección de la comparación posterior. Este enfoque elimina la influencia de factores aleatorios y permite evaluar objetivamente la calidad de los algoritmos.
Ahora le presentamos los resultados de las pruebas.
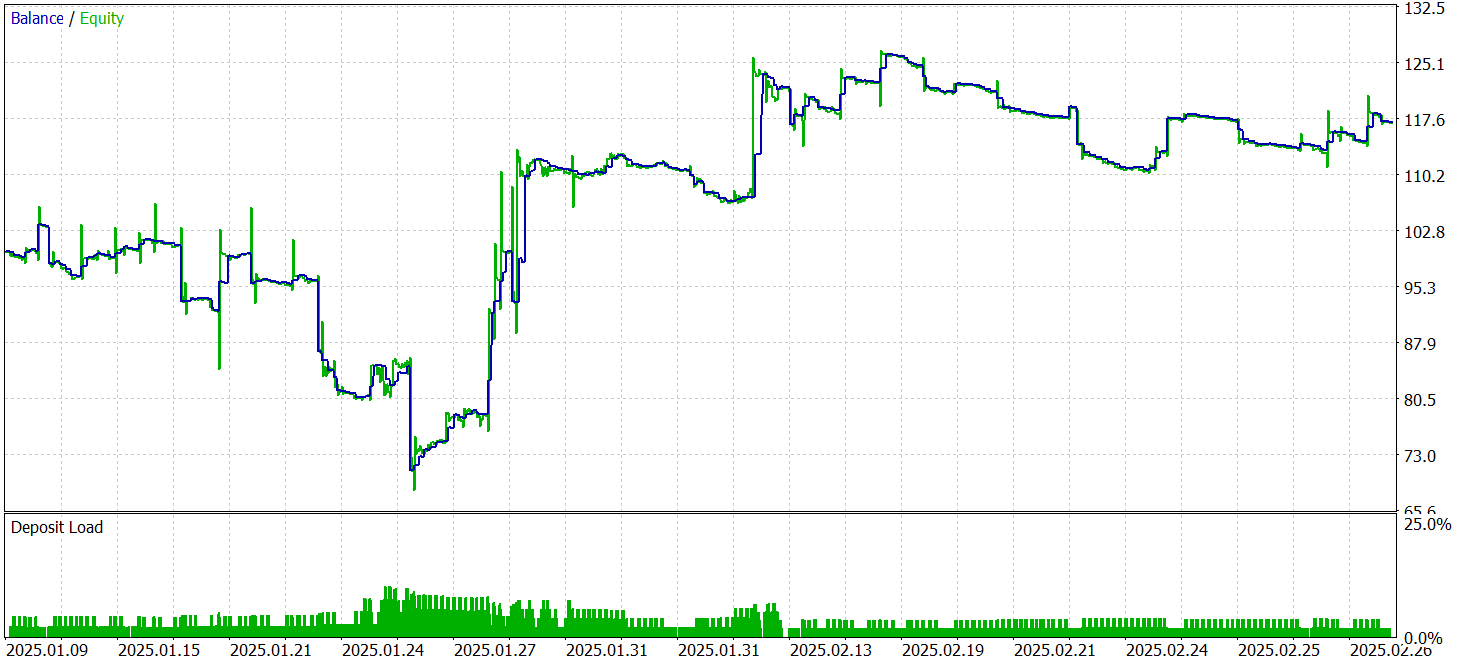
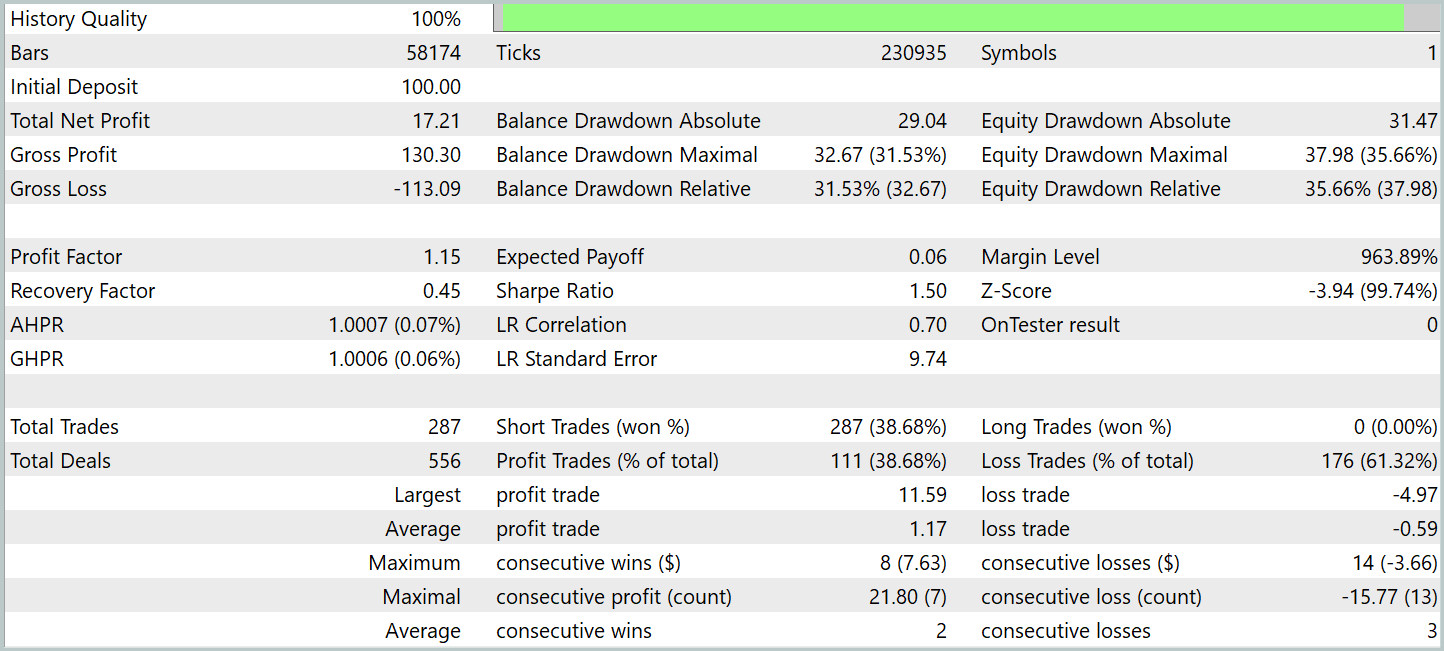
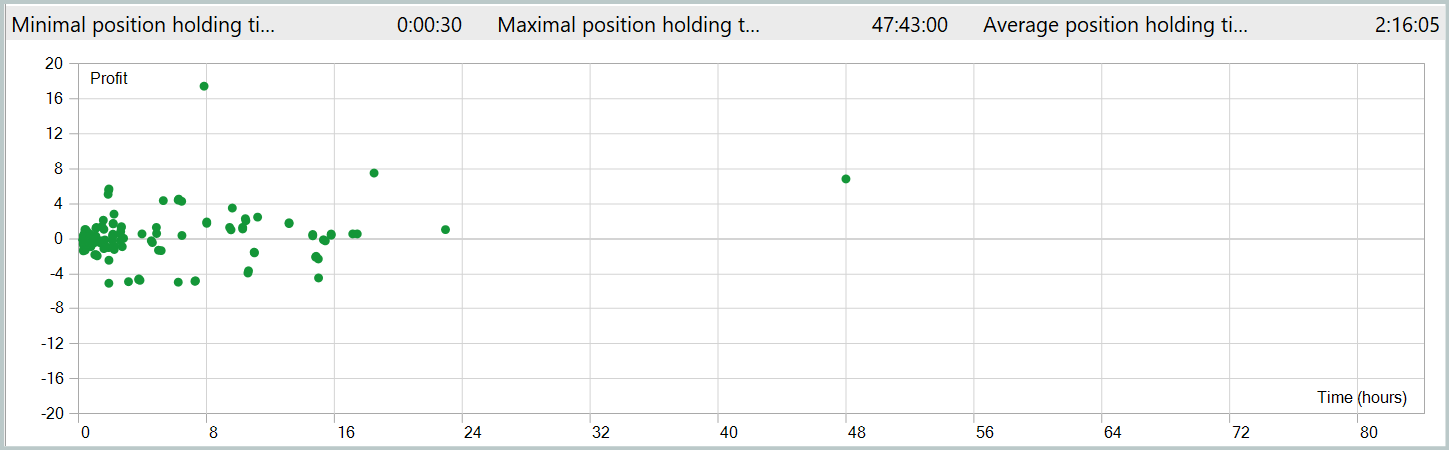
Durante el periodo de prueba, el modelo ha realizado 287 transacciones comerciales, de las que casi el 39% se han cerrado con beneficios. A pesar del porcentaje relativamente bajo de transacciones exitosas, la estrategia ha demostrado un resultado positivo debido a la relación beneficios/pérdidas. En particular, el beneficio medio de una transacción exitosa ha sido el doble de la pérdida media, lo que ha permitido compensar las transacciones con menos éxito, alcanzando un resultado financiero global positivo y fijando el factor de beneficio en 1,15.
El tiempo medio de mantenimiento de la posición ha superado las 2 horas, lo que indica la propensión del modelo a tomar decisiones comerciales a corto y medio plazo. Sin embargo, llama especialmente la atención el caso del mantenimiento máximo de posición, que ha ascendido a casi dos días. Este hecho requiere un análisis más profundo.
Conclusión
Hoy nos hemos familiarizado con el framework Attraos, que utiliza conceptos de la teoría del caos para resolver problemas de previsión de series temporales. Los autores del framework integran enfoques de análisis no lineal, reconstrucción del espacio de fases, memoria dinámica con distintos niveles de resolución y algoritmos adaptativos. Estas tecnologías ayudan a elaborar previsiones más precisas y a adaptar los modelos comerciales a las cambiantes condiciones del mercado.
En la parte práctica, hemos implementado nuestra propia visión de los enfoques propuestos utilizando herramientas MQL5, y además hemos construido y entrenado modelos sobre datos históricos reales. Los resultados de la prueba del modelo entrenado con datos históricos no incluidos en la muestra de entrenamiento indican la capacidad del modelo para generar beneficios con datos nuevos. Sin embargo, los resultados también han revelado algunos problemas. En particular, estamos viendo mantenimientos largos en algunas posiciones. Y el gráfico de balance no es tan fluido como nos gustaría. De todo ello podemos concluir que el modelo tiene potencial, pero debemos seguir trabajando para optimizarlo.
Nótese que las conclusiones extraídas solo son pertinentes para esta aplicación. La versión del autor no se ha probado en este artículo.
Enlaces
- Attractor Memory for Long-Term Time Series Forecasting: A Chaos Perspective
- Otros artículos de la serie
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor experto para recopilar ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de modelos |
| 4 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 5 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema y la arquitectura del modelo |
| 6 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código del programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/17371
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Algoritmo del restaurador de éxito — Successful Restaurateur Algorithm (SRA)
Algoritmo del restaurador de éxito — Successful Restaurateur Algorithm (SRA)
 Creación de un Panel de administración de operaciones en MQL5 (Parte IX): Organización del código (II): Modularización
Creación de un Panel de administración de operaciones en MQL5 (Parte IX): Organización del código (II): Modularización
 Desarrollo de un kit de herramientas para el análisis de la acción del precio (Parte 13): Herramienta RSI Sentinel
Desarrollo de un kit de herramientas para el análisis de la acción del precio (Parte 13): Herramienta RSI Sentinel
 Creación de una estrategia de retorno a la media basada en el aprendizaje automático
Creación de una estrategia de retorno a la media basada en el aprendizaje automático
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso