Predicción de tipos de cambio mediante métodos clásicos de aprendizaje automático: Modelos Logit y Probit

Introducción

Los investigadores de los mercados financieros siempre se enfrentarán a la difícil tarea de elegir un modelo matemático que les ayude a predecir el futuro comportamiento de los instrumentos comerciales. Hasta la fecha, se ha desarrollado un gran número de modelos de este tipo. Así que nos surgen las preguntas: ¿cómo no ahogarnos en toda esta variedad de métodos y enfoques? ¿Por dónde empezar? ¿En qué modelos es mejor centrarse, especialmente si estamos empezando a realizar predicciones con modelos de aprendizaje automático? Si intentamos reducir la tarea de la previsión a una simple respuesta a la pregunta "¿será mañana el precio de cierre superior al de hoy?", la opción lógica serían los modelos de clasificación binaria. Algunas de las más sencillas y utilizadas son la regresión logit y probit. Estos modelos pertenecen a la forma más común de aprendizaje automático, el llamado aprendizaje supervisado.

La tarea del aprendizaje supervisado, a su vez, consiste en enseñar a nuestro modelo a mapear un conjunto de entradas {x} (predictores o características) en un conjunto de salidas {y} (objetivos o etiquetas). En este artículo, solo pronosticaremos dos estados del mercado: la subida o la bajada del precio de un par de divisas. Por consiguiente, tendremos solo dos clases de etiquetas y ∊ {1,0}. Los predictores serán patrones de precios, es decir, incrementos de precios normalizados con un cierto desfase. Estos datos formarán nuestro conjunto de entrenamiento {x, y} sobre el que estimaremos los parámetros de nuestros modelos. El modelo predictivo basado en clasificadores entrenados se implementará como LogitExpert.

Regresión Logit y Probit binaria

Veamos brevemente la parte teórica. Cabe decir que el modelo más sencillo de elección binaria es un modelo de probabilidad lineal en el que la probabilidad de que se produzca un suceso P(yn=1|xn) es una función lineal de las variables explicativas:

P(yn=1|xn) = w0*1 + w1x1 + w2x2 + … + wkxk

Por desgracia, este modelo tiene un inconveniente muy grave: el valor predicho puede ser mayor que uno o menor que cero, lo cual a su vez no permite interpretar el valor predicho como una probabilidad. Por consiguiente, para resolver este problema, se propuso utilizar funciones de distribución de probabilidad conocidas en las que se sustituirían los valores de la función lineal.

El modelo probit se basa en la ley de distribución normal estándar N(0,1):

P(yn=1|xn) = F(xnw)=μn

• n - índice inferior que denota el número de observación (ejemplo),

• yn - etiqueta de clase,

• F( ) - función de distribución de ley normal (función de activación),

• xn – vector de características,

• w - vector de parámetros del modelo,

• xnw - logit o preactivación (representa el producto escalar de un vector de características y un vector de parámetros)

xnw = w0*1 + w1x1 + w2x2 + … + wkxk

A su vez, el modelo logit se basa en la ley logística de distribución de probabilidades:

                                                      P(yn=1|xn) = L(xnw) = exp(xnw)/(1 + exp(xnw)) = μn

Las funciones de distribución de la distribución logística y normal son bastante parecidas, y resultan casi idénticas en el intervalo [-1,2;1,2]. Por ello, los modelos logit y probit suelen dar resultados similares a menos que la probabilidad sea cercana a cero o a uno. Así, estos modelos, al sustituir un vector de características, nos permiten calcular las probabilidades de las etiquetas de clase y, por lo tanto, la probabilidad de la dirección futura del movimiento de los precios.

Preparación de los datos

Antes de estimar los parámetros del modelo, deberemos definir las características, normalizarlas y representarlas de forma adecuada para la función que encontrará los parámetros óptimos (en el sentido de minimizar la función de pérdida). La función GetDataset se encargará de este trabajo:

• InpCount_ - indica el número de ejemplos para el entrenamiento

• lag_ - número de características analizadas (incrementos de precio con lag)

• string X - par de divisas para el que se calculan las características

• string y - par de divisas para el que se calculan las etiquetas

• int start - número de barra a partir del cual empezamos a tomar ejemplos para el entrenamiento

Como ejemplo ilustrativo, usaremos los incrementos de retardo del precio de un par de divisas. Por ejemplo, si establecemos el argumento de la función lag_ = 4, entonces las características serán x{return-4,return-3,return-2,return-1} y tendremos exactamente (InpCount_- lag_) elementos para el entrenamiento.

//+------------------------------------------------------------------+
//|Get data for analysis: features and corresponding labels          |
//+------------------------------------------------------------------+
bool GetDataset(int InpCount_,int lag_,int start,matrix &Input_X,vector & Target_y,string X,string y)
  {

   matrix rates;
   matrix target;
   target.CopyRates(y, PERIOD_CURRENT, COPY_RATES_OHLC, start+1, InpCount_);
   rates.CopyRates(X, PERIOD_CURRENT, COPY_RATES_OHLC, start+2, InpCount_-1);
   rates = rates.Transpose();
   target = target.Transpose();
   int Class_ [];
   ArrayResize(Class_,InpCount_);
   for(int i=0; i<InpCount_; i++)
     {
      if(target[i,3] >  target[i,0])
         Class_[i] = 1;
      else
         Class_[i] = 0;
     }

   vector label=vector::Zeros(InpCount_-lag_);
   for(int i=0; i<InpCount_-lag_; i++)
     {
      label[i] = Class_[i+lag_]; // class label
     }

   matrix returns=matrix::Zeros(InpCount_-lag_, lag_);
   for(int j=0; j<lag_; j++)
     {
      for(int i=0; i<InpCount_-lag_; i++)
        {
         returns[i,j] =rates[i+j,3] - rates[i+j,0]  ; // Input Data
        }
     }

   vector cols_mean=returns.Mean(0);
   vector cols_std=returns.Std(0);

   mean_ = cols_mean[lag_-1];
   std_ = cols_std[lag_-1];

   for(int j=0; j<lag_; j++)
     {
      for(int i=0; i<InpCount_-lag_; i++)
        {
         returns[i,j] = (returns[i,j] - cols_mean[lag_-1])/cols_std[lag_-1];
        }
     }
   Input_X = returns;
   Target_y = label;

   return true;
  }

En la salida obtendremos una matriz de características Input_X y un vector de etiquetas Target_y. Una vez generado el conjunto de entrenamiento, procederemos a la estimación de los parámetros.

Estimación de los parámetros del modelo

La estimación de los parámetros suele realizarse según el método de máxima verosimilitud. En el caso binario, los modelos logit y probit suponen que la variable dependiente y tiene una distribución Bernoulli. Y como este es el caso, entonces la función de verosimilitud logarítmica será igual:

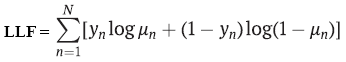
• yn - etiqueta de clase,

• μn - probabilidad de predecir la clase, utilizando la regresión logit o probit,

• N - número de ejemplos de entrenamiento

Para estimar los parámetros necesitaremos encontrar el máximo de esta función, pero como en el aprendizaje automático es habitual minimizar la función de pérdida, y todos los optimizadores están configurados principalmente para minimizar las funciones objetivo, simplemente añadiremos un signo menos a la función de verosimilitud. Como resultado, obtendremos la denominada probabilidad logarítmica negativa (NLL). Minimizaremos esta función de pérdida utilizando el método de optimización cuasi-newtoniano de segundo orden L-BFGS implementado en la biblioteca Alglib. Este método numérico es el que se suele usar para hallar los parámetros de los modelos logit y probit. Otro método de optimización muy usado es el de mínimos cuadrados con recálculo iterativo de pesos (IRLS).

//+------------------------------------------------------------------+
//| Derived class from CNDimensional_Func                            |
//+------------------------------------------------------------------+
class CNDimensional_Logit : public CNDimensional_Func
  {
public:
                     CNDimensional_Logit(void) {}
                    ~CNDimensional_Logit(void) {}
   virtual void      Func(CRowDouble &w,double &func,CObject &obj);
  };

//+------------------------------------------------------------------+
//| Objective Function: Logit Negative loglikelihood                 |
//+------------------------------------------------------------------+
void CNDimensional_Logit::Func(CRowDouble &w,double &func,CObject &obj)
  {

   double LLF[],probit[],probitact[];
   vector logitact;
   ArrayResize(LLF,Rows_);
   ArrayResize(probit,Rows_);
   vector params=vector::Zeros(Cols_);

   for(int i = 0; i<Cols_; i++)
     {
      params[i] =  w[i]; // vector of parameters
     }

   vector logit=vector::Zeros(Rows_);
   logit = Input_X_gl.MatMul(params);

   for(int i=0; i <Rows_; i++)
     {
      probit[i] = logit[i];
     }

   if(probit_)
      MathCumulativeDistributionNormal(probit,0,1,probitact); // Probit activation
   else
      logit.Activation(logitact,AF_SIGMOID); // Logit activation

//--------------------to avoid NAN error when calculating logarithm ------------------------------------
   if(probit_)
     {
      for(int i = 0; i<Rows_; i++)
        {
         if(probitact[i]==1)
            probitact[i]= 0.999;
         if(probitact[i]==0)
            probitact[i]= 0.001;
        }
     }
   else
     {
      for(int i = 0; i<Rows_; i++)
        {
         if(logitact[i]==1)
            logitact[i]= 0.999;
         if(logitact[i]==0)
            logitact[i]= 0.001;
        }
     }
//-------------------------------------------------------------------------------------------------
   double L2_reg;
   if(L2_)
      L2_reg = 0.5 * params.Dot(params); //  L2_regularization
   else
      L2_reg =0;

//------------------ calculate loss function-------------------------------------------------------------
   if(probit_)
     {
      for(int i = 0; i<Rows_; i++)
        {

         LLF[i]=target_y_gl[i]*MathLog(probitact[i]) + (1-target_y_gl[i])*MathLog(1-probitact[i]) ;

         if(!MathIsValidNumber(LLF[i]))
           {
            break;
           }
        }
     }
   else
     {
      for(int i = 0; i<Rows_; i++)
        {

         LLF[i]=target_y_gl[i]*MathLog(logitact[i]) + (1-target_y_gl[i])*MathLog(1-logitact[i]);

         if(!MathIsValidNumber(LLF[i]))
           {
            break;
           }
        }
     }

   func = -MathSum(LLF) + L2_reg/(Rows_*C_); // Negative Loglikelihood + L2_regularization
//------------------------------------------------------------------------------------------------------
   func_ = func;
  }

Pero no basta con calcular las estimaciones de los parámetros; nos gustaría obtener los errores estándar de estas estimaciones para comprender hasta qué punto son significativas nuestras características.

Por ejemplo, la popular biblioteca de aprendizaje automático scikit-learn, por alguna razón, no calcula esta información para el modelo logit. Hemos implementado el cálculo de errores estándar tanto para modelos logit como probit, de modo que ahora podemos ver si algunas características específicas tienen un impacto estadísticamente significativo en la previsión o no. Esta es una de las razones por las que prefiero escribir yo mismo el código del modelo logit en MQL en lugar de utilizar la conversión ONNX de modelos ya hechos de paquetes populares de aprendizaje automático. Otra razón es que necesitamos un modelo dinámico que pueda reoptimizar los parámetros del clasificador en cada barra o a una frecuencia establecida deseada.

Pero volvamos a nuestra función de pérdida. Debemos decir que necesita algunos retoques. La cosa es que nuestros clasificadores, así como los métodos avanzados de redes neuronales, son propensos al sobreentrenamiento. Esto se manifiesta en valores anormalmente grandes de las estimaciones de los parámetros; para evitar este fenómeno negativo, necesitamos un método que limite dichas estimaciones. Este método se denomina regularización L2:

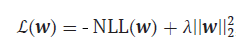
• λ = 1/С , С = (0,1]

Aquí simplemente añadiremos a nuestra función de pérdida existente el cuadrado de la norma del vector de parámetros multiplicado por el hiperparámetro λ lambda. Cuanto mayor sea lambda, más penalizados estarán los parámetros para valores grandes y más intensa será la regularización.

La función FitLogitRegression se encargará de estimar los parámetros del clasificador:

• bool L2 = false - por defecto la regularización L2 está desactivada,
• doble C=1,0 - hiperparámetro de intensidad de regularización, cuanto más pequeño sea, más se limitarán los valores de los parámetros optimizados,
• bool probit = false - el modelo logit estará activado por defecto,
• doble alfa - nivel de significación alfa Chi-cuadrado de la distribución estadística LR

Esta función tomará como argumento una matriz de características y le añadirá una variable denominada condicional o ficticia que tomará valores iguales a uno en todas las observaciones. Esto será necesario para poder estimar el parámetro w0(desplazamiento) en nuestro modelo. Además de las estimaciones de los parámetros, esta función también calculará sus matrices de covarianza para calcular los errores estándar.

//+------------------------------------------------------------------+
//| Finding the optimal parameters for the Logit or Probit model     |
//+------------------------------------------------------------------+
vector FitLogitRegression(matrix &input_X, vector &target_y,bool L2 = false, double C=1.0,bool probit = false,double alpha = 0.05)
  {
   L2_=L2;
   probit_ = probit;
   C_ = C;
   double              w[],s[];
   CObject             obj;
   CNDimensional_Logit ffunc;
   CNDimensional_Rep   frep;
   ulong Rows = input_X.Rows();
   ulong Cols = input_X.Cols();
   matrix One=matrix::Ones(int(Rows),int(Cols+1));
   for(int i=0;i<int(Cols); i++)
     {
      One.Col(input_X.Col(i),i+1);  // design matrix
     }
   input_X = One;
   Cols = input_X.Cols();
   Rows_ = int(Rows);
   Cols_ = int(Cols);
   Input_X_gl = input_X;
   target_y_gl = target_y;
   ArrayResize(w,int(Cols));
   ArrayResize(s,int(Cols));
//--- initialization
   ArrayInitialize(w,0.0);
   ArrayInitialize(s,1.0);
//--- optimization stop conditions
   double epsg=0.000001;
   double epsf=0.000001;
   double epsx=0.000001;
   double diffstep=0.000001;
   int maxits=0;
//------------------------------
   CMinLBFGSStateShell state;
   CMinLBFGSReportShell rep;
   CAlglib::MinLBFGSCreateF(1,w,diffstep,state);
   CAlglib::MinLBFGSSetCond(state,epsg,epsf,epsx,maxits);
   CAlglib::MinLBFGSSetScale(state,s);
   CAlglib::MinLBFGSOptimize(state,ffunc,frep,0,obj);
   CAlglib::MinLBFGSResults(state,w,rep);
   Print("TerminationType ="," ",rep.GetTerminationType());
   Print("IterationsCount ="," ",rep.GetIterationsCount());

   vector parameters=vector::Zeros(Cols);
   for(int i = 0; i<int(Cols); i++)
     {
      parameters[i]= w[i];
     }
   Print("Parameters = "," ",parameters);

//-------Likelihood Ratio Test LR-----------------------------------------
   double S = target_y.Sum();   // number of "success"
   ulong All = target_y.Size(); // all data
   double L0 = S*MathLog(S/All) + (All-S)*MathLog((All-S)/All); // Log-likelihood for the trivial model
 //  Print("L0 = ",L0);
 //  Print("LLF = ",func_);
   double LR;
   LR = 2*(-func_ - L0); // Likelihood Ratio Test LR
   int err;
   double Chi2 = MathQuantileChiSquare(1-alpha,Cols-1,err); // If H0 true ---> Chi2Distribution(alpha,v)
   Print("LR ",LR," ","Chi2 = ",Chi2);
//--------------------------------------------------------------------------------
//-------------- calculate if model significant or not
   if(LR > Chi2)
      ModelSignificant = true;
   else
      ModelSignificant = false;
//----------------------------------------------------

//-------------Estimation of the covariance matrix of parameters for the Probit model------------
   vector logit = input_X.MatMul(parameters);  //
   vector activation;
   logit.Activation(activation,AF_SIGMOID); // Logit activation
   double probit_SE[],probitact[];
   ArrayResize(probit_SE,Rows_);

   for(int i=0; i <Rows_; i++)
     {
      probit_SE[i] = logit[i];
     }

   if(probit_)
     {
      ulong size_parameters = parameters.Size();
      matrix CovProbit=matrix::Zeros(int(size_parameters),int(size_parameters));
      int err;
      vector a_=vector::Zeros(Rows_);
      vector b=vector::Zeros(Rows_);
      vector c=vector::Zeros(Rows_);
      vector xt=vector::Zeros(int(size_parameters));

      for(int i = 0; i<Rows_; i++)
        {
         a_[i] = MathPow((MathProbabilityDensityNormal(probit_SE[i],0,1,err)),2);
         b[i] = MathCumulativeDistributionNormal(probit_SE[i],0,1,err);
         c[i] = a_[i]/(b[i]*(1-b[i]));
         xt = input_X.Row(i);
         CovProbit = CovProbit + c[i]*xt.Outer(xt);
        }
      CovProbit = CovProbit.Inv();
      vector SE;
      SE = CovProbit.Diag(0);
      SE = MathSqrt(SE);  // standard errors of parameters
      Print("Probit_SE = ", SE);
     }
   else
     {
      //-------------Estimation of the covariance matrix of parameters for the Logit model------------
      vector v = vector::Zeros(Rows_);

      for(int i = 0; i<Rows_; i++)
        {
         v[i] = activation[i]*(1-activation[i]);
        }

      matrix R,Hesse,X,a,CovLogit;
      R.Diag(v,0);
      X = input_X.Transpose();
      a = X.MatMul(R);
      Hesse = a.MatMul(input_X);
      CovLogit = Hesse.Inv();
      vector SE;
      SE = CovLogit.Diag(0);
      SE = MathSqrt(SE); // standard errors of parameters
      Print("Logit_SE = ", SE);
      //-----------------------------------------------
     }
   return parameters;
  }

Una vez hallados los parámetros y calculadas sus matrices de covarianza, podremos proceder a la previsión.

Previsión

La función Trade_PredictedTarget se encargará de predecir las etiquetas de clase y, por tanto, las señales de compra o venta. Tomará los parámetros optimizados como entrada y emitirá la etiqueta de clase predicha. A continuación, LogitExpert generará las reglas para la apertura de posiciones. Son bastante sencillas. Si obtenemos una señal de compra (señal = 1) - abriremos una posición larga. Si ya existe una posición larga, seguiremos manteniéndola. Cuando se reciba una señal de venta, se cerrará la posición larga y se abrirá inmediatamente una posición corta.

El propio código de LogitExpert

//+------------------------------------------------------------------+
//|                                                  LogitExpert.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"

#include <\LogitReg.mqh>
#include <Trade\Trade.mqh>
#include <Trade\PositionInfo.mqh>
CTrade m_trade;
CPositionInfo m_position;

sinput string   symbol_X       = "EURUSD";    // Input symbol
sinput string   symbol_y       = "EURUSD";    // Target symbol
input bool     _probit_        = false;       // Probit model
input  int      InpCount       = 20;          // Depth of history
input  int     _lag_           = 4;           // Number of features
input bool     _L2_            = false;       // L2_regularization
input double   _C_             = 1;           // C(0,1) inverse of regularization strength
input double   alpha_          = 0.05;        // Significance level Alpha (0,1)
input int      reoptimize_step = 2;           // Reoptimize step

#define MAGIC_NUMBER 23092024

int prev_bars = 0;
MqlTick ticks;
double min_lot;
vector params_;
matrix _Input_X;
vector _Target_y;
static int count_ = 0;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   m_trade.SetExpertMagicNumber(MAGIC_NUMBER);
   m_trade.SetTypeFillingBySymbol(Symbol());
   m_trade.SetMarginMode();
   min_lot = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);

   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   Print(__FUNCTION__," Deinitialization reason code = ",reason);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
   if(!isnewBar(PERIOD_CURRENT))
      return;

   double step;
   step = count_ % reoptimize_step;
//------------------------------------Train Dataset-------------------------------------------------
   int start = 0;
   if(step == 0)
     {
      GetDataset(InpCount,_lag_,start,_Input_X,_Target_y,symbol_X,symbol_y);
      params_ = FitLogitRegression(_Input_X,_Target_y,_L2_,_C_,_probit_,alpha_);
     }
   count_ = count_+1;
//--------------------------------------------------------------------------------------------------

//--- Get trade signal
   int signal = Trade_PredictedTarget(params_,start,_lag_,InpCount,symbol_X);
   Comment("Trade signal: ",signal,"  ","ModelSignificant: ",ModelSignificant);  
//---------------------------------------------

//--- Open trades based on Signals
   SymbolInfoTick(Symbol(), ticks);
   if(signal==1)
     {
      if(!PosExists(POSITION_TYPE_BUY) && ModelSignificant)
        {
         m_trade.Buy(min_lot,Symbol(), ticks.ask);
         PosClose(POSITION_TYPE_SELL);
        }
      else
        {
         PosClose(POSITION_TYPE_SELL);
        }
     }
   else
     {
      if(!PosExists(POSITION_TYPE_SELL) && ModelSignificant)
        {
         m_trade.Sell(min_lot,Symbol(), ticks.bid);
         PosClose(POSITION_TYPE_BUY);
        }
      else
        {
         PosClose(POSITION_TYPE_BUY);
        }
     }
  }
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//|   Function tracks the occurrence of a new bar event              |
//+------------------------------------------------------------------+
bool isnewBar(ENUM_TIMEFRAMES TF)
  {
   if(prev_bars == 0)
      prev_bars = Bars(Symbol(), TF);

   if(prev_bars != Bars(Symbol(), TF))
     {
      prev_bars = Bars(Symbol(), TF);
      return true;
     }

   return false;
  }

//+------------------------------------------------------------------+
//|Function determines whether there is an open buy or sell position |
//+------------------------------------------------------------------+
bool PosExists(ENUM_POSITION_TYPE type)
  {
   for(int i=PositionsTotal()-1; i>=0; i--)
      if(m_position.SelectByIndex(i))
         if(m_position.Symbol()==Symbol() && m_position.Magic() == MAGIC_NUMBER && m_position.PositionType()==type)
            return true;

   return false;
  }
//+------------------------------------------------------------------+
//|The function closes a long or short trade                         |
//+------------------------------------------------------------------+
void PosClose(ENUM_POSITION_TYPE type)
  {
   for(int i=PositionsTotal()-1; i>=0; i--)
      if(m_position.SelectByIndex(i))
         if(m_position.Symbol()==Symbol() && m_position.Magic() == MAGIC_NUMBER && m_position.PositionType()==type)
            if(!m_trade.PositionClose(m_position.Ticket()))
               printf("Failed to close position %d Err=%s",m_position.Ticket(),m_trade.ResultRetcodeDescription());
  }

¿Qué distingue a este experto de los demás enfoques? En primer lugar, permite reoptimizar los parámetros del clasificador cada barra (reoptimize_step). En segundo lugar, no se limita a estimar los parámetros del modelo, sino que presta atención a los errores estándar de dichas estimaciones, algo que mucha gente suele pasar por alto. No basta con encontrar los parámetros "óptimos" en la muestra, hay que comprobar si estos parámetros o el modelo en su conjunto son significativos. Al fin y al cabo, si los parámetros no son significativos, lo lógico sería ignorar la señal comercial, ¿no?

Por ello, este EA también incluye un procedimiento para comprobar la significación de la hipótesis del modelo. En este caso, la hipótesis nula afirmará que todos los parámetros del modelo son cero (H0:w1=0,w2=0,w3=0,..., wk=0), mientras que la hipótesis alternativa H1 afirmará que algunos parámetros no son cero y, por tanto, el modelo resultará útil en la predicción. Para comprobar esta hipótesis, se utilizará el criterio de la razón de verosimilitud (LR), que evalúa la diferencia entre el modelo inferido y el modelo trivial:

LR = 2(LLF – LLF0)

• LLF - valor encontrado del logaritmo de la función de verosimilitud,

• LLF0 - logaritmo de verosimilitud bajo la hipótesis nula, es decir, para el modelo trivial

p0 = ∑(yn =1)/N - tasa de éxito de la muestra,

LLF0 = N(p0*Ln(p0) + (1- p0)*Ln(1 – p0))

Cuanto mayor sea la diferencia, mejor será el modelo completo antes que el modelo trivial. Cuando se cumpla la hipótesis nula, el estadístico LR tendrá una distribución Chi-cuadrado con v grados de libertad (v será igual al número de características). Si el valor calculado del estadístico LR cae en la zona crítica, es decir, LR > X²crit (alpha; v=lag_), entonces se rechazará la hipótesis H0 y, por tanto, no se ignorará la señal comercial y se abrirá una posición comercial.

Un de los escenarios posibles. GBPUSD, Daily

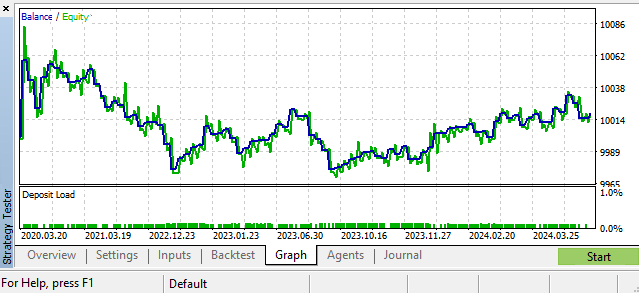
Hiperparámetros

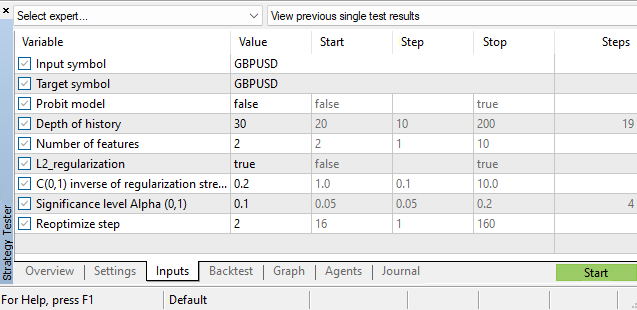
Merece la pena decir que, además de la estimación de los parámetros de los propios modelos clasificadores, seguiremos teniendo un gran bagaje de hiperparámetros:

• profundidad de la historia
• número de funciones
• nivel de significación alfa
• paso de reoptimización

Estos hiperparámetros se seleccionarán en el simulador de estrategias de MetaTrader 5. Una de las tareas que pueden mejorar el rendimiento del asesor experto es construir una función de dependencia del parámetro de profundidad histórica del estado actual del mercado, es decir, hacerlo dinámico de la misma manera que se ha hecho con los parámetros del modelo logit y breakout. Pero esa es otra historia. Como pista, puede leer mi artículo «El criterio de homogeneidad de Smirnov como indicador de la no estacionariedad de las series temporales», donde se discute la cuestión de la construcción de un indicador de discordancia.

Conclusión

En este artículo hemos analizado modelos de regresión con resultados binarios, hemos aprendido a estimar los parámetros de estos modelos y hemos implementado el asesor experto comercial LogitExpert para probar y ajustar estos modelos. Su especialidad reside en la capacidad de reentrenar sobre la marcha los parámetros del clasificador basándose en los datos más recientes y actualizados.

También hemos prestado especial atención a la estimación de los errores estándar de los parámetros, para lo cual ha sido necesario estimar las matrices de covarianza de los modelos logit y probit.

Utilizando el criterio de la razón de verosimilitud, hemos realizado la prueba de significación de la ecuación del modelo clasificador en su conjunto. Sobre esta estadística se ha construido un filtro para cribar las señales comerciales que no sean fiables desde el punto de vista estadístico.