Elementos del análisis de correlación en MQL5: Prueba chi-cuadrado de Pearson de independencia y ratio de correlación.

Introducción

En este artículo, me gustaría abordar una sección tan importante de la estadística matemática como el análisis de correlación, que incluye la detección y evaluación de dependencias entre variables aleatorias. La herramienta más popular en el arsenal del análisis de correlación es, por supuesto, el ratio de correlación. Sin embargo, el cálculo del ratio de correlación por sí solo es completamente insuficiente si queremos evaluar dependencias en los datos, especialmente como los incrementos del precio de las acciones. En primer lugar, la ratio sólo evalúa la dependencia lineal. En segundo lugar, los valores cero de la ratio de correlación no significan la ausencia de dependencia si la muestra de datos a partir de la que se calcula tiene una distribución distinta de la normal. Para responder a la pregunta de si los datos son dependientes, debemos definir los criterios de independencia. Hablaremos del criterio más famoso: la prueba chi-cuadrado de independencia de Pearson. También hablaremos de una característica numérica como la ratio de correlación, que ayuda a determinar si la dependencia estudiada es no lineal.

La hipótesis de la independencia

Se supone que los datos representan observaciones de alguna variable aleatoria bidimensional (X, Y) con una función de distribución desconocida F(X, Y), sobre la que se requiere probar la hipótesis de independencia H0 : F(X, Y) = F(X)*F(Y), donde F(X) y F(Y) son funciones de distribución unidimensionales.

Por variables aleatorias X e Y en este artículo me referiré o bien a incrementos de los logaritmos de los precios de diferentes instrumentos financieros, o bien a incrementos de los precios de un instrumento tomados con el desfase de uno.

Prueba de independencia chi-cuadrado de Pearson

El criterio de independencia chi-cuadrado se utiliza tanto para variables aleatorias discretas con un número finito de resultados como para variables aleatorias continuas, pero con la condición obligatoria de su agrupación previa. En este caso, el conjunto de todos los valores posibles de la variable aleatoria X se divide en i intervalos no intersecantes A1, A2, Ai, y el conjunto de todos los valores de Y se divide en un conjunto de j intervalos no intersecantes B1, B2, Bj. Así, el conjunto de valores de una cantidad bidimensional (X, Y) se divide en i*j rectángulos (celdas). Para mayor claridad, estos datos se presentan en forma de la denominada tabla de contingencia de características (tabla de correlaciones, tabla de distribución de probabilidades de una variable aleatoria bidimensional, etc.).

                              

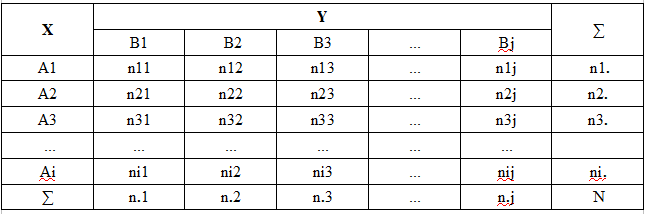
En la tabla:

• Ai = (Xi-1, Xi) : i-ésimo intervalo de una agrupación aleatoria de valores X

• Bj = (Yj-1,Yj) : j-ésimo intervalo de una agrupación aleatoria de valores Y

• nij : frecuencia real del grupo de celdas (número de esos pares de observaciones (X, Y) cuyos valores caen dentro del intervalo Ai y Bj)

• ni. : número de observaciones en la fila i

• n.j : número de observaciones en la j-ésima columna

• N : volumen de muestra

La siguiente estadística se utiliza como prueba chi-cuadrado de independencia:

CHI2 = (Real – Esperado) ^2 / Esperado,

donde

• Real : (celdas nij) frecuencia de grupo real,

• Esperado : (celdas nij) frecuencia esperada del grupo

Estos datos estadísticos tienen una distribución chi-cuadrado con v = (j-1)(i-1) grados de libertad.

La hipótesis nula de independencia se rechaza si el estadístico CHI2 estimado supera los valores críticos de la distribución chi-cuadrado con v grados de libertad a un determinado nivel de significación «alfa».

Calcularemos las frecuencias reales basándonos en los datos de la muestra. El principio para construir las frecuencias esperadas es el siguiente: si las variables aleatorias X e Y son independientes, entonces es válida la siguiente ecuación:

P {Ai, Bj} = P {Ai}*P{Bj},

en otras palabras, la probabilidad de que se produzcan simultáneamente los sucesos Ai y Bj es igual al producto de la probabilidad de que se produzcan los sucesos Ai y la probabilidad de que se produzcan los sucesos Bj.

Para hallar las expectativas matemáticas de los sucesos {Ai, Bj}, {Ai} y {Bj}, multiplique ambas partes de esta igualdad por N*N, es decir, por el cuadrado del número de observaciones.

N*N * P {Ai, Bj} = N *P{Ai} * N* P{Bj}

Entonces obtenemos:

• N*P{Ai} : expectativa matemática del número de observaciones en la i-ésima fila

• N* P{Bj} : expectativa matemática del número de observaciones en la j-ésima columna

• N * P {Ai, Bj} = (N *P{Ai} * N* P{Bj})/N : expectativa matemática del número de coincidencias de celdas en la intersección de la i-ésima fila y la j-ésima columna

Luego, sustituyendo las estimaciones ni y nj en lugar de las expectativas matemáticas N *P{Ai} y N* P{Bj} (las frecuencias reales de la tabla de correlación), obtenemos la estimación deseada de las frecuencias esperadas.

Esperado = (ni. *n.j)/N

Así, según la hipótesis de independencia, la frecuencia esperada de acertar una celda en la intersección de la i-ésima fila y la j-ésima columna es igual al producto de las sumas del número de observaciones en la i-ésima fila y la j-ésima columna dividido por el tamaño de la muestra.

Por lo tanto, al calcular el criterio, es natural esperar que cuanto más difieran las frecuencias reales de las esperadas, mayor será la probabilidad de que los datos no sean independientes.

Indicador Chi2Test

El cálculo de la prueba de independencia chi-cuadrado de Pearson se implementa en el indicador Chi2Test. El indicador comprueba la hipótesis de independencia en cada barra entre incrementos de precios adyacentes para un mismo instrumento financiero.

El indicador tiene cuatro entradas:

• alpha : nivel de significación

• Data : ventana de datos para el cálculo

• Tails : número de desviaciones típicas

• Coeficiente de contingencia

Para calcular el estadístico chi-cuadrado, primero tenemos que calcular las frecuencias reales en la tabla de contingencia de características. Para ello se utiliza la función de tabulación cruzada.

//+------------------------------------------------------------------+
//|  Calculate the table of contingency of two random values (X,Y)   |
//+------------------------------------------------------------------+
bool Crosstab(const double &dataX[],const double &dataY[],const double &bins[],matrix &freq)
  {

   int datasizeX=ArraySize(dataX);
   int datasizeY=ArraySize(dataY);
   int binssize=ArraySize(bins);
   if(datasizeX==0 || datasizeY==0 || binssize==0)
      return(false);
   if(datasizeX != datasizeY)
      return(false);

   for(int i=0; i<datasizeX; i++)
     {
      if(!MathIsValidNumber(dataX[i]) || !MathIsValidNumber(dataY[i]))
         return(false);
     }

   matrix m_freq=matrix::Zeros(binssize, binssize);
   
   for(int x=0; x<binssize; x++)
     {
      for(int i=0; i<datasizeX; i++)
        {
         for(int y=0; y<binssize; y++)
           {
            if(dataX[i]<=bins[x] && dataY[i]<=bins[y]) 
              {
               m_freq[x,y]=m_freq[x,y]+1;
               break;
              }
           }
        }
     }
     
   matrix Actual = m_freq;
   vector p1,p2,diffp;
   for (int j=1; j<binssize; j++)
   {
   p1 = m_freq.Row(j-1);
   p2 = m_freq.Row(j);
   diffp = p2-p1;
   Actual.Row(diffp,j);   
   }
   freq = Actual; 
   
   return(true);
  }

Como los datos con los que trabajamos son continuos, lo primero que tenemos que hacer es agruparlos. En este caso, podemos encontrar recomendaciones que indican que, para calcular correctamente la prueba, es conveniente que el valor mínimo de la frecuencia esperada en las casillas no sea inferior a uno, mientras que el número de casillas, en las que la frecuencia esperada es inferior a cinco, no debe ser grande (por ejemplo, se permiten dos casillas de este tipo si el número total de casillas es inferior a 10). Dado que las distribuciones de los datos bursátiles tienen colas pesadas, surge cierta dificultad para construir intervalos de agrupación que puedan cumplir los requisitos anteriores.

Propongo agrupar los datos después de normalizarlos. A continuación, recorte las colas pesadas de la distribución a 2-3-4 sigma, en función del volumen de datos analizados. En el indicador, esto se hace mediante el parámetro Tails. Por ejemplo, si el volumen de datos es pequeño (200-300 valores), entonces debemos elegir el valor Tails igual a 2 sigma. Como resultado, obtenemos intervalos de agrupación: (-2,-1), (-1,0), (0,1), (1,2) y, en consecuencia, una tabla de contingencia de 4x4 características. Por lo tanto, combinaremos intervalos de agrupación adyacentes con frecuencias esperadas pequeñas para calcular correctamente la estadística de chi-cuadrado.

Coeficiente de contingencia de Cramer

Desafortunadamente, la estadística CHI2 no puede servir como una medida numérica de dependencia de la probabilidad, por lo que se utiliza el coeficiente de contingencia de Cramer para este propósito. Sus valores varían de cero a uno. Cero significa que no hay dependencia entre los datos, uno significa dependencia funcional.

El coeficiente de contingencia de Cramer se basa en la estadística de chi-cuadrado:

Coeficiente de contingencia = sqrt (CHI2 / N*(Bins_count-1)),

donde Bins_count es un número de filas (o columnas) en la tabla de contingencia de características.

De este modo, en un único indicador se implementan de hecho dos estadísticas: la estadística principal de chi-cuadrado y el coeficiente de contingencia calculado sobre su base.

Si desea probar la independencia de dos instrumentos financieros diferentes, utilice el script Crosstab. Para ello, active el parámetro X vs Y (verdadero). De lo contrario, el script calcula estadísticas basadas en los datos del símbolo actual. Los datos de muestra para el cálculo se cuentan desde la penúltima barra del gráfico.

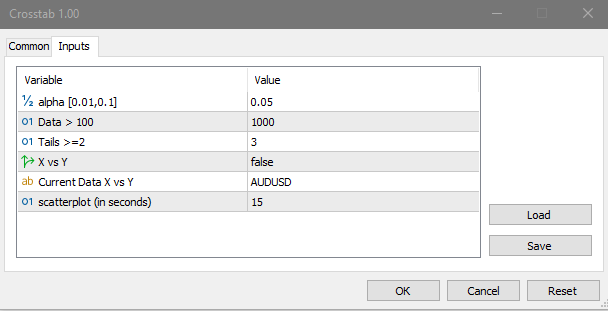
El script Crosstab calcula y registra la siguiente información:

• Matriz de frecuencias reales (Actual) y esperadas (Expected)

• Ratio de correlación r calculada a partir de datos agrupados

• Ratio de correlación de Pearson calculada a partir de datos no agrupados (para comparar la precisión de los cálculos, ya que las estadísticas calculadas a partir de datos agrupados son menos precisas)

• Nxy, Nyx (ratio de correlación) ratio de correlación

• resultados de la prueba de la hipótesis de ausencia de dependencia de correlación (estadística f de independencia de correlación)

• resultados de la prueba de la hipótesis de la linealidad de la dependencia de la correlación (estadística f lineal/no lineal),

• Estadísticas de chi-cuadrado CHI2

• Coeficiente de contingencia de Cramer

También se muestra en la pantalla un diagrama de dispersión (campo de correlación) para la evaluación visual de la dependencia del par.

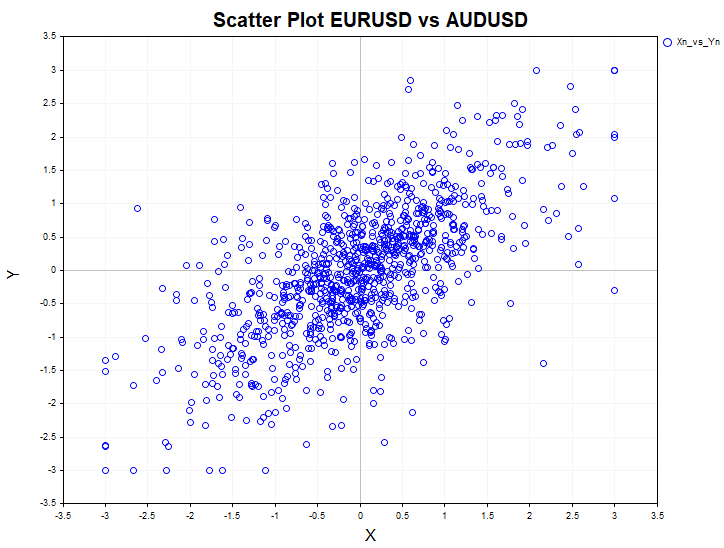
Utilice el script Crosstab_Models para probar la independencia de los datos del modelo. Los modelos utilizados son distribución uniforme, autorregresión de primer orden, heterocedasticidad condicional autorregresiva ARCH y mapeo logístico.

Los datos del modelo sirven como una especie de plantilla utilizada para comparar resultados obtenidos a partir de datos reales. Por ejemplo, así es como se ve una dependencia no lineal en un sistema dinámico no lineal unidimensional: un mapeo logístico:

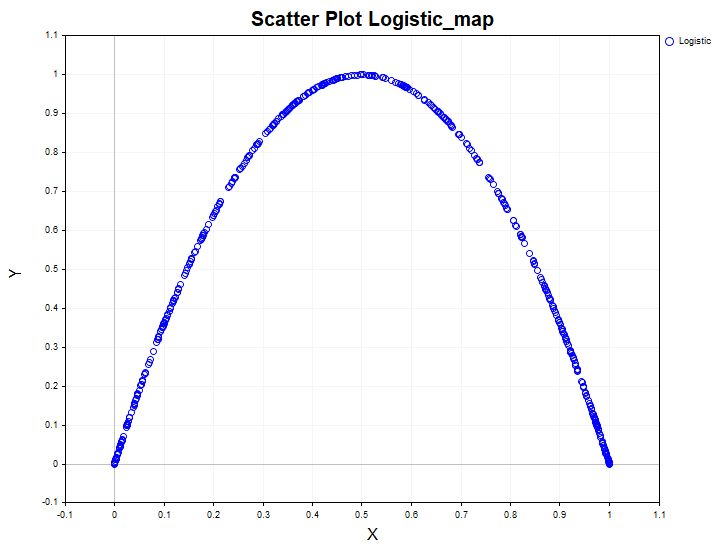
Al analizar los datos de dicho sistema utilizando únicamente la ratio de correlación lineal, se podría concluir erróneamente que este proceso es ruido blanco. Al mismo tiempo, la prueba de independencia de chi-cuadrado revela fácilmente que los datos son dependientes y la ratio de correlación confirma que la dependencia no es lineal.

Ratio de correlación

El ratio de correlación se utiliza para evaluar la no linealidad de la dependencia de correlación:

Nyx = sqrt (D[E(Y|X)]/Sy)

Nxy = sqrt (D[E(X|Y)])/Sx)

donde:

• E(Y|X) : expectativa matemática condicional del valor aleatorio Y

• E(X|Y) : expectativa matemática condicional del valor aleatorio X

• D[E(Y|X)] : varianza de la expectativa matemática condicional del valor aleatorio Y

• D[E(X|Y)] : varianza de la expectativa matemática condicional del valor aleatorio X

• Sy, Sx : varianzas incondicionales de los valores aleatorios Y y X

Recordemos que:

• La expectativa matemática condicional E(Y|X) es un valor aleatorio.

• E[E(Y|X)] = E[Y] (la expectativa matemática del valor aleatorio Y es igual a la expectativa matemática incondicional Y).

• La dispersión de Y es D[Y] = E[(Y – E(Y) )^2)] expectativa matemática del cuadrado de la desviación del valor aleatorio de Y respecto de la expectativa matemática E[Y].

• Entonces D[E(Y|X)] = E{[ E(Y|X) – E[Y] ] ^ 2}. En otras palabras, la varianza de la expectativa matemática incondicional E(Y|X) es igual a la expectativa matemática del cuadrado de la desviación de la expectativa matemática incondicional E(Y|X) respecto de la expectativa matemática incondicional E[Y].

En otras palabras, el ratio de correlaciónes la raíz cuadrada del ratio de dos varianzas: condicional e incondicional. El ratio de correlación sólo se puede calcular en base a la tabla de correlación, es decir, en base a datos agrupados. Enumeremos las propiedades que tiene:

• La ratio de correlación es asimétrica con respecto a X e Y, es decir, Nxy != Nyx.

• 0 ≤ | r | ≤ Nxy ≤ 1, 0 ≤ | r | ≤ Nyx ≤ 1, los valores del indicador se encuentran dentro del rango [0,1] y siempre son mayores o iguales que la razón lineal de correlación r, que se toma módulo.

• Si los datos son independientes, entonces Nxy=Nyx=0. Lo contrario no es cierto, es decir, la falta de correlación no implica independencia.

• Si | r | = Nyx = Nyx < 1, entonces la correlación entre X e Y es lineal, es decir, no se puede encontrar una curva mejor que una línea recta para la ecuación de regresión.

• Si la correlación entre X e Y no es lineal, entonces | r | < min (Nxy, Nyx). Cuanto menor sea la diferencia entre la ratio de correlación y la relación de correlación, más cercana será la relación entre X e Y a la lineal.

Calculando la relación de correlación de muestra, podemos comprobar la hipótesis de la ausencia de correlación entre dos variables aleatorias (H0: Nyx = 0).

Para ello se calculan las siguientes estadísticas:

F = Nyx^2 * (N-Bins_count) / (1- Nyx^2) *(Bins_count-1)

Si la hipótesis probada es verdadera, la estadística F se distribuye de acuerdo con la ley de Fisher con v1 = Bins_count-1 y v2 = N-Bins_count grados de libertad.

La hipótesis nula se rechaza en el nivel de significación alfa si el valor calculado de la estadística F excede el valor crítico de esta estadística (entonces se acepta la alternativa H1: Nyx >0)

Digamos que estamos convencidos de que la dependencia de correlación está presente. Surge la pregunta: ¿esta dependencia es lineal o no lineal? La hipótesis sobre la linealidad de la dependencia de correlación entre dos variables aleatorias responde esta pregunta.

Para probar la hipótesis sobre la linealidad de la dependencia de correlación de Y sobre X (H0: Nyx^2 = r^2), se utilizan las siguientes estadísticas:

F = (Nyx^2 - r^2) * (N-Bins_count) / (1- Nyx^2) *(Bins_count-2)

Si la hipótesis probada es verdadera, la estadística F se distribuye de acuerdo con la ley de Fisher con v1 = Bins_count-2 y v2 = N-Bins_count grados de libertad.

La hipótesis nula sobre la linealidad de la correlación se rechaza en el nivel de significación alfa si el valor calculado de la estadística F excede el valor crítico de esta estadística (entonces se acepta la alternativa H1: Nyx^2 != r^2 )

Conclusión

El artículo examinó herramientas tan importantes del análisis de correlación como la prueba de independencia de chi-cuadrado de Pearson y la ratio de correlación. Con su ayuda, es posible evaluar con mucha más precisión la presencia de relaciones ocultas en los datos. El indicador CHI2Test prueba la hipótesis de independencia, permitiéndonos obtener conclusiones estadísticamente válidas sobre la presencia de relaciones en los datos.

Además de las estadísticas de chi-cuadrado, los scripts Crosstab y Crosstab_Models también calculan la relación de correlación y prueban la hipótesis sobre la dependencia de la correlación y la linealidad de esta dependencia, incluso para los datos del modelo. Además, se muestra un gráfico de campo de correlación en la pantalla para una evaluación visual de la dependencia del par. El usuario puede regular la precisión de las pruebas estadísticas eligiendo el nivel de significación alfa deseado. Cuanto menor sea el nivel de significación, menos probable será obtener una respuesta falsa.