Forecasting exchange rates using classic machine learning methods: Logit and Probit models

Introduction

Financial market researchers will always face the difficult task of choosing a mathematical model to predict the future behavior of trading instruments. To date, a huge number of such models have been developed. So the question arises: how not to drown in all this variety of methods and approaches, where to start and which models are best to focus on, especially if you are just starting to forecast using machine learning models? If we try to reduce the forecasting task to a simple answer to the question - "will the tomorrow's closing price be higher than the ones of today?", then the logical choice would be binary classification models. Some of the simplest and most widely used are logit and probit regression. These models belong to the most common form of machine learning, so-called supervised learning.

The task of supervised learning, in turn, is to teach our model to display a set of inputs {x} (predictors or features) into a set of outputs {y} (targets or labels). Here we will predict only two market conditions - the rise or fall of the currency pair price. Therefore, we will have only two classes of labels y ∊ {1,0}. Price patterns, namely standardized price increments with a certain lag, will act as predictors. This data will form our {x, y} training set to be used to estimate the parameters of our models. The predictive model based on trained classifiers is implemented as LogitExpert EA.

Binary logit and probit regression

Let's briefly go over the theoretical part. The simplest model of a binary choice is a linear probability model, in which the probability of a successful event of P(yn=1|xn) is a linear function of the explanatory variables:

P(yn=1|xn) = w0*1 + w1x1 + w2x2 + … + wkxk

Unfortunately, such a model has a very serious drawback - the predicted value can be greater than one or less than zero, and this in turn does not allow the predicted value to be interpreted as a probability. Therefore, to solve this problem, it was proposed to use known probability distribution functions the values of the linear function would be substituted into.

The probit model is based on the standard normal distribution law N(0,1):

P(yn=1|xn) = F(xnw)=μn

• n – lower index indicating the observation (example) number,

• yn - class label,

• F( ) - normal distribution function (activation function),

• xn – feature vector,

• w – vector of model parameters,

• xnw – logit or preactivation (represents the scalar product of the feature vector and the parameter vector)

xnw = w0*1 + w1x1 + w2x2 + … + wkxk

In turn, the logit model is based on the logistic law of probability distribution:

                                                      P(yn=1|xn) = L(xnw) = exp(xnw)/(1 + exp(xnw)) = μn

The distribution functions of the logistic and normal distributions are quite close, and on the [-1.2;1.2] interval they are almost identical. Therefore, logit and probit models often give similar results unless the probability is close to zero or one. Thus, when these models are substituted with a feature vector, we can calculate the probabilities of class labels, and therefore the probability of the future price movement direction.

Data preparation

Before estimating the parameters of the model, we need to define the features, then standardize them and present them in the proper form for the function that will find the optimal parameters (in the sense of minimizing the loss function). The responsible function is GetDataset:

• InpCount_ - set the number of examples for training

• lag_ - number of analyzed features (price increments with lag)

• string X — currency pair the features are calculated for

• string y — currency pair labels are calculated for

• int start — number of a bar we start taking training examples from

As an illustrative example, we will use the lag increments of the price of a currency pair as signs. For example, if we set the function argument lag_ = 4, then the features will be x{return-4,return-3,return-2,return-1} and we will have exactly (InpCount_- lag_) examples for training.

//+------------------------------------------------------------------+
//|Get data for analysis: features and corresponding labels          |
//+------------------------------------------------------------------+
bool GetDataset(int InpCount_,int lag_,int start,matrix &Input_X,vector & Target_y,string X,string y)
  {

   matrix rates;
   matrix target;
   target.CopyRates(y, PERIOD_CURRENT, COPY_RATES_OHLC, start+1, InpCount_);
   rates.CopyRates(X, PERIOD_CURRENT, COPY_RATES_OHLC, start+2, InpCount_-1);
   rates = rates.Transpose();
   target = target.Transpose();
   int Class_ [];
   ArrayResize(Class_,InpCount_);
   for(int i=0; i<InpCount_; i++)
     {
      if(target[i,3] >  target[i,0])
         Class_[i] = 1;
      else
         Class_[i] = 0;
     }

   vector label=vector::Zeros(InpCount_-lag_);
   for(int i=0; i<InpCount_-lag_; i++)
     {
      label[i] = Class_[i+lag_]; // class label
     }

   matrix returns=matrix::Zeros(InpCount_-lag_, lag_);
   for(int j=0; j<lag_; j++)
     {
      for(int i=0; i<InpCount_-lag_; i++)
        {
         returns[i,j] =rates[i+j,3] - rates[i+j,0]  ; // Input Data
        }
     }

   vector cols_mean=returns.Mean(0);
   vector cols_std=returns.Std(0);

   mean_ = cols_mean[lag_-1];
   std_ = cols_std[lag_-1];

   for(int j=0; j<lag_; j++)
     {
      for(int i=0; i<InpCount_-lag_; i++)
        {
         returns[i,j] = (returns[i,j] - cols_mean[lag_-1])/cols_std[lag_-1];
        }
     }
   Input_X = returns;
   Target_y = label;

   return true;
  }

At the output, we obtain the Input_X feature matrix and the Target_y label vector. After the training set has been formed, we move on to estimating the parameters.

Estimation of model parameters

Most often, parameter estimates are found using the maximum likelihood method. In the binary case, the logit and probit models assume that the y dependent variable y has a Bernoulli distribution. If so, then the logarithmic likelihood function will be equal to:

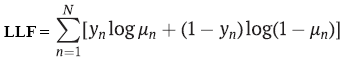
• yn – class label,

• μn - probability of predicting a class using logit or probit regression,

• N – number of training examples

To estimate the parameters, we need to find the maximum of this function, but since it is customary in machine learning to minimize the loss function, and all optimizers are mainly configured to minimize the target functions, then a minus sign is simply added to the likelihood function. The result is the so-called negative log-likelihood (NLL). We will minimize this loss function using the L-BFGS second-order quasi-Newtonian optimization method implemented in the Alglib library. This numerical method is usually used to find the parameters of logit and probit models. Another popular optimization method is the iterative least squares (IRLS) method.

//+------------------------------------------------------------------+
//| Derived class from CNDimensional_Func                            |
//+------------------------------------------------------------------+
class CNDimensional_Logit : public CNDimensional_Func
  {
public:
                     CNDimensional_Logit(void) {}
                    ~CNDimensional_Logit(void) {}
   virtual void      Func(CRowDouble &w,double &func,CObject &obj);
  };

//+------------------------------------------------------------------+
//| Objective Function: Logit Negative loglikelihood                 |
//+------------------------------------------------------------------+
void CNDimensional_Logit::Func(CRowDouble &w,double &func,CObject &obj)
  {

   double LLF[],probit[],probitact[];
   vector logitact;
   ArrayResize(LLF,Rows_);
   ArrayResize(probit,Rows_);
   vector params=vector::Zeros(Cols_);

   for(int i = 0; i<Cols_; i++)
     {
      params[i] =  w[i]; // vector of parameters
     }

   vector logit=vector::Zeros(Rows_);
   logit = Input_X_gl.MatMul(params);

   for(int i=0; i <Rows_; i++)
     {
      probit[i] = logit[i];
     }

   if(probit_)
      MathCumulativeDistributionNormal(probit,0,1,probitact); // Probit activation
   else
      logit.Activation(logitact,AF_SIGMOID); // Logit activation

//--------------------to avoid NAN error when calculating logarithm ------------------------------------
   if(probit_)
     {
      for(int i = 0; i<Rows_; i++)
        {
         if(probitact[i]==1)
            probitact[i]= 0.999;
         if(probitact[i]==0)
            probitact[i]= 0.001;
        }
     }
   else
     {
      for(int i = 0; i<Rows_; i++)
        {
         if(logitact[i]==1)
            logitact[i]= 0.999;
         if(logitact[i]==0)
            logitact[i]= 0.001;
        }
     }
//-------------------------------------------------------------------------------------------------
   double L2_reg;
   if(L2_)
      L2_reg = 0.5 * params.Dot(params); //  L2_regularization
   else
      L2_reg =0;

//------------------ calculate loss function-------------------------------------------------------------
   if(probit_)
     {
      for(int i = 0; i<Rows_; i++)
        {

         LLF[i]=target_y_gl[i]*MathLog(probitact[i]) + (1-target_y_gl[i])*MathLog(1-probitact[i]) ;

         if(!MathIsValidNumber(LLF[i]))
           {
            break;
           }
        }
     }
   else
     {
      for(int i = 0; i<Rows_; i++)
        {

         LLF[i]=target_y_gl[i]*MathLog(logitact[i]) + (1-target_y_gl[i])*MathLog(1-logitact[i]);

         if(!MathIsValidNumber(LLF[i]))
           {
            break;
           }
        }
     }

   func = -MathSum(LLF) + L2_reg/(Rows_*C_); // Negative Loglikelihood + L2_regularization
//------------------------------------------------------------------------------------------------------
   func_ = func;
  }

However, calculating parameter estimates alone is not enough; we would also like to obtain standard errors of these estimates in order to understand how significant our features are.

For example, the popular machine learning library scikit-learn for some reason does not calculate this information for the logit model. I implemented the calculation of standard errors for both the logit and probit models, so now you can see whether any specific features have a statistically significant effect on the forecast or not. This is one of the reasons why I prefer to write the logit model code myself in MQL, rather than use ONNX to convert ready-made models from popular machine learning packages. Another reason is that I need a dynamic model that can re-optimize the classifier parameters on every bar or at a desired specified frequency.

But let's get back to our loss function. It should be said that it requires some revision. The whole point is that our classifiers, just like advanced neural network methods, are prone to overfitting. This manifests itself in abnormally large values of parameter estimates and in order to prevent this negative phenomenon, we need a method that would limit such estimates. This method is called L2 regularization:

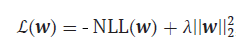
• λ = 1/С , С = (0,1]

Here we simply add the square of the norm of the parameter vector multiplied by the λ lambda hyperparameter to our existing loss function. The larger the lambda, the more the parameters are penalized for large values and the stronger the regularization.

The function responsible for evaluating the classifier parameters is FitLogitRegression:

• bool L2 = false — by default L2 regularization is disabled,
• double C=1.0 — regularization strength hyperparameter, the smaller it is, the more the values of the optimized parameters are limited,
• bool probit = false — logit model is enabled by default,
• double alpha — alpha significance level Chi-square distribution of LR statistics

This function takes a matrix of features as an argument and adds to it a so-called conditional or dummy variable that takes values equal to one in all observations. This is necessary so that we can estimate the parameter w0(bias) in our model. In addition to the parameter estimates, this function also computes their covariance matrices to calculate standard errors.

//+------------------------------------------------------------------+
//| Finding the optimal parameters for the Logit or Probit model     |
//+------------------------------------------------------------------+
vector FitLogitRegression(matrix &input_X, vector &target_y,bool L2 = false, double C=1.0,bool probit = false,double alpha = 0.05)
  {
   L2_=L2;
   probit_ = probit;
   C_ = C;
   double              w[],s[];
   CObject             obj;
   CNDimensional_Logit ffunc;
   CNDimensional_Rep   frep;
   ulong Rows = input_X.Rows();
   ulong Cols = input_X.Cols();
   matrix One=matrix::Ones(int(Rows),int(Cols+1));
   for(int i=0;i<int(Cols); i++)
     {
      One.Col(input_X.Col(i),i+1);  // design matrix
     }
   input_X = One;
   Cols = input_X.Cols();
   Rows_ = int(Rows);
   Cols_ = int(Cols);
   Input_X_gl = input_X;
   target_y_gl = target_y;
   ArrayResize(w,int(Cols));
   ArrayResize(s,int(Cols));
//--- initialization
   ArrayInitialize(w,0.0);
   ArrayInitialize(s,1.0);
//--- optimization stop conditions
   double epsg=0.000001;
   double epsf=0.000001;
   double epsx=0.000001;
   double diffstep=0.000001;
   int maxits=0;
//------------------------------
   CMinLBFGSStateShell state;
   CMinLBFGSReportShell rep;
   CAlglib::MinLBFGSCreateF(1,w,diffstep,state);
   CAlglib::MinLBFGSSetCond(state,epsg,epsf,epsx,maxits);
   CAlglib::MinLBFGSSetScale(state,s);
   CAlglib::MinLBFGSOptimize(state,ffunc,frep,0,obj);
   CAlglib::MinLBFGSResults(state,w,rep);
   Print("TerminationType ="," ",rep.GetTerminationType());
   Print("IterationsCount ="," ",rep.GetIterationsCount());

   vector parameters=vector::Zeros(Cols);
   for(int i = 0; i<int(Cols); i++)
     {
      parameters[i]= w[i];
     }
   Print("Parameters = "," ",parameters);

//-------Likelihood Ratio Test LR-----------------------------------------
   double S = target_y.Sum();   // number of "success"
   ulong All = target_y.Size(); // all data
   double L0 = S*MathLog(S/All) + (All-S)*MathLog((All-S)/All); // Log-likelihood for the trivial model
 //  Print("L0 = ",L0);
 //  Print("LLF = ",func_);
   double LR;
   LR = 2*(-func_ - L0); // Likelihood Ratio Test LR
   int err;
   double Chi2 = MathQuantileChiSquare(1-alpha,Cols-1,err); // If H0 true ---> Chi2Distribution(alpha,v)
   Print("LR ",LR," ","Chi2 = ",Chi2);
//--------------------------------------------------------------------------------
//-------------- calculate if model significant or not
   if(LR > Chi2)
      ModelSignificant = true;
   else
      ModelSignificant = false;
//----------------------------------------------------

//-------------Estimation of the covariance matrix of parameters for the Probit model------------
   vector logit = input_X.MatMul(parameters);  //
   vector activation;
   logit.Activation(activation,AF_SIGMOID); // Logit activation
   double probit_SE[],probitact[];
   ArrayResize(probit_SE,Rows_);

   for(int i=0; i <Rows_; i++)
     {
      probit_SE[i] = logit[i];
     }

   if(probit_)
     {
      ulong size_parameters = parameters.Size();
      matrix CovProbit=matrix::Zeros(int(size_parameters),int(size_parameters));
      int err;
      vector a_=vector::Zeros(Rows_);
      vector b=vector::Zeros(Rows_);
      vector c=vector::Zeros(Rows_);
      vector xt=vector::Zeros(int(size_parameters));

      for(int i = 0; i<Rows_; i++)
        {
         a_[i] = MathPow((MathProbabilityDensityNormal(probit_SE[i],0,1,err)),2);
         b[i] = MathCumulativeDistributionNormal(probit_SE[i],0,1,err);
         c[i] = a_[i]/(b[i]*(1-b[i]));
         xt = input_X.Row(i);
         CovProbit = CovProbit + c[i]*xt.Outer(xt);
        }
      CovProbit = CovProbit.Inv();
      vector SE;
      SE = CovProbit.Diag(0);
      SE = MathSqrt(SE);  // standard errors of parameters
      Print("Probit_SE = ", SE);
     }
   else
     {
      //-------------Estimation of the covariance matrix of parameters for the Logit model------------
      vector v = vector::Zeros(Rows_);

      for(int i = 0; i<Rows_; i++)
        {
         v[i] = activation[i]*(1-activation[i]);
        }

      matrix R,Hesse,X,a,CovLogit;
      R.Diag(v,0);
      X = input_X.Transpose();
      a = X.MatMul(R);
      Hesse = a.MatMul(input_X);
      CovLogit = Hesse.Inv();
      vector SE;
      SE = CovLogit.Diag(0);
      SE = MathSqrt(SE); // standard errors of parameters
      Print("Logit_SE = ", SE);
      //-----------------------------------------------
     }
   return parameters;
  }

Once the parameters have been found and their covariance matrices have been calculated, we can move on to forecasting.

Prediction

The function responsible for predicting class labels and, therefore, buy or sell signals is Trade_PredictedTarget. It receives the parameters to be optimized as inputs, and outputs the predicted class label. After that, the LogitExpert EA forms the rules for opening positions. They are quite simple. If we receive a buy signal (signal = 1), we open a long position. If a long position already exists, we continue to hold it. When a sell signal is received, the long position is closed and a short position is immediately opened.

The actual code of the LogitExpert EA

//+------------------------------------------------------------------+
//|                                                  LogitExpert.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"

#include <\LogitReg.mqh>
#include <Trade\Trade.mqh>
#include <Trade\PositionInfo.mqh>
CTrade m_trade;
CPositionInfo m_position;

sinput string   symbol_X       = "EURUSD";    // Input symbol
sinput string   symbol_y       = "EURUSD";    // Target symbol
input bool     _probit_        = false;       // Probit model
input  int      InpCount       = 20;          // Depth of history
input  int     _lag_           = 4;           // Number of features
input bool     _L2_            = false;       // L2_regularization
input double   _C_             = 1;           // C(0,1) inverse of regularization strength
input double   alpha_          = 0.05;        // Significance level Alpha (0,1)
input int      reoptimize_step = 2;           // Reoptimize step

#define MAGIC_NUMBER 23092024

int prev_bars = 0;
MqlTick ticks;
double min_lot;
vector params_;
matrix _Input_X;
vector _Target_y;
static int count_ = 0;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   m_trade.SetExpertMagicNumber(MAGIC_NUMBER);
   m_trade.SetTypeFillingBySymbol(Symbol());
   m_trade.SetMarginMode();
   min_lot = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);

   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   Print(__FUNCTION__," Deinitialization reason code = ",reason);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
   if(!isnewBar(PERIOD_CURRENT))
      return;

   double step;
   step = count_ % reoptimize_step;
//------------------------------------Train Dataset-------------------------------------------------
   int start = 0;
   if(step == 0)
     {
      GetDataset(InpCount,_lag_,start,_Input_X,_Target_y,symbol_X,symbol_y);
      params_ = FitLogitRegression(_Input_X,_Target_y,_L2_,_C_,_probit_,alpha_);
     }
   count_ = count_+1;
//--------------------------------------------------------------------------------------------------

//--- Get trade signal
   int signal = Trade_PredictedTarget(params_,start,_lag_,InpCount,symbol_X);
   Comment("Trade signal: ",signal,"  ","ModelSignificant: ",ModelSignificant);  
//---------------------------------------------

//--- Open trades based on Signals
   SymbolInfoTick(Symbol(), ticks);
   if(signal==1)
     {
      if(!PosExists(POSITION_TYPE_BUY) && ModelSignificant)
        {
         m_trade.Buy(min_lot,Symbol(), ticks.ask);
         PosClose(POSITION_TYPE_SELL);
        }
      else
        {
         PosClose(POSITION_TYPE_SELL);
        }
     }
   else
     {
      if(!PosExists(POSITION_TYPE_SELL) && ModelSignificant)
        {
         m_trade.Sell(min_lot,Symbol(), ticks.bid);
         PosClose(POSITION_TYPE_BUY);
        }
      else
        {
         PosClose(POSITION_TYPE_BUY);
        }
     }
  }
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//|   Function tracks the occurrence of a new bar event              |
//+------------------------------------------------------------------+
bool isnewBar(ENUM_TIMEFRAMES TF)
  {
   if(prev_bars == 0)
      prev_bars = Bars(Symbol(), TF);

   if(prev_bars != Bars(Symbol(), TF))
     {
      prev_bars = Bars(Symbol(), TF);
      return true;
     }

   return false;
  }

//+------------------------------------------------------------------+
//|Function determines whether there is an open buy or sell position |
//+------------------------------------------------------------------+
bool PosExists(ENUM_POSITION_TYPE type)
  {
   for(int i=PositionsTotal()-1; i>=0; i--)
      if(m_position.SelectByIndex(i))
         if(m_position.Symbol()==Symbol() && m_position.Magic() == MAGIC_NUMBER && m_position.PositionType()==type)
            return true;

   return false;
  }
//+------------------------------------------------------------------+
//|The function closes a long or short trade                         |
//+------------------------------------------------------------------+
void PosClose(ENUM_POSITION_TYPE type)
  {
   for(int i=PositionsTotal()-1; i>=0; i--)
      if(m_position.SelectByIndex(i))
         if(m_position.Symbol()==Symbol() && m_position.Magic() == MAGIC_NUMBER && m_position.PositionType()==type)
            if(!m_trade.PositionClose(m_position.Ticket()))
               printf("Failed to close position %d Err=%s",m_position.Ticket(),m_trade.ResultRetcodeDescription());
  }

What distinguishes this EA from a number of other approaches? First, it allows reoptimization of classifier parameters every (reoptimize_step) bars. Second, it does not simply estimate the parameters of the model, it pays attention to the standard errors of these estimates, which is often overlooked. It is insufficient to find the "optimal" parameters for a sample. It is also necessary to check how significant these parameters or the model as a whole are. After all, if the parameters are not significant, then it would be more logical to ignore such a trading signal.

Therefore, this EA also includes a procedure for testing the model hypothesis for significance. In this case, the null hypothesis will state that all model parameters are equal to zero (H0:w1=0,w2=0,w3=0,..., wk=0), while the alternative H1 hypothesis will state that some parameters are not equal to zero and, therefore, the model is useful in prediction. To test such a hypothesis, the likelihood ratio (LR) criterion is used, which evaluates the difference between the assumed and the trivial model:

LR = 2(LLF – LLF0)

• LLF – the found value of the logarithm of the likelihood function,

• LLF0 - the likelihood logarithm under the null hypothesis, i.e. for the trivial model

p0 = ∑(yn =1)/N  – sample success rate,

LLF0 = N(p0*Ln(p0) + (1- p0)*Ln(1 – p0))

The greater the difference, the better the full model compared to the trivial one. When the null hypothesis is satisfied, the LR statistic has a Chi-square distribution with v degrees of freedom (v is equal to the number of features). If the calculated value of the LR statistic falls into the critical region, i.e. LR > X²crit (alpha; v=lag_), then H0 hypothesis is rejected, and therefore the trading signal is not ignored and a trading position is opened.

One of the possible scenarios. GBPUSD, Daily

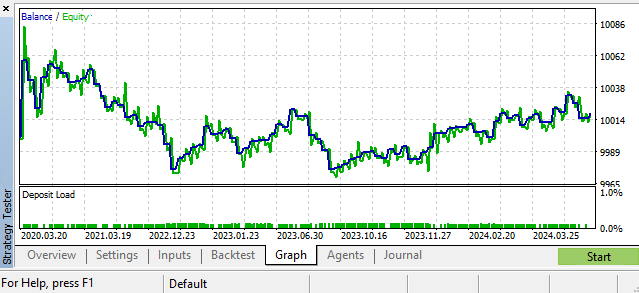
Hyperparameters

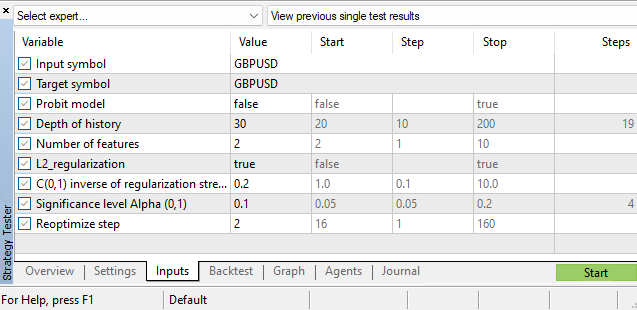
In addition to evaluating the parameters of the classifier models themselves, we also have a large baggage of hyperparameters:

• history depth
• the number of features,
• alpha significance level
• reoptimization step

The hyperparameters are selected in the MetaTrader 5 strategy tester. One of the tasks that can improve the EA performance is to build a function of the dependence of the history depth parameter on the current state of the market, that is, to make it dynamic in the same way as we did with the parameters of the logit and probit models. But that is another story. For a hint, see my article "Two-sample Kolmogorov-Smirnov test as an indicator of time series non-stationarity" considering the issue of constructing a disorder indicator.

Conclusion

In this article, we looked at regression models with binary performance indicators, learned how to evaluate the parameters of these models, and also implemented the LogitExpert trading EA for testing and setting up these models. Its unique feature is that it allows us to retrain the classifier parameters on the fly, based on the most recent and relevant data.

Particular attention was paid to the estimation of standard errors of parameters, which required estimating covariance matrices for logit and probit models.

The likelihood ratio criterion is used to test the significance of the classifier model equation as a whole. This statistics is used to sort out statistically unreliable trading signals.