Reimaginando las estrategias clásicas (Parte VIII): Los mercados de divisas y metales preciosos en el USDCAD

A lo largo de esta serie de artículos, pretendemos explorar el vasto panorama de las posibles aplicaciones de la IA en las estrategias de negociación. Nuestro objetivo es brindarle la información que necesita para llegar a una decisión informada antes de invertir su capital con una estrategia basada en IA. Con suerte, podrá identificar una estrategia que sea adecuada para sus niveles particulares de tolerancia al riesgo.

Descripción general de la estrategia de negociación

En el artículo de hoy, trataremos de descubrir las relaciones entre los mercados de divisas y de metales preciosos. Los metales preciosos constituyen una parte integral de cualquier economía moderna. Esto se debe a sus amplios usos industriales, que van desde la electrónica hasta la atención sanitaria. Las fluctuaciones en el precio de los metales preciosos generan inflación para los productores de bienes terminados, lo que puede hacer caer los niveles de producción nacional o, por el contrario, puede conducir a una caída de los niveles de demanda de los países que exportan estos metales.

El oro es uno de los principales minerales de exportación de Canadá y Estados Unidos. La resistencia natural del oro a la corrosión hace que sea un material muy demandado tanto por los desarrolladores de equipos electrónicos sensibles como por los joyeros. El paladio, por otro lado, es demandado por muchas industrias, especialmente la industria automotriz. Hay más de 20 componentes diferentes en un automóvil que requieren convertidores catalíticos, los más conocidos son los que están integrados en los tubos de escape. Cada uno de estos convertidores contiene, en parte, cantidades significativas de paladio. Canadá y Estados Unidos son líderes en la exportación de vehículos. Por lo tanto, los precios de estos metales preciosos tendrán algún efecto en la producción interna de estos dos países.

En el pasado, la correlación entre el precio del oro y el dólar era inversa. Siempre que el dólar tenía un mal desempeño, los inversores tendían a cerrar todas las posiciones que tenían apostando al dólar y en su lugar cubrían su dinero en oro. Sin embargo, en los tiempos de flexibilización cuantitativa que vivimos, las correlaciones ya no son tan claras.

Descripción general de la metodología

Nos gustaría que nuestro ordenador aprendiera su propia estrategia a partir de los precios de estos tres mercados. Naturalmente, podemos tener cierta tendencia a creer en estrategias que nos resultan atractivas o tienen sentido intuitivo, en lugar de en estrategias que no lo tienen. Sin embargo, al aprender algorítmicamente una estrategia, nuestra computadora podría aprender relaciones que a nosotros nos habría llevado toda la vida descubrir. Alternativamente, también podría exponer limitaciones en la precisión de nuestra estrategia.

Evaluar la confiabilidad de los mercados de valores a la hora de pronosticar los mercados de divisas. Intentamos pronosticar el tipo de cambio USDCAD utilizando tres grupos de predictores:

1. Cotizaciones del par USDCAD
2. Cotizaciones de XAUUSD y XPDUSD
3. Un conjunto de lo anterior.

Obtuvimos todos nuestros datos directamente desde el terminal MetaTrader 5 usando un script personalizado que escribimos en MQL5. Escribimos los datos en formato CSV y los procesamos en Python. Además, observamos niveles negativos significativos de correlación, -0,5 entre XAUUSD y USDCAD y por último -0,66 entre XPDUSD y USDCAD. Sin embargo, sólo observamos niveles moderados de correlación directamente entre los dos metales, 0,37.

Intentamos visualizar los datos. Sin embargo, no pudimos observar ninguna relación perceptible en los datos. Intentamos representar gráficamente los datos en dimensiones superiores, utilizando un diagrama de dispersión 3D, pero sin éxito. Parece difícil separar los datos.

A partir de ahí, entrenamos varios modelos para pronosticar el tipo de cambio del USDCAD utilizando los tres grupos de predictores que describimos anteriormente; el modelo con mejor rendimiento fue el modelo lineal que utilizó el primer grupo de predictores. Sin embargo, dado que el modelo lineal no tiene parámetros que podamos ajustar, seleccionamos el segundo mejor modelo, el Regresor de vectores de soporte lineal (Linear Support Vector Regressor, LSVR), como nuestro modelo con mejor rendimiento.

Ajustamos con éxito los hiperparámetros del modelo LSVR sin sobreajustarlos al conjunto de entrenamiento, como es evidente por el hecho de que superamos al modelo LSVR predeterminado en datos no vistos. Desafortunadamente, no pudimos superar al modelo lineal en los mismos datos de validación. Utilizamos el RMSE promedio calculado mediante una validación cruzada de series de tiempo de 5 veces sin mezcla aleatoria para realizar la selección de modelos tanto en el entrenamiento como en la validación.

Luego, exportamos nuestro modelo LSVR personalizado al formato ONNX y construimos nuestro propio Asesor Experto con IA integrada utilizando MQL5.

Recopilación de datos

He incluido un script útil que puede utilizar para obtener datos de su terminal MetaTrader 5. Simplemente adjunte el script a cualquier gráfico que desee analizar y comience.

El script simplemente buscará tantas barras como especifique en la entrada y las escribirá en formato CSV. Escribir la hora es vital porque la usaremos más adelante cuando deseemos unir nuestros archivos CSV en un marco de datos fusionado en Python. Fusionaremos nuestros datos sólo en los días que todos tengan en común.

Fíjate que incluimos la propiedad: «#property script_show_inputs» si no incluyes esta propiedad en tus scripts, no podrás ajustar las entradas del script.

//+------------------------------------------------------------------+
//|                                                     ProjectName  |
//|                                     Copyright 2020, CompanyName  |
//|                                     http://www.companyname.net   |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link          "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//---Amount of data requested
input int size = 100000; //How much data should we fetch?

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void OnStart()
  {
//---File name
   string file_name = "Market Data " + Symbol() + ".csv";

//---Write to file
   int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");

   for(int i= size;i>=0;i--)
        {
        if(i == size)
        {
        FileWrite(file_handle,"Time","Open","High","Low","Close");
        }

        else
        {
        FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i),
                iOpen(Symbol(),PERIOD_CURRENT,i),
                iHigh(Symbol(),PERIOD_CURRENT,i),
                iLow(Symbol(),PERIOD_CURRENT,i),
                iClose(Symbol(),PERIOD_CURRENT,i));
        }
        }

  }
//+------------------------------------------------------------------+

Ahora que nuestros datos están listos, podemos empezar a limpiar los datos en Python.

Limpieza de datos

Primero, importaremos las bibliotecas estándar que necesitamos.

#Import the libraries we need
import pandas as pd
import numpy as np

Esta es la versión de la biblioteca que estamos usando en esta demostración.

#Display library versions
print(f"Pandas version {pd.__version__}")
print(f"Numpy version {np.__version__}")

Versión de Pandas 2.2.1
Versión de Numpy 1.26.4

Ahora, lea los datos CSV que obtuvimos.

#Read in the data we need
usdcad = pd.read_csv("\\home\\volatily\\.wine\\drive_c\\Program Files\\MetaTrader 5\\MQL5\\Files\\Market Data USDCAD.csv")
usdcad = usdcad[::-1]
xauusd = pd.read_csv("\\home\\volatily\\.wine\\drive_c\\Program Files\\MetaTrader 5\\MQL5\\Files\\Market Data XAUUSD.csv")
xauusd = xauusd[::-1]
xpdusd = pd.read_csv("\\home\\volatily\\.wine\\drive_c\\Program Files\\MetaTrader 5\\MQL5\\Files\\Market Data XPDUSD.csv")
xpdusd = xpdusd[::-1]

Utilice la columna de tiempo como índice.

#Set the time column as the index
usdcad.set_index("Time",inplace=True)
xauusd.set_index("Time",inplace=True)
xpdusd.set_index("Time",inplace=True)

Fusionar los datos.

#Let's merge the data
merged_data = usdcad.merge(xauusd,suffixes=('',' XAU'),left_index=True,right_index=True)
merged_data = merged_data.merge(xpdusd,suffixes=('',' XPD'),left_index=True,right_index=True)

Así es como se ven nuestros datos.

merged_data

Figura 1: Nuestro marco de datos fusionado.

Definamos hasta qué punto en el futuro deseamos pronosticar.

#Define the forecast horizon
look_ahead = 20

Defina los 3 grupos de predictores que deseamos probar.

#Define the predictors and target
ohlc_predictors = ['Open','High','Low','Close']
new_predictors = ['Open XAU','High XAU','Low XAU','Close XAU','Open XPD','High XPD','Low XPD','Close XPD']
predictors = ohlc_predictors + new_predictors

Etiquetado de los datos.

#Let's add labels to the data
merged_data["Target"] = merged_data["Close"].shift(-look_ahead)

También crearemos etiquetas que serán útiles cuando visualicemos los datos. Estas etiquetas resumirán los cambios en cada mercado.

#Let's also add labels to help us visualize the relationships
merged_data["Binary Target"] = np.nan
merged_data["XAU Target"] = np.nan
merged_data["XPD Target"] = np.nan

#Define the target values
#Changes in the USDCAD Exchange rate
merged_data.loc[merged_data["Close"] > merged_data["Target"],"Binary Target"] = 0
merged_data.loc[merged_data["Close"] < merged_data["Target"],"Binary Target"] = 1
#Changes in the price of Gold
merged_data.loc[merged_data["Close XAU"] > merged_data["Close XAU"].shift(-look_ahead),"XAU Target"] = 0
merged_data.loc[merged_data["Close XAU"] < merged_data["Close XAU"].shift(-look_ahead),"XAU Target"] = 1
#Changes in the price of Palladium
merged_data.loc[merged_data["Close XPD"] > merged_data["Close XPD"].shift(-look_ahead),"XPD Target"] = 0
merged_data.loc[merged_data["Close XPD"] < merged_data["Close XPD"].shift(-look_ahead),"XPD Target"] = 1

#Drop any NA values
merged_data.dropna(inplace=True)

Análisis exploratorio de datos

Para visualizar nuestros datos, primero importaremos las librerías necesarias.

#Explorartory data analysis
import seaborn as sns
import matplotlib.pyplot as plt

Visualización de las versiones de la biblioteca.

#Display library version
print(f"Seaborn version: {sns.__version__}")

Versión de Seaborn: 0.13.2

Primero, restablezcamos el índice de nuestro marco de datos fusionado.

#Reset the index
merged_data.reset_index(inplace=True)

Ahora, vamos a crear un mapa de calor de correlación. Como podemos ver, existen niveles significativamente fuertes de correlación entre los dos metales preciosos y el par USDCAD. Esto está en línea con nuestro análisis fundamental de los papeles que juegan estos metales en el Producto Interior Bruto (Gross Domestic Product, GDP) de ambos países. Lamentablemente, esto no resultó en un mejor desempeño al intentar pronosticar el tipo de cambio USDCAD.

#Correlation heatmap
fig , ax = plt.subplots(figsize=(7,7))
sns.heatmap(merged_data.loc[:,predictors].corr(),annot=True,ax=ax)

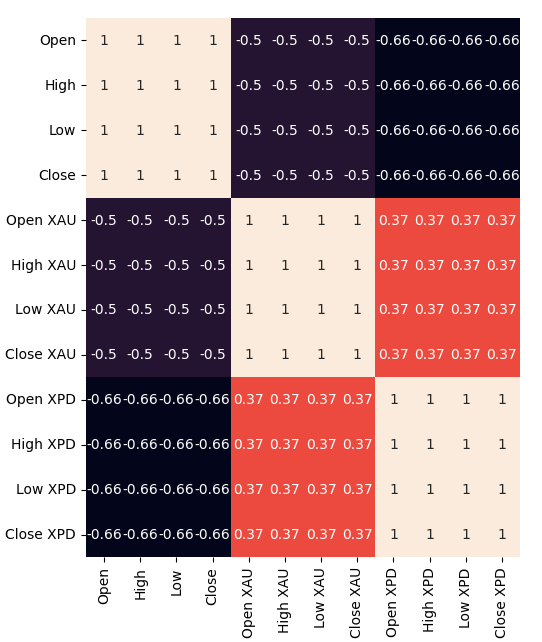
Figura 2: Nuestro mapa de calor de correlación.

Creamos dos gráficos categóricos que resumen todos los casos en los que el precio del oro o del paladio subió (columna 1) o bajó (columna 2). A partir de allí, coloreamos cada uno de los puntos para indicar si el tipo de cambio USDCAD subió, indicado por los puntos naranjas, o bajó, indicado por los puntos azules. Como se puede ver, tenemos una mezcla de ambos resultados en ambas columnas. Posiblemente sugiera que los cambios en el tipo de cambio USDCAD son independientes de los cambios en los metales preciosos que hemos elegido.

#Let's create categorical plots
sns.catplot(data=merged_data,x="XAU Target",y="Close",hue="Binary Target")

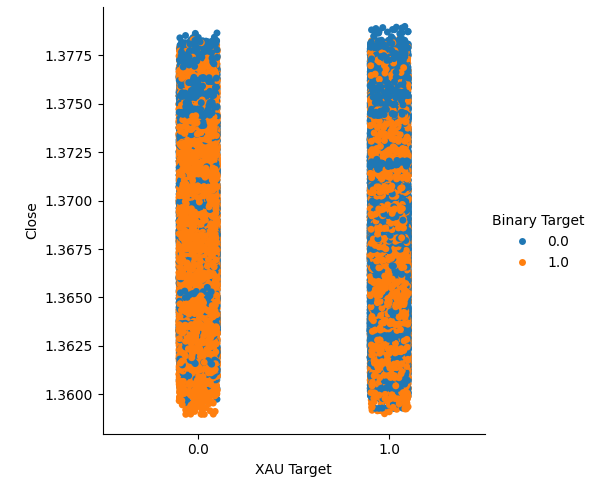
Figura 3: Gráfico categórico del precio del oro y el precio de cierre del USDCAD.

#Let's create categorical plots
sns.catplot(data=merged_data,x="XPD Target",y="Close",hue="Binary Target")

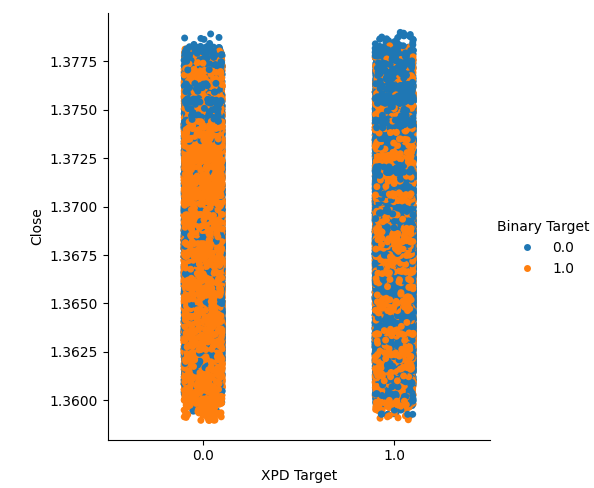
Figura 4: Gráfico categórico del precio del paladio frente al precio del USDCAD.

Posteriormente, creamos gráficos de dispersión, para visualizar la varianza entre el precio de cierre del mercado de Paladio y USDCAD. Lamentablemente, esto no produjo ninguna relación discernible que pudiéramos aprovechar. Coloreamos cada punto utilizando el mismo mapa de colores naranja y azul delineado arriba.

#Let's visualize scatter plots
sns.scatterplot(data=merged_data,x="Close XPD",y="Close",hue="Binary Target")

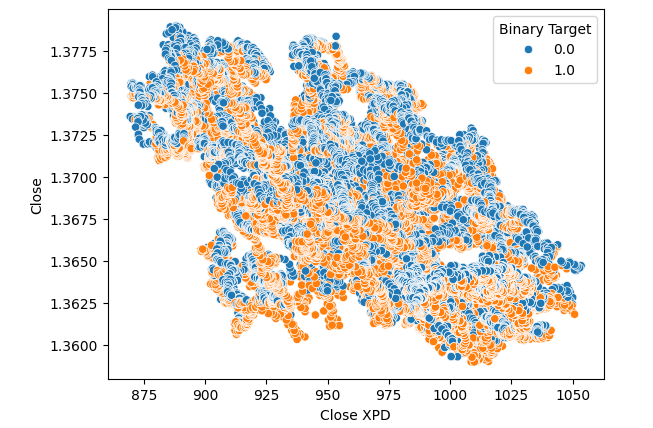
Figura 5: Diagrama de dispersión de XPDUSD frente a USDCAD.

No se produjeron mejoras cuando sustituimos el precio del oro en lugar del paladio en el diagrama de dispersión.

#Let's visualize scatter plots
sns.scatterplot(data=merged_data,x="Close XAU",y="Close",hue="Binary Target")

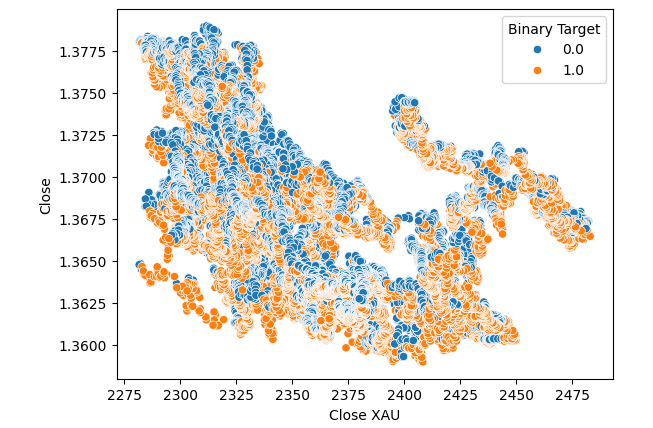
Figura 6: Un diagrama de dispersión del cierre del XAUUSD frente al USDCAD.

Pensamos en intentar comprobar si existe una relación entre los dos metales. Sin embargo, la relación aún no nos resultaba evidente. Creamos un gráfico de dispersión del precio del oro frente al precio del paladio y usamos el cambio en el par USDCAD para colorear cada punto, pero esto no produjo ninguna mejora.

#Let's visualize scatter plots
sns.scatterplot(data=merged_data,x="Close XPD",y="Close XAU",hue="Binary Target")

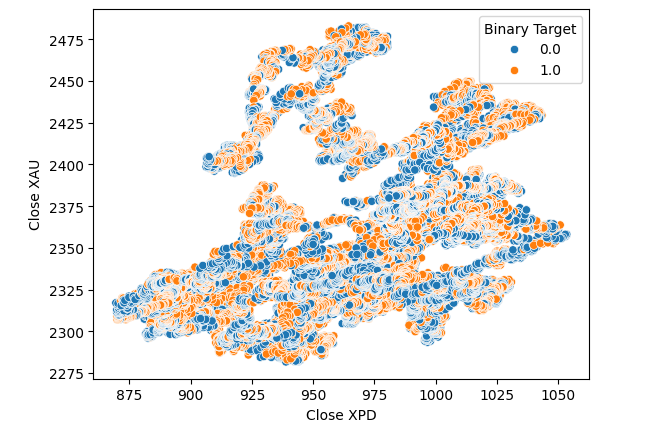
Figura 7: Un diagrama de dispersión de XAUUSD frente a XPDUSD.

A veces, las relaciones pueden estar ocultas porque no estamos viendo suficientes variables al mismo tiempo para ver el efecto. Creamos un gráfico de dispersión 3D, utilizando el precio de cierre del paladio, el oro y el USDCAD. Lamentablemente, el gráfico resultante destacó lo que parecían ser grupos en los datos que tienen bajos niveles de separación, lo que en esencia reafirma lo que ya sabemos hasta ahora.

#Visualizing 3D data
fig = plt.figure(figsize=(7,7))
ax = fig.add_subplot(111,projection='3d')
colors = ['blue' if movement == 0 else 'orange' for movement in merged_data.loc[0:1100,"Binary Target"]]
ax.scatter(merged_data.loc[0:1100,"Close"],merged_data.loc[0:1100,"Close XAU"],merged_data.loc[0:1100,"Close XPD"],c=colors)

#Set labels
ax.set_xlabel('USDCAD')
ax.set_ylabel('XAUUSD')
ax.set_zlabel('XPDUSD')

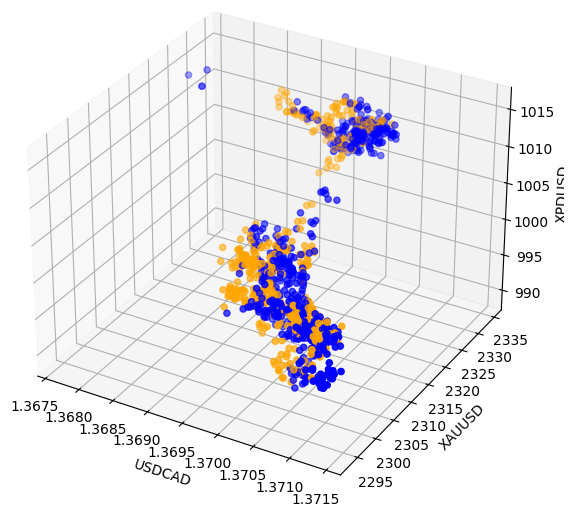
Figuraa 8: Visualización de nuestros datos de mercado en 3D.

Modelado de datos

Preparémonos para comenzar a modelar nuestros datos. Primero, importaremos las bibliotecas estándar.

#Modelling the data
import sklearn
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import RobustScaler

Mostrando la versión de la biblioteca.

#Print library version
print(f"Sklearn version {sklearn.__version__}")

Versión Sklearn 1.4.1.post1

Antes de comenzar a entrenar cualquier modelo, primero debemos escalar y estandarizar los datos.

#Scale the data
scaled_data = pd.DataFrame(RobustScaler().fit_transform(merged_data.loc[:,predictors]),columns=predictors)

Ahora dividiremos los datos en dos mitades, una para entrenamiento y optimización y la segunda para validación y prueba de sobreajuste.

#Split the data
train_X,test_X,train_y,test_y = train_test_split(scaled_data,merged_data.loc[:,"Target"],shuffle=False,test_size=0.5)

Ahora importe los modelos.

#Preparing to model the data
from sklearn.model_selection import TimeSeriesSplit
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor , GradientBoostingRegressor , BaggingRegressor
from sklearn.svm import LinearSVR
from sklearn.neighbors import KNeighborsRegressor
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import root_mean_squared_error

Crear el objeto de división de series de tiempo.

#Create the time series split object
tscv = TimeSeriesSplit(gap=look_ahead,n_splits=5)

Almacene los modelos en una lista para que podamos iterarlos.

#Create a list of models
models = [
        LinearRegression(),
        RandomForestRegressor(),
        GradientBoostingRegressor(),
        BaggingRegressor(),
        LinearSVR(),
        KNeighborsRegressor(),
        MLPRegressor(hidden_layer_sizes=(100,10))
]

Cree un marco de datos para almacenar nuestros niveles de precisión.

#List of models
columns = [
        "Linear Regression",
        "Random Forest",
        "Gradient Boost",
        "Bagging",
        "Linear SVR",
        "K-Neighbors",
        "Neural Network"
]

#Create a dataframe to store our error metrics
ohlc_error = pd.DataFrame(columns=columns,index=np.arange(0,5))
new_error = pd.DataFrame(columns=columns,index=np.arange(0,5))
all_error = pd.DataFrame(columns=columns,index=np.arange(0,5))

Definir los predictores a utilizar.

#Setting the current predictors
current_predictors = predictors

Valide de forma cruzada cada modelo utilizando los predictores definidos anteriormente.

#Perform cross validation
for j in np.arange(0,len(models)):
        model = models[j]
        for i,(train,test) in enumerate(tscv.split(train_X)):
        model.fit(train_X.loc[train[0]:train[-1],current_predictors],train_y.loc[train[0]:train[-1]])
        all_error.iloc[i,j] = root_mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],current_predictors]))

Observemos nuestros niveles de error utilizando datos OHLC ordinarios. De nuestras visualizaciones y las estadísticas de resumen, queda claro que el modelo de regresión lineal tuvo el mejor desempeño en esta tarea.

ohlc_error

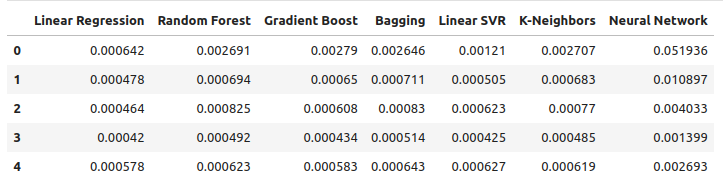
Figura 9: Nuestros niveles de error al pronosticar utilizando datos OHLC USDCAD.

Graficar los datos.

ohlc_error.plot()

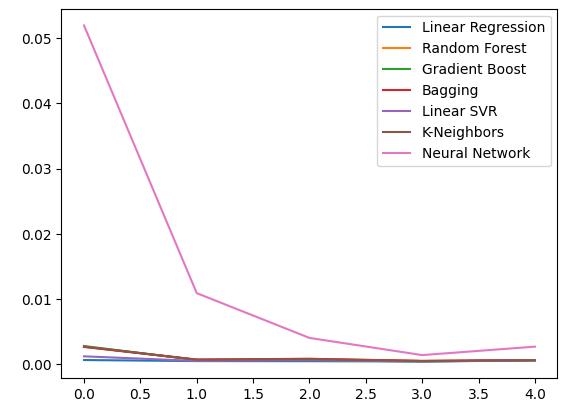
Figura 10: La precisión de nuestro modelo utilizando el primer conjunto de predictores.

Creación de gráficos de cajas.

fig = plt.figure(figsize=(5,5))
plt.boxplot(ohlc_error)

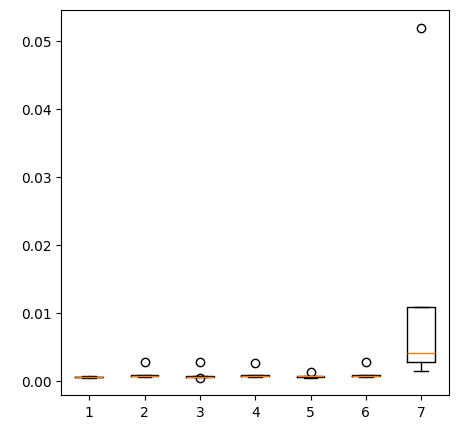
Figura 11: La precisión de nuestro modelo al pronosticar con el primer grupo de predictores.

Observemos nuestros niveles de error al utilizar metales preciosos para pronosticar el tipo de cambio USDCAD. La regresión lineal sigue siendo el modelo con mejor rendimiento, aunque ya no por un amplio margen.

new_error

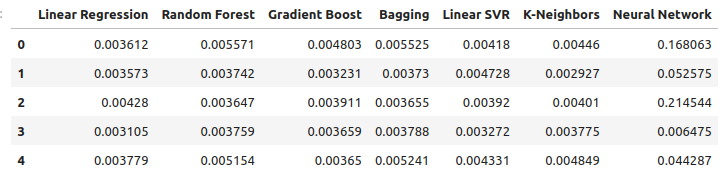
Figura 12: Nuestros nuevos niveles de error.

Gráfico de los nuevos niveles de error.

new_error.plot()

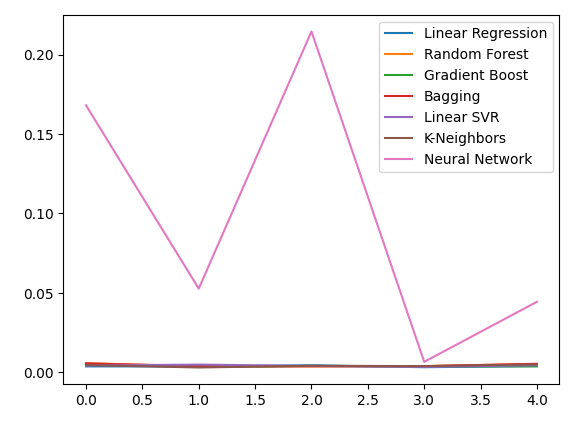
Figura 13: Nuestros nuevos niveles de error.

Creación de un diagrama de los nuevos resultados.

fig = plt.figure(figsize=(5,5))
plt.boxplot(new_error)

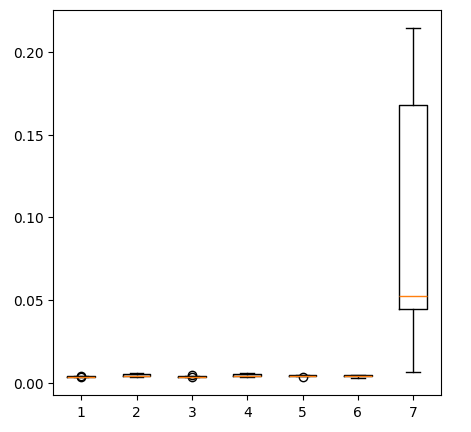
Figura 14: Nuestros niveles de error al utilizar datos del mercado de metales preciosos.

Ahora consideremos nuestro desempeño al utilizar todos los datos disponibles. Todavía observamos que el modelo lineal tiene un rendimiento muy superior al de cualquier otro modelo que tenemos. Intentemos optimizar el segundo mejor modelo, el LinearSVR, para superar a la regresión lineal.

all_error

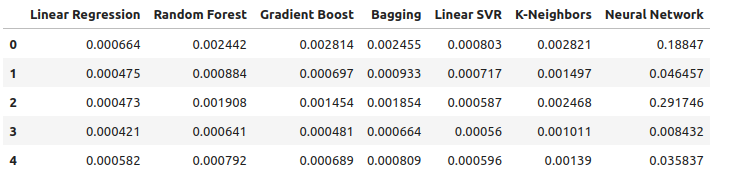
Figura 15: Nuestra precisión al utilizar todos los datos que tenemos.

Gráfico de los niveles de error.

all_error.plot()

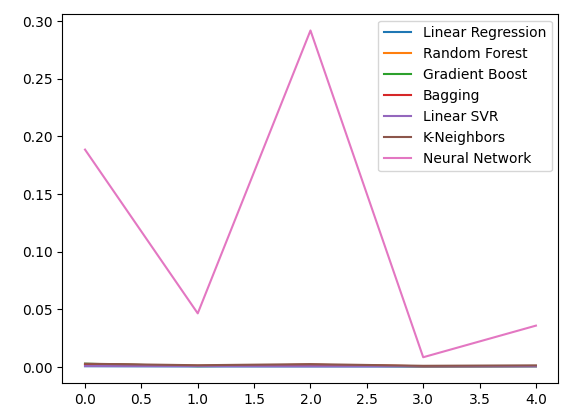
Figura 16: Gráficos de líneas de nuestra precisión al utilizar todos los datos que tenemos.

La creación de un diagrama de los niveles de error que obtuvimos al utilizar todos los datos que tenemos, muestra que la regresión lineal simple sigue siendo nuestra mejor opción.

fig = plt.figure(figsize=(5,5))
plt.boxplot(all_error)

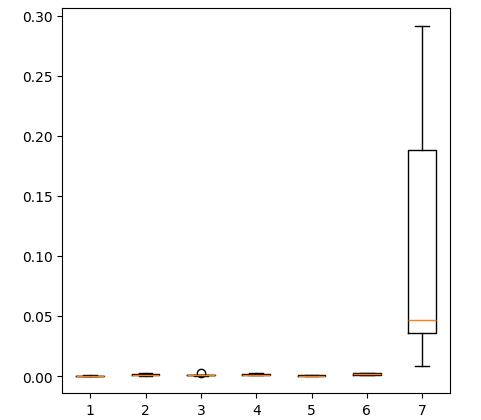
Figura 17: Diagramas de caja de nuestra precisión al utilizar todos los datos de que disponemos.

Los niveles de error medios de nuestros modelos en los cinco conjuntos de validación muestran claramente que el modelo lineal es nuestra mejor opción hasta ahora. Sin embargo, el LinearSVR no se queda atrás.

all_error.mean()

Linear Regression 0.000523
Random Forest      0.001333
Gradient Boost       0.001227
Bagging                  0.001343
Linear SVR             0.000653
K-Neighbors            0.001837
Neural Network       0.114188
dtype: object

Importancia de las características

Antes de comenzar a optimizar nuestro modelo, evaluemos primero qué características parecen importantes; esperamos que nuestros datos relacionados con el mercado de metales preciosos muestren su valor en esta prueba. Primero probaremos los niveles de información mutua (Mutual Information, MI). MI es una medida de cuánta certeza se obtiene acerca del valor del objetivo al conocer el valor de uno de los predictores. El MI se mide en una escala logarítmica, por lo que en la práctica es raro encontrar un puntaje de MI superior a 2.

Comenzamos importando las librerías que necesitamos.

#Mutual information score
from sklearn.feature_selection import mutual_info_regression

Ahora calculamos las puntuaciones MI para cada uno de nuestros predictores.

#Prepare the data for plotting
mi = mutual_info_regression(train_X,train_y)
mi = mi.reshape(1,12)
mi_scores = pd.DataFrame(mi,columns=predictors)

La representación gráfica de nuestras puntuaciones MI nos sugiere que los datos del mercado USDCAD pueden ser más informativos que todos los datos del mercado de metales preciosos. Esto queda validado por nuestra prueba de validación cruzada, en la que observamos que el modelo lineal que utiliza solo las cotizaciones del mercado USDCAD produjo el error más bajo.

#Prepare the data for plotting
mi = mutual_info_regression(train_X,train_y)
mi = mi.reshape(1,12)
mi_scores = pd.DataFrame(mi,columns=predictors)
#Plot the scores
mi_scores.plot.bar()

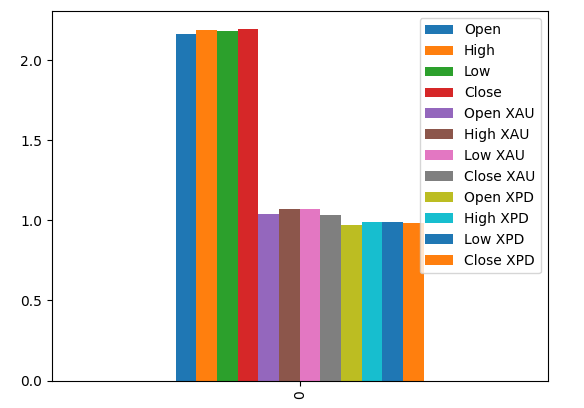
Figura 18: Puntuaciones de información mutua en nuestros 3 conjuntos de datos.

A continuación calcularemos los valores SHAP. Los valores SHAP son explicadores de caja negra que nos ayudan a identificar la importancia de las características globales en nuestros modelos de aprendizaje automático.

Importar la biblioteca SHAP.

#The Linear SVR appears to be performing second best
import shap

Inicializar el modelo LSVR.

#Initialize the model
model = LinearSVR()
model.fit(train_X,train_y)

Calcular valores SHAP.

#Compute SHAP values
explainer = shap.Explainer(model,train_X)
explanations = explainer(train_X)

Mostrar la importancia de las características globales.

#Plot SHAP values
shap.plots.violin(explanations)

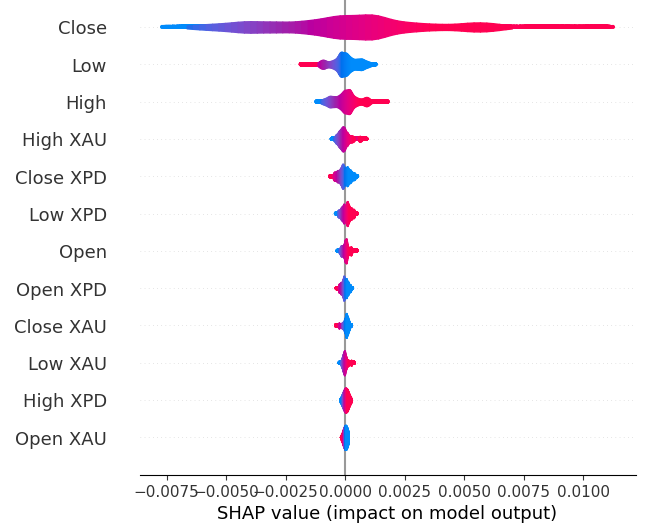
Figura 19: Nuestros niveles de importancia SHAP.

Nuestras explicaciones SHAP no concuerdan con nuestra evaluación de información mutua. Hemos abordado ampliamente el problema del desacuerdo en artículos anteriores, pero lo mejor que se puede decir es que la importancia de las características puede ser difícil de evaluar y debe tomarse con cautela. Sin embargo, ambas explicaciones sugieren que existe cierta información útil contenida en los mercados de metales preciosos.

Ajuste de hiperparámetros

Ajustar nuestro modelo puede permitirnos obtener mejores resultados con datos no vistos de lo que podríamos lograr si usáramos el modelo predeterminado.

Para ajustar nuestro modelo, primero importemos las bibliotecas que necesitamos.

#Parameter tuning
from sklearn.model_selection import RandomizedSearchCV

Ahora inicialice el modelo.

#Reinitialize the model
model = LinearSVR()

Luego definimos nuestros parámetros de ajuste. Pasamos el modelo y un diccionario de posibles valores de parámetros, seguido del número total de iteraciones que deseamos realizar. Nos gustaría realizar una validación cruzada de 5 veces para medir el error cuadrático medio negativo, esto significa que seleccionaremos el modelo con el error de validación más bajo. Por último, establecer n_jobs en menos 1 permite realizar la búsqueda en paralelo en todos los núcleos de CPU disponibles.

#Define the tuner
tuner = RandomizedSearchCV(
        model,
        {
        "epsilon" : [0,10,100,1000],
        "tol":[0.01,0.001,0.0001,0.00001,0.0000001],
        "C":[1,10,100,1000,10000],
        "loss":['epsilon_insensitive', 'squared_epsilon_insensitive']  
        },
        n_iter=1000,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

Coloca el ajustador.

#Let's fit the tuner
tuner_results = tuner.fit(train_X,train_y)

Los mejores parámetros que hemos encontrado.

#Let's see the best parameters we found
tuner_results.best_params_

{'tol': 1e-05, 'loss': 'squared_epsilon_insensitive', 'epsilon': 0, 'C': 10000}

Pruebas de sobreajuste

Para comprobar si hay sobreajuste, primero tenemos que inicializar nuestros modelos.

#Testing for overfitting
benchmark =  LinearRegression()
default_lsvr = LinearSVR()
customized_lsvr = LinearSVR(tol=1e-05,loss='squared_epsilon_insensitive',epsilon=0,C=10000)

Ahora restablece los índices para que podamos realizar la validación cruzada.

#Reset the indexes
test_y = test_y.reset_index()
test_X = test_X.reset_index()

Formatea los datos.

#Format the data
test_y = test_y.loc[:,"Target"]
test_X = test_X.loc[:,predictors]

Crear marcos de datos para almacenar nuestros niveles de error.

#Create dataframes to store our error levels
test_error = pd.DataFrame(columns=["Linear Regression","LSVR","Customized LSVR"],index=[0,1,2,3,4])

Entrene los modelos en el conjunto de entrenamiento.

#Fit the models on the training set
benchmark.fit(train_X,train_y)
default_lsvr.fit(train_X,train_y)
customized_lsvr.fit(train_X,train_y)

Almacene los modelos en una lista.

models = [benchmark,default_lsvr,customized_lsvr]

Validación cruzada de cada modelo en el conjunto de pruebas.

for j in np.arange(0,len(models)):
        model = models[j]
        for i,(train,test) in enumerate(tscv.split(test_X)):
        model.fit(test_X.loc[train[0]:train[-1],:],test_y.loc[train[0]:train[-1]])
        test_error.iloc[i,j] = root_mean_squared_error(test_y.loc[test[0]:test[-1]],model.predict(test_X.loc[test[0]:test[-1],:]))

Nuestro error de prueba.

test_error

Linear Regression	LSVR	Customized LSVR
0.000598	0.000542	0.000743
0.000472	0.000573	0.000722
0.000318	0.000451	0.000333
0.000341	0.000366	0.000499
0.00043	0.000839	0.00043

De acuerdo con nuestro desempeño promedio en los cinco aspectos, nuestro modelo lineal sigue siendo el modelo con mejor desempeño. Sin embargo, logramos superar el modelo predeterminado.

#Let's calculate our mean performances
test_error.mean()

Linear Regression      0.000432
LSVR                          0.000554
Customized LSVR      0.000545
dtype: object

Visualizando nuestro error de prueba.

#Let's visualize our error
test_error.plot()

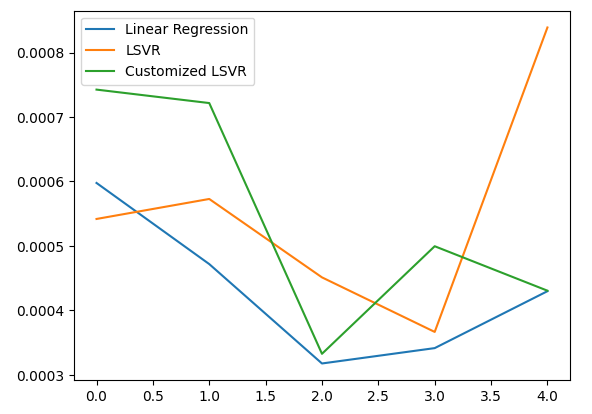
Figura 20: Visualizando nuestro error de prueba.

Creación de un diagrama de caja de nuestras tasas de error de prueba.

#Create a boxplot of the error
sns.boxplot(data=test_error)

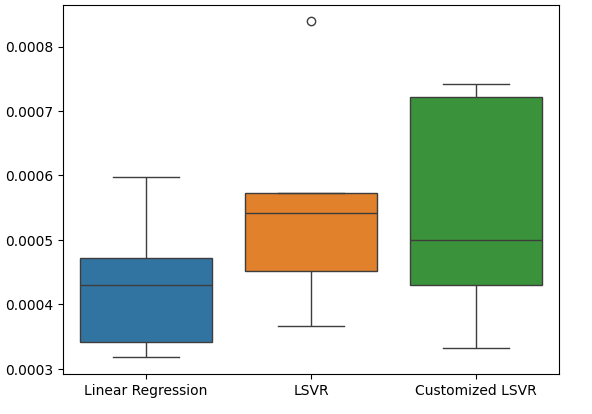
Figura 21: Visualizando nuestro error de prueba.

Preparación del modelo para exportar a ONNX

Antes de poder exportar nuestro modelo al formato ONNX, primero necesitamos escalar y estandarizar los datos restando la media y dividiéndolos por la desviación estándar. Desde allí escribiremos nuestros factores de escala en CSV para que podamos reproducir el procedimiento en MQL5.

Primero, crea el marco de datos para almacenar nuestros factores de escala.

#Let's scale our data
scaling_factors = pd.DataFrame(columns=predictors,index=['mean','standard deviation'])
X = merged_data.loc[:,predictors]
y = merged_data.loc[:,"Target"]

Luego almacene la media y la desviación estándar y, finalmente, realice el procedimiento de escala.

#Let's fill each column
for i in np.arange(0,len(predictors)):
        scaling_factors.iloc[0,i] = X.iloc[:,i].mean()
        scaling_factors.iloc[1,i] = X.iloc[:,i].std()
        X.iloc[:,i] = ( ( X.iloc[:,i] - scaling_factors.iloc[0,i] ) / scaling_factors.iloc[1,i])

Guarde los factores de escala.

#Save the scaling factors as a CSV
scaling_factors.to_csv("/home/volatily/.wine/drive_c/Program Files/MetaTrader 5/MQL5/Files/usd_cad_xau_xpd_scaling_factors.csv")

Exportar el modelo a ONNX

ONNX significa Open Neural Network Exchange (ONNX) y es un marco de aprendizaje automático interoperable de código abierto que permite a los desarrolladores crear, compartir e implementar modelos de aprendizaje automático en un marco independiente del lenguaje. Esto se logra representando cada modelo de aprendizaje automático como un árbol de nodos y gráficos que pueden volver a ensamblarse al modelo original mediante cualquier lenguaje que admita la API ONNX.

Primero, importaremos las bibliotecas que necesitamos.

#Let's prepare to export our model to ONNX format
import onnx
import netron
import skl2onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType

Visualización de las versiones de la biblioteca.

#Display library versions
print(f"Onnx version: {onnx.__version__}")
print(f"Netron version: {netron.__version__}")
print(f"Skl2onnx version: {skl2onnx.__version__}")

Versión de ONNX: 1.15.0
Versión de Netron: 7.8.0
Versión de Skl2onnx: 1.16.0

Ahora definiremos los tipos de entrada de nuestro modelo.

#Define the input type
initial_types = [('float_input',FloatTensorType([1,12]))]

Entrenemos el modelo con todos los datos que tenemos.

#Train the model on all the data we have
customized_lsvr = LinearSVR(tol=1e-05,loss='squared_epsilon_insensitive',epsilon=0,C=10000)
customized_lsvr.fit(X,y)

Convierte el modelo al formato ONNX.

#Covert the sklearn model
onnx_model = convert_sklearn(customized_lsvr,initial_types=initial_types)

Guarde el modelo ONNX.

#Save the onnx model
onnx_name = "USDCAD XAUUSD XPDUSD M1 Float.onnx"
onnx.save(onnx_model,onnx_name)

Ver el modelo ONNX.

#View the onnx model
netron.start(onnx_name)

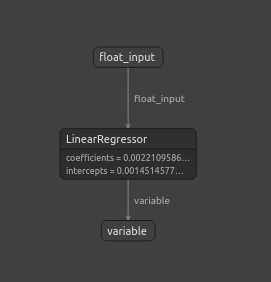
Figura 22: Visualización de nuestro modelo ONNX en Netron.

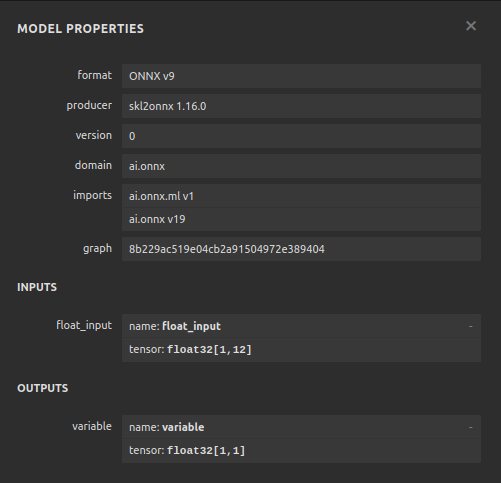
Figura 23: Nuestros parámetros del modelo ONNX se alinean con nuestras expectativas para la entrada y la salida del modelo.

Implementación en MQL5

Para implementar un Asesor Experto integrado con IA en MQL5, primero tenemos que cargar el modelo ONNX que exportamos anteriormente.

//+------------------------------------------------------------------+
//|                                                    USDCAD AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Resources                                                        |
//+------------------------------------------------------------------+
#resource  "\\Files\\USDCAD XAUUSD XPDUSD M1 Float.onnx" as const uchar onnx_buffer[];

A continuación, debemos cargar la biblioteca de operaciones para poder abrir y cerrar posiciones.

//+------------------------------------------------------------------+
//| Libraries we need                                                |
//+------------------------------------------------------------------+
#include <Trade/Trade.mqh>
CTrade Trade;

Definamos también algunas variables globales que necesitaremos a lo largo de nuestro programa.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
long onnx_model;
double mean_values[12],std_values[12];
vectorf model_output = vectorf::Zeros(1);
int model_forecast,state;
double ask,bid;

Definamos las funciones auxiliares que usaremos en nuestro programa, necesitamos una función responsable de cargar nuestro modelo ONNX y configurar sus formas de entrada y salida. Lo haremos usando una función que devuelve verdadero si fue exitoso y falso en caso contrario. Nuestra función primero crea el modelo a partir del buffer que creamos anteriormente, luego intenta establecer y validar las formas de entrada y salida.

//+------------------------------------------------------------------+
//| This function is responsible for loading our ONNX model          |
//+------------------------------------------------------------------+
bool load_onnx(void)
  {
//--- First we must create the model from the buffer
   onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT);

//--- Now we shall define our I/O shape
   ulong input_shape [] = {1,12};
   ulong output_shape []  = {1,1};

   if(!OnnxSetInputShape(onnx_model,0,input_shape))
        {
        Comment("Failed to set ONNX input shape!");
        return(false);
        }

   if(!OnnxSetOutputShape(onnx_model,0,output_shape))
        {
        Comment("Failed to set ONNX output shape!");
        return(false);
        }

//--- Everything went fine
   return(true);
  }
//+------------------------------------------------------------------+

Esta función es responsable de leer el archivo CSV que tiene nuestros valores de escala y almacenarlos en las matrices de alcance global que definimos.

//+------------------------------------------------------------------+
//| This function will read our scaling factors and store them       |
//+------------------------------------------------------------------+
bool load_scaling_factors(void)
  {
//--- Read in the file
   string file_name = "usd_cad_xau_xpd_scaling_factors.csv";

//--- Try open the file
   int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols).

//--- Check the result
   if(result != INVALID_HANDLE)
        {
        Print("Opened the file");
        //--- Store the values of the file

        int counter = 0;
        string value = "";

        while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end
        {

        if(counter > 100)  //if you aim to read 10 values set a break point after 10 elements have been read
                break; //stop the reading progress

        value = FileReadString(result);
        Print("Trying to read string: ",value," count value: ",counter);

        //--- Check where we are
        if((counter >= 14) && (counter < 26))
        {
                mean_values[counter - 14] = (float) value;
        }
        //--- Check where we are
        if((counter >= 27) && (counter < 39))
        {
                std_values[counter - 27] = (float) value;
        }
        //--- Reading a new row
        if(FileIsLineEnding(result))
        {
                Print("row++");
        }

        counter++;
        }
        //---Close the file
        ArrayPrint(mean_values);
        ArrayPrint(std_values);
        FileClose(result);
        return(true);
        }
//--- We failed to find the file
   else
        {
        Comment("Failed to find the file containing scaling factors");
        return(false);
        }
  }

También necesitamos una función responsable de obtener las cotizaciones de precios actualizadas del mercado.

//+------------------------------------------------------------------+
//| Update market prices                                             |
//+------------------------------------------------------------------+
void update_market_prices(void)
  {
   ask = SymbolInfoDouble(_Symbol,SYMBOL_ASK);
   bid = SymbolInfoDouble(_Symbol,SYMBOL_BID);
  }

Por último, necesitamos una función para obtener predicciones de nuestro modelo. Nuestra función de predicción primero escalará los datos antes de pasarlos a nuestro modelo.

//+------------------------------------------------------------------+
//| Model predict                                                    |
//+------------------------------------------------------------------+
void model_predict(void)
  {
//--- First fetch the market data

   vectorf model_input  =
        {
        iOpen("USDCAD",PERIOD_CURRENT,0),iHigh("USDCAD",PERIOD_CURRENT,0),iLow("USDCAD",PERIOD_CURRENT,0),iClose("USDCAD",PERIOD_CURRENT,0),
        iOpen("XAUUSD",PERIOD_CURRENT,0),iHigh("XAUUSD",PERIOD_CURRENT,0),iLow("XAUUSD",PERIOD_CURRENT,0),iClose("XAUUSD",PERIOD_CURRENT,0),
        iOpen("XPDUSD",PERIOD_CURRENT,0),iHigh("XPDUSD",PERIOD_CURRENT,0),iLow("XPDUSD",PERIOD_CURRENT,0),iClose("XPDUSD",PERIOD_CURRENT,0)
        };

//--- Now standardize and scale the data
   for(int i =0; i < 12; i++)
        {
        model_input[i] = ((model_input[i] - mean_values[i]) / std_values[i]);
        }

//--- Now fetch a prediction from our model
   OnnxRun(onnx_model,ONNX_DEFAULT,model_input,model_output);

//--- Store our model's forecat
   if(model_output[0] > iClose("USDCAD",PERIOD_CURRENT,0))
        {
        model_forecast = 1;
        }
   else
        if(model_output[0] < iClose("USDCAD",PERIOD_CURRENT,0))
        {
        model_forecast = -1;
        }
  }

Al inicializar nuestro Asesor Experto, primero cargaremos nuestro archivo ONNX y luego leeremos los valores de escala. Si alguno de estos procedimientos falla, abortaremos todo el proceso.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- This function will load our ONNX model
   if(!load_onnx())
        {
        return(INIT_FAILED);
        }

//--- This function will load our scaling factors
   if(!load_scaling_factors())
        {
        return(INIT_FAILED);
        }
//---
   return(INIT_SUCCEEDED);
  }

Cada vez que nuestro Asesor Experto sea eliminado del gráfico, liberemos los recursos que ya no necesitamos.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free up the resources we do not need
   OnnxRelease(onnx_model);
   ExpertRemove();
  }

Finalmente, cada vez que recibamos cambios en los precios de compra y venta, almacenaremos el precio actualizado en memoria y obtendremos una nueva predicción de nuestro modelo de IA. Si no tenemos posiciones abiertas, tomaremos la posición sugerida por nuestro modelo de IA; sin embargo, si tenemos una posición abierta, comprobaremos que la predicción de nuestro modelo de IA no contradiga nuestra posición actual.

void OnTick()
  {
//--- Update the market prices
   update_market_prices();

//--- Fetch a forecast from our model
   model_predict();

//--- Find a trading oppurtunity
   if(PositionsTotal() == 0)
        {
        if(model_forecast == -1)
        {
        Trade.Sell(0.2,_Symbol,ask,0,0,"USDCAD AI");
        state = -1;
        }

        else
        if(model_forecast == 1)
        {
                Trade.Buy(0.2,_Symbol,ask,0,0,"USDCAD AI");
                state = 1;
        }
        }

//--- Check for reversals
   if(PositionsTotal() > 0)
        {
        if(state != model_forecast)
        {
        Alert("Reversal detected by our AI system, closing all positions now!");
        Trade.PositionClose(_Symbol);
        }
        }

  }
//+------------------------------------------------------------------+

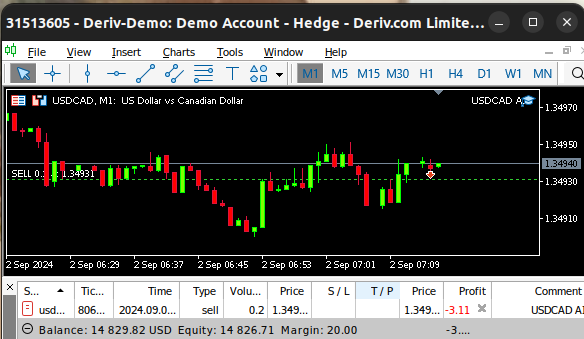
Figura 24: Nuestro asesor experto en acción.

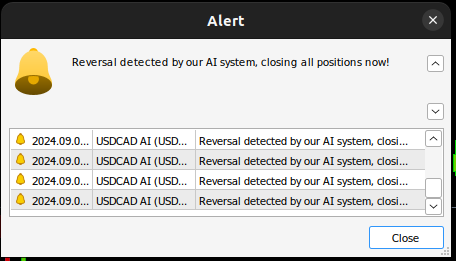
Figura 25: Nuestro sistema de IA ha detectado una posible reversión.

Conclusión

En el artículo de hoy, demostramos cómo descubrir relaciones ocultas que pueden existir entre mercados interrelacionados. Sin embargo, vale la pena señalar que nuestro análisis empírico nos muestra que podemos tener más éxito si utilizamos únicamente datos de mercado ordinarios y modelos lineales más simples. Esto puede ser cierto porque, como todos sabemos bien, los datos del mercado pueden ser ruidosos. Y en casos de datos ruidosos, los modelos más simples tienden a superar a los modelos más complejos porque los modelos complejos son sensibles a la variación en los datos de entrada.