Herramientas econométricas para la previsión de la volatilidad: el modelo GARCH

Introducción

La volatilidad supone una medida importante a la hora de evaluar la volatilidad de los precios de los activos financieros. Al analizar las cotizaciones, se ha observado desde hace tiempo que las grandes variaciones de precios suelen conllevar cambios aún mayores, sobre todo en tiempos de crisis financiera. A su vez, los pequeños cambios suelen ir seguidos de pequeñas variaciones de precio. Así, a periodos tranquilos de volatilidad siguen otros de relativa inestabilidad.

El primer modelo que intentó explicar este fenómeno fue el modelo ARCH, desarrollado por Engle, la Heteroscedasticidad condicional autorregresiva (heterogeneidad). Además del efecto de agrupamiento (agrupación de los rendimientos en conjuntos de valores grandes y pequeños), este modelo también explicaba la aparición de colas pesadas y curtosis positiva, característica de todas las distribuciones de incrementos de precio. El éxito del modelo gaussiano condicional ARCH ha dado lugar a la aparición de una serie de generalizaciones del modelo ARCH para explicar otros fenómenos observados en el análisis de series temporales financieras. Históricamente, una de las primeras generalizaciones del modelo ARCH es el modelo GARCH, (Generalized ARCH).

La principal ventaja de GARCH en comparación con ARCH es que es más parsimonioso y no requiere una estructura long-lag al ajustar los datos de muestra. En este artículo, queremos ofrecer una descripción de lo que es un GARCH y, lo que es más importante, ofrecer una herramienta de previsión de la volatilidad basada en él, ya que la previsión es uno de los principales objetivos del análisis de datos financieros.

Enfoque no paramétrico de la estimación de la volatilidad

El uso de la volatilidad para evaluar el riesgo es un tema bastante popular entre los tráders. La forma más habitual de estimar la volatilidad consiste simplemente en calcular la desviación típica a lo largo de un determinado periodo temporal.

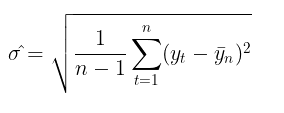
Se trata del denominado enfoque no paramétrico de la estimación de la volatilidad. La volatilidad calculada de esta forma se denomina volatilidad histórica o empírica. En el modelo de paseo aleatorio gaussiano, es la principal medida de la incertidumbre y la variabilidad, ya que se supone que la volatilidad es constante en el tiempo.

Enfoque paramétrico de la estimación de la volatilidad

El modelo GARCH, a su vez, supone que la volatilidad es una variable aleatoria (la propia volatilidad es volátil). Eso se acerca más a la realidad de la situación. El proceso GARCH se establece con las siguientes ecuaciones:

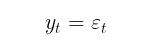
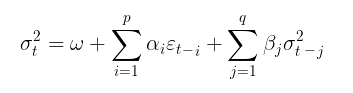
dónde,

• Yt – incrementos logarítmicos de los precios,
• ε t - residuos del modelo
• σt ² - varianza condicional
• zt = i.i.d. N(0,1) – distribución gaussiana estándar
• zt = i.i.d. t-Student(v) – Distribución estándar de Student con v grados de libertad
• (omega,alpha,beta,v) – parámetros del modelo que deben estimarse a partir de la muestra de datos

A los parámetros del modelo se le imponen las siguientes restricciones:

• omega >0, la condición para que la varianza sea positiva,
• alpha≥0,
• beta≥0,
• ∑alphai + ∑betaj <1 , condición de estacionariedad,
• v>2

Si beta = 0, el modelo GARCH se convertirá en un modelo ARCH .

Normalmente, el modelo GARCH se complementa con el modelo de esperanza matemática, ya sea condicional o incondicional. Como modelo de la esperanza matemática condicional podemos tomar, por ejemplo, un proceso autorregresivo de primer orden AR(1):

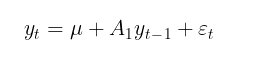
dónde,

• u - parámetro de intercepción,
• A 1 - parámetro del modelo autorregresivo

El objetivo del modelado de la media condicional será determinar la serie de cuadrados de los residuos (εt²) con la que hallaremos la varianza condicional. Si no hay autocorrelación en la serie de rendimientos, como suele ser el caso, podremos pasar al modelo de esperanza matemática incondicional:

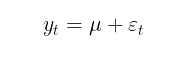
En este artículo, para simplificar los cálculos, utilizaremos el modelo sin estimar la autocorrelación de los rendimientos. Así, el problema de la estimación de la volatilidad en el modelo GARCH se reducirá al problema paramétrico de hallar los coeficientes del modelo (μ, ω, alpha, beta, v).

Estimación de los parámetros del modelo GARCH usando el método de máxima verosimilitud

El método de máxima verosimilitud suele usarse para hallar los parámetros desconocidos. Suponiendo una distribución gaussiana de los residuos et, la función logarítmica de verosimilitud adoptará el aspecto:

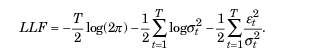
Si se detectan desviaciones de la normalidad, la distribución estandarizada de Student podría ser una distribución adecuada. Para valores pequeños del parámetro v (grado de libertad) presenta curtosis positiva y colas más pesadas que la distribución normal. En este caso, la función de verosimilitud adoptará la forma:

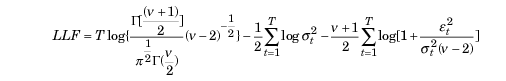
Dónde,

• D - función gamma
• T - volumen de muestreo de datos

Optimizador ALGLIB MinBLEIC

Para encontrar los valores de los parámetros del modelo GARCH, deberemos maximizar la función de verosimilitud. Para ello tendremos que usar técnicas de optimización. En este sentido, puede servir de ayuda la biblioteca de análisis numérico ALGLIB. Para maximizar la función objetivo, hemos elegido el algoritmo MinBLEIC(Bounded Linear Equality Inequality Constraints).

//+------------------------------------------------------------------+
//|  Objective Function: Gaussian loglikelihood                      |
//+------------------------------------------------------------------+
void CNDimensional_GaussianFunc::Func(CRowDouble &x,double &func,CObject &obj)
  {
//x[0] - mu;
//x[1] - omega;
//x[2] - alpha;
//x[3] - beta;
   double returns[];
   ArrayResize(returns,N1);
   for(int i=0;i<N1;i++)
     {
      returns[i] = MathLog(close[i+1]/close[i]);
     }

   double residuals[];
   ArrayResize(residuals,N1);
   for(int i = 0; i<N1; i++)
     {
      residuals[i] = (returns[i] - x[0]);
     }

   double condVar[];
   ArrayResize(condVar,N1);
   condVar[0] = x[1]/(1-x[2]-x[3]);  // Unconditional Variance

   for(int i=1; i<N1; i++)
     {
      condVar[i] = x[1] + x[2]*MathPow(residuals[i-1],2) + x[3]*condVar[i-1]; // Conditional Variance
     }

   double LLF[],a[],b[];
   ArrayResize(LLF,N1);
   ArrayResize(a,N1);
   ArrayResize(b,N1);
   for(int i=0; i<N1; i++)
     {

      a[i]= 1/sqrt(2*M_PI*condVar[i]);
      if(!MathIsValidNumber(a[i]))
        {
         break;
        }

      b[i]= MathExp(- MathPow(residuals[i],2)/(2 * condVar[i]));
      if(!MathIsValidNumber(b[i]))
        {
         break;
        }

      LLF[i]=MathLog(a[i]*b[i]);
      if(!MathIsValidNumber(LLF[i]))
        {
         break;
        }
     }

   func = -MathSum(LLF); // Loglikelihood
  }

En la función GARCH, que recurre directamente a la función objetivo y encuentra los valores óptimos de los parámetros, será necesario:

• especificar los valores iniciales de los parámetros,
• establecer la escala de datos (un punto muy importante del que depende el éxito de la optimización),
• especificar los límites dentro de los cuales podrán modificarse los parámetros,
• escribir las limitaciones-desigualdades lineales (solo tenemos una para la estacionariedad alpha + beta <1),
• especificar las condiciones para detener el algoritmo de optimización,
• especificar el paso de diferenciación.

//+------------------------------------------------------------------+
//|  Function GARCH  Gaussian                                        |
//+------------------------------------------------------------------+
vector GARCH()
  {
   double              x[],s[];
   int                 ct[];
   CMatrixDouble       c;
   CObject Obj;
   CNDimensional_GaussianFunc ffunc;
   CNDimensional_Rep frep;

   double returns[];
   ArrayResize(returns,N1);
   for(int i=0;i<N1;i++)
     {
      returns[i] = MathLog(close[i+1]/close[i]);
     }
   double returns_mean  = MathMean(returns);
   double returns_var = MathVariance(returns);
   double KurtosisReturns = MathKurtosis(returns);
// Print("KurtosisReturns= ",KurtosisReturns);

// Initial parameters ---------------------------
   ArrayResize(x,4);
   x[0]=returns_mean;  //  Mu
   x[1]=returns_var;  // Omega
   x[2]=0.0;         // alpha
   x[3]=0.0;        // beta
//------------------------------------------------------------
   double mu;
   if(NormalizeDouble(returns_mean,10)==0)
     {
      mu = 0.0000001;
     }
   else
      mu = NormalizeDouble(returns_mean,10);
// Set Scale-----------------------------------------------
   ArrayResize(s,4);
   s[0] = NormalizeDouble(returns_mean,10);  //  Mu
   s[1] = NormalizeDouble(returns_var,10); // omega
   s[2] =1;
   s[3] =1;
//---------------------------------------------------------------
// Linearly inequality constrained: --------------------------------
   c.Resize(1,5);
   c.Set(0,0,0);
   c.Set(0,1,0);
   c.Set(0,2,1);
   c.Set(0,3,1);
   c.Set(0,4,0.999); // alpha + beta <= 0.999
   ArrayResize(ct,1);
   ct[0]=-1; // {-1:<=},{+1:>=},{0:=}
//--------------------------------------------------------------
// Box constraints ------------------------------------------------
   double bndl[4];
   double bndu[4];

   bndl[0] = -0.01;  // mu
   bndl[1] = NormalizeDouble(returns_var/20,10);  // omega
   bndl[2] = 0.0;  // alpha
   bndl[3] = 0.0;  // beta

   bndu[0] = 0.01;  // mu
   bndu[1] = NormalizeDouble(returns_var,10);  // omega
   bndu[2] = 0.999;  // alpha
   bndu[3] = 0.999;  // beta
//--------------------------------------------------------------
   CMinBLEICStateShell state;
   CMinBLEICReportShell rep;
   double epsg=0;
   double epsf=0;
   double epsx=0.00001;
   double diffstep=0.0001;
//--- These variables define stopping conditions for the outer iterations:
//--- * epso controls convergence of outer iterations;algorithm will stop
//---   when difference between solutions of subsequent unconstrained problems
//---   will be less than 0.0001
//--- * epsi controls amount of infeasibility allowed in the final solution
   double epso=0.00001;
   double epsi=0.00001;

   CAlglib::MinBLEICCreateF(x,diffstep,state); //---  create optimizer
   CAlglib::MinBLEICSetBC(state,bndl,bndu);  //--- add boundary constraints
   CAlglib::MinBLEICSetLC(state,c,ct);
   CAlglib::MinBLEICSetScale(state,s);
   CAlglib::MinBLEICSetPrecScale(state); // Preconditioner
   CAlglib::MinBLEICSetInnerCond(state,epsg,epsf,epsx);
   CAlglib::MinBLEICSetOuterCond(state,epso,epsi);
   CAlglib::MinBLEICOptimize(state,ffunc,frep,0,Obj);
   CAlglib::MinBLEICResults(state,x,rep);   // Get parameters
//---------------------------------------------------------

   double residuals[],resSquared[],Realised[];
   ArrayResize(residuals,N1);
   for(int i = 0; i<N1; i++)
     {
      residuals[i] = (returns[i] - x[0]);
     }

   MathPow(residuals,2,resSquared);
   ArrayCopy(resSquared_,resSquared,0,0,WHOLE_ARRAY);
   MathSqrt(resSquared,Realised);

   double condVar[],condStDev[];
   double ForecastCondVar,PriceConf_Upper,PriceConf_Lower;
   ArrayResize(condVar,N1);
   condVar[0] = x[1]/(1-x[2]-x[3]);
   for(int i = 1; i<N1; i++)
     {
      condVar[i] = x[1] + x[2]*MathPow(residuals[i-1],2) + x[3]*condVar[i-1];
     }

   double PlotUncondStDev[];
   ArrayResize(PlotUncondStDev,N1);
   ArrayFill(PlotUncondStDev,0,N1,sqrt(condVar[0])); // for Plot
   ArrayCopy(PlotUncondStDev_,PlotUncondStDev,0,0,WHOLE_ARRAY);
   MathSqrt(condVar,condStDev);
// Print("мат ожидание условного ст отклонения = "," ",MathMean(condStDev));

   ArrayCopy(Real,Realised,0,0,WHOLE_ARRAY);
   ArrayCopy(GARCH_,condStDev,0,0,WHOLE_ARRAY);

   vector v_Realised, v_condStDev;
   v_Realised.Assign(Realised);
   v_condStDev.Assign(condStDev);
   double MSE=v_condStDev.Loss(v_Realised,LOSS_MSE); // Mean Squared Error
//-----------------------------------------------------------------------------
//-------- Standardize Residuals--------------------------------------
   double z[];
   ArrayResize(z,N1);
   for(int i = 0; i<N1; i++)
     {
      z[i] = residuals[i]/sqrt(condVar[i]);
     }
   ArrayCopy(Z,z,0,0,WHOLE_ARRAY);
//----------------------------------------------------------------------------------

//-------------- JarqueBeraTest for Normality  ----------------------------------
   double pValueJB;
   int JBTestH;
   CAlglib::JarqueBeraTest(z,N1,pValueJB);
   if(pValueJB <0.05)
      JBTestH =1;
   else
      JBTestH=0; // H=0 - data Normal, H=1 data are not Normal
   double Kurtosis = MathKurtosis(z); // Kurosis = 0 for Normal distribution
//---------------------------------------------------------------------------------

//-------------------------------------------------------------------------------------
//-------- Forecast Conditional Variance for m bars
   double FCV[];
   ArrayResize(FCV,forecast_m);
   for(int i = 0; i<forecast_m; i++)
     {
      FCV[i] = sqrt(x[1]*((1-MathPow(x[2]+x[3],i+1))/(1-x[2]-x[3])) + MathPow(x[2]+x[3],i)*(x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1])) ;
     }
   ArrayCopy(FCV_,FCV,0,0,WHOLE_ARRAY);
//-----------------------------------------------------------------------------------
   double LLF[];
   double Loglikelihood;
   ArrayResize(LLF,N1);
   for(int i = 0; i<N1; i++)
     {
      LLF[i] = MathLog(1/sqrt(2*M_PI*condVar[i])*MathExp(- MathPow(residuals[i],2)/(2*condVar[i])));
     }
   Loglikelihood = MathSum(LLF);
//--------------------------------------------------------------------------

   ForecastCondVar= x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1];
   int err1;
   PriceConf_Lower = close[N1]*MathExp(-MathAbs(MathQuantileNormal((1-pci)/2,0,1,err1))*sqrt(x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1])); // confidence interval pci%
   PriceConf_Upper = close[N1]*MathExp(MathAbs(MathQuantileNormal((1-pci)/2,0,1,err1))*sqrt(x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1]));  // confidence interval pci%

//--------------------------------------------------------------------------------------
   vector result= {x[0],x[1],x[2],x[3],rep.GetTerminationType(),ForecastCondVar,PriceConf_Lower,PriceConf_Upper,MSE,Loglikelihood,condVar[0],returns_var,JBTestH,Kurtosis};
   return (result);
  }
//+------------------------------------------------------------------+

Previsión de la volatilidad con el modelo GARCH(1,1)

Previsión puntual de la volatilidad

Una vez encontrados los parámetros del modelo, podemos pasar a la tarea principal: la previsión de la volatilidad. La previsión de volatilidad para el modelo GARCH(1,1) para m pasos por delante se calculará mediante la fórmula:

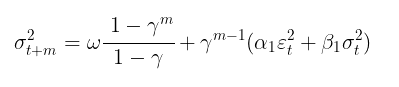
dónde,

• γ = α1 + β 1.

Esta previsión m →∞ converge con la varianza condicional teórica GARCH (si se cumple la condición de estacionariedad α1+ β1 < 1).

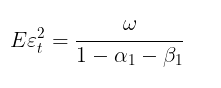
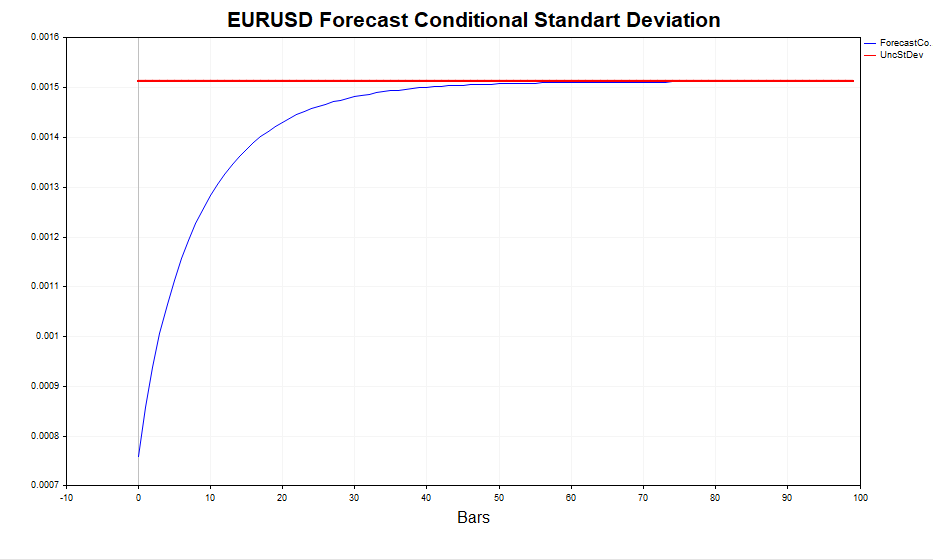
En otras palabras, cuanto más lejana sea la predicción, más se acercarán sus valores al valor estacionario de la varianza incondicional. El script GARCH nos permite calcular una previsión de la volatilidad m pasos por delante y comparar estos valores con el valor Eεt ², confirmando que efectivamente es así.

Previsión de intervalos

Una previsión puntual de la volatilidad es buena, pero resulta más importante obtener una estimación probabilística de dónde se situarán los futuros incrementos de precios, es decir, obtener intervalos de confianza con un cierto nivel de significación.

Bajo el supuesto de normalidad z t= i.i.d. Los N(0,1) intervalos de confianza N(0,1) se calcularán mediante la fórmula:

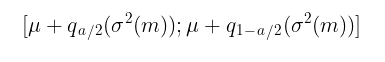
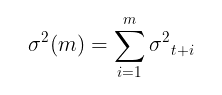
dónde,

• q – cuantil de la distribución normal estándar

Por ejemplo, para un intervalo de confianza con un nivel de confianza del 90% (a = 1-0,9), este sería el intervalo:

[ u – 1,65σ ; u + 1,65σ ]

Las cosas se ponen mucho más difíciles cuando presuponemos que zt = i.i.d. t-Student(v). En tal caso, no existe una fórmula analítica para la inversa de la función de distribución. Por ello, tendremos que utilizar simulaciones Monte Carlo para construir intervalos de confianza.

//+-------------------------------------------------------------------------+
//|Function calculate Forecast Confidence intervals using Monte-Carlo method|
//+-------------------------------------------------------------------------+
bool MCForecastStandardized_t(const double DoF,const double CondStDevForecast,const double prob, double & F_lower[],double & F_upper[])
  {

   double alpha = 1-prob;
   double qlower[1] = {alpha/2};       // q (a/2)
   double qupper[1] = {1-alpha/2};  // q (1-a/2)

   int N = 10000; //number Monte-Carlo simulates
   double h_St[];
   ArrayResize(h_St,N);
   for(int i=0;i<N;i++)
     {
      h_St[i] = CondStDevForecast * Standardized_t(DoF);   // GARCH-Student(1,1)
     }
   MathQuantile(h_St,qlower,F_lower);
   MathQuantile(h_St,qupper,F_upper);
   return(true);
  }

//+--------------------------------------------------------------------------+
//| Function calculate i.i.d. standardized t-distributed variable            |                              |
//+--------------------------------------------------------------------------+
double  Standardized_t(const double DoF)
  {
   double randStandStudent;
   int err;
   randStandStudent = MathRandomNormal(0,1,err) * sqrt(DoF/((MathRandomGamma(DoF/2.0,1)*2.0)));
   randStandStudent = randStandStudent/sqrt(DoF/(DoF-2.0));
   return(randStandStudent);
  }
//+------------------------------------------------------------------+

Resulta evidente que cuanto mayor sea el número de simulaciones (10 000 por defecto), más precisa será la previsión, pero al mismo tiempo aumentará el tiempo necesario para los cálculos. La cifra más aceptable será 100 000, entonces los intervalos de confianza parecerán más simétricos.

Comprobación de la adecuación del modelo GARCH gaussiano condicional

Para comprobar la capacidad del modelo GARCH para captar la heteroscedasticidad de la volatilidad, deberemos comprobar la presencia de autocorrelación en los residuos normalizados y su conformidad con una distribución normal estándar. Los residuos normalizados son simplemente los incrementos de precios menos la esperanza matemática condicional (o incondicional) dividida por la desviación típica condicional calculada utilizando el modelo GARCH.

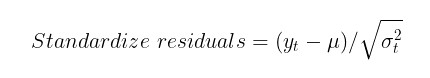
Si el modelo GARCH resulta adecuado para los datos reales, los residuos normalizados serán variables normales estándar independientes e idénticamente distribuidas.

Como ejemplo de análisis de residuos, tomaremos los datos diarios de EURUSD de los últimos cuatro años y calcularemos los parámetros del modelo.

Ahora comprobaremos los cuadrados de los residuos en busca de autocorrelación.

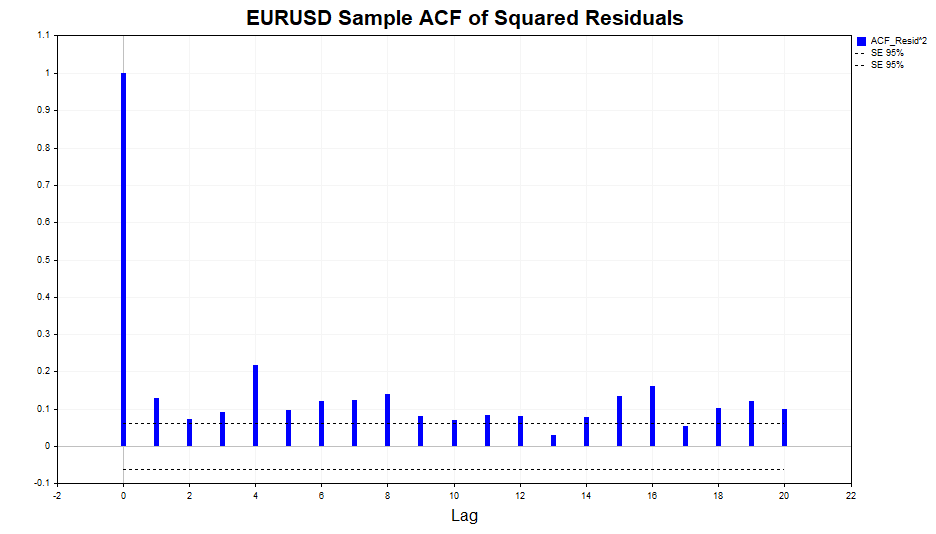
Como podemos ver, existe una ligera dependencia en los datos, hasta el lag 20 inclusive. Ahora comprobaremos los cuadrados de los residuos normalizados en busca de autocorrelación y veremos si el modelo GARCH(1,1) podría describir adecuadamente esta relación.

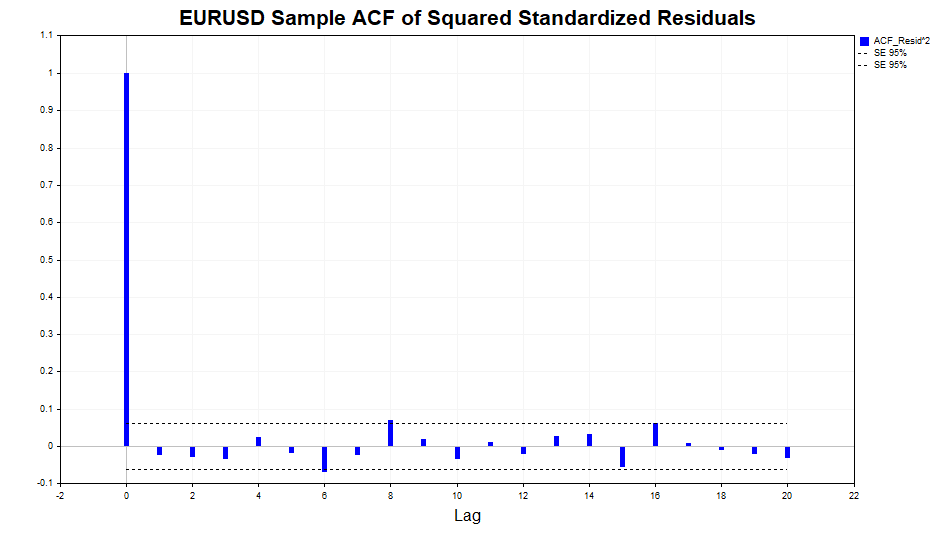
Como podemos ver, el modelo ha funcionado bien, no hay correlación significativa en los datos.

Veamos ahora la volatilidad realizada calculada (cuadrado de los incrementos logarítmicos de los precios) y la desviación típica condicional (GARCH). El modelo reacciona bastante bien a los cambios de volatilidad. La desviación típica incondicional actuará como la media en torno a la cual fluctúa la volatilidad GARCH.

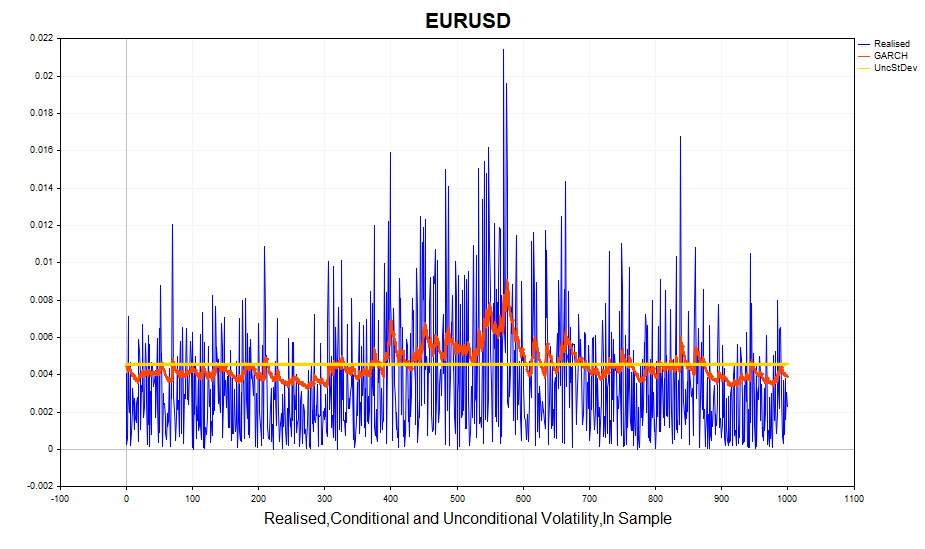
Ahora comprobaremos la normalidad de los residuos normalizados.

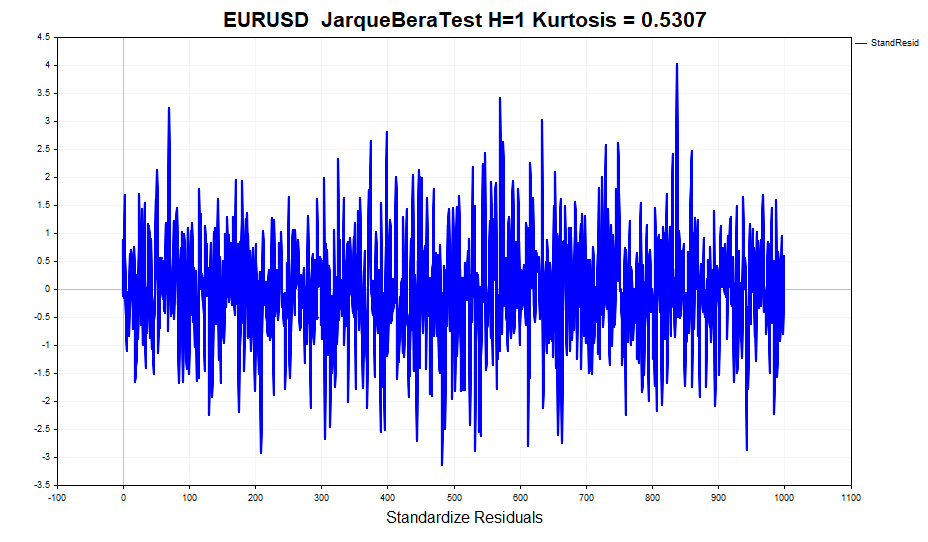
A primera vista, los datos parecen bastante normales, puede decirse que no hay colas pesadas. Pero las pruebas formales de normalidad, como JarqueBeraTest, rechazarán la hipótesis nula. Toda la culpa la tiene el exceso (0,5307), ligeramente distinto de lo normal. Al mismo tiempo, el valor de curtosis para los rendimientos es de 1,2904. Es decir, el modelo GARCH ha tenido parcialmente en cuenta este efecto de insularidad de la distribución, aunque no completamente. Recordemos que la distribución incondicional del proceso GARCH tiene colas gruesas. Esto se debe a que una mezcla de distribuciones gaussianas con distinta varianza da lugar a una distribución con colas pesadas y curtosis positiva.

Por consiguiente, se incumplirá uno de los supuestos del modelo GARCH según el cual los residuos normalizados tienen una distribución normal condicional. Por ello, las estimaciones de los parámetros del modelo obtenidas por el método de máxima verosimilitud pierden algunas propiedades útiles, a saber, dejan de ser asintóticamente eficientes (en otras palabras, se pueden encontrar estimaciones de parámetros más precisas en muestras grandes).

En este caso, la distribución de Student puede tomarse como alternativa a la distribución normal, ya que tiene curtosis positiva y colas pesadas para grados de libertad pequeños. Además, el número de grados de libertad se convierte en un parámetro desconocido adicional que deberá estimarse a partir de la muestra.

Todas las acciones relacionadas con la presentación visual de diversas estadísticas que acabamos de comentar brevemente, se colocarán en el script GARCH para facilitar el análisis.

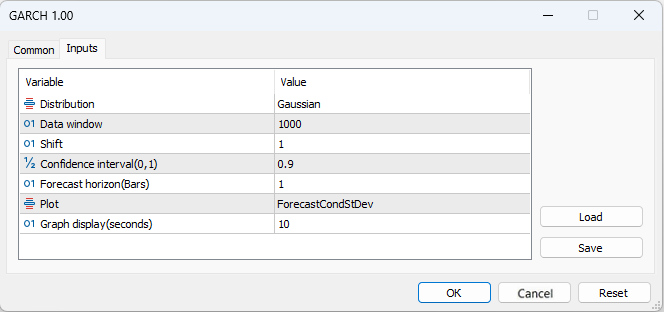
• Distribution – distribución normal estándar o distribución estándar de Student
• Data window - ventana de datos para calcular los parámetros del modelo
• Shift – desplazamiento de la ventana de datos (1- penúltima barra del gráfico)
• Confidence interval – nivel de significación del intervalo de confianza (cuanto mayor sea el nivel de significación, más amplio será el intervalo de confianza).
• Forecast horizon – previsión de la volatilidad para el número especificado de barras por delante
• Plot – representa en el gráfico: la previsión de volatilidad, los residuos normalizados, la comparación de la volatilidad realizada y GARCH, la función de autocorrelación de los cuadrados de los residuos, la función de autocorrelación de los cuadrados normalizados de los residuos.

Indicador iGARCH

Para hacernos una primera idea del modelo y de los datos a los que queremos aplicar este modelo, el script GARCH resultará bastante adecuado. Pero para estimar y prever la volatilidad en tiempo real, querríamos disponer de un algoritmo que recalculara los parámetros del modelo en cada nueva barra, ajustándose rápidamente a los constantes cambios del mercado. El indicador adaptativo iGARCH será la solución a este problema.

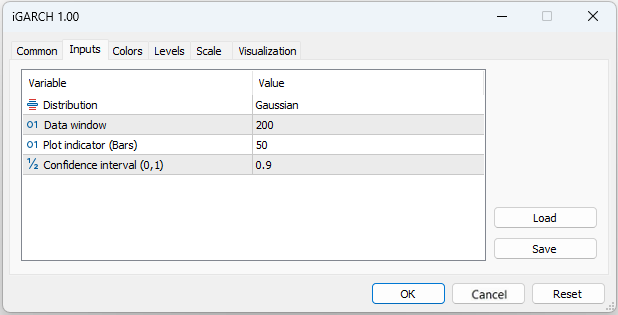
• Plot indicator – número de barras para las que se calculará el indicador

El indicador preverá la volatilidad (desviación típica condicional) y los intervalos de confianza para los futuros incrementos de precio con un cierto nivel de fiabilidad un paso por delante. La previsión se mostrará en la barra cero, los datos para el cálculo de los parámetros (Data window) se tomarán de la primera barra. Como los parámetros del modelo se optimizan en cada barra, no le recomendamos fijar valores de Plot indicator(Bars) demasiado altos, ya que el cálculo podría llevar bastante tiempo (especialmente para el modelo con distribución de Student).

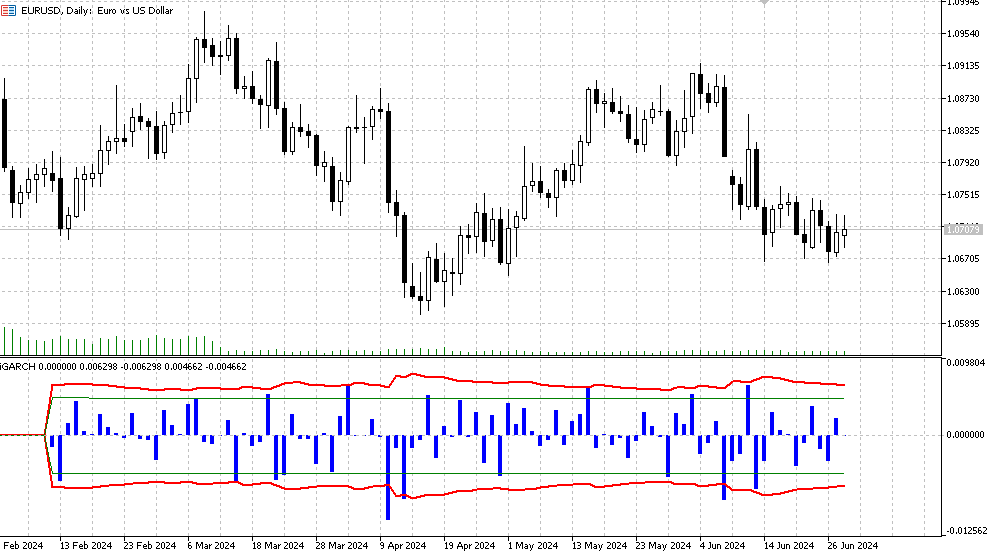
• Histograma - valores de los rendimientos logarítmicos LN(Yt/Yt-1),
• La línea roja será el límite superior e inferior de la predicción de la desviación típica condicional definida para el nivel de significación confidence interval (90% por defecto). Esto significa que aproximadamente el 90% de las veces, los incrementos logarítmicos de los precios se situarán dentro de estos límites,
• Las líneas verdes representarán la volatilidad histórica normal y los límites inferior y superior, respectivamente.

Además, se enviará la siguiente información al registro, que se actualizará con cada nueva barra:

• los últimos valores de los parámetros optimizados (mu, omega, alpha, beta, v),
• los valores de la función de verosimilitud (LLF),
• los niveles de precio previstos para el nivel de significación seleccionado,
• el informe sobre la finalización exitosa de la optimización,
• los valores de la desviación típica condicional prevista,
• los valores de la desviación típica GARCH teórica incondicional
• los valores de la desviación típica histórica.

Conclusión

En este artículo, hemos considerado uno de los modelos más populares de heteroscedasticidad condicional, el modelo GARCH. Asimismo, hemos observado que los métodos habituales de estimación de la volatilidad, que suponen su constancia en el tiempo, no reflejan la situación real. En cambio, el modelo GARCH considera la variabilidad de la volatilidad a lo largo del tiempo, lo cual lo hace más adecuado para analizar las condiciones del mercado.

Usando el modelo GARCH(1,1) como ejemplo, hemos desarrollado un indicador adaptativo que nos permite prever la volatilidad y los intervalos de confianza de los logaritmos de los incrementos de precio un paso por delante en el tiempo. Y esto nos da la oportunidad de obtener una evaluación probabilística de los futuros movimientos de los precios y, por tanto, de gestionar los riesgos de las posiciones abiertas con mayor eficacia.

Este indicador permite elegir no solo el modelo clásico de residuos gaussianos, sino también un modelo que supone que los residuos siguen una distribución de Student. Al mismo tiempo, los parámetros del modelo se optimizan en cada nueva barra, lo cual permite reaccionar rápidamente a la situación actual del mercado.

Además, hemos utilizado el algoritmo de optimización MinBLEIC de la biblioteca de análisis numérico ALGLIB para estimar los parámetros del modelo usando el método de máxima verosimilitud. El script GARCH calcula todas las estadísticas necesarias asociadas al modelo y ofrece ayudas visuales para evaluar las dependencias en los datos.

Así pues, la aplicación del modelo GARCH en la investigación econométrica y el análisis financiero permite obtener previsiones de volatilidad más precisas, lo cual mejora notablemente la gestión del riesgo y la toma de decisiones de inversión.