Características del Wizard MQL5 que debe conocer (Parte 33): Núcleos de procesos gaussianos

Introducción

Proceso gaussiano: Los núcleos son funciones de covarianza que se utilizan en los procesos gaussianos para medir las relaciones entre los puntos de datos, como en una serie temporal. Estos núcleos generan matrices que capturan la relación intradatos, lo que permite que el proceso gaussiano realice proyecciones o pronósticos asumiendo que los datos siguen una distribución normal. Como estas series buscan explorar nuevas ideas y al mismo tiempo examinar cómo se pueden explotar estas ideas, los núcleos de proceso gaussiano (Gaussian Process, GP) sirven como tema para construir una señal personalizada.

Recientemente hemos cubierto muchos artículos relacionados con el aprendizaje automático en los últimos cinco artículos, por lo que para este "tomamos un descanso" y analizamos las buenas y antiguas estadísticas. En la naturaleza del desarrollo de sistemas, muy a menudo ambos están casados; sin embargo, al desarrollar esta señal personalizada en particular, no complementaremos ni consideraremos ningún algoritmo de aprendizaje automático. Los kernels GP se destacan por su flexibilidad.

Se pueden utilizar para modelar una amplia variedad de patrones de datos que varían en enfoque desde la periodicidad hasta las tendencias o incluso relaciones no lineales. Sin embargo, lo más importante es que, a la hora de predecir, hacen más que proporcionar un único valor. En lugar de ello, proporcionan una estimación de la incertidumbre que incluiría el valor deseado, así como un valor de límite superior y un valor de límite inferior. Estos rangos límite a menudo se proporcionan con un índice de confianza, lo que facilita aún más el proceso de toma de decisiones de un comerciante cuando se le presenta un valor previsto. Estas calificaciones de confianza también pueden ser reveladoras y ayudar a comprender mejor los valores negociados al comparar diferentes bandas de pronóstico que están marcadas con diferentes niveles de confianza.

Además, son buenos para manejar datos ruidosos ya que permiten incrementar un valor de ruido en la matriz K creada (ver más abajo), y también se pueden usar incorporando conocimiento previo en ellos, además de que son muy escalables. Hay una gran variedad de kernels diferentes para elegir. La lista incluye (pero no se limita a): núcleo exponencial cuadrado, núcleo lineal, núcleo periódico, núcleo cuadrático racional, núcleo materno, núcleo exponencial, núcleo polinomial, núcleo de ruido blanco, núcleo de producto escalar, núcleo de mezcla espectral, núcleo constante, núcleo de coseno, núcleo de red neuronal (arcoseno) y núcleos de producto y suma.

En este artículo solo analizaremos el kernel RBF, también conocido como kernel de función de base radial (Radial Basis Function, RBF). Como la mayoría de los núcleos, mide la similitud entre dos puntos de datos centrándose en la distancia entre ellos con el supuesto básico subyacente de que cuanto más alejados estén los puntos, menos similares serán y viceversa. Esto se rige por la siguiente ecuación:

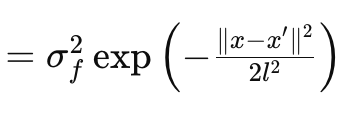
Donde:

• x y x′: Estos son los vectores de entrada o puntos en el espacio de entrada.
• σ f²: Este es el parámetro de varianza del kernel, que sirve como parámetro predeterminado u optimizable.
• l se suele denominar parámetro de escala de longitud. Controla la suavidad de la función resultante. Una l más pequeña (o una escala de longitud más corta) da como resultado una función que varía rápidamente, mientras que una l más grande (o una escala de longitud más larga) da como resultado una función más suave.
• exp:Esta es la función exponencial.

Este núcleo se puede codificar en MQL5 fácilmente como:

//+------------------------------------------------------------------+
// RBF Kernel Function
//+------------------------------------------------------------------+
matrix CSignalGauss::RBF_Kernel(vector &Rows, vector &Cols)
{  matrix _rbf;
   _rbf.Init(Rows.Size(), Cols.Size());
   for(int i = 0; i < int(Rows.Size()); i++)
   {  for(int ii = 0; ii < int(Cols.Size()); ii++)
      {  _rbf[i][ii] = m_variance * exp(-0.5 * pow(Rows[i] - Cols[ii], 2.0) / pow(m_next, 2.0));
      }
   }
   return(_rbf);
}

Procesos gaussianos en series temporales financieras

Los procesos gaussianos son un marco probabilístico donde los pronósticos se realizan en términos de distribuciones en lugar de valores fijos. Es por esto que también se le conoce como un marco no parametrizado. Los pronósticos de salida incluyen una predicción media y una varianza (o incertidumbre) en torno a este pronóstico. La varianza de GPs representa la incertidumbre o confianza en el pronóstico realizado. Esta incertidumbre es en principio aleatoria, dado que se basa en la distribución normal del GP. Sin embargo, debido a que implica un intervalo y un nivel de confianza (generalmente basado en el 95%), no es necesario cumplir todas sus predicciones. En comparación con otros métodos de pronóstico estadístico como ARIMA, GP es altamente flexible y capaz de modelar relaciones no lineales complejas con incertidumbre cuantificada, mientras que ARIMA funciona mejor con series de tiempo estacionarias con estructuras establecidas. La principal desventaja de GP es que es computacionalmente costoso, mientras que métodos como ARIMA no lo son.

El núcleo RBF

El cálculo del kernel GP implica principalmente 6 matrices y 2 vectores. Todas estas matrices y vectores se utilizan en nuestra función 'GetOutput', cuyo código se detalla resumidamente a continuación:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalGauss::GetOutput(double BasisMean, vector &Output)
{  
   ...

   matrix _k = RBF_Kernel(_past_time, _past_time);
   matrix _noise;
   _noise.Init(_k.Rows(), _k.Cols());
   _noise.Fill(fabs(0.05 * _k.Min()));
   _k += _noise;
   matrix _norm;
   _norm.Init(_k.Rows(), _k.Cols());
   _norm.Identity();
   _norm *= 0.0005;
   _k += _norm;
   vector _next_time;
   _next_time.Init(m_next);
   for(int i = 0; i < m_next; i++)
   {  _next_time[i] = _past_time[_past_time.Size() - 1] + i + 1;
   }
   matrix _k_s = RBF_Kernel(_next_time, _past_time);
   matrix _k_ss = RBF_Kernel(_next_time, _next_time);
// Compute K^-1 * y
   matrix _k_inv = _k.Inv();
   if(_k_inv.Rows() > 0 && _k_inv.Cols() > 0)
   {  vector _alpha = _k_inv.MatMul(_past);
      // Compute mean predictions: mu_* = K_s * alpha
      vector _mu_star = _k_s.MatMul(_alpha);
      vector _mean;
      _mean.Init(_mu_star.Size());
      _mean.Fill(BasisMean);
      _mu_star += _mean;
   // Compute covariance: Sigma_* = K_ss - K_s * K_inv * K_s^T
      matrix _v = _k_s.MatMul(_k_inv);
      matrix _sigma_star = _k_ss - (_v.MatMul(_k_s.Transpose()));
      vector _variances = _sigma_star.Diag();
      //Print(" sigma star: ",_sigma_star);
      Print(" pre variances: ",_variances);
      Output = _mu_star;
      SetOutput(Output);
      SetOutput(_variances);
      Print(" variances: ",_variances);
   }
}

Para detallarlos, son:

• _k
• _k_s
• _k_ss
• _k_inv
• _v
• y _sigma_star

_k es la matriz de covarianzas ancla y principal. Captura las relaciones entre el par de vectores de entrada y la función kernel en uso. Estamos utilizando el kernel de función de base radial (RBF), y su código fuente ya se ha compartido anteriormente. Dado que estamos haciendo un pronóstico para una serie de tiempo, la entrada a nuestro kernel RBF serían dos vectores de tiempo similares que registran los índices de tiempo de la serie de datos que buscamos pronosticar. Al codificar las similitudes entre los puntos de tiempo registrados, esto sirve como base para determinar la estructura general. Tenga en cuenta que hay muchos otros formatos de kernel, como se ve en los catorce enumerados anteriormente, y en artículos futuros podríamos considerar estas alternativas como una clase de señal personalizada.

Esto nos lleva a la matriz de covarianza _k_s. Esta matriz actúa como un puente hacia los siguientes índices de tiempo también a través de un núcleo RBF como la matriz _k. La longitud o el número de estos índices de tiempo establece el número de proyecciones que se realizarán y está definido por el parámetro de entrada length-scale. Nos referimos a este parámetro como m_next en la clase de señal personalizada. Al establecer un puente entre los índices de tiempo pasado y los índices de tiempo próximo _k_s sirve para proyectar una relación entre los datos conocidos y los próximos datos desconocidos y esto, como es de esperar, es útil en la previsión. Esta matriz en particular es muy sensible a la proyección realizada, por lo que su precisión debe ser exacta, y con mucho gusto nuestro código y la función del núcleo RBF manejan esto sin problemas. No obstante, los dos parámetros ajustables de varianza y escala de longitud deben ajustarse con cuidado para garantizar la máxima precisión de la proyección.

Esta matriz puede definirse como:

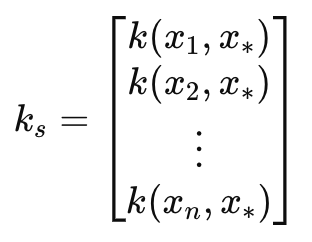
Donde:

• k(x i , y i ) es una Función de Base Radial entre dos valores de los vectores x e y en el índice i. En nuestro caso, x e y son el mismo vector temporal de entrada, por lo que ambos vectores se etiquetan como x. x suelen ser los datos de entrenamiento, mientras que y es un marcador de posición para los datos de prueba.
• k s es el vector de covarianza (o matriz en la escala de longitud par o número de proyecciones superior a 1) entre los datos de entrenamiento y el punto de prueba x∗.
• x 1 , x 2 ,..., xn, son los puntos de entrada de los datos de entrenamiento.
• x∗ es el punto de datos de prueba de entrada en el que se van a realizar las predicciones.

Esto conduce a la matriz _k_ss que en esencia es una imagen especular de la matriz _k , con la diferencia clave de que es una covarianza de los índices de tiempo de pronóstico. Por lo tanto, sus dimensiones coinciden con el parámetro de entrada de escala de longitud. Es fundamental para calcular la parte de estimación de incertidumbre del pronóstico. Mide la varianza sobre los índices de tiempo de pronóstico antes de que se incorporen los datos. Esto se puede resumir en una fórmula como la siguiente:

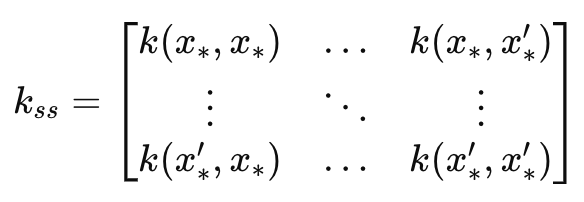
Donde:

• k ss es la matriz de covarianza de los puntos de datos de prueba.
• x∗, x∗′ son los puntos de datos de prueba de entrada donde se realizarán las predicciones.
• k(x∗,x∗′) es la función kernel aplicada al par de puntos de prueba 𝑥∗ y 𝑥∗′.

La matriz _k_inv, como su nombre indica, es la inversa de la matriz k. La inversión de matrices se maneja mediante funciones integradas, sin embargo, no está libre de fallas ya que a menudo la inversión puede no ser posible. Por eso, en nuestro código, verificamos si la matriz invertida tiene filas o columnas. Si no hay ninguno presente, implica que la inversión ha fallado. Esta inversión es importante para calcular las ponderaciones aplicadas a los datos de entrenamiento durante el pronóstico. Se podrían considerar métodos personalizados alternativos para realizar esta inversión, como Cholesky (asumiendo que no es el enfoque incorporado); sin embargo, la codificación de ellos como opciones depende del lector.

El vector de peso se utiliza para combinar los resultados del entrenamiento en función de su estructura de covarianza. _alpha determina cuánta influencia tienen los nuevos puntos de datos en la predicción sobre los puntos de prueba/escala de longitud. Obtenemos alfa del producto matricial de la matriz k invertida y los datos antiguos sin procesar para los que buscamos un pronóstico. Esto nos lleva a nuestro objetivo, el vector _mu_star. Esto finalmente registra las previsiones sobre el período de escala de longitud de entrada basado en los datos anteriores que, cuyo tamaño se define por el parámetro de entrada m_past en la clase de señal personalizada. Así, el número de medias proyectadas está determinado por la escala de longitud a la que nos referimos como m_next en la clase y debido a que los vectores en MQL5 no están ordenados como series (al copiar y tratar con índices), el índice más alto de este vector de previsión se proyecta para que ocurra en último lugar mientras que el índice cero está destinado a ocurrir de forma inminente. Esto implica que, además de estimar qué valores se van a producir a continuación en la serie, podemos proyectar también la tendencia que va a seguir, en función del tamaño del parámetro de escala de longitud. Estos valores proyectados también se denominan puntos de prueba.

Una vez que tenemos medias indicativas, el proceso GP también proporciona un sentido de incertidumbre en torno a estos valores a través de la matriz _sigma_star. Lo que sí captura es la covarianza entre diferentes predicciones en distintos puntos del futuro o entre los puntos de prueba. Dado que estamos haciendo un número específico de predicciones, una para cada punto de prueba, solo nos interesan los valores diagonales de esta matriz. No nos interesa la covarianza entre predicciones. La fórmula para esta matriz viene dada por:

Donde:

• k ss es la matriz de covarianza de los nuevos puntos de datos descrita anteriormente como _k_ss.
• k s es la matriz de covarianza entre los nuevos puntos de datos y los datos de entrenamiento, también como ya se ha mencionado anteriormente como _k_s.
• K es la matriz de covarianza de los datos de entrenamiento, la primera matriz que definimos.

A partir de nuestra ecuación anterior, la matriz _v se indica como el producto entre _k_s y la inversa K^-1. Estamos probando para un 95% de confianza, y gracias a las tablas de distribución normal esto significa que para cada punto de prueba el valor del límite superior es la media del pronóstico más 1,96 veces el valor de varianza respectivo en la matriz. Por el contrario, el valor del límite inferior es la media predicha menos 1,96 veces el valor de la varianza de nuestra matriz _sigma_star . Esta varianza ayuda a cuantificar nuestra confianza en las predicciones medias con, y esto es importante, valores mayores que indican una mayor incertidumbre. Por tanto, cuanto más amplio sea el intervalo de confianza (desde el valor del límite superior hasta el valor del límite inferior), menor será la confianza.

Como nota al margen, pero no por ello menos importante, los cálculos del kernel de GP implican encontrar la inversión de la matriz y, como ya se ha mencionado anteriormente, el lector puede personalizarlo aún más considerando enfoques como la descomposición de Cholesky para minimizar los errores y los NaN. Además de esto, una técnica de normalización común que se aplica a la matriz _k desde el principio del proceso del núcleo GP, es la adición de un pequeño valor distinto de cero a través de su diagonal con el fin de evitar o prevenir que los valores negativos aparezcan en la matriz _sigma_star . Recordemos que esta matriz tiene valores de desviación estándar al cuadrado o los valores de varianza, por lo tanto, todos sus valores deben ser positivos. Y, por extraño que parezca, la omisión de esta pequeña adición en la diagonal de la matriz _k puede hacer que esta matriz tenga valores negativos. Así que es un paso importante, y se indica en el listado de la función get output anterior.

Así pues, nuestras previsiones nos dan dos cosas: la previsión y la "confianza" que debemos tener en ella. Para este artículo, como puede verse a continuación, estamos realizando pruebas basándonos únicamente en la proyección bruta sin tener en cuenta los niveles de confianza como implica la matriz _sigma_star . En muchos sentidos, esto supone una enorme infrarrepresentación de los núcleos de GP, por lo que, ¿cómo podríamos tener en cuenta la confianza implícita de una previsión en nuestra señal personalizada? Hay una variedad de maneras en que esto se puede lograr, pero incluso antes de que estos se consideran, una solución rápida sería por lo general fuera de la clase de señal personalizada mediante el uso de la magnitud de la confianza para guiar el tamaño de la posición.

Esto implicaría que, además de tener un núcleo GP en una clase de señal personalizada, también tendríamos otro núcleo GP en una clase de gestión monetaria personalizada. Y en esta situación, tanto la clase de señal como las clases de gestión de dinero tendrían que utilizar conjuntos de datos de entrada y varianzas similares, así como parámetros de escala de longitud. Sin embargo, dentro de la clase de señal personalizada, una incorporación fácil sería crear un vector de varianzas que copie la diagonal de la matriz _sigma_star, normalizarla con nuestra función 'SetOutput' y luego determinar el índice con el valor más bajo. Este índice se utilizaría entonces en el vector _mu_star para determinar el estado de la señal personalizada. Dado que _mu_star también se normaliza con la misma función, entonces cualquier valor por debajo de 0,5 se asignaría a cambios negativos que serían bajistas mientras que cualquier valor por encima de 0,5 sería alcista.

Otro método de utilizar la incertidumbre cuantificada de una previsión dentro de una clase de señal personalizada podría ser si tomamos la media ponderada de todas las previsiones o proyecciones a través de todos los puntos de prueba pero utilizamos el valor de varianza normalizado como peso inverso. Sería inverso, es decir, lo restamos de uno o lo invertimos añadiendo un valor pequeño al denominador. Esta inversión es importante porque, como se ha subrayado anteriormente, una varianza mayor implica más incertidumbre. Estos enfoques sobre el uso de la incertidumbre sólo se mencionan aquí, pero no se implementan en el código ni durante la ejecución de nuestras pruebas. El lector puede dar un paso más y realizar sus propias pruebas.

Preprocesamiento y normalización de datos

Los kernels GP pueden utilizarse para una gran variedad de datos de series temporales financieras. En términos generales, estos datos pueden estar en formato absoluto, como los precios absolutos, o en formato incremental, como los cambios en los precios. Para este artículo, vamos a probar el kernel GP RBF con este último. Para ello, como se puede ver en el listado 'GetOutput' anterior, comenzamos llenando el vector '_past' con la diferencia de otros dos vectores que copiaron precios de cierre de diferentes puntos, con 1 barra de diferencia.

Además, podríamos haber normalizado estos cambios de precios convirtiéndolos desde sus puntos brutos y tenerlos en un rango de -1,0 a +1,0. La función 'SetOutput' que se utiliza para la post-normalización u otro método personalizado, podría utilizarse también para este pre-procesamiento de datos. Sin embargo, para nuestras pruebas utilizamos los cambios de precios brutos en formato de datos flotantes (double) y solo aplicamos la normalización a los valores de pronóstico (lo que llamamos puntos de prueba anteriormente). Esto se realiza con la función 'SetOutput', cuyo código se detalla a continuación:

//+------------------------------------------------------------------+
//|
//+------------------------------------------------------------------+
void CSignalGauss::SetOutput(vector &Output)
{  vector _copy;
   _copy.Copy(Output);
   if(Output.HasNan() == 0 && _copy.Max() - _copy.Min() > 0.0)
   {  for (int i = 0; i < int(Output.Size()); i++)
      {  if(_copy[i] >= 0.0)
         {  Output[i] = 0.5 + (0.5 * ((_copy[i] - _copy.Min()) / (_copy.Max() - _copy.Min())));
         }
         else if(_copy[i] < 0.0)
         {  Output[i] = (0.5 * ((_copy[i] - _copy.Min()) / (_copy.Max() - _copy.Min())));
         }
      }
   }
   else
   {  Output.Fill(0.5);
   }
}

Hemos utilizado esta normalización en artículos anteriores dentro de esta serie y todo lo que estamos haciendo es reescalar los valores vectoriales proyectados para que estén en el rango de 0,0 a +1,0 con la advertencia principal de que cualquier valor menor a 0,5 habría sido negativo en la serie desnormalizada, mientras que cualquier valor superior a 0,5 habría sido positivo.

Pruebas y evaluación

Para nuestras ejecuciones de prueba en un kernel GP RBF, estamos probando el par EURUSD para el año 2023 en el marco de tiempo diario. Como suele suceder, aunque no siempre, estos ajustes se obtienen a partir de un período de optimización muy breve y no se verifican con un recorrido hacia adelante. La aplicación de nuestro Asesor Experto ensamblado por un asistente a condiciones reales del mercado requerirá una mayor diligencia independiente por parte del lector para garantizar que se realicen pruebas exhaustivas en más historial y con recorridos hacia adelante (validación cruzada). A continuación se presentan los resultados:

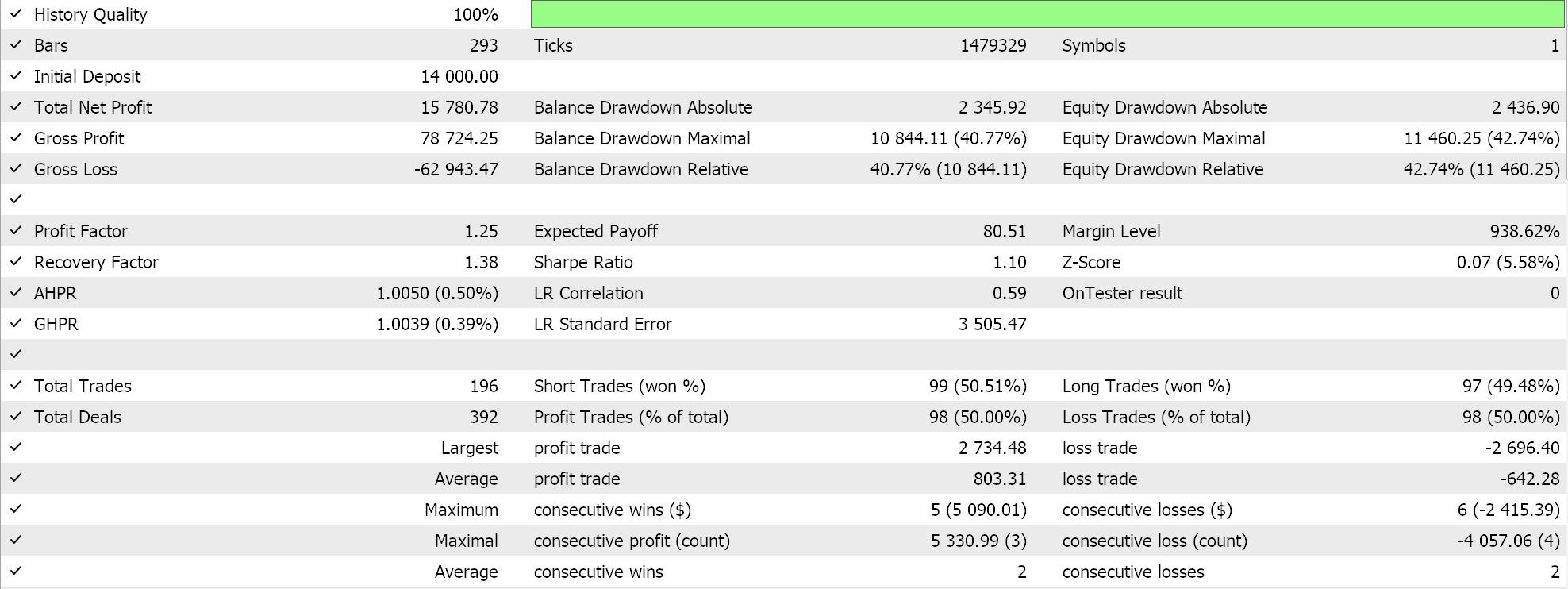
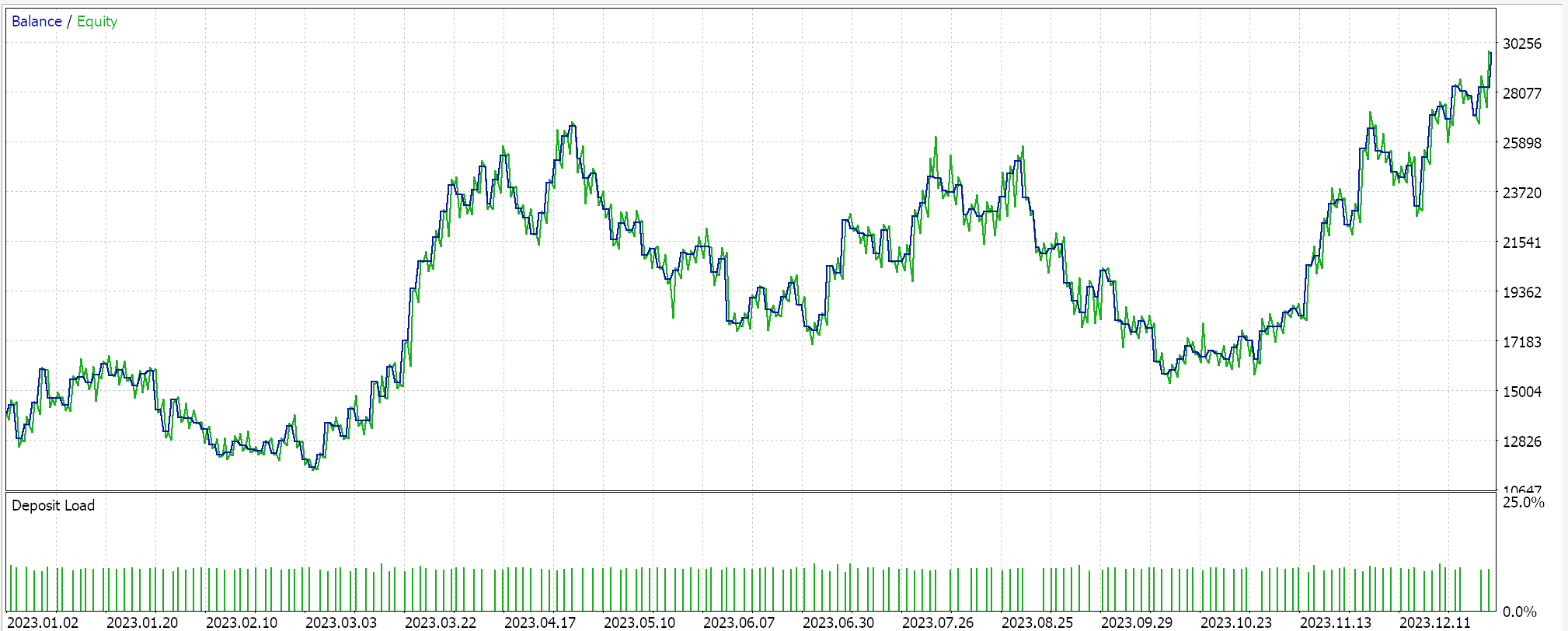
Conclusión

En conclusión, hemos analizado los núcleos del proceso gaussiano como una señal potencial para un sistema comercial. "Gaussiano" a menudo invoca el azar o la presunción de que un sistema que se utiliza supone que su entorno es aleatorio y, por lo tanto, está apostando a probabilidades de 50-50 para ganar dinero. Sin embargo, sus defensores sostienen que utilizan una muestra de datos proporcionada para realizar pronósticos durante un período predefinido con un marco probabilístico. Se argumenta que este método permite una mayor flexibilidad ya que no se hacen suposiciones sobre a qué se adhieren los datos estudiados (es decir, no es paramétrico). El único supuesto general es que los datos siguen una distribución gaussiana. Por lo tanto, se argumentó que la incertidumbre se incorpora al proceso y a los resultados porque el proceso no está centrado en el azar.

Además, a partir de nuestra codificación y prueba de los núcleos del proceso gaussiano no hemos explotado la cuantificación de la incertidumbre que, se podría decir, lo distingue de otros métodos de pronóstico. Dicho esto, el uso y la confianza en distribuciones normales plantean la pregunta de si los núcleos del proceso gaussiano están pensados para utilizarse de forma independiente o funcionan mejor cuando se combinan con una señal alternativa. El asistente de MQL5, en el que los nuevos lectores pueden encontrar orientación aquí y aquí, permite probar fácilmente más de una señal en un solo Asesor Experto ya que cada señal seleccionada se puede optimizar con una ponderación adecuada. ¿Qué señal alternativa vale la pena emparejar con estos núcleos? Bueno, la mejor respuesta a esta pregunta solo la puede proporcionar el lector a partir de sus propias pruebas, sin embargo, si tuviera que sugerirlo, deberían ser osciladores como el RSI, o el oscilador estocástico o el volumen en equilibrio e incluso algunos indicadores de sentimiento de noticias. Además, los indicadores como las medias móviles simples, los cruces de medias móviles, el canal de precios y los indicadores en general con un desfase considerable pueden no funcionar bien cuando se combinan con núcleos de procesos gaussianos.

También hemos examinado sólo un tipo de kernel, la Función de Base Radial, los otros formatos serán examinados en próximos artículos en configuraciones alteradas.