트레이딩에서 카오스 이론(2부): 더 깊이 알아보기

이전 글 요약

첫 번째 기고글에서 우리는 카오스 이론의 기본 개념과 금융 시장에의 적용에 대해 살펴봤습니다. 어트랙터, 프랙탈, 나비 효과와 같은 주요 개념을 살펴보고 시장 역학에서 이러한 개념이 어떻게 사용되는지에 대해 알아보았습니다. 여기서 우리는 금융의 맥락에서 혼란스러운 시스템의 특성과 변동성의 개념에 특히 주의 깊게 살펴보았습니다.

또한 고전적 카오스 이론과 빌 윌리엄스의 접근법을 비교하여 트레이딩에서 이러한 개념을 과학적으로 적용하는 것과 실제로 적용하는 것 사이의 차이점을 더 잘 이해할 수 있었습니다. 금융 시계열을 분석하는 도구로서의 리아푸노프 지수는 글에서 주인공으로서의 역할을 하였습니다. 우리는 카오스 이론의 이론적 의미와 MQL5 언어로 계산을 실제로 구현하는 방법을 모두 살펴보았습니다.

글의 마지막 부분은 리아푸노프 지수를 사용한 추세 반전 및 지속에 대한 통계적 분석에 대해 다뤘습니다. 그리고 1시간 주기 EURUSD 차트에서 이 분석을 실제로 어떻게 적용할 수 있는지 시연하고 얻은 결과의 해석에 대해 논의하였습니다.

글은 금융시장의 맥락에서 카오스 이론을 이해하기 위한 토대를 마련하고 트레이딩에 적용할 수 있는 실용적인 도구를 제시했습니다. 두 번째 기고글에서는 이 주제에 대해 보다 복잡한 측면과 실제 적용에 초점을 맞추어 심화해 다뤄 보겠습니다.

가장 먼저 다룰 내용은 시장 혼란의 척도인 프랙탈 차원입니다.

시장 혼란의 척도로서의 프랙탈 차원

프랙탈 차원은 카오스 이론과 금융 시장을 포함한 복잡한 시스템 분석에서 중요한 역할을 하는 개념입니다. 이는 대상이나 프로세스의 복잡성과 자기 유사성을 정량적으로 측정할 수 있는 지표로 시장 움직임의 무작위성의 정도를 평가하는 데 특히 유용합니다.

금융 시장의 맥락에서 프랙탈 차원은 가격 차트의 '들쭉날쭉함'을 측정하는 데 사용할 수 있습니다. 프랙탈 차원이 높을수록 가격 구조가 더 복잡하고 혼란스러운 반면 차원이 낮을수록 움직임이 더 부드럽고 예측 가능함을 나타낼 수 있습니다.

프랙탈 차원을 계산하는 방법에는 여러 가지가 있습니다. 가장 많이 사용되는 방법 중 하나는 박스 카운팅 메서드입니다. 이 방법은 다양한 크기의 셀 그리드로 차트를 덮고 차트를 덮는 데 필요한 셀의 수를 다양한 배율로 세는 것입니다.

이 메서드를 사용하여 프랙탈 차원 D를 계산하는 방정식은 다음과 같습니다:

D = -lim(ε→0) [log N(ε)/log(ε)]

여기서 N(ε)는 대상을 덮는 데 필요한 사이즈 ε의 셀 수입니다.

트레이더들과 애널리스트들은 프랙탈 차원을 금융 시장 분석에 적용해서 시장 움직임의 본질에 대한 추가적인 통찰력을 얻을 수 있습니다. 예를 들어:

• 시장 모드 파악하기: 프랙탈 차원에서의 변화는 추세, 횡보 또는 카오스적인 기간과 같은 다양한 시장 상태 사이의 전환을 나타낼 수 있습니다.
• 변동성 평가: 프랙탈 차원이 높다는 것은 변동성이 커진 기간이라는 의미인 경우가 많습니다.
• 예측: 시간의 경과에 따른 프랙탈 차원에서의 변화를 분석하면 향후 시장 움직임을 예측하는 데 도움이 될 수 있습니다.
• 트레이딩 전략 최적화: 시장의 프랙탈 구조를 이해하면 트레이딩 알고리즘을 개발하고 최적화하는 데 도움이 될 수 있습니다.

이제 MQL5 언어에서 프랙탈 차원을 계산하는 실제 구현에 대해 살펴보겠습니다. 우리는 MQL5에서 실시간으로 가격 차트의 프랙탈 차원을 계산하는 지표를 개발할 것입니다.

이 지표는 박스 카운팅 메서드를 사용하여 프랙탈 차원을 추정합니다.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Fractal Dimension"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpBoxSizesCount = 5;    // Number of box sizes
input int    InpMinBoxSize    = 2;    // Minimum box size
input int    InpMaxBoxSize    = 100;  // Maximum box size
input int    InpDataLength    = 1000; // Data length for calculation

double FractalDimensionBuffer[];

int OnInit()
{
   SetIndexBuffer(0, FractalDimensionBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Fractal Dimension");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      FractalDimensionBuffer[i] = CalculateFractalDimension(close, i);
   }
   
   return(rates_total);
}

double CalculateFractalDimension(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double x[]; 
   double y[];
   ArrayResize(x, InpBoxSizesCount);
   ArrayResize(y, InpBoxSizesCount);
   
   for(int i = 0; i < InpBoxSizesCount; i++)
   {
      int boxSize = (int)MathRound(MathPow(10, MathLog10(InpMinBoxSize) + (MathLog10(InpMaxBoxSize) - MathLog10(InpMinBoxSize)) * i / (InpBoxSizesCount - 1)));
      x[i] = MathLog(1.0 / boxSize);
      y[i] = MathLog(CountBoxes(price, index, boxSize));
   }
   
   double a, b;
   CalculateLinearRegression(x, y, InpBoxSizesCount, a, b);
   
   return a; // The slope of the regression line is the estimate of the fractal dimension
}

int CountBoxes(const double &price[], int index, int boxSize)
{
   double min = price[index - InpDataLength];
   double max = min;
   
   for(int i = index - InpDataLength + 1; i <= index; i++)
   {
      if(price[i] < min) min = price[i];
      if(price[i] > max) max = price[i];
   }
   
   return (int)MathCeil((max - min) / (boxSize * _Point));
}

void CalculateLinearRegression(const double &x[], const double &y[], int count, double &a, double &b)
{
   double sumX = 0, sumY = 0, sumXY = 0, sumX2 = 0;
   
   for(int i = 0; i < count; i++)
   {
      sumX += x[i];
      sumY += y[i];
      sumXY += x[i] * y[i];
      sumX2 += x[i] * x[i];
   }
   
   a = (count * sumXY - sumX * sumY) / (count * sumX2 - sumX * sumX);
   b = (sumY - a * sumX) / count;
}

이 지표는 박스 카운팅 메서드를 사용하여 가격 차트의 프랙탈 차원을 계산합니다. 프랙탈 차원은 차트의 '들쭉날쭉함' 또는 복잡성을 측정하는 척도로 시장의 혼란 정도를 평가하는 데 사용할 수 있습니다.

입력:

• InpBoxSizesCount - 계산을 위한 다양한 "box" 사이즈의 수입니다.
• InpMinBoxSize - 최소 "box" 사이즈
• InpMaxBoxSize - 최대 "box" 사이즈
• InpDataLength - 계산에 사용되는 캔들 수

지표의 작동 알고리즘:

1. 차트의 각 포인트에 대해 지표는 마지막 InpDataLength 캔들에 대한 데이터를 사용하여 프랙탈 차원을 계산합니다.
2. 박스 카운팅 메서드는 InpMinBoxSize부터 InpMaxBoxSize까지 다양한 "박스" 사이즈로 적용됩니다.
3. 차트를 덮는 데 필요한 '상자'의 수는 각 '상자' 사이즈에 대해 계산됩니다.
4. '상자' 사이즈의 로그에 대한 '상자' 수의 로그 의존성 그래프가 생성됩니다.
5. 그래프 기울기는 프랙탈 차원의 추정치인 선형 회귀 메서드를 사용하여 계산됩니다.

프랙탈 차원에서의 변화는 시장 모드에서의 변화를 의미할 수 있습니다.

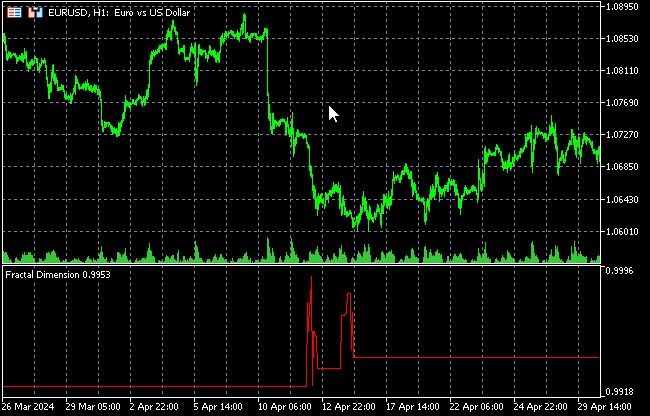
가격 변동에 숨겨진 패턴을 발견하는 반복 분석

반복 분석은 금융 시장의 역학을 연구하는 데 효과적으로 적용할 수 있는 강력한 비선형 시계열 분석 메서드입니다. 이러한 접근 방식을 통해 금융 시장을 포함한 복잡한 동적 시스템에서 반복되는 패턴을 시각화하고 정량화할 수 있습니다.

반복 분석의 주요 도구는 반복 플롯입니다. 이 다이어그램은 시간 경과에 따라 반복되는 시스템 상태를 시각적으로 표현한 것입니다. 반복 다이어그램에서 포인트(i, j)는 특정한 시각에서 i와 j의 상태가 비슷한 경우 색이 칠해집니다.

재무 시계열의 순환 다이어그램을 만들려면 다음 단계를 따르세요:

1. 위상 공간 재구성: 지연 메서드를 사용하여 1차원 가격 시계열을 다차원 위상 공간으로 변환합니다.
2. 유사성 기준값 결정하기: 두 상태가 비슷한 것으로 간주할 기준을 선택합니다.
3. 반복 행렬의 구성: 각 시점 포인트 쌍에 대해 해당 상태가 유사한지 여부를 결정합니다.
4. 시각화: 반복 행렬은 2차원 이미지로 표시되며 유사한 상태는 점으로 표시됩니다.

반복 다이어그램을 사용하면 시스템에서 다양한 유형의 역학 관계를 파악할 수 있습니다:

• 균질 영역은 정지된 기간을 나타냅니다.
• 대각선은 결정론적 역학을 나타냅니다.
• 수직 및 수평 구조는 층류 상태를 나타낼 수 있습니다.
• 구조가 없는 것은 무작위 프로세스의 특징입니다.

반복 다이어그램의 구조를 정량화하기 위해 반복 비율, 대각선의 엔트로피, 대각선의 최대 길이 등 다양한 반복 측정이 사용됩니다.

재무 시계열에 반복 분석을 적용하면 도움이 될 수 있습니다:

1. 다양한 시장 모드(추세, 보합, 혼돈 상태) 파악하기
2. 모드 변경 감지
3. 다양한 기간에서 시장의 예측 가능성 평가
4. 숨겨진 주기적 패턴 파악

거래에서 반복 분석을 실제로 구현하기 위해 MQL5 언어로 지표를 개발하여 반복 다이어그램을 구축하고 실시간으로 반복 측정값을 계산할 수 있습니다. 이러한 지표는 특히 다른 기술적 분석 방법과 결합할 경우 트레이딩 결정을 내리는 추가적인 도구로 사용될 수 있습니다.

다음 섹션에서는 이러한 지표를 구체적으로 어떻게 개발하는지 살펴보고 트레이딩 전략의 맥락에서 해당 지표를 해석하는 방법에 대해 논의하겠습니다.

MQL5의 반복 분석 지표

이 지표는 금융 시장의 역학을 연구하기 위한 반복 분석 메서드를 구현합니다. 반복의 세 가지 주요 측정값인 반복 수준, 결정론, 층류성을 계산합니다.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 3
#property indicator_plots   3
#property indicator_label1  "Recurrence Rate"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Determinism"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed
#property indicator_label3  "Laminarity"
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrGreen

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 1;     // Time delay
input int    InpThreshold          = 10;    // Threshold (in points)
input int    InpWindowSize         = 200;   // Window size

double RecurrenceRateBuffer[];
double DeterminismBuffer[];
double LaminarityBuffer[];

int minRequiredBars;

int OnInit()
{
   SetIndexBuffer(0, RecurrenceRateBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, DeterminismBuffer, INDICATOR_DATA);
   SetIndexBuffer(2, LaminarityBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Recurrence Analysis");
   
   minRequiredBars = InpWindowSize + (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   if(rates_total < minRequiredBars) return(0);
   
   int start = (prev_calculated > 0) ? MathMax(prev_calculated - 1, minRequiredBars - 1) : minRequiredBars - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      CalculateRecurrenceMeasures(close, rates_total, i, RecurrenceRateBuffer[i], DeterminismBuffer[i], LaminarityBuffer[i]);
   }
   
   return(rates_total);
}

void CalculateRecurrenceMeasures(const double &price[], int price_total, int index, double &recurrenceRate, double &determinism, double &laminarity)
{
   if(index < minRequiredBars - 1 || index >= price_total)
   {
      recurrenceRate = 0;
      determinism = 0;
      laminarity = 0;
      return;
   }

   int windowStart = index - InpWindowSize + 1;
   int matrixSize = InpWindowSize - (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   int recurrenceCount = 0;
   int diagonalLines = 0;
   int verticalLines = 0;
   
   for(int i = 0; i < matrixSize; i++)
   {
      for(int j = 0; j < matrixSize; j++)
      {
         bool isRecurrent = IsRecurrent(price, price_total, windowStart + i, windowStart + j);
         if(isRecurrent)
         {
            recurrenceCount++;
            
            // Check for diagonal lines
            if(i > 0 && j > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j - 1))
               diagonalLines++;
            
            // Check for vertical lines
            if(i > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j))
               verticalLines++;
         }
      }
   }
   
   recurrenceRate = (double)recurrenceCount / (matrixSize * matrixSize);
   determinism = (recurrenceCount > 0) ? (double)diagonalLines / recurrenceCount : 0;
   laminarity = (recurrenceCount > 0) ? (double)verticalLines / recurrenceCount : 0;
}

bool IsRecurrent(const double &price[], int price_total, int i, int j)
{
   if(i < 0 || j < 0 || i >= price_total || j >= price_total) return false;

   double distance = 0;
   for(int d = 0; d < InpEmbeddingDimension; d++)
   {
      int offset = d * InpTimeDelay;
      if(i + offset >= price_total || j + offset >= price_total) return false;
      double diff = price[i + offset] - price[j + offset];
      distance += diff * diff;
   }
   distance = MathSqrt(distance);
   
   return (distance <= InpThreshold * _Point);
}

지표의 주요 특징

지표는 가격 차트 아래에 별도의 창으로 표시되며 3개의 버퍼를 사용하여 데이터를 저장하고 표시합니다. 이 지표는 세 가지 메트릭을 계산합니다: 전반적인 반복 수준을 나타내는 반복률(파란색 선), 시스템 예측 가능성을 측정하는 결정성(빨간색 선), 시스템이 특정 상태에 머무르는 경향을 평가하는 층류성(녹색 선)이 있습니다.

지표 입력은 다음과 같습니다. 위상 공간 재구성을 위한 임베딩 차원을 정의하는 InpEmbeddingDimension(기본값 3), 재구성 중 시간 지연을 나타내는 InpTimeDelay(기본값 1), 포인트의 상태 유사성 기준값을 나타내는 InpThreshold(기본값 10), 분석 창 크기를 설정하는 InpWindowSize(기본값 200)가 있습니다.

지표의 작동 알고리즘은 1차원 시계열 가격에서 위상 공간을 재구성하는 지연 방식을 기반으로 합니다. 분석 창의 각 포인트에서 다른 포인트와 관련한 '반복'이 계산됩니다. 그런 다음 이렇게 얻은 반복 구조를 기반으로 세 가지 측정값이 계산됩니다: 전체 포인트 수에서 반복 포인트가 차지하는 비율을 결정하는 반복률, 대각선을 이루는 반복 포인트의 비율을 보여주는 결정성, 수직선을 이루는 반복 포인트의 비율을 추정하는 층류성입니다.

변동성 예측에 타켄스(Takens)의 임베딩 정리 적용하기

타켄스의 임베딩 정리는 금융 데이터를 포함한 시계열 분석에서 중요한 의미를 가지는 동적 시스템 이론의 기본적인 결과입니다. 이 정리는 시간 지연 방법을 사용하여 단 하나의 변수를 관측하는 것으로부터 동적 시스템이 재구성될 수 있다는 것을 나타냅니다.

금융 시장의 맥락에서 타켄스의 정리를 사용하면 가격이나 수익률의 1차원 시계열에서 다차원 위상 공간을 재구성할 수 있는데 이는 금융 시장의 주요 특징인 변동성을 분석할 때 특히 유용합니다.

변동성 예측에 타켄스의 정리를 적용하는 기본 단계는 다음과 같습니다:

1. 위상 공간 재구성:
   • 임베딩 차원 선택(m)
   • 시간 지연(τ) 선택
   • 원본 시계열에서 m차원 벡터 만들기
2. 재구성된 공간 분석:
   • 각 포인트에서 최인접 이웃 찾기
   • 로컬 포인트 밀도 추정
3. 변동성 예측:
   • 로컬 밀도 정보를 사용하여 미래 변동성 예측하기

이러한 단계를 더 자세히 살펴보겠습니다.

위상 공간 재구성:

종가 {p(t)}의 시계열이 있다고 가정해 보겠습니다. 다음과 같이 M차원 벡터를 생성합니다:

x(t) = [p(t), p(t+τ), p(t+2τ), ..., p(t+(m-1)τ)]

여기서 m은 임베딩 차원이고 τ는 시간 지연입니다.

성공적인 재구성을 위해서는 m과 τ의 올바른 값을 선택하는 것이 중요합니다. 일반적으로 τ는 상호 정보 또는 자동 상관 함수 메서드를 사용하여 선택되며 m은 거짓 최인접 이웃 메서드를 사용하여 선택됩니다.

재구성된 공간 분석:

위상 공간을 재구성한 후 시스템 어트랙터의 구조를 분석할 수 있습니다. 변동성 예측의 경우 위상 공간에서 포인트의 국부적 밀도에 대한 정보가 특히 중요합니다.

각 포인트 x(t)에 대해 가장 최인접 이웃 k 개를 구하고(일반적으로 k는 5~20 범위에서 선택됨) 이 이웃과의 평균 거리를 계산합니다. 이 거리는 로컬 밀도, 즉 로컬 변동성을 측정하는 척도로 사용됩니다.

변동성 예측

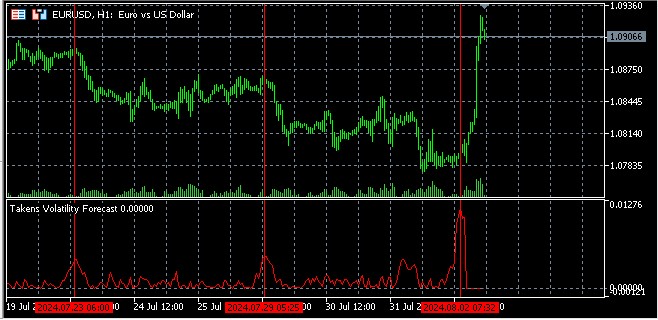
재구성된 위상 공간을 사용하여 변동성을 예측하는 기본 개념은 이 공간에 가까운 포인트들이 가까운 미래에 비슷한 움직임을 보일 가능성이 높다는 것입니다.

t+h 시점의 변동성을 예측합니다:

• 재구성된 공간에서 현재 x(t) 포인트의 최인접 이웃 k 개를 구합니다.
• h 단계 앞서 이러한 이웃에 대한 실제 변동성을 계산합니다.
• 이러한 변동성의 평균을 예측값으로 사용합니다.

이는 수학적으로는 다음과 같이 표현될 수 있습니다:

σ̂(t+h) = (1/k) Σ σ(ti+h), 여기서 ti는 x(t)의 가장 가까운 k개 이웃의 인덱스입니다.

이러한 접근 방식의 장점:

• 비선형적인 시장 역학을 고려합니다.
• 수익률 분포에 대한 가정이 필요하지 않습니다.
• 변동성의 복잡한 패턴을 포착할 수 있습니다.

단점:

• 매개변수의(m, τ, k) 선택에 민감합니다.
• 대용량 데이터의 경우 계산 비용이 많이 들 수 있습니다.

구현

이 변동성 예측 메서드를 구현할 MQL5 지표를 만들어 보겠습니다:

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Predicted Volatility"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double PredictedVolatilityBuffer[];

int OnInit()
{
   SetIndexBuffer(0, PredictedVolatilityBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Takens Volatility Forecast");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedVolatilityBuffer[i] = PredictVolatility(close, i);
      }
   }
   
   return(rates_total);
}

double PredictVolatility(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }
   
   double distances[];
   ArrayResize(distances, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double sum = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         sum += diff * diff;
      }
      distances[i] = sqrt(sum);
   }
   
   int sortedIndices[];
   ArrayCopy(sortedIndices, distances);
   ArraySort(sortedIndices);
   
   double sumVolatility = 0;
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - sortedIndices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double futureReturn = (price[neighborIndex + InpForecastHorizon] - price[neighborIndex]) / price[neighborIndex];
      sumVolatility += MathAbs(futureReturn);
   }
   
   return sumVolatility / InpNeighbors;
}

시간 지연 및 임베딩 차원을 결정하는 방법

타켄스의 정리를 사용하여 위상 공간을 재구성할 때는 시간 지연(τ)과 임베딩 차원(m)이라는 두 가지 주요 파라미터를 올바르게 선택하는 것이 중요합니다. 이러한 매개변수를 잘못 선택하면 재구성이 잘못되어 결과적으로 잘못된 결론에 도달할 수 있습니다. 이러한 매개 변수를 결정하는 두 가지 주요 메서드에 대해 알아 보겠습니다.

시간 지연을 결정하는 자동 상관 함수(ACF) 메서드

이 메서드는 시간 지연 τ를 선택하는 아이디어를 기반으로 하며 이 때 자동 상관 함수가 먼저 0을 넘거나 특정 낮은 값(예: 초기 값의 1/e)에 도달합니다. 이를 통해 시계열의 연속적인 값이 서로 충분히 독립적이 되는 지연을 선택할 수 있습니다.

MQL5에서 ACF 메서드의 구현은 다음과 같습니다:

int FindOptimalLagACF(const double &price[], int maxLag, double threshold = 0.1)
{
   int size = ArraySize(price);
   if(size <= maxLag) return 1;
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += price[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(price[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (price[i] - mean) * (price[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

이 구현에서는 먼저 시계열의 평균과 분산을 계산합니다. 그런 다음 1에서 최대 지연까지 각 지연에 대해 자동 상관 관계 함수의 값을 계산합니다. ACF 값이 지정된 기준값(기본값 0.1)보다 작아지면 이 지연을 최적의 시간 지연으로 반환합니다.

ACF 메서드에는 장단점이 있습니다. 한편으로는 구현하기 쉽고 직관적입니다. 반면에 데이터의 비선형 종속성을 고려하지 않기 때문에 비선형적인 동작을 보이는 재무 시계열을 분석할 때 큰 단점이 될 수 있습니다.

시간 지연을 결정하는 상호 정보(MI) 메서드

이 메서드는 정보 이론을 기반으로 하며 데이터에서 비선형 종속성을 고려할 수 있습니다. 상호 정보 함수의 첫 번째 국부 최소값에 해당하는 지연 τ를 선택하는 것이 아이디어입니다.

MQL5에서 상호 정보 메서드의 구현은 다음과 같습니다:

double CalculateMutualInformation(const double &price[], int lag, int bins = 20)
{
   int size = ArraySize(price);
   if(size <= lag) return 0;
   
   double minPrice = price[ArrayMinimum(price)];
   double maxPrice = price[ArrayMaximum(price)];
   double binSize = (maxPrice - minPrice) / bins;
   
   int histogram[];
   ArrayResize(histogram, bins * bins);
   ArrayInitialize(histogram, 0);
   
   int totalPoints = 0;
   
   for(int i = 0; i < size - lag; i++)
   {
      int bin1 = (int)((price[i] - minPrice) / binSize);
      int bin2 = (int)((price[i + lag] - minPrice) / binSize);
      if(bin1 >= 0 && bin1 < bins && bin2 >= 0 && bin2 < bins)
      {
         histogram[bin1 * bins + bin2]++;
         totalPoints++;
      }
   }
   
   double mutualInfo = 0;
   for(int i = 0; i < bins; i++)
   {
      for(int j = 0; j < bins; j++)
      {
         if(histogram[i * bins + j] > 0)
         {
            double pxy = (double)histogram[i * bins + j] / totalPoints;
            double px = 0, py = 0;
            for(int k = 0; k < bins; k++)
            {
               px += (double)histogram[i * bins + k] / totalPoints;
               py += (double)histogram[k * bins + j] / totalPoints;
            }
            mutualInfo += pxy * MathLog(pxy / (px * py));
         }
      }
   }
   
   return mutualInfo;
}

int FindOptimalLagMI(const double &price[], int maxLag)
{
   double minMI = DBL_MAX;
   int optimalLag = 1;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double mi = CalculateMutualInformation(price, lag);
      if(mi < minMI)
      {
         minMI = mi;
         optimalLag = lag;
      }
      else if(mi > minMI)
      {
         break;
      }
   }
   
   return optimalLag;
}

이 구현에서는 먼저 주어진 지연에 대해 원본 시리즈와 시프트 된 버전 간의 상호 정보를 계산하는 CalculateMutualInformation 함수를 정의합니다. 그런 다음 FindOptimalLagMI 함수에서 서로 다른 지연 값을 반복해서 상호 정보의 첫 번째 로컬 최소값을 찾습니다.

상호 정보 메서드는 데이터의 비선형 종속성을 고려할 수 있다는 점에서 ACF 방식에 비해 장점이 있습니다. 따라서 복잡하고 비선형적인 동작을 보이는 재무 시계열을 분석하는 데 더 적합합니다. 하지만 이 메서드는 구현하기가 더 복잡하고 더 많은 계산이 필요합니다.

ACF와 MI 메서드 중에 무엇을 선택할지는 특정 작업과 분석 대상 데이터의 특성에 따라 달라집니다. 경우에 따라 두 가지 메서드를 모두 사용하고 결과를 비교하는 것이 유용할 수 있습니다. 특히 재무 시계열의 경우 시간이 지남에 따라 최적의 시간 지연이 달라질 수 있습니다. 그러므로 이 매개변수는 주기적으로 다시 계산하는 것이 좋습니다.

최적의 임베딩 차원을 결정하기 위한 거짓 최인접 이웃 알고리즘

최적의 시간 지연이 결정되면 위상 공간 재구성에서 중요한 단계는 적절한 임베딩 차원을 선택하는 것입니다. 이를 위해 가장 많이 사용되는 방법 중 하나는 거짓 가장 가까운 이웃(FNN; False Nearest Neighbors) 알고리즘입니다.

FNN 알고리즘의 아이디어는 위상 공간에서 어트랙터의 기하학적 구조를 올바르게 재현할 수 있는 최소 임베딩 차원을 찾는 것입니다. 이 알고리즘은 올바르게 재구성된 위상 공간에서 고차원 공간으로 이동할 때 가까운 포인트가 가깝게 유지되어야 한다는 가정을 기반으로 합니다.

이제 MQL5 언어에서 FNN 알고리즘을 구현하는 방법을 살펴보겠습니다:

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

int FindOptimalEmbeddingDimension(const double &price[], int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = ArraySize(price);
   int minRequiredSize = (maxDim - 1) * delay + 1;
   if(size < minRequiredSize) return 1;
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = price[i - k * delay] - price[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(price, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

IsFalseNeighbor 함수는 두 포인트가 거짓 이웃인지 여부를 결정합니다. 현재 차원과 더 큰 차원에 있는 포인트 사이의 거리가 1보다 큰 거리를 계산합니다. 거리의 상대적 변화가 주어진 기준값을 초과하면 해당 포인트는 거짓 이웃으로 간주됩니다.

주 함수 FindOptimalEmbeddingDimension은 1에서 maxDim까지 차원을 반복합니다. 이제 각 차원에 대해 시계열의 모든 포인트를 거쳐갑니다. 각 포인트에 대해 현재 차원에서 가장 가까운 이웃을 찾습니다. 그런 다음 찾은 이웃이 IsFalseNeighbor 함수를 사용하여 거짓인지 확인합니다. 총 이웃 수와 거짓 이웃 수를 계산합니다. 그런 다음 거짓 이웃의 비율을 계산합니다. 거짓 이웃의 비율이 지정된 허용 오차 기준값보다 작으면 현재 차원이 최적이라고 간주하고 반환합니다.

이 알고리즘에서 주요한 변수는 다음과 같습니다. delay - 이전에 ACF 또는 MI 메서드로 결정한 시간 지연. maxDim - 고려할 최대 임베딩 차원. threshold - 거짓 이웃을 감지하기 위한 기준값. tolerance - 거짓 이웃의 비율에 대한 허용 오차 기준값입니다. 이러한 매개변수의 선택은 결과에 큰 영향을 미칠 수 있으므로 다양한 값으로 실험하고 분석 대상의 데이터 특성을 고려해야 합니다.

FNN 알고리즘에는 여러 가지 장점이 있습니다. 위상 공간에서 데이터의 기하학적 구조를 고려합니다. 이 메서드는 데이터의 노이즈에 매우 강력합니다. 연구 중인 시스템의 특성에 대한 사전 가정이 필요하지 않습니다.

MQL5에서 카오스 이론에 기반한 예측 메서드 구현하기

위상 공간 재구성을 위한 최적의 파라미터를 결정하면 카오스 이론 기반의 예측 메서드의 구현을 시작할 수 있습니다. 이 메서드는 위상 공간에서 가까운 상태는 가까운 미래에 비슷한 진화를 보일 것이라는 아이디어에 기반합니다.

이 메서드의 기본 개념은 다음과 같습니다: 현재 상태에 가장 가까운 과거의 시스템 상태를 찾고 향후 행동을 기반으로 현재 상태를 예측합니다. 이러한 접근 방식을 아날로그 또는 최근접 이웃 메서드라고 합니다.

MetaTrader 5의 지표로 이 메서드를 구현하는 방법에 대해 살펴 보겠습니다. 지표는 다음 단계를 수행합니다:

1. 시간 지연 메서드를 사용한 위상 공간 재구성.
2. 시스템의 현재 상태에 대한 가장 가까운 이웃 k 개를 찾습니다.
3. 발견된 이웃의 행동을 기반으로 미래 가치를 예측합니다.

다음은 이 메서드를 구현하는 지표의 코드입니다:

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_chart_window
#property indicator_buffers 2
#property indicator_plots   2
#property indicator_label1  "Actual"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Predicted"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double ActualBuffer[];
double PredictedBuffer[];

int OnInit()
{
   SetIndexBuffer(0, ActualBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, PredictedBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, _Digits);
   IndicatorSetString(INDICATOR_SHORTNAME, "Chaos Theory Predictor");
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      ActualBuffer[i] = close[i];
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedBuffer[i] = PredictPrice(close, i);
      }
   }
   
   return(rates_total);
}

double PredictPrice(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;

   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }

   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);

   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }

   // Custom sort function for sorting distances and indices together
   SortDistancesWithIndices(distances, indices, dataSize);

   double prediction = 0;
   double weightSum = 0;

   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - indices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double weight = 1.0 / (distances[i] + 0.0001);  // Avoid division by zero
      prediction += weight * price[neighborIndex + InpForecastHorizon];
      weightSum += weight;
   }

   return prediction / weightSum;
}

void SortDistancesWithIndices(double &distances[], int &indices[], int size)
{
   for(int i = 0; i < size - 1; i++)
   {
      for(int j = i + 1; j < size; j++)
      {
         if(distances[i] > distances[j])
         {
            double tempDist = distances[i];
            distances[i] = distances[j];
            distances[j] = tempDist;

            int tempIndex = indices[i];
            indices[i] = indices[j];
            indices[j] = tempIndex;
         }
      }
   }
}

지표는 위상 공간을 재구성하고 현재 상태에서 가장 가까운 이웃을 찾은 다음 미래 값을 사용하여 예측을 수행합니다. 실제 값과 예측 값을 모두 차트에 표시하여 예측의 품질을 시각적으로 평가할 수 있습니다.

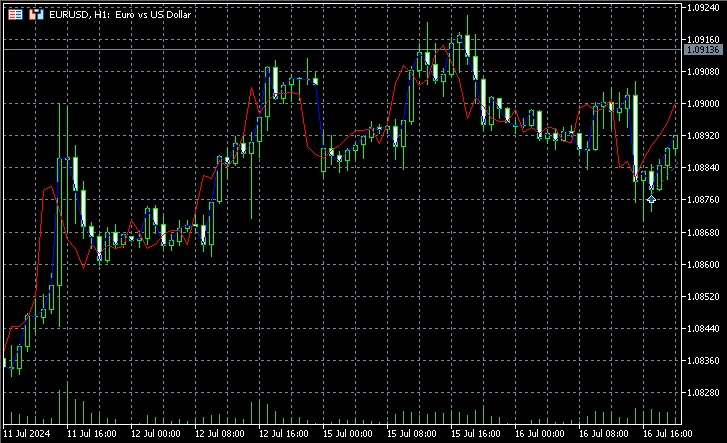
구현에서 중요한 부분은 각 이웃의 가중치가 현재 상태와의 거리에 반비례하는 가중 평균을 예측에 사용한다는 점입니다. 이를 통해 가까운 이웃이 더 정확한 예측을 할 가능성이 높다는 점을 고려할 수 있습니다. 스크린샷을 보면 지표는 가격 움직임의 방향을 여러 바에서 미리 예측합니다.

컨셉 EA 만들기

이제 우리는 가장 흥미로운 부분에 도달했습니다. 아래는 카오스 이론에 기반한 완전 자동화 작업 코드입니다:

#property copyright "Copyright 2024, Author"
#property link      "https://www.example.com"
#property version   "1.00"
#property strict

#include <Arrays\ArrayObj.mqh>
#include <Trade\Trade.mqh>
CTrade Trade;
input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period
input double InpLotSize            = 0.1;   // Lot size

ulong g_ticket = 0;
datetime g_last_bar_time = 0;
double optimalTimeDelay;
double optimalEmbeddingDimension;
int OnInit()
{
   return(INIT_SUCCEEDED);
}

void OnDeinit(const int reason)
{
}

void OnTick()
{  
   OptimizeParameters();
   
   if(g_last_bar_time == iTime(_Symbol, PERIOD_CURRENT, 0)) return;
   g_last_bar_time = iTime(_Symbol, PERIOD_CURRENT, 0);
   
   double prediction = PredictPrice(iClose(_Symbol, PERIOD_CURRENT, 0), 0);
   Comment(prediction);
   
   if(prediction > iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close selling
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close SELL position: ", GetLastError());
         }
      }
      
      // Open buy
      double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
      ulong ticket = Trade.Buy(InpLotSize, _Symbol, ask, 0, 0, "ChaosBuy");
      if(ticket == 0)
         Print("Failed to open BUY position: ", GetLastError());
   }
   else if(prediction < iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close buying
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close BUY position: ", GetLastError());
         }
      }
      
      // Open sell
      double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
      ulong ticket = Trade.Sell(InpLotSize, _Symbol, bid, 0, 0, "ChaosSell");
      if(ticket == 0)
         Print("Failed to open SELL position: ", GetLastError());
   }
}

double PredictPrice(double price, int index)
{
   int vectorSize = optimalEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      currentVector[i] = iClose(_Symbol, PERIOD_CURRENT, index + i * optimalTimeDelay);
   }
   
   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         double diff = currentVector[j] - iClose(_Symbol, PERIOD_CURRENT, index + i + j * optimalTimeDelay);
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }
   
   // Use SortDoubleArray to sort by 'distances' array values
   SortDoubleArray(distances, indices);
   
   double prediction = 0;
   double weightSum = 0;
   
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index + indices[i];
      double weight = 1.0 / (distances[i] + 0.0001);
      prediction += weight * iClose(_Symbol, PERIOD_CURRENT, neighborIndex + InpForecastHorizon);
      weightSum += weight;
   }
   
   return prediction / weightSum;
}

void SortDoubleArray(double &distances[], int &indices[])
{
    int size = ArraySize(distances);
    for(int i = 0; i < size - 1; i++)
    {
        for(int j = i + 1; j < size; j++)
        {
            if(distances[i] > distances[j])
            {
                // Swap distances
                double tempDist = distances[i];
                distances[i] = distances[j];
                distances[j] = tempDist;
                
                // Swap corresponding indices
                int tempIndex = indices[i];
                indices[i] = indices[j];
                indices[j] = tempIndex;
            }
        }
    }
}

int FindOptimalLagACF(int maxLag, double threshold = 0.1)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += series[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(series[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (series[i] - mean) * (series[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

int FindOptimalEmbeddingDimension(int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = series[i - k * delay] - series[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(series, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

void OptimizeParameters()
{
   double optimalTimeDelay = FindOptimalLagACF(50);
   double optimalEmbeddingDimension = FindOptimalEmbeddingDimension(optimalTimeDelay, 10);
   Print("Optimal Time Delay: ", optimalTimeDelay);
   Print("Optimal Embedding Dimension: ", optimalEmbeddingDimension);
}

이 코드는 카오스 이론의 개념을 사용하여 금융 시장의 가격을 예측하는 MetaTrader 5용 EA입니다. EA는 재구성된 위상 공간에서 최근접 이웃 메서드를 기반으로 예측 방법을 구현합니다.

EA에는 다음과 같은 입력이 있습니다:

• InpEmbeddingDimension - 위상 공간 재구성을 위한 임베딩 차원(기본값 - 3)
• InpTimeDelay - 재구성을 위한 시간 지연(기본값 - 5)
• InpNeighbors - 예측을 위한 최근접 이웃의 수(기본값 - 10)
• InpForecastHorizon - 예측 수평선(기본값 - 10)
• InpLookback - 분석용 룩백 기간(기본값 - 1000)
• InpLotSize - 랏 크기(기본값 - 0.1)

EA는 다음과 같이 작동합니다:

1. 각각의 새로운 바에서 각각 자동 상관 함수(ACF) 메서드와 거짓 최인접 이웃(FNN) 알고리즘을 사용하여 최적 시간 지연 및 최적 임베딩 차원 매개 변수를 최적화합니다.
2. 그런 다음 최근접 이웃 메서드를 사용하여 시스템의 현재 상태를 기반으로 가격을 예측합니다.
3. 가격 예측이 현재 가격보다 높으면 EA는 모든 매도 포지션을 청산하고 새로운 매수 포지션을 오픈합니다. 가격 예측이 현재 가격보다 낮으면 EA는 모든 오픈 매수 포지션을 청산하고 새 매도 포지션을 오픈합니다.

EA는 PredictPrice 함수를 사용하는데 다음과 같습니다:

• 최적의 임베딩 차원과 시간 지연을 사용하여 위상 공간을 재구성합니다.
• 시스템의 현재 상태와 룩백 기간의 모든 상태 사이의 거리를 구합니다.
• 거리가 먼 순서로 상태를 정렬합니다.
• 각 이웃의 가중치는 현재 상태와의 거리에 반비례하여 정률적으로 배분된 InpNeighbors 이웃에 대한 미래 가격의 가중치 평균을 계산합니다.
• 가중 평균을 가격 예측으로 반환합니다.

또한 EA에는 각각 최적TimeDelay 및 optimalEmbeddingDimension 파라미터를 최적화하는 데 사용되는 FindOptimalLagACF 및 FindOptimalEmbeddingDimension 함수도 포함되어 있습니다.

전반적으로 EA는 카오스 이론의 개념을 사용하여 금융 시장의 가격을 예측하는 혁신적인 접근 방식을 제공하며 트레이더가 더 많은 정보를 바탕으로 의사결정을 내리고 잠재적으로 투자 수익을 높이는 데에 도움을 줍니다.

자동 최적화를 통한 테스트

몇 가지 심볼에서의 경우를 살펴보겠습니다. 첫 번째 통화쌍인 EURUSD의 기간은 2016년 1월 1일부터입니다:

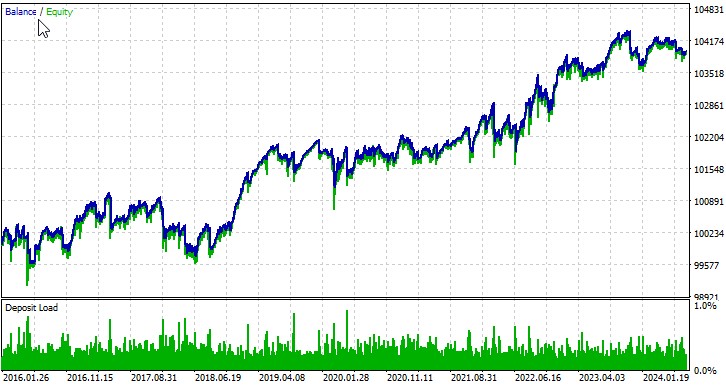
두 번째 쌍, AUD:

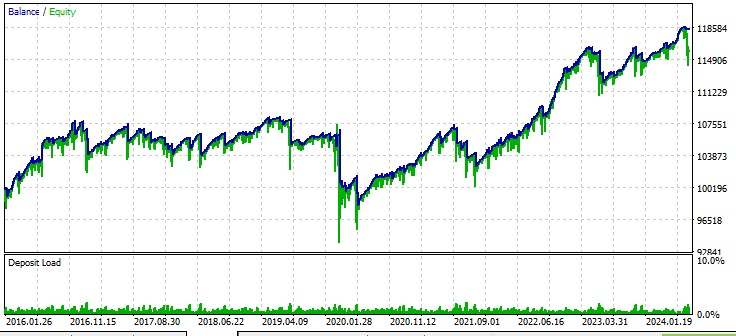
세 번째 쌍, GBPUSD:

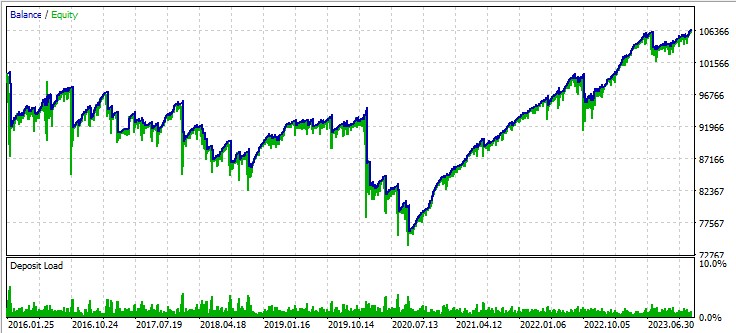
다음 단계

카오스 이론 기반인 우리의 EA를 더욱 심화하여 개발하는 데에는 심층적인 테스트와 최적화가 필요합니다. 다양한 시장 상황에 대응하는 EA의 효율성을 더 잘 이해하려면 다양한 기간과 금융 상품에 걸쳐 대규모 테스트가 필요합니다. 머신 러닝을 사용하면 EA 매개변수를 최적화하여 변화하는 시장 현실에 대한 적응력을 높일 수 있습니다.

또한 리스크 관리 시스템을 개선하는 데 특히 주의를 기울여야 합니다. 현재 시장 변동성과 혼란스러운 변동성 예측을 고려한 동적 포지션 크기 관리를 구현하면 전략을 크게 향상시킬 수 있습니다.

결론

이 글에서는 카오스 이론을 금융 시장 분석과 예측에 적용하는 방법을 살펴봤습니다. 위상 공간 재구성, 최적의 임베딩 차원 및 시간 지연 결정, 최근접 이웃 예측 방법과 같은 핵심 개념에 대해 알아보았습니다.

우리가 개발한 EA는 알고리즘 트레이딩에서 카오스 이론을 사용할 수 있다는 잠재력을 보여줍니다. 다양한 통화쌍에 대한 테스트 결과 이 전략은 상품에 따라 성공 정도는 다르지만 수익을 창출할 수 있는 것으로 나타났습니다.

그러나 카오스 이론을 금융에 적용하는 데에는 여러 가지 어려움이 따른다는 점에 유의해야 합니다. 금융 시장은 많은 요인에 영향을 받는 매우 복잡한 시스템이며 그 중 상당수는 모델에서 고려하기 어렵거나 심지어 불가능합니다. 또한 혼란스러운 시스템의 특성상 장기적인 예측은 근본적으로 불가능하며 이는 진지한 연구자들이 당연한 것으로 간주하는 것 중 하나입니다.

결론적으로 카오스 이론이 시장 예측의 거룩한 성배는 아니지만 금융 분석 및 알고리즘 트레이딩 분야에서 향후 연구 및 개발의 유망한 방향성을 제시합니다. 카오스 이론 방법을 머신러닝 및 빅데이터 분석과 같은 다른 접근 방식과 결합하면 새로운 가능성을 열 수 있다는 것은 분명합니다.