La teoría del caos en el trading (Parte 1): Introducción, aplicación a los mercados financieros e indicador de Lyapunov

Introducción a la teoría del caos y su relación con los mercados financieros

¿Qué es la teoría del caos y cómo podemos aplicarla a los mercados financieros? Hoy nos ocuparemos de esta cuestión.

Nuestra intención es escribir una serie de artículos que respondan a las preguntas: ¿qué es la teoría del caos, en qué se diferencia el concepto de caos en el mercado de Bill Williams de la teoría clásica fundamentada científicamente? ¿Cómo describe la teoría el mercado? ¿Cómo podemos utilizarla y en qué ámbitos del trading? 

Nos encargaremos tanto de desglosar el marco teórico como de crear una serie de herramientas que puedan ayudar a los tráders a la hora de negociar.

Conceptos básicos de la teoría del caos: atractores, fractales y efecto mariposa

La teoría del caos es un interesante campo de las matemáticas y la física que nos ayuda a comprender mejor sistemas complejos como los mercados financieros. Vamos a desglosar las tres ideas principales de esta teoría:

1. Atractores: Son como imanes para los estados de un sistema: el sistema gravita hacia ellos a lo largo del tiempo. En los mercados financieros, pueden determinarse precios o patrones recurrentes a los que el mercado vuelve una y otra vez. Resultan especialmente interesantes los atractores extraños que podemos encontrar en los sistemas caóticos. Estos parecen complejos y pueden revelar un orden oculto en el comportamiento aleatorio del mercado.

2. Fractales: Son formas geométricas que tienen el mismo aspecto con cualquier nivel de aumento. En los mercados financieros, los fractales pueden observarse en los gráficos de precio: el mismo patrón puede verse tanto en periodos cortos como largos. Gracias a ello, podemos aplicar los mismos métodos de análisis a distintos intervalos temporales, lo que ayuda a analizar las variaciones de precios y evaluar los riesgos.

3. Efecto mariposa: Este efecto demuestra que incluso los cambios en principio más pequeños pueden tener consecuencias posteriores grandes e inesperadas. En el mundo de las finanzas, esto significa que pequeños cambios en los datos o en el modelo pueden suponer una gran diferencia en las predicciones. Esto dificulta el pronóstico a largo plazo en los mercados financieros y subraya la importancia de actualizar y adaptar constantemente nuestros modelos a las nuevas condiciones.

Comprender estas ideas ayuda a los analistas y tráders a observar los mercados de una forma nueva, descubrir pautas ocultas y posibles puntos de entrada o salida. La teoría del caos abre nuevas vías de análisis y predicción que van más allá de los modelos convencionales.

Sistemas caóticos en el contexto de los mercados financieros

Los mercados financieros poseen características de los sistemas caóticos, lo cual resulta importante a la hora de analizarlos y predecirlos.

• No linealidad: Pequeños cambios provocan fluctuaciones no proporcionales.
• Sensibilidad a las condiciones iniciales: Pequeños eventos pueden provocar grandes movimientos.
• Autoorganización: Formación de tendencias y patrones sin control externo.
• Estructura fractal: Los gráficos de precio muestran propiedades fractales.
• Previsibilidad limitada: La precisión de las previsiones disminuye a medida que aumenta el horizonte.
• Atractores extraños: Fluctuaciones en torno a determinados niveles o estados.
• Transiciones entre estados: Transiciones repentinas de la estabilidad a la volatilidad.

Comprender esto ayudará a desarrollar sofisticados algoritmos de análisis, gestión de riesgos y negociación.

Volatilidad en el trading

La volatilidad es un concepto crucial en el trading y las finanzas relacionado con la teoría del caos. Esta mide cuánto varía el precio de un activo en un tiempo determinado. En el trading, la volatilidad nos ayuda a evaluar el riesgo, valorar las opciones y desarrollar estrategias de negociación.

Los mercados financieros suelen comportarse como sistemas caóticos, y pueden reaccionar inesperadamente a pequeños cambios, de forma similar al efecto mariposa. Los mercados también pueden autoorganizarse, creando tendencias y patrones sin intervención externa, mientras que los gráficos de precio muestran similitudes en diferentes escalas temporales, lo que se denomina propiedades fractales.

La teoría del caos ofrece herramientas únicas para el análisis de la volatilidad, como la reconstrucción del espacio de fases y el exponente de Lyapunov, que ayudan a encontrar patrones ocultos y evaluar la previsibilidad. Estos modelos caóticos pueden complementar los métodos tradicionales, como los modelos GARCH, especialmente al identificar regímenes de mercado y predecir cambios bruscos en la volatilidad.

Comprender la naturaleza caótica de la volatilidad abre nuevas oportunidades para el análisis y ayuda a lograr una previsión más precisa de la dinámica del mercado, lo cual posibilita el desarrollo de estrategias comerciales y técnicas de gestión del riesgo eficaces.

Teoría clásica del caos y enfoque de Bill Williams

La teoría clásica del caos y el concepto de "caos" de Bill Williams son muy distintos. La teoría clásica del caos se basa en principios matemáticos rigurosos y usa herramientas sofisticadas para analizar los sistemas. Williams, por su parte, usa un enfoque intuitivo e indicadores técnicos como Alligator y Fractales, que no están directamente relacionados con la teoría matemática del caos.

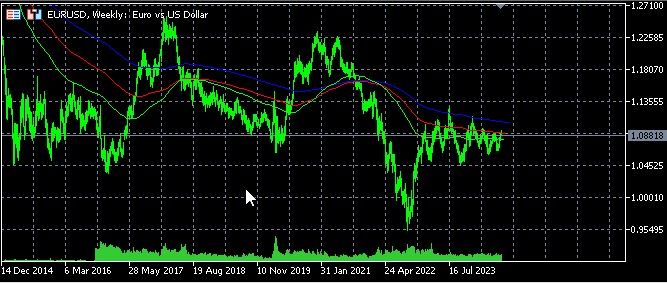
La teoría clásica se basa en principios matemáticos rigurosos y en la investigación científica de la dinámica no lineal. Considera el caos como un comportamiento determinista pero impredecible, analizado con ayuda de métodos matemáticos exactos. Williams, por su parte, usa el término "caos" de forma más libre, refiriéndose a la imprevisibilidad general de los mercados. Sus métodos se orientan más a aplicaciones prácticas en el trading que al análisis profundo de la naturaleza caótica de los mercados.

Aunque Williams ha adaptado algunos términos de la teoría del caos, su enfoque utiliza más el análisis técnico y la interpretación personal de los movimientos del mercado. Esto ha suscitado las críticas de expertos en el campo de la teoría del caos, que consideran engañoso el uso del término "caos" en dicho contexto.

La teoría del caos en el análisis de los mercados

La teoría del caos ofrece una nueva perspectiva del análisis de la dinámica de los mercados, reconociendo la complejidad e imprevisibilidad de los mercados financieros. A diferencia de los métodos tradicionales, la teoría del caos considera la no linealidad y la complejidad de los procesos de mercado.

Este enfoque ayuda a explicar por qué pequeños eventos pueden dar lugar a importantes movimientos del mercado y por qué las previsiones a largo plazo suelen resultar inexactas. La teoría del caos permite analizar fenómenos como los desplomes y las burbujas del mercado, ofreciendo nuevas herramientas para un análisis más preciso y adaptable de los mercados.

El exponente de Lyapunov y su aplicación al análisis de series temporales financieras

El exponente de Lyapunov es una herramienta de la teoría del caos que ayuda a comprender la sensibilidad de un sistema a las condiciones iniciales. En los mercados financieros, esto es importante porque permite valorar cuánto cambiarán los precios ante pequeños cambios en las condiciones del mercado.

Si el exponente de Lyapunov es positivo, esto significará que el sistema se comportará de forma caótica: pequeños cambios podrán provocar grandes fluctuaciones en el futuro. Si el exponente es negativo, el sistema será más estable y los precios variarán menos.

Con este exponente, podemos determinar cuándo el mercado se volverá más volátil y predecible. Los valores altos pueden indicar posibles variaciones bruscas de los precios, lo cual resulta útil para evaluar el riesgo y ajustar las estrategias comerciales.

Para calcular el exponente de Lyapunov en datos financieros, deberemos crear un espacio de fases analizando lo cerca que divergen los puntos de este espacio. Este proceso requerirá la selección de los parámetros adecuados, como la dimensionalidad y el retardo temporal.

Un aspecto importante del uso del exponente de Lyapunov es la estimación del tiempo durante el que serán precisas las previsiones. Cuanto mayor sea el valor del indicador, más corto será el periodo en el que las previsiones seguirán siendo fiables. Esto resultará especialmente útil para las operaciones a corto plazo y la gestión de riesgos.

Ahora podemos comenzar a implementar el exponente de Lyapunov en MQL5.

Implementación del exponente de Lyapunov con MQL5

Este indicador implementará el cálculo del exponente de Lyapunov para analizar series temporales financieras. Esto permitirá evaluar el grado de aleatoriedad del mercado y la previsibilidad potencial de los movimientos de precio.

Parámetros de entrada:

input int    InpTimeLag = 1;       // Time lag
input int    InpEmbedDim = 2;      // Embedding dimension
input int    InpDataLength = 1000; // Data length for calculation

• InpTimeLag: define el retardo para la reconstrucción del espacio de fases.
• InpEmbedDim: indica la dimensionalidad de la incorporación para la reconstrucción del espacio de fases.
• InpDataLength: establece el número de velas usadas para calcular el indicador.

Hay una variable global:

double LyapunovBuffer[];

Inicialización:

int OnInit()
{
   SetIndexBuffer(0, LyapunovBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Lyapunov Exponent");
   return(INIT_SUCCEEDED);
}

En la función OnInit() configuraremos el búfer de indicador, fijaremos la precisión de visualización en 5 decimales y estableceremos un nombre breve para el indicador.

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      LyapunovBuffer[i] = CalculateLyapunovExponent(close, i);
   }
   
   return(rates_total);
}

La función OnCalculate() se llamará en cada tick y realizará el cálculo del exponente de Lyapunov para cada vela a partir de InpDataLength .

Cálculo del exponente de Lyapunov:

double CalculateLyapunovExponent(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double sum = 0;
   int count = 0;
   
   for(int i = 0; i < InpDataLength - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      int nearestNeighbor = FindNearestNeighbor(price, index - InpDataLength + i, index);
      if(nearestNeighbor != -1)
      {
         double initialDistance = MathAbs(price[index - InpDataLength + i] - price[nearestNeighbor]);
         double finalDistance = MathAbs(price[index - InpDataLength + i + InpTimeLag] - price[nearestNeighbor + InpTimeLag]);
         
         if(initialDistance > 0 && finalDistance > 0)
         {
            sum += MathLog(finalDistance / initialDistance);
            count++;
         }
      }
   }
   
   if(count > 0)
      return sum / (count * InpTimeLag);
   else
      return 0;
}

La función CalculateLyapunovExponent() implementará el algoritmo para calcular el exponente local de Lyapunov. Usará el método de los vecinos más próximos para estimar la divergencia de las trayectorias en el espacio de fases reconstruido.

Búsqueda del vecino más próximo:

int FindNearestNeighbor(const double &price[], int startIndex, int endIndex)
{
   double minDistance = DBL_MAX;
   int nearestIndex = -1;
   
   for(int i = startIndex; i < endIndex - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      if(MathAbs(i - startIndex) > InpTimeLag)
      {
         double distance = 0;
         for(int j = 0; j < InpEmbedDim; j++)
         {
            distance += MathPow(price[startIndex + j * InpTimeLag] - price[i + j * InpTimeLag], 2);
         }
         distance = MathSqrt(distance);
         
         if(distance < minDistance)
         {
            minDistance = distance;
            nearestIndex = i;
         }
      }
   }
   
   return nearestIndex;
}

La función FindNearestNeighbor() buscará el punto más cercano en el especio de fases reconstruido utilizando la distancia euclidiana.

Interpretación de los resultados

• Los valores positivos del indicador indicarán la presencia de un comportamiento caótico del mercado.
• Los valores negativos indicarán una tendencia de precios más estable y potencialmente predecible.
• Cuanto mayor sea el valor absoluto del indicador, más pronunciada será la característica correspondiente (caótica o estable).

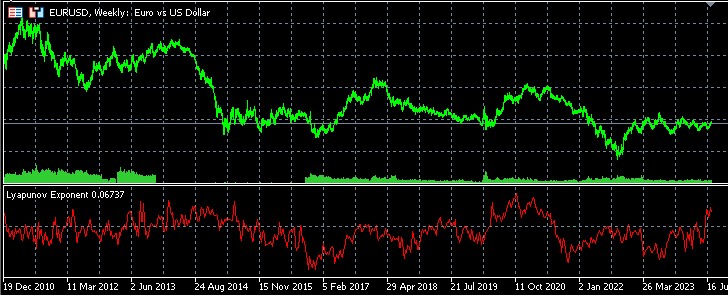
Análisis estadístico de inversiones y continuaciones de tendencia usando el exponente de Lyapunov

Para estudiar en profundidad la relación entre el exponente de Lyapunov y la dinámica de los mercados financieros, hemos desarrollado un script especializado usando MQL5. Esta herramienta nos permitirá realizar un análisis estadístico detallado de las inversiones y continuaciones de tendencia en el contexto de los valores del exponente de Lyapunov, proporcionando a los tráders y analistas información valiosa sobre el comportamiento del mercado.

El script trabajará con los datos históricos del instrumento financiero seleccionado, analizando un número determinado de barras. Para cada barra, se calculará el exponente local de Lyapunov mediante el método de reconstrucción del espacio de fases y la búsqueda del vecino más próximo. Este enfoque permitirá evaluar el grado de comportamiento caótico del sistema en un momento dado.

Simultáneamente con el cálculo del exponente de Lyapunov, el script analizará la dinámica de los precios, identificando los retrocesos y la continuación de la tendencia. Una inversión se definirá como una situación en la que el precio de cierre actual se encuentra por encima del precio anterior y el precio de cierre siguiente se encuentra por debajo del precio actual (o viceversa). Todos los demás casos se tratarán como una continuación de la tendencia.

La característica clave del script será su capacidad para comparar los momentos de las inversiones y continuaciones de tendencia con los valores del exponente de Lyapunov. Esto nos permitirá identificar regularidades estadísticas entre el comportamiento caótico del mercado y su dinámica de precios. El script contará el número de inversiones y continuaciones de tendencia que se producen en valores positivos y negativos del exponente de Lyapunov.

Una vez finalizado el análisis, el script generará estadísticas detalladas, incluidos los valores absolutos y los porcentajes de inversiones y continuaciones de tendencia para los valores positivos y negativos del exponente de Lyapunov. Esta información permitirá a los tráders evaluar con qué frecuencia las inversiones de tendencia coinciden con periodos de mayor caos en el mercado y, a la inversa, con qué frecuencia las continuaciones de tendencia corresponden a periodos más estables.

Interpretación de los resultados de los análisis estadísticos

Los resultados obtenidos del análisis estadístico de las inversiones y continuaciones de tendencia usando el exponente de Lyapunov nos ofrecen datos interesantes sobre la dinámica del mercado EURUSD en el marco temporal horario.

En primer lugar, llama la atención la distribución casi equitativa de eventos entre valores positivos y negativos del exponente de Lyapunov. Tanto las inversiones como las continuaciones de tendencia se observan en aproximadamente la mitad de los casos con Lyapunov positivo y negativo. Esto puede indicar que el mercado EURUSD en el gráfico horario está mostrando un equilibrio entre periodos de relativa estabilidad y caos.

Los valores positivos del exponente de Lyapunov, que suelen vincularse con un comportamiento más caótico e impredecible, se observan en algo más de la mitad de los casos (50,61% para las inversiones y 51,09% para las continuaciones). Esto puede indicar una ligera prevalencia de periodos de mayor volatilidad o incertidumbre en el mercado.

Los valores negativos del exponente de Lyapunov, que suelen interpretarse como una señal de comportamientos más ordenados y menos caóticos del sistema, se observan en el 49,39% de los casos para las inversiones y en el 48,91% para las continuaciones de tendencia. Estos periodos pueden caracterizarse por movimientos de precio más predecibles que siguen determinados patrones.

Resulta interesante observar que el porcentaje de inversiones y continuaciones de tendencia resulta casi idéntico para los valores de Lyapunov positivos y negativos. La diferencia es inferior al 0,5% en ambos casos. Esto puede indicarnos que el exponente de Lyapunov en sí no es un factor determinante para predecir la inversión o la continuación de la tendencia.

Esta distribución uniforme de eventos entre valores de Lyapunov positivos y negativos puede indicar la naturaleza compleja del mercado EURUSD, en el que los periodos de estabilidad y aleatoriedad se alternan con una frecuencia aproximadamente igual. 

Conclusión

La teoría del caos aporta un enfoque innovador al análisis de los mercados financieros, permitiéndonos tener una comprensión más profunda de su naturaleza compleja y no lineal. En este artículo hemos repasado los conceptos clave de la teoría del caos -atractores, fractales y efecto mariposa- y su aplicación a las series temporales financieras. Asimismo, hemos prestado especial atención al exponente de Lyapunov como herramienta para evaluar el grado de dinámica caótica del mercado.