La théorie du chaos dans le trading (partie 2) : Plongée en profondeur

Résumé de l'article précédent

Le premier article examine les concepts de base de la théorie du chaos et leur application à l'analyse des marchés financiers. Nous avons examiné des concepts clés, tels que les attracteurs, les fractales et l'effet papillon, et discuté de la manière dont ils se révèlent dans la dynamique du marché. Une attention particulière a été accordée aux caractéristiques des systèmes chaotiques dans le contexte de la finance et au concept de volatilité.

Nous avons également comparé la théorie classique du chaos avec l'approche de Bill Williams, ce qui nous a permis de mieux comprendre les différences entre l'application scientifique et pratique de ces concepts dans le domaine du trading. L'exposant de Lyapounov en tant qu'outil d'analyse des séries temporelles financières occupe une place centrale dans l'article. Nous avons examiné à la fois sa signification théorique et une mise en œuvre pratique de son calcul dans le langage MQL5.

La dernière partie de l'article est consacrée à l'analyse statistique des renversements et des prolongements de tendance à l'aide de l'exposant de Lyapounov. En prenant pour exemple la paire EURUSD sur la période H1, nous avons démontré comment cette analyse peut être appliquée en pratique et discuté de l'interprétation des résultats obtenus.

L'article pose les bases de la compréhension de la théorie du chaos dans le contexte des marchés financiers et présente des outils pratiques pour l'appliquer au trading. Dans le deuxième article, nous continuerons à approfondir notre compréhension de ce sujet, en nous concentrant sur des aspects plus complexes et leurs applications pratiques.

La première chose dont nous parlerons est la dimension fractale comme mesure du chaos du marché.

La dimension fractale comme mesure du chaos du marché

La dimension fractale est un concept qui joue un rôle important dans la théorie du chaos et l'analyse des systèmes complexes, y compris les marchés financiers. Elle fournit une mesure quantitative de la complexité et de l'auto-similarité d'un objet ou d'un processus, ce qui la rend particulièrement utile pour évaluer le degré d'aléa dans les mouvements du marché.

Dans le contexte des marchés financiers, la dimension fractale peut être utilisée pour mesurer l'irrégularité des graphiques de prix. Une dimension fractale élevée indique une structure de prix plus complexe et chaotique, alors qu'une dimension plus faible peut indiquer un mouvement plus régulier et prévisible.

Il existe plusieurs méthodes pour calculer la dimension fractale. L'une des plus populaires est la méthode du comptage des boîtes. Cette méthode consiste à recouvrir le graphique d'une grille de cellules de différentes tailles et à compter le nombre de cellules nécessaires pour couvrir le graphique à différentes échelles.

L'équation permettant de calculer la dimension fractale D à l'aide de la méthode est la suivante :

D = -lim(ε→0) [log N(ε) / log(ε)].

où N(ε) est le nombre de cellules de taille ε nécessaires pour couvrir l'objet.

L'application de la dimension fractale à l'analyse des marchés financiers peut fournir aux traders et aux analystes des informations supplémentaires sur la nature des mouvements du marché. Par exemple :

• Identifier les modes de marché : les changements dans la dimension fractale peuvent indiquer des transitions entre différents états du marché, tels que des tendances, des mouvements plats ou des périodes chaotiques.
• Evaluation de la volatilité : une dimension fractale élevée correspond souvent à des périodes de volatilité accrue.
• Prévisions : l'analyse de l'évolution de la dimension fractale dans le temps peut aider à prévoir les mouvements futurs du marché.
• Optimisation des stratégies de trading : La compréhension de la structure fractale du marché peut aider à développer et à optimiser les algorithmes de trading.

Voyons maintenant la mise en œuvre pratique du calcul de la dimension fractale dans le langage MQL5. Nous allons développer un indicateur qui calculera la dimension fractale du graphique des prix en temps réel dans MQL5.

L'indicateur utilise la méthode du comptage de boîtes pour estimer la dimension fractale.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/fr/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Fractal Dimension"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpBoxSizesCount = 5;    // Number of box sizes
input int    InpMinBoxSize    = 2;    // Minimum box size
input int    InpMaxBoxSize    = 100;  // Maximum box size
input int    InpDataLength    = 1000; // Data length for calculation

double FractalDimensionBuffer[];

int OnInit()
{
   SetIndexBuffer(0, FractalDimensionBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Fractal Dimension");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      FractalDimensionBuffer[i] = CalculateFractalDimension(close, i);
   }
   
   return(rates_total);
}

double CalculateFractalDimension(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double x[]; 
   double y[];
   ArrayResize(x, InpBoxSizesCount);
   ArrayResize(y, InpBoxSizesCount);
   
   for(int i = 0; i < InpBoxSizesCount; i++)
   {
      int boxSize = (int)MathRound(MathPow(10, MathLog10(InpMinBoxSize) + (MathLog10(InpMaxBoxSize) - MathLog10(InpMinBoxSize)) * i / (InpBoxSizesCount - 1)));
      x[i] = MathLog(1.0 / boxSize);
      y[i] = MathLog(CountBoxes(price, index, boxSize));
   }
   
   double a, b;
   CalculateLinearRegression(x, y, InpBoxSizesCount, a, b);
   
   return a; // The slope of the regression line is the estimate of the fractal dimension
}

int CountBoxes(const double &price[], int index, int boxSize)
{
   double min = price[index - InpDataLength];
   double max = min;
   
   for(int i = index - InpDataLength + 1; i <= index; i++)
   {
      if(price[i] < min) min = price[i];
      if(price[i] > max) max = price[i];
   }
   
   return (int)MathCeil((max - min) / (boxSize * _Point));
}

void CalculateLinearRegression(const double &x[], const double &y[], int count, double &a, double &b)
{
   double sumX = 0, sumY = 0, sumXY = 0, sumX2 = 0;
   
   for(int i = 0; i < count; i++)
   {
      sumX += x[i];
      sumY += y[i];
      sumXY += x[i] * y[i];
      sumX2 += x[i] * x[i];
   }
   
   a = (count * sumXY - sumX * sumY) / (count * sumX2 - sumX * sumX);
   b = (sumY - a * sumX) / count;
}

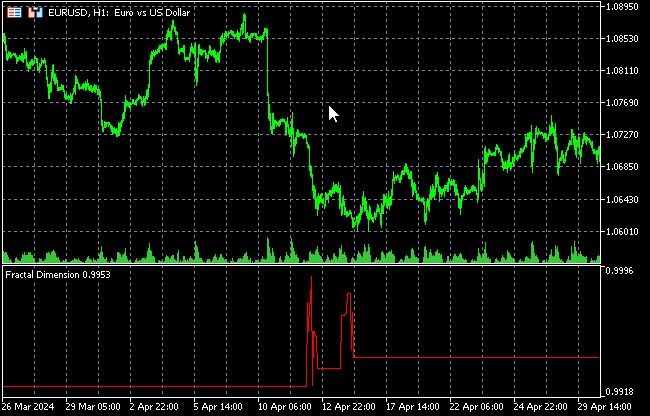
L'indicateur calcule la dimension fractale d'un graphique de prix en utilisant la méthode de comptage de boîtes. La dimension fractale est une mesure de la "dentelure" ou de la complexité d'un graphique et peut être utilisée pour évaluer le degré de chaos sur le marché.

Entrées :

• InpBoxSizesCount - le nombre de tailles de boîtes différentes pour le calcul
• InpMinBoxSize - la taille minimale d’une "boîte".
• InpMaxBoxSize - la taille maximale d’une "boîte".
• InpDataLength - le nombre de bougies utilisées pour le calcul

Algorithme de fonctionnement de l'indicateur :

1. Pour chaque point du graphique, l'indicateur calcule la dimension fractale en utilisant les données des dernières InpDataLength bougies.
2. La méthode de comptage des boîtes est appliquée avec différentes tailles de "boîtes" allant de InpMinBoxSize à InpMaxBoxSize.
3. Le nombre de "boîtes" nécessaires pour couvrir la carte est calculé pour chaque taille de "boîte".
4. Un graphique de dépendance entre le logarithme du nombre de "boîtes" et le logarithme de la taille de la "boîte" est créé.
5. La pente du graphique est calculée à l'aide de la méthode de régression linéaire, qui est une estimation de la dimension fractale.

Les changements dans la dimension fractale peuvent signaler un changement dans le mode de marché.

L'analyse des récurrences pour découvrir des modèles cachés dans les mouvements de prix

L'analyse des récurrences est une méthode puissante d'analyse des séries temporelles non linéaires qui peut être appliquée efficacement à l'étude de la dynamique des marchés financiers. Cette approche nous permet de visualiser et de quantifier les schémas récurrents dans les systèmes dynamiques complexes, dont les marchés financiers font certainement partie.

Le principal outil de l'analyse de récurrence est le graphique de récurrence. Ce diagramme est une représentation visuelle des états répétitifs d'un système dans le temps. Dans un diagramme de récurrence, un point (i, j) est coloré si les états aux moments i et j sont similaires dans un certain sens.

Pour construire un diagramme de récurrence d'une série temporelle financière, suivez les étapes suivantes :

1. Reconstruction de l'espace de phase : en utilisant la méthode des délais, nous transformons les séries temporelles de prix unidimensionnelles en un espace de phase multidimensionnel.
2. Détermination du seuil de similarité : nous sélectionnons un critère selon lequel nous considérons que 2 états sont similaires.
3. Construction de la matrice de récurrence : pour chaque paire de points dans le temps, nous déterminons si les états correspondants sont similaires.
4. Visualisation : nous affichons la matrice de récurrence sous la forme d'une image bidimensionnelle, où les états similaires sont indiqués par des points.

Les diagrammes de récurrence nous permettent d'identifier différents types de dynamiques dans un système :

• Les régions homogènes indiquent des périodes stationnaires
• Les lignes diagonales indiquent une dynamique déterministe
• Les structures verticales et horizontales peuvent indiquer des conditions laminaires.
• L'absence de structure est caractéristique d'un processus aléatoire.

Pour quantifier les structures d'un diagramme de récurrence, diverses mesures de récurrence sont utilisées, telles que le pourcentage de récurrence, l'entropie des lignes diagonales, la longueur maximale d'une ligne diagonale, etc.

L'application de l'analyse de récurrence aux séries chronologiques financières peut être utile pour :

1. Identifier les différents modes de marché (tendance, stagnation, état chaotique)
2. Détecter le changement de mode
3. Évaluer la prévisibilité du marché à différentes périodes
4. Révéler les modèles cycliques cachés

Pour la mise en œuvre pratique de l'analyse récurrente dans le trading, nous pouvons développer un indicateur en langage MQL5, qui construira un diagramme de récurrence et calculera les mesures de récurrence en temps réel. Un tel indicateur peut servir d'outil supplémentaire pour prendre des décisions de trading, en particulier lorsqu'il est combiné à d'autres méthodes d'analyse technique.

Dans la section suivante, nous examinerons une implémentation spécifique de cet indicateur et nous discuterons de la manière d'interpréter ses résultats dans le contexte d'une stratégie de trading.

Indicateur d'analyse de récurrence dans MQL5

L'indicateur met en œuvre la méthode d'analyse des récurrences pour étudier la dynamique des marchés financiers. Il calcule 3 mesures clés de la récurrence : le niveau de récurrence, le déterminisme et la laminarité.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/fr/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 3
#property indicator_plots   3
#property indicator_label1  "Recurrence Rate"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Determinism"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed
#property indicator_label3  "Laminarity"
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrGreen

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 1;     // Time delay
input int    InpThreshold          = 10;    // Threshold (in points)
input int    InpWindowSize         = 200;   // Window size

double RecurrenceRateBuffer[];
double DeterminismBuffer[];
double LaminarityBuffer[];

int minRequiredBars;

int OnInit()
{
   SetIndexBuffer(0, RecurrenceRateBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, DeterminismBuffer, INDICATOR_DATA);
   SetIndexBuffer(2, LaminarityBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Recurrence Analysis");
   
   minRequiredBars = InpWindowSize + (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   if(rates_total < minRequiredBars) return(0);
   
   int start = (prev_calculated > 0) ? MathMax(prev_calculated - 1, minRequiredBars - 1) : minRequiredBars - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      CalculateRecurrenceMeasures(close, rates_total, i, RecurrenceRateBuffer[i], DeterminismBuffer[i], LaminarityBuffer[i]);
   }
   
   return(rates_total);
}

void CalculateRecurrenceMeasures(const double &price[], int price_total, int index, double &recurrenceRate, double &determinism, double &laminarity)
{
   if(index < minRequiredBars - 1 || index >= price_total)
   {
      recurrenceRate = 0;
      determinism = 0;
      laminarity = 0;
      return;
   }

   int windowStart = index - InpWindowSize + 1;
   int matrixSize = InpWindowSize - (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   int recurrenceCount = 0;
   int diagonalLines = 0;
   int verticalLines = 0;
   
   for(int i = 0; i < matrixSize; i++)
   {
      for(int j = 0; j < matrixSize; j++)
      {
         bool isRecurrent = IsRecurrent(price, price_total, windowStart + i, windowStart + j);
         if(isRecurrent)
         {
            recurrenceCount++;
            
            // Check for diagonal lines
            if(i > 0 && j > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j - 1))
               diagonalLines++;
            
            // Check for vertical lines
            if(i > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j))
               verticalLines++;
         }
      }
   }
   
   recurrenceRate = (double)recurrenceCount / (matrixSize * matrixSize);
   determinism = (recurrenceCount > 0) ? (double)diagonalLines / recurrenceCount : 0;
   laminarity = (recurrenceCount > 0) ? (double)verticalLines / recurrenceCount : 0;
}

bool IsRecurrent(const double &price[], int price_total, int i, int j)
{
   if(i < 0 || j < 0 || i >= price_total || j >= price_total) return false;

   double distance = 0;
   for(int d = 0; d < InpEmbeddingDimension; d++)
   {
      int offset = d * InpTimeDelay;
      if(i + offset >= price_total || j + offset >= price_total) return false;
      double diff = price[i + offset] - price[j + offset];
      distance += diff * diff;
   }
   distance = MathSqrt(distance);
   
   return (distance <= InpThreshold * _Point);
}

Principales caractéristiques de l'indicateur :

L'indicateur est affiché dans une fenêtre séparée sous le graphique des prix et utilise 3 buffers pour stocker et afficher les données. L'indicateur calcule 3 paramètres : le taux de récurrence (ligne bleue), qui indique le niveau global de récurrence, le déterminisme (ligne rouge), qui est une mesure de la prévisibilité du système, et la laminarité (ligne verte), qui évalue la tendance du système à rester dans un certain état.

Les entrées de l'indicateur comprennent InpEmbeddingDimension (par défaut 3), qui définit la dimension d'intégration pour la reconstruction de l'espace des phases, InpTimeDelay (par défaut 1) pour le délai pendant la reconstruction, InpThreshold (par défaut 10) pour le seuil de similarité d'état en points, et InpWindowSize (par défaut 200) pour la définition de la taille de la fenêtre d'analyse.

L'algorithme de fonctionnement de l'indicateur est basé sur la méthode des délais pour reconstruire l'espace de phase à partir d'une série temporelle unidimensionnelle de prix. Pour chaque point de la fenêtre d'analyse, sa "récurrence" par rapport aux autres points est calculée. Ensuite, sur la base de la structure récurrente obtenue, 3 mesures sont calculées : Le taux de récurrence, qui détermine la proportion de points de récurrence par rapport au nombre total de points, le déterminisme, qui indique la proportion de points de récurrence qui forment des lignes diagonales, et la laminarité, qui estime la proportion de points de récurrence qui forment des lignes verticales.

Application du théorème d'intégration de Takens aux prévisions de volatilité

Le théorème d'intégration de Takens est un résultat fondamental de la théorie des systèmes dynamiques qui a des implications importantes pour l'analyse des séries temporelles, y compris des données financières. Ce théorème stipule qu'un système dynamique peut être reconstruit à partir des observations d'une seule variable en utilisant la méthode du décalage temporel.

Dans le contexte des marchés financiers, le théorème de Takens nous permet de reconstruire un espace de phase multidimensionnel à partir d'une série temporelle unidimensionnelle de prix ou de rendements. Ceci est particulièrement utile pour analyser la volatilité, qui est une caractéristique clé des marchés financiers.

Les étapes de base de l'application du théorème de Takens à la prévision de la volatilité sont les suivantes :

1. Reconstruction de l'espace de phase :
   • Sélection de la dimension d'intégration (m)
   • Sélection du délai (τ)
   • Création de vecteurs à m dimensions à partir de la série temporelle originale
2. Analyse de l'espace reconstruit :
   • Recherche des voisins les plus proches pour chaque point
   • Estimation de la densité locale des points
3. Prévisions de volatilité :
   • Utilisation d'informations sur la densité locale pour estimer la volatilité future

Examinons ces étapes plus en détail.

Reconstruction de l'espace de phase :

Disposons d'une série temporelle de prix de clôture {p(t)}. Nous créons des vecteurs à m dimensions comme suit :

x(t) = [p(t), p(t+τ), p(t+2τ), ..., p(t+(m-1)τ)]

où m est une dimension d'intégration et τ un délai.

Le choix des valeurs correctes de m et de τ est essentiel pour une reconstruction réussie. Généralement, τ est choisi à l'aide des méthodes d'information mutuelle ou de fonction d'autocorrélation, et m est choisi à l'aide de la méthode du faux plus proche voisin.

Analyse de l'espace reconstruit :

Après avoir reconstruit l'espace des phases, nous pouvons analyser la structure de l'attracteur du système. Pour la prévision de la volatilité, les informations sur la densité locale des points dans l'espace des phases sont particulièrement importantes.

Pour chaque point x(t), nous trouvons ses k plus proches voisins (en général, k est choisi entre 5 et 20) et calculons la distance moyenne par rapport à ces voisins. Cette distance sert à mesurer la densité locale et donc la volatilité locale.

Prévisions de volatilité

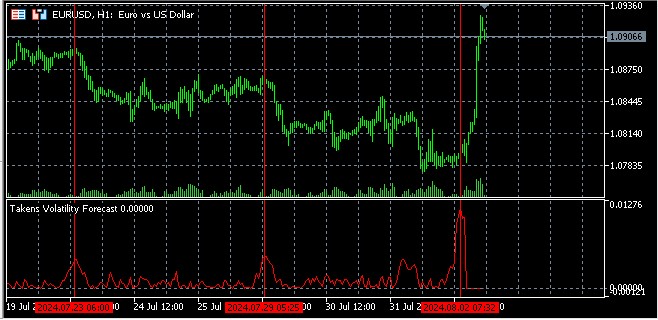
L'idée de base de la prévision de la volatilité à l'aide de l'espace de phase reconstruit est que les points proches dans cet espace sont susceptibles d'avoir un comportement similaire dans un avenir proche.

Pour prévoir la volatilité à l'instant t+h, nous :

• Trouvons les k plus proches voisins du point x(t) actuel dans l'espace reconstruit
• Calculons la volatilité réelle de ces voisins à h pas d'avance
• Utilisons la moyenne de ces volatilités comme prévision

Mathématiquement, cela peut s'exprimer comme suit :

σ̂(t+h) = (1/k) Σ σ(ti+h), où ti sont les indices des k plus proches voisins de x(t).

Les avantages de cette approche :

• Elle tient compte de la dynamique non linéaire du marché
• Elle ne nécessite pas d'hypothèses sur la distribution des rendements
• Nous sommes capables d'identifier des schémas complexes dans la volatilité

Inconvénients :

• Elle est sensible au choix des paramètres (m, τ, k)
• Elle peut s'avérer coûteuse en termes de calcul pour de grandes quantités de données.

Implémentation

Créons un indicateur MQL5 qui mettra en œuvre cette méthode de prévision de la volatilité :

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/fr/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Predicted Volatility"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double PredictedVolatilityBuffer[];

int OnInit()
{
   SetIndexBuffer(0, PredictedVolatilityBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Takens Volatility Forecast");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedVolatilityBuffer[i] = PredictVolatility(close, i);
      }
   }
   
   return(rates_total);
}

double PredictVolatility(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }
   
   double distances[];
   ArrayResize(distances, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double sum = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         sum += diff * diff;
      }
      distances[i] = sqrt(sum);
   }
   
   int sortedIndices[];
   ArrayCopy(sortedIndices, distances);
   ArraySort(sortedIndices);
   
   double sumVolatility = 0;
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - sortedIndices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double futureReturn = (price[neighborIndex + InpForecastHorizon] - price[neighborIndex]) / price[neighborIndex];
      sumVolatility += MathAbs(futureReturn);
   }
   
   return sumVolatility / InpNeighbors;
}

Méthodes de détermination d'un délai et d'une dimension d'intégration

Lors de la reconstruction de l'espace des phases à l'aide du théorème de Takens, il est essentiel de choisir correctement 2 paramètres clés : le délai (τ) et la dimension d'intégration (m). Une mauvaise sélection de ces paramètres peut conduire à une reconstruction incorrecte et, par conséquent, à des conclusions erronées. Examinons deux méthodes principales pour déterminer ces paramètres.

Méthode de la fonction d'autocorrélation (ACF) pour déterminer le retard temporel

La méthode repose sur l'idée de choisir un délai τ, à partir duquel la fonction d'autocorrélation passe pour la première fois par 0 ou atteint une certaine valeur faible, par exemple 1/e de la valeur initiale. Cela permet de choisir un délai à partir duquel les valeurs successives de la série temporelle deviennent suffisamment indépendantes les unes des autres.

L'implémentation de la méthode ACF dans MQL5 peut ressembler à ceci :

int FindOptimalLagACF(const double &price[], int maxLag, double threshold = 0.1)
{
   int size = ArraySize(price);
   if(size <= maxLag) return 1;
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += price[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(price[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (price[i] - mean) * (price[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

Dans cette mise en œuvre, nous calculons d'abord la moyenne et la variance de la série temporelle. Ensuite, pour chaque retard de 1 à maxLag, nous calculons la valeur de la fonction d'autocorrélation. Une fois que la valeur de l'ACF devient inférieure ou égale à un seuil donné (par défaut 0,1), ce décalage est considéré comme le délai optimal.

La méthode ACF a ses avantages et ses inconvénients. D'une part, il est facile à mettre en œuvre et intuitif. D'autre part, elle ne tient pas compte des dépendances non linéaires dans les données, ce qui peut constituer un inconvénient important lors de l'analyse de séries chronologiques financières, qui présentent souvent un comportement non linéaire.

Méthode d'information mutuelle (MI) pour déterminer le délai d'attente

Cette méthode est basée sur la théorie de l'information et permet de prendre en compte les dépendances non linéaires dans les données. L'idée est de choisir un délai τ qui correspond au premier minimum local de la fonction d'information mutuelle.

L'implémentation de la méthode de l'information mutuelle dans MQL5 peut se présenter comme suit :

double CalculateMutualInformation(const double &price[], int lag, int bins = 20)
{
   int size = ArraySize(price);
   if(size <= lag) return 0;
   
   double minPrice = price[ArrayMinimum(price)];
   double maxPrice = price[ArrayMaximum(price)];
   double binSize = (maxPrice - minPrice) / bins;
   
   int histogram[];
   ArrayResize(histogram, bins * bins);
   ArrayInitialize(histogram, 0);
   
   int totalPoints = 0;
   
   for(int i = 0; i < size - lag; i++)
   {
      int bin1 = (int)((price[i] - minPrice) / binSize);
      int bin2 = (int)((price[i + lag] - minPrice) / binSize);
      if(bin1 >= 0 && bin1 < bins && bin2 >= 0 && bin2 < bins)
      {
         histogram[bin1 * bins + bin2]++;
         totalPoints++;
      }
   }
   
   double mutualInfo = 0;
   for(int i = 0; i < bins; i++)
   {
      for(int j = 0; j < bins; j++)
      {
         if(histogram[i * bins + j] > 0)
         {
            double pxy = (double)histogram[i * bins + j] / totalPoints;
            double px = 0, py = 0;
            for(int k = 0; k < bins; k++)
            {
               px += (double)histogram[i * bins + k] / totalPoints;
               py += (double)histogram[k * bins + j] / totalPoints;
            }
            mutualInfo += pxy * MathLog(pxy / (px * py));
         }
      }
   }
   
   return mutualInfo;
}

int FindOptimalLagMI(const double &price[], int maxLag)
{
   double minMI = DBL_MAX;
   int optimalLag = 1;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double mi = CalculateMutualInformation(price, lag);
      if(mi < minMI)
      {
         minMI = mi;
         optimalLag = lag;
      }
      else if(mi > minMI)
      {
         break;
      }
   }
   
   return optimalLag;
}

Dans cette implémentation, nous définissons d'abord la fonction CalculateMutualInformation qui calcule l'information mutuelle entre la série originale et sa version décalée pour un décalage donné. Ensuite, dans la fonction FindOptimalLagMI, nous recherchons le premier minimum local d'information mutuelle en itérant sur différentes valeurs de décalage.

La méthode de l'information mutuelle présente l'avantage, par rapport à la méthode ACF, de pouvoir prendre en compte les dépendances non linéaires dans les données. Elle est donc plus adaptée à l'analyse des séries temporelles financières, qui présentent souvent un comportement complexe et non linéaire. Toutefois, cette méthode est plus complexe à mettre en œuvre et nécessite davantage de calculs.

Le choix entre les méthodes ACF et MI dépend de la tâche spécifique et des caractéristiques des données analysées. Dans certains cas, il peut être utile d'utiliser les deux méthodes et de comparer les résultats. Il est également important de se rappeler que le délai optimal peut changer au fil du temps, en particulier pour les séries chronologiques financières, et qu'il peut donc être judicieux de recalculer ce paramètre périodiquement.

Algorithme des faux voisins les plus proches pour déterminer la dimension d'encastrement optimale

Une fois le délai optimal déterminé, l'étape suivante de la reconstruction de l'espace des phases est le choix d'une dimension d'intégration appropriée. L'une des méthodes les plus populaires à cette fin est l'algorithme des Faux Plus Proches Voisins (False Nearest Neighbors, ou FNN).

L'idée de l'algorithme FNN est de trouver une dimension d'intégration minimale telle que la structure géométrique de l'attracteur dans l'espace des phases soit correctement reproduite. L'algorithme est basé sur l'hypothèse que dans un espace de phase correctement reconstruit, les points proches devraient rester proches lors du passage à un espace de dimension supérieure.

Examinons l'implémentation de l'algorithme FNN dans le langage MQL5 :

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

int FindOptimalEmbeddingDimension(const double &price[], int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = ArraySize(price);
   int minRequiredSize = (maxDim - 1) * delay + 1;
   if(size < minRequiredSize) return 1;
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = price[i - k * delay] - price[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(price, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

La fonction IsFalseNeighbor détermine si deux points sont de faux voisins. Il calcule la distance entre les points de la dimension courante et de la dimension supérieure d'une unité. Si la variation relative de la distance dépasse un seuil donné, les points sont considérés comme de faux voisins.

La fonction principale FindOptimalEmbeddingDimension parcourt les dimensions de 1 à maxDim. Pour chaque dimension, nous passons en revue tous les points de la série temporelle. Pour chaque point, nous trouvons le voisin le plus proche dans la dimension courante. Nous vérifions ensuite si le voisin trouvé est faux à l'aide de la fonction IsFalseNeighbor. On compte le nombre total de voisins et le nombre de faux voisins. On calcule ensuite la proportion de faux voisins. Si la proportion de faux voisins est inférieure au seuil de tolérance spécifié, la dimension actuelle est considérée comme optimale et est renvoyée.

L'algorithme comporte plusieurs paramètres importants. delay — un délai préalablement déterminé par la méthode ACF ou MI. maxDim — la dimension d'intégration maximale à prendre en compte. threshold — le seuil de détection des faux voisins. tolerance — le seuil de tolérance pour la proportion de faux voisins. Le choix de ces paramètres peut affecter de manière significative le résultat, il est donc important d'expérimenter différentes valeurs et de prendre en compte les spécificités des données analysées.

L'algorithme FNN présente un certain nombre d'avantages. Il prend en compte la structure géométrique des données dans l'espace des phases. La méthode est assez robuste au bruit dans les données. Elle ne nécessite aucune hypothèse préalable sur la nature du système étudié.

Implémentation de la méthode de prévision basée sur la théorie du chaos dans MQL5

Une fois que nous avons déterminé les paramètres optimaux pour reconstruire l'espace des phases, nous pouvons commencer à mettre en œuvre la méthode de prédiction basée sur la théorie du chaos. Cette méthode repose sur l'idée que les états proches dans l'espace des phases auront une évolution similaire dans un avenir proche.

L'idée de base de la méthode est la suivante : nous trouvons les états du système dans le passé qui sont les plus proches de l'état actuel. Sur la base de leur comportement futur, nous établissons une prévision pour l'état actuel. Cette approche est connue sous le nom de méthode analogique ou méthode du plus proche voisin.

Examinons la mise en œuvre de cette méthode en tant qu'indicateur pour MetaTrader 5. L'indicateur effectue les opérations suivantes :

1. Reconstruction de l'espace de phase à l'aide de la méthode du délai.
2. Recherche des k plus proches voisins pour l'état actuel du système.
3. Prédiction de la valeur future sur la base du comportement des voisins trouvés.

Voici le code de l'indicateur qui implémente cette méthode :

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/fr/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_chart_window
#property indicator_buffers 2
#property indicator_plots   2
#property indicator_label1  "Actual"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Predicted"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double ActualBuffer[];
double PredictedBuffer[];

int OnInit()
{
   SetIndexBuffer(0, ActualBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, PredictedBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, _Digits);
   IndicatorSetString(INDICATOR_SHORTNAME, "Chaos Theory Predictor");
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      ActualBuffer[i] = close[i];
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedBuffer[i] = PredictPrice(close, i);
      }
   }
   
   return(rates_total);
}

double PredictPrice(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;

   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }

   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);

   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }

   // Custom sort function for sorting distances and indices together
   SortDistancesWithIndices(distances, indices, dataSize);

   double prediction = 0;
   double weightSum = 0;

   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - indices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double weight = 1.0 / (distances[i] + 0.0001);  // Avoid division by zero
      prediction += weight * price[neighborIndex + InpForecastHorizon];
      weightSum += weight;
   }

   return prediction / weightSum;
}

void SortDistancesWithIndices(double &distances[], int &indices[], int size)
{
   for(int i = 0; i < size - 1; i++)
   {
      for(int j = i + 1; j < size; j++)
      {
         if(distances[i] > distances[j])
         {
            double tempDist = distances[i];
            distances[i] = distances[j];
            distances[j] = tempDist;

            int tempIndex = indices[i];
            indices[i] = indices[j];
            indices[j] = tempIndex;
         }
      }
   }
}

L'indicateur reconstruit l'espace des phases, trouve les voisins les plus proches de l'état actuel et utilise leurs valeurs futures pour faire des prédictions. Il affiche les valeurs réelles et les valeurs prévues sur un graphique, ce qui permet d'évaluer visuellement la qualité de la prévision.

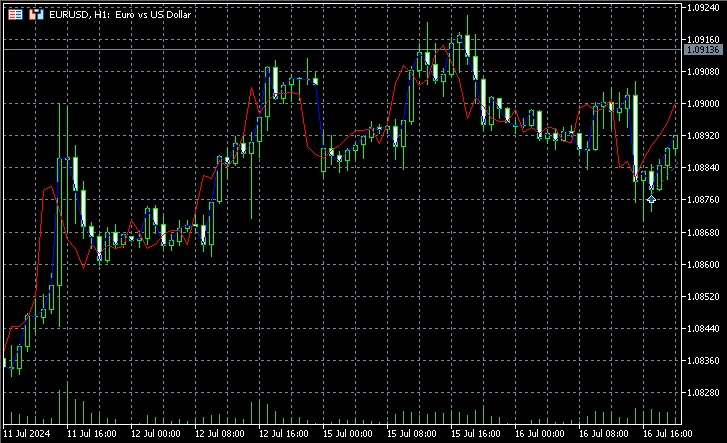
Les principaux aspects de la mise en œuvre comprennent l'utilisation d'une moyenne pondérée pour la prédiction, où le poids de chaque voisin est inversement proportionnel à sa distance par rapport à l'état actuel. Cela nous permet de tenir compte du fait que les voisins les plus proches sont susceptibles de fournir des prévisions plus précises. A en juger par les captures d'écran, l'indicateur prédit la direction du mouvement des prix plusieurs barres à l'avance.

Création d'un EA de concept

Nous sommes arrivés à la partie la plus intéressante. Vous trouverez ci-dessous le code d'un travail entièrement automatisé basé sur la théorie du chaos :

#property copyright "Copyright 2024, Author"
#property link      "https://www.example.com"
#property version   "1.00"
#property strict

#include <Arrays\ArrayObj.mqh>
#include <Trade\Trade.mqh>
CTrade Trade;
input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period
input double InpLotSize            = 0.1;   // Lot size

ulong g_ticket = 0;
datetime g_last_bar_time = 0;
double optimalTimeDelay;
double optimalEmbeddingDimension;
int OnInit()
{
   return(INIT_SUCCEEDED);
}

void OnDeinit(const int reason)
{
}

void OnTick()
{  
   OptimizeParameters();
   
   if(g_last_bar_time == iTime(_Symbol, PERIOD_CURRENT, 0)) return;
   g_last_bar_time = iTime(_Symbol, PERIOD_CURRENT, 0);
   
   double prediction = PredictPrice(iClose(_Symbol, PERIOD_CURRENT, 0), 0);
   Comment(prediction);
   
   if(prediction > iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close selling
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close SELL position: ", GetLastError());
         }
      }
      
      // Open buy
      double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
      ulong ticket = Trade.Buy(InpLotSize, _Symbol, ask, 0, 0, "ChaosBuy");
      if(ticket == 0)
         Print("Failed to open BUY position: ", GetLastError());
   }
   else if(prediction < iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close buying
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close BUY position: ", GetLastError());
         }
      }
      
      // Open sell
      double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
      ulong ticket = Trade.Sell(InpLotSize, _Symbol, bid, 0, 0, "ChaosSell");
      if(ticket == 0)
         Print("Failed to open SELL position: ", GetLastError());
   }
}

double PredictPrice(double price, int index)
{
   int vectorSize = optimalEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      currentVector[i] = iClose(_Symbol, PERIOD_CURRENT, index + i * optimalTimeDelay);
   }
   
   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         double diff = currentVector[j] - iClose(_Symbol, PERIOD_CURRENT, index + i + j * optimalTimeDelay);
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }
   
   // Use SortDoubleArray to sort by 'distances' array values
   SortDoubleArray(distances, indices);
   
   double prediction = 0;
   double weightSum = 0;
   
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index + indices[i];
      double weight = 1.0 / (distances[i] + 0.0001);
      prediction += weight * iClose(_Symbol, PERIOD_CURRENT, neighborIndex + InpForecastHorizon);
      weightSum += weight;
   }
   
   return prediction / weightSum;
}

void SortDoubleArray(double &distances[], int &indices[])
{
    int size = ArraySize(distances);
    for(int i = 0; i < size - 1; i++)
    {
        for(int j = i + 1; j < size; j++)
        {
            if(distances[i] > distances[j])
            {
                // Swap distances
                double tempDist = distances[i];
                distances[i] = distances[j];
                distances[j] = tempDist;
                
                // Swap corresponding indices
                int tempIndex = indices[i];
                indices[i] = indices[j];
                indices[j] = tempIndex;
            }
        }
    }
}

int FindOptimalLagACF(int maxLag, double threshold = 0.1)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += series[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(series[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (series[i] - mean) * (series[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

int FindOptimalEmbeddingDimension(int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = series[i - k * delay] - series[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(series, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

void OptimizeParameters()
{
   double optimalTimeDelay = FindOptimalLagACF(50);
   double optimalEmbeddingDimension = FindOptimalEmbeddingDimension(optimalTimeDelay, 10);
   Print("Optimal Time Delay: ", optimalTimeDelay);
   Print("Optimal Embedding Dimension: ", optimalEmbeddingDimension);
}

Ce code est un EA pour MetaTrader 5 qui utilise les concepts de la théorie du chaos pour prévoir les prix sur les marchés financiers. L'EA met en œuvre la méthode de prévision basée sur la méthode du plus proche voisin dans l'espace des phases reconstruit.

L'évaluation environnementale comprend les éléments suivants :

• InpEmbeddingDimension - la dimension d'intégration pour la reconstruction de l'espace de phase (par défaut : 3)
• InpTimeDelay - le délai de reconstruction (5 par défaut)
• InpNeighbors - le nombre de voisins les plus proches pour les prévisions (par défaut - 10)
• InpForecastHorizon - l’horizon de prévision (par défaut - 10)
• InpLookback - la période de rétroaction pour l'analyse (par défaut : 1000)
• InpLotSize - la taille du lot pour le trading (par défaut - 0,1)

L'EA fonctionne comme suit :

1. À chaque nouvelle barre, il optimise les paramètres optimalTimeDelay et optimalEmbeddingDimension en utilisant la méthode de la fonction d'autocorrélation (ACF) et l'algorithme des faux voisins les plus proches (FNN), respectivement.
2. Il fait ensuite une prévision de prix basée sur l'état actuel du système en utilisant la méthode des voisins les plus proches.
3. Si le prix prévu est supérieur au prix actuel, l'EA ferme toutes les positions de vente ouvertes et ouvre une nouvelle position d'achat. Si le prix prévu est inférieur au prix actuel, l'EA ferme toutes les positions d'achat ouvertes et ouvre une nouvelle position de vente.

L'EA utilise la fonction PredictPrice, qui :

• Reconstruit l'espace de phase en utilisant une dimension d'intégration et un délai optimaux.
• Détermine les distances entre l'état actuel du système et tous les états de la période de recul.
• Trie les états par ordre croissant de distance.
• Calcule une moyenne pondérée des prix futurs pour les voisins les plus proches de InpNeighbors, où le poids de chaque voisin est inversement proportionnel à sa distance par rapport à l'état actuel.
• Renvoie une moyenne pondérée comme prévision de prix.

L'EA comprend également les fonctions FindOptimalLagACF et FindOptimalEmbeddingDimension, qui sont utilisées pour optimiser les paramètres OptimalTimeDelay et OptimalEmbeddingDimension, respectivement.

Dans l'ensemble, l'évaluation environnementale propose une approche innovante de la prévision des prix sur les marchés financiers en utilisant les concepts de la théorie du chaos. Elle peut aider les opérateurs à prendre des décisions plus éclairées et à augmenter potentiellement le rendement de leurs investissements.

Test avec auto-optimisation

Examinons le travail de notre EA sur plusieurs symboles. La première paire de devises, EURUSD, depuis le 01/01/2016 :

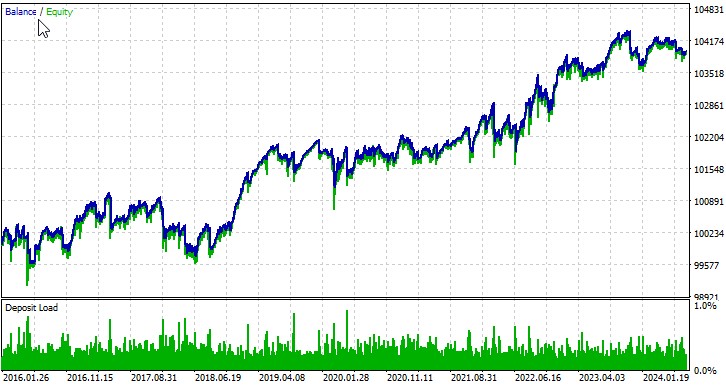
Deuxième paire, AUD :

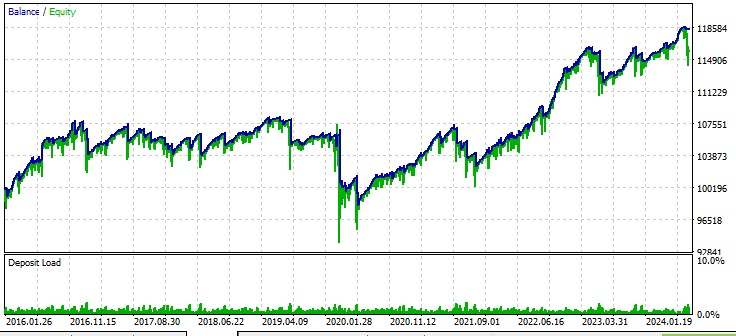
Troisième paire, GBPUSD :

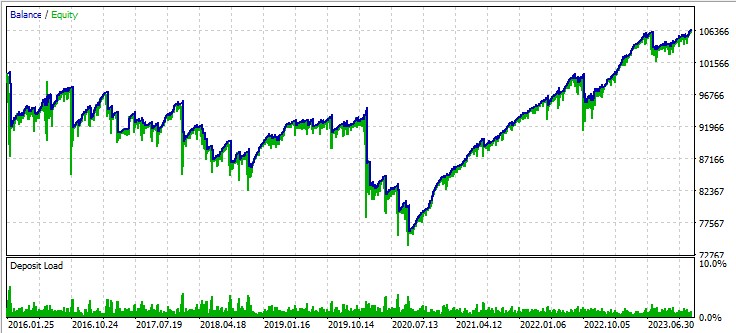
Prochaines étapes

La poursuite du développement de notre EA basée sur la théorie du chaos nécessitera des tests approfondis et une optimisation. Des tests à grande échelle portant sur différents délais et instruments financiers sont nécessaires pour mieux comprendre son efficacité dans différentes conditions de marché. L'utilisation de méthodes d'apprentissage automatique peut contribuer à optimiser les paramètres de l'EA et à accroître sa capacité d'adaptation à l'évolution des réalités du marché.

Une attention particulière devrait être accordée à l'amélioration du système de gestion des risques. La mise en œuvre d'une gestion dynamique du dimensionnement des positions, qui tient compte de la volatilité actuelle du marché et des prévisions de volatilité chaotique, peut améliorer considérablement la résilience de la stratégie.

Conclusion

Dans cet article, nous avons examiné l'application de la théorie du chaos à l'analyse et aux prévisions des marchés financiers. Nous avons étudié des concepts clés tels que la reconstruction de l'espace de phase, la détermination de la dimension d'intégration optimale et du délai, ainsi que la méthode de prédiction du plus proche voisin.

L'EA que nous avons développé démontre le potentiel de l'utilisation de la théorie du chaos dans le trading algorithmique. Les résultats des tests effectués sur différentes paires de devises montrent que la stratégie est capable de générer des bénéfices, bien qu'avec des degrés de réussite variables selon les instruments.

Cependant, il est important de noter que l'application de la théorie du chaos à la finance s'accompagne d'un certain nombre de défis. Les marchés financiers sont des systèmes extrêmement complexes influencés par de nombreux facteurs, dont beaucoup sont difficiles, voire impossibles, à prendre en compte dans un modèle. De plus, la nature même des systèmes chaotiques rend la prévision à long terme fondamentalement impossible - c'est l'un des principaux postulats des chercheurs sérieux.

En conclusion, si la théorie du chaos n'est pas le Saint Graal de la prévision des marchés, elle représente une direction prometteuse pour la poursuite de la recherche et du développement dans les domaines de l'analyse financière et du trading algorithmique. Il est clair que la combinaison des méthodes de la théorie du chaos avec d'autres approches, telles que l'apprentissage automatique et l'analyse de données massives, peut ouvrir de nouvelles possibilités.