La teoria del caos nel trading (parte 2): Immergendosi in profondità

Riassunto dell'articolo precedente

Il primo articolo ha considerato i concetti di base della teoria del caos e la loro applicazione all'analisi dei mercati finanziari. Abbiamo analizzato i concetti chiave, come gli attrattori, i frattali e l'effetto farfalla, e abbiamo discusso come si rivelano nelle dinamiche di mercato. Particolare attenzione è stata dedicata alle caratteristiche dei sistemi caotici nel contesto della finanza e al concetto di volatilità.

Abbiamo anche confrontato la teoria del caos classica con l'approccio di Bill Williams, che ci ha permesso di comprendere meglio le differenze tra l'applicazione scientifica e pratica di questi concetti nel trading. L'esponente di Lyapunov come strumento per l'analisi delle serie temporali finanziarie ha assunto un ruolo centrale nell'articolo. Abbiamo considerato sia il suo significato teorico sia un'implementazione pratica del suo calcolo nel linguaggio MQL5.

La parte finale dell'articolo è stata dedicata all'analisi statistica delle inversioni e delle continuazioni dei trend utilizzando l'esponente di Lyapunov. Utilizzando come esempio la coppia EURUSD sul timeframe H1, abbiamo dimostrato come questa analisi possa essere applicata nella pratica e abbiamo discusso l'interpretazione dei risultati ottenuti.

L'articolo ha posto le basi per la comprensione della teoria del caos nel contesto dei mercati finanziari e ha presentato strumenti pratici per la sua applicazione al trading. Nel secondo articolo continueremo ad approfondire la comprensione di questo argomento, concentrandoci su aspetti più complessi e sulle loro applicazioni pratiche.

La prima cosa di cui parleremo è la dimensione frattale come misura del caos del mercato.

La dimensione frattale come misura del caos del mercato

La dimensione frattale è un concetto che svolge un ruolo importante nella teoria del caos e nell'analisi dei sistemi complessi, compresi i mercati finanziari. Fornisce una misura quantitativa della complessità e dell'autosimilarità di un oggetto o di un processo, rendendola particolarmente utile per valutare il grado di casualità dei movimenti del mercato.

Nel contesto dei mercati finanziari, la dimensione frattale può essere utilizzata per misurare "l’irregolarità" dei grafici dei prezzi. Una dimensione frattale più elevata indica una struttura dei prezzi più complessa e caotica, mentre una dimensione più bassa può indicare un movimento più regolare e prevedibile.

Esistono diversi metodi per calcolare la dimensione frattale. Uno dei più popolari è il metodo del conteggio dei box. Questo metodo prevede di coprire il grafico con una griglia di celle di dimensioni variabili e di contare il numero di celle necessarie per coprire il grafico a scale differenti.

L'equazione per calcolare la dimensione frattale D utilizzando il metodo è la seguente:

D = -lim(ε→0) [log N(ε) / log(ε)]

dove N(ε) è il numero di celle di dimensione ε necessarie per coprire l'oggetto.

L'applicazione della dimensione frattale all'analisi dei mercati finanziari può fornire ai trader e agli analisti ulteriori indicazioni sulla natura dei movimenti di mercato. Per esempio:

• Identificare le modalità di mercato: I cambiamenti nella dimensione frattale possono indicare transizioni tra diversi stati del mercato, come trend, movimenti laterali o periodi caotici.
• Valutazione della volatilità: Una dimensione frattale elevata corrisponde spesso a periodi di maggiore volatilità.
• Previsioni: L'analisi delle variazioni della dimensione frattale nel tempo può aiutare a prevedere i futuri movimenti del mercato.
• Ottimizzazione delle strategie di trading: La comprensione della struttura frattale del mercato può aiutare a sviluppare e ottimizzare gli algoritmi di trading.

Vediamo ora l'implementazione pratica del calcolo della dimensione frattale nel linguaggio MQL5. Svilupperemo un indicatore che calcolerà la dimensione frattale del grafico dei prezzi in tempo reale in MQL5.

L'indicatore utilizza il metodo del conteggio dei box per stimare la dimensione frattale.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Fractal Dimension"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpBoxSizesCount = 5;    // Number of box sizes
input int    InpMinBoxSize    = 2;    // Minimum box size
input int    InpMaxBoxSize    = 100;  // Maximum box size
input int    InpDataLength    = 1000; // Data length for calculation

double FractalDimensionBuffer[];

int OnInit()
{
   SetIndexBuffer(0, FractalDimensionBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Fractal Dimension");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      FractalDimensionBuffer[i] = CalculateFractalDimension(close, i);
   }
   
   return(rates_total);
}

double CalculateFractalDimension(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double x[]; 
   double y[];
   ArrayResize(x, InpBoxSizesCount);
   ArrayResize(y, InpBoxSizesCount);
   
   for(int i = 0; i < InpBoxSizesCount; i++)
   {
      int boxSize = (int)MathRound(MathPow(10, MathLog10(InpMinBoxSize) + (MathLog10(InpMaxBoxSize) - MathLog10(InpMinBoxSize)) * i / (InpBoxSizesCount - 1)));
      x[i] = MathLog(1.0 / boxSize);
      y[i] = MathLog(CountBoxes(price, index, boxSize));
   }
   
   double a, b;
   CalculateLinearRegression(x, y, InpBoxSizesCount, a, b);
   
   return a; // The slope of the regression line is the estimate of the fractal dimension
}

int CountBoxes(const double &price[], int index, int boxSize)
{
   double min = price[index - InpDataLength];
   double max = min;
   
   for(int i = index - InpDataLength + 1; i <= index; i++)
   {
      if(price[i] < min) min = price[i];
      if(price[i] > max) max = price[i];
   }
   
   return (int)MathCeil((max - min) / (boxSize * _Point));
}

void CalculateLinearRegression(const double &x[], const double &y[], int count, double &a, double &b)
{
   double sumX = 0, sumY = 0, sumXY = 0, sumX2 = 0;
   
   for(int i = 0; i < count; i++)
   {
      sumX += x[i];
      sumY += y[i];
      sumXY += x[i] * y[i];
      sumX2 += x[i] * x[i];
   }
   
   a = (count * sumXY - sumX * sumY) / (count * sumX2 - sumX * sumX);
   b = (sumY - a * sumX) / count;
}

L'indicatore calcola la dimensione frattale di un grafico dei prezzi utilizzando il metodo del conteggio dei box. La dimensione frattale è una misura della "frastagliatura" o complessità di un grafico e può essere utilizzata per valutare il grado di caos del mercato.

Inputs:

• InpBoxSizesCount - numero delle diverse dimensioni del "box" per il calcolo
• InpMinBoxSize - dimensioni minime del "box"
• InpMaxBoxSize - dimensioni massime del "box"
• InpDataLength - numero di candele utilizzate per il calcolo

Algoritmo di funzionamento dell'indicatore:

1. Per ogni punto sul grafico, l'indicatore calcola la dimensione frattale utilizzando i dati delle ultime candele InputDataLength.
2. Il metodo di conteggio dei box viene applicato con diverse dimensioni dei "box", da InpMinBoxSize a InpMaxBoxSize.
3. Il numero di "box" necessari per coprire il grafico viene calcolato per ogni dimensione del "box".
4. Viene creato un grafico di dipendenza del logaritmo del numero di "box" dal logaritmo della dimensione del "box".
5. La pendenza del grafico viene calcolata con il metodo della regressione lineare, che rappresenta una stima della dimensione frattale.

Le variazioni della dimensione frattale possono segnalare un cambiamento nella modalità di mercato.

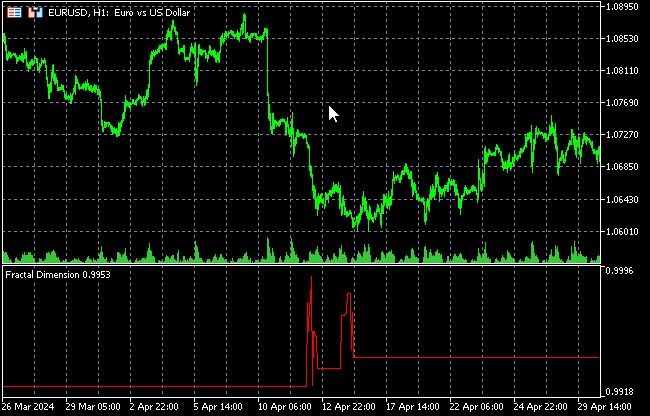
Analisi della ricorrenza per scoprire modelli nascosti nei movimenti dei prezzi

L'analisi della ricorrenza è un potente metodo di analisi delle serie temporali non lineari che può essere efficacemente applicato per studiare la dinamica dei mercati finanziari. Questo approccio ci permette di visualizzare e quantificare gli schemi ricorrenti nei sistemi dinamici complessi, tra i quali rientrano certamente i mercati finanziari.

Lo strumento principale dell'analisi delle ricorrenze è il diagramma di ricorrenza. Questo diagramma è una rappresentazione visiva degli stati ripetuti di un sistema nel tempo. In un diagramma di ricorrenza, un punto (i, j) viene colorato se gli stati ai tempi i e j sono simili in un certo senso.

Per costruire un diagramma di ricorrenza di una serie temporale finanziaria, procedere come segue:

1. Ricostruzione dello spazio di fase: Utilizzando il metodo del ritardo, trasformiamo le serie temporali dei prezzi unidimensionali in uno spazio di fase multidimensionale.
2. Determinazione della soglia di somiglianza: Selezioniamo un criterio in base al quale consideriamo due stati essere simili.
3. Costruzione della matrice di ricorrenza: Per ogni coppia di punti temporali, determiniamo se gli stati corrispondenti sono simili.
4. Visualizzazione: La matrice di ricorrenza viene visualizzata come un'immagine bidimensionale, in cui gli stati simili sono indicati da punti.

I diagrammi di ricorrenza ci permettono di identificare diversi tipi di dinamiche in un sistema:

• Le regioni omogenee indicano periodi stazionari
• Le linee diagonali indicano le dinamiche deterministiche
• Le strutture verticali e orizzontali possono indicare condizioni laminari
• L'assenza di una struttura è caratteristica di un processo casuale.

Per quantificare le strutture in un diagramma di ricorrenza, si utilizzano varie misure di ricorrenza, come la percentuale di ricorrenza, l'entropia delle linee diagonali, la lunghezza massima di una linea diagonale e altre.

L'applicazione dell'analisi delle ricorrenze alle serie temporali finanziarie può essere d'aiuto a:

1. Individuare le diverse modalità di mercato (trend, laterale, stato caotico)
2. Rilevare il cambio di modalità
3. Valutare la prevedibilità del mercato in periodi diversi
4. Rivelare modelli ciclici nascosti

Per l'implementazione pratica dell'analisi ricorrente nel trading, possiamo sviluppare un indicatore nel linguaggio MQL5, che costruirà un diagramma di ricorrenza e calcolerà le misure di ricorrenza in tempo reale. Un indicatore di questo tipo può servire come strumento aggiuntivo per prendere decisioni di trading, soprattutto se combinato con altri metodi di analisi tecnica.

Nella prossima sezione esamineremo un'implementazione specifica di tale indicatore e discuteremo come interpretare le sue letture nel contesto di una strategia di trading.

Indicatore di analisi della ricorrenza in MQL5

L'indicatore implementa il metodo dell'analisi della ricorrenza per studiare la dinamica dei mercati finanziari. Calcola tre misure chiave della ricorrenza: livello di ricorrenza, determinismo e laminarità.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 3
#property indicator_plots   3
#property indicator_label1  "Recurrence Rate"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Determinism"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed
#property indicator_label3  "Laminarity"
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrGreen

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 1;     // Time delay
input int    InpThreshold          = 10;    // Threshold (in points)
input int    InpWindowSize         = 200;   // Window size

double RecurrenceRateBuffer[];
double DeterminismBuffer[];
double LaminarityBuffer[];

int minRequiredBars;

int OnInit()
{
   SetIndexBuffer(0, RecurrenceRateBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, DeterminismBuffer, INDICATOR_DATA);
   SetIndexBuffer(2, LaminarityBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Recurrence Analysis");
   
   minRequiredBars = InpWindowSize + (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   if(rates_total < minRequiredBars) return(0);
   
   int start = (prev_calculated > 0) ? MathMax(prev_calculated - 1, minRequiredBars - 1) : minRequiredBars - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      CalculateRecurrenceMeasures(close, rates_total, i, RecurrenceRateBuffer[i], DeterminismBuffer[i], LaminarityBuffer[i]);
   }
   
   return(rates_total);
}

void CalculateRecurrenceMeasures(const double &price[], int price_total, int index, double &recurrenceRate, double &determinism, double &laminarity)
{
   if(index < minRequiredBars - 1 || index >= price_total)
   {
      recurrenceRate = 0;
      determinism = 0;
      laminarity = 0;
      return;
   }

   int windowStart = index - InpWindowSize + 1;
   int matrixSize = InpWindowSize - (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   int recurrenceCount = 0;
   int diagonalLines = 0;
   int verticalLines = 0;
   
   for(int i = 0; i < matrixSize; i++)
   {
      for(int j = 0; j < matrixSize; j++)
      {
         bool isRecurrent = IsRecurrent(price, price_total, windowStart + i, windowStart + j);
         if(isRecurrent)
         {
            recurrenceCount++;
            
            // Check for diagonal lines
            if(i > 0 && j > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j - 1))
               diagonalLines++;
            
            // Check for vertical lines
            if(i > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j))
               verticalLines++;
         }
      }
   }
   
   recurrenceRate = (double)recurrenceCount / (matrixSize * matrixSize);
   determinism = (recurrenceCount > 0) ? (double)diagonalLines / recurrenceCount : 0;
   laminarity = (recurrenceCount > 0) ? (double)verticalLines / recurrenceCount : 0;
}

bool IsRecurrent(const double &price[], int price_total, int i, int j)
{
   if(i < 0 || j < 0 || i >= price_total || j >= price_total) return false;

   double distance = 0;
   for(int d = 0; d < InpEmbeddingDimension; d++)
   {
      int offset = d * InpTimeDelay;
      if(i + offset >= price_total || j + offset >= price_total) return false;
      double diff = price[i + offset] - price[j + offset];
      distance += diff * diff;
   }
   distance = MathSqrt(distance);
   
   return (distance <= InpThreshold * _Point);
}

Caratteristiche principali dell'indicatore:

L'indicatore viene visualizzato in una finestra separata sotto il grafico dei prezzi e utilizza tre buffer per memorizzare e visualizzare i dati. L'indicatore calcola tre metriche: Tasso di Ricorrenza (linea blu), che mostra il livello complessivo di ricorrenza, Determinismo (linea rossa), che è una misura della prevedibilità del sistema, e Laminarità (linea verde), che valuta la tendenza del sistema a rimanere in un determinato stato.

Gli input dell'indicatore includono InpEmbeddingDimension (valore predefinito 3), che definisce la dimensione di incorporazione per la ricostruzione dello spazio di fase, InpTimeDelay (valore predefinito 1) per il ritardo durante la ricostruzione, InpThreshold (valore predefinito 10) per la soglia di somiglianza dello stato in punti e InpWindowSize (valore predefinito 200) per l'impostazione delle dimensioni della finestra in analisi.

L'algoritmo di funzionamento dell'indicatore si basa sul metodo del ritardo per ricostruire lo spazio delle fasi da una serie temporale unidimensionale di prezzi. Per ogni punto della finestra in analisi viene calcolata la sua "ricorrenza" rispetto agli altri punti. In seguito, sulla base della struttura ricorrente ottenuta, vengono calcolate tre misure: Tasso di Ricorrenza, che determina la proporzione dei punti di ricorrenza sul numero totale di punti, Determinismo, che mostra la proporzione dei punti di ricorrenza che formano linee diagonali, e Laminarità, che stima la proporzione dei punti di ricorrenza che formano linee verticali.

Applicazione del teorema dell'incorporazione di Takens nella previsione della volatilità

Il teorema dell’incorporazione di Takens è un risultato fondamentale della teoria dei sistemi dinamici che ha importanti implicazioni nell'analisi delle serie temporali, compresi i dati finanziari. Questo teorema afferma che un sistema dinamico può essere ricostruito dalle osservazioni di una sola variabile utilizzando il metodo del time-lag.

Nel contesto dei mercati finanziari, il teorema di Takens ci permette di ricostruire uno spazio di fase multidimensionale da una serie temporale unidimensionale di prezzi o rendimenti. Ciò è particolarmente utile quando si analizza la volatilità, che è una caratteristica fondamentale dei mercati finanziari.

Le fasi fondamentali dell'applicazione del teorema di Takens alla previsione della volatilità sono:

1. Ricostruzione dello spazio di fase:
   • Selezione della dimensione di incorporazione (m)
   • Selezione del ritardo temporale (τ)
   • Creazione di vettori m-dimensionali dalle serie temporali originali
2. Analisi dello spazio ricostruito:
   • Trovare i vicini più prossimi per ciascun punto
   • Stima della densità locale dei punti
3. Previsione della volatilità:
   • Utilizzo delle informazioni sulla densità locale per stimare la volatilità futura

Analizziamo questi passaggi in modo più dettagliato.

Ricostruzione dello spazio di fase:

Disponiamo di una serie temporale dei prezzi di chiusura {p(t)}. Creiamo vettori m-dimensionali come segue:

x(t) = [p(t), p(t+τ), p(t+2τ), ..., p(t+(m-1)τ)]

dove m è una dimensione di incorporazione e τ è un ritardo temporale.

La scelta dei valori corretti di m e τ è fondamentale per il successo della ricostruzione. In genere, τ viene scelto con i metodi dell'informazione reciproca o della funzione di autocorrelazione, mentre m viene scelto con il metodo del falso più vicino.

Analisi dello spazio ricostruito:

Dopo aver ricostruito lo spazio delle fasi, possiamo analizzare la struttura dell'attrattore del sistema. Per la previsione della volatilità, le informazioni sulla densità locale dei punti nello spazio delle fasi sono particolarmente importanti.

Per ogni punto x(t), troviamo i suoi k vicini più prossimi (di solito k viene scelto in un intervallo compreso tra 5 e 20) e calcoliamo la distanza media da questi vicini. Questa distanza serve a misurare la densità locale e quindi la volatilità locale.

Previsione della volatilità

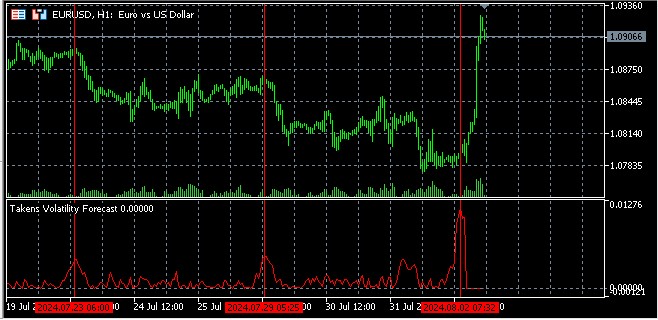
L'idea di base della previsione della volatilità utilizzando lo spazio di fase ricostruito è che punti vicini in questo spazio avranno probabilmente un comportamento simile nel prossimo futuro.

Per prevedere la volatilità al punto temporale t+h, bisogna:

• Trovare i k vicini più prossimi per il punto x(t) corrente nello spazio ricostruito
• Calcolare la volatilità effettiva per questi vicini h passi avanti
• Utilizzare la media di queste volatilità come previsione

Matematicamente, ciò può essere espresso come segue:

σ̂(t+h) = (1/k) Σ σ(ti+h), dove ti sono gli indici dei k vicini più prossimi di x(t)

I vantaggi di questo approccio:

• Tiene conto delle dinamiche di mercato non lineari
• Non richiede supposizioni sulla distribuzione dei rendimenti.
• Siamo in grado di cogliere schemi complessi nella volatilità

Contro:

• È sensibile alla scelta dei parametri (m, τ, k)
• Può essere computazionalmente costoso per grandi quantità di dati.

Implementazione

Creiamo un indicatore MQL5 che implementerà questo metodo di previsione della volatilità:

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Predicted Volatility"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double PredictedVolatilityBuffer[];

int OnInit()
{
   SetIndexBuffer(0, PredictedVolatilityBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Takens Volatility Forecast");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedVolatilityBuffer[i] = PredictVolatility(close, i);
      }
   }
   
   return(rates_total);
}

double PredictVolatility(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }
   
   double distances[];
   ArrayResize(distances, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double sum = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         sum += diff * diff;
      }
      distances[i] = sqrt(sum);
   }
   
   int sortedIndices[];
   ArrayCopy(sortedIndices, distances);
   ArraySort(sortedIndices);
   
   double sumVolatility = 0;
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - sortedIndices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double futureReturn = (price[neighborIndex + InpForecastHorizon] - price[neighborIndex]) / price[neighborIndex];
      sumVolatility += MathAbs(futureReturn);
   }
   
   return sumVolatility / InpNeighbors;
}

Metodi per la determinazione di un ritardo temporale e di una dimensione di incorporazione

Quando si ricostruisce lo spazio delle fasi utilizzando il teorema di Takens, è fondamentale scegliere correttamente due parametri chiave: il ritardo temporale (τ) e la dimensione di incorporazione (m). Una selezione errata di questi parametri può portare a una ricostruzione non corretta e di conseguenza, a conclusioni errate. Consideriamo due metodi principali per determinare questi parametri.

Metodo della funzione di autocorrelazione (ACF) per la determinazione del ritardo temporale

Il metodo si basa sull'idea di scegliere un ritardo temporale τ, in corrispondenza del quale la funzione di autocorrelazione attraversa per la prima volta lo zero o raggiunge un certo valore basso, ad esempio 1/e del valore iniziale. Ciò consente di scegliere un ritardo al quale i valori successivi della serie temporale diventano sufficientemente indipendenti l'uno dall'altro.

L'implementazione del metodo ACF in MQL5 può apparire come segue:

int FindOptimalLagACF(const double &price[], int maxLag, double threshold = 0.1)
{
   int size = ArraySize(price);
   if(size <= maxLag) return 1;
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += price[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(price[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (price[i] - mean) * (price[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

In questa implementazione, calcoliamo innanzitutto la media e la varianza della serie temporale. Quindi, per ogni lag da 1 a maxLag, si calcola il valore della funzione di autocorrelazione. Una volta che il valore ACF diventa inferiore o uguale a una determinata soglia (predefinita 0.1), si restituisce questo ritardo come ritardo ottimale.

Il metodo ACF ha i suoi pro e i suoi contro. Da un lato, è facile da implementare e intuitivo. Dall'altra parte, non tiene conto delle dipendenze non lineari nei dati, il che può essere un inconveniente significativo nell'analisi delle serie temporali finanziarie, che spesso presentano un comportamento non lineare.

Metodo dell'informazione reciproca (MI) per la determinazione del ritardo temporale

Questo metodo si basa sulla teoria dell'informazione ed è in grado di tenere conto delle dipendenze non lineari dei dati. L'idea è di scegliere un ritardo τ che corrisponde al primo minimo locale della funzione di informazione reciproca.

L'implementazione del metodo dell'informazione reciproca in MQL5 può apparire come segue:

double CalculateMutualInformation(const double &price[], int lag, int bins = 20)
{
   int size = ArraySize(price);
   if(size <= lag) return 0;
   
   double minPrice = price[ArrayMinimum(price)];
   double maxPrice = price[ArrayMaximum(price)];
   double binSize = (maxPrice - minPrice) / bins;
   
   int histogram[];
   ArrayResize(histogram, bins * bins);
   ArrayInitialize(histogram, 0);
   
   int totalPoints = 0;
   
   for(int i = 0; i < size - lag; i++)
   {
      int bin1 = (int)((price[i] - minPrice) / binSize);
      int bin2 = (int)((price[i + lag] - minPrice) / binSize);
      if(bin1 >= 0 && bin1 < bins && bin2 >= 0 && bin2 < bins)
      {
         histogram[bin1 * bins + bin2]++;
         totalPoints++;
      }
   }
   
   double mutualInfo = 0;
   for(int i = 0; i < bins; i++)
   {
      for(int j = 0; j < bins; j++)
      {
         if(histogram[i * bins + j] > 0)
         {
            double pxy = (double)histogram[i * bins + j] / totalPoints;
            double px = 0, py = 0;
            for(int k = 0; k < bins; k++)
            {
               px += (double)histogram[i * bins + k] / totalPoints;
               py += (double)histogram[k * bins + j] / totalPoints;
            }
            mutualInfo += pxy * MathLog(pxy / (px * py));
         }
      }
   }
   
   return mutualInfo;
}

int FindOptimalLagMI(const double &price[], int maxLag)
{
   double minMI = DBL_MAX;
   int optimalLag = 1;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double mi = CalculateMutualInformation(price, lag);
      if(mi < minMI)
      {
         minMI = mi;
         optimalLag = lag;
      }
      else if(mi > minMI)
      {
         break;
      }
   }
   
   return optimalLag;
}

In questa implementazione, definiamo innanzitutto la funzione CalculateMutualInformation che calcola l'informazione reciproca tra la serie originale e la sua versione traslata per un determinato ritardo. Poi, nella funzione FindOptimalLagMI, cerchiamo il primo minimo locale dell'informazione reciproca iterando su diversi valori di ritardo.

Il metodo dell'informazione reciproca ha un vantaggio rispetto al metodo ACF, in quanto è in grado di tenere conto delle dipendenze non lineari dei dati. Ciò lo rende più adatto all'analisi delle serie temporali finanziarie, che spesso presentano un comportamento complesso e non lineare. Tuttavia, questo metodo è più complesso da implementare e richiede un maggior numero di calcoli.

La scelta tra i metodi ACF e MI dipende dal compito specifico e dalle caratteristiche dei dati da analizzare. In alcuni casi, può essere utile utilizzare entrambi i metodi e confrontare i risultati. È inoltre importante ricordare che il ritardo temporale ottimale può cambiare nel tempo, soprattutto per le serie temporali finanziarie, per cui può essere consigliabile ricalcolare questo parametro periodicamente.

Algoritmo dei falsi vicini per la determinazione della dimensione di incorporazione ottimale

Una volta determinato il ritardo temporale ottimale, il passo successivo importante nella ricostruzione dello spazio di fase è la scelta di una dimensione di incorporazione appropriata. Uno dei metodi più diffusi per questo scopo è l'algoritmo False Nearest Neighbors (FNN).

L'idea dell'algoritmo FNN è quella di trovare una dimensione minima di incorporazione tale da riprodurre correttamente la struttura geometrica dell'attrattore nello spazio delle fasi. L'algoritmo si basa sul presupposto che in uno spazio di fase correttamente ricostruito, i punti vicini dovrebbero rimanere tali anche quando si passa a uno spazio di dimensioni superiori.

Diamo un’occhiata all'implementazione dell'algoritmo FNN nel linguaggio MQL5:

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

int FindOptimalEmbeddingDimension(const double &price[], int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = ArraySize(price);
   int minRequiredSize = (maxDim - 1) * delay + 1;
   if(size < minRequiredSize) return 1;
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = price[i - k * delay] - price[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(price, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

La funzione IsFalseNeighbor determina se due punti sono falsi vicini. Calcola la distanza tra i punti della dimensione corrente e quelli della dimensione aumentata di uno. Se la variazione relativa della distanza supera una determinata soglia, i punti sono considerati falsi vicini.

La funzione principale FindOptimalEmbeddingDimension itera attraverso le dimensioni da 1 a maxDim. Per ogni dimensione, si esaminano tutti i punti della serie temporale. Per ogni punto, troviamo il vicino più prossimo nella dimensione corrente. Quindi si controlla se il vicino trovato è falso utilizzando la funzione IsFalseNeighbor. Conta il numero totale di vicini e il numero di falsi vicini. Successivamente, calcolare la proporzione di falsi vicini. Se la proporzione di falsi vicini è inferiore alla soglia di tolleranza specificata, considera la dimensione corrente come ottimale e la restituisce.

L'algoritmo ha diversi parametri importanti. delay - ritardo temporale precedentemente determinato dal metodo ACF o MI. maxDim - dimensione massima di incorporazione da considerare. threshold - soglia per il rilevamento dei falsi vicini. tolerance - soglia di tolleranza per la proporzione di falsi vicini. La scelta di questi parametri può influenzare significativamente il risultato, quindi è importante sperimentare diversi valori e tenere conto delle specificità dei dati analizzati.

L'algoritmo FNN presenta una serie di vantaggi. Tiene conto della struttura geometrica dei dati nello spazio delle fasi. Il metodo è abbastanza robusto al rumore dei dati. Non richiede alcuna ipotesi preliminare sulla natura del sistema da studiare.

Implementazione del metodo di previsione basato sulla teoria del caos in MQL5

Una volta determinati i parametri ottimali per la ricostruzione dello spazio delle fasi, possiamo iniziare a implementare il metodo di previsione basato sulla teoria del caos. Questo metodo si basa sull'idea che gli stati vicini nello spazio delle fasi avranno un'evoluzione simile nel futuro prossimo.

L'idea di base del metodo è la seguente: troviamo gli stati del sistema nel passato che sono più vicini allo stato attuale. In base al loro comportamento futuro, facciamo una previsione sullo stato attuale. Questo approccio è noto come metodo analogo o metodo del vicino più prossimo.

Vediamo l'implementazione di questo metodo come indicatore per MetaTrader 5. L'indicatore eseguirà le seguenti operazioni:

1. Ricostruzione dello spazio di fase utilizzando il metodo del ritardo temporale.
2. Trovare i k vicini più prossimi per lo stato attuale del sistema.
3. Previsione del valore futuro in base al comportamento dei vicini trovati.

Ecco il codice dell'indicatore che implementa questo metodo:

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_chart_window
#property indicator_buffers 2
#property indicator_plots   2
#property indicator_label1  "Actual"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Predicted"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double ActualBuffer[];
double PredictedBuffer[];

int OnInit()
{
   SetIndexBuffer(0, ActualBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, PredictedBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, _Digits);
   IndicatorSetString(INDICATOR_SHORTNAME, "Chaos Theory Predictor");
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      ActualBuffer[i] = close[i];
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedBuffer[i] = PredictPrice(close, i);
      }
   }
   
   return(rates_total);
}

double PredictPrice(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;

   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }

   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);

   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }

   // Custom sort function for sorting distances and indices together
   SortDistancesWithIndices(distances, indices, dataSize);

   double prediction = 0;
   double weightSum = 0;

   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - indices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double weight = 1.0 / (distances[i] + 0.0001);  // Avoid division by zero
      prediction += weight * price[neighborIndex + InpForecastHorizon];
      weightSum += weight;
   }

   return prediction / weightSum;
}

void SortDistancesWithIndices(double &distances[], int &indices[], int size)
{
   for(int i = 0; i < size - 1; i++)
   {
      for(int j = i + 1; j < size; j++)
      {
         if(distances[i] > distances[j])
         {
            double tempDist = distances[i];
            distances[i] = distances[j];
            distances[j] = tempDist;

            int tempIndex = indices[i];
            indices[i] = indices[j];
            indices[j] = tempIndex;
         }
      }
   }
}

L'indicatore ricostruisce lo spazio delle fasi, trova i vicini più prossimi per lo stato attuale e utilizza i loro valori futuri per fare previsioni. Mostra sia i valori effettivi che quelli previsti su un grafico permettendoci di valutare visivamente la qualità della previsione.

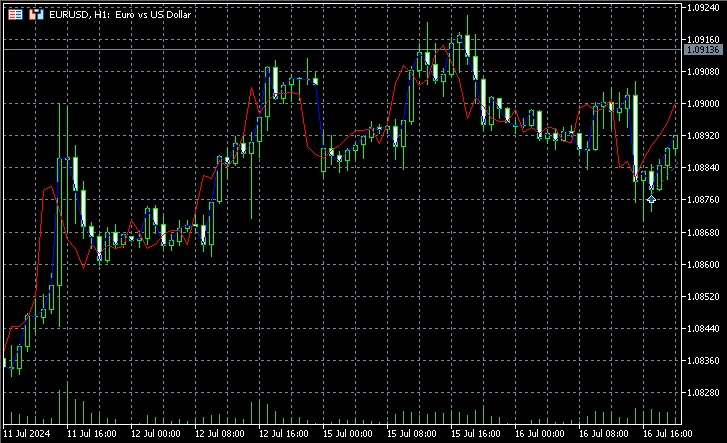
Gli aspetti chiave dell'implementazione includono l'uso di una media ponderata per la previsione, in cui il peso di ogni vicino è inversamente proporzionale alla sua distanza dallo stato corrente. Questo ci permette di tenere conto del fatto che i vicini più vicini probabilmente forniscono una previsione più accurata. A giudicare dalle schermate, l'indicatore prevede la direzione del movimento dei prezzi con diverse barre di anticipo.

Creazione di un EA concettuale

Siamo arrivati alla parte più interessante. Di seguito è riportato il codice per un lavoro completamente automatizzato basato sulla teoria del caos:

#property copyright "Copyright 2024, Author"
#property link      "https://www.example.com"
#property version   "1.00"
#property strict

#include <Arrays\ArrayObj.mqh>
#include <Trade\Trade.mqh>
CTrade Trade;
input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period
input double InpLotSize            = 0.1;   // Lot size

ulong g_ticket = 0;
datetime g_last_bar_time = 0;
double optimalTimeDelay;
double optimalEmbeddingDimension;
int OnInit()
{
   return(INIT_SUCCEEDED);
}

void OnDeinit(const int reason)
{
}

void OnTick()
{  
   OptimizeParameters();
   
   if(g_last_bar_time == iTime(_Symbol, PERIOD_CURRENT, 0)) return;
   g_last_bar_time = iTime(_Symbol, PERIOD_CURRENT, 0);
   
   double prediction = PredictPrice(iClose(_Symbol, PERIOD_CURRENT, 0), 0);
   Comment(prediction);
   
   if(prediction > iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close selling
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close SELL position: ", GetLastError());
         }
      }
      
      // Open buy
      double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
      ulong ticket = Trade.Buy(InpLotSize, _Symbol, ask, 0, 0, "ChaosBuy");
      if(ticket == 0)
         Print("Failed to open BUY position: ", GetLastError());
   }
   else if(prediction < iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close buying
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close BUY position: ", GetLastError());
         }
      }
      
      // Open sell
      double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
      ulong ticket = Trade.Sell(InpLotSize, _Symbol, bid, 0, 0, "ChaosSell");
      if(ticket == 0)
         Print("Failed to open SELL position: ", GetLastError());
   }
}

double PredictPrice(double price, int index)
{
   int vectorSize = optimalEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      currentVector[i] = iClose(_Symbol, PERIOD_CURRENT, index + i * optimalTimeDelay);
   }
   
   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         double diff = currentVector[j] - iClose(_Symbol, PERIOD_CURRENT, index + i + j * optimalTimeDelay);
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }
   
   // Use SortDoubleArray to sort by 'distances' array values
   SortDoubleArray(distances, indices);
   
   double prediction = 0;
   double weightSum = 0;
   
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index + indices[i];
      double weight = 1.0 / (distances[i] + 0.0001);
      prediction += weight * iClose(_Symbol, PERIOD_CURRENT, neighborIndex + InpForecastHorizon);
      weightSum += weight;
   }
   
   return prediction / weightSum;
}

void SortDoubleArray(double &distances[], int &indices[])
{
    int size = ArraySize(distances);
    for(int i = 0; i < size - 1; i++)
    {
        for(int j = i + 1; j < size; j++)
        {
            if(distances[i] > distances[j])
            {
                // Swap distances
                double tempDist = distances[i];
                distances[i] = distances[j];
                distances[j] = tempDist;
                
                // Swap corresponding indices
                int tempIndex = indices[i];
                indices[i] = indices[j];
                indices[j] = tempIndex;
            }
        }
    }
}

int FindOptimalLagACF(int maxLag, double threshold = 0.1)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += series[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(series[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (series[i] - mean) * (series[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

int FindOptimalEmbeddingDimension(int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = series[i - k * delay] - series[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(series, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

void OptimizeParameters()
{
   double optimalTimeDelay = FindOptimalLagACF(50);
   double optimalEmbeddingDimension = FindOptimalEmbeddingDimension(optimalTimeDelay, 10);
   Print("Optimal Time Delay: ", optimalTimeDelay);
   Print("Optimal Embedding Dimension: ", optimalEmbeddingDimension);
}

Questo codice è un EA per MetaTrader 5 che utilizza i concetti della teoria del caos per prevedere i prezzi dei mercati finanziari. L'EA implementa il metodo di previsione basato sul metodo dei vicini più prossimi nello spazio di fase ricostruito.

L'EA ha i seguenti input:

• InpEmbeddingDimension - dimensione di incorporamento per la ricostruzione dello spazio di fase (valore predefinito - 3)
• InpTimeDelay - ritardo temporale per la ricostruzione (valore predefinito - 5)
• InpNeighbors - numero di vicini più prossimi per la previsione (default - 10)
• InpForecastHorizon - orizzonte di previsione (predefinito - 10)
• InpLookback - periodo di lookback per l'analisi (default - 1000)
• InpLotSize - dimensione del lotto per la negoziazione (predefinito - 0.1)

L'EA funziona come segue:

1. A ogni nuova barra, ottimizza i parametri optimalTimeDelay e optimalEmbeddingDimension utilizzando rispettivamente il metodo della funzione di autocorrelazione (ACF) e l'algoritmo dei falsi vicini (FNN).
2. Quindi fa una previsione del prezzo in base allo stato attuale del sistema utilizzando il metodo dei vicini più prossimi.
3. Se il prezzo previsto è superiore al prezzo corrente, l'EA chiude tutte le posizioni di vendita aperte e apre una nuova posizione di acquisto. Se il prezzo previsto è inferiore al prezzo corrente, l'EA chiude tutte le posizioni di acquisto aperte e apre una nuova posizione di vendita.

L'EA utilizza la funzione PredictPrice, che:

• Ricostruisce lo spazio di fase utilizzando una dimensione di incorporazione ottimale e un ritardo temporale.
• Trova le distanze tra lo stato attuale del sistema e tutti gli stati nel periodo di lookback.
• Ordina gli stati in base alla distanza crescente.
• Calcola una media ponderata dei prezzi futuri dei vicini di InpNeighbors, dove il peso di ogni vicino è inversamente proporzionale alla sua distanza dallo stato corrente.
• Restituisce una media ponderata come previsione di prezzo.

L'EA include anche le funzioni FindOptimalLagACF e FindOptimalEmbeddingDimension, utilizzate per ottimizzare rispettivamente i parametri optimalTimeDelay e optimalEmbeddingDimension.

Nel complesso, l'EA fornisce un approccio innovativo alla previsione dei prezzi nei mercati finanziari utilizzando i concetti della teoria del caos. Può aiutare i trader a prendere decisioni più informate e potenzialmente ad aumentare i rendimenti degli investimenti.

Test con l'ottimizzazione automatica

Consideriamo il lavoro del nostro EA su diversi simboli. La prima coppia di valute, EURUSD, periodo dal 01.01.2016:

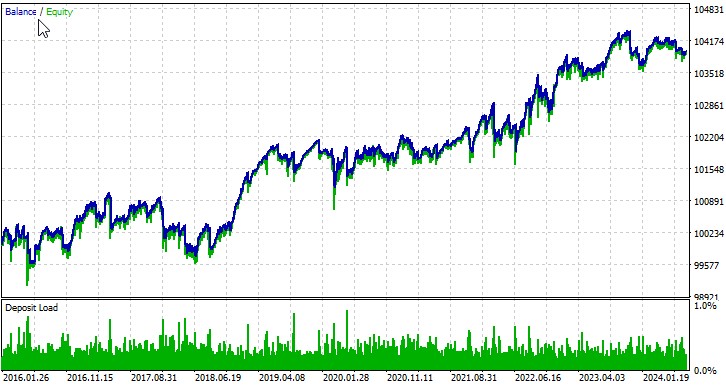
Seconda coppia, AUDUSD:

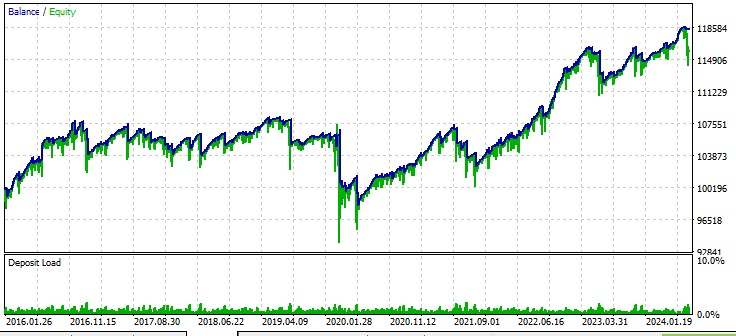
Terza coppia, GBPUSD:

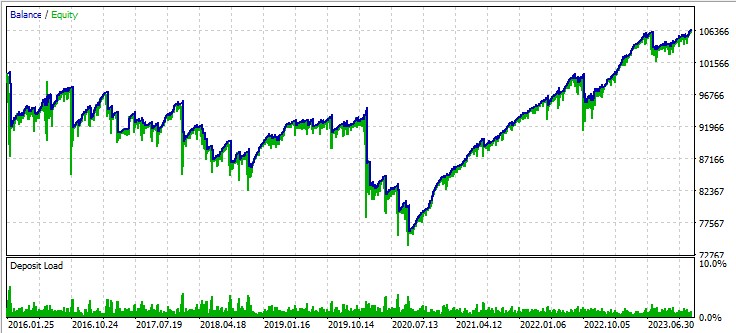
I prossimi passi

L'ulteriore sviluppo del nostro EA basato sulla teoria del caos richiederà test approfonditi e ottimizzazioni. Per comprendere meglio la sua efficienza in diverse condizioni di mercato, sono necessari test su larga scala su diversi periodi e strumenti finanziari. L'uso di metodi di apprendimento automatico può aiutare a ottimizzare i parametri dell'EA aumentandone l'adattabilità alle mutevoli realtà del mercato.

Particolare attenzione deve essere prestata al miglioramento del sistema di gestione del rischio. L'implementazione di una gestione dinamica del dimensionamento delle posizioni, che tenga conto della volatilità attuale del mercato e delle previsioni di volatilità caotica, può migliorare significativamente la resilienza della strategia.

Conclusioni

In questo articolo abbiamo esaminato l'applicazione della teoria del caos all'analisi e alla previsione dei mercati finanziari. Abbiamo studiato concetti chiave come la ricostruzione dello spazio di fase, la determinazione della dimensione ottimale di incorporazione e del ritardo temporale e il metodo di previsione del vicino più prossimo.

L'EA che abbiamo sviluppato dimostra il potenziale dell'utilizzo della teoria del caos nel trading algoritmico. I risultati dei test su varie coppie di valute dimostrano che la strategia è in grado di generare profitti, anche se con diversi gradi di successo sui vari strumenti.

Tuttavia, è importante notare che l'applicazione della teoria del caos alla finanza comporta una serie di sfide. I mercati finanziari sono sistemi estremamente complessi influenzati da numerosi fattori, molti dei quali sono difficili o addirittura impossibili da prendere in considerazione in un modello. Inoltre, la natura stessa dei sistemi caotici rende fondamentalmente impossibile la previsione a lungo termine - questo è uno delle principali supposizioni dei ricercatori seri.

In conclusione, sebbene la teoria del caos non sia il Santo Graal per le previsioni di mercato, rappresenta una direzione promettente per ulteriori ricerche e sviluppi nei campi dell'analisi finanziaria e del trading algoritmico. È chiaro che la combinazione dei metodi della teoria del caos con altri approcci, come l'apprendimento automatico e l'analisi dei big data, può aprire nuove possibilità.