Características del Wizard MQL5 que debe conocer (Parte 16): Método de componentes principales con vectores propios

Introducción

El Método de Componentes Principales (Principal Component Analysis, PCA) se centra únicamente en los "componentes principales" entre muchas dimensiones de un conjunto de datos, cuyas dimensiones se reducen ignorando las partes "no principales". Quizá el ejemplo más sencillo de reducción de la dimensionalidad sea una matriz como la presentada a continuación:

Si fuera un punto de datos, podría representarse como un único valor:

Así, este único valor implica reducir la dimensionalidad de 9 a 1. Nuestra ilustración anterior reduce una matriz a su determinante, lo cual equivale aproximadamente a una reducción de la dimensionalidad.

El PCA ofrece un enfoque más profundo utilizando valores y vectores propios. Normalmente, los conjuntos de datos procesados con PCA poseen una estructura matricial, mientras que los componentes principales que se buscan en la matriz suponen una única columna vectorial (o fila) que es la más significativa entre los demás vectores de la matriz y puede bastar como representante de toda la matriz. Como ya hemos mencionado en la introducción, este vector contendrá los componentes principales de toda la matriz, de ahí el nombre PCA. Sin embargo, la identificación de este vector no tiene que hacerse necesariamente usando vectores y valores propios. Otras variantes alternativas serían la descomposición en valores singulares (singular value decomposition, SVD) y el método de las potencias.

La SVD consigue reducir la dimensionalidad partiendo el conjunto de datos matriciales en tres matrices separadas, una de las cuales, la matriz Σ, definirá las direcciones más importantes de la varianza en los datos. Esta matriz, también conocida como matriz diagonal, contiene valores singulares que representan los valores de varianza a lo largo de cada dirección predeterminada (escrita en otra de las tres matrices, con frecuencia denominada U). Cuanto mayor sea el valor singular, más significativa será la dirección correspondiente para explicar la variabilidad de los datos. Esto hace que la columna U con el valor singular más alto se seleccione como representativa de toda la matriz, reduciendo de hecho la dimensionalidad de la matriz a un único vector.

Por el contrario, el método de las potencias refina iterativamente la estimación del vector tendiendo al vector propio dominante. Este vector propio captará la dirección con los cambios más significativos en los datos y representará la dimensionalidad reducida de la matriz de origen.

Sin embargo, como en este artículo nos centramos en los vectores y valores propios, podemos transformar una matriz n x n en n vectores posibles de tamaño n, asignando a cada uno de estos vectores un valor propio. Este valor propio determinará entonces la elección de un único vector propio para representar mejor la matriz; en este caso, además, un valor más alto indicará de nuevo una mayor correlación positiva para explicar la variabilidad de los datos.

Entonces, ¿para qué sirve la reducción de la dimensionalidad de los conjuntos de datos? Resumiendo, creo que se trata de la gestión del ruido blanco Sin embargo, una respuesta más significativa sería la mejora de la visualización, ya que los datos de alta dimensionalidad resultan más difíciles de mostrar y presentar en una forma familiar como el diagrama de puntos y otros formatos gráficos convencionales. En este caso, la reducción de la dimensionalidad (coordenadas del sector) a 2 ó 3 puede servir de ayuda. Otra ventaja importante es la reducción del coste computacional de la comparación de los puntos de datos en la previsión.

Esta comparación se realiza durante el entrenamiento del modelo, lo cual ahorra tiempo de entrenamiento y potencia de cálculo. Esto conduce a la "maldición de la dimensionalidad", en la que los datos de alta dimensionalidad tienden a dar resultados precisos cuando se prueban en una muestra durante el entrenamiento, pero este rendimiento se degrada más rápidamente que para los datos de baja dimensionalidad cuando se validan de forma cruzada. Reducir el tamaño puede ayudarnos a solucionar este problema. Además, la reducción de la dimensionalidad se traduce en menos ruido en los conjuntos de datos, lo cual en teoría debería mejorar el rendimiento. Por último, los datos de menor dimensionalidad ocupan menos espacio y, por tanto, se gestionan con mayor eficiencia, especialmente cuando se entrenan modelos de gran tamaño.

PCA y vectores propios

Formalmente, los vectores propios se definen usando la ecuación:

Av =λv

donde:

• A — matriz de transformación
• v — vector a transformar
• a y λ — factor de escala aplicado al vector.

El principio central de los vectores propios es que para muchas (pero no para todas) matrices cuadradas A de tamaño n x n, existen n vectores, cada uno de tamaño n, tales que cuando la matriz A se aplica a cualquiera de estos vectores, la dirección del producto resultante conserva la misma dirección que el vector original, siendo el único cambio la escala proporcional de los valores del vector original. En la ecuación anterior, dicha escala se etiqueta como lambda y se denomina más correctamente valor propio. Existe un valor propio por cada vector propio.

No todas las matrices producen el número necesario de vectores propios porque algunas están deformadas, pero por cada vector producido, existe un candidato para una dimensionalidad reducida de la matriz original. El ganador entre estos vectores se elige según el valor propio, correspondiendo los valores más altos a una mejor cobertura de la varianza del conjunto de datos y una menor cobertura de su ruido.

El proceso de determinación del vector propio empieza normalizando la matriz del conjunto de datos. Esto puede hacerse de varias maneras. En este artículo, utilizaremos la normalización z. Después de normalizar los datos de la matriz, se calcula el equivalente de la matriz de covarianza. Cada elemento de la matriz refleja la covarianza entre dos elementos cualesquiera; en este caso, además, la diagonal refleja la covarianza de cada elemento consigo mismo. Además de la mayor eficiencia computacional en el cálculo de los vectores propios y los valores al usarse la matriz de covarianza, los valores de los datos obtenidos utilizando la matriz de covarianza reflejan las relaciones lineales entre los puntos de datos de la matriz y proporcionan una imagen clara de cómo cada punto de datos de la matriz se compara con otros puntos.

El cálculo de la matriz de covarianza para los tipos de datos matriciales se realiza con la ayuda de las funciones incorporadas de MQL5, en este caso, la función Cov(). Una vez obtenida la matriz de covarianza, podemos calcular los vectores propios y sus valores mediante la función incorporada Eig(). Tras obtener los vectores propios y sus valores correspondientes, transpondremos la matriz de vectores propios y la multiplicaremos por la matriz original de rendimientos. Las filas de la matriz representan los pesos de la varianza de cada portafolio, por lo que el portafolio seleccionado dependerá de estos pesos. Esto se debe a que su dirección refleja la varianza máxima de los datos dentro del conjunto de datos seleccionados.

Podemos crear una ilustración sencilla que explique la esencia de la fijación de la varianza máxima tomando las coordenadas x e y a lo largo de una curva elíptica como un conjunto de datos en el que cada punto de datos tiene dos dimensiones x e y. Si representáramos esta elipse en un gráfico, tendría el aspecto siguiente:

fuente 

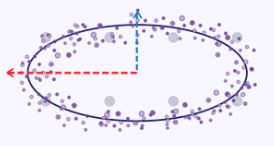
Por lo tanto, si nos proponemos reducir estas dimensiones x e y a un único número (menor) de medidas, como puede verse en la imagen del gráfico anterior, los valores de las coordenadas x serán más representativos de las dos, ya que la elipse tiende a estirarse con más fuerza a lo largo de su eje x que a lo largo de su eje y.

En general, sin embargo, debemos elegir entre reducir las mediciones y preservar la información. Aunque la reducción de la dimensionalidad tiene las ventajas enumeradas anteriormente, tenemos que considerar su interpretación y la sencillez de su explicación.

Implementación con MQL5

Un sistema comercial que utilice PCA con vectores propios suele hacerlo seleccionando de forma óptima un portafolio a partir de un conjunto o conjuntos de iteraciones diferentes. Para ilustrar esto, podemos tomar la matriz de la que hablamos en la introducción anterior simplemente como una parte compuesta de vectores, donde cada vector representa el rendimiento por dólar invertido en cada activo con tres modos de asignación diferentes. La asignación de pesos real de cada vector (portafolio) solo adquiere importancia una vez elegido el vector propio, y la asignación de activos que debe adoptarse en función de este vector se requiere entonces para futuras inversiones.

Si nuestros activos son SPY, TLT y PDBC, entonces su distribución estimada, en base a los rendimientos a 5 años de cada uno de estos ETF, será:

Así pues, el PCA con vectores propios nos ayudará a elegir el portafolio (asignación de activos) ideal entre estas 3 opciones en función de su rendimiento en los últimos 5 años. Enumerando los pasos anteriores, lo primero que deberemos hacer siempre es normalizar el conjunto de datos y, como ya hemos mencionado, para ello utilizaremos la normalización z. A continuación mostramos el código fuente:

//+------------------------------------------------------------------+
//| Z-Normalization                                                  |
//+------------------------------------------------------------------+
matrix ZNorm(matrix &M)
{  matrix _z;
   _z.Init(M.Rows(), M.Cols());
   _z.Copy(M);
   if(M.Rows() > 0 && M.Cols() > 0)
   {  double _std_min = (M.Max() - M.Min()) / (M.Rows() * M.Cols());
      if(_std_min > 0.0)
      {  double _mean = M.Mean();
         double _std = fmax(_std_min, M.Std());
         for(ulong i = 0; i < M.Rows(); i++)
         {  for(ulong ii = 0; ii < M.Cols(); ii++)
            {  _z[i][ii] = (M[i][ii] - _mean) / _std;
            }
         }
      }
   }
   return(_z);
}

Después de normalizar la matriz de rendimientos, calcularemos la matriz de covarianza de lo que hemos normalizado. El tipo de datos incorporado en MQL5 para las matrices puede hacer esto por nosotros en una línea:

   matrix _z = ZNorm(_m);
   matrix _cov_col = _z.Cov(false);

Con las relaciones de covarianza de cada dato de la matriz, podremos calcular los vectores y valores propios. El cálculo también ocupará una línea:

   matrix _e_vectors;
   vector _e_values;
   _cov_col.Eig(_e_vectors, _e_values);

La salida de la función anterior será dual. Nos interesan sobre todo los vectores propios retornados en forma de matriz. Esta matriz, transpuesta y multiplicada por la matriz de rendimiento original, nos dará lo que buscamos, la matriz de proyección P. Se trata de una matriz con filas para cada uno de los portafolios posibles, donde la columna de cada fila representa el factor de ponderación para cada uno de los tres vectores propios generados. Por ejemplo, en la primera fila, el valor mayor estará en la primera columna. Esto significa que la mayor parte de la varianza de los rendimientos de este portafolio se deberá al primer vector propio. Si nos fijamos en el valor propio de este vector propio, veremos que es el mayor de los tres. Por lo tanto, esto significa que entre los tres portafolios, el primero será responsable de la mayoría de los patrones (o tendencias) significativos presentados en la matriz de datos.

En nuestro caso, todos los portafolios han generado rendimientos positivos cuando se suman sus valores en todas las columnas, ya que cada columna representa un portafolio. De hecho, los únicos rendimientos negativos se producen al invertir en ETF de bonos PDBC, independientemente de la asignación. Esto significa que si alguien quiere "perpetuar" esa rentabilidad cubierta, diversificada o de buena beta, tendrá que quedarse con el portafolio 1. Una vez más, la tendencia general de la matriz de datos de rentabilidad será de rentabilidades positivas en acciones y materias primas y negativas en bonos. Así, el PCA con vectores propios puede clasificar el portafolio entre los que tienen más probabilidades de continuar la tendencia, como en el caso del portafolio 1, o incluso hacer lo contrario, que en nuestro caso sería el portafolio 3, ya que en la matriz de proyección el valor máximo de la 3ª fila está en la columna 3 y el 3er vector propio tenía el valor más bajo.

En particular, este portafolio no tiene el rendimiento más alto, y el propio proceso no lo selecciona como tal. Lo único que hace es ofrecer estimaciones provisionales del mantenimiento del statu quo. Todo esto parece innecesariamente complicado respecto a decisiones que podrían tomarse fácilmente en la verificación, y sin embargo, a medida que los datos retornados o las matrices analizadas se hacen más grandes, con más filas y columnas (el PCA con vectores propios requiere matrices cuadradas), este proceso empieza a pasar factura.

Para demostrar el PCA en la clase de señal, nos veremos limitados por el hecho de que, por defecto, solo se puede probar un símbolo en un único marco temporal, lo cual significa que los conceptos anteriores sobre la selección de portafolios no se aplicarán inicialmente. Existen soluciones para estas limitaciones, y quizá podamos abordarlas en otro artículo futuro, pero por ahora trabajaremos con estas restricciones.

Analizaremos las variaciones de precio de cada día de la semana, símbolo por símbolo, en el marco temporal diario. Como en una semana hay 5 días de negociación, nuestra matriz tendrá 5 columnas y, para obtener las 5 filas necesarias para analizar los vectores propios del PCA, consideraremos 5 tipos diferentes de precios, a saber, Open, High, Low, Close y Typical. La determinación de los vectores propios y sus valores seguirá los pasos ya mencionados.

Lo mismo ocurre con la obtención de la matriz de proyección, y una vez que la tengamos, podremos identificar fácilmente el día de negociación de la semana y el tipo de precio aplicado que reflejen la mayor varianza. Si seguimos el código del script de abajo:

   matrix _t = _e_vectors.Transpose();
   matrix _p = _m * _t;
   //Print(" projection: \n", _p);
   vector _max_row = _p.Max(0);
   vector _max_col = _p.Max(1);
   double _days[];
   _max_row.Swap(_days);
   PrintFormat(" best trade day is: %s", EnumToString(ENUM_DAY_OF_WEEK(ArrayMaximum(_days)+1)));
   ENUM_APPLIED_PRICE _price[__SIZE];
   _price[0] = PRICE_OPEN;
   _price[1] = PRICE_WEIGHTED;
   _price[2] = PRICE_MEDIAN;
   _price[3] = PRICE_CLOSE;
   _price[4] = PRICE_TYPICAL;
   double _prices[];
   _max_col.Swap(_prices);
   PrintFormat(" best applied price is: %s", EnumToString(_price[ArrayMaximum(_prices)]));
   PrintFormat(" worst trade day is: %s", EnumToString(ENUM_DAY_OF_WEEK(ArrayMinimum(_days)+1)));
   PrintFormat(" worst applied price is: %s", EnumToString(_price[ArrayMinimum(_prices)]));

Los mensajes en el registro se recogerán en la sección "Pruebas y resultados de la estrategia".

Así, a partir de los registros anteriores, podemos ver que la mayoría de las fluctuaciones en los precios del símbolo cuyo gráfico se adjunta al script (EURJPY) se producen los jueves en los precios de cierre. ¿Y qué significa eso? Esto significa que si alguien encuentra interesante la tendencia general y el comportamiento del precio del EURJPY y quiere jugar a un juego similar en el futuro, será mejor que centre sus transacciones en el jueves y utilice un rango de precios de cierre. Supongamos que el EURJPY forma parte de una posición establecida en el portafolio de alguien, y posteriormente se reduce la influencia de EURJPY. ¿Cómo podemos ayudar a la matriz de posiciones? Los "peores" días de negociación y series de precios pueden usarse para determinar cuándo y cómo cerrar las posiciones en EURJPY.

Por lo tanto, nuestra matriz de posición nos recomienda ciertos días de negociación y ciertas series de precios, así que vamos a utilizar a continuación una clase de señal simple que tenga esto en cuenta.

   int _buffer_size = CopyRates(Symbol(), Period(), __start, __stop, _rates);
   PrintFormat(__FUNCSIG__+" buffered: %i",_buffer_size);
   if(_buffer_size >= 1)
   {  for(int i = 1; i < _buffer_size - 1; i++)
      {  TimeToStruct(_rates[i].time,_datetime);
         int _iii = int(_datetime.day_of_week)-1;
         if(_datetime.day_of_week == SUNDAY || _datetime.day_of_week == SATURDAY)
         {  _iii = 0;
         }
         for(int ii = 0; ii < __SIZE; ii++)
         {  
                ...

                ...
         }
      }
   }

Pruebas de la estrategia y resultados

Para realizar pruebas sobre la historia utilizando el asesor experto incorporado en el Wizard MQL5, primero tendremos que ejecutar el script en el gráfico y el marco temporal del símbolo que vamos a probar. En nuestro ejemplo será EURUSD H4. Si ejecutamos el script en el gráfico, obtendremos el viernes y el precio ponderado como los parámetros "ideales" o determinantes de la varianza para EURUSD H4. Los mensajes de registro serán los siguientes:

2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      best trade day is: FRIDAY
2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      best applied price is: PRICE_WEIGHTED
2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      worst trade day is: TUESDAY
2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      worst applied price is: PRICE_OPEN

Nuestro script también tiene dos parámetros de entrada que definirán el periodo a analizar, a saber, la fecha inicial y la fecha final. Ambas serán variables de tipo datetime. Las fijaremos en el 2022.01.01 y el 2023.01.01 para probar primero nuestro EA en este periodo, y luego realizaremos una comprobación cruzada con los mismos ajustes en el periodo del 2023.01.01.01 al 2024.01.01. El script recomienda el viernes y el precio ponderado como las mejores variables para determinar la varianza. ¿Cómo utilizaremos esta información al diseñar una clase de señal? Como siempre, existe una serie de opciones a considerar, pero analizaremos un simple indicador de cruce de precios con una media móvil. Usando la media móvil del precio aplicado recomendado y realizando operaciones solo en el día de la semana recomendado, intentaremos comprobar la lógica de nuestro script. Así, el código para nuestra clase de señales será muy sencillo:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalPCA::LongCondition(void)
{  int _result = 0;
   m_MA.Refresh(-1);
   m_close.Refresh(-1);
   m_time.Refresh(-1);
//
   if(m_MA.Main(StartIndex()+1) > m_close.GetData(StartIndex()+1) && m_MA.Main(StartIndex()) < m_close.GetData(StartIndex()))
   {  _result = 100;
      //PrintFormat(__FUNCSIG__);
   }
   if(m_pca)
   {  TimeToStruct(m_time.GetData(StartIndex()),__D);
      if(__D.day_of_week != m_day)
      {  _result = 0;
      }
   }
//
   return(_result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalPCA::ShortCondition(void)
{  int _result = 0;
   m_MA.Refresh(-1);
   m_close.Refresh(-1);
//
   if(m_MA.Main(StartIndex()+1) < m_close.GetData(StartIndex()+1) && m_MA.Main(StartIndex()) > m_close.GetData(StartIndex()))
   {  _result = 100;
      //PrintFormat(__FUNCSIG__);
   }
   if(m_pca)
   {  TimeToStruct(m_time.GetData(StartIndex()),__D);
      if(__D.day_of_week != m_day)
      {  _result = 0;
      }
   }
//
   return(_result);
}

Como siempre, no utilizaremos niveles de precios para el take profit o el stop loss y usaremos estrictamente órdenes límite. Esto significa que una vez que una posición sea abierta por nuestro EA, se cerrará solo en la reversión. Claro que puede resultar un enfoque de alto riesgo, pero para nuestros fines será suficiente. Si hacemos un test histórico sobre el primer periodo, obtendremos el siguiente informe y curva de capital:

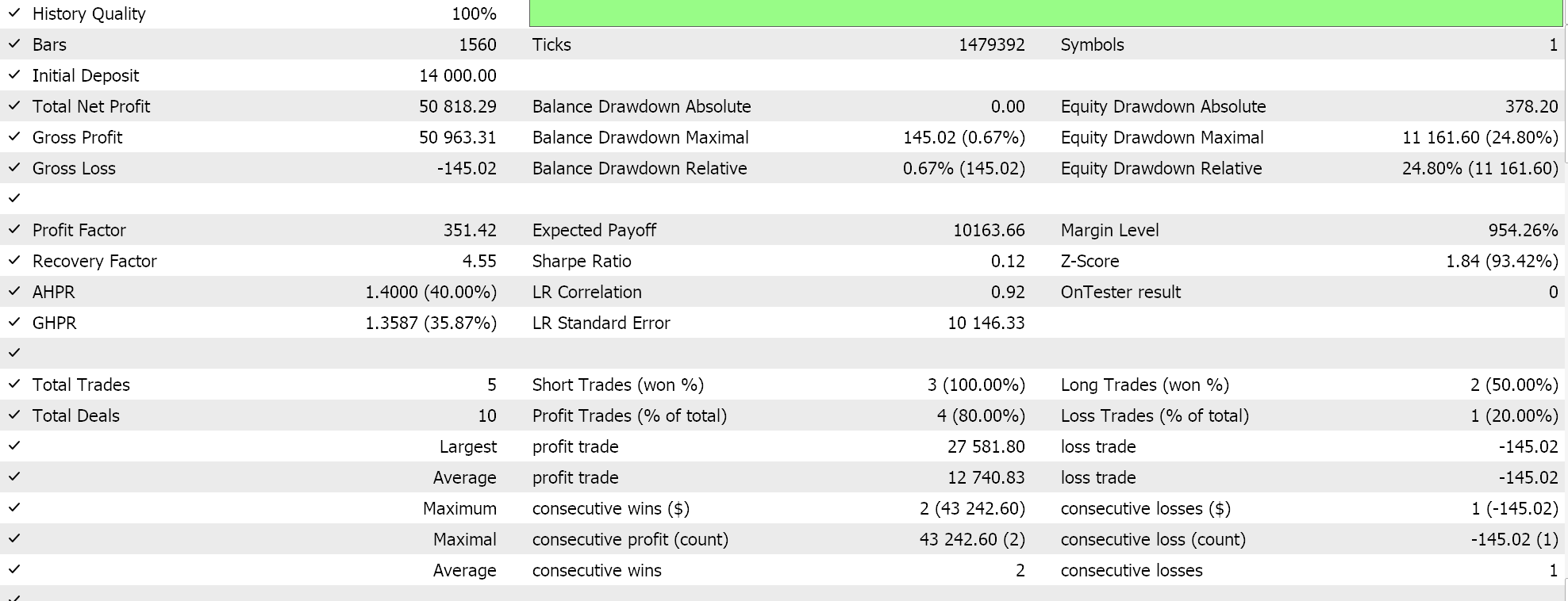
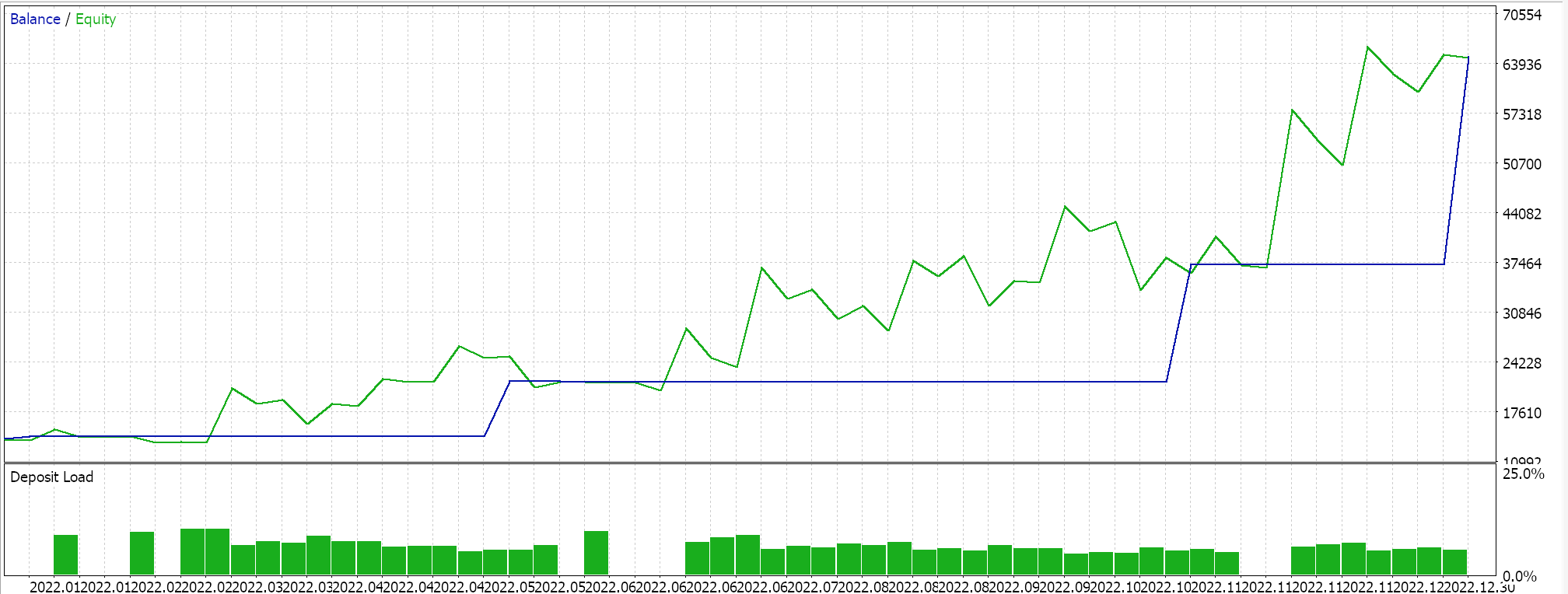
Los resultados anteriores se corresponden con el periodo comprendido entre el 01.01.2022 y el 01.01.2023. Si intentamos hacer una prueba con la misma configuración durante un periodo más largo que el periodo de análisis del script, del 2022.01.01 al 2024.01.01, obtendremos los siguientes resultados:

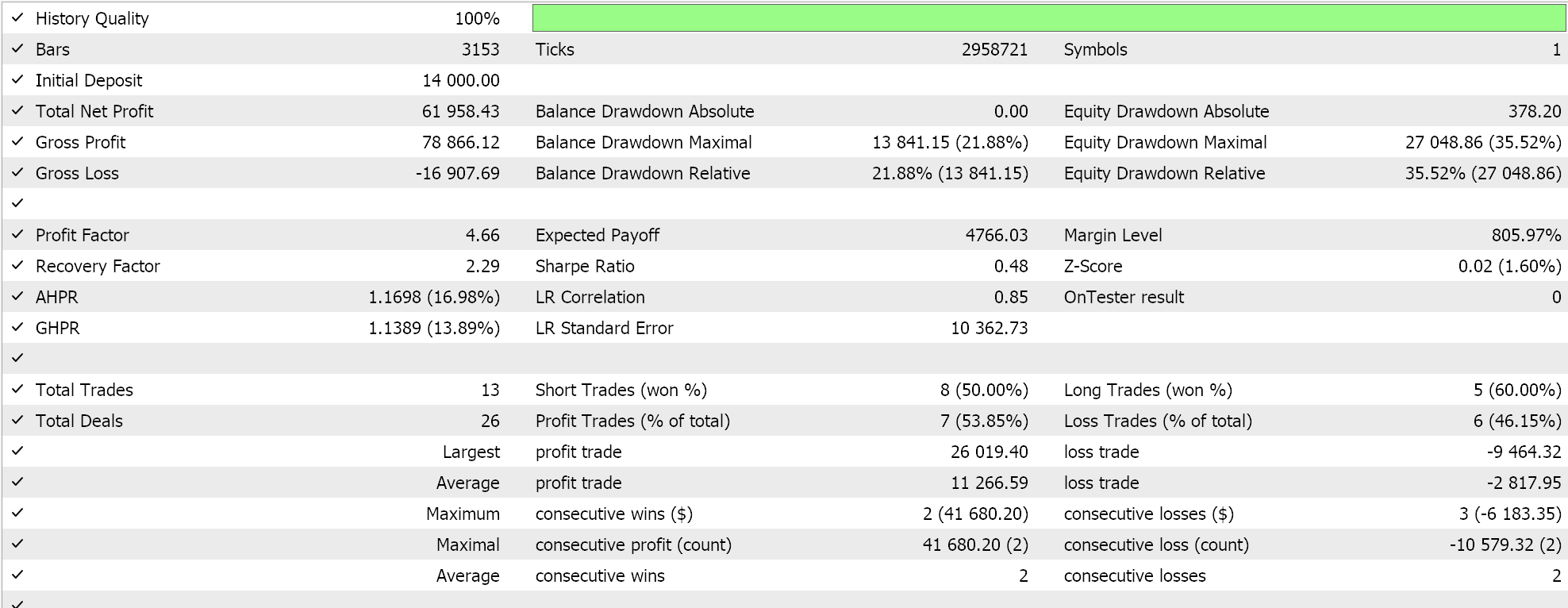
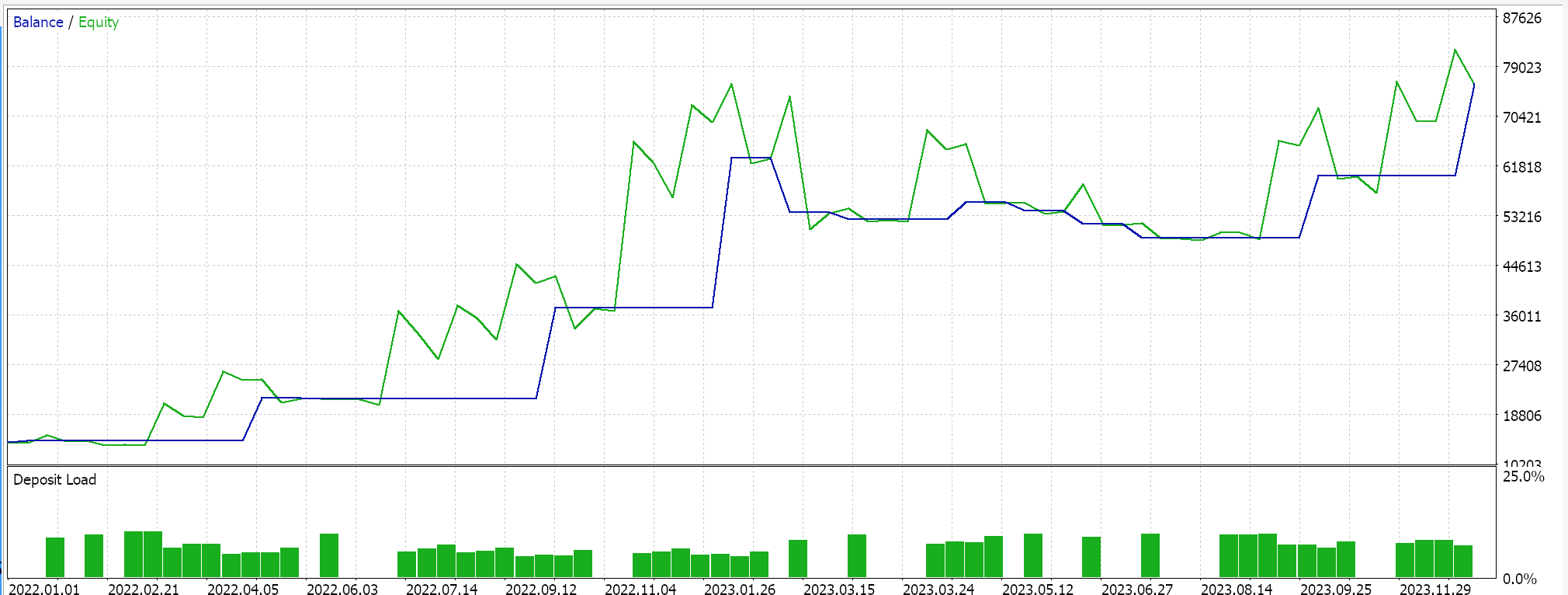
Nuestra señal contiene bastantes limitaciones y no se realizan muchas transacciones, lo cual hace que la eficacia de las pruebas sea cuestionable. Tanto más que los periodos de prueba de varios años no son fiables. A modo de control, además de la comprobación cruzada descrita anteriormente, también podemos realizar pruebas con diferentes precios aplicados mientras negociamos en cualquier día de la semana con la misma configuración del EA. Los resultados serán los siguientes:

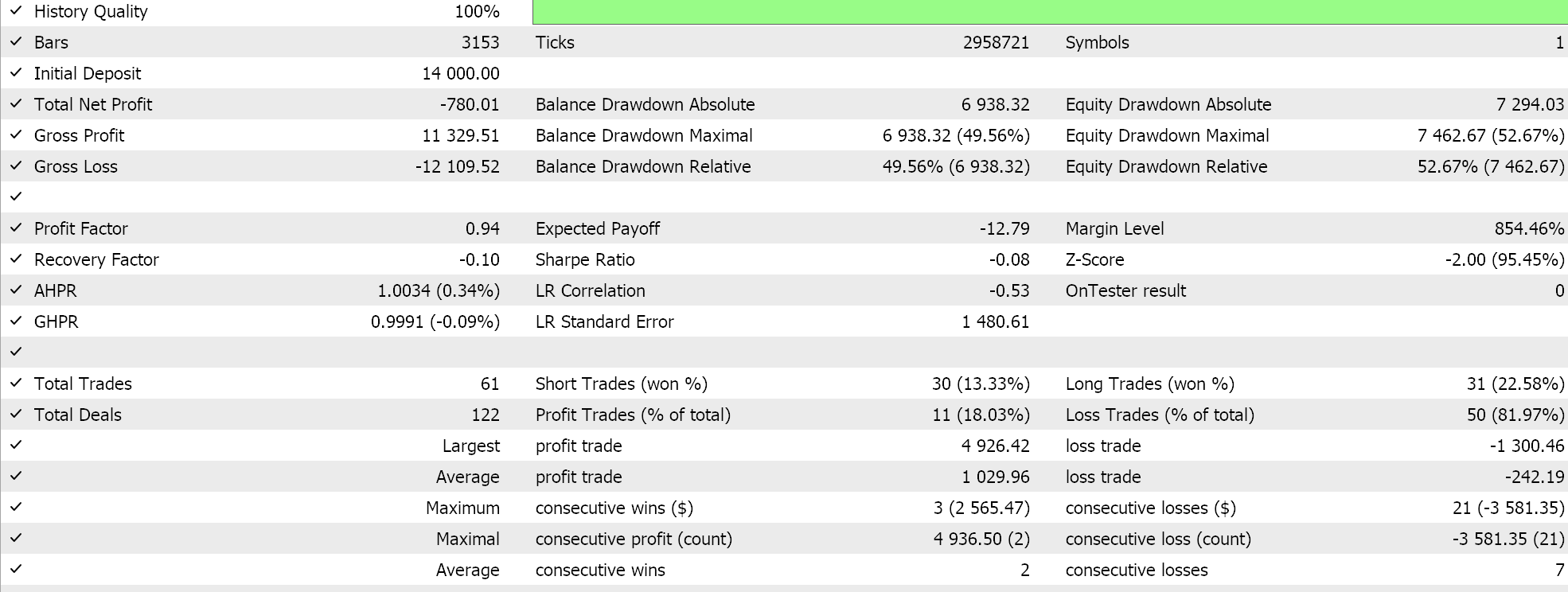
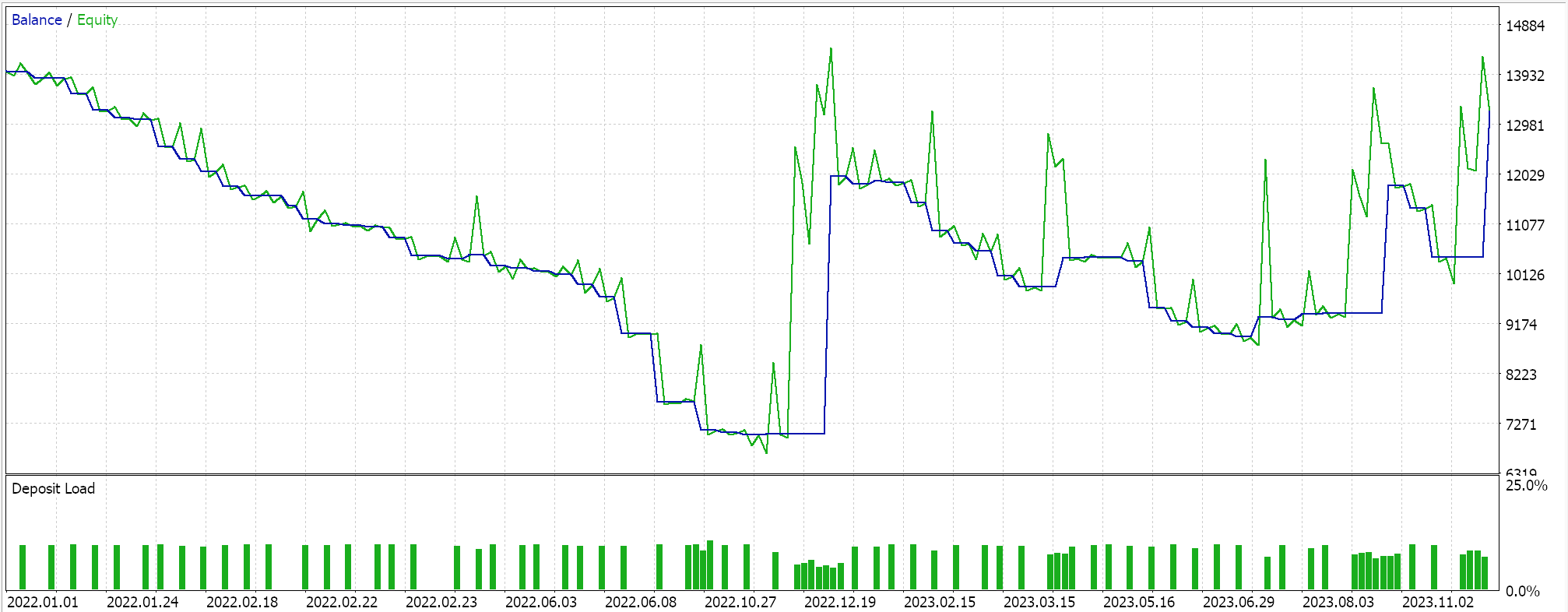
El rendimiento global se resiente claramente en cuanto superamos las recomendaciones del escenario del PCA, pero ¿por qué? ¿Por qué negociar solo con los parámetros que definen la varianza ofrece mejores resultados que hacerlo sin restricciones? Creo que es una pregunta relevante, ya que la influencia sobre la varianza no implica necesariamente una mayor rentabilidad, puesto que la tendencia general del conjunto de datos estudiado puede estar sesgada. Por este motivo, la selección de los ajustes más determinantes de la varianza solo debe realizarse si las tendencias básicas y generales del conjunto de datos estudiado son coherentes con los objetivos generales del tráder.

Si nos fijamos en el gráfico de EURUSD, podemos ver que durante el periodo de análisis de PCA del 2022.01.01 al 2023.01.01, el par ha demostrado en su mayoría una tendencia a la baja antes de revertir brevemente en octubre. Sin embargo, durante el periodo de control cruzado, en 2023, el par ha fluctuado bruscamente sin formar ninguna tendencia importante como en 2022. Esto puede significar que, realizando el análisis en los principales periodos de tendencia, podemos captar mejor los parámetros de varianza que marcan la tendencia, y estos pueden resultar útiles incluso en situaciones de reversión brusca, como ha quedado patente en 2023.

Conclusión

Hemos visto que el PCA es esencialmente una herramienta analítica destinada a reducir la dimensionalidad de un conjunto o varios conjuntos de datos mediante la identificación de las dimensiones (o componentes del conjunto de datos) más responsables a la hora de identificar sus tendencias básicas. Existen muchas herramientas disponibles para reducir la dimensionalidad de los datos y, a primera vista, el PCA puede parecer primitivo, pero requiere un análisis y una interpretación cuidadosos, dado que siempre se basa en las tendencias básicas del conjunto de datos estudiado.

En el ejemplo que hemos analizado en la prueba, las tendencias básicas para el símbolo estudiado eran bajistas, y basándonos en esto, en la comprobación cruzada la mayoría de las transacciones realizadas de la muestra han sido cortas. Si hipotéticamente estudiáramos un mercado alcista para el símbolo en cuestión, entonces cualquier estrategia comercial que adoptemos basada en la configuración recomendada del PCA tendría que capitalizar el entorno alcista. Por el contrario, en tales situaciones, tendrá sentido seleccionar configuraciones que expliquen la menor cantidad de varianza si pretendemos sacar provecho de un mercado bajista, ya que los mercados bajistas y los alcistas son polos opuestos. Además, el PCA genera más de un par de configuraciones, cada una con un valor de peso, o valor propio, lo cual implica que puede aceptarse más de una configuración si sus valores de peso superan un umbral determinado. Esto no lo hemos analizado en el presente artículo, así que proponemos al lector que explore por sí mismo: el código fuente se adjunta a continuación. El uso de este código en el Wizard MQL5 para construir un asesor experto se puede ver aquí.

Sin embargo, un enfoque que podríamos usar para dar cabida a más configuraciones de PCA en el script de análisis y el EA sería simplemente normalizar los valores propios de manera que, por ejemplo, todos sean positivos y estén entre 0,0 y 1,0. A continuación, podremos definir umbrales de selección para los vectores propios que seleccionaremos en cada análisis. Por ejemplo, si el análisis de PCA de una matriz de 3 x 3 arroja inicialmente valores de 2,94, 1,92, 0,14, normalizaremos estos valores al intervalo 0-1 de la siguiente manera: 0,588, 0,384 y 0,028. Al utilizar valores normalizados, un valor umbral como 0,3 puede permitir una selección no sesgada de los vectores propios para análisis múltiples. Un reanálisis con un conjunto de datos diferente e incluso un tamaño de matriz distinto puede tener vectores propios seleccionados de forma similar. Para el script, esto significaría iterar sobre los valores propios y añadir dos propiedades cruzadas por cada valor coincidente a la lista o array de salida. Este array puede ser una estructura que registre las propiedades x e y en la matriz del conjunto de datos. Al utilizar el EA, deberemos introducir las propiedades del filtro como valores string separados por comas para facilitar la escalabilidad. Esto implicará analizar la línea y extraer las propiedades en un formato estándar que el EA pueda entender.