Aprendizaje automático y data science (Parte 06): Descenso de gradiente
880
0
La optimización prematura es la raíz de todos (o la mayoría) de los problemas de programación.
(Donald Knuth)
Introducción
Según la Wikipedia,el descenso de gradiente es un método para encontrar un mínimo local de una función en la dirección del gradiente utilizando métodos de optimización unidimensionales. La idea consiste en repetir los pasos en dirección opuesta al gradiente (o gradiente aproximado) de la función en el punto actual, porque esa será la dirección de mayor descenso. Por el contrario, un paso en la dirección del gradiente dará como resultado un máximo local de esta función. Este proceso se llama ascenso de gradiente. En esencia, el descenso de gradiente es un algoritmo de optimización usado para encontrar el mínimo de una función:
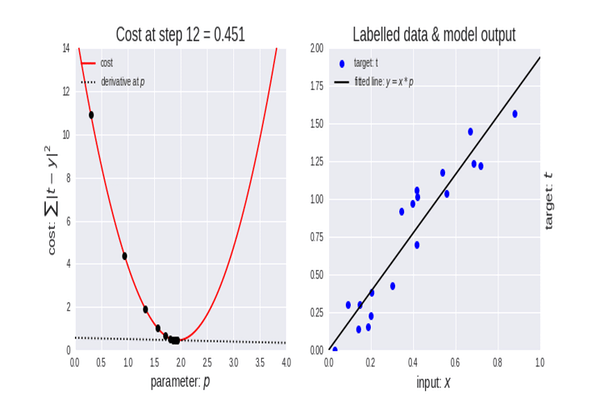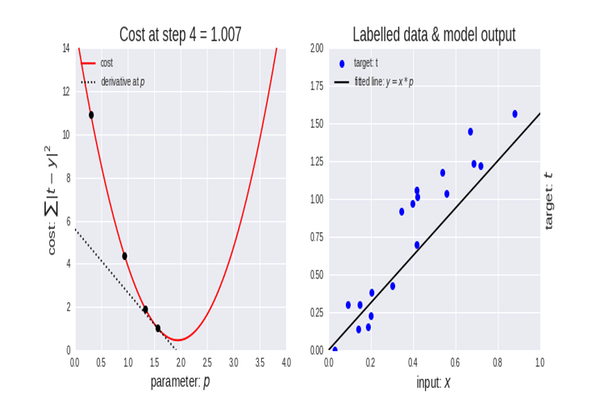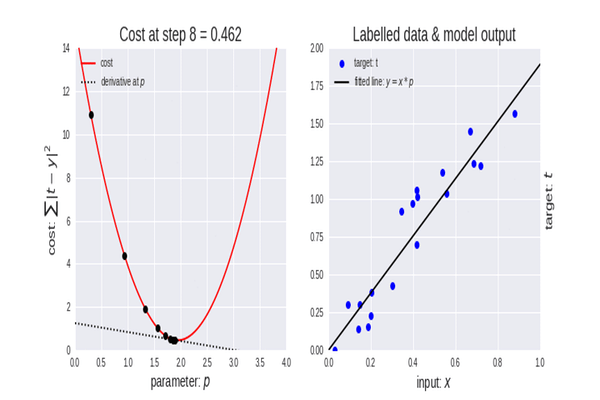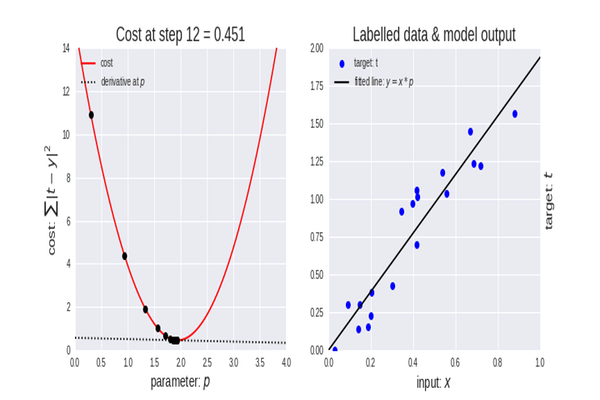
Función de coste
También se la llama función de pérdida, quizás alguien esté más familiarizado con este nombre. Se trata de una métrica que calcula cómo de bien o mal predice nuestro modelo la relación entre los valores de x e y.
Hay muchas métricas diferentes que se pueden utilizar para determinar la calidad predictiva de un modelo. Pero, a diferencia de todas las demás, la función de coste encuentra la pérdida promedio en todo el conjunto de datos, y cuanto mayor sea la función de coste, peores relaciones encontrará nuestro modelo en este conjunto de datos.
El objetivo del descenso de gradiente es minimizar la función de coste porque el modelo con la función de coste/pérdida más pequeña será el mejor modelo. Para entender mejor lo que acabamos de explicar, vamos a ver el siguiente ejemplo.
Supongamos que nuestra función de coste es la ecuación
Si construimos el gráfico de esta función usando el lenguaje Python, se verá así:
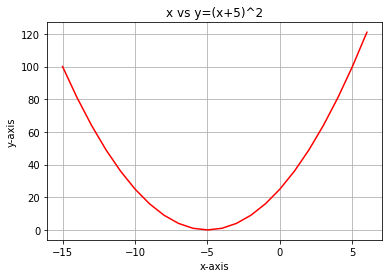
El primer paso que debemos dar con nuestra función de coste es diferenciar la función de coste usando la regla de la cadena, o Chain rule.
La ecuación y= (x+5)^2 es una función compuesta (una función en otra). La función externa es (x+5)^2, mientras que la interna es(x+5). Para distinguirlas, aplicaremos la regla de la cadena. Mire la imagen:
Al final hay un enlace a un vídeo en el que realizamos operaciones matemáticas a mano, si le resulta difícil entender la idea con palabras. Bien, ahora esta característica que acabamos de obtener es un gradiente. El proceso de encontrar el gradiente de la ecuación es el paso más importante. Ojalá mi profesor de matemáticas me dijera ese día en la escuela que el propósito de diferenciar una función es obtener el gradiente de la misma.
Este es el primer paso, y el más importante. Luego viene el segundo.
Paso 2
Nos movemos en la dirección negativa del gradiente. Aquí nos surge la pregunta, ¿hasta dónde llegar? Precisamente ahí entra en juego la tasa de aprendizaje.
Coeficiente de tasa de aprendizaje
Por definición, se trata del tamaño de paso en cada iteración al avanzar hacia la minimización de la función de pérdida. Podemos comparar esto con una persona que baja una montaña: sus pasos serían la tasa de aprendizaje, y cuanto más pequeños sean los pasos, más tiempo le llevará a la persona llegar al pie de la montaña y viceversa.Si reducimos la tasa de aprendizaje a, digamos, 0,0001, aumentaremos el tiempo de ejecución del programa, ya que el algoritmo puede tardar más en alcanzar los valores mínimos. Por el contrario, el uso de valores elevados para el coeficiente de tasa de aprendizaje hará que el algoritmo dé pasos demasiado grandes y, finalmente, pierda el valor mínimo objetivo.
La tasa de aprendizaje por defecto es 0,01.
Vamos a iniciar las iteraciones de ejecución para ver cómo funciona el algoritmo.
Iteración uno: tomamos cualquier punto aleatorio como punto de partida para el algoritmo. Hemos elegido que el primer valor para x sea 0, mientras que actualizaremos los valores de x usando esta fórmula:
En cada iteración, descenderemos en la dirección del valor mínimo de la función, de hecho, de ahí viene el nombre "Descenso de gradiente". Ahora queda más claro, ¿no?
Veamos ahora con detalle cómo funciona esto. Vamos a calcular manualmente los valores en dos iteraciones para tener una idea clara de lo que está pasando.
Primera iteración
Fórmula: x1 = x0 - Learning Rate * ( 2*(x+5) )
x1 = 0 - 0.01 * 0.01 * 2*(0+5)
x1 = -0.01 * 10
x1 = -0.1 (finalmente)
Y luego actualizamos los valores asignando los nuevos valores a los antiguos. Luego, repetimos el proceso con iteraciones hasta llegar al valor mínimo de la función.
x0 = x1
Segunda iteración
x1 = -0.1 - 0.01 * 2*(-0.1+5)
x1 = -0.198
Entonces: x0 = x1
Si repetimos este proceso varias veces, para las primeras diez iteraciones, el resultado será:
RS 0 17:15:16.793 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction CUSTOM QQ 0 17:15:16.793 gradient-descent test (EURUSD,M1) 1 x0 = 0.0000000000 x1 = -0.1000000000 CostFunction = 10.0000000000 ES 0 17:15:16.793 gradient-descent test (EURUSD,M1) 2 x0 = -0.1000000000 x1 = -0.1980000000 CostFunction = 9.8000000000 PR 0 17:15:16.793 gradient-descent test (EURUSD,M1) 3 x0 = -0.1980000000 x1 = -0.2940400000 CostFunction = 9.6040000000 LE 0 17:15:16.793 gradient-descent test (EURUSD,M1) 4 x0 = -0.2940400000 x1 = -0.3881592000 CostFunction = 9.4119200000 JD 0 17:15:16.793 gradient-descent test (EURUSD,M1) 5 x0 = -0.3881592000 x1 = -0.4803960160 CostFunction = 9.2236816000 IG 0 17:15:16.793 gradient-descent test (EURUSD,M1) 6 x0 = -0.4803960160 x1 = -0.5707880957 CostFunction = 9.0392079680 IG 0 17:15:16.793 gradient-descent test (EURUSD,M1) 7 x0 = -0.5707880957 x1 = -0.6593723338 CostFunction = 8.8584238086 JF 0 17:15:16.793 gradient-descent test (EURUSD,M1) 8 x0 = -0.6593723338 x1 = -0.7461848871 CostFunction = 8.6812553325 NI 0 17:15:16.793 gradient-descent test (EURUSD,M1) 9 x0 = -0.7461848871 x1 = -0.8312611893 CostFunction = 8.5076302258 CK 0 17:15:16.793 gradient-descent test (EURUSD,M1) 10 x0 = -0.8312611893 x1 = -0.9146359656 CostFunction = 8.3374776213
Echemos un vistazo a los otros diez valores del algoritmo cuando estamos muy cerca del mínimo de la función:
GK 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1052 x0 = -4.9999999970 x1 = -4.9999999971 CostFunction = 0.0000000060 IH 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1053 x0 = -4.9999999971 x1 = -4.9999999971 CostFunction = 0.0000000059 NH 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1054 x0 = -4.9999999971 x1 = -4.9999999972 CostFunction = 0.0000000058 QI 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1055 x0 = -4.9999999972 x1 = -4.9999999972 CostFunction = 0.0000000057 II 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1056 x0 = -4.9999999972 x1 = -4.9999999973 CostFunction = 0.0000000055 RN 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1057 x0 = -4.9999999973 x1 = -4.9999999973 CostFunction = 0.0000000054 KN 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1058 x0 = -4.9999999973 x1 = -4.9999999974 CostFunction = 0.0000000053 JO 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1059 x0 = -4.9999999974 x1 = -4.9999999974 CostFunction = 0.0000000052 JO 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1060 x0 = -4.9999999974 x1 = -4.9999999975 CostFunction = 0.0000000051 QL 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1061 x0 = -4.9999999975 x1 = -4.9999999975 CostFunction = 0.0000000050 QL 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1062 x0 = -4.9999999975 x1 = -4.9999999976 CostFunction = 0.0000000049 HP 0 17:15:16.800 gradient-descent test (EURUSD,M1) Local minimum found =-4.999999997546217
Después de 1062 (mil sesenta y dos) iteraciones, el algoritmo ha podido alcanzar el mínimo local de esta función. ¡Ta-dam!
A qué prestar atención en este algoritmo
Al observar los valores de la función de coste, notaremos un gran cambio en los valores al principio, pero muy poco cambio notorio en los últimos valores de la función de coste.
El descenso de gradiente hace grandes pasos al principio cuando aún está lejos del mínimo de la función, y luego los pasos disminuyen a medida que el algoritmo se aproxima al mínimo de la función. Hacemos lo mismo cuando nos encontramos al pie de la montaña. Entonces, ¡ahora entendemos que el descenso de gradiente es bastante inteligente!
Como resultado, conseguimos un mínimo local
HP 0 17:15:16.800 gradient-descent test (EURUSD,M1) Local minimum found =-4.999999997546217
Este es un valor muy preciso, porque el mínimo de la función es -5.0.
¡Atención, pregunta!
¿Cómo sabe el gradiente cuándo detenerse? Después de todo, el algoritmo puede continuar repitiéndose indefinidamente, o al menos hasta que se agote la potencia de cálculo de la computadora.
Cuando la función de coste sea cero, sabremos que el descenso de gradiente ha hecho su trabajo.
Ahora vamos a escribir todo este proceso en MQL5
while (true) { iterations++; x1 = x0 - m_learning_rate * CustomCostFunction(x0); printf("%d x0 = %.10f x1 = %.10f CostFunction = %.10f",iterations,x0,x1,CustomCostFunction(x0)); if (NormalizeDouble(CustomCostFunction(x0),8) == 0) { Print("Local minimum found =",x0); break; } x0 = x1; }
El bloque de código anterior pudo darnos los resultados deseados, pero no es el único de la clase CGradientDescent. CustomCostFunction es donde se ha almacenado y calculado nuestra ecuación diferenciada. Aquí está:
double CGradientDescent::CustomCostFunction(double x) { return(2 * ( x + 5 )); }
¿Cuál es el objetivo?
Uno podría preguntarse cuál es el objetivo de todos estos cálculos, ya que podemos usar simplemente el modelo lineal predeterminado creado en las bibliotecas anteriores que analizamos en esta serie de artículos con anterioridad. Pero un modelo construido con valores por defecto no es necesariamente el mejor modelo. Por lo tanto, la computadora deberá aprender los mejores parámetros para que el modelo tenga pocos errores (sea el mejor modelo).
Ya estamos algunos artículos más cerca de construir redes neuronales artificiales. Aquí estamos tratando de analizar con detalle y de forma simple cómo aprenden las redes neuronales (autoaprendizaje) en el proceso de retropropagación y otros métodos. El descenso de gradiente es el algoritmo más popular que ha hecho de todo esto algo posible. Sin una comprensión clara de este proceso básico, resultará imposible entender el resto, porque todo se complicará más a partir de aquí.
El descenso de gradiente para el modelo de regresión
Usando un conjunto de datos de salarios como ejemplo, vamos a construir un modelo mejor usando el descenso de gradiente.
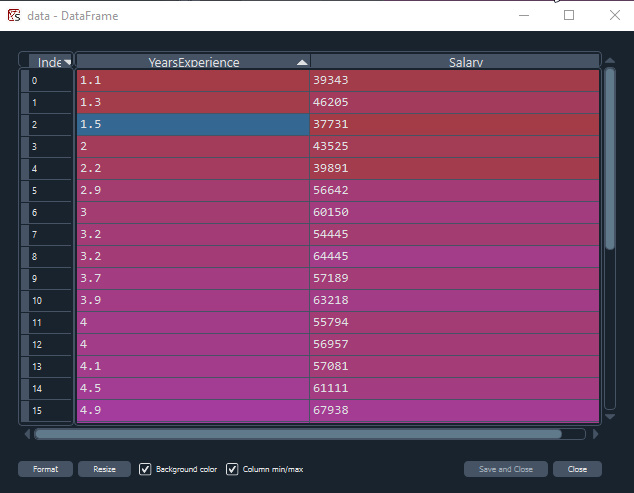
Visualización de datos en Python
import pandas as pd import numpy as np import matplotlib.pyplot as plt data = pd.read_csv(r"C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\Salary_Data.csv") print(data.head(10)) x = data["YearsExperience"] y = data["Salary"] plt.figure(figsize=(16,9)) plt.title("Experience vs Salary") plt.scatter(x,y,c="green") plt.xlabel(xlabel="Years of Experience") plt.ylabel(ylabel="Salary") plt.show()
Este será nuestro gráfico.
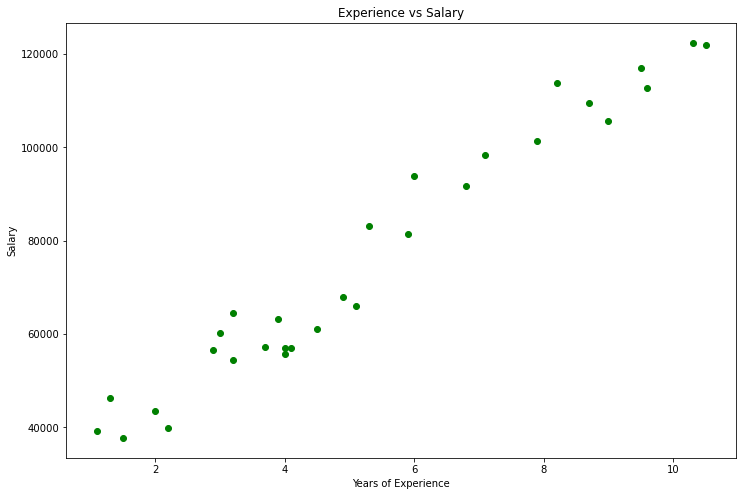
Mirando nuestro conjunto de datos, no podemos dejar de notar que este conjunto está diseñado para problemas de regresión. Pero podemos tener un millón de modelos para hacer una predicción o lo que sea que tratemos de conseguir.
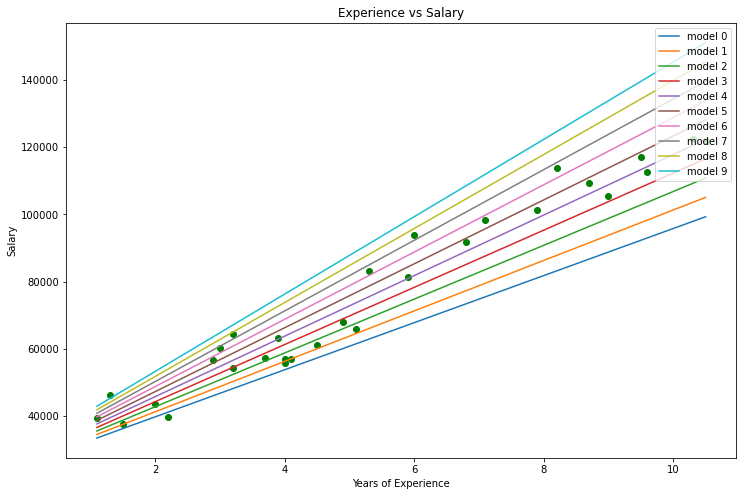
¿Cuál es el mejor modelo para predecir la experiencia y el salario de una persona? Esto es lo que averiguaremos, pero primero, vamos a derivar la función de coste para nuestro modelo de regresión.
Teoría
Volvamos a la regresión lineal.
Sabemos con certeza que cada modelo lineal tiene sus propios errores. Igualmente, sabemos que podemos crear un millón de líneas en este gráfico, y la mejor línea siempre será la que tenga menos errores.
La función de coste es el error entre los valores reales y predichos. Podemos escribir una fórmula para la función de coste, que será igual a:
Coste = Y real - Y predicho. Como tenemos el valor del error que estamos elevando al cuadrado, nuestra fórmula ahora se convertirá en:
Pero estamos buscando errores en todo nuestro conjunto de datos, por lo que deberemos sumar:
Finalmente, dividiremos la suma de errores por m, el número de elementos en el conjunto de datos:
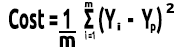
En el vídeo a continuación, todos los cálculos matemáticos se realizan manualmente.
Tenemos la función de coste. Ahora podemos codificar el descenso de gradiente y encontrar los mejores parámetros para dos valores: el factor X (inclinación), indicado como Bo, y la intersección Y, indicada como B1
double cost_B0=0, cost_B1=0; if (costFunction == MSE) { int iterations=0; for (int i=0; i<m_iterations; i++, iterations++) { cost_B0 = Mse(b0,b1,Intercept); cost_B1 = Mse(b0,b1,Slope); b0 = b0 - m_learning_rate * cost_B0; b1 = b1 - m_learning_rate * cost_B1; printf("%d b0 = %.8f cost_B0 = %.8f B1 = %.8f cost_B1 = %.8f",iterations,b0,cost_B0,b1,cost_B1); DBL_MAX_MIN(b0); DBL_MAX_MIN(cost_B0); DBL_MAX_MIN(cost_B1); if (NormalizeDouble(cost_B0,8) == 0 && NormalizeDouble(cost_B1,8) == 0) break; } printf("%d Iterations Local Minima are\nB0(Intercept) = %.5f || B1(Coefficient) = %.5f",iterations,b0,b1); }
Prestemos atención a algunas cosas del código de descenso de gradiente:
- El proceso sigue siendo el mismo que implementamos antes, pero esta vez encontramos y actualizamos los valores dos veces, simultáneamente para Bo y B1.
- Vamos a limitar el número de iteraciones. Alguien dijo una vez que la mejor manera de hacer un ciclo infinito es utilizar un ciclo while, pero esta vez no estamos usando un ciclo while. Aún así, limitaremos el número de activaciones del algoritmo en las que buscaremos los coeficientes para el mejor modelo.
- DBL_MAX_MIN es una función destinada a la depuración, y se encarga de comprobar si hemos llegado al límite de las capacidades matemáticas del ordenador y mostrar un aviso sobre ello.
A continuación, le mostramos el resultado del algoritmo cuando Learning Rate = 0.01 y el número de iteraciones Iterations = 10000
PD 0 17:29:17.999 gradient-descent test (EURUSD,M1) [20] 91738.0000 98273.0000 101302.0000 113812.0000 109431.0000 105582.0000 116969.0000 112635.0000 122391.0000 121872.0000 JS 0 17:29:17.999 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction MSE RF 0 17:29:17.999 gradient-descent test (EURUSD,M1) 0 b0 = 1520.06000000 cost_B0 = -152006.00000000 B1 = 9547.97400000 cost_B1 = -954797.40000000 OP 0 17:29:17.999 gradient-descent test (EURUSD,M1) 1 b0 = 1995.08742960 cost_B0 = -47502.74296000 B1 = 12056.69235267 cost_B1 = -250871.83526667 LP 0 17:29:17.999 gradient-descent test (EURUSD,M1) 2 b0 = 2194.02117366 cost_B0 = -19893.37440646 B1 = 12707.81767044 cost_B1 = -65112.53177770 QN 0 17:29:17.999 gradient-descent test (EURUSD,M1) 3 b0 = 2319.78332575 cost_B0 = -12576.21520809 B1 = 12868.77569178 cost_B1 = -16095.80213357 LO 0 17:29:17.999 gradient-descent test (EURUSD,M1) 4 b0 = 2425.92576238 cost_B0 = -10614.24366387 B1 = 12900.42596039 cost_B1 = -3165.02686058 GH 0 17:29:17.999 gradient-descent test (EURUSD,M1) 5 b0 = 2526.58198175 cost_B0 = -10065.62193621 B1 = 12897.99808257 cost_B1 = 242.78778134 CJ 0 17:29:17.999 gradient-descent test (EURUSD,M1) 6 b0 = 2625.48307920 cost_B0 = -9890.10974571 B1 = 12886.62268517 cost_B1 = 1137.53974060 DD 0 17:29:17.999 gradient-descent test (EURUSD,M1) 7 b0 = 2723.61498028 cost_B0 = -9813.19010723 B1 = 12872.93147573 cost_B1 = 1369.12094310 HF 0 17:29:17.999 gradient-descent test (EURUSD,M1) 8 b0 = 2821.23916252 cost_B0 = -9762.41822398 B1 = 12858.67435081 cost_B1 = 1425.71249248 <<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< Last Iterations >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> EI 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6672 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 NG 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6673 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 GD 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6674 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 PR 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6675 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 IS 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6676 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 RQ 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6677 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 KN 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6678 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 DL 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6679 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 RM 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6680 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 IK 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6681 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 PH 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6682 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 GF 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6683 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 MG 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6684 b0 = 25792.20019866 cost_B0 = -0.00000000 B1 = 9449.96232146 cost_B1 = 0.00000000 LE 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6684 Iterations Local Minima are OJ 0 17:29:48.247 gradient-descent test (EURUSD,M1) B0(Intercept) = 25792.20020 || B1(Coefficient) = 9449.96232
Construiremos el gráfico con la ayuda de matplotlib
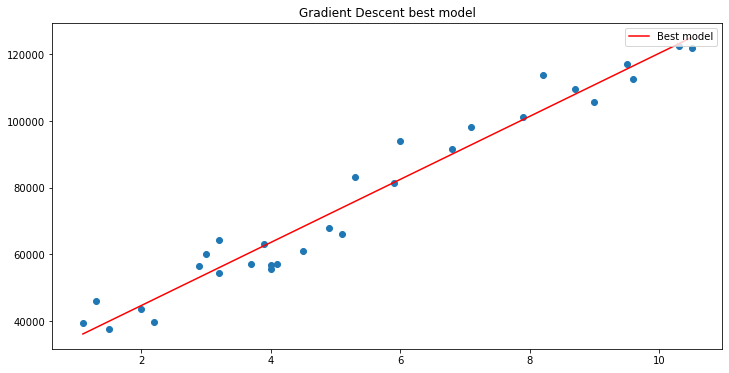
¡Ta-dam! El descenso de gradiente ha logrado obtener con éxito el mejor modelo de los 10 000 modelos probados. Genial, pero hay un paso importante que estamos omitiendo, y esto puede provocar que nuestro modelo se comporte de forma extraña y obtengamos resultados que no necesitamos.
Normalizando los datos de las variables de entrada de la regresión lineal
Sabemos que para diferentes conjuntos de datos, los mejores modelos se pueden encontrar después de un número de iteraciones distinto: algunos pueden necesitar 100 iteraciones para llegar a los mejores modelos, mientras que otros pueden necesitar 10 000 o incluso un millón para que la función de coste se vuelva igual a cero. Eso por no mencionar que si usamos valores incorrectos para el coeficiente de tasa de aprendizaje, podríamos terminar perdiendo los mínimos locales. Y si nos saltamos este objetivo, terminaremos chocando con los límites matemáticos de la computadora. Veamos todo esto con un ejemplo concreto.
Tasa de aprendizaje = 0,1, iteraciones = 1000
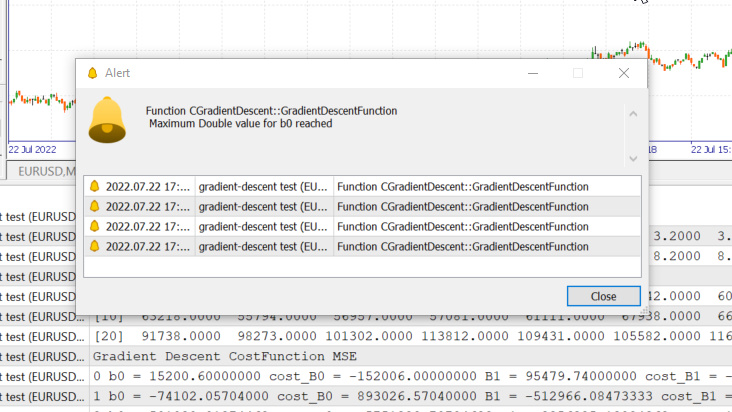
Acabamos de alcanzar el valor máximo del tipo double permitido por el sistema. Podemos ver esto en el log.
GM 0 17:28:14.819 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction MSE OP 0 17:28:14.819 gradient-descent test (EURUSD,M1) 0 b0 = 15200.60000000 cost_B0 = -152006.00000000 B1 = 95479.74000000 cost_B1 = -954797.40000000 GR 0 17:28:14.819 gradient-descent test (EURUSD,M1) 1 b0 = -74102.05704000 cost_B0 = 893026.57040000 B1 = -512966.08473333 cost_B1 = 6084458.24733333 NM 0 17:28:14.819 gradient-descent test (EURUSD,M1) 2 b0 = 501030.91374462 cost_B0 = -5751329.70784622 B1 = 3356325.13824362 cost_B1 = -38692912.22976952 LH 0 17:28:14.819 gradient-descent test (EURUSD,M1) 3 b0 = -3150629.51591119 cost_B0 = 36516604.29655810 B1 = -21257352.71857720 cost_B1 = 246136778.56820822 KD 0 17:28:14.819 gradient-descent test (EURUSD,M1) 4 b0 = 20084177.14287909 cost_B0 = -232348066.58790281 B1 = 135309993.40314889 cost_B1 = -1565673461.21726084 OQ 0 17:28:14.819 gradient-descent test (EURUSD,M1) 5 b0 = -127706877.34210962 cost_B0 = 1477910544.84988713 B1 = -860620298.24803317 cost_B1 = 9959302916.51181984 FM 0 17:28:14.819 gradient-descent test (EURUSD,M1) 6 b0 = 812402202.33122230 cost_B0 = -9401090796.73331833 B1 = 5474519904.86084747 cost_B1 = -63351402031.08880615 JJ 0 17:28:14.819 gradient-descent test (EURUSD,M1) 7 b0 = -5167652856.43381691 cost_B0 = 59800550587.65039062 B1 = -34823489070.42410278 cost_B1 = 402980089752.84948730 MP 0 17:28:14.819 gradient-descent test (EURUSD,M1) 8 b0 = 32871653967.62362671 cost_B0 = -380393068240.57440186 B1 = 221513298448.70788574 cost_B1 = -2563367875191.31982422 MM 0 17:28:14.819 gradient-descent test (EURUSD,M1) 9 b0 = -209097460110.12799072 cost_B0 = 2419691140777.51611328 B1 = -1409052343513.33935547 cost_B1 = 16305656419620.47265625 HD 0 17:28:14.819 gradient-descent test (EURUSD,M1) 10 b0 = 1330075004152.67309570 cost_B0 = -15391724642628.00976562 B1 = 8963022367351.18359375 cost_B1 = -103720747108645.23437500 DP 0 17:28:14.819 gradient-descent test (EURUSD,M1) 11 b0 = -8460645083849.12207031 cost_B0 = 97907200880017.93750000 B1 = -57014041694401.67187500 cost_B1 = 659770640617528.50000000
Esto significa que si elegimos el coeficiente de tasa de aprendizaje incorrecto, podríamos tener una posibilidad mínima de encontrar un modelo mejor, y las posibilidades de que eventualmente lleguemos al límite matemático de la computadora son altas, como acabamos de ver en el ejemplo.
Pero si intentamos usar 0.01 para la tasa de aprendizaje con este conjunto de datos, no tendremos problemas, aunque el proceso de aprendizaje será mucho más lento. Pero si usamos esa tasa de aprendizaje para este conjunto de datos,eventualmente se alcanzará el límite matemático. Así que ahora sabemos que cada conjunto de datos tiene su propia tasa de aprendizaje. Pero a veces puede que no resulte posible optimizar la tasa de aprendizaje porque haya conjuntos de datos complejos con múltiples variables.
La solución sería normalizar todo el conjunto de datos para que se encuentre en la misma escala. Esto mejorará la legibilidad cuando los valores se muestren en el mismo eje, y también mejorará el tiempo de aprendizaje, porque los valores normalizados suelen estar entre 0 y 1. Además, no tendremos que preocuparnos por la tasa de aprendizaje, porque cuando solo tenemos un parámetro para la misma, podemos usarlo con cualquier conjunto de datos que encontremos. Por ejemplo, en nuestro caso, es una tasa de aprendizaje de 0,01. Podrá leer más sobre la normalización aquí.
Y por último, pero no menos importante.
También sabemos que los valores de los datos sobre salarios se encuentran en el intervalo de 39.343 a 121.782, y los valores de experiencia van de 1,1 a 10,5 años. Si los datos se guardan de esta manera, los valores salariales serán tan grandes que podrán hacer que el modelo piense que el salario es más importante que cualquier valor. Por lo tanto, tendrán una gran influencia en comparación con los años de experiencia, y necesitamos que todas las variables independientes tengan un impacto al nivel de las otras. Ahora puede ver lo importante que es normalizar los valores.
(Normalización) Escalar Min-Max
En este enfoque, los datos se normalizan para que se hallen en el rango de 0 a 1. La fórmula de normalización es:
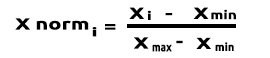
Si traducimos esta fórmula a líneas de código, obtendremos:
void CGradientDescent::MinMaxScaler(double &Array[]) { double mean = Mean(Array); double max,min; double Norm[]; ArrayResize(Norm,ArraySize(Array)); max = Array[ArrayMaximum(Array)]; min = Array[ArrayMinimum(Array)]; for (int i=0; i<ArraySize(Array); i++) Norm[i] = (Array[i] - min) / (max - min); printf("Scaled data Mean = %.5f Std = %.5f",Mean(Norm),std(Norm)); ArrayFree(Array); ArrayCopy(Array,Norm); }
La función std() solo es necesaria para que podamos averiguar la desviación estándar después de normalizar los datos. Aquí tenemos su código:
double CGradientDescent::std(double &data[]) { double mean = Mean(data); double sum = 0; for (int i=0; i<ArraySize(data); i++) sum += MathPow(data[i] - mean,2); return(MathSqrt(sum/ArraySize(data))); }
Ahora llamaremos a todo esto y mostraremos el resultado:
void OnStart() { //--- string filename = "Salary_Data.csv"; double XMatrix[]; double YMatrix[]; grad = new CGradientDescent(1, 0.01,1000); grad.ReadCsvCol(filename,1,XMatrix); grad.ReadCsvCol(filename,2,YMatrix); grad.MinMaxScaler(XMatrix); grad.MinMaxScaler(YMatrix); ArrayPrint("Normalized X",XMatrix); ArrayPrint("Normalized Y",YMatrix); grad.GradientDescentFunction(XMatrix,YMatrix,MSE); delete (grad); }
Resultado
OK 0 18:50:53.387 gradient-descent test (EURUSD,M1) Scaled data Mean = 0.44823 Std = 0.29683 MG 0 18:50:53.387 gradient-descent test (EURUSD,M1) Scaled data Mean = 0.45207 Std = 0.31838 MP 0 18:50:53.387 gradient-descent test (EURUSD,M1) Normalized X JG 0 18:50:53.387 gradient-descent test (EURUSD,M1) [ 0] 0.0000 0.0213 0.0426 0.0957 0.1170 0.1915 0.2021 0.2234 0.2234 0.2766 0.2979 0.3085 0.3085 0.3191 0.3617 ER 0 18:50:53.387 gradient-descent test (EURUSD,M1) [15] 0.4043 0.4255 0.4468 0.5106 0.5213 0.6064 0.6383 0.7234 0.7553 0.8085 0.8404 0.8936 0.9043 0.9787 1.0000 NQ 0 18:50:53.387 gradient-descent test (EURUSD,M1) Normalized Y IF 0 18:50:53.387 gradient-descent test (EURUSD,M1) [ 0] 0.0190 0.1001 0.0000 0.0684 0.0255 0.2234 0.2648 0.1974 0.3155 0.2298 0.3011 0.2134 0.2271 0.2286 0.2762 IS 0 18:50:53.387 gradient-descent test (EURUSD,M1) [15] 0.3568 0.3343 0.5358 0.5154 0.6639 0.6379 0.7151 0.7509 0.8987 0.8469 0.8015 0.9360 0.8848 1.0000 0.9939
Los gráficos se verán así:
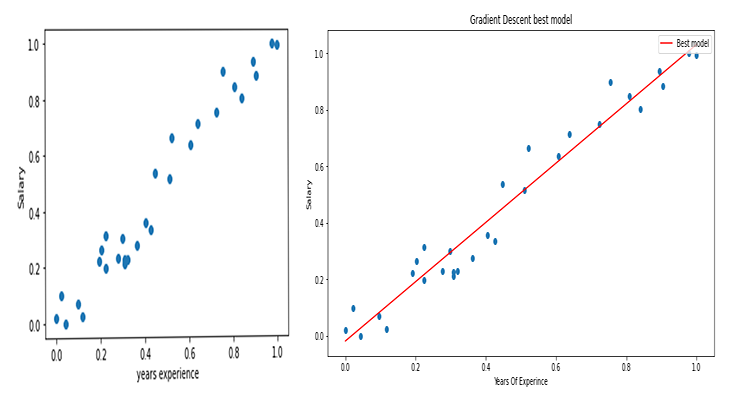
Descenso de gradiente para la regresión logística
Hemos visto el lado lineal del descenso de gradiente, ahora vamos a ver el lado logístico.
Aquí haremos lo mismo que acabamos de hacer en la parte de la regresión lineal, porque están involucrados exactamente los mismos procesos, solo que el proceso de diferenciación de la regresión logística se vuelve más complicado que en el modelo lineal. Veamos primero la función de coste.
Ya hemos hablado en el segundo artículo de la serie sobre la regresión logística. La función de coste de un modelo de regresión logística es la entropía cruzada binaria, o función logarítmica de pérdida Log Loss, mostrada a continuación.
Primero haremos la parte difícil: diferenciar esta función para obtener su gradiente.
Luego hallaremos las derivadas
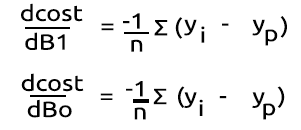
A continuación, convertimos las fórmulas en código MQL5 dentro de la función BCE, que significa Binary Cross Entropy (entropía cruzada binaria).
double CGradientDescent::Bce(double Bo,double B1,Beta wrt) { double sum_sqr=0; double m = ArraySize(Y); double x[]; MatrixColumn(m_XMatrix,x,2); if (wrt == Slope) for (int i=0; i<ArraySize(Y); i++) { double Yp = Sigmoid(Bo+B1*x[i]); sum_sqr += (Y[i] - Yp) * x[i]; } if (wrt == Intercept) for (int i=0; i<ArraySize(Y); i++) { double Yp = Sigmoid(Bo+B1*x[i]); sum_sqr += (Y[i] - Yp); } return((-1/m)*sum_sqr); }
Como estamos tratando con un modelo de clasificación, seleccionaremos el conjunto de datos del Titanic con el que trabajamos en el artículo sobre regresión logística. Tenemos la variable independiente Pclass (clase de pasajeros) y la variable dependiente Survived en el otro lado.
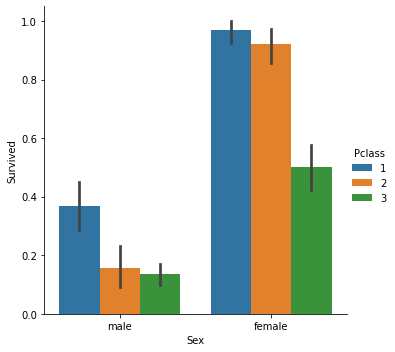
Gráfico de dispersión
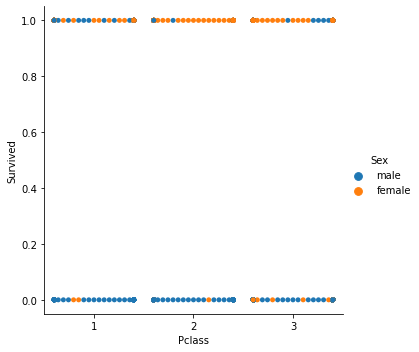
Ahora llamaremos a la clase Gradient Descent, pero esta vez con BCE (entropía cruzada binaria) como una función de coste.
filename = "titanic.csv"; ZeroMemory(XMatrix); ZeroMemory(YMatrix); grad.ReadCsvCol(filename,3,XMatrix); grad.ReadCsvCol(filename,2,YMatrix); grad.GradientDescentFunction(XMatrix,YMatrix,BCE); delete (grad);
Veamos los resultados.
CP 0 07:19:08.906 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction BCE KD 0 07:19:08.906 gradient-descent test (EURUSD,M1) 0 b0 = -0.01161616 cost_B0 = 0.11616162 B1 = -0.04057239 cost_B1 = 0.40572391 FD 0 07:19:08.906 gradient-descent test (EURUSD,M1) 1 b0 = -0.02060337 cost_B0 = 0.08987211 B1 = -0.07436893 cost_B1 = 0.33796541 KE 0 07:19:08.906 gradient-descent test (EURUSD,M1) 2 b0 = -0.02743120 cost_B0 = 0.06827832 B1 = -0.10259883 cost_B1 = 0.28229898 QE 0 07:19:08.906 gradient-descent test (EURUSD,M1) 3 b0 = -0.03248925 cost_B0 = 0.05058047 B1 = -0.12626640 cost_B1 = 0.23667566 EE 0 07:19:08.907 gradient-descent test (EURUSD,M1) 4 b0 = -0.03609603 cost_B0 = 0.03606775 B1 = -0.14619252 cost_B1 = 0.19926123 CF 0 07:19:08.907 gradient-descent test (EURUSD,M1) 5 b0 = -0.03851035 cost_B0 = 0.02414322 B1 = -0.16304363 cost_B1 = 0.16851108 MF 0 07:19:08.907 gradient-descent test (EURUSD,M1) 6 b0 = -0.03994229 cost_B0 = 0.01431946 B1 = -0.17735996 cost_B1 = 0.14316329 JG 0 07:19:08.907 gradient-descent test (EURUSD,M1) 7 b0 = -0.04056266 cost_B0 = 0.00620364 B1 = -0.18958010 cost_B1 = 0.12220146 HE 0 07:19:08.907 gradient-descent test (EURUSD,M1) 8 b0 = -0.04051073 cost_B0 = -0.00051932 B1 = -0.20006123 cost_B1 = 0.10481129 ME 0 07:19:08.907 gradient-descent test (EURUSD,M1) 9 b0 = -0.03990051 cost_B0 = -0.00610216 B1 = -0.20909530 cost_B1 = 0.09034065 JQ 0 07:19:08.907 gradient-descent test (EURUSD,M1) 10 b0 = -0.03882570 cost_B0 = -0.01074812 B1 = -0.21692190 cost_B1 = 0.07826600 <<<<<< Last 10 iterations >>>>>> FN 0 07:19:09.725 gradient-descent test (EURUSD,M1) 6935 b0 = 1.44678930 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 PN 0 07:19:09.725 gradient-descent test (EURUSD,M1) 6936 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 NM 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6937 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 KL 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6938 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 PK 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6939 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 RK 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6940 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 MJ 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6941 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 HI 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6942 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 CH 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6943 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 MH 0 07:19:09.727 gradient-descent test (EURUSD,M1) 6944 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 QG 0 07:19:09.727 gradient-descent test (EURUSD,M1) 6945 b0 = 1.44678931 cost_B0 = -0.00000000 B1 = -0.85010666 cost_B1 = 0.00000000 NG 0 07:19:09.727 gradient-descent test (EURUSD,M1) 6945 Iterations Local Minima are MJ 0 07:19:09.727 gradient-descent test (EURUSD,M1) B0(Intercept) = 1.44679 || B1(Coefficient) = -0.85011
No normalizaremos ni escalaremos los datos clasificados para la regresión logística como se hizo en la regresión lineal.
Aquí tenemos un descenso de gradiente para dos de los modelos de aprendizaje automático más importantes. Esperamos que sea claro y útil. El código de Python utilizado en el artículo, así como el conjunto de datos, están disponibles en el repositorio de GitHub.
Conclusión
En el presente artículo, hemos analizado el descenso de gradiente para una variable independiente y una dependiente. Para el conjunto de variables independientes, debemos usar vectores/matrices de la ecuación. Creo que esta vez será más fácil para los lectores probar todo por su cuenta, porque recientemente se ha lanzado una biblioteca de funciones de matricesen MQL5. Si necesita ayuda con las matrices, no dude en ponerse en contacto conmigo; estaré encantado de asistirle.
Reciba mis mejores deseos
Lista de vídeos con los cálculos:
- https://www.youtube.com/watch?v=5yfh5cf4-0w
- https://www.youtube.com/watch?v=yg_497u6JnA
- https://www.youtube.com/watch?v=HaHsqDjWMLU
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/11200
DoEasy. Elementos de control (Parte 9): Reorganizando los métodos de los objetos WinForms, los controles "RadioButton" y "Button"
Aprendiendo a diseñar un sistema de trading con la desviación estándar
Redes neuronales: así de sencillo (Parte 19): Reglas asociativas usando MQL5
Aprendiendo a diseñar un sistema de trading con Williams PR
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso